Time-varying effect models for ordinal responses with applications in substance abuse research

Abstract

Ordinal responses are very common in longitudinal data collected from substance abuse research or other behavioral research. This study develops a new statistical model with free SAS macro’s that can be applied to characterize time-varying effects on ordinal responses. Our simulation study shows that the ordinal-scale time-varying effects model has very low estimation bias and sometimes offers considerably better performance when fitting data with ordinal responses than a model that treats the response as continuous. Contrary to a common assumption that an ordinal scale with several levels can be treated as continuous, our results indicate that it is not so much the number of levels on the ordinal scale but rather the skewness of the distribution that makes a difference on relative performance of linear versus ordinal models. We use longitudinal data from a well-known study on youth at high risk for substance abuse as a motivating example to demonstrate that the proposed model can characterize the time-varying effect of negative peer influences on alcohol use in a way that is more consistent with the developmental theory and existing literature, in comparison to the linear time-varying effect model.

Introduction

Substance use outcomes are often ordinal in nature with participants classified in terms of degrees of use [1]. For example, a well-known annual survey of U.S. high school seniors, Monitoring The Future [2], asked the participants to report their alcohol or other substance use in their lifetime, during the last 12 months, or during the last 30 days on an ordinal scale: (1) 0 occasions; (2) 1–2; (3) 3–5; (4) 6–9; (5) 10–19; (6) 20–39; (7) 40 or more. An important feature of this type of data is that they tend to be skewed to the right due to high frequencies at the lower end. Although it is common practice to use linear models (for continuous responses) to analyze ordinal responses with several categories, such practice has been shown to produce misleading results, especially when the data contain excess minimum values [3].

Bauer and Sterba [4] investigated the common practice of analyzing longitudinal data with ordinal outcomes and pointed out the main reasons why researchers may be reluctant to fit an ordinal rather than linear mixed model [5], including familiarity with linear models and lack of existing studies that expressly examined the consequences of fitting a linear mixed model to ordinal outcomes. To fill in the important knowledge gap, they conducted a simulation study and found that when the longitudinal response was ordinal, the performance of the linear mixed model was acceptable (i.e. with bias < 10%) only if the response had 7 or more categories and was distributed like a bell shape; the generalized linear mixed model [6] with a cumulative logit link, on the other hand, performed well across different numbers of categories (3, 5, 7) and distribution shapes (bell shaped, polarized, skewed).

Linear mixed models [5] and generalized linear mixed models [6] have been applied mostly in the settings involving time-invariant effects (i.e. assuming that the association between an outcome of interest and a covariate is constant over time). This convention, however, has been challenged in recent years because there are many practical settings where the phenomenon of time-varying associations exists [7]. For example, a smoking-cessation study found that the effect of negative affect on urge to smoke changed in a complex and dynamic way during various stages of the smoking-cessation process [8]. Tan and colleagues [9] introduced a time-varying effect model (TVEM) for longitudinal data with continuous responses to social and behavioral science researchers. They also developed a SAS macro to implement a P-spline approach to estimating TVEM using SAS PROC MIXED. This macro was later extended to handle binary, count, and zero-inflated count responses [10]. Yet, the TVEM for ordinal responses has not become available. Furthermore, it is unclear if the consequences of fitting a linear mixed model to ordinal outcomes found in the previous study [4] can be generalized to the case of TVEM.

This paper aims to fill in the current knowledge gap by extending the TVEM to handle ordinal responses and conducting a simulation study to examine the consequences of fitting the linear TVEM to ordinal responses. We also evaluate the performance of the proposed proportional odds TVEM when the number of levels on the ordinal scale, the sample size, the number of waves, and the distribution shape were varied. We organize the paper as follows. In Section 2, we specify the ordinal TVEM and propose the procedures to practically implement the estimation. In Section 3, we present a motivational example using longitudinal data from the Flint Adolescent Study (FAS). In Section 4, we conduct a simulation study to assess the performance of the ordinal TVEM relative to the linear TVEM under different situations. Discussion and concluding remarks are presented in Section 5. Example SAS codes are given in the appendix to demonstrate how to use the SAS macro’s developed in this study.

2. The Statistical Model

Consider the following proportional odds model for time-varying effects on an ordinal response Y. Label the categories on Y as 0, 1, …, K − 1. Let X₁, …, X_P be the covariates whose relationships with Y are assumed to vary over time, and U₁, …, U_Q be the covariates whose relationships with Y are assumed to be constant at each time. For observation j on subject i, taken at time t_ij, we define a continuous latent variable Ў_ij as follows:

$${Ў}_{ij}={\beta }_0(t_{ij})+\sum _{p=1}^P{\beta }_p(t_{ij})X_{pij}+\sum _{q=1}^Q{\gamma }_q{U}_{qij}+a_i+e_{ij}$$

where a_i is a random effect for subject i (assumed normal with a variance of τ²) and e_ij is a standard logistic error term (hence has a variance of π²/3 ≈ 3.29). We then assume that the ordinal variable is defined by the following thresholding rule:

$$Y_{ij}=\{\begin{array}{cc}0\hfill & \text{if}{Ў}_{ij}\le {\theta }_1\hfill \\ k\hfill & \text{if}{\theta }_k<{Ў}_{ij}\le {\theta }_{k+1},k=1,\dots ,K-2\hfill \\ K-1\hfill & \text{if}{\theta }_{K-1}<{Ў}_{ij}\hfill \end{array}$$

where θ₁ < … < θ_K−1. Thus

$$\text{logit}[\text{Pr}(Y_{ij}\ge k)]=\text{logit}\left[\text{Pr}\right({Ў}_{ij}>{\theta }_k\left)\right]={\beta }_0(t_{ij})+\sum _{p=1}^P{\beta }_p(t_{ij})X_{pij}+\sum _{q=1}^Q{\gamma }_q{U}_{qij}+a_i-{\theta }_k$$ (1)

for k = 1, …, K − 1.

As in much previous work (e.g., [9][11]), we represent the time-varying coefficients using basis expansions. Thus, the nonparametric function β_p (t) is treated as a linear combination of several known parametric functions ϕ₁(t), …, ϕ_D(t). We chose to use a spline basis to represent β_p(t) as a piecewise cubic function. On each of several intervals defined by knots, the spline function is cubic. At a knot, the spline function is continuous and has continuous first and second derivatives, although the third derivative may be discontinuous at the knots. This allows any smooth shape to be approximated well if enough knots are used. Specifically, we use a B-spline basis (see [12] for technical details and the recursive formula for computing ϕ_d(t)), which can be automatically generated by most commonly used statistical software packages such as SAS and R, for a given set of knots. The basis functions are always nonnegative, and each is zero over most of the interval, so that each knot’s basis function is orthogonal to the other basis functions except for its closest knot neighbors. This is more favorable from a numerical standpoint than alternatives such as a polynomial regression basis or a truncated power spline basis ([13]), because those functions tend to be highly intercorrelated and thus can potentially lead to a poorly conditioned regression matrix. Nevertheless, overfitting may still occur with a B-spline basis if too many knots are used. For simplicity, in this paper, we follow Shiyko and colleagues [14] in using a small number of equally spaced knots and treat the selection of the number of basis functions D as a model selection problem.

After defining the basis functions using the B-spline formula, the problem can be treated as parametric with (P + 1)D + Q scalar regression coefficients ζ, with K − 1 scalar threshold coefficients θ, and with one variance component τ². Specifically, Equation (1) becomes

$$\text{logit}(\text{Pr}(Y_{ij}\ge k))=\sum _{d=1}^D{\zeta }_d{\varphi }_d(t_{ij})+\sum _{p=1}^P\sum _{d=1}^D{\zeta }_{(pD+d)}{\varphi }_d(t_{ij})X_{pij}+\sum _{q=1}^Q{\zeta }_{((P+1)D+q)}{U}_{qij}+a_i-{\theta }_k$$ (2)

where ϕ₁, …, ϕ_D are known functions of time defined using the recursive B-spline formulas. One could use different numbers of knots for different parameters, but we use the same D for each here for simplicity. The parameters are estimated by maximum likelihood.

Because Equation (2) is a generalized linear mixed model (GLMM), the log-likelihood is complex and dealing with it directly would involve difficult numerical integration. Standard software such as SAS PROC GLIMMIX handles this problem using successive approximation. The default approach in GLIMMIX is a doubly iterative method in which the nonlinear model is successively locally approximated as a linear mixed model that is estimated using the Newton- Raphson algorithm. Specifically, it involves the residual pseudo-likelihood with subject-specific linear approximation (see the technical details in [15] and Pages 2829, 2945–2950 in [16]). An alternative approach, also available in GLIMMIX, is to fit the GLMM model directly, but approximate the likelihood function using Gaussian quadrature (see the technical details in [17] and Pages 2831, 2953–2954 in [16]). The quadrature approach may offer reduced small-sample bias (see [18] and Pages 2957–2958 in [16]). Based on our preliminary simulations employing both approaches, the quadrature approach tends to be superior in terms of bias so we adopt it in our simulation study. As a caveat, it is possible that the subject-specific linear approximation approach might work better in other conditions differing from those in the simulation study (perhaps with fewer subjects and more observations per subject). Future research might clarify this further. In this study, we have developed a SAS macro that offers both approaches as options (see the Appendix). In either case, we also include a small ridge penalty to facilitate convergence of the Newton-Raphson algorithm (this is available as an option in GLIMMIX and has been recommended [19]).

The maximum likelihood procedure used by SAS provides an estimate for the ζ, θ and τ² parameters, and the covariance matrix of the ζ parameters. The estimated β_p(t) function is then reconstructed as ${\mathrm{\beta ̂}}_p(t)={\sum }_{d=1}^D{\mathrm{\zeta ̂}}_{(pD+d)}{\varphi }_d(t)$ and can be plotted as a function of t across the interval of interest. Cramér’s delta method [20] can then be used in a straightforward way to estimate the variance of β_p(t) at any time t of interest, and thus provides approximate pointwise confidence intervals for fitted values of β_p(t). These calculations are carried out automatically in the macro we developed.

3. A Motivating Example: The Flint Adolescent Study (FAS)

3.1. Description of the study and data

The Flint Adolescent Study (FAS) is an ongoing longitudinal study that aims to investigate both risk and protective factors for health risk behaviors including substance use, violence, and HIV risk sexual behaviors from adolescence to adulthood [21]. The study recruited ninth-grade students with a GPA of 3.0 and below from the four public high schools in an economically disadvantaged school district in Midwest. The grade cutoff was used to select the youth who were at high risk for many deleterious outcomes. The high percentage (over 80%) of Blacks makes the sample unique because the few large scale longitudinal studies of the risk and protective factors include predominantly White samples. We know relatively little about these issues among Black youth. A face-to-face interview was conducted annually from adolescence to adulthood in school or a location that participants identified as convenient for them and that provided adequate privacy with no interruptions. In addition, a questionnaire on substance use related behaviors was self-administered at the end of the interview to avoid under-report.

In this study, we analyzed longitudinal data from a sample of 698 participants (about 50% males) who completed at least four waves of assessment during the critical developmental period of substance use (ages 15–25). The impact of peer factors is, in general, hypothesized to become stronger during the course of adolescence and into early adulthood, as the youth gradually establishes his/her own social network outside the home. However, few studies have found that the developmental change in this effect may be nonlinear with the effect being nonsignificant at some points of time [22][23][24]. Our investigation, thus, aims to characterize the time-varying effect of negative peer influences (NPI) on alcohol use across this critical period of human development. The outcome variable is alcohol use in past 30 days with a 0–6 ordinal scale (0=0 occasions; 1=1–2 occasions; 2=3–5 occasions; 3=6–9 occasions; 4=10–19 occasions; 5=20–39 occasions; 6=40 or more occasions). The risk factor, NPI, was measured by the mean score of the following 13 items about how many of the participant’s friends were involved in delinquent or violent behaviors:

1. Drink beer or wine at least once a month?

2. Drink hard liquor (gin, whiskey, etc.) at least once a month?

3. Have a drug or alcohol problem?

4. Smoke marijuana at least once a month?

5. Have used cocaine?

6. Have been busted for selling drugs?

7. Have been busted for having drugs?

8. Get into fights?

9. Have carried a knife or razor?

10. Have carried a gun?

11. Shoplift from stores?

12. Have been busted for burglary or robbery?

13. Have dropped out of high school

Each item was coded as a 1–5 ordinal scale (1=none; 2=some; 3=many; 4=most; 5=all). Thus, the scale of NPI was continuous with the range of 1–5. This measure had high internal consistency with Cronbach’s α = 0.88 – 0.90 across waves [25].

3.2. Fitting TVEM on the data

For observation j on participant i, let t_ij be his/her age, X_ij be the score of NPI (centered by subtracting the grand mean for all included observations), and Y_ij be alcohol use in past 30 days. We consider two TVEM models for modeling Y_ij, conditional on t_ij and X_ij

• Normal linear TVEM with random subject effects:

  • Y_ij = β₀(t_ij) + β₁(t_ij)X_ij + a_i + e_ij, with a_i ~ N(0; τ²), e_ij ~ N(0; σ²).
• Proportional odds TVEM with random subject effects:

  • logit (Pr(Y_ij ≥ k)) = β₀(t_ij) + β₁(t_ij)X_ij + a_i − θ_k, for θ₁ < … < θ₆.

For each model, we estimated the coefficients by an unpenalized B-spline basis expansion, using AIC [26] to choose the optimal number of knots (0 to 10) and the optimal function order (linear, quadratic or cubic) between knots, as Shiyko and colleagues [14] did for linear TVEM models. For simplicity, we assume the same number of knots and function order for β₀(t) as for β₁(t), and equal knot spacing. For the linear TVEM model, a cubic spline with 3 knots was chosen. For the proportional odds TVEM model, a cubic spline with 2 knots was selected.

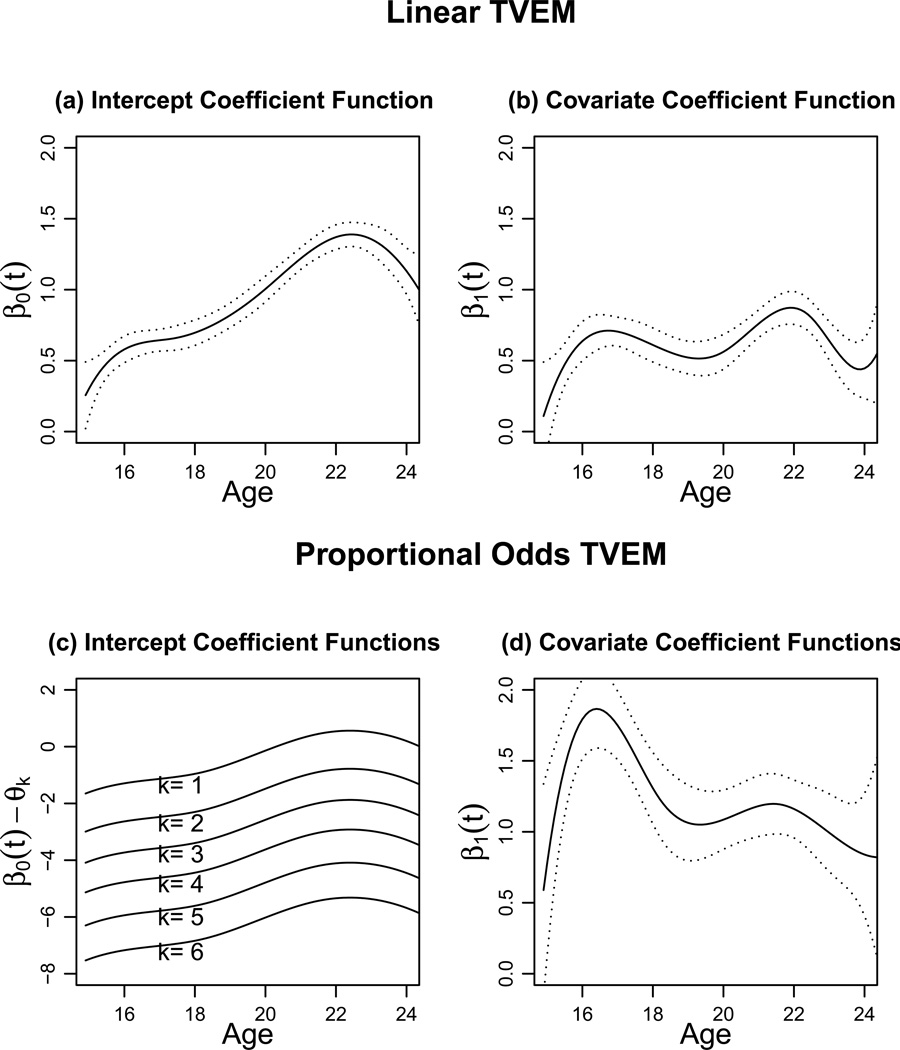
The fitted functions for the linear TVEM are plotted in the upper two panels of Figure 1. Dotted lines represent estimated 95% pointwise confidence intervals. Times past age 24 are not shown because sparse data there caused an edge effect (wide confidence intervals and difficult-to-interpret local parameter values for the linear TVEM model). β₀(t) here can be interpreted as the estimated mean drinking level for all population members having age t and the sample average level of NPI (because NPI was centered to have average 0). β₁(t) can be interpreted as the estimated difference in mean drinking levels between population members at age t differing by 1 unit on the NPI scale. A disadvantage of this interpretation is that it is difficult to define what an average or difference represents on an ordinal scale which is simply being represented by integers, or to imagine how this would have a linear form. The estimated variance components are τ² = .4404 and σ² = 1.0566. Thus, the estimated intraclass correlation within persons is τ²/(τ² + σ²) = .2942 [27].

Figure 1.

The fitted TVEM models on the FAS data.

The fitted functions for proportional odds TVEM are plotted in the lower two panels of Figure 1. β₀(t) in this model is not well-identified in isolation, because one could obtain the same probability model by adding a constant to β₀(t) and also adding the same constant to each threshold θ_k. Therefore, β₀(t) − θ_k is plotted instead. β₀(t) − θ_k represents the log odds of a drinking response greater than or equal to k, for a person with an average level of NPI (hence X_ij = 0) and the average value of the random effect (hence a_i = 0). By contrast, β₁(t) is easier to interpret. It represents the log odds ratio for higher drinking levels between population members at age t having the same value on the random effect and differing by 1 unit on the NPI scale. The estimated random effects variance is τ² = 2.2156. Thus, the estimated intraclass correlation within persons for the latent Ў is τ²/(τ² + τ²/3) ≈ .4024 [27].

Comparison between Figure 1b and Figure 1d demonstrates different time-varying effects of NPI on drinking as characterized by the two models. The different magnitudes of the coefficients is not inherently of interest because they represent different models. However, the shapes of the coefficients differ. In particular, the linear TVEM suggests that the time of greatest peer influence is around age 22, while the proportional odds TVEM suggests that the time of greatest peer influence is around age 17. The later result is more consistent with the findings of existing studies [22][23][24]. Thus, this fitted proportional odds TVEM model was adopted as the true model to generate data in the simulation study.

4. Simulation

We adopted the fitted proportional odds TVEM model in the motivating example as the true model to generate simulated data that closely represent the structure of real data so that the results can be more generalizable to the substance abuse field [28]. The true β₀(t) and true β₁(t) functions were taken from the estimates based on the empirical data as a cubic spline with 2 equally spaced interior knots. We examined the effects of four factors on the performance of the proportional odds TVEM model, and on the relative performance of the linear TVEM model when it was used to fit on the ordinal data. The following factors were varied:

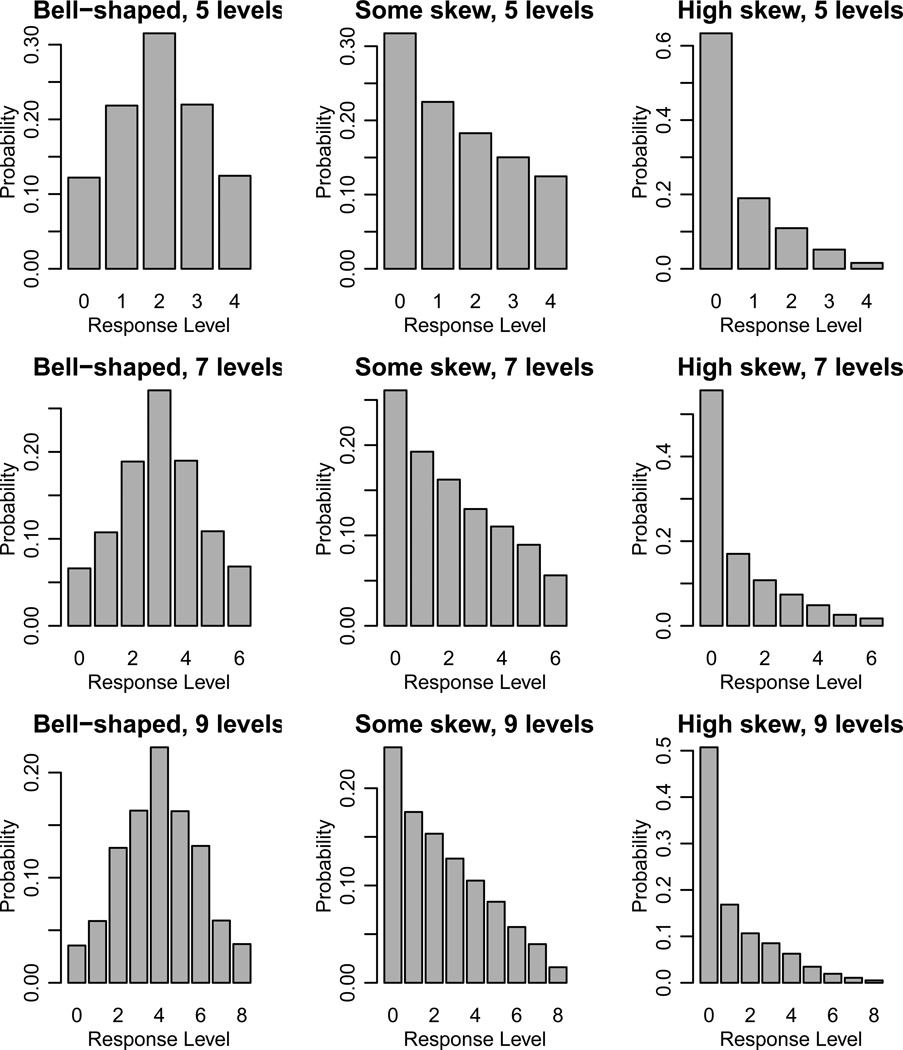
• The distribution of the ordinal response y had 5 levels (0 through 4), 7 levels (0 through 6), or 9 levels (0 through 8).

• The number of subjects n was 300, 500 or 700.

• The number of observations (waves) per subject was J = 5, 7, or 9.

• The marginal distribution of y was bell-shaped (roughly as in the simulations of Bauer and Sterba [4]), somewhat skewed, or highly skewed. The highly skewed distribution was based on the marginal distribution observed in the FAS data.

For each of these 3 × 3 × 3 × 3 = 81 conditions, 1000 random data sets were simulated.

The observation times t_ij (considered as the age of simulated participants at each observation) was random but roughly equally spaced: specifically, for the jth wave in a J-wave scenario, subject i was sampled at age $13.25+11\frac{j}{J}+u_{ij}$ where u_ij comes from a standard uniform distribution between 0 and 1.

For each subject i, the values of x_ij were generated as follows. A latent normal value of z_ij was generated from a N(0,1) distribution with intraclass correlation 0.5, and then transformed to have a marginal Beta(1,4) distribution. Denoting the resulting variate as z_ij, we let x_ij = 4z_ij + 1. This procedure, thus, produced correlated skewed data with a marginal distribution very similar to the observed values of NPI in the empirical data. For simplicity, we set the marginal probability distribution of x to be independent of time, because x did not appear to have much systematic change over time in the empirical data.

The response values y_ij were then generated from a proportional odds TVEM model with the same β₀(t) and β₁(t) as the estimates based on the FAS data, and with θ parameters chosen to give approximately the marginal distributions (across time and subjects) shown in Figure 2. The estimated τ² parameter from the FAS data, 2.2156, was taken as the true value here. This leads to an ICC for the latent Ў|X of .4024 [27], or an estimated ICC for Y|X in the linear TVEM model of .29 to .40 depending on the condition.

Figure 2.

The distribution shapes by response levels manipulated in the simulations.

Both the linear TVEM model and the proportional odds TVEM model were fit to each simulated data set. For simplicity, the number and location of knots were considered known and set to those of the data-generating model. The relative predictive accuracy of the two methods was compared as follows. For each observation Y_ij, the fitted value ŷ_ij from the linear model was defined as the best linear unbiased prediction (BLUP) from the linear mixed model. For the proportional odds model, the BLUP for the subject-specific probability of each response level was obtained, and then used to calculate ŷ_ij as Σ y_ij Pr(y_ij). The fitted value ŷ_ij was compared with the subject-specific expected value μ_ij = E(Y_ij|t_ij, x_ij, a_ij) based on the true model, and the sum of squared error Σ_i Σ_j (ŷ_ij − μ_ij)² and the prediction bias $n^{-1}{J}^{-1}{\sum }_{i=1}^n{\sum }_{j=1}^J({ŷ}_{ij}-{\mu }_{ij})$ were calculated for each method. The relative efficiency for the proportional odds model was defined as the average across simulations of the ratio of the sum squared error of the linear model to that of the proportional odds model. Thus, a relative efficiency greater than one implies that the proportional odds model does a better job at predicting the expected value than the linear model.

For prediction, both the linear TVEM and proportional odds TVEM had very little bias in all conditions. Mean absolute prediction bias was always less than .003 for the linear TVEM model, and ranged from .002 to .030 for the proportional odds TVEM model, depending on the condition. The bias associated with the proportional odds TVEM model sometimes tended to represent a slight underestimate of the mean in scenarios with moderate or high skewness; it may have been related to the fact that the predicted response mean had to be estimated indirectly from the predicted response probabilities.

The relative efficiencies of proportional odds TVEM versus linear TVEM for prediction are shown in Table 1. The proportional odds TVEM model always performed better than the linear TVEM model (relative efficiency > 1). Thus, although the linear TVEM estimate of the response was unbiased, it still had higher overall error than the proportional odds TVEM estimate because it did not take the true nature of the response distribution into account. In general, the number of subjects, the number of waves, or the number of levels of the ordinal scale had very little effect on relative efficiency. When the distribution of the ordinal responses was a bell shape, the two models performed at about the same level. However, when skewness was involved, the linear model’s performance was worse. This is particularly salient in the case of high skewness, which is very common in data on substance abuse.

Table 1.

Relative efficiency of proportional odds TVEM versus linear TVEM.

#Levels	#Subjects	#Waves	Relative Efficiency
			(Bell-shaped)	(Some skew)	(High skew)
5	300	5	1.0257	1.0761	1.1880
5	300	7	1.0395	1.1140	1.2793
5	300	9	1.0505	1.1506	1.3627
5	500	5	1.0272	1.0795	1.1991
5	500	7	1.0397	1.1186	1.2890
5	500	9	1.0518	1.1546	1.3732
5	700	5	1.0275	1.0813	1.2036
5	700	7	1.0411	1.1194	1.2924
5	700	9	1.0524	1.1557	1.3797
7	300	5	1.0261	1.0876	1.2201
7	300	7	1.0372	1.1241	1.3141
7	300	9	1.0438	1.1586	1.4019
7	500	5	1.0283	1.0890	1.2270
7	500	7	1.0370	1.1260	1.3223
7	500	9	1.0454	1.1625	1.4099
7	700	5	1.0282	1.0910	1.2325
7	700	7	1.0379	1.1272	1.3250
7	700	9	1.0459	1.1623	1.4137
9	300	5	1.0290	1.0963	1.2157
9	300	7	1.0381	1.1351	1.3043
9	300	9	1.0426	1.1694	1.3882
9	500	5	1.0288	1.0989	1.2251
9	500	7	1.0378	1.1388	1.3165
9	500	9	1.0445	1.1716	1.3985
9	700	5	1.0284	1.1015	1.2306
9	700	7	1.0377	1.1396	1.3170
9	700	9	1.0443	1.1754	1.4035

For the proportional odds model, it is also of interest to compare the true and estimated β₁(t) function. We omit this for the linear model, because the β₁(t) function there requires different interpretations for the true (proportional odds) and fitted (linear) models, and therefore direct comparisons are less meaningful. In all conditions, the average bias for proportional odds TVEM in estimating β₁ (t) was essentially zero (between −.002 and .002). In addition to the bias, we calculated the mean squared error (MSE) in estimating β₁(t) averaging over observation times t for the proportional odds TVEM. The results for MSE are summarized in Table 2. The MSE tended to be higher in scenarios where skewness was greater, or when the number of subjects, waves, or response levels was smaller. Pointwise coverage for 95% nominal confidence intervals for β(t) was also assessed. On average across replications and sampling times, this coverage was very close to nominal (94.4% to 95.7%). The Monte Carlo error rate for 1000 simulations is $\pm 1.96\times \sqrt{0.05\times 0.95÷1000}=\pm 1.35\%$. Thus, the confidence intervals have excellent coverage.

Table 2.

MSE in coefficient function estimation for proportional odds TVEM.

#Levels	#Subjects	#Waves	MSE for β1(t)
			(Bell-shaped)	(Some skew)	(High skew)
5	300	5	0.0453	0.0453	0.0638
5	300	7	0.0306	0.0312	0.0432
5	300	9	0.0245	0.0241	0.0309
5	500	5	0.0261	0.0271	0.0355
5	500	7	0.0183	0.0186	0.0255
5	500	9	0.0138	0.0144	0.0185
5	700	5	0.0189	0.0186	0.0250
5	700	7	0.0127	0.0132	0.0174
5	700	9	0.0100	0.0103	0.0127
7	300	5	0.0422	0.0417	0.0522
7	300	7	0.0277	0.0297	0.0355
7	300	9	0.0214	0.0216	0.0278
7	500	5	0.0247	0.0250	0.0315
7	500	7	0.0171	0.0167	0.0211
7	500	9	0.0129	0.0135	0.0165
7	700	5	0.0178	0.0178	0.0225
7	700	7	0.0121	0.0123	0.0151
7	700	9	0.0093	0.0094	0.0119
9	300	5	0.0405	0.0419	0.0515
9	300	7	0.0284	0.0286	0.0342
9	300	9	0.0212	0.0211	0.0270
9	500	5	0.0239	0.0246	0.0296
9	500	7	0.0161	0.0170	0.0206
9	500	9	0.0124	0.0130	0.0162
9	700	5	0.0170	0.0172	0.0213
9	700	7	0.0116	0.0121	0.0141
9	700	9	0.0091	0.0093	0.0110

5. Discussion

This study developed a new statistical model with free SAS macro’s that can be applied to characterize time-varying effects of risk factors on ordinal outcomes, which are very common in longitudinal data collected from substance abuse research. We also examined the consequences of fitting the linear TVEM to ordinal responses through simulations. The design of our simulation study is unique because it represents the special features of a well-known longitudinal study on youth at high risk for substance abuse so that the results can inform future applications of the methodology to the substance abuse field.

The proposed model, in general, produced very small biases across different numbers of levels on the ordinal scale, sample sizes, numbers of waves, and distribution shapes, although there was a tendency for some slight bias to be found in more skewed distributions with fewer levels. Further, the MSE tended to be higher in scenarios where skewness was greater, or when the number of subjects, waves, or response levels was smaller. Our simulation also shows that fitting the linear TVEM to ordinal responses was particularly problematic when the ordinal scale was highly skewed. Contrary to a common assumption that an ordinal scale with several levels can be treated as a continuous scale, our results indicate that it is not so much the number of levels on the ordinal scale but rather the skewness of the distribution that makes a difference on relative performance of linear versus ordinal models.

The motivating example in this study demonstrates that the proposed model that was designed for longitudinal ordinal responses can characterize the time-varying effect of negative peer influences on alcohol use in a way that is more consistent with the developmental theory and existing literature in comparison to the linear TVEM model. Furthermore, Bauer and Sterba [4] provided some arguments against the use of linear models with ordinal outcomes, such as the possibility of generating impossible predicted values outside the range of the ordinal scale and the concern of dealing with heteroscedasticity. There is also another important practical advantage to modeling ordinal responses as they are: we can use the regression coefficients to calculate probabilities or odds ratios (e.g. the probability of engaging in binge drinking). A linear model is not adapted for this purpose.

Our approach to model selection in this paper and the accompanying macro is a rather simple one. We assumed that each coefficient function could be represented as a spline with the same number of knots, and used the BIC penalized fit statistic to choose the best number of knots. It would be beneficial in the future to make the process more flexible. This can be done in one of two ways. The easiest way is to allow different numbers of knots for different functions (so that β₀(t) might have a complicated shape while β₁(t) had a simple one, or vice versa). However, a fit statistic would still have to be used to loop through each possible number of knots for each coefficient, and to choose the best combination, which may become time-consuming. A more automatic approach would use many knots but then implement a complexity penalty function (e.g. [29]) to regulate the magnitude of the change in the function which may occur at each knot. However, in our experience it was computationally difficult to estimate a model which included both a complexity penalty and a random effect in a generalized linear model using standard software. Therefore, more research here is needed.

The proposed model was built upon the assumption of proportional odds which has the advantages of ensuring the proper order among the cumulative probabilities and providing simple interpretation of the effects of covariates. In some practical settings, however, this assumption may need to be relaxed. Interested readers may refer to [30] for a comprehensive review of alternative approaches. Particularly, in substance abuse research where the shift from no use to any use may be qualitatively different from shifts in level of use, the zero-inflated proportional odds model [31] may be considered.

Model (1) accounts for subject-specific effects only through a random intercept at the latent level. Thus, latent values ў_ij and ў_ij′ are treated as equally correlated regardless of the size of the time difference between t_ij and t_ij′, and this may not be realistic in some settings. Popular longitudinal models assuming autocorrelation for the residuals e_ij (such as AR-1), on the other hand, treat the lag between each consecutive pair of measurements t_ij and t_i,j+1 as equivalent. This assumption may not apply to those settings that involve random or inconsistent measurement times. A more straightforward way to incorporate longitudinal correlation, therefore, is to add a random subject-level slope b_i alongside a_i. That is, one can add a new term b_it_ij to the right-hand side of Equation (1). This approach of adding a simple parametric random effects structure to a rich nonparametric fixed effects structure can work well and in fact has some precedent in the literature [32]. We adopted this approach to re-analyze the empirical data but found that the estimated curves are not noticeably different from those in Figure 1. We also attempted to repeat the simulations as well to include a random slope, but we found that the GLIMMIX procedure sometimes failed to converge when faced with a proportional odds model with two random effects. Further research is, thus, warranted regarding how best to implement more complex random effect structures while still allowing the time-varying effects to be easily estimated and interpreted with standard software. Another option, besides random effects, could have been to take a marginal (GEE) approach with sandwich standard errors [33]. This is, however, beyond the scope of this paper.

Appendix

SAS program example for using macro’s OrdinalTvem & OrdinalTvemLoop

In this study, we have developed two SAS macro’s that can be downloaded from the web site of the Methodology Center at the Pennsylvania State University (http://methodology.psu.edu/OrdinalTvemPropOdds). The principal macro is OrdinalTvem which fits either a linear or proportional odds TVEM model with one or more covariates and an ordinal response. The macro optionally includes (1) no random effects, (2) a random intercept alone, or (3) a random intercept and random slope, in the model. The second macro, OrdinalTvemLoop, calls OrdinalTvem in a loop in order to facilitate the choice of the degree of spline and the number of knots. The input data format requires one row for each wave (see an example in [10]).

The code shown below runs an analysis similar to the one included in the paper, but with an addition of two covariates, family history of alcoholism and depression, which are assumed to have time-invariant effects on alcohol use. Note that whether a covariate’s value is time-varying is independent of whether its effect is time-varying. All four combinations are possible. For example, family history of alcoholism is time-invariant but may have different effects on alcohol use at different developmental stages. On the other hand, a time-varying covariate such as depression can be given a constant coefficient for the sake of parsimony if its estimated coefficient function appears flat. While it is not necessary to tell the macro whether the value of a covariate is time-varying, covariates with time-invariant effects are indicated with cov and covariates with time-varying effects are specified under tcov.

%INCLUDE "C:\Documents\OrdinalTvem.sas";
/* substitute  here the location at which the macro is stored */
%OrdinalTvem(dataset=usable,  /*data set name*/
   id=ID,  /* ID variable */
   t=age,  /* time variable */
   cov=FamHistory Depression, /* name of the covariate(s) with time-invariant effect */
   tcov=NegPeer, /* name of the covariate(s) with time-varying effect */
   y=Drink30day, /* response variable name */
   UsePropOdds=1,/* use a proportional odds TVEM;
                    specify "UsePropOdds=0" if using a linear TVEM */
   UseRandom=1, /* 0 indicates no random effects;
                   1 indicates a random intercept;
                   2 indicates a random intercept and slope */
   deg=3, /* the degree of the spline */
   MinTToPlot=15, /* lower end of plot */
   MaxTToPlot=25, /* upper end of plot */
   NumInteriorKnots=3 /* the number of interior knots, assumed evenly spaced */);

The calculations for the macro mainly involve SAS PROC GLIMMIX (see the details in Section 2) so SAS version 9.2 or higher is required. In addition to the time-varying coefficients for the covariates specified under tcov (it is permissible to specify none at all), the macro automatically fits a time-varying intercept using B-splines without a penalty. When calling PROC GLIMMIX for proportional odds regression, we use the DESCENDING option and then reverse the signs of the resulting intercept constants [16]. This is needed because the default approach to proportional odds regression in SAS would model the probability of getting a lower, not higher value, which would make the interpretation of the β functions less intuitive. We reverse the signs of the intercept constants (so that θ₁ < … < θ_K−1 instead of θ_K−1 < … < θ₁) to make them more easily interpretable as thresholds which the latent variable must exceed in order for the observed variable to pass to the next level.

Three different approaches to doing the internal calculations can be specified in OrdinalTvem or OrdinalTvemLoop, using the optional keyword ComputationOption. If ComputationOption=1 is specified, then doubly iterative pseudolikelihood is used, with no nonnegativity constraint on the subject-level covariance parameter. If ComputationOption=2 is specified, then doubly iterative pseudolikelihood is used, but with a nonnegativity constraint on the subject-level covariance parameter. If ComputationOption=3 is specified, then approximate maximum likelihood by Gaussian quadrature is used. Based on our preliminary simulations, Option 3 is recommended.

Besides plots, several useful data files are created. The most useful are:

• DataWithFitted The input dataset, merged with the fitted values and confidence intervals for the beta function of each covariate at each observed time point.

• DataWithFittedByLevel Fitted values at the logit scale for each observation, for each level (in the proportional odds model).

• Covparms Estimate for the random effects variance, if any.

• ParameterEstimates Estimates for the regression parameters corresponding to the terms in the spline basis. Also, estimates for the level-specific cutoff parameters θ.

• InvariantEffects Estimates and standard errors for the regression parameters, if any, specified by the user to have constant regression coefficients.

• TheseFitStats Fit statistics for the model (e.g., AIC, BIC)

The second macro developed from this study is OrdinalTvemLoop which calls OrdinalTvem in a loop in order to facilitate the choice of the degree of spline and the number of knots. This macro creates an output data set called FitStats which contains fit statistics including AIC and BIC for each of many combinations of choices for degree and number of knots. These fit statistics come from PROC GLIMMIX via OrdinalTvem. The following is sample code for this macro.

%OrdinalTvemLoop(dataset=usable,
id=ID,
t=age,
cov=FamHistory Depression,
tcov=NegPeer,
y=Drink30day,
UsePropOdds=1,
UseRandom=1,
ComputationOption=3);

PROC PRINT DATA=FitStats;
     VAR degNumInteriorKnots
         AIC___smaller_is_better_ BIC___smaller_is_better_;
     RUN;