Combining growth curves when a longitudinal study switches measurement tools

Abstract

When longitudinal studies are performed to investigate the growth of traits in children, the measurement tool being used to quantify the trait may need to change as the subjects age throughout the study. Changing the measurement tool at some point in the longitudinal study makes the analysis of that growth challenging which, in turn, makes it difficult to determine what other factors influence the growth rate. We developed a Bayesian hierarchical modeling framework that relates the growth curves per individual for each of the different measurement tools and allows for covariates to influence the shapes of the curves by borrowing strength across curves. The method is motivated by and demonstrated by speech perception outcome measurements of children who were implanted with cochlear implants. Researchers are interested in assessing the impact of age at implantation, and comparing the growth rates of children who are implanted under the age of two versus those implanted between the ages of two and four.

1 Introduction

Although there are statistical methods to address occurrences such as dropouts and missing data in longitudinal studies, these problems can be exacerbated in studies involving children. One critical problem often encountered in longitudinal studies of children is finding a measurement tool that is appropriate across all ages of the study period. For example, when the measurements involve psychological or linguistic variables, the measurement tool administered to a 5 year old is not always an appropriate measurement tool to be used with a 10 year old. That is true even though the tool at 5 years old is intended to measure the same underlying construct as the tool for 10 year olds. If the 10 year old took the 5 year old measurement they would likely score at the ceiling level. Vice versa, if the 5 year old took the measurement designed for 10 year olds then they would score at floor level. The focus in this paper will be on longitudinal growth curves of measurements involving children, accomplished via correlated growth curves of two different measurement tools reflecting the same underlying construct. In our motivating study, one growth curve is for a speech perception measure administered at younger ages and another correlated growth curve is for a speech perception measure administered at older ages. Even though the methods are presented in terms of studies involving growth in children, the methods discussed and developed within are appropriate for any set of correlated growth curves.

Methods have existed for many years to model growth curves. Linear growth curve analysis is well established^1,2 and has been extended to include the linear mixed-effects models,³ as recently summarized in Fitzmaurice et al.⁴ The nonlinear mixed-effects model is similar to that of the linear mixed-effects model, except the function allows the subject-specific growth profile to be nonlinear such as the logistic or Gompertz function. Alternatively there are nonparametric mixed-effects models including local polynomial mixed-effects, regression spline mixed-effects and smoothing spline mixed-effects. A Bayesian nonparametric mixed-effects model is also available.^5,6 In this paper we will specifically examine the nonlinear Gompertz growth curve. An advantage of this particular curve is the distinctive growth shape that the nonlinear function allows, which will be demonstrated with the data analysis. In addition, the parametric function will make it easier to borrow strength across curves by better specifying what the functional form will be when observed data points are lacking. These methods could be easily extended to other linear and nonlinear growth curves.

In addition to the growth curves, another critical motivation of this work is the development of a method to combine two different, but related, measurement tools into one single measure which could be used in a longitudinal analysis. Effective methods do exist for combining two measurement tools within the same study. However, these methods tend to require both measurement items being recorded at the same time for each individual, which may not be feasible when testing a child with a short attention span or when facing the constraints of a longitudinal protocol. There is a large body of work on item response theory which allows for the correlation between the two scores to be evaluated and a new construct variable to be devised; using such an approach, a new numerical scale is produced.^7,8 Hoffman et al.⁹ have used item response theory to compare estimates of vocabulary ability from different test forms. Burgette and Reiter¹⁰ present a nonparametric approach for imputing one measurement from another when the measurement of interest changes during the study. Their approach is based on the ranks of the two measurement items and works very well, but only incorporates a single time period. Unfortunately, in observational longitudinal studies, the subjects may not always be evaluated at regular intervals. In fact, each subject may have a different number of visits with different lags between them. With our proposed methods, we combine the measurement items but allow for each individual in the study to return for a differing number of visits, where the time between visits may vary. The time and amount of overlap between the two measurement tools may not be consistent either. Our approach not only equates scores from one measure to those of a parallel measure, but also addresses the challenge within a framework that uses data over time and over individuals of modeling the individual specific growth functions.

Many of the methods discussed previously have been constructed in the Bayesian paradigm. Addressing the many challenges presented can be made easier in a hierarchical and conditional setting, which lends itself to a Bayesian analysis. The nonlinear model that allows for subject specific random effects and borrowing strength from another curve can be built in an intuitive hierarchical Bayesian approach.

In this paper we produce one system that will evaluate the underlying growth curve construct from two related measurement items, and can ultimately impute one of the measurements given an observed score on the other measurement item. The remainder of the paper is organized as follows. We present the motivating study for this research in Section 2. The Bayesian hierarchical model is presented in Section 3, along with procedures for posterior predictions and estimation. The motivating study is analyzed and the results described in Section 4. We close with our conclusions in Section 5.

2 Motivating Study

Hearing loss in early childhood is known to affect the development of essential learning skills including speech perception, language development, and reading skills. Children who have a hearing loss ranging from mild to severe can receive help from hearing aids but for children with profound degrees of sensorineural hearing loss, hearing aids do not provide adequate acoustic input. For those children, a cochlear implant (CI) is often a more viable option.

Cochlear implants are designed to provide access to environmental sounds for individuals with severe to profound deafness. The device receives acoustic signals through an externally-worn microphone. These signals are processed to filter and transmit those components of sound critically important for speech perception. From there, those components are transmitted via electrical signals to an array of electrodes in the cochlea, resulting in electrical stimulation of the auditory nerve. The central auditory pathway then receives the signal for interpretation, which does not produce an exact replica of normal hearing. However, when using current CI technology, the majority of CI recipients who are post-lingually deaf score above 80% on high-context sentences in quiet listening conditions, even without visual cues.¹¹

It is typically thought that age at implantation influences outcomes for pediatric CI recipients. In particular, the earlier a child receives a CI, the better their developmental outcomes will be.^12,13 Presumably, this is because earlier implantation takes advantage of neural plasticity in the brain and sensitive periods in language development.^14,15,16 The question is, how early does this need to be? Although current Food and Drug Administration guidelines recommend implantation at 12 months or older, some CI centers advocate for implantation as young as 6 months of age.

While earlier implantation is beneficial, by providing earlier opportunities for hearing and speech and language development, these benefits may not be long lasting.¹⁷ Early implantation (prior to 2 years) is often advocated, but as children grow older there are other factors such as general cognitive development and educational environment that affect their outcomes. For that reason, Dunn et al.¹⁷ investigated the long-term outcomes of children with CIs to assess whether the differences in outcomes changed during the growth of the children. In this paper, we focus on one particular aspect of their study. The data come from the Iowa Cochlear Implant Clinical Research Center’s longitudinal database for speech perception outcomes. A team of audiologists and speech and language scientists have collected data annually with this population since 1990.

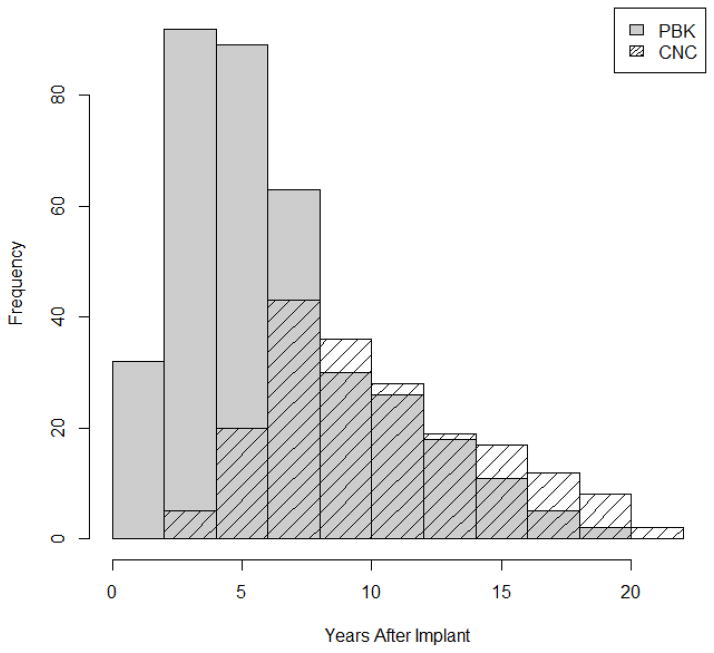
Speech perception was measured in quiet using recorded Consonant-Nucleus-Consonant (CNC) monosyllabic words¹⁸ and Phonetically Balanced-Kindergarten (PBK) words.¹⁹ Due to the influence of vocabulary on the speech perception word lists, PBK lists in this study were administered to children between 4 to 22 years of age whereas CNC words were administered to children between 6 to 25 years of age. In our analysis, we set the baseline as the time of implant and measured longitudinally according to the number of years since implant. Time could be measured either as chronological age (time since birth) or as hearing age (time since implant). Using hearing age allows us to model the growth from time of implant to evaluate how quickly the children progress in their speech perception scores. For PBK, the hearing age ranges from 1 to 19 years, and from 3 to 22 years for CNC, as shown in Figure 1.

Figure 1.

Distribution of ages that participants were administered the two measures PBK and CNC.. The PBK distribution is shown in gray and the CNC distribution is shown by the dashed lines.

Both the CNC and PBK scoring is based on percent-correct performance at both the word and the phoneme levels. One or two 50-word lists of CNC words are presented to each child per visit, depending upon the attention span. Individual children are assessed at each visit, and if a child does not have the language skills to move on to CNC, then the PBK is administered again. The result is that many children in this study continue to take the PBK test, as evidenced in Figure 1. In general, the children do not take both the PBK and CNC tests at the same age, but the age at which they transfer from one test to the other is individual specific. The result is a great deal of overlap at each age, but without the same child taking both tests, we lose the correlation structure needed to utilize the methods mentioned in the introduction. This highlights one of the advantages of our method. There are more data on the PBK scores, but our inferential interest is more focused on the CNC test. Thus, we want to borrow strength from the PBK curve to create a more secure CNC curve as we evaluate the age of implantation for cochlear implants.

In the previous analysis, the CNC and PBK speech perception scores were combined as if they were the exact same measurement. That is, a score of 20 on the PBK was assumed to equal a score of 20 on the CNC. Such an assumption was deemed reasonable based on analyzing the scores from those children who took both tests on the same day. The concordance correlation coefficient²⁰ was 83%, suggesting that PBK and CNC were highly reliable measures of each other. The previous analysis was based on a linear mixed model, using regression splines to follow the unique curvature of speech perception growth curves. Along with speech perception scores, the authors also evaluated other measures such as reading comprehension and determined that on most measures there are not long lasting effects on the children who are implanted later. The analysis was limited to only the testing under the age of thirteen years, because no children implanted at less than two years of age had any measurements beyond age thirteen. They found that mean speech perception scores between younger and older implanted children were significantly different at five years of age, but were no longer significantly different by seven years of age. However, there appeared to be a threshold that was reached at age seven between the two groups, as there were significant differences again at eight, nine, ten, and twelve years of age.

The same speech perception dataset is investigated in this paper, but we use all of the available measurements per person to help inform the entire growth curve trajectory. The proposed methods shed new light on long term speech perception differences according to age at implant. Rather than using regression splines, we choose a Bayesian parametric nonlinear growth curve model. We see many benefits to this approach. With a growth curve, we can explicitly specify a maximum to the growth. This maximum value is important to ascertain if one group will eventually reach that threshold; the regression spline has no such maximum restriction. We also view the growth as monotonically increasing, which is implicit in the growth curve model. Even though a semi-parametric regression spline is more general and allows for increases and decreases, decreases are not warranted theoretically in monotonic growth functions of speech perception. A Gompertz growth curve has three critical parameters to estimate, while the regression spline is based on a cubic polynomial and does require the choice of knots. The knots could be chosen on the population curve and have individual deviations from the curve, similar to what we propose. We prefer a Bayesian approach, but the basic model could be implemented using standard software such as PROC NLMIXED of SAS or the nlme package in R.

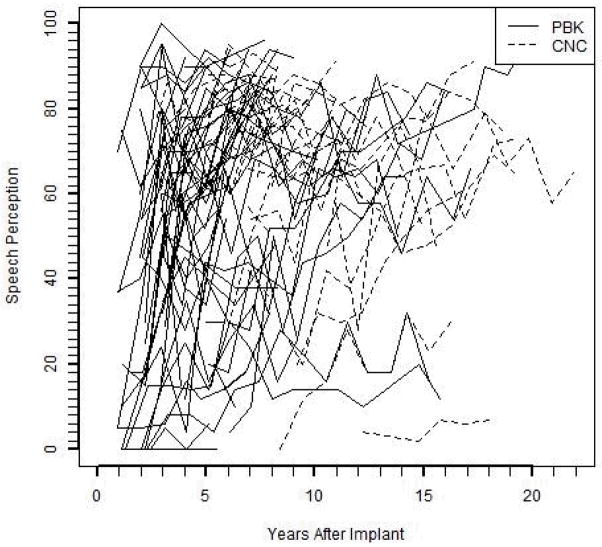
The study involves 66 total children; 28 were implanted before the age of 2 years and 38 were implanted between the ages of 2 and 4 years. The fewest number of visits was 1 and the largest number of visits was 18. The number of months between visits are designed to be every 12 months, but the observed range is from 7 to 30 months between visits. The sporadic nature of the visits is illustrated in Figure 2.

Figure 2.

Individual observed PBK curves are shown in solid lines. Individual observed CNC curves are shown by dashed lines.

3 Methods

3.1 Data and Process Models

Let Y_1i(t) denote the score of individual i at time t of the first measure while Y_2i(t) denotes the score on the second measure for i = 1,…, N. The same individual is allowed to have both measures at any particular time t. Assume a normal distribution for each outcome variable such that

$$\begin{array}{l}{Y}_{1i}(t)\mid {\mu }_{1i}(t),{\sigma }_1^2~N({\mu }_{1i}(t),{\sigma }_1^2)\\ Y_{2i}(t)\mid {\mu }_{2i}(t),{\sigma }_2^2~N({\mu }_{2i}(t),{\sigma }_2^2)\end{array}$$ (1)

Note that each individual has his/her own mean function specified at time t. As part of the model specification, we assume that the Y_1i(t) and the Y_2i(t) are conditionally independent given μ_1i(t) and μ_2i(t). Intuitively, this implies that the deviations between a subject’s scores and the subject-specific mean function do not exhibit any type of dependence (temporal, between subject, within subject, etc.). The model also implies homoscedasticity in these deviations across subjects for each measure.

In some cases, the underlying assumptions for the model may not be met because the variation in the difference of the two measures may depend on the subject. However, the heterogeneity in variation is likely to be small relative to the other factors in the study making the impact of the dependence negligible.

We consider the growth to follow the nonlinear Gompertz curve, although other similar growth curves or a regression spline could be used. Let l = 1,2 denote whether the outcome is based on measure 1 or 2. The Gompertz growth curves can then be written as

$${\mu }_{li}(t)={\alpha }_{li}\mathit{exp}(-{\beta }_{li}\mathit{exp}(-{\gamma }_{li}\ast t))$$ (2)

where α_li denotes the individual maximum for outcome l, β_li can be conceived as a measure of the vertical intercept for outcome l, and γ_li can be conceived as a measure of the growth rate (slope) for outcome l. We expect these parameters to be similar for the two outcomes, meaning that the individual level growth curves for each outcome variable will follow similar paths.

Even with similar growth patterns, the outcome measures are unique and their differences need to be quantified and included in the model. Therefore, within this modeling framework, we specify both the population growth curve and subject specific curves for each outcome variable. The differences between the outcome variables will be accounted for by an offset term multiplied by an indicator variable, and the three terms that specify a Gompertz curve will each have a random subject effect which will allow for subject specific curves. To characterize the three terms, let

$$\begin{array}{l}{\alpha }_{li}=a+{\theta }_a{1}_{l=2}+{{\mathbf{X}}_i}^{\prime }{\mathbf{\delta }}_a+U_i\\ {\beta }_{li}=b+{\theta }_b{1}_{l=2}+{{\mathbf{X}}_i}^{\prime }{\mathbf{\delta }}_b+V_i\\ {\gamma }_{li}=c+{\theta }_c{1}_{l=2}+{{\mathbf{X}}_i}^{\prime }{\mathbf{\delta }}_c+W_i\end{array}$$ (3)

The parameters a, b, and c correspond to intercept values for the three models in equation (3). The value of the indicator 1_l=2 equals 1 if the score resulted from outcome measure Y₂ and equals 0 if the score resulted from outcome measure Y₁. Thus, θ_a, θ_b, and θ_c are the measures of offset for outcome Y₁ from Y₂ for the parameters of the curve, with Y₁ serving as the reference level. Let X be an N × k design matrix representing k covariates and interaction terms, where X_i′ is the row vector containing the values for the ith person, while δ_a, δ_b, and δ_c are k dimensional vectors containing the corresponding coefficients. In our implementation of the model, we will focus on a single dichotomous covariate X (specifically, age at implant), and include an interaction between 1_l=2 and X so that the covariate is allowed to impact Y₁ and Y₂ differently.

These equations reconcile the obvious similarities between the two outcomes by borrowing strength via shared components, but still allow for unique curves between the different outcomes. The approach also accommodates the assessment of the separation of the two curves through the estimates of θ_a, θ_b, and θ_c. In addition, we may be interested in how a specific single covariate X₀ measured at baseline (e.g., age at implant) impacts the curve. Specifically, the combination of the terms a + θ_a1_l=2 + X_0iδ_a + 1_l=2X_0iν_a, b + θ_b + X_0iδ_b + 1_l=2X_0iν_b, and c + θ_c + X_0iδ_c + 1_l=2 X_0iν_c specifies the population Gompertz growth curve for the two outcome measures, where the δ parameters represent the main effects of the covariate and the ν terms represent the interaction effects.

The random subject effects (U_i, V_i, W_i) give the subject specific curves, allowing each individual to deviate from the population curve. We assume the same random subject effects for both outcome measures. Having shared random subject effects imposes the assumption that the effect of an individual on the second tool will be the same as it is for the first tool. This is accomplished by having the deviation from the mean levels of α_li, β_li, and γ_li be the same for each measurement tool. An advantage of borrowing strength through this shared effect assumption is that it facilitates a realistic prediction of the missing Y_2i(t) when the model assumptions are met. In certain instances, the assumption of a shared effect may be unduly restrictive and it could be necessary to include separate random subject effects for each outcome measure.

3.2 Prior Distributions

In a Bayesian hierarchical model, the parameters in the model are assigned prior distributions. Assume a normal distribution prior for a with mean zero and large variance ${\sigma }_a^2$. The values of b and c are restricted to be positive so we assume a gamma prior, Gamma(q, r), for each. The parameters θ_a, θ_b, θ_c, δ_a, δ_b, and δ_c can be viewed as linear regression coefficients, for which we assume a normal distribution with mean zero and large variance ${\sigma }_{\theta }^2$. The random subject effects, U_i, V_i, W_i, are given the traditional normal distribution prior with mean zero and variances ${\sigma }_U^2,{\sigma }_V^2,{\sigma }_W^2$, respectively. Finally, the variance components ${\sigma }_1^2,{\sigma }_2^2,{\sigma }_U^2,{\sigma }_V^2$, and ${\sigma }_W^2$ are each assigned the prior Inverse Gamma(q, r).

In addition, we must specify the following hyperparameters: ${\sigma }_{\theta }^2,{\sigma }_a^2$, q, and r. The choices for these parameters are discussed in Section 3.4.

3.3 Posterior Predictions

Bayesian inference is often framed in terms of the parameters from the posterior distribution. We have separate models for the outcome measures Y₁ and Y₂, as specified in equation (1), that share components given in equation (2), because we expect those parameters specifying the growth curves from the two different outcome variables to be related. One way to evaluate the growth or impact of covariates is to perform inference on the shared variables in equation (3).

Alternatively, one of our study goals is to demonstrate how to transform Y₁ and Y₂ to the same scale so that there can be a single dataset for statistical analysis. This can be done by creating an entirely new scale, such as done in item response theory. A drawback to that approach is that one loses any interpretation of the score. Instead, we could predict the second from the first or vice versa, calling the prediction $Y_{2i}^{(\mathit{pred})}(t)$. This then becomes a missing data problem where we impute a $Y_{2i}^{(\mathit{pred})}(t)$ value from the posterior predictive distribution $Y_{2i}^{(\mathit{pred})}\mid Y_{1i}(t)$. Using the model in Section 3.1, we impute a Y_2i(t) value for every observed Y_1i(t) value, a process known as single imputation²¹. The resulting filled-in dataset could be used in future analyses, but the imputation uncertainty needs to be appropriately accounted for.

The posterior predictive distribution of $Y_{2i}^{(\mathit{pred})}(t)\mid Y_{1i}(t)$ is found by integrating out the additional parameters, which we denote here by ψ. Thus, a distribution for the yet unobserved $Y_{2i}^{(\mathit{pred})}(t)$, given the likelihood, is obtained based on a particular value of Y_1i(t). The predictive distribution is formulated as

$$Y_{2i}^{(\mathit{pred})}(t)\mid Y_{1i}(t)=\underset{\psi }{\int }\left(Y_{2i}^{(\mathit{pred})}(t)\mid \psi \right)\left(\psi \mid Y_{1i}(t)\right)d\psi$$ (4)

In this way, we construct a predictive distribution for $Y_{2i}^{(\mathit{pred})}(t)$ after observing Y_1i(t). The predictive distribution can be approximated using Bayesian estimation, as outlined in Section 3.4.

3.4 Bayesian Estimation

We use vague priors for all parameters in the model to reflect a lack of pre-existing information on the parameters. Normal distributions were specified to have large variances with ${\sigma }_{\theta }^2=1,000$ and ${\sigma }_a^2=10,000$. The hyperparameters of the Inverse Gamma were flat with q = 0.01 and r = 0.01.

Given that the Bayesian hierarchical model is largely composed of conjugate priors, the MCMC sampling is implemented using WinBUGS.²² Sample WinBUGS code can be obtained from the first author. Convergence was assessed by examining trace plots and using the Geweke diagnostic criterion with α = 0.05.²³ The chain was run for 11,000 iterations with the first 4,000 being burn-in.

The distribution specified in equation (4) is estimated by randomly generating a $Y_{2i}^{(\mathit{pred})}(t)$ value from equation (1) at every iteration of the MCMC chain using the current states of μ_2i(t) and ${\sigma }_2^2$. The result is a distribution of predicted $Y_{2i}^{(\mathit{pred})}(t)$ values for an observed Y_1i(t) value of person i at time t.

4 Data Analysis

4.1 Speech Perception

Age at implantation, as discussed in Section 2, was included as a covariate in the analysis. Age could realistically impact α_li, β_li, and γ_li, and it could also impact PBK and CNC differently. We allowed for δ_a, δ_b, and δ_c to be in the model and for CNC and PBK to differ through interaction terms. Therefore, the full model can be written as

$$\begin{array}{l}{\alpha }_{li}=a+{\theta }_a{1}_{\mathit{CNC}}+X_{1i}{\delta }_a+X_{1i}{1}_{\mathit{CNC}}{\nu }_a+U_i\\ {\beta }_{li}=b+{\theta }_b{1}_{\mathit{CNC}}+X_{1i}{\delta }_b+X_{1i}{1}_{\mathit{CNC}}{\nu }_b+V_i\\ {\gamma }_{li}=c+{\theta }_c{1}_{\mathit{CNC}}+X_{1i}{\delta }_c+X_{1i}{1}_{\mathit{CNC}}{\nu }_c+W_i\end{array}$$ (5)

where we let 1_CNC = 1 with l =CNC if measuring CNC and 1_CNC = 0 with l =PBK if measuring PBK. Also, let X_1i equal one if individual i was implanted under the age of two and equal zero if implanted between the ages of two and four. The interaction term, X_1i1_CNC, allows the CNC and PBK curves to behave differently based on age at implantation. Although results reported here dichotomize age at implant into two groups, we also examined the curves using a continuous value of age at implantation, which yielded similar results but a slightly higher value of the deviance information criterion (DIC).

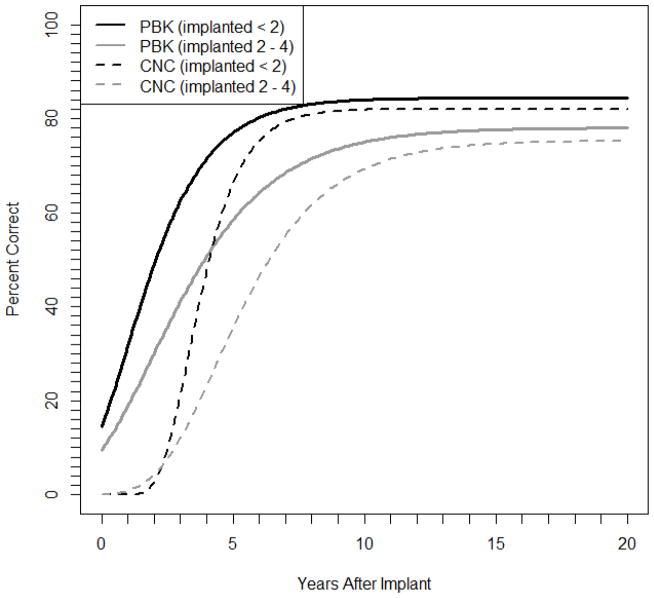
The prior distributions, chosen hyperparameters, and parameter estimates are shown in Table 1. Flat priors were used for all parameters to reflect the lack of prior knowledge on the specific shapes of the growth curves. The estimated population shape parameters for the PBK and CNC curves, given in Table 2, are found by plugging the parameter estimates from Table 1 into equation (5) and setting the subject specific deviations U_i, V_i, and W_i all to zero. The PBK curves are portrayed in Figure 3 as solid lines and CNC as dashed lines, with black denoting the younger group and gray the older group. We clearly see that immediately after implant the scores are low but increase at different rates until approximately five years after implant, when the PBK population averaged curve begins to approach the asymptote. As expected, it takes much longer for the CNC scores to reach an asymptote, which is at approximately ten years after implant.

Table 1.

Hyperparameters and posterior estimates of parameters from the speech perception analysis.

Parameter	Prior Distribution	Posterior Mean (SD)	95% Credible Interval
a	N(0, 1002)	78.05 (2.30)	(73.67, 82.62)
b	Gamma(0.1, 0.1)	2.11 (0.33)	(1.49, 2.80)
c	Gamma(0.1, 0.1)	0.40 (0.15)	(0.19, 0.62)
θa	Normal(0, 1000)	−2.77 (1.63)	(−5.98, 0.39)
θb	Normal(0, 1000)	4.82 (3.13)	(0.29, 13.05)
θc	Normal(0, 1000)	0.05 (0.03)	(−0.02, 0.11)
δa	Normal(0, 1000)	6.35 (3.31)	(0.04, 12.95)
δb	Normal(0, 1000)	−0.34 (0.56)	(−1.30, 0.99)
δc	Normal(0, 1000)	−0.19 (0.22)	(−0.57, 0.13)
νa	Normal(0, 1000)	0.42 (2.83)	(−5.16, 6.04)
νb	Normal(0, 1000)	14.73 (13.88)	(−0.81, 49.52)
νc	Normal(0, 1000)	−0.28 (0.12)	(−0.52, −0.06)
${\sigma }_1^2$	IG(0.01, 0.01)	105.30 (9.43)	(88.30, 125.30)
${\sigma }_2^2$	IG(0.01, 0.01)	62.84 (8.20)	(48.44, 80.78)
${\sigma }_U^2$	IG(0.01, 0.01)	33.72 (18.29)	(7.94, 79.08)
${\sigma }_V^2$	IG(0.01, 0.01)	1.23 (0.54)	(0.40, 2.49)
${\sigma }_W^2$	IG(0.01, 0.01)	0.17 (0.06)	(0.07, 0.31)

Table 2.

Group specific solutions to equation (5) that determine the shape of each curve in Figure 3.

Word List	Age	α̂	β̂	γ̂
PBK	< 2	84.40	1.77	0.59
PBK	2–4	78.05	2.11	0.40
CNC	< 2	82.05	21.32	0.92
CNC	2–4	75.28	6.93	0.45

Figure 3.

Estimated population curves. The solid lines represent the PBK growth curves and the dashed lines represent CNC growth curves. The black lines represent the older implanted children and the gray lines represent the younger implanted children.

It is informative to evaluate each of the specific parameters on their own to know more about the similarities and differences between the trajectories of the two age groups. For the terms in the equation for α_li, we find that δ_a has a 95% credible interval that does not include zero. Because the 95% credible interval excludes zero we can be confident that the speech perception score does result in a significantly higher maximum if the parents have their child implanted before the age of two than if the parents wait. Also note that the asymptotes are lower for CNC scores than for PBK scores, which is suitable because the CNC test is theoretically more difficult and should have a lower upper limit than the PBK test.

Another pronounced difference between the two speech perception tests appears to be in the intercepts. The quantity θ̂_b = 4.82 denotes the offset between the baseline scores of CNC and PBK for the older implanted group, which does show a noteworthy effect as the 95% credible interval does not include zero. We also see that the slopes for the younger group are steeper than the slopes for the older group. In other words, not only does the younger group have a higher maximum value, but it also achieves that maximum more rapidly. The difference in growth rates between PBK and CNC is evaluated by θ_c, and its 95% credible interval barely includes zero, but the interval for ν_c does not include zero. We can see in Figure 3 the culmination of these estimated parameters on the overall shape of the curves. The PBK curves clearly start higher than the CNC curves. However, their growth rates appear similar with the CNC curves being slightly steeper. The curves both increase rapidly until nearing the asymptote, with CNC reaching the asymptote at a later age due, in part, to its lower intercept.

Recall the large amount of variability inherent in speech perception scores, as demonstrated in Figure 2, both within a subject and between subjects. The estimated values of ${\sigma }_1^2$ and ${\sigma }_2^2$ reflect within-subject variability, and the estimated values of ${\sigma }_U^2,{\sigma }_V^2$, and ${\sigma }_W^2$ reflect between-subject variability. Of particular interest is the large estimated value of ${\sigma }_U^2$. The importance of this term is that it captures the large amount of variability between individual curves and where individual subjects reach the asymptote. Each individual realistically has a different maximum value, and U_i is the parameter that accommodates this heterogeneity. The values of ${\sigma }_U^2,{\sigma }_V^2$, and ${\sigma }_W^2$ are all large relative to the values of a, b, and c.

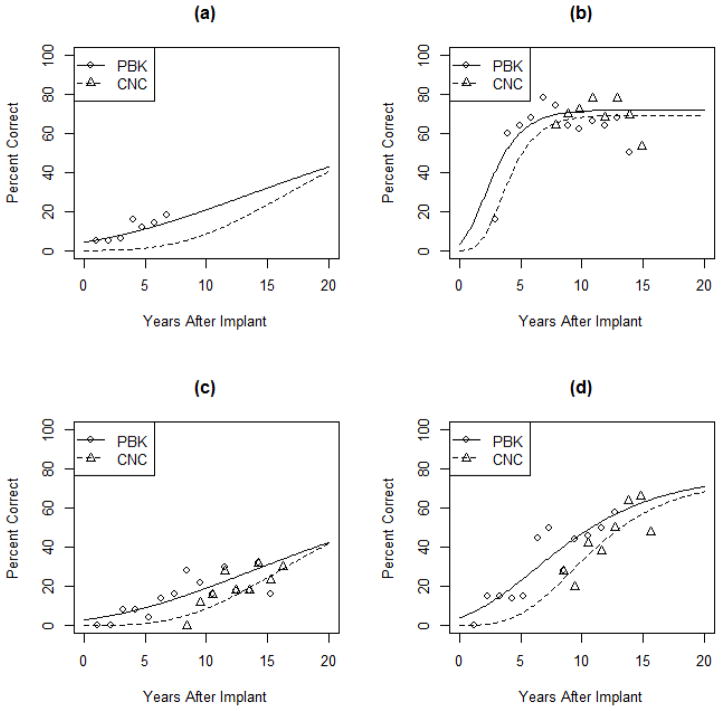
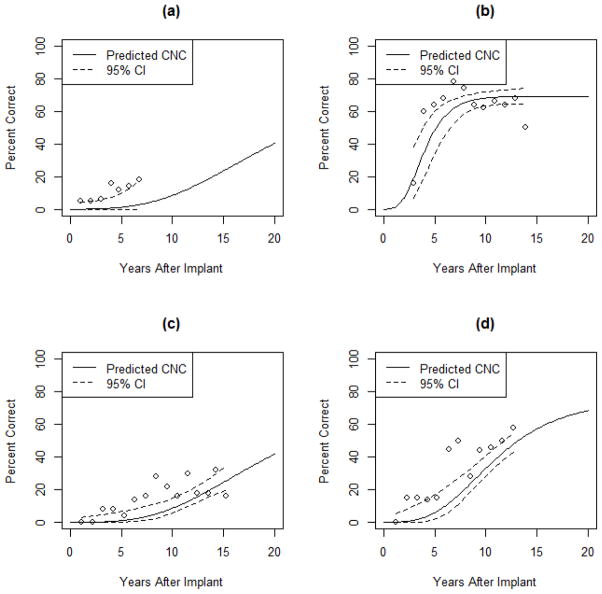
This approach to modeling allows for individual specific curves. We obtain an individual specific curve by incorporating the subject specific deviations U_i, V_i, and W_i into the determination of α_li, β_li, and γ_li in equation (5). We have selected a few subjects to demonstrate these curves in Figure 4, where we see their individual specific curves along with their raw data. These plots demonstrate the flexibility of this model to characterize both the individual specific curves and the population level curves. In Figure 4(a), the individual only had PBK scores with no CNC scores. The model then draws upon the population average and the random subject effect to specify how far apart the CNC curve should be from the PBK curve for this individual. In Figures 4(b)–4(d), we see different variants for how the individuals deviate from the population value. The individual in 4(b) asymptotes soon after implantation. The person in 4(c) is not performing well and has yet to reach the threshold. The person in 4(d) exhibits a moderate increase and appears to be reaching his maximum. The modeling clearly is equipped to match many various types of individual growth curves while simultaneously evaluating the population averaged curve.

Figure 4.

Subject specific curves. Observed PBK scores are denoted by circles and observed CNC scores are denoted by triangles. The estimated individual growth curves for PBK are given by the solid lines and estimated individual growth curves for CNC are given by the dotted lines.

4.2 Imputation Results

Another goal of this analysis was to put all of the observations (PBK and CNC) on the same scale. In this section we present the results of imputing CNC scores when the children took the PBK test.

We obtained predicted values and 95% credible intervals for each PBK observation. The individual CNC curves presented in Figure 4 also serve as the posterior predicted CNC curves. In Figure 5, we see how the prediction worked for the same four subjects featured in Figure 4. The observed PBK scores are represented by the dots, which are shown alongside each predicted CNC curve denoted by the solid line. The point on the curve corresponding to the age at which the PBK score was taken is the predicted CNC score. We also see the 95% credible interval for the predicted value shown as dotted lines. The intervals are relatively narrow. These predictions could be used in a follow-up analysis of only CNC scores.

Figure 5.

Dots represent the observed PBK scores. The solid lines provide the predicted CNC scores. 95% credible intervals are given by the dotted lines.

5 Discussion

Longitudinal dropouts and sporadic return visits can make statistical analysis in biomedical research studies more difficult. We examined a longitudinal study where we experienced multiple data collection issues but were also interested in studying correlated growth curves on a single underlying construct. This happens when the observational measurement tool changes over time, which frequently occurs when measuring the growth development in children. Our Bayesian hierarchical growth model accounts for all of these factors.

A Gompertz growth curve was used for both measurements, but the curves borrowed strength from each other by sharing specific model components. If a study subject has ample data on one of the tools then their individual data specifies the shape of the curve. If there are less data on one of the study measurements, then population level parameters guide the shape and location of the individual specific curve. Since the two curves share subject specific random effects the curves will move together even with small amounts of data.

This model instituted a maximum threshold whereas prior analyses using splines did not. The results here are consistent with what has previously been published regarding the relationship between speech perception scores and age at implantation, showing a long-term advantage for receipt of a CI prior to 2 years of age. In the prior analysis,¹⁶ the effect of age of implantation was marginal out to 15 years of age, at which point the variance became large enough to conclude no significant differences between the age groups. This analysis used chronological age at testing for the purpose of comparing the two groups at specific ages.

The construct being measured is fairly clear cut and the task is expected to asymptote as this ability should be constant over time so long as the device is working the same. The interesting clinical questions become why do we see growth, and when and where does the growth end? The value of this analytical method is that it allows us to address these questions by measuring the entire longitudinal growth curve. So now, we can take these data and explore what accounts for the growth. This value underscores the multilevel analytic potential, where we can incorporate possible explanatory factors that may account for this growth. Such an approach will accommodate the adjustment of important covariates in biomedical studies.

The individual specific curves allow us to predict one score from the other. These predicted scores can be used to have one measurement tool across the entire study period. Some researchers may prefer this method so that only one model is required rather than having the two correlated growth curves. Although practitioners may prefer a more simplistic imputation where they adjust one score by adding or multiplying by a constant, we prefer the model-based approach.