Abstract
The mammalian auditory system includes a brainstem-mediated efferent pathway from the superior olivary complex by way of the medial olivocochlear system, which reduces the cochlear response to sound (Warr and Guinan, 1979; Liberman et al., 1996). The human medial olivocochlear response has an onset delay of between 25 and 40 ms and rise and decay constants in the region of 280 and 160 ms, respectively (Backus and Guinan, 2006). Physiological studies with nonhuman mammals indicate that onset and decay characteristics of efferent activation are dependent on the temporal and level characteristics of the auditory stimulus (Bacon and Smith, 1991; Guinan and Stankovic, 1996). This study uses a novel psychoacoustical masking technique using a precursor sound to obtain a measure of the efferent effect in humans. This technique avoids confounds currently associated with other psychoacoustical measures. Both temporal and level dependency of the efferent effect was measured, providing a comprehensive measure of the effect of human auditory efferents on cochlear gain and compression. Results indicate that a precursor (>20 dB SPL) induced efferent activation, resulting in a decrease in both maximum gain and maximum compression, with linearization of the compressive function for input sound levels between 50 and 70 dB SPL. Estimated gain decreased as precursor level increased, and increased as the silent interval between the precursor and combined masker-signal stimulus increased, consistent with a decay of the efferent effect. Human auditory efferent activation linearizes the cochlear response for mid-level sounds while reducing maximum gain.
Keywords: cochlear, compression, efferent, gain, masking, neural
Introduction
In addition to ascending (afferent) neural pathways, the mammalian auditory system comprises descending (efferent) neural projections from higher to lower levels of the auditory system: ipsilateral and contralateral efferent systems of cat (Liberman, 1988; Huffman and Henson, 1990) and human (Guinan, 2006). An efferent pathway from the olivocochlear bundle (OCB) in the brainstem [in particular from the medial olivocochlear (MOC) bundle] reduces the cochlear gain applied over time to the basilar membrane (BM) response to sound (electrical stimulation of the OCB in guinea-pigs) (Murugasu and Russell, 1996). Depending on the species, the total number of OCB neurons innervating a given cochlea differ (Warr, 1992; Sánchez-González et al., 2003). The proportions of lateral olivocochlear (LOC) and MOC neurons are ∼65% (LOC) and 35% (MOC) in both cats and mice (Campbell and Henson, 1988; Warr et al., 2002) and 70% (LOC) and 30% (MOC) in humans (Arnesen, 1984). In humans, this MOC feedback is suggested to be involved in improving speech perception in noisy environments (Clarke et al., 2012) by reducing the effect of noise masking (Kawase et al., 1993). A schematic of the MOC efferent feedback to the right cochlea is shown in Figure 1. Human otoacoustic emission (OAE) studies indicate that the MOC response is sluggish; with an onset delay of ∼25 ms and rise and decay time constants of ∼280 and 160 ms, respectively (James et al., 2002; Backus and Guinan, 2006). Because OAEs are easily diminished by a hearing impairment, they cannot be used to infer response characteristics of the efferent effect in the presence of a mild hearing loss (Bhatia et al., 2013). An advantage of psychoacoustical methods is that they can be used to infer characteristics of the efferent effect in both normal and mildly impaired hearing (Strickland and Krishnan, 2005). Psychoacoustical methods often use a procedure called forward masking, in which detection thresholds are measured for a short-duration signal presented close to the offset of a masker that is preceded by another sound (precursor) of a duration and intensity sufficient to elicit efferent activation (Strickland, 2001, 2004).
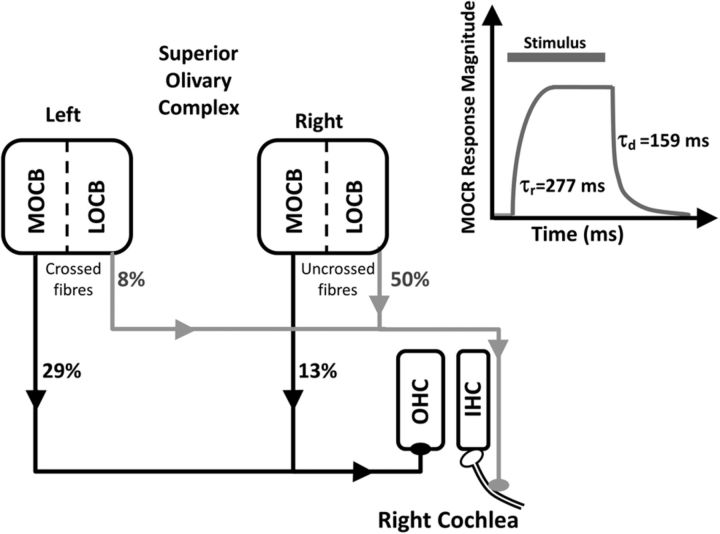
Figure 1.
Origin and distribution of efferent fibers of the right and left OCB in the superior olivary complex, to the right cochlea. Percentages (cat data) (Warr, 1978) indicate the proportion of crossed and uncrossed fibers projecting from each medial OCB (MOCB) and lateral OCB (LOCB) to inner hair cells (IHCs) and outer hair cells (OHCs) of the right cochlea. Because this schematic represents only innervation of the right cochlea, only the crossed fibers from the left OCB and uncrossed fibers from the right OCB are shown. MOCB efferent fibers predominantly terminate at the base of the OHCs, whereas LOCB efferent fibers predominantly project to the dendritic processes of the Type I spiral ganglion auditory neurons that innervate IHCs (Spangler and Warr, 1991). Top right, Medial olivocochlear response (MOCR) magnitude as a function of time after stimulus onset. Typical MOCR rise and decay time constants (human otoacoustic emission data) (Backus and Guinan, 2006) are also shown (τr and τd, respectively).
Physiological studies [e.g., cat (Guinan and Stankovic, 1996) and guinea-pig (Murugasu and Russell, 1996)] and psychoacoustical studies with humans (e.g., Strickland, 2008) show that the efferent effect is level dependent, suggesting an interaction between increase and decay of the efferent effect and eliciting sound levels (Bacon and Smith, 1991). It is not clear how such a temporal- and level-dependent efferent interaction affects cochlear gain and compression.
The present study investigates the effects of the temporal- and level-dependent human efferent effect on cochlear gain and compression using the psychoacoustical fixed-duration masking curve (FDMC) method (Yasin et al., 2013a,b), which avoids confounds of previous psychoacoustical methods used to measure the efferent effect. The main aims of the current study were as follows: (1) to characterize changes in cochlear gain and compression associated with increasing efferent effect mediated by increasing precursor level and (2) to characterize decay of the efferent effect, measured by increasing the silent temporal interval between precursor and masker.
Materials and Methods
Listeners.
Six normal-hearing listeners, L1-L6 (4 males, 2 females; age, 21–44 years), with absolute thresholds >20 dB HL for sound frequencies between 0.25 and 8 kHz (American National Standards Institute, 1996), took part in this study. Listeners L1-L5 undertook 4–10 hours of training on subsets of the stimuli used for the main experiment. Listeners L1-L3 were experienced listeners in FDMC tasks and required less training than L4-L6. Listener L6 found the task difficult and needed an additional 12 h of training, including higher signal sensation levels. Apart from L1 (author V.D.), L2-L6 were paid £6 per hour of participation.
Stimuli.
Cochlear gain and compression were measured using the FDMC method (Yasin et al., 2013a,b). The signal was a 4 kHz sinusoid, and the masker was either an off-frequency (1.8 kHz) or on-frequency (4 kHz) sinusoidal masker. Both signal and masker always began in sine phase. The shortest signal used had a total duration of 6 ms (3 ms onset and offset ramps, 0 ms steady state). Absolute thresholds for this signal, presented to the left ear, were 18.2, 11.6, 18.5, 10.8, 15.1, and 14.1 dB SPL for listeners L1-L6, respectively. The off- or on-frequency masker-plus-signal total duration was always 25 ms, and the masker-signal (M-S) interval was fixed at 0 ms (for a schematic of the stimuli, see Fig. 2). The combined duration of the FDMC masker-plus-signal stimulus (25 ms) is within the efferent onset delay. The effect of efferent activation can then be separately studied by presenting a precursor sound of different levels and silent temporal intervals before the onset of the combined FDMC masker-signal stimulus. The masker and signal used raised-cosine onset and offset ramps of equal duration, where ramp durations were 2 ms for the masker and 3 ms for the signal. Across trial blocks for on-frequency maskers, signal steady-state portions varied from 0 to 15 ms in 2.5 ms increments, whereas complementary masker steady-state portions varied from 15 to 0 ms, providing seven possible signal durations. Across trial blocks for off-frequency maskers, signal steady-state portions varied from 0 to 10 ms in 2.5 ms increments, whereas complementary masker steady-state portions varied from 15 to 5 ms, providing five possible signal durations because practice trials showed that most listeners' masker thresholds exceeded 100 dB SPL if the two longest signal durations were used. Under some precursor conditions for some listeners, only the shortest four (or, rarely, the shortest three) signal durations were used if practice trials showed off-frequency masker thresholds >100 dB SPL. The precursor, when present, was a 500 ms (10 ms onset and offset ramps, 480 ms steady state), 1-kHz-wide noiseband centered on 4 kHz. Signal level was set separately per listener and per precursor level and P-M interval. Because the precursor acted as a forward masker on the signal, precursor-only masked thresholds were first measured for the shortest (6 ms) signal in the absence of the tonal masker, using precursor and signal timings as if the masker was present. The signal level was then set at 10 dB (listeners L1-L5) or 15 dB (listener L6) above this level to measure the FDMCs. As a check, precursor-only masked thresholds were also measured for the longest (21 ms) signal at a 0 ms P-M interval for each precursor level (including no precursor). Across listeners and precursor levels, signal level at threshold for the longest signal was consistently less than or equal to that for the shortest signal, so setting FDMC signal levels based upon the shortest signal duration was deemed appropriate. For the shortest and longest 4 kHz signal durations, the equivalent rectangular bandwidths were 250 and 53 Hz, respectively. The complementary equivalent rectangular bandwidths for the longest and shortest 4 kHz masker durations were 57 and 375 Hz, respectively. In all cases, both signal and masker spectral splatter fell within the auditory filter centered at 4 kHz (equivalent rectangular bandwidth of 457 Hz, using the equation in Moore, 1995).
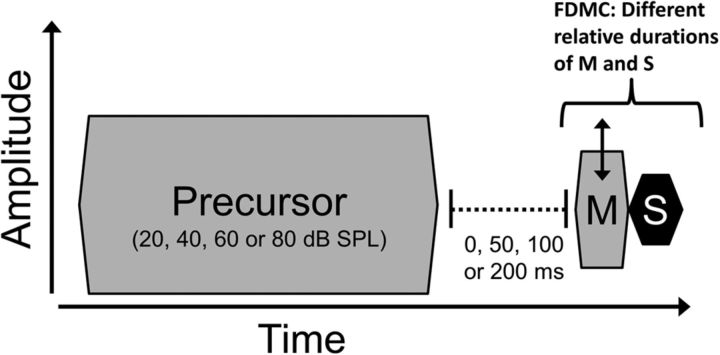
Figure 2.
Schematic of the stimuli used. Masker (M) level at threshold for the signal (S) was measured using the FDMC method. Off-frequency or on-frequency masker-plus-signal total duration was always 25 ms, and the masker-signal temporal interval was fixed at 0 ms. Signal steady-state portions varied in complement to masker steady-state durations. A precursor was presented before the FDMC combined masker-signal stimulus. The precursor was presented before the masker at levels of 20, 40, 60, and 80 dB SPL, with silent temporal intervals between precursor offset and masker onset of 0, 50, 100, and 200 ms. Double-headed arrow indicates the masker stimulus that was adaptively varied in each stimulus trial.
All stimuli were digitally generated and gated on a PC using custom software written in MATLAB R2010b (MathWorks 2010) and output via an E-MU 0202 (24-bit, 96 kHz) USB 2.0 soundcard external to the PC. Antialiasing was provided by built-in filters. Stimuli were presented via the left channel of a pair of Sennheiser HD 600 headphones. The headphone input came directly from the analog output of the soundcard. The headphones were calibrated with respect to their acoustic output at 1 kHz. The calibration was performed using a Brüel&Kjaer (B&K) measuring amplifier (Type 2636), a B&K artificial ear (Type 4153) with its flat-plate coupler, and a B&K microphone (Type 4134). Responses at 2, 4, and 6 kHz were within ±1.5 dB of the response at 1 kHz. Listeners were tested in an IAC triple-walled sound-attenuating booth while seated in front of a computer screen and keyboard.
Conditions.
For all listeners, FDMCs were obtained by measuring the masker level at threshold for seven signal durations for the on-frequency masker and typically five (but occasionally four or three) signal durations for the off-frequency masker. FDMCs were also obtained in the presence of a precursor. When present, the precursor was presented before the combined masker-signal stimulus at precursor levels of 20, 40, 60, and 80 dB SPL. For each precursor level, FDMCs were obtained for different temporal delays of the precursor with respect to the masker, at precursor-to-masker (P-M) silent intervals (precursor end to masker start zero-to-zero window points) of 0, 50, 100, and 200 ms. There were a total of 16 possible combinations of precursor level and P-M interval and an additional condition with no precursor using the same within-trial timing as for a P-M interval of 0 ms.
Procedure.
A two-interval, two-alternative forced choice adaptive tracking procedure was implemented. The interstimulus interval between the two observation intervals of each trial was 500 ms. The second observation interval was followed by a decision interval of variable length determined by the listener (typically <2 s). A computer-simulated response box appeared on the screen providing lights that coincided with each observation interval and a feedback interval of 500 ms duration at the end of each trial. At the end of the feedback interval, a 400 ms duration silent interval occurred before the start of the next trial. The signal was randomly presented in one of the two observation intervals, and the listener's task was to indicate which interval contained the signal by pressing a button on the keyboard. Trial-by-trial feedback was provided. For the preliminary precursor-only masked thresholds (with tonal masker absent), the signal level began ∼30–40 dB above threshold and was varied adaptively (using a 2-down 1-up rule) to obtain the signal level required to achieve 70.7% correct (Levitt, 1971). For the FDMC thresholds (with signal level fixed and tonal masker present), the masker level began at 0 dB SPL for on-frequency maskers and 40 dB SPL for off-frequency maskers, and was varied adaptively (using a 2-up 1-down rule) to obtain the masker level required to achieve 70.7% correct (Levitt, 1971). For each block of trials, the initial adaptive track step size was 5 dB, which reduced to 2 dB after four reversals. Threshold was obtained by averaging stimulus levels for the next eight reversals, but the block was rerun if the SD was >6 dB, or the nominal masker level reached ≥108 dB SPL (due to soundcard output clipping). Some settings where clipping occurred repeatedly were not rerun. Occasionally, very high level thresholds (∼102–105 dB SPL) were still obtained for a block of trials when one or, at most, two reversals occurred at (nominally) ≥108 dB, by substituting a value of 108 dB SPL for those reversals.
Listeners ran in 2 h sessions, taking breaks as needed and typically completing runs for two precursor conditions within a session. Only one precursor condition was run at a time, consisting of 10–12 adaptive tracking blocks of 3–4 min duration each. Signal duration and masker frequency were randomized across blocks per condition. Condition order was randomized within and across sessions. Reported threshold values are the mean of either two (for listeners L1, L3, and L6) or three (for listeners L2, L4, and L5) separate threshold estimates, but in cases when only three signal durations could be used for off-frequency FDMCs because of the high threshold values (mostly for listener L4), reported threshold values are the mean of four separate threshold estimates for each of the three signal durations.
Results
Deriving inferred BM response functions
The main drawback of current psychoacoustical methods, such as the temporal masking curve and growth of masking methods for deriving cochlear response functions is that aspects of the stimulus design may, in some circumstances, compromise estimates of cochlear gain and compression. Particularly with the growth of masking method, there can be a potential confound with masking by a precursor sound (e.g., Strickland, 2008; Jennings et al., 2009). The main advantages of the FDMC method used in the current study over temporal masking curve and growth of masking methods (Yasin et al., 2013a,b) are as follows: (1) estimates of gain and compression are less likely to be confounded by efferent activation; (2) the masker-signal silent interval is maintained at 0 ms, reducing the possibility of an appreciable difference in internal decay of masking between off- and on-frequency maskers (Wojtczak and Oxenham, 2010); (3) the signal is maintained at a low sensation level, minimizing spread of excitation of the response to the signal along the cochlea, thereby improving reliability of the gain and compression estimate (Oxenham and Plack, 1997; Nelson et al., 2001); and (4) unlike the temporal masking curve method, because the masker-signal interval is maintained at 0 ms, the FDMC method can be used to estimate effects of efferent activation when used in conjunction with precursor sounds presented at variable silent intervals before the masker-signal stimulus.
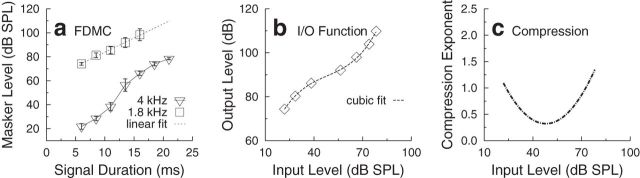
Inferred BM response functions were derived from the FDMC data using the procedure described by Yasin et al. (2013a,b). In summary, the off-frequency data are first fitted with a linear regression fit to the data. Linear regression provided good fits to the slopes of off-frequency FDMCs with mean slopes (across listeners and all experimental conditions) of 2.60 dB/ms (average R2 of 0.94). The response to the off-frequency masker is assumed to be linear at the signal place on the BM. Hence, the off-frequency masker level at threshold is an estimate of the BM excitation at the signal place required to mask the signal (give or take an additive constant in dB). For the same signal duration, the on-frequency masker level at threshold is an estimate of the input level required to produce that same BM excitation (taking into account any compression). Hence, a plot of off-frequency masker level (BM excitation) versus on-frequency masker level (input level required to produce that BM excitation) defines the inferred BM response function (Yasin et al., 2013a). For each signal duration, the values from the linear fit to the off-frequency (output) masker-level data were paired with the on-frequency (input) masker-level data values. The paired values were then fitted with a third-order polynomial. The first derivative (slope of the inferred BM response function) provides an estimate of the compression exponent. Figure 3 presents the steps in converting the mean FDMC data for the no-precursor condition (Figure 3a) to an inferred BM response function (or inferred BM input–output function; Figure 3b) and estimation of the compression exponent as a function of the 4 kHz input masker level (Figure 3c).
Figure 3.
Example of the stages involved in converting FDMC data to inferred BM response functions and derivation of compression exponents. In this example, mean data (across listeners) for the no-precursor condition are shown. a, FDMC for on-frequency masker levels (inverted open triangles) and off-frequency masker levels (open squares) at threshold for the signal, as a function of signal duration. Dotted line indicates the linear fit to the off-frequency masker data. Error bars indicate ±1 SE. b, Inferred BM response function [BM input/output (I/O) function] derived from the FDMC shown in a, by plotting the values from the linear fit to the off-frequency masker level data (output masker levels) versus the on-frequency masker levels (input masker levels), paired by signal duration. Dashed line indicates the third-order polynomial fit to the BM response function. c, Estimated compression exponents as a function of input masker level, obtained by differentiating the third-order polynomial fit to the data shown in b.
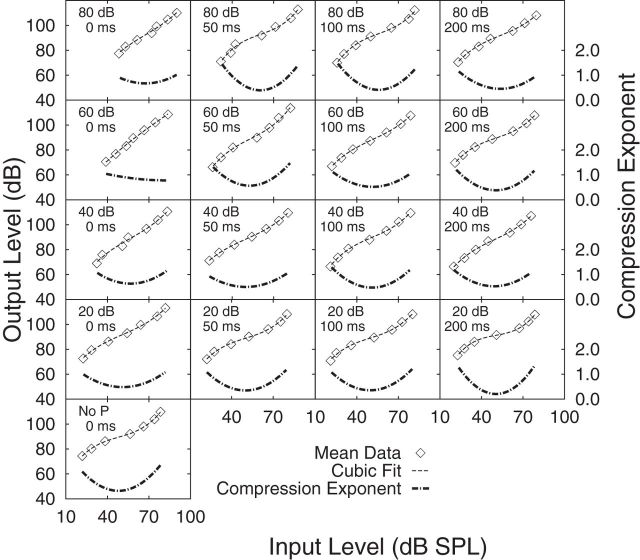
Figure 4 shows the mean (across six listeners) inferred BM response functions (left-hand y-axis) for the 16 conditions of increasing precursor level (presented from bottom to top panels) and increasing P-M interval (presented from left to right panels), plus the no-precursor condition (single bottom panel). The mean data points are represented by open unconnected diamond symbols, which are overlaid by a faint dashed line representing the third-order polynomial fit to the mean data. The mean SE per condition ranged from 1.7 to 4.2 (across the 16 precursor level and precursor-masker conditions) for the on-frequency masked thresholds and 2.8 to 3.9 for the off-frequency masked thresholds. Polynomial coefficients for each fit to the mean data were obtained by minimizing the sum-of-squared-error (dB) of the actual versus predicted values. Model fitting was constrained to allow only non-negative response function slope fits to the data. Fits resulting in slope values >1.0 (expansive) were permitted by the fitting procedure because constraining the fitting to permit slope values only between 0 and 1, inclusive, provided nonmeaningful fits to the data for some of the listeners.
Figure 4.
Mean inferred BM response functions are presented. Unconnected open diamonds represent mean data points overlaid by a third-order polynomial fit to the mean (faint dashed line; left-hand y-axis). The compression exponent is the first derivative of the slope of the BM response function (thick dashed line; right-hand y-axis). Inferred BM response functions and compression exponents are presented for each of the 16 combinations of precursor level and precursor-masker silent temporal intervals. Increasing precursor level is shown in panels from bottom to top. Increasing precursor-masker silent temporal interval is shown in panels from left to right. The single panel at the bottom represents the mean data for the no-precursor (No P) condition. The mean SE per condition ranged from 1.7 to 4.2 (across the 16 precursor level and precursor-masker conditions) for the on-frequency masked thresholds and 2.8 to 3.9 for the off-frequency masked thresholds.
For most listeners, the inferred BM response functions show typical nonlinear characteristics: that is, a steep portion for low-level inputs up to ∼40 to 50 dB SPL, and a shallow portion for mid-level inputs of ∼50 to 70 dB SPL. In comparison with the no-precursor condition, as precursor level increases (e.g., when P-M interval is 0 ms), the inferred BM response function is shifted rightwards to higher input masker levels (representing a decrease in gain). Similarly, in comparison with the no-precursor condition, as P-M interval increases (e.g., a 60-dB SPL precursor), the inferred BM response function is shifted leftwards to lower input masker levels (representing an increase in gain). The maximum value of BM gain (Gainmax) was estimated for the shortest signal duration as the difference between off-frequency and on-frequency masker values, where the former was taken from the linear fit to the off-frequency data.
For any given input masker level, the slope of the cubic fit was used as an estimate of compression. The slope provides an estimate of the compression exponent, which is inversely related to the magnitude of BM compression. Two estimates of compression exponent were of interest per listener: an average value of compression exponent associated with input masker levels between 50 and 70 dB SPL (CE50–70) and a minimum value of compression exponent (CEmin). An input masker range of 50–70 dB SPL was chosen for estimates of CE50–70 as this range of masker levels defined the shallowest part of the inferred BM response functions (slopes are less than unity) common to all conditions and listeners. Estimates of BM compression exponent as a function of the input masker level were obtained by differentiating the third-order polynomial fits to the inferred BM response functions (as presented in Fig. 3). The compression exponents as a function of input level for each experimental condition are displayed in Figure 4 (right-hand y-axis). In general, for all conditions, the minimum value of compression exponent was associated with an input masker range of between 50 and 70 dB SPL.
Table 1 presents the mean values of Gainmax, CEmin, and CE50–70, for each experimental condition. Also shown is the input masker level associated with CEmin (ILCE). In general, as precursor level increased up to 60 dB SPL (for a 0 ms P-M interval), CEmin and CE50–70 increased, as Gainmax decreased. As P-M interval increased, values of CEmin, CE50–70, and Gainmax approached those found in the no-precursor condition. In general, ILCE tended to decrease as P-M interval increased (for a given precursor level) and increased as precursor level increased.
Table 1.
Estimates of gain and compression (averaged across listeners) are presented, for the no-precursor condition (No P), and for the 16 conditions of precursor level (P level) and precursor-masker silent interval (P-M interval). Presented in columns from left to right are values for maximum gain (Gainmax), the minimum value of the compression exponent (CEmin) together with the value of the input masker level associated with the minimum compression exponent (ILCE), and the averaged compression exponent across an input masker level range of 50–70 dB SPL (CE50–70). Gainmax (dB) and ILCE (dB SPL) values are shown to one decimal place. CEmin and CE50–70 values are shown to two decimal places
| P level (dB SPL) | P-M interval (ms) | GainMax | CEMin; ILCE | CE50–70 |
|---|---|---|---|---|
| No P | No P | 52.3 | 0.21; 46.4 | 0.50 |
| 20 | 0 | 49.8 | 0.21; 41.1 | 0.45 |
| 50 | 50.2 | 0.21; 48.3 | 0.45 | |
| 100 | 49.5 | 0.31; 39.7 | 0.55 | |
| 200 | 52.5 | 0.17; 51.7 | 0.39 | |
| 40 | 0 | 36.3 | 0.46; 54.9 | 0.56 |
| 50 | 47.2 | 0.39; 44.9 | 0.58 | |
| 100 | 45.0 | 0.33; 49.6 | 0.58 | |
| 200 | 46.4 | 0.36; 49.5 | 0.58 | |
| 60 | 0 | 29.4 | 0.61; 60.8 | 0.78 |
| 50 | 38.7 | 0.42; 66.8 | 0.56 | |
| 100 | 44.4 | 0.27; 52.8 | 0.47 | |
| 200 | 48.3 | 0.26; 49.5 | 0.48 | |
| 80 | 0 | 27.1 | 0.26; 71.4 | 0.85 |
| 50 | 39.1 | 0.33; 59.5 | 0.40 | |
| 100 | 44.3 | 0.25; 56.1 | 0.36 | |
| 200 | 47.4 | 0.32; 53.5 | 0.45 |
Effect of efferent activation on gain and compression
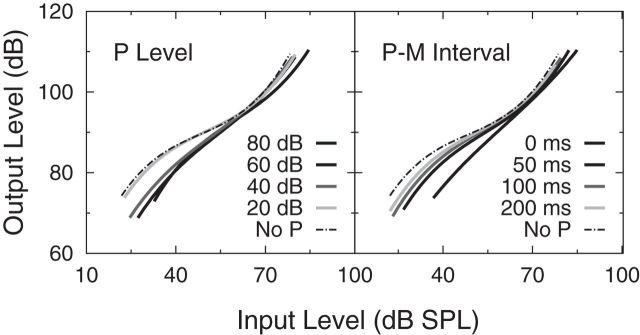
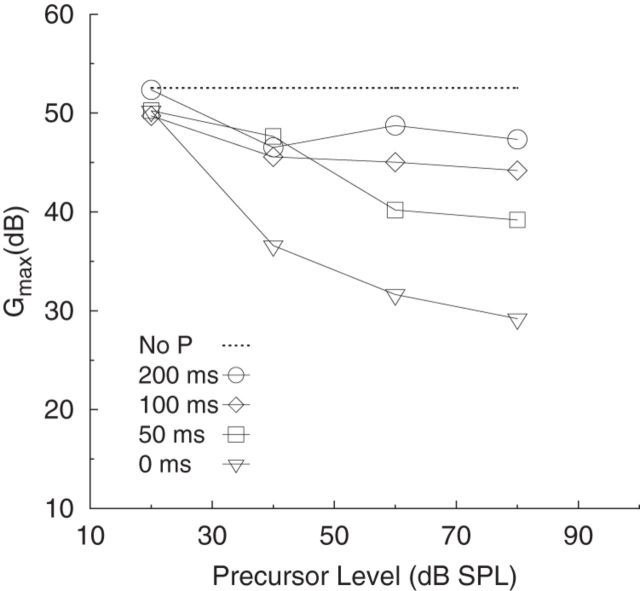
Summary plots of the effects of efferent activation on BM gain and compression are shown in Figure 5. Figure 5 presents the mean data across listeners for the third-order polynomial fits to the mean inferred BM response functions as a function of precursor level (averaged across P-M interval), in the left panel, and as a function of P-M interval (averaged across precursor level), in the right panel. Per panel, increasing precursor level or decreasing P-M interval is represented by increasing depth of grayscale. The polynomial fit to the mean inferred BM response function for the no-precursor condition is represented by the dashed line. As precursor level increased, the slope of the inferred BM response function tended to increase, whereas Gainmax decreased (rightward shift of the response function). As P-M interval increased, the slope of the inferred BM response function decreased, whereas Gainmax increased (leftward shift of the response function). The mean decrease in Gainmax as a function of precursor level for all P-M intervals, including the no precursor condition, is also shown in Figure 6. The decrease in gain per 10 dB increase in precursor level (e.g., 40–50 dB SPL) is dependent on the P-M interval, such that gain decreases by ∼3.3 dB per 10 dB increase in precursor level at a P-M interval of 0 ms and gain decreases by ∼1.3 dB per 10 dB increase in precursor level for a P-M interval of 100 ms.
Figure 5.
Left, Mean inferred BM response functions (mean data across listeners) for precursor levels 20–80 dB SPL, averaged across P-M interval. Right, Mean inferred BM response functions for P-M intervals 0–200 ms, averaged across precursor level. Within each panel, lines of increasing darkness represent increasing precursor level (left) or decreasing P-M interval (right). The dashed line in each panel indicates the mean inferred BM response function for the no-precursor (No P) condition.
Figure 6.
Maximum gain (Gmax) plotted as a function of precursor level for each P-M interval (open symbols) and for the no-precursor (No P) condition (dashed line). The mean data across listeners are shown.
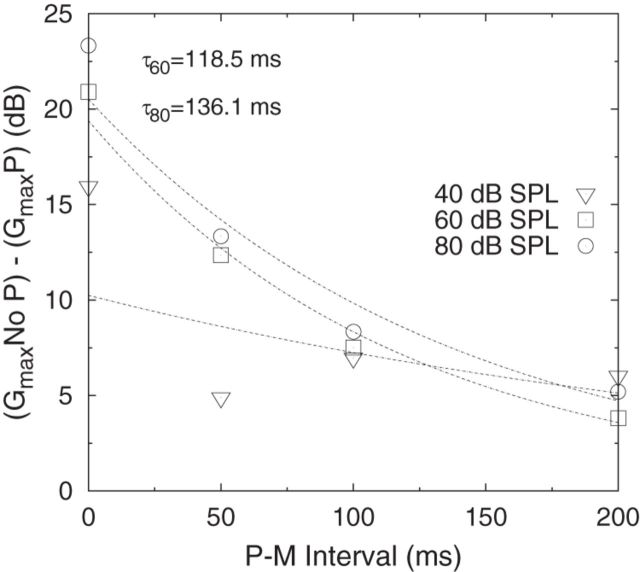
If the change in maximum gain (Gmax in the absence of a precursor − Gmax in the presence of a precursor) is plotted as a function of P-M interval (across listeners), and exponential decay functions are fitted to the data (Fig. 7), the time constants associated with decay of the efferent effect can be estimated. R2 values for the fits to the 60 and 80 dB SPL data were 0.99 and 0.95, respectively. An accurate estimate of the decay constant associated with the 40 dB precursor could not be obtained because of a poor fit to the data (R2 = 0.33). For clarity, the differences in gain for the 20 dB SPL precursor condition are not shown because the difference in gain was close to zero across all P-M intervals. The estimated decay time constants for the present study are 118.5 ms for the 60 dB SPL precursor and 136.1 ms for the 80 dB SPL precursor, indicating that the recovery of gain occurs at a similar rate with presentation of 60 or 80 dB SPL precursors.
Figure 7.
Difference in maximum gain (Gmax in the absence of a precursor − Gmax in the presence of a precursor) plotted as a function of P-M interval. The mean data across listeners is shown. For clarity, only the mean data for the 40 (open triangle), 60 (open square), and 80 (open circle) dB SPL precursor conditions are shown because the difference in maximum gain estimated for the 20 dB SPL precursor was close to zero for all P-M intervals. Exponential functions are fitted to the data, with good fits to the 60 and 80 dB SPL data (R2 = 0.99 and R2 = 0.95, respectively) and poor fit to the 40 dB SPL data (R2 = 0.33). The estimated time constants associated with the decay of the efferent effect for the 60 and 80 dB SPL conditions are given by τ(60) = 116.5 ms and τ(80) = 136.1 ms, respectively.
The data were normally distributed; and before conducting the ANOVAs, Levene's test for equality of variances was performed. In all cases, the Levene's test was not significant (p > 0.05), indicating that the groups were homogeneous. A two-way ANOVA was conducted on the Gainmax estimates with main factors of precursor level (20, 40, 60, and 80 ms) and P-M interval (0, 50, 100, and 200 ms). Results showed a significant effect of precursor level (F(3,15) = 18.25, p < 0.001, with effect size, η2 = 0.79), P-M interval (F(3,15) = 10.86, p < 0.001, with effect size, η2 = 0.69), and interaction between precursor level and P-M interval (F(9,45) = 5.58, p < 0.001, with effect size, η2 = 0.53).
Post hoc t tests (Bonferroni corrected) showed that the effect of P-M interval on Gainmax increases with precursor level (for levels between 40 and 80 dB SPL). For the 40, 60, and 80 dB SPL precursors, there was a significant increase in Gainmax when P-M interval was increased from 0 to 50, 100, and 200 ms (p < 0.05, one-tailed).
A two-way ANOVA was conducted on the values for CEmin with main factors of precursor level and P-M interval. There was a significant main effect of precursor level (F(3,15) = 6.26, p < 0.01, with effect size, η2 = 0.56) and a significant interaction between precursor level and P-M interval (F(9,45) = 3.21, p < 0.01, with effect size, η2 = 0.39). There was no significant main effect of P-M interval. There was a significant recovery of BM compression (decrease in CEmin) for a relatively high precursor level of 60 dB SPL, as P-M interval increased from 50 to 200 ms (mean difference = 0.19, SD = 0.17, t(5) = 2.63, p < 0.05, two-tailed).
A two-way ANOVA was conducted on the values of ILCE with main factors of precursor level and P-M interval. There was a significant effect of precursor level (F(3,15) = 22.72, p < 0.001, with effect size, η2 = 0.82), P-M interval (F(3,15) = 5.72, p < 0.01, with effect size, η2 = 0.53), and a significant interaction between precursor level and P-M interval (F(9,45) = 2.80, p < 0.05, with effect size, η2 = 0.36).
Post hoc paired t tests (Bonferroni corrected) revealed that there was a greater reduction in ILCE with increasing P-M interval, for relatively high-level precursors compared with low-level precursors. For an 80 dB SPL precursor, there was a significant decrease in ILCE as P-M interval increased from 0 to 50, 100, and 200 ms and 50 to 200 ms (p < 0.05, two-tailed).
A two-way ANOVA was conducted on the values of CE50–70 with main factors of precursor level and P-M interval. There was a significant interaction between precursor level and P-M interval (F(9,45) = 3.23, p < 0.01, with effect size, η2 = 0.39). There were no significant main effects. Post hoc paired t tests (Bonferroni corrected) revealed that there was a significant linearization of the inferred BM response function in the presence of a high-level 60 dB SPL precursor presented at the shortest P-M interval of 0 ms or a 40 dB SPL precursor presented at increasing P-M intervals of 50 and 200 ms (p < 0.05, two-tailed).
Comparing the effect of precursor addition at the P-M interval of 0 ms, to the absence of a precursor, there was found to be no significant difference in Gainmax, CEmin, and ILCE with the addition of a 20 dB SPL precursor. However, there was a significant decrease in Gainmax, with the addition of a 40, 60, and 80 dB SPL precursor (p < 0.05, two-tailed), a significant increase in CEmin (compared with the no-precursor condition) in the presence of a 40 and 60 dB SPL precursor (p < 0.05, two-tailed), and a significant increase in ILCE (compared with the no-precursor condition) only with the addition of an 80 dB SPL precursor (p < 0.01, two-tailed).
Discussion
There is increased interest in developing accurate psychoacoustical techniques to measure the efferent effect in both normal and impaired-hearing populations. The present results, using the psychoacoustical FDMC method, show that efferent activation reduces maximum cochlear gain by ∼3.3 dB per 10 dB increase in precursor level (for a P-M interval of 0 ms). This is close to the lower end of the estimated range for efferent-mediated gain reduction reported in the literature: 2.5–9.0 dB reduction in maximum gain per 10 dB level increase of an ipsilateral 160 ms precursor (Krull and Strickland, 2008) and 4–6 dB reduction in maximum gain per 10 dB increase in level of an ipsilateral 205 ms notched-noise precursor (Strickland, 2008). These current estimates of maximum gain reduction are slightly lower than previously reported, perhaps because of possible forward masking by the precursor itself in the previous studies (Strickland, 2008).
There are only a few physiological studies with nonhuman mammals that have measured gain reduction inferred from electrical stimulation of the efferent system. Direct comparisons between gain and compression estimates obtained in the current study and physiological measures of the efferent effect are problematic for the main reason that the majority of studies have not measured the BM or cochlear response as a function of electrical (either ipsilateral or contralateral) stimulation of the OCB but have measured changes in neural firing patterns (e.g., Guinan and Gifford, 1988; Guinan and Stankovic, 1996) or inferred reduced activity from lesion studies (e.g., Brown et al., 2003). Only a few studies have directly measured changes in BM response characteristics with efferent activation (Russell and Murugasu, 1997; e.g., Dolan et al., 1997), the results of which may be pertinent to the current study. Dolan et al. (1997) studied changes in BM response with electrical stimulation of the OCB in guinea pigs and showed that the BM response function shifts to higher sound levels with efferent activation with a gain reduction of ∼10 dB (Dolan et al., 1997) (Figs. 1, 2, and 3). A similar rightward shift of the inferred BM response function with efferent activation is observed in the current study.
In the current study, maximum gain increased as the P-M silent interval increased, indicating a recovery from the efferent effect at a P-M interval of 200 ms, corresponding to the estimated MOC response offset and decay (Backus and Guinan, 2006) and decrease in temporal effect with a 100 ms precursor (Roverud and Strickland, 2010). The recovery from the efferent effect for a 60-dB SPL precursor resulted in a gain increase of ∼8 dB per 100 ms increase in P-M interval. The present findings indicate that gain decrease per 10 dB increase in precursor level is dependent on the P-M interval, such that gain decreases by ∼3.3 dB and 1.3 dB (per 10 dB increase in precursor level) at P-M intervals of 0 and 100 ms, respectively. These estimates of gain decrease with increasing precursor level are within the range estimated from psychoacoustical studies, at a range of P-M levels (Carlyon, 1987, 1989; McFadden, 1989; Schmidt and Zwicker, 1991; Overson et al., 1996; Roverud and Strickland, 2010).
Estimated decay time constants associated with gain recovery in the present study were 118.5 ms and 136.1 ms for the 60 and 80 dB SPL precursors, respectively, indicating that gain recovery occurs at a similar rate with 60 or 80 dB SPL precursors. These time constants are within the range of decay time constants reported with ipsilateral acoustic stimulation of the efferent system using stimulus-frequency OAEs in humans (159 ± 54 ms) (Backus and Guinan, 2006) and distortion-product OAEs in cats (∼100 ms) (Liberman et al., 1996). The present study shows that, with efferent activation elicited by relatively higher-level precursors (60 dB SPL), not only is maximum compression reduced, but the inferred BM response function is linearized across input sound levels of 50–70 dB SPL, resulting in an increase in mean CE50–70 (decrease in mean compression ratio) from 0.50 (no precursor) to 0.78 (with an 80-dB SPL precursor). Few physiological studies with nonhuman mammals have suggested linearization of the BM response function. Russell and Murugasu (1997) (Fig. 3d) showed that, with electrical stimulation of the guinea-pig MOC, there was a shift of the BM vibrational response (as a function of sound level) to higher sound levels (∼20 dB reduction in maximum gain) and an associated linearization of the BM response across an input sound-level range of 50–75 dB SPL, which corresponds to the input-masker level range showing the largest effect of linearization in the current study.
The estimate of mean CEmin (across listeners) in the absence of a precursor was 0.21, which is within the range reported by previous psychoacoustical studies (e.g., Nelson et al., 2001; Lopez-Poveda et al., 2003; Plack and Drga, 2003; Yasin and Plack, 2003; Rosengard et al., 2005; Williams and Bacon, 2005). The estimate of CEmin (across listeners) with increasing precursor did not show a significant change in the present study, although other psychoacoustical studies have reported an increase in mean CEmin with increasing precursor level of 0.41–0.71 (Krull and Strickland, 2008) and 0.33–0.63 (averaged results across three listeners) (Strickland, 2008).
Another efferent pathway from the superior olivary complex that could affect responses at the cochlear level is the middle-ear muscle reflex (MEMR). A high-level sound stimulus can activate the MEMR, resulting in contraction of the stapedius muscles of the ossicular chain (Møller, 2012). This contraction decreases the transmission of ossicular vibration to the cochlea (by increasing middle-ear impedance). It is possible that high-level precursors used in the present study could have activated the MEMR and affected the results for estimated gain and compression, although this seems unlikely for two main reasons. One reason is that, although the MEMR can be elicited by sounds of various frequencies, the increased impedance affects mostly sound transmission for frequencies <2 kHz (Møller, 1965; Feeney et al., 2004). So it is unlikely that a high-level 4 kHz precursor could affect the response of the subsequently presented on-frequency masker and signal. The second reason is that, in the present study, the MEMR is also unlikely to have affected the response to the 1.8 kHz masker because an ipsilateral 4 kHz activator (or elicitor) has to reach a level of ∼90 dB SPL to activate the MEMR and have an effect on sound frequencies between 0.38 and 2.8 kHz (Keefe et al., 2010); in the present study, the ipsilateral 4 kHz precursor level had a maximum level of 80 dB SPL.
It is unlikely that the present results may have been influenced by activation of the LOC, which affects neural output after any BM differential frequency response to on- and off-frequency maskers. Overall, little is known about the precise function and role of the LOC, and its associated neurotransmitter release is still being debated (Le Prell et al., 2014). LOC neurons are small with unmyelinated axons and have high thresholds, which makes them difficult to stimulate separately from MOC axons (Guinan, 1996; Sterenborg et al., 2010). Continued physiological research into auditory lateral efferent projections, and their function is required to fully answer how this system modulates auditory sensitivity.
Any physiological interpretation of data based on psychoacoustical measurements necessarily involves a series of assumptions. The inferred BM input–output functions (used for gain estimation) are based on the physiological finding of a differential response at a given BM location for sounds with frequencies about an octave apart (on- and off-frequency maskers) (Yates, 1990; Ruggero et al., 1992, 1997). It is assumed that any nonlinearity subsequent to the BM is not frequency dependent (affecting on-and off-frequency maskers equally) and should not affect our findings. Recent physiological in vivo techniques, such as those used by Subhash et al. (2011) and Choudhury et al. (2011) may, in the future, shed further light on the issue of any frequency-dependent nonlinearities subsequent to the BM.
Overall, the current results show that efferent activation affects estimates of both CEmin and CE50–70. In particular, the estimate of CE50–70 was found to be significantly increased in the presence of 40 and 60 dB SPL precursors and may provide a more representative estimate of inferred BM response linearization. The present results indicate that the input masker level associated with CEmin (ILCE) may also change in the presence of efferent activation. This may be the case if the lower portion of the BM response function extends to higher input masker levels, such that CEmin remains relatively unchanged, but CE50–70 increases because of linearization of the BM function at lower input masker levels. Bhagat and Carter (2010) reported such an extension of the linear portion of the BM response function derived using distortion product OAEs in the presence of efferent activation by a contralateral precursor. Overall, the current psychoacoustical results support the idea that MOC efferents may decrease BM gain with partial linearization to extend the neural response to the signal above that of moderate noise (Geisler, 1974; Winslow and Sachs, 1987; Kawase et al., 1993; Brown et al., 2010; Chintanpalli et al., 2012).
Footnotes
This work was supported by an Engineering & Physical Sciences Research Council (EPSRC) Project Grant EP/H022732/1. We thank the Editor and two anonymous reviewers for their helpful comments.
The authors declare no competing financial interests.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/3.0), which permits unrestricted use, distribution and reproduction in any medium provided that the original work is properly attributed.
References
- American National Standards Institute. ANSI S3.6–1996 specification for audiometers. New York: American National Standards Institute; 1996. [Google Scholar]
- Arnesen AR. Fibre population of the vestibulocochlear anastomosis in humans. Acta Otolaryngol. 1984;98:501–518. doi: 10.3109/00016488409107591. [DOI] [PubMed] [Google Scholar]
- Backus BC, Guinan JJ., Jr Time-course of the human medial olivocochlear reflex. J Acoust Soc Am. 2006;119:2889–2904. doi: 10.1121/1.2169918. [DOI] [PubMed] [Google Scholar]
- Bacon SP, Smith MA. Spectral, intensive, and temporal factors influencing overshoot. Q J Exp Psychol A. 1991;43:373–399. doi: 10.1080/14640749108400978. [DOI] [PubMed] [Google Scholar]
- Bhagat SP, Carter PH. Efferent-induced change in human cochlear compression and its influence on masking of tones. Neurosci Lett. 2010;485:94–97. doi: 10.1016/j.neulet.2010.08.069. [DOI] [PubMed] [Google Scholar]
- Bhatia P, Mintz S, Hecht BF, Deavenport A, Kuo AA. Early identification of young children with hearing loss in federally qualified health centers. J Dev Behav Pediatr. 2013;34:15–21. doi: 10.1097/DBP.0b013e318279899c. [DOI] [PubMed] [Google Scholar]
- Brown GJ, Ferry RT, Meddis R. A computer model of auditory efferent suppression: implications for the recognition of speech in noise. J Acoust Soc Am. 2010;127:943–954. doi: 10.1121/1.3273893. [DOI] [PubMed] [Google Scholar]
- Brown MC, de Venecia RK, Guinan JJ., Jr Responses of medial olivocochlear neurons: specifying the central pathways of the medial olivocochlear reflex. Exp Brain Res. 2003;153:491–498. doi: 10.1007/s00221-003-1679-y. [DOI] [PubMed] [Google Scholar]
- Campbell JP, Henson MM. Olivocochlear neurons in the brainstem of the mouse. Hear Res. 1988;35:271–274. doi: 10.1016/0378-5955(88)90124-4. [DOI] [PubMed] [Google Scholar]
- Carlyon RP. A release from masking by continuous, random, notched noise. J Acoust Soc Am. 1987;81:418–426. doi: 10.1121/1.395117. [DOI] [PubMed] [Google Scholar]
- Carlyon RP. Changes in the masked thresholds of brief tones produced by prior bursts of noise. Hear Res. 1989;41:223–235. doi: 10.1016/0378-5955(89)90014-2. [DOI] [PubMed] [Google Scholar]
- Chintanpalli A, Jennings SG, Heinz MG, Strickland EA. Modeling the anti-masking effects of the olivocochlear reflex in auditory nerve responses to tones in sustained noise. J Assoc Res Otolaryngol. 2012;13:219–235. doi: 10.1007/s10162-011-0310-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choudhury N, Zheg Y, Fridberger A, Chen F, Zha D, Nuttall AL, Wang RK. Imaging vibration of the cochlear partition of an excised guinea pig cochlea using phase-sensitive Fourier domain optical coherence tomography. Proc SPIE 7889, Optical Coherence Tomography and Coherence Domain Optical Methods in Biomedicine XV 788930.2011. [Google Scholar]
- Clark NR, Brown GJ, Jürgens T, Meddis R. A frequency-selective feedback model of auditory efferent suppression and its implications for the recognition of speech in noise. J Acoust Soc Am. 2012;132:1535–1541. doi: 10.1121/1.4742745. [DOI] [PubMed] [Google Scholar]
- Dolan DF, Guo MH, Nuttall AL. Frequency-dependent enhancement of basilar membrane velocity during olivocochlear bundle stimulation. J Acoust Soc Am. 1997;102:3587–3596. doi: 10.1121/1.421008. [DOI] [PubMed] [Google Scholar]
- Feeney MP, Keefe DH, Sanford CA. Wideband reflectance measures of the ipsilateral acoustic stapedius reflex threshold. Ear Hear. 2004;25:421–430. doi: 10.1097/01.aud.0000145110.60657.73. [DOI] [PubMed] [Google Scholar]
- Geisler CD. Hypothesis on the function of the crossed olivocochlear bundle. J Acoust Soc Am. 1974;56:1908–1909. doi: 10.1121/1.1903532. [DOI] [PubMed] [Google Scholar]
- Guinan JJ., Jr . The physiology of olivocochlear efferents. In: Dallos P, Popper AN, Fay RR, editors. The cochlea. New York: Springer; 1996. pp. 435–502. [Google Scholar]
- Guinan JJ., Jr Olivocochlear efferents: anatomy, physiology, function, and the measurement of efferent effects in humans. Ear Hear. 2006;27:589–607. doi: 10.1093/eurheartj/ehi728. [DOI] [PubMed] [Google Scholar]
- Guinan JJ, Jr, Gifford ML. Effects of electrical stimulation of efferent olivocochlear neurons on cat auditory-nerve fibres: I. Rate-level functions. Hear Res. 1988;33:97–113. doi: 10.1016/0378-5955(88)90023-8. [DOI] [PubMed] [Google Scholar]
- Guinan JJ, Jr, Stankovic KM. Medial efferent inhibition produces the largest equivalent attenuations at moderate to high sound levels in cat auditory-nerve fibers. J Acoust Soc Am. 1996;100:1680–1690. doi: 10.1121/1.416066. [DOI] [PubMed] [Google Scholar]
- Huffman RF, Henson OW., Jr The descending auditory pathway and acousticomotor systems: connections with the inferior colliculus. Brain Res Rev. 1990;15:295–323. doi: 10.1016/0165-0173(90)90005-9. [DOI] [PubMed] [Google Scholar]
- James AL, Mount RJ, Harrison RV. Contralateral suppression of DPOAE measured in real time. Clin Otolaryngol. 2002;27:106–112. doi: 10.1046/j.1365-2273.2002.00541.x. [DOI] [PubMed] [Google Scholar]
- Jennings SG, Strickland EA, Heinz MG. Precursor effects on behavioral estimates of frequency selectivity and gain in forward masking. J Acoust Soc Am. 2009;125:2172–2181. doi: 10.1121/1.3081383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawase T, Delgutte B, Liberman MC. Antimasking effects of the olivocochlear reflex: II. Enhancement of auditory-nerve response to masked tones. J Neurophysiol. 1993;70:2533–2549. doi: 10.1152/jn.1993.70.6.2533. [DOI] [PubMed] [Google Scholar]
- Keefe DH, Fitzpatrick D, Liu YW, Sanford CA, Gorga MP. Wideband acoustic-reflex test in a test battery to predict middle-ear dysfunction. Hear Res. 2010;263:52–65. doi: 10.1016/j.heares.2009.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krull V, Strickland EA. The effect of a precursor on growth of forward masking. J Acoust Soc Am. 2008;123:4352–4357. doi: 10.1121/1.2912440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Le Prell CG, Hughes LF, Bledsoe SC., Jr Dynorphin release by the lateral olivocochlear efferents may inhibit auditory nerve activity: a cochlear drug delivery system. Neurosci Lett. 2014;571:17–22. doi: 10.1016/j.neulet.2014.04.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levitt H. Transformed up-down methods in psychoacoustics. J Acoust Soc Am. 1971;49(Suppl 2):467–477. doi: 10.1121/1.1912375. [DOI] [PubMed] [Google Scholar]
- Liberman MC. Response properties of cochlear efferent neurons: monaural vs. binaural stimulation and the effects of noise. J Neurophysiol. 1988;60:1779–1798. doi: 10.1152/jn.1988.60.5.1779. [DOI] [PubMed] [Google Scholar]
- Liberman MC, Puria S, Guinan JJ., Jr The ipsilaterally evoked olivocochlear reflex causes rapid adaptation of the 2f1-f2 distortion product otoacoustic emission. J Acoust Soc Am. 1996;99:3572–3584. doi: 10.1121/1.414956. [DOI] [PubMed] [Google Scholar]
- Lopez-Poveda EA, Plack CJ, Meddis R. Cochlear nonlinearity between 500 and 8000 Hz in listeners with normal hearing. J Acoust Soc Am. 2003;113:951–960. doi: 10.1121/1.1534838. [DOI] [PubMed] [Google Scholar]
- McFadden D. Spectral differences in the ability of temporal gaps to reset the mechanisms underlying overshoot. J Acoust Soc Am. 1989;85:254–261. doi: 10.1121/1.397732. [DOI] [PubMed] [Google Scholar]
- Møller AR. An experimental study of the acoustic impedance of the middle ear system and its transmission properties. Acta Otolaryngol. 1965;60:129–149. doi: 10.3109/00016486509126996. [DOI] [PubMed] [Google Scholar]
- Møller AR. Hearing: anatomy, physiology and disorders of the auditory system. San Diego: Plural; 2012. Acoustic middle ear reflex. [Google Scholar]
- Moore BCJ. Frequency analysis and masking. In: Moore BCJ, editor. Hearing. London: Academic; 1995. pp. 161–205. [Google Scholar]
- Murugasu E, Russell IJ. The effect of efferent stimulation on basilar membrane displacement in the basal turn of the guinea pig cochlea. J Neurosci. 1996;16:325–332. doi: 10.1523/JNEUROSCI.16-01-00325.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelson DA, Schroder AC, Wojtczak M. A new procedure for measuring peripheral compression in normal-hearing and hearing-impaired listeners. J Acoust Soc Am. 2001;110:2045–2064. doi: 10.1121/1.1404439. [DOI] [PubMed] [Google Scholar]
- Overson GJ, Bacon SP, Webb TM. The effect of level and relative frequency region on the recovery of overshot. J Acoust Soc Am. 1996;99:1059–1065. doi: 10.1121/1.415232. [DOI] [PubMed] [Google Scholar]
- Oxenham AJ, Plack CJ. A behavioral measure of basilar-membrane nonlinearity in listeners with normal and impaired hearing. J Acoust Soc Am. 1997;101:3666–3675. doi: 10.1121/1.418327. [DOI] [PubMed] [Google Scholar]
- Plack CJ, Drga V. Psychophysical evidence for auditory compression at low characteristic frequencies. J Acoust Soc Am. 2003;113:1574–1586. doi: 10.1121/1.1538247. [DOI] [PubMed] [Google Scholar]
- Rosengard PS, Oxenham AJ, Braida LD. Comparing different estimates of cochlear compression in listeners with normal and impaired hearing. J Acoust Soc Am. 2005;117:3028–3041. doi: 10.1121/1.1883367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roverud E, Strickland EA. The time course of cochlear gain reduction measured using a more efficient psychophysical technique. J Acoust Soc Am. 2010;128:1203–1214. doi: 10.1121/1.3473695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruggero MA, Robles L, Rich NC. Two-tone suppression in the basilar membrane of the cochlea: mechanical basis of auditory-nerve rate suppression. J Neurophysiol. 1992;68:1087–1099. doi: 10.1152/jn.1992.68.4.1087. [DOI] [PubMed] [Google Scholar]
- Ruggero MA, Rich NC, Recio A, Narayan SS, Robles L. Basilar-membrane responses to tones at the base of the chinchilla cochlea. J Acoust Soc Am. 1997;101:2151–2163. doi: 10.1121/1.418265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Russell IJ, Murugasu E. Medial efferent inhibition suppresses basilar membrane responses to near characteristic frequency tones of moderate to high intensities. J Acoust Soc Am. 1997;102:1734–1738. doi: 10.1121/1.420083. [DOI] [PubMed] [Google Scholar]
- Sánchez-González MA, Warr WB, López DE. Anatomy of olivocochlear neurons in the hamster studied with FluoroGold. Hear Res. 2003;185:65–76. doi: 10.1016/S0378-5955(03)00213-2. [DOI] [PubMed] [Google Scholar]
- Schmidt S, Zwicker E. The effect of masker spectral asymmetry on overshoot in simultaneous masking. J Acoust Soc Am. 1991;89:1324–1330. doi: 10.1121/1.400656. [DOI] [PubMed] [Google Scholar]
- Spangler KM, Warr WB. The descending auditory system. In: Altschuler RA, Bobbin RP, Clopton BM, Hoffman DW, editors. Neurobiology of hearing: the central auditory system. New York: Raven; 1991. pp. 27–45. [Google Scholar]
- Sterenborg JC, Pilati N, Sheridan CJ, Uchitel OD, Forsythe ID, Barnes-Davies M. Lateral olivocochlear (LOC) neurons of the mouse LSO receive excitatory and inhibitory synaptic inputs with slower kinetics than LSO principal neurons. Hear Res. 2010;270:119–126. doi: 10.1016/j.heares.2010.08.013. [DOI] [PubMed] [Google Scholar]
- Strickland EA. The relationship between frequency selectivity and overshoot. J Acoust Soc Am. 2001;109:2062–2073. doi: 10.1121/1.1357811. [DOI] [PubMed] [Google Scholar]
- Strickland EA. The temporal effect with notched-noise maskers: analysis in terms of input–output functions. J Acoust Soc Am. 2004;115:2234–2245. doi: 10.1121/1.1691036. [DOI] [PubMed] [Google Scholar]
- Strickland EA. The relationship between precursor level and the temporal effect. J Acoust Soc Am. 2008;123:946–954. doi: 10.1121/1.2821977. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strickland EA, Krishnan LA. The temporal effect in listeners with mild to moderate cochlear hearing impairment. J Acoust Soc Am. 2005;118:3211–3217. doi: 10.1121/1.2074787. [DOI] [PubMed] [Google Scholar]
- Subhash HM, Davila V, Sun H, Nguyen-Huynh AT, Shi X, Nuttall AL. Volumetric in vivo imaging of microvascular perfusion within the intact cochlea in mice using ultra-high sensitive optical microangiography. IEEE Trans Med Imag. 2011;30:224–230. doi: 10.1109/TMI.2010.2072934. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Warr WB. The olivocochlear bundle: its origins and terminations in the cat. In: Naunton RF, Fernandez C, editors. Evoked electrical activity in the auditory nervous system. London: Academic; 1978. pp. 43–65. [Google Scholar]
- Warr WB. Organization of olivocochlear efferent systems in mammals. In: Webster DB, Popper AN, Fay RR, editors. The mammalian auditory pathway: neuroanatomy. New York: Springer; 1992. pp. 410–448. [Google Scholar]
- Warr WB, Guinan JJ., Jr Efferent innervation of the organ of Corti: two separate systems. Brain Res. 1979;173:152–155. doi: 10.1016/0006-8993(79)91104-1. [DOI] [PubMed] [Google Scholar]
- Warr WB, Beck Boche JE, Ye Y, Kim DO. Organization of olivocochlear neurons in the cat studied with retrograde tracer cholera toxin-B. J Assoc Res Otolaryngol. 2002;3:457–478. doi: 10.1007/s10162-002-2046-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams EJ, Bacon SP. Compression estimates using behavioral and otoacoustic emission measures. Hear Res. 2005;201:44–54. doi: 10.1016/j.heares.2004.10.006. [DOI] [PubMed] [Google Scholar]
- Winslow RL, Sachs MB. Effect of electrical stimulation of the crossed olivocochlear bundle on auditory nerve response to tones in noise. J Neurophysiol. 1987;57:1002–1021. doi: 10.1152/jn.1987.57.4.1002. [DOI] [PubMed] [Google Scholar]
- Wojtczak M, Oxenham AJ. Recovery from on- and off-frequency forward masking in listeners with normal and impaired hearing. J Acoust Soc Am. 2010;128:247–256. doi: 10.1121/1.3436566. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yasin I, Plack CJ. The effects of a high-frequency suppressor on tuning curves and derived basilar membrane response estimates. J Acoust Soc Am. 2003;114:322–332. doi: 10.1121/1.1579003. [DOI] [PubMed] [Google Scholar]
- Yasin I, Drga V, Plack CJ. Estimating peripheral gain and compression using fixed-duration masking curves. J Acoust Soc Am. 2013a;133:4145–4155. doi: 10.1121/1.4802827. [DOI] [PubMed] [Google Scholar]
- Yasin I, Drga V, Plack CJ. Improved psychophysical methods to estimate peripheral gain and compression. In: Moore BCJ, Patterson RD, Winter IM, Carlyon RP, Gockel HE, editors. Basic aspects of hearing: physiology and perception. Heidelberg: Springer; 2013b. pp. 39–46. [DOI] [PubMed] [Google Scholar]
- Yates GK. Basilar membrane nonlinearity and its influence on auditory nerve rate-intensity functions. Hear Res. 1990;50:145–162. doi: 10.1016/0378-5955(90)90041-M. [DOI] [PubMed] [Google Scholar]