Free-energy landscape of the GB1 hairpin in all-atom explicit solvent simulations with different force fields: Similarities and differences

Abstract

Although it is now possible to fold peptides and miniproteins in molecular dynamics simulations, it is well appreciated that force fields are not all transferable to different proteins. Here, we investigate the influence of the protein force field and the solvent model on the folding energy landscape of a prototypical two-state folder, the GB1 hairpin. We use extensive replica-exchange molecular dynamics simulations to characterize the free-energy surface as a function of temperature. Most of these force fields appear similar at a global level, giving a fraction folded at 300 K between 0.2 and 0.8 in all cases, which is a difference in stability of 2.8 kT, and are generally consistent with experimental data at this temperature. The most significant differences appear in the unfolded state, where there are different residual secondary structures which are populated, and the overall dimensions of the unfolded states, which in most of the force fields are too collapsed relative to experimental Förster Resonance Energy Transfer (FRET) data.

INTRODUCTION

To identify the molecular details of protein folding, computer simulations can provide information that is not easily accessible to experiments. However, brute force molecular simulations can only reach time and length scales relevant for peptides and miniproteins. The synergy between experiment and simulation using these miniproteins — which can be analyzed in both computer and laboratory experiments — therefore supplies information that can be used to address longstanding questions in protein folding.^1–3

We have previously addressed a principal remaining challenge in protein folding simulations, namely the transferability of the energy function (force field) used to represent protein and solvent molecules: although some force fields are known to be suitable for folding α-helical proteins in computer simulations, others are biased toward β-structures.⁴ This is clearly illustrated by folding simulations of the all-β pin WW domain with the CHARMM 27 force field (which has a known α-helical bias), where only helical structures were formed in a 10-μs simulation starting from a completely unfolded structure.⁵ We have shown that a simple backbone modification can redress this deficiency in the folding of several peptides and proteins.^6,7 Specifically, we used an optimized energy function Amber 03* to fold Pin WW domain, Villin HP35, GB1 hairpin, and Trp cage starting from completely unfolded states.

Going beyond this fundamental issue of “balancing” α and β structures, it is natural to ask what the remaining similarities and differences between various force fields are. We address this question using a prototypical model of β hairpin folding, namely the GB1 hairpin (Fig. 1), residues 41—56 of the immunoglobulin-binding domain of streptococcal protein G. This molecule was observed to fold independently⁸ into a hairpin similar to that in the native protein structure,⁹ and the coincidence of melting curves derived from different probes indicates that folding is cooperative.^10,11 It is ~50% folded at room temperature and folds in ~6 ls at 300 K.¹⁰ We use long replica-exchange molecular dynamics (REMD) simulations to obtain converged equilibrium properties. For a meaningful comparison, we focus only on a limited set of energy functions currently known to fold proteins with β-structures (although there are certainly other force fields for which the hairpin is stable that we have not considered). For example, starting from the native fold, we had previously obtained almost exclusively helical structures in REMD simulations of this peptide with Amber ff03.⁶ Similarly, we did not investigate CHARMM 27, because it was found to form more helix than ff03 for short peptides;⁴ folding simulations of the all-β pin WW domain also resulted in only helical structures,⁵ subsequently shown to be lower in free energy than the folded state¹² in this force field.

Figure 1.

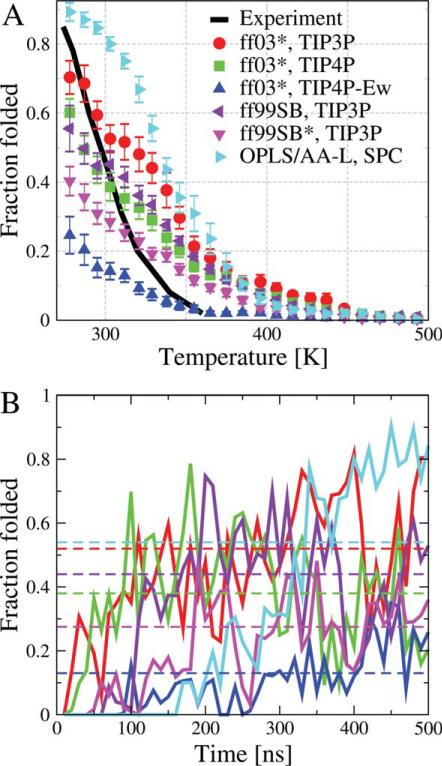
Equilibrium folded population. (A) The fraction folded is shown as a function of temperature, as determined from REMD simulations. The first 200 ns of simulation were discarded from these averages except for OPLS/AA-L for which 400 ns of simulation were discarded. Experimentally determined populations are shown by a solid black line.¹⁰ (B) Averages of the folded population over a moving window of 10 ns are shown as a function of the window origin at T = 303 K by solid lines. The horizontal dashed lines are the equilibrium fraction folded averaged over last 300 ns. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Being of a size amenable to simulation, the GB1 hairpin has been the subject of numerous simulation studies, with coarse-grained models¹³ and atomistic models with either implicit,^14–20 or explicit solvent^21–34 using a variety of sampling schemes. However, there is some disagreement on the mechanism of hairpin formation both between the simulation studies and with experiment. Using an implicit solvent model, Zagrovic et al.¹⁵ proposed an intermediate with a collapsed hydrophobic core, from which the final hydrophobic packing and hydrogen bond formation occur; most of the simulation studies have inferred a “hydrophobic collapse” mechanism where, in contrast to the “zipper”, the hydrophobic interactions in the center of the peptide drive an initial collapse, followed by the formation of the backbone hydrogen bonds. Although our work does not explicitly address the question of mechanism, it is relevant because differences between the folding free-energy-landscape of the peptide in different force fields could influence the mechanism obtained.

We find that most of the force fields considered here appear similar at a global level, giving a fraction folded at 300 K between 0.2 and 0.8 in all cases (a difference in stability of 2.8 kT). In the unfolded state, there are differences in the residual secondary structures which are populated, as well as in the overall degree of “collapse”— indeed most of the force fields are too collapsed relative to experimental FRET data. Despite the differences in unfolded state structure, agreement with the experimental NMR and FRET data does not clearly discriminate between the different force fields. A remaining challenge in seeking optimal force fields will therefore be to obtain more accurate methods of calculating experimental parameters from the simulation data, in order that different force fields may be better distinguished, and more high-resolution experimental data on these short peptides.

SIMULATION METHOD

REMD simulations of the GB1 hairpin were performed using the Gromacs 4.0.5 simulation package.^35–37 The Amber ff03* force field (Amber ff03³⁸ with a modified Ψ torsion potential³⁹) was used to represent the protein with a solvent model combination of TIP3P, TIP4P, or TIP4P-Ew.^40–42 In addition to Amber ff03*, we use Amber ff99SB⁴³ and Amber ff99SB*39 with the TIP3P water model and OPLS/AA-L⁴⁴ with the SPC water model.⁴⁵ Although OPLS/AA-L is intended for use with TIP3P, we use it with SPC following the success of this combination in Zhou and Bolhuis's work.^{16,25,26,31,46,47} The structure of the 16 residue GB1 hairpin was taken from residues 41–56 of the full-length GB1 protein (PDB: 1GB1) and solvated in a truncated octahedron simulation cell with 3.5 nm between the nearest faces, containing 984 water molecules, six sodium ions, and three chloride ions to neutralize the charge. The termini of the peptide were unblocked, corresponding to the experimental conditions.10 For the GB1 hairpin, the salt bridge between the charged termini is expected to be an important contribution to the stability, analogous to the introduction of additional salt bridges between the ter-mini by mutation.⁴⁸ All REMD simulations were performed at constant volume with long-range electrostatics calculated using PME with a 1.2Å grid spacing and 9Å cutoff. A Langevin algorithm was used with a friction of 1/ps to propagate the dynamics, and replica exchange was attempted every 10 ps (every 5000 steps with a time step of 2 fs). The temperatures of the replicas spanned a range of 278–595 K with 32 replicas. The temperatures used were as follows: 278, 287, 295, 303, 312, 321, 329, 338, 346, 355, 365, 375, 385, 396, 406, 416, 427, 437, 448, 459, 470, 482, 493, 505, 517, 528, 539, 551, 562, 573, 584, and 595. REMD simulations were initiated with all the replicas in the unfolded state, and the unfolded states were drawn at regular intervals from a constant volume trajectory at 1000 K. All REMD runs were propagated for 0.5 μs per replica, for a total of 16 μs for each force field considered here. The global cluster analysis of the equilibrium configurations is performed using the single linkage algorithm with all-atom RMSD as a distance metric. This is an agglomerative clustering algorithm, which can be summarized as follows: each structure is initially assigned to a different cluster. Clusters are then successively merged if any element of one cluster is within a cutoff distance (here 0.15 nm) of an element of another cluster. The procedure terminates when no further clusters are within the cutoff distance of each other. Initially, we used several values of cluster cutoff distance to identify the dependence of results on a particular value. We find that the number of structures in the most dominant cluster plateaus around cutoff 0.15 nm (see Supporting Information Fig. 1), and, therefore, we use this value for all our further analysis. A cluster radius value larger than 0.15 nm results in structures with similar backbone but different side-chain arrangement (e.g., cluster 1 and 5 in case of ff03* with TIP3P in Fig. 3) clustered together, which we wanted to avoid.

Figure 3.

Structural ensemble at 303 K. Representative structures from the five most populated clusters (% population indicated) are shown for various force fields. Hydrophobic side chains forming a “hydrophobic cluster” in the folded state are drawn as sticks. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

RESULTS AND DISCUSSION

Equilibrium folding of GB1 hairpin

In the REMD simulations that start from unfolded structure in all the replicas, we observe a folded population, defined as having a backbone d_RMS < 1.5Å, showing that the folded structures can be obtained with all the force fields used in this study. Backbone d_RMS is defined as $d_{\mathrm{RMS}}={\left[N_{\mathrm{bb}}^{-1}{\sum }_{(i,j)}{(r_{ij}-r_{ij}^0)}^2\right]}^{1∕2}$, where the sum runs over the N_bb backbone native contacts (i,j) of native amino acid contacts which are separated by distances r_ij in the configuration of interest and by $r_{ij}^0$ in the native state. On the basis of the native structure, we define a contact between a backbone atom (CA, C, N, or O) in residue i and a second backbone atom in residue j to be native if the distance between them is less than 4.5Å and | i – j | > 2. Representative folded structures obtained from the simulations starting from unfolded configurations are shown in Figure 3.

For each case, we observe multiple folding and unfolding events during the simulations. Although the REMD simulations result in discontinuous trajectories at a single temperature, we obtain continuous trajectories by following a given replica through the exchanges in temperature space. The trajectories reveal cooperative folding and unfolding events for each peptide (not shown). In Figure 1, we show the fraction of folded molecules as a function of the replica temperature, finding folded populations at 300 K of ~20–90%, in reasonable agreement with the experimental values of ~30,49 respectively. ~50,¹⁰ and ~75 %,⁵⁰ We note that the experimental temperature dependence of the folded population is not reproduced with any of the force fields.

A concern with any simulation study is whether the length of the runs is sufficient to obtain representative sampling of the phase space, such that accurate equilibrium averages may be obtained. A stringent test of such “convergence” for protein folding is the comparison between the results of simulations started from folded and unfolded configurations. We have previously shown that REMD simulations of the order of 500 ns per replica are sufficient to obtain converged results in the low-temperature replicas for GB1 hairpin and Trp cage.⁶ In this previous study, we found that by discarding the first 0.2 μs of each simulation, we obtain well-converged results from the final 0.3 μs, with similar folded populations starting from either folded or unfolded structure. By plotting the average folded population in the 303 K replica, averaged over a moving “window” of 10 ns, we are able to assess how fast the averages for the simulations for different force fields converge [Fig. 1(B)]. We find that ~200 ns is sufficient for most of the force fields used, although longer times are needed for OPLS/AA-L. This suggests that the protein dynamics with OPLS/AA-L may be more sluggish than Amber-based force fields, and longer simulations may be needed with this energy function. We use the same length REMD runs for all the force fields used, but a longer equilibration time (400 ns) for OPLS/AAL, versus 200 ns for the other force fields. In future studies, we plan to revisit the issue of equilibration time difference between various force fields.

Folding free-energy surfaces

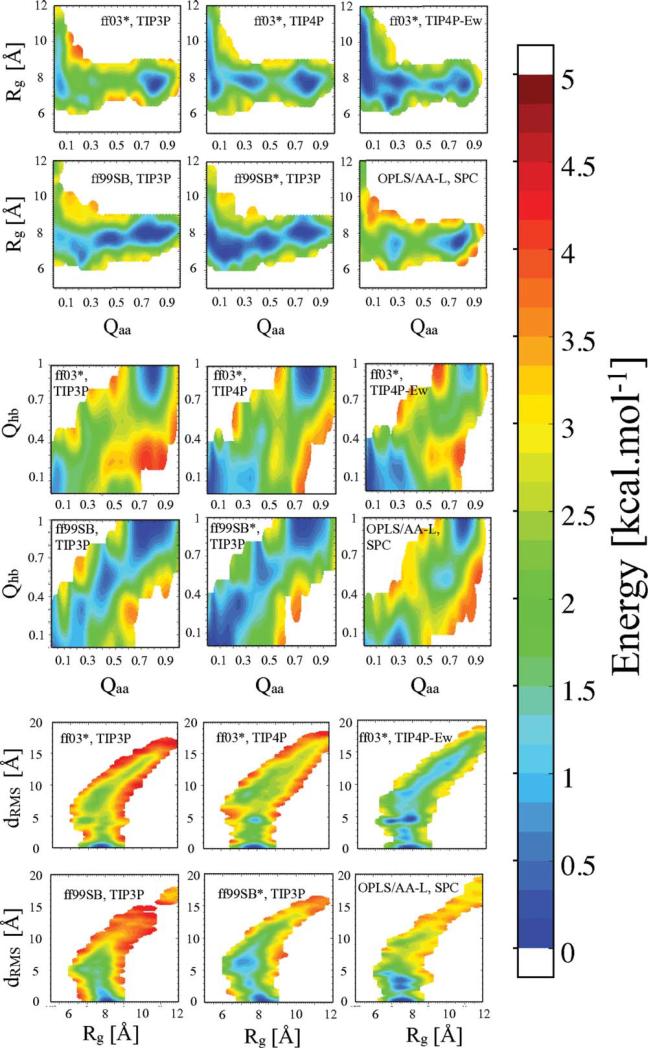
We characterize the energy landscape by calculating two-dimensional free-energy surfaces for projections onto selected reaction coordinates. We use several coordinates to overcome likely deficiencies in the individual coordinates chosen.⁵¹ We use a set of coordinates designed to capture both local and global structure formation. As a measure of global contact formation, we use the fraction of native contacts (excluding hydrogen atoms), $Q_{\mathrm{aa}}=N_{\mathrm{aa}}^{-1}{\sum }_{(i,j)}{[1+\exp \left(\beta (r_{ij}-\lambda r_{ij}^0)\right)]}^{-1}$, where the sum runs over the N_aa pairs (i,j) of native amino acid contacts which are separated by distances r_ij in the configuration of interest and by $r_{ij}^0$ in the native state (β = 5 Å⁻¹; λ = 1.5 ). The parameter λ accounts for the fluctuations in distance between residues in contact in the native state, while β controls the steepness of the contact step function.^6,52 If one considers two atoms in contact to be at the minimum of a Lennard–Jones-type potential, then choosing λ= 1.5 includes all interactions where the pair energy is higher than ≈15 % of the minimum pair energy. The value of β was chosen such that the step function is smoothly switched over a range of ≈1 Å, to give a continuous, smooth coordinate. We define a contact between the two heavy atoms to be native if the distance between these atoms is less than 4.5Å and | i − j | > 3. As Q_aa does not distinguish well between structures which are far from native, we augment this information with the fraction of native hydrogen bonds Q_hb, defined in an analogous fashion to Q_aa. We also consider the radius of gyration R_g as a measure of overall compaction and backbone d_RMS as a measure of backbone native structure formation.

The free-energy surfaces are presented in Figure 2. They each reveal two dominant minima, an “unfolded” state near Q_aa 5 0.1 and a “folded” state near Q_aa 5 0.8. In our previous study with Amber ff03*, we found that the free-energy surfaces calculated from REMD starting from either folded or unfolded are very similar, even for the low-temperature replicas. The unfolded state shows considerable heterogeneity with structures varying considerably in compactness, as evident in the R_g distribution. The unfolded structures all contain very few native hydrogen bonds, indicating the absence of native-like secondary structure from the unfolded state.

Figure 2.

Folding free-energy surfaces at 303 K. Two-dimensional potentials of mean force have been calculated from projections onto the radius of gyration R_g, the all-atom fraction of native contacts Q_aa, backbone d_RMS, and the fraction of native hydrogen bonds Q_hb. The primary data have been smoothed using Gaussians of width comparable to the grid spacing.

In addition to the folded states at high Q_aa ~0.8 and the unfolded states at Q_aa ~0.2, of in some the force fields there are intermediate states with Q_aa 0.5. In the case of Amber ff03*, we have previously shown that this minimum comes from an off-pathway intermediate with a considerable number of native-like contacts.⁶ The minimum near Q_aa = 0.5 in Amber 99SB and Amber 99SB* is even more pronounced; however, the origin is different. Inspection of the Q_aa and Q_hb surfaces indicates that the intermediate is stabilized by native-like hydrogen bonds (partially formed intermediates) when compared with the simulations with Amber ff03*, where no native-like hydrogen bonds are formed.

In terms of the overall radius of gyration, R_g, there are some significant differences between the unfolded states in the various force fields. In TIP3P, or TIP4P water, the unfolded states for the Amber force fields span a similar range of R_g, ~6–10Å. The combination of TIP4P-Ew water in conjunction with Amber ff03* results in a much more expanded unfolded state. This result is consistent with earlier, less well-converged results on an unfolded protein (CspTm).⁵³ The effect of changing the water model demonstrates the critical importance of balancing the solute–solvent and solute–solute interactions in determining the properties of the folding free-energy landscape.

To gain some insight into the most favored structures on the free-energy landscape, we have performed a global cluster analysis of the equilibrium configurations at 303 K using the linkage algorithm with all-atom RMSD as a distance metric and 0.15 nm as the cluster radius. The centroid structure from top five clusters is shown in Figure 3. We observe a single dominant cluster with population ranging from 44.6% (Amber ff03* with TIP3P water) to 21% (Amber ff99SB*) except for Amber ff03* with TIP4P-Ew water, corresponding to the correctly folded hairpin. For Amber ff03* with TIP4P-Ew water, we observe folded structures with varying degree of sheet “twist” and side-chain packing. The remaining “unfolded” clusters all have varying population less than 12.5% and comprise a great diversity of structures. These structures indicate that in the most frequently visited clusters of the unfolded state, there is considerable population of non-native secondary structure, including both helical and non-native sheets and hairpins. Note that although short helices are present for all force fields except OPLS-AA/L, these represent a small fraction of the total ensemble. This may still reflect too great a propensity for the formation of local secondary structure in most of the currently used force fields as we discuss next.

Secondary structure populations

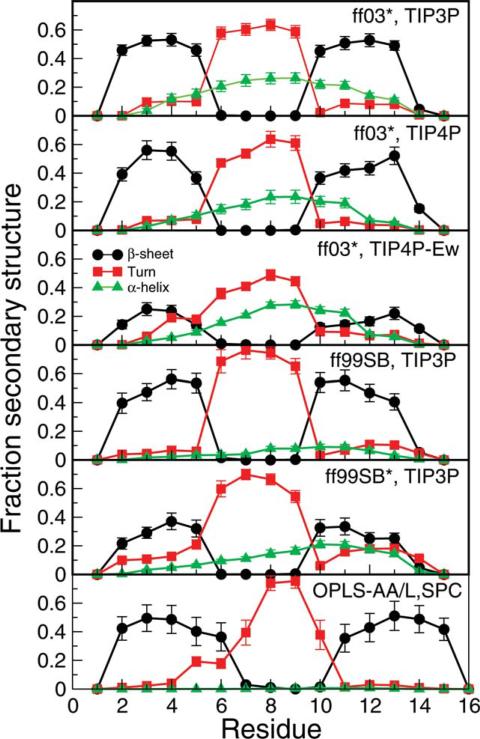
We characterize the secondary structure propensities of the different force fields considered by calculating the fraction of time a given type of secondary structure is observed for residues in the GB1 hairpin sequence using DSSP. Figure 4 shows this data for β-sheet, turn, and α-helix structures, which are the dominant secondary structures detected by DSSP in the simulation data. We find differences in secondary structure preference, despite the overall similarity in folded population. In most of the force fields, there is significant α-helical population, particularly toward the center of the peptide, consistent with the cluster analysis. This helical population seems too high for a peptide with native β-structure. On the other hand, no helical population is observed in the case of OPLS-AA/L in SPC water. At first sight, this would appear to be more consistent with expectations based on the folded structure. However, we have found that this force field has a low helix-forming propensity with any sequence, even those known to form helices (unpublished data). Therefore, the helical population in the unfolded states may be a necessary consequence of achieving a balance between α and β structures. This may be a side effect of insufficiently cooperative secondary structure formation in force fields (e.g., in backbone hydrogen bonding³⁹); thus it cannot be completely eliminated by simply shifting the α/β balance. On the other hand, it is known that the GB1 hairpin sequence is not inconsistent with helical structure, as was elegantly demonstrated by the engineering of a folded full-length GB1 mutant in which the sequence of the helix was almost completely replaced by that of the C-terminal hairpin⁵⁴ while preserving the helical structure. In the end, such non-native structure can only be discounted via direct comparison with experimental data as presented later.

Figure 4.

Secondary structure populations at 303 K. Fraction of time a residue is found in a given structure (defined based on DSSP criteria) as a function of residue number is shown for various force fields. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Comparison of equilibrium simulation results with experiment: FRET efficiencies

Although all the force fields studied give folded populations at 300 K consistent with experiment, there are substantial differences in structure in the unfolded state. To avoid speculating as to which observations are closer to expectations, we compare the simulation data directly with two types of experimental data: FRET efficiencies and NMR chemical shifts. To calculate FRET efficiencies, we initially assume that the conformational dynamics is much slower than the donor fluorescence lifetime (≈3 ns for Trp). A more sophisticated approach would involve calculating the average transfer efficiency using a time-dependent transfer rate,⁵⁵ but this is not straightforward, because our simulations are interrupted by replica-exchange moves. With this assumption of “slow” peptide conformational dynamics, and also that either the donor or acceptor orientation decays on a timescale faster than the fluorescence lifetime, the FRET efficiency may be calculated from:^55,56

$$\langle E\left(R\right)\rangle =\langle \frac{1}{1+{(R∕R_0)}^6}\rangle ,$$ (1)

where R is the distance between donor and acceptor chromophores and R₀ is the spectroscopically determined Förster radius (2.2 nm). Although the donor Trp is explicitly present in our simulations, the acceptor (a Dansylated Lys at the C-terminus) is not. To model the acceptor chromophore and its lysine linker, we developed an AMBER-type force-field model for Dansylated lysine, using RESP57 charges for the chromophore. Supporting Information Figure 3 and Table S1 gives the AMBER 9958 atom types and partial charges for this residue. A 20-ns simulation of the chromophore attached to folded GB1 was run in explicit TIP3P water using the same protocol as for the other simulations. We defined a local reference frame at the Cα of Glu 16 and measure the position of the C10 in the Dansyl relative to the Glu 16 Cα, r_E-Dan. For each frame in the simulation, we calculate the Trp-Dansyl vector r_W-Dan, between the CD2 of Trp and C10 of the Dansyl, as r_W-Dan = r_W-E + Tr_E-Dan, where r_W-E is the Trp-Glu displacement in the simulation, r_E-Dan is a Glu-Dansyl orientation chosen at random from the explicit chromophore simulation, and T is a unitary transformation rotating r_E-Dan from the reference frame to the simulation frame.

In previous work, we had added a fixed distance of δR = 0.2 nm to that between the Trp and the Glu, which gives similar results although slightly lower efficiency for the unfolded state. This analysis is presented in Supporting Information Figure 4.

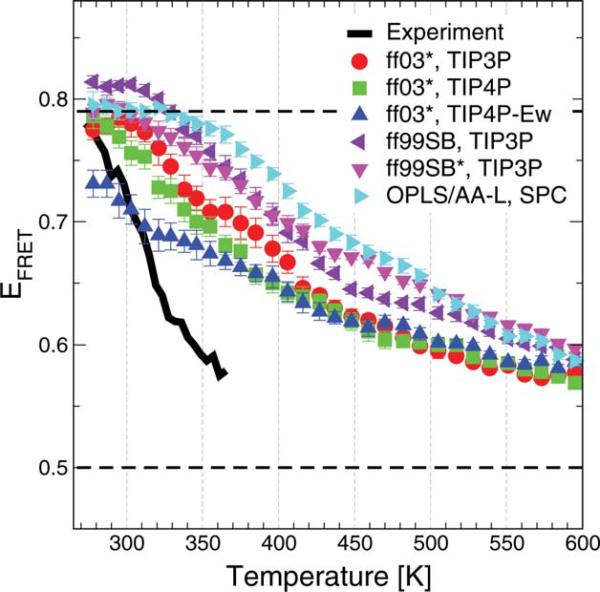
The calculated FRET efficiencies are shown in Figure 5. We obtain reasonable agreement with the experimental efficiencies near 300 K for all the force fields, with some marked differences apparent in the temperature dependence. For all the force fields the overall temperature dependence is much weaker than observed experimentally.¹⁰ This is due to a combination of the too-weak temperature dependence of the folded population (as shown earlier) and a high efficiency for the unfolded state (see efficiency for highest temperature replicas). This latter effect can be attributed to an unfolded state that is too “collapsed” or structured as discussed above. The collapsed structures in the unfolded state are most apparent for OPLS/AA-L, where the FRET efficiency is significantly higher than the other force fields at low temperatures, and to some extent for AMBER ff99SB. A similar collapsed unfolded state using OPLS/AA-L with TIP3P water has also been seen in simulations of unfolded CspTm.⁵³ We note that the question about non-native secondary structure population in the unfolded state has been studied previously⁵⁹, and the answer may actually be context dependent. Our analysis suggests that the simulated unfolded structures may be too structured, but the alternate possibility that experiments have not been able to capture these structures cannot be discounted. Future experimental and computational studies need to resolve this issue if simulation is to be used to interpret and predict properties of unfolded proteins and intrinsically disordered proteins.

Figure 5.

Trp-Dansyl FRET transfer efficiencies. FRET efficiencies were calculated from the simulations as described in the text. We assume slow chain dynamics relative to donor lifetime. Black solid line: experimental data from Mũnoz et al.;¹⁰ black broken lines: folded and unfolded efficiencies from two-state experimental analysis. Efficiencies from simulation are as indicated in the legend. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Comparison of equilibrium results with experiment: NMR chemical shifts

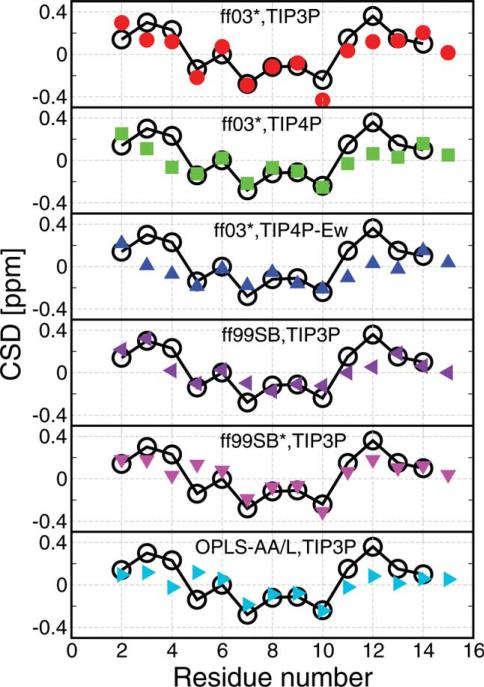
The second experimental measure that we consider is NMR chemical shifts, which are a sensitive measure of peptide conformation, reflecting both backbone structure and side-chain packing. A number of accurate empirical algorithms have been developed for the calculation of shifts from structure, based on correlations of chemical shifts with simple geometrical properties.^60,61,62 Here, we have calculated chemical shifts based on CamShift algorithm⁶⁰ to assess our simulation results; we have previously obtained similar results with other algorithms.⁶ We focus on H^α shifts, which can be most accurately predicted by these approaches, reported as a chemical shift deviation, the difference from standardized “random-coil” chemical shifts.

At low temperature (278 K), we obtain reasonable agreement with the experimental data with all the force fields as shown in Figure 6. Some notable differences that we find for various force fields are as follows. For all the force fields, residues around W3 and F12 show a significant difference from experiment. This discrepancy may be related to ring current effects not well captured by current chemical shift prediction algorithms. For Amber ff03* with TIP3P water, K10 shows a slight deviation from experiment. It is interesting that K10 in the native state is found in α_L, and previous tests with this force field on Ala-5 suggested that α_L structures may be less stable than expected based on frequency of occurrence in loop regions in the PDB.

Figure 6.

Comparison with experimental NMR chemical shift deviations (CSD).

The calculated H^α CSD (obtained experimentally by subtracting the random coil shift) is shown for 278 K replicas by using CamShift algorithm.⁶⁰ Black empty circles are the experimental data at 278 K.⁴⁹ α-Helical structure is usually associated with a negative CSD and extended structures with a positive CSD.⁶³ Note that although two α proton shifts can be measured for Gly, CamShift reports only a single value. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

These results mainly confirm the accuracy of the folded structures obtained, because these are the majority of the population at low temperature except for Amber ff03* with TIP4P-Ew, which shows significant differences from experimental data; this case can be explained by the low population of native structure near 300 K.

Origin of differences between force fields and directions for improvement

Parameterization of modern all-atom force fields is a complex process, and the procedures used by different groups vary in the emphasis placed on matching different types of data, obtained either from ab initio quantum mechanical calculations or experiment. In general, bonded terms (bonds, angles, and dihedrals) are obtained from ab initio calculations.⁶⁴ The main differences in parameterization occur in the fitting of non-bonded parameters, particularly electrostatic parameters. The AMBER family of force fields generally derive atomic partial charges by fitting them to an electro-static potential map at the molecular surface, calculated by ab initio methods.^38,58 In contrast, the OPLS44 and GROMOS⁶⁵ force fields were derived by matching the solvation thermodynamics of small model compounds. The CHARMM force field uses ab initio binding energies of water molecules to model peptides as part of the parameterization. In this work, we consider only AMBER and OPLS force fields. Clearly, with thousands of parameters in each force field, it would be generally very hard to attribute the differences in properties of different energy functions to specific parameters. However, by considering closely related force fields, useful conclusions can be drawn. Here, we consider the Amber ff03* force field in conjunction with three different water models: TIP3P, TIP4P, and TIP4PEw. We also consider the Amber ff99SB force field both with and without a backbone modification (ff99SB*) designed to reproduce helical propensities in alanine-based peptides. The OPLS/AA-L protein force field with SPC water was studied because this combination had been used in several previous folding studies,^25,26,47 but is hard to compare because both protein and water models are different from the other cases. This difference is evident in the relatively large differences in unfolded state dimensions, and in the different secondary structure propensities, relative to the AMBER force fields.

In comparing variations across the different water models used in conjunction with AMBER ff03*, we find that using TIP4P-Ew results in a substantially lower fraction folded than obtained using TIP3P, with TIP4P only lowering the fraction folded relative to TIP3P slightly. The similarities between TIP3P and TIP4P can be rationalized given that they were both parameterized using similar target data and a similar treatment of nonbonded interactions (9Å spherical cutoffs). However, more recent models, such as TIP4PEw⁴² and TIP4P/2005,⁶⁶ were parameterized using a particle-mesh Ewald approach to treat the long-range electrostatics, and with corrections to empirical data (e.g., enthalpies of vaporization) to account for the fact that the computational model is not polarizable. These water models result in stronger interactions between the peptide and the water, and a larger enthalpy of solvation.⁶⁷ As a result, the unfolded state using such force fields is more expanded and becomes less expanded with increasing temperature, in agreement with experiment.^53,68 Does the use of this water model (which gives a better description of bulk water than TIP3P) represent an improvement for hairpin folding? Although there is some disagreement about the fraction of GB1, which is folded at room temperature (some estimates are as low as 30%,⁴⁹) on the whole the evidence suggests that the hairpin is too unstable in this force field. This is clearly evident from the NMR chemical shift analysis, Figure 6. Therefore, despite the promising results in terms of unfolded state dimensions, it is clear that further refinement would be needed before the ff03*/TIP4P-Ew combination would be suitable for general use. For example, in recent work using the related water model TIP4P/2005, we have found that the effects of the water model on helix stability could be compensated by a backbone modification.⁶⁸ These results together indicate that using more accurate water models appears to be a promising direction for improvement, but that careful testing will be needed when such models are combined with existing protein force fields.

The backbone modification of AMBER ff99SB,⁴³ termed ff99SB*,³⁹ is a relatively small change in the Ψ torsion potential in favor of helical over extended secondary structure. It is therefore not too surprising, then that ff99SB* results in a lower fraction of hairpin than ff99SB. Although ff99SB* represents an improvement in terms of helical propensity for the Ac-(AAQAA)-NH₂ peptide on which it was parameterized, the available experimental data do not distinguish which of ff99SB or ff99SB* better captures the hairpin folding, both being within the range of experimental estimates of fraction folded at 300 K, and both producing chemical shift predictions in similar agreement with experiment. As discussed below, this highlights a need for more quantitative experimental data on similar peptide systems.

Finally, we can compare AMBER ff03* and ff99SB* in TIP3P water, where we observe that ff99SB* is generally more compact than ff03*. Both of these force fields have been subjected to a backbone “correction” to produce a similar overall helix propensity. The most likely source of the difference is in the parameterization of the charges, with AMBER ff03 being parameterized using a higher level of theory in conjunction with an implicit solvent model.³⁸ Both force fields result in similar agreement with NMR experimental data and the folded fraction, but the FRET calculation indicates that ff99SB is slightly more compact.

CONCLUSIONS

We have compared the folding free-energy landscape of the GB1 hairpin for six different protein force field and water combinations for which the hairpin is stable. Despite the overall similarity in fraction folded, we find significant differences in the structures populated in the unfolded state, with most force fields giving an unexpectedly large amount of helix for a hairpin-forming peptide. The exception to this is OPLS-AA/L, which is biased toward β structure. It is hard to say from the available experimental data whether this residual helix is in fact incorrect. Further experimental NMR data on unfolded peptides, particularly recorded over a range of temperatures, would help to resolve this issue.

A key finding is that the dimensions of the unfolded state, as measured by FRET, are too small, suggesting that all the force fields considered produce too “collapsed” an unfolded state. This suggests that the balance between protein–protein and protein–solvent interactions needs to be carefully considered in the development and validation of new force fields.

An important point for further development will be a more accurate quantitative comparison with experiment, because the present results suggest that from the point of view of the experimental data, most of the force fields are similarly good. In the case of FRET measurements, this may come from the direct inclusion of the chromophores in the simulation in order to capture more accurately their distribution of relative distances and orientations, as well as the appropriate dynamic averaging regime. For scalar couplings, inclusion of substituent effects in the parameters for the Karplus equation (e.g., by DFT calculations⁶⁹) should provide more quantitative results. In the case of chemical shifts, current prediction algorithms, although accurate, have several known deficiencies (e.g., treatment of ring current effects)—if these could be reduced, or the circumstances in which uncertainty arises better identified, then the (relatively small) differences between experimental and calculated shifts could be used for a more quantitative force-field assessment.