Econometric Mediation Analyses: Identifying the Sources of Treatment Effects from Experimentally Estimated Production Technologies with Unmeasured and Mismeasured Inputs

Abstract

This paper presents an econometric mediation analysis. It considers identification of production functions and the sources of output effects (treatment effects) from experimental interventions when some inputs are mismeasured and others are entirely omitted.

JEL Code: D24, C21, C43, C38

1 Introduction

William Barnett is a pioneer in the development and application of index theory and productivity accounting analyses. He has also pioneered the estimation of production functions. This paper follows in the tradition of Barnett’s work. It develops an econometric mediation analysis to explain the sources of experimental treatment effects. It considers how to use experiments to identify production functions in the presence of unmeasured and mismeasured inputs. The goal of the analysis is to determine the causes of effects: sources of the treatment effects properly attributable to experimental variation in measured inputs.

Social experiments usually proceed by giving a vector of inputs to the treatment group and withholding it from the control group. Analysts of social experiments report a variety of treatment effects. Our goal is to go beyond the estimation of treatment effects and examine the mechanisms through which experiments generate these effects. Thus we seek to use experiments to estimate the production functions producing treatment effects. This exercise is called mediation analysis in the statistics literature (Imai et al., 2011, 2010; Pearl, 2011). Such analyses have been used for decades in economics (Klein and Goldberger, 1955; Theil, 1958) and trace back to the work on path analysis by Sewall Wright (1921; 1934).

We provide an economically motivated interpretation of treatment effects. Treatment may affect outcomes through changing inputs. Treatment may also affect outcomes through shifting the map between inputs and outputs for treatment group members. When there are unmeasured (by the analyst) inputs, empirically distinguishing these two cases becomes problematic. We present a framework for making this distinction in the presence of unmeasured inputs and when the measured inputs are measured with error.

A fundamental problem of mediation analysis is that even though we might observe experimental variation in some inputs and outputs, the relationship between inputs and outputs might be confounded by unobserved variables. There may exist relevant unmeasured inputs changed by the experiment that impact outputs. If unmeasured inputs are not statistically independent of measured ones, then the observed empirical relation between measured inputs and outputs might be due to the confounding effect of experimentally induced changes in unmeasured inputs. In this case, treatment effects on outputs can be wrongly attributed to the enhancement of measured inputs instead of experimentally induced increase in unmeasured inputs.

Randomized Controlled Trials (RCTs) generate independent variation of treatment which allows the analyst to identify the causal effect of treatment on measured inputs and outputs. Nevertheless, RCTs unaided by additional assumptions do not allow the analyst to identify the causal effect of increases in measured inputs on outputs nor do they allow the analyst to distinguish between treatment effects arising from changes in production functions induced by the experiment or changes in unmeasured inputs when there is a common production function for treatments and controls.

This paper examines these confounding effects in mediation analysis. We demonstrate how econometric methods can be used to address them. We show how experimental variation can be used to increase the degree of confidence in the validity of the exogeneity assumptions needed to make valid causal statements. In particular, we show that we can test some of the strong assumptions implicitly invoked to infer causal effects in statistical mediation analyses. We analyze the invariance of our estimates of the sources of treatment effects to changes in measurement schemes.

The paper is organized in the following fashion. Section 2 discusses the previous literature and defines the mediation problem as currently framed in the statistics literature. Section 3 presents a mediation analysis within a linear framework with both omitted and mismeasured inputs. Section 4 discusses identification. Section 5 presents an estimation method. Section 6.1 discusses an invariance property when input measures are subject to affine transformations. Section 6.2 discusses further invariance results for general monotonic transformations of measures and for nonlinear technologies. Section 7 concludes.

2 Assumptions in Statistical Mediation Analysis

The goal of mediation analysis as framed in the literature in statistics is to disentangle the average treatment effect on outputs that operates through two channels: (1) Indirect output effects arising from the effect of treatment on measured inputs and (2) Direct output effects that operate through channels other than changes in the measured inputs. The mediation literature often ignores the point that Direct Effects are subject to some ambiguity: they can arise from inputs changed by the experiment that are not observed by the analyst, but can also arise from changes in the map between inputs and the outputs.

To clarify ideas it is useful to introduce some general notation. Let D denote treatment assignment. D = 1, if an agent is treated and D = 0 otherwise. Let Y₁ and Y₀ be counterfactual outputs when D is fixed at “1” and “0” respectively. By fixing, we mean an independent manipulation where treatment status is set at d. The distinction between fixing and conditioning traces back to Haavelmo (1943). For recent discussions see Pearl (2001, 2011) and Heckman and Pinto (2012). We use the subscript d ∈ {0, 1} to represent variables when treatment is fixed at d. In this notation Y_d represents output Y when treatment status is fixed at d and the realized output is given by

$$Y=D{Y}_1+(1-D)Y_0.$$ (1)

In our notation, the average treatment effect between treatment and control groups is given by

$$\mathit{ATE}=E(Y_1-Y_0).$$ (2)

We define a vector of inputs when treatment is fixed at d by ${\mathit{\theta }}_d=({\theta }_d^j:j\in \mathcal{J})$, where 𝒥 is an index set for inputs. We define the vector of realized inputs by θ in a fashion analogous to Y : θ = Dθ₁ + (1 − D)θ₀. While output Y is assumed to be observed, we allow for some inputs to be unobserved. Notationally, let 𝒥_p ⊆ 𝒥 be the index set of proxied inputs—inputs for which we have observed measurements. We represent the vector of proxied inputs by ${\mathit{\theta }}_d^p=({\theta }_d^j:j\in {\mathcal{J}}_p)$. We allow for the possibility that observed measurements may be imperfect proxies of measured inputs so that measured inputs may not be observed directly. We denote the remaining inputs indexed by 𝒥\𝒥_p as unmeasured inputs, which are represented by ${\mathit{\theta }}_d^u=({\theta }_d^j:j\in \mathcal{J}\backslash {\mathcal{J}}_p)$.

We postulate that the output Y is generated through a production function whose arguments are both measured and unmeasured inputs in addition to an auxiliary set of baseline variables X. Variables in X are assumed not to be caused by treatment D that affects output Y in either treatment state. The production function for each treatment regime is

$$Y_d=f_d({\mathit{\theta }}_d^p,{\mathit{\theta }}_d^u,\mathit{X}),d\in \{0,1\}.$$ (3)

Equation (3) states that output Y_d under treatment regime D = d is generated by ( ${\mathit{\theta }}_d^p,{\mathit{\theta }}_d^u$, X) according to function f_d such that d ∈ {0, 1}. If f₁ = f₀, functions (f₁, f₀) are said to be invariant across treatment regimes. Invariance means that the relationship between inputs and output is determined by a stable mechanism defined by a deterministic function unaffected by treatment.

From Equation (2), the average treatment effect or ATE is given by:

$$\mathit{ATE}=E(f_1({\mathit{\theta }}_1^p,{\mathit{\theta }}_1^u,\mathit{X})-f_0({\mathit{\theta }}_0^p,{\mathit{\theta }}_0^u,\mathit{X})).$$

Expectations are computed with respect to all inputs. Treatment effects operate through the impact of treatment D on inputs ( ${\mathit{\theta }}_d^p,{\mathit{\theta }}_d^u$), dε{0, 1} and also by changing the map between inputs and the outcome, namely, f_d(·); d ∈ {0, 1}. Observed output is given by $Y={\sum }_{d\in \{0,1\}}\mathbf{1}[D=d]·f_d({\mathit{\theta }}_d^p,{\mathit{\theta }}_d^u,\mathit{X})$.

We are now equipped to define mediation effects. Let $Y_{d,{\stackrel{\sim }{\mathit{\theta }}}_d^p}$ represent the counterfactual output when treatment status D is fixed at d and proxied inputs are fixed at the some value ${\overline{\mathit{\theta }}}_d^p\in \text{supp}{\mathit{\theta }}_{\mathit{d}}^{\mathit{p}}$. From production function (3),

$$Y_{d,{\overline{\mathit{\theta }}}^p}=f_d({\overline{\mathit{\theta }}}_d^p,{\mathit{\theta }}_d^u,\mathit{X}),d\in \{0,1\}.$$ (4)

Note that the subscript d of Y_d,θ̄^p arises both from the selection of the production function f_d(·), from the choice of d, and from changes in unmeasured inputs ${\mathit{\theta }}_d^u$. Moreover, conditional on X and fixing ${\mathit{\theta }}_d^p={\overline{\mathit{\theta }}}_d^p$, the source of variation of Y_d,θ̄^p is attributable to unmeasured inputs ${\mathit{\theta }}_d^u$. Keeping X implicit, use $Y_{d,{\overline{\mathit{\theta }}}_{d^{\prime }}^p}$ to represent the value output would take fixing D to d and simultaneously fixing measured inputs to be ${\overline{\mathit{\theta }}}_{d^{\prime }}^p$.

In the mediation literature, ATE is called the total treatment effect. It is often decomposed into direct and indirect treatment effects. The indirect effect (IE) is the effect of changes in the distribution of proxied inputs (from ${\mathit{\theta }}_0^p$ to ${\mathit{\theta }}_1^p$) on mean outcomes while holding the technology f_d and the distribution of unmeasured inputs ${\mathit{\theta }}_d^u$ fixed at treatment status d. Formally, the indirect effect is

$$\begin{array}{l}IE(d)=E(Y_d({\mathit{\theta }}_1^p)-Y_d({\mathit{\theta }}_0^p))\\ =E(f_d({\mathit{\theta }}_1^p,{\mathit{\theta }}_d^u,\mathit{X})-f_d({\mathit{\theta }}_0^p,{\mathit{\theta }}_d^u,\mathit{X})).\end{array}$$

Here expectations are taken with respect to ${\mathit{\theta }}_d^u$ and X. One definition of the direct effect (DE) is the average effect of treatment holding measured inputs fixed at the level appropriate to treatment status d but allowing technologies and associated distributions of unobservables to change with treatment regime:

$$\begin{array}{l}DE(d)=E(Y_{1,{\mathit{\theta }}_d^p}-Y_{0,{\mathit{\theta }}_d^p})\\ =E(f_1({\mathit{\theta }}_d^p,{\mathit{\theta }}_1^u,\mathit{X})-f_0({\mathit{\theta }}_d^p,{\mathit{\theta }}_0^u,\mathit{X})).\end{array}$$ (5)

Robin (2003) terms these effects as the pure, direct, and indirect effects, while Pearl (2001) calls them the natural direct and indirect effects.

We can further decompose the direct effect of Equation (5) into portions associated with the change in the distribution of ${\mathit{\theta }}_d^u$; d ∈ {0, 1} and the change in the map between inputs and outputs f_d(·); d ∈ {0, 1}. Define

$$D{E}^{\prime }(d,d^{\prime })=E(f_1({\mathit{\theta }}_{\mathit{d}}^{\mathit{p}},{\mathit{\theta }}_{{\mathit{d}}^{\prime }}^{\mathit{u}},\mathit{X})-f_0({\mathit{\theta }}_{\mathit{d}}^{\mathit{p}},{\mathit{\theta }}_{{\mathit{d}}^{\prime }}^{\mathit{u}},\mathit{X})).$$ (6)

DE′(d, d′) is the treatment effect mediated by changes in the map between inputs and outputs when fixing the distribution of measured inputs at ${\mathit{\theta }}_{\mathit{d}}^{\mathit{p}}$, and unmeasured inputs at ${\mathit{\theta }}_{{\mathit{d}}^{\prime }}^{\mathit{u}}$ for d, d′ ∈ {0, 1}. Define

$$D{E}^{″}(d,d^{\prime })=E(f_{d^{\prime }}({\mathit{\theta }}_{\mathit{d}}^{\mathit{p}},{\mathit{\theta }}_{\mathbf{1}}^{\mathit{u}},\mathit{X})-f_{d^{\prime }}({\mathit{\theta }}_{\mathit{d}}^{\mathit{p}},{\mathit{\theta }}_{\mathbf{0}}^{\mathit{u}},\mathit{X})).$$ (7)

DE″ (d, d′) is the treatment effect mediated by changes unmeasured inputs from ${\mathit{\theta }}_{\mathbf{0}}^{\mathit{u}}$ to ${\mathit{\theta }}_{\mathbf{1}}^{\mathit{u}}$ while setting the production function at f_d′ (·) where measured inputs are fixed at ${\mathit{\theta }}_{\mathit{d}}^{\mathit{p}}$ for d, d′ ∈ {0, 1}.

The definition of direct effect in Equation (5) is implicit in the mediation literature. Definitions (6) – (7) are logically coherent. Direct effects (5) can be written alternatively as:

$$\begin{array}{l}DE(d)=D{E}^{\prime }(d,1)+D{E}^{″}(d,0);\\ DE(d)=D{E}^{\prime }(d,0)+D{E}^{″}(d,1).\end{array}$$

The source of the direct treatment effect is often ignored in the statistical literature. It can arise from changes in unobserved inputs induced by the experiment (from ${\mathit{\theta }}_0^u$ to ${\mathit{\theta }}_1^u$). It could also arise from an empowerment effect e.g. that treatment modifies the technology that maps inputs into outputs (from f₀ to f₁). The change in technology may arise from new inputs never previously available such as parenting information as studied by Cunha (2012) and Heckman et al. (2012). If both measured and unmeasured inputs were known (including any new inputs never previously available to the agent), then the causal relationship between inputs and outputs could be estimated. Using the production function for each treatment state, one could decompose treatment effects into components associated with changes in either measured or unmeasured inputs. Since unmeasured inputs are not observed, the estimated relationship between measured inputs and outputs may be confounded with changes in unmeasured inputs induced by the experiment.

In this framework, under the definition of a direct effect (Equation 5), we can decompose the total treatment effect into the direct and indirect effect as follows:

$$\begin{array}{l}\mathit{ATE}=E(Y_1({\mathit{\theta }}_1^p)-Y_0({\mathit{\theta }}_0^p))\\ =\underset{DE(1)}{\underbrace{E(Y_1({\mathit{\theta }}_1^p)-Y_0({\mathit{\theta }}_1^p))}}+\underset{IE(0)}{\underbrace{E(Y_0({\mathit{\theta }}_1^p)-Y_0({\mathit{\theta }}_0^p))}}\\ =\underset{DE(0)}{\underbrace{E(Y_1({\mathit{\theta }}_0^p)-Y_0({\mathit{\theta }}_0^p))}}+\underset{IE(1)}{\underbrace{E(Y_1({\mathit{\theta }}_1^p)-Y_1({\mathit{\theta }}_0^p))}}.\end{array}$$

The literature of mediation analysis deals with the problem of confounding effects of unobserved inputs and the potential technology changes by invoking different assumptions. We now examine those assumptions.

The standard literature on mediation analysis in psychology regresses outputs on mediator inputs (Baron and Kenny, 1986). The assumptions required to give these regressions a causal interpretation are usually not explicitly stated. This approach often adopts the strong assumption of no variation in unmeasured inputs conditional on the treatment. Under this assumption, measured and unmeasured inputs are statistically independent. Moreover, the effect of unmeasured inputs ${\mathit{\theta }}_d^u$ are fully summarized by a dummy variable for treatment status. In addition, this literature assumes full invariance of the production function, that is, f₁(·) = f₀(·). Under these assumptions, function (3) reduces to

$$Y_d=f({\mathit{\theta }}_d^p,d,\mathit{X})$$ (8)

which can readily be identified and estimated. A similar framework is also used by in Pearl (2001).

Imai et al. (2011, 2010) present a different analysis and invoke two conditions in their Sequential Ignorability Assumption. Their approach does not explicitly account for unobserved inputs. They invoke statistical relationships that can be interpreted as a double randomization, i.e., they assume that both treatment status and measured inputs are randomized. More specifically, their approach assumes independence of both treatment status D and measured inputs ${\mathit{\theta }}_d^p$ with respect to $Y_{d,{\overline{\mathit{\theta }}}_d^p}$ conditional on covariates X.

Assumption A-1. Sequential Ignorability (Imai et al., 2011, 2010)

$$(Y_{d,{\overline{\mathit{\theta }}}_d^p},{\mathit{\theta }}_{d^{\prime }}^p)⫫D\mid \mathit{X};d,d^{\prime }\in \{0,1\}$$ (i)

$$Y_{d,{\overline{\mathit{\theta }}}_d^p}⫫{\mathit{\theta }}_{d^{\prime }}^p\mid D,\mathit{X};d,d^{\prime }\in \{0,1\}$$ (ii)

$$0<Pr(D=d\mid \mathit{X})<1\text{and}0<Pr({\mathit{\theta }}_d^p=\mathit{\theta }\mid D=d,\mathit{X})<1;d\in \{0,1\},\forall {\mathit{\theta }}_d^p,\mathit{\theta }\in \text{supp}({\mathit{\theta }}_d^p)$$ (iii)

Condition (i) of Assumption (A-1) states that both counterfactual outputs and counterfactual measured inputs are independent of D conditional on pre-program variables. These statistical relationships are generated by a RCT that randomly assigns treatment status D given X. Indeed, if treatment status D were randomly assigned by a randomization protocol that conditions on preprogram variables X, then Y_d ⫫ D|X (see e.g. Heckman et al. (2010) for a discussion). But proxied and unmeasured inputs are also outcomes in a RCT, and therefore $({\mathit{\theta }}_d^p,{\mathit{\theta }}_d^u⫫D\mid \mathit{X})$. Condition (i) of Assumption (A-1) is invoked to eliminate the dependence arising from the fact that for fixed X the source of variation of $Y_{d,{\overline{\mathit{\theta }}}_d^p}$ is ${\mathit{\theta }}_d^u$.

Condition (ii) declares that counterfactual outcomes given d and ${\overline{\mathit{\theta }}}_d^p$ are independent of unmeasured inputs given the observed treatment status and the pre-program variables X. In other words, input ${\mathit{\theta }}_{d^{\prime }}^p$ is statistically independent of potential outputs when treatment is fixed at D = d and measured inputs are fixed at ${\overline{\mathit{\theta }}}_{d^{\prime }}^p$ conditional on treatment assignment D and same pre-program characteristics X. The same randomization rationale used to interpret Condition (i) can be applied to Condition (ii). Thus Condition (ii) can be understood as if a second RCT were implemented for each treatment group such that measured inputs are randomized through a randomization protocol conditional on pre-program variables X and treatment status D. This randomization is equivalent to assuming that ${\mathit{\theta }}_d^p⫫{\mathit{\theta }}_{d^{\prime }}^0$ for all d and d′. Condition (iii) is a support condition that allows the estimation of treatment effects conditioned on the values X takes. Even though the Imai et al. (2010) and Imai et al. (2011) approach is weaker than the Pearl (2001) solution which is based on lack of variation of unobserved inputs, their assumptions are nonetheless still quite strong.

Imai et al. (2010) show that under Assumption A-1, the direct and indirect effects are given by:

$$E(IE(d)\mid \mathit{X})=\int E(Y\mid {\mathit{\theta }}^p=t,D=d,\mathit{X})({dF}_{({\mathit{\theta }}^p\mid D=1,\mathit{X})}(t)-{dF}_{({\mathit{\theta }}^p\mid D=0,\mathit{X})}(t))$$ (9)

$$E(DE(d)\mid \mathit{X})=\int (E(Y\mid {\mathit{\theta }}^p=t,D=1,\mathit{X})-E(Y\mid {\mathit{\theta }}^p=t,D=0,\mathit{X})){dF}_{({\mathit{\theta }}^p\mid D=1,\mathit{X})}(t).$$ (10)

Pearl (2011) uses the term Mediation Formulas for Equations (9)–(10). Like Imai et al. (2010), Pearl (2011) invokes the assumption of exogeneity on mediators conditioned on variables X to generate these equations.

Identification of the direct and indirect effects under the strong implicit assumption A-1, translates to an assumption of no-confounding effects on both treatment and measured inputs. This assumption does not follow from a randomized assignment of treatment. Randomized trials ensure independence between treatment status and counterfactual inputs/outputs, namely Y_d ⫫ D|X and ${\mathit{\theta }}_d^p⫫D\mid \mathit{X}$. Thus RCTs identify treatment effects for proxied inputs and for outputs. However, random treatment assignment does not imply independent variation between proxied inputs ${\mathit{\theta }}_d^p$ and unmeasured inputs ${\mathit{\theta }}_d^u$. In particular, it does not guarantee independence between counterfactual outputs $Y_{d,{\overline{\mathit{\theta }}}_d^p}$, which is generated in part by ${\mathit{\theta }}_d^u$, and measured inputs ${\mathit{\theta }}_{d^{\prime }}^p$ as assumed in Condition (ii) of Assumption A-1.

2.1 Mediation Analysis under RCT

It is useful to clarify the strong causal relationships implied by Condition (ii) of Assumption A-1 in light of a mediation model based on a RCT. To this end, we first start by defining a standard confounding model arising from uncontrolled pre-program unobserved variables. We then introduce a general RCT model and establish the benefits of RCTs in comparison with models that rely on standard matching assumptions. We then define a general mediation model with explicitly formulated measured and unmeasured inputs. We then examine the causal relationships of the mediation model that are implied by Condition (ii) of Assumption A-1. We show that the assumptions made in Assumption A-1 are stronger than standard assumptions invoked in matching.

A standard confounding model can be represented by three variables: (1) An output of interest Y ; (2) A treatment indicator D that causes the output of interest. As before, we use D = 1 for treated and D = 0 for untreated; (3) An unobserved variable V that causes both D and Y. A major difference between unobserved variable V and unobserved input ${\mathit{\theta }}_d^u$ is that V is not caused by treatment D while we allow ${\mathit{\theta }}_d^u$ to be determined by treatment. Thus, ${\mathit{V}}_1\stackrel{\mathit{dist}}{=}{\mathit{V}}_0$, where $\stackrel{\mathit{dist}}{=}$ means equal in distribution. We discuss the relationship between unobserved variable ${\mathit{\theta }}_d^u$ and V in presenting our mediation model.

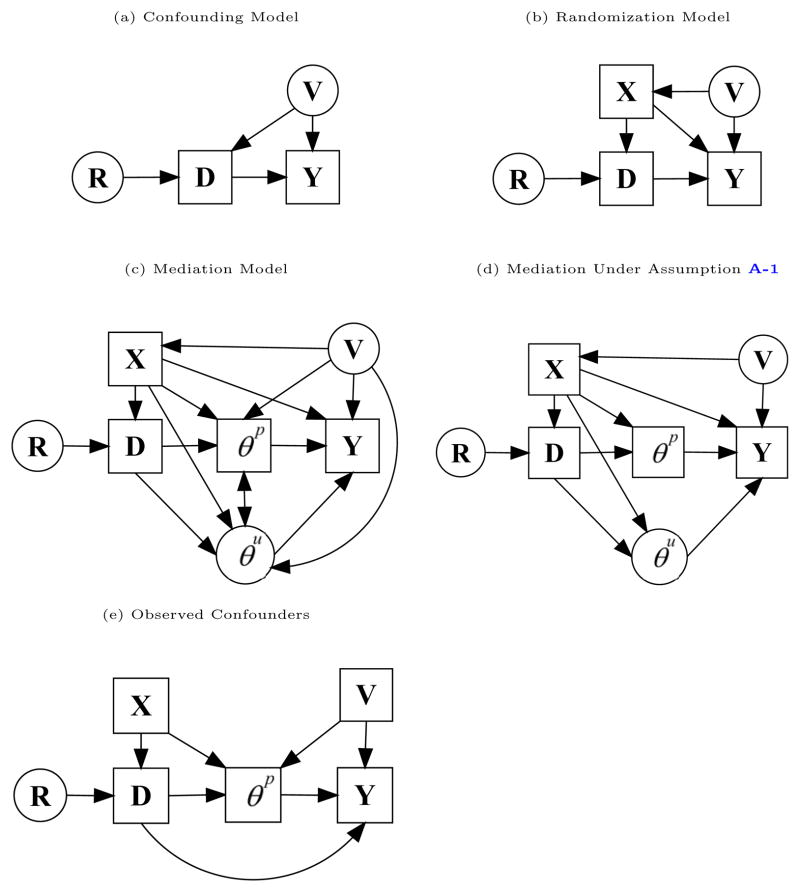
Model (a) of Figure 1 represents the standard confounding model as a Directed Acyclic Graph (DAG).¹ In this model, (Y₁, Y₀) ⫫ D does not hold due to confounding effects of unobserved variables V. As a consequence, the observed empirical relationship between output Y and treatment D is not causal and ATE cannot be evaluated by the conditional difference in means between treated and untreated subjects, i.e., E(Y |D = 1) − E(Y |D = 0). Nevertheless, if V were observed, ATE could be identified from ∫ E(Y |D = 1, V = υ) − E(Y |D = 0, V = υ)dF_V (υ) as (Y₁, Y₀) ⫫ D|V holds.

Figure 1.

Mechanisms of Causality for Treatment Effects

Notes: This chart represents five causal models as directed acyclic graphs. Arrows represent causal relationships. Circles represent unobserved variables. Squares represent observed variables. Y is an output of interest. V are unobserved variables. D is the treatment variable. X are pre-program variables. R is the random device used in RCT models to assign treatment status. θ_p are measured inputs. θ_u are unmeasured inputs. Both θ_p and θ_u play the role of mediation variables. Figure (a) shows a standard confounding model. Figure (b) shows a general randomized trial model. Figure (c) shows a general mediation model where unobserved variables V cause mediation variable (θ_p; θ_u): Figure (d) shows the causal relationships of a mediation model that are allowed to exist for Assumption A-1 to hold. Figure (e) shows the mediation model presented in Pearl (2001).

The literature on matching (Rosenbaum and Rubin, 1983) solves the problem of confounders by assumption. It postulates that a set of observed pre-program variables, say X, spans the space generated by unobserved variables V although it offers no guidance on how to select this set. Thus it assumes that observed pre-program variables X can be found such that (Y₁, Y₀) ⫫ D|X holds. In this case, ATE can be computed by

$$E(Y_1-Y_0)=\int E(Y\mid D=1,X=x)-E(Y\mid D=0,X=x){dF}_X(x).$$

For a review of matching assumptions and their limitations see Heckman and Navarro (2004) and Heckman and Vytlacil (2007).

Randomized controlled trials solve the problem of confounders by design. A standard RCT model for confounders can be represented by five variables: (1) An output of interest Y ; (2) A treatment indicator D that causes the output of interest and is generated by a random device R and variables X used in the randomization protocol; (3) Pre-program variables X used in the randomization protocol; (4) A random device R that assigns treatment status. (5) An unobserved variable V that causes both X and Y. Model (b) in Figure 1 represents the RCT model as a DAG.

In the RCT model, potential confounding effects of unobserved variables V are eliminated by observed variables X. ATE can be identified by

$$E(Y_1-Y_0)=\int E(Y\mid D=1,X=x)-E(Y\mid D=0,X=x){dF}_X(x).$$

While (Y₁, Y₀) ⫫ D|X holds in both matching and RCT models, it holds by assumption in matching models and by design in RCT models.

We now examine mediation analysis under the assumption that treatment status is generated by a RCT. To this end, we explicitly include measured and unmeasured inputs (θ^p, θ^u) to our RCT framework depicted in Model (b) of Figure 1. Inputs mediate treatment effects, i.e. inputs are caused by D and cause Y. Moreover, we also allow pre-program variables X to cause mediators θ^p, θ^u. The most general mediation model is described by the following relationships: (R1) mediators θ^p, θ^u are caused by unobserved variable V ; and (R2) measured inputs can cause unmeasured ones and vice-versa. Model (c) of Figure 1 represents this mediation model for RCT as a Directed Acyclic Graph (DAG).

A production function representation that rationalizes the mediation model is

$$Y_d=f_d({\mathit{\theta }}_d^p,{\mathit{\theta }}_d^u,\mathit{V},\mathit{X}),d\in \{0,1\}.$$ (11)

Equation (11) differs from Equation (3) by explicitly introducing pre-program unobserved variables V. Y_d,θ̄^p is now defined as:

$$Y_{d,{\overline{\mathit{\theta }}}^p}=f_d({\overline{\mathit{\theta }}}_d^p,{\mathit{\theta }}_d^u,\mathit{V},\mathit{X}).$$ (12)

It is the variation in ${\mathit{\theta }}_d^u$, V, and X that generate randomness in outcome Y_d, fixing θ̄^p.

We gain further insight into Assumption A-1 by examining it in light of the mediation model. The mediation model is constructed under the assumption that treatment status is generated by a RCT. Therefore Condition (i) of Assumption A-1 holds. However randomization does not generate Condition (ii) of Assumption A-1. If either R1 or R2 occurs, measured and unmeasured inputs will not be independent conditioned on observed variables (D, X). As a consequence, $Y_{d,{\overline{\mathit{\theta }}}_d^p}⫫̸{\mathit{\theta }}_{d^{\prime }}^p\mid D$. Model (d) of Figure 1 represents a mediation model in which Assumption A-1 holds, but neither R1 nor R2 occurs.

Condition (ii) is stronger than the conditions invoked in conventional matching analyses. Indeed, if V is assumed to be observed (a matching assumption), then relationship R1 reduces to a causal relationship among observed variables. Nevertheless, the matching assumption does not rule out R2. Relationship R2 would not apply if we adopt the strong assumption that unmeasured inputs have no variation conditional on the treatment.² The no-variation assumption assures that measured and unmeasured mediators are statistically independent conditional on D. This model is represented as a DAG in Model (e) of Figure 1. Pearl (2001) shows why Condition (ii) will not hold for Model (e) of Figure 1. However the direct effect (Equation 5) can be computed by Condition (ii):

$$DE(d)=\int \int (E(Y\mid D=1,{\mathit{\theta }}^p=t,V=v)-E(Y\mid D=0,{\mathit{\theta }}^p=t,V=v)){dF}_V(v)\int {dF}_{{\mathit{\theta }}^p\mid D=d,\mathit{X}=x,V=v}(t){dF}_{\mathit{X}}(x).$$

A general solution to the mediation problem is outside the scope of this paper. Instead we use a linear model to investigate how experimental variation coupled with additional econometric exogeneity assumptions can produce a credible mediation analysis for the case where some inputs are unobserved (but may be changed by the experiment) and proxied variables θ^p are measured with error. Our analysis is based on the production function defined in Equation (3). We assume that the map between inputs ${\mathit{\theta }}_d^p,{\mathit{\theta }}_d^u$ and output Y_d is given by a linear function. We then show how multiple measures on inputs and certain assumptions about the exogeneity of inputs allow us to test for invariance, i.e. whether f₁(·) is equal to f₀(·). Alternatively, invoking invariance we show how to test the hypothesis that increments in ${\mathit{\theta }}_d^p$ are statistically independent of ${\mathit{\theta }}_d^u$.

3 A Linear Model for Meditation Analysis

We focus on examining a linear model for the production function of output in sector d. The benefit of the linear model stems from its parsimony in parameters, which facilitates reliable estimation in small samples. Non-linear or non-parametric procedures require large samples often not available in RCTs. We write:

$$Y_d={\kappa }_d+{\mathit{\alpha }}_d{\mathit{\theta }}_d+{\mathit{\beta }}_d\mathit{X}+{\stackrel{\sim }{\epsilon }}_d,d\in \{0,1\},$$ (13)

where κ_d is an intercept, α_d and β_d are, respectively, |𝒥|-dimensional and |X|-dimensional vectors of parameters where |Q| denotes the number of elements in Q. Pre-program variables X are assumed not to be affected by the treatment, their effect on Y can be affected by the treatment. ε̃_d is a zero-mean error term assumed to be independent of regressors θ_d and X.

Technology (13) is compatible with a Cobb-Douglas model using linearity in logs. Thus an alternative to (13) is

$$log(Y_d)={\kappa }_d+{\mathit{\alpha }}_{d}log({\mathit{\theta }}_d)+{\mathit{\beta }}_{d}log(\mathit{X})+{\stackrel{\sim }{\epsilon }}_d,\text{or}$$ (14)

$$Y_d={\kappa }_d+{\mathit{\alpha }}_{d}log({\mathit{\theta }}_d)+{\mathit{\beta }}_{d}log(\mathit{X})+{\stackrel{\sim }{\epsilon }}_d,d\in \{0,1\}.$$ (15)

We discuss the estimation of θ_d in Section 3.1. There, we also adopt a linear specification for the measurement system that links unobserved inputs θ with measurements M. The Cobb-Douglas specification can be applied to the linear measurement system by adopting a linear-in-logs specification in the same fashion as used in outcome equations (14)–(15).

Analysts of experiments often collect an array of measures of the inputs. However, it is very likely that there are relevant inputs not measured. We decompose the term α_dθ_d in equation (13) into components due to inputs that are measured and inputs that are not:

$$\begin{array}{l}{Y}_d={\kappa }_d+\sum _{j\in \mathcal{J}}{\alpha }_d^j{\theta }_d^j+{\mathit{\beta }}_d\mathit{X}+{\stackrel{\sim }{\epsilon }}_d\\ ={\kappa }_d+\underset{\begin{array}{l}\text{inputs}\text{on}\text{which}\text{we}\\ \text{have}\text{measurements}\end{array}}{\underbrace{\sum _{j\in {\mathcal{J}}_p}{\alpha }_d^j{\theta }_d^j}}+\underset{\begin{array}{c}\text{inputs}\text{on}\text{which}\text{we}\\ \text{have}\text{no}\text{measurements}\end{array}}{\underbrace{\sum _{j\in \mathcal{J}\backslash {\mathcal{J}}_p}{\alpha }_d^j{\theta }_d^j}}+{\mathit{\beta }}_d\mathit{X}+{\stackrel{\sim }{\epsilon }}_d\\ ={\tau }_d+\sum _{j\in {\mathcal{J}}_p}{\alpha }_d^j{\theta }_d^j+{\mathit{\beta }}_d\mathit{X}+{\epsilon }_d,\end{array}$$ (16)

where d ∈ {0, 1}, ${\tau }_d={\kappa }_d+{\sum }_{j\in \mathcal{J}\backslash {\mathcal{J}}_p}{\alpha }_d^{j}E({\theta }_d^j)$, and ε_d is a zero-mean error term defined by ${\epsilon }_d={\stackrel{\sim }{\epsilon }}_d+{\sum }_{j\in \mathcal{J}\backslash {\mathcal{J}}_p}{\alpha }_d^j({\theta }_d^j-E({\theta }_d^j))$. Any differences in the error terms between treatment and control groups can be attributed to differences in the inputs on which we have no measurements. Without loss of generality we assume that ${\stackrel{\sim }{\epsilon }}_1\stackrel{\mathit{dist}}{=}{\stackrel{\sim }{\epsilon }}_0$, where $\stackrel{\mathit{dist}}{=}$ means equality in distribution. Note that the error term ∊_d is correlated with the measured inputs if measured inputs are correlated with unmeasured inputs.

We seek to decompose treatment effects into components attributable to changes in the inputs that we can measure. Assuming that changes in unmeasured inputs attributable to the experiment are independent of X, treatment effects can be decomposed into components due to changes in inputs E(Δθ^j) and components due to changes in parameters $\mathrm{\Delta }{\alpha }^j(={\alpha }_1^j-{\alpha }_0^j)$:

$$\begin{array}{l}E(\mathrm{\Delta }{Y}_d\mid \mathit{X})=E(Y_1-Y_0\mid \mathit{X})\\ =({\tau }_1-{\tau }_0)+E\left(\sum _{j\in {\mathcal{J}}_p}\left({\alpha }_1^j{\theta }_1^j-{\alpha }_0^j{\theta }_0^j\right)\right)+({\mathit{\beta }}_1-{\mathit{\beta }}_0)\mathit{X}\\ =({\tau }_1-{\tau }_0)+\sum _{j\in {\mathcal{J}}_p}\left(\left(\mathrm{\Delta }{\alpha }^j+{\alpha }_0^j\right)E(\mathrm{\Delta }{\theta }^j)+(\mathrm{\Delta }{\alpha }^j)E\left({\theta }_0^j\right)\right)+({\mathit{\beta }}_1-{\mathit{\beta }}_0)\mathit{X}.\end{array}$$ (17)

Equation (17) can be simplified if treatment affects inputs, but not the impact of inputs and background variables on outcomes, i.e. ${\alpha }_1^j={\alpha }_0^j$; j ∈ 𝒥_p and β₁ = β₀.⁴ This says that all treatment effects are due to changes in inputs. Under this assumption, the term associated with X drops from the decomposition. Note that under this assumption there still may be a direct effect (Equation 5) but it arises from experimentally induced shifts in unmeasured inputs.

If measured and unmeasured inputs are independent in the no-treatment outcome equation, α₀ can be consistently estimated by standard methods. Under this assumption, we can test if the experimentally-induced increments in unmeasured inputs are independent of the experimentally induced increments in measured inputs. This allows us to test a portion of Condition (ii) of Assumption A-1. The intuition for this test is as follows. The inputs for treated participants are the sum of the inputs they would have had if they were assigned to the control group plus the increment due to treatment. If measured and unmeasured input increments are independent, α₁ is consistently estimated by standard methods and we can test H₀ : plim α̂₁ = plim α̂₀ where (α̂₁, α̂ ₀) are least squares estimators of (α₁, α₀). Notice that even if α̂₀ is not consistently estimated, the test of the independence of the increments from the base is generally valid. Assuming the exogeneity of X, we can also test if plim β̂₁ = plim β̂₀.

Note further that if we maintain that measured inputs are independent of unmeasured inputs for both treatment and control groups, we can test the hypothesis of autonomy H₀ : α₁ = α₀. Thus there are two different ways to use the data from an experiment (a) to test the independence of the increments given that unmeasured inputs are independent of measured inputs or (b) to test H₀ : α₁ = α₀ maintaining full independence.

Imposing autonomy simplifies the notation. Below we show conditions under which we can test for autonomy. Equation (16) can be expressed as

$$Y_d={\tau }_d+\sum _{j_{\epsilon }\mathcal{J}}{\mathit{\alpha }}^{\mathit{j}}{\theta }^j+\mathit{\beta }\mathit{X}+{\epsilon }_d,d\in \{0,1\}.$$ (18)

In this notation, the observed outcome can be written as:

$$\begin{array}{l}Y=D\underset{Y_1}{\underbrace{({\tau }_1+\sum _{j\in {\mathcal{J}}_p}{\alpha }^j{\theta }_1^j+\mathit{\beta }\mathit{X}+{\epsilon }_1)}}+(1-D)\underset{Y_0}{\underbrace{({\tau }_0+\sum _{j\in {\mathcal{J}}_p}{\alpha }^j{\theta }_0^j+\mathit{\beta }\mathit{X}+{\epsilon }_0)}}\\ ={\tau }_0+\tau D+\sum _{j\in {\mathcal{J}}_p}{\alpha }^j{\theta }^j+\mathit{\beta }\mathit{X}+\epsilon ,\end{array}$$ (19)

where τ = τ₁ − τ₀ is the contribution of unmeasured variables to mean treatment effects, ε = D_ε1 + (1 − D)_ε0 is a zero-mean error term, and ${\theta }^j=D{\theta }_1^j+(1-D){\theta }_0^j$, j ∈ 𝒥_p denotes the inputs that we can measure.

If the ${\theta }_d^j$, j ∈ 𝒥_p are measured without error and are independent of the error term ∊, least squares estimators of the parameters of equation (19) are unbiased for α^j, j ∈ 𝒥_p. If, on the other hand, the unmeasured inputs are correlated with both measured inputs and outputs, least squares estimators of α^j, j ∈ 𝒥_p, are biased and capture the effect of changes in the unmeasured inputs as they are projected onto the measured components of θ, in addition to the direct effects of changes in measured components of θ on Y.

The average treatment effect is

$$E(Y_1-Y_0)=\underset{\begin{array}{c}\text{treatment}\text{effect}\text{due}\\ \text{to}\text{unmeasured}\text{inputs}\end{array}}{\underbrace{({\tau }_1-{\tau }_0)}}+\underset{\begin{array}{c}\text{treatment}\text{effect}\text{due}\\ \text{to}\text{measured}\text{inputs}\end{array}}{\underbrace{\sum _{j\in {\mathcal{J}}_p}{\alpha }^{j}E({\theta }_1^j-{\theta }_0^j)}}.$$ (20)

Input j can explain treatment effects only if it affects outcomes (α^j ≠ 0) and, on average, is affected by the experiment ( $E({\theta }_1^j-{\theta }_0^j)\ne 0$). Using experimental data it is possible to test both conditions.

Decomposition (20) would be straightforward to identify if the measured variables are independent of the unmeasured variables, and the measurements are accurate. The input term of Equation (20) is easily constructed by using consistent estimates of the α^j and the effects of treatment on inputs. However, measurements of inputs are often riddled with measurement error. We next address this problem.

3.1 Addressing the Problem of Measurement Error

We assume access to multiple measures on each input. This arises often in many studies related to the technology of human skill formation. For example, there are multiple psychological measures of the same underlying development trait. (See e.g., Cunha and Heckman (2008) and Cunha et al. (2010)). More formally, let the index set for measures associated with factor j ∈ 𝒥_p be ℳ^j. Denote the measures for factor j by $M_{m^j,d}^j$, where m^j ∈ ℳ^j, d ∈ {0, 1}. θ_d denotes the vector of factors associated with the inputs that can be measured in treatment state d, i.e., ${\mathit{\theta }}_d=({\theta }_d^j:j\in {\mathcal{J}}_p)$ d ∈ {0, 1}.

We assume that each input measure is associated with at most one factor. The following equation describes the relationship between the measures associated with factor j and the factor:

$$\text{Measures}:M_{m^j,d}^j={\nu }_{m^j}^j+{\phi }_{m^j}^j{\theta }_d^j+{\eta }_{m^j}^j,j\in {\mathcal{J}}_p,m^j\in {\mathcal{M}}^j.$$ (21)

To simplify the notation, we keep the covariates X implicit. Parameters ${\nu }_{m^j}^j$ are measure-specific intercepts. Parameters ${\phi }_{m^j}^j$ are factor loadings. The ∊_d in (18) and ${\eta }_{m^j}^j$ are mean-zero error terms assumed to be independent of θ_d; d ∈ {0, 1}, and of each other. The factor structure is characterized by the following equations:

$$\text{Factor}\text{Means}:E[{\theta }_d^j]={\mu }_d^j,j\in {\mathcal{J}}_p$$ (22)

$$\text{Factor}\text{Covariance}:\text{Var}[{\mathit{\theta }}_d]={\mathit{\sum }}_{{\mathit{\theta }}_d},d\in \{0,1\}.$$ (23)

The assumption that the parameters ${\nu }_{m^j}^j,{\phi }_{m^j}^j,\text{Var}({\eta }_{m^j}^j):m^j\in {\mathcal{M}}^j$, j ∈ 𝒥_p, do not depend on d simplifies the notation, as well as the interpretation of the estimates obtained from our procedure. It implies that the effect of treatment on the measured inputs operates only through the latent inputs and not the measurement system for those inputs. However, these assumptions are not strictly required. They can be tested by estimating these parameters separately for treatment and control groups and checking if measurement equation factor loadings and measurement equation intercepts differ between treatment and control groups.

4 Identification

Identification of factor models requires normalizations that set the location and scale of the factors (e.g., Anderson and Rubin, 1956 ). We set the location of each factor by fixing the intercepts of one measure—designated “the first”— to zero, i.e. ${\nu }_1^j=0$, j ∈ 𝒥_p. This defines the location of factor j for each counterfactual condition. We set the scale of the factor by fixing the factor loadings of the first measure of each skill to one, i.e. ${\phi }_1^j=1$, j ∈ 𝒥_p. For all measures that are related to a factor (i.e. have a non-zero loading on the factor, ${\phi }_{m^j}^j$) , the decomposition of treatment effects presented in this paper is invariant to the choice of which measure is designated as the “first measure” for each factor provided that the normalizing measure has a non-zero loading on the input. The decompositions are also invariant to any affine transformations of the measures. Our procedure can be generalized to monotonic nonlinear transformations of the measures.

Identification is established in four steps. First, we identify the means of the factors, ${\mu }_d^j$. Second, we identify the measurement factor loadings ${\phi }_{m^j}^j$, the variances $\text{Var}({\eta }_{m^j}^j)$ of the measurement system, and the factor covariance structure Σ_θd. Third, we use the parameters identified from the first and second steps to secure identification of the measurement intercepts ${\nu }_{m^j}^j$. Finally, we use the parameters identified in the first three steps to identify the factor loadings α and intercept τ_d of the outcome equations. We discuss each of these steps.

1. Factor Means

We identify ${\mu }_1^j$ and ${\mu }_0^j$ from the mean of the designated first measure for treatment and control groups: $E(M_{1,d}^j)={\mu }_d^j$, j ∈ 𝒥_p, d ∊; {0,1}.

2. Measurement Loadings

From the covariance structure of the measurement system, we can identify: (a) the factor loadings of the measurement system ${\phi }_{m^j}^j$; (b) the variances of the measurement error terms, $\text{Var}({\eta }_{m^j}^j)$; and (c) the factor covariance matrix, Σ_θd. Factors are allowed to be freely correlated. We need at least three measures for each input j ∈ 𝒥_p, all with non-zero factor loadings. The ${\phi }_{m^j}^j$ can depend on d ∈ {0, 1}, and we can identify ${\phi }_{m^j,d}^j$. Thus we can test if $H_0:{\phi }_{m^j,1}^j={\phi }_{m^j,0}^j$, j ∈ 𝒥_p, and do not have to impose autonomy on the measurement system.

3. Measurement Intercepts

From the means of the measurements, i.e. $E(M_{m^j,d}^j)={\nu }_{m^j}^j+{\phi }_{m^j}^j{\mu }_d^j$, we identify ${\nu }_{m^j}^j$, m^j ∈ ℳ^j\{1}, j ∈ 𝒥_p. Recall that the factor loadings ${\phi }_{m^j}^j$ and factor means ${\mu }_d^j$ are identified. Assuming equality of the intercepts ( ${\nu }_{m^j}^j$) between treatment and control groups guarantees that treatment effects on measures, i.e. $E(M_{m^j,1}^j)-E(M_{m^j,0}^j)$, operate solely through treatment effects on factor means, i.e. ${\mu }_1^j-{\mu }_0^j$. However, identification of our decomposition requires intercept equality only for the designated first measure of each factor. We can test $H_0:{\nu }_{m^j,1}^j={\nu }_{m^j,0}^j$ for all m^j ∈ ℳ^j\{1}, j ∈ 𝒥_p, and hence do not have to impose autonomy on the full measurement system.

4. Outcome Equation

Outcome factor loadings in equation (18) can be identified using the covariances between outcomes and the designated first measure of each input. We form the co-variances of each outcome Y_d with the designated first measure of each input j ∈ 𝒥_pto obtain Cov(Y_d, M_1,d) = Σ_θdα where α = (α^j, j ∈ 𝒥_p). By the previous argument, Σ_θd is identified. Thus α is identified whenever det(Σ_θd ≠ 0. We do not have to impose autonomy or structural invariance. Outcome factor loadings α can depend on d ∈ {0, 1}, as they can be identified through Cov(Y_d, M_1,d) = Σ_θdα_d which can be identified separately for treatments and controls. We can test $H_0:{\alpha }_1^j={\alpha }_0^j$, j ∈ 𝒥_p. Using E(Y_d), we can identify τd because all of the other parameters of each outcome equation are identified.

5 Estimation Procedure

We can estimate the model using a simple three stage procedure. First, we estimate the measurement system. Second, from these equations we can estimate the skills for each participant. Third, we estimate the relationship between participant skills and outcomes. Proceeding in this fashion makes identification and estimation transparent.

Step 1

For a given set of dedicated measurements, and choice of the number of factors, we estimate the factor model using measurement system (21)–(23). There are several widely used procedures to determine the number of factors. Examples of these procedures are the scree test (Cattell, 1966), Onatski’s criterion (2009), and Horn’s (1965) parallel analysis test. In addition, the Guttman-Kaiser rule (Guttman, 1954, and Kaiser, 1960, 1961 ) is well known to overestimate the number of factors (see Zwick and Velicer, 1986, Gorsuch, 2003, and Thompson, 2004). We refer to Heckman et al. (2013) for a detailed discussion of the selection of number of factors.

Step 2

We use the measures and factor loadings estimated in the first step to compute a vector of factor scores for each participant i. We form unbiased estimates of the true vector of skills ${\mathit{\theta }}_i=({\theta }_i^j;j\in {\mathcal{J}}_p)$ for agent i. The factor measure equations contain X which we suppress to simplify the expressions. Notationally, we represent the measurement system for agent i as

$$\underset{\mid \mathcal{M}\mid \times 1}{\underbrace{{\mathit{M}}_i}}=\underset{\mid \mathcal{M}\mid \times \mid {\mathcal{J}}_p\mid }{\underbrace{\mathit{j}}}\underset{\mid {\mathcal{J}}_p\mid \times 1}{\underbrace{{\mathit{\theta }}_i}}+\underset{\mid \mathcal{M}\mid \times 1}{\underbrace{{\mathit{\eta }}_i}},$$ (24)

where φ represents a matrix of the factor loadings estimated in first step and M_i is the vector of stacked measures for participant i subtracting the intercepts ${\nu }_{m^j}^j$ of equation (21). The dimension of each element in equation (24) is shown beneath it, where

$$\mathcal{M}={\cup }_{j\in {\mathcal{J}}_p}{\mathcal{M}}^j$$

is the union of all the index sets of the measures. The error term for agent i, η_i, has zero mean and is independent of the vector of skills θ_i. Cov(η_i, η_i) = Ω. The most commonly used estimator of factor scores is based on a linear function of measures: θ_S,i = L′M_i. Unbiasedness requires that L′φ =L_|𝒥|, where L_|𝒥| is a |𝒥|-dimensional identity matrix.⁵ To achieve unbiasedness, L must satisfy L′ = (φ′Ω⁻¹φ)⁻¹φ′ɷ⁻¹. The unbiased estimator of the factor is:

$${\mathit{\theta }}_{S,i}={\mathit{L}}^{\prime }{\mathit{M}}_i={({\mathit{j}}^{\prime }{\mathit{\Omega }}^{-1}\mathit{j})}^{-1}{\mathit{j}}^{\prime }{\mathit{\Omega }}^{-1}{\mathit{M}}_i.$$

Factor score estimates can be interpreted as the output of a GLS estimation procedure where measures are taken as dependent variables and factor loadings are treated as regressors. By the Gauss-Markov theorem, for a known φ the proposed estimator is the best linear unbiased estimator of the vector of inputs θ_i.⁶

Step 3

The use of factor scores instead of the true factors to estimate equation (18) generates biased estimates of outcome coefficients α. Even though estimates of θ_i are unbiased, there is still a discrepancy between the true and measured θ_i due to estimation error. To correct for the bias, we propose a bias-correction procedure. Because we estimate the variance of θ and the variance of the measurement errors in the first step of our procedure, we can eliminate the bias created by the measurement error.

Consider the outcome model for agent i :

$$Y_i=\mathit{\alpha }{\mathit{\theta }}_i+\mathit{\gamma }{\mathit{Z}}_i+{\mathit{\epsilon }}_i,$$ (25)

where (θ_i, Z_i) ⫫ ∊_i and E(∊_i) = 0. For brevity of notation, we use Z_i to denote pre-program variables, treatment status indicators, and the intercept term of equation (18). From equation (24), the factor scores θ_S,i can be written as the inputs θ_i plus a measurement error V_i, that is,

$${\mathit{\theta }}_{S,i}={\mathit{\theta }}_i+{\mathit{V}}_i\text{such}\text{that}({\mathit{Z}}_i,{\mathit{\theta }}_i)⫫{\mathit{V}}_i\text{and}E({\mathit{V}}_i)=0.$$ (26)

Replacing θ_i with θ_S,i yields Y_i = αθ_S,i + γZ_i + ∊_i − αV_i. The linear regression estimator of α and γ is inconsistent:

$$\text{plim}\left(\begin{array}{c}\widehat{\mathit{\alpha }}\\ \widehat{\mathit{\gamma }}\end{array}\right)\underset{\mathit{A}}{\underbrace{={\left(\begin{array}{cc}\text{Cov}({\mathit{\theta }}_S,{\mathit{\theta }}_S)& \text{Cov}({\mathit{\theta }}_S,\mathit{Z})\\ \text{Cov}(\mathit{Z},{\mathit{\theta }}_S)& \text{Cov}(\mathit{Z},\mathit{Z})\end{array}\right)}^{-1}\left(\begin{array}{cc}\text{Cov}(\mathit{\theta },\mathit{\theta })& \text{Cov}(\mathit{\theta },\mathit{Z})\\ \text{Cov}(\mathit{Z},\mathit{\theta })& \text{Cov}(\mathit{Z},\mathit{Z})\end{array}\right)}}\left(\begin{array}{c}\mathit{\alpha }\\ \mathit{\gamma }\end{array}\right).$$ (27)

This is the multivariate version of the standard one-variable attenuation bias formula. All covariances in A can be computed directly except for the terms that involve θ. Cov(θ, θ) is estimated in step (1). Using equation (26), we can compute Cov(Z, θ_S) = Cov(Z, θ). Thus, A is identified. Our bias-correction procedure consists of pre-multiplying the least squares estimators (α̂,γ̂) by A⁻¹, thus providing consistent estimates of (α,γ).⁷ A one step maximum likelihood procedure, while less intuitive, directly estimates the parameters without constructing the factors and accounts for measurement error. It is justified in large samples under standard regularity conditions.

6 Invariance to Transformation of Measures

We present some invariance results regarding the decomposition of treatment effects under transformations of the measures used to proxy the inputs. Our analysis is divided into two parts. Section 6.1 examines the invariance of the decomposition for affine transformation of measures under the linear model discussed in the previous section. Section 6.2 relaxes the linearity assumption of Section 6.1 and discusses some generalized results for the case of non-linear monotonic transformations using the analysis of Cunha et al. (2010).

6.1 Invariance to Affine Transformations of Measures

We first establish conditions under which outcome decomposition (20), relating treatment effects to experimentally induced changes in inputs, is invariant to affine transforms of any measure of input for any factor. Decomposition (20) assumes α₁ = α₀. We also consider forming decompositions for the more general nonautonomous case where α₁ ≠ α₀. We establish the invariance of the treatment effect due to measured inputs (see Equation (20)) but not of other terms in the decompositions that arise in the more general case. Throughout we assume autonomy of the measurement system so that intercepts and factor loadings are the same for treatments and controls for all measurement equations. Our analysis can be generalized to deal with that case but at the cost of greater notational complexity.

Before presenting a formal analysis, it is useful to present an intuitive motivation. Let ${\stackrel{\sim }{M}}_{m^j,d}^j$ be an affine transformation of the measure $M_{m^j,d}^j$, for some j ∈ 𝒥_p and m^j ∈ ℳ^j. Specifically, define ${\stackrel{\sim }{M}}_{m^j,d}^j$ by:

$${\stackrel{\sim }{M}}_{m^j,d}^j=a{M}_{m^j,d}^j+b\text{such}\text{that}a\in ℝ\backslash \{0\},b\in ℝ,\text{and}d\in \{0,1\},\text{for}\text{all}j\in {\mathcal{J}}_p.$$ (28)

Let ${\stackrel{\sim }{\phi }}_{m^j}^j,{\stackrel{\sim }{\eta }}_{m^j}^j,{\stackrel{\sim }{\nu }}_{m^j}^j$ be the factor loading, error term and intercept associated with the transformed measure ${\stackrel{\sim }{M}}_{m^j,d}^j$, d ∈ {0, 1}. The key condition for the invariance of decomposition (20) to linear transformations of the different measures is that ${\displaystyle \sum _{j\in {\mathcal{J}}_p}}{\alpha }^{j}E({\theta }_1^j-{\theta }_0^j)$ be invariant.

We apply the same normalization to the transformed system as we do to the original system. Suppose that the measure transformed is a “first measure” so m_j = 1. Recall that in the original system, ${\nu }_1^j=0$ and ${\phi }_1^j=1$. Transformation (28) can be expressed as

$${\stackrel{\sim }{M}}_{1,d}^j=b+a{\theta }_d^j+a{\eta }_1^j.$$

Applying the normalization rule to this equation defines factor θ̃_j = b + aθ_j, i.e. the scale and the location of the factor are changed, so that in the transformed system the intercept is 0 and the factor loading 1:

$${\stackrel{\sim }{M}}_{1,d}^j={\stackrel{\sim }{\theta }}_d^j+{\stackrel{\sim }{\eta }}_1^j$$

where ${\stackrel{\sim }{\eta }}_1^j=\alpha {\eta }_1^j$ is a rescaled mean zero error term. This transformation propagates through the entire system, where ${\theta }_d^j$ is replaced by ${\stackrel{\sim }{\theta }}_d^j$.

Notice that in decomposition (20), the induced shift in the mean of the factor is irrelevant. It differences out in the decomposition. The scale of θ^j is affected. The covariance matrix Σ_θd is transformed to Σ_θ̃d where

$${\mathit{\sum }}_{{\stackrel{\sim }{\mathit{\theta }}}_{\mathit{d}}}={\mathit{I}}_a{\mathit{\sum }}_{{\mathit{\theta }}_{\mathit{d}}}{\mathit{I}}_a$$

where I_a is a square diagonal matrix of the same dimension as the number of measured factors and the j^th diagonal is a and the other elements are unity. The factor loading for the outcome function for the set of transformed first measures, M̃_1,d =M_1,dI_a, is the solution to the system of equations

$$\text{Cov}(Y_d,{\stackrel{\sim }{\mathit{M}}}_{1,d})={\mathit{\sum }}_{{\stackrel{\sim }{\mathit{\theta }}}_{\mathit{d}}}{\stackrel{\sim }{\mathit{\alpha }}}_d.$$

Thus

$$\begin{array}{l}{\stackrel{\sim }{\mathit{\alpha }}}_{\mathit{d}}={\mathit{\sum }}_{{\stackrel{\sim }{\mathit{\theta }}}_{\mathit{d}}}^{-1}\text{Cov}({\mathit{Y}}_d,{\stackrel{\sim }{\mathit{M}}}_{1,d})\\ ={\mathit{I}}_a^{-1}{\mathit{\sum }}_{{\mathit{\theta }}_{\mathit{d}}}^{-1}{\mathit{I}}_a^{-1}\text{Cov}({\mathit{Y}}_d,{\stackrel{\sim }{\mathit{M}}}_{\mathbf{1},\mathit{d}})\\ ={\mathit{I}}_a^{-1}{\mathit{\sum }}_{{\mathit{\theta }}_{\mathit{d}}}^{-1}\text{Cov}({\mathit{Y}}_d,{\mathit{M}}_{1,d})\\ ={\mathit{I}}_a^{-1}{\mathit{\alpha }}_{\mathit{d}}.\end{array}$$

Since θ̃_d = I_aθ_d, it follows trivially that decomposition (20), ${\mathit{\alpha }}_{\mathit{D}}^{\prime }({\mathit{\theta }}_{\mathbf{1}}-{\mathit{\theta }}_{\mathbf{0}})$, is invariant to transformations.

Suppose next that the transformation is applied to any measure other than a first measure. Invoking the same kind of reasoning, it is evident that θ̃_d = θ_d and α̃_d = α_d. Thus the decomposition is invariant. Clearly, however, the intercept of the transformed measure becomes

$${\stackrel{\sim }{\nu }}_{m_j}^j=b+a{\nu }_{m_j}^j$$

and the factor loading becomes

$${\stackrel{\sim }{\phi }}_{m_j}^j={\phi }_{m_j}^{j}a.$$

The preceding analysis assumes that the outcome system is autonomous: α₀ = α₁, and β₀ = β₁. Suppose that α₁ ≠ α₀. To simplify the argument, we continue to assume that β₀ = β₁. In this case

$$E(Y_1-Y_0)=E({\mathit{\alpha }}_{\mathbf{1}}^{\prime }{\mathit{\theta }}_{\mathbf{1}}-{\mathit{\alpha }}_{\mathbf{0}}^{\prime }{\mathit{\theta }}_{\mathbf{0}}).$$

In the general case, the decomposition is not unique due to a standard index number problem. Using the notation Δα = α₁ − α₀,

$$\begin{array}{l}E(Y_1-Y_0)=\underset{\begin{array}{c}\text{invariant}\text{to}\text{affine}\\ \text{transformations}\text{of}\\ \text{measures}\end{array}}{\underbrace{{\mathit{\alpha }}_{\mathbf{0}}^{\prime }E({\mathit{\theta }}_{\mathbf{1}}-{\mathit{\theta }}_{\mathbf{0}})}}+\underset{\begin{array}{c}\text{non}\text{invariant}\text{to}\text{affine}\\ \text{transformations}\text{of}\\ \text{measures}\end{array}}{\underbrace{{(\mathrm{\Delta }\mathit{\alpha })}^{\prime }E({\mathit{\theta }}_{\mathbf{1}})}}\\ =\underset{\begin{array}{c}\text{invariant}\text{to}\text{affine}\\ \text{transformations}\text{of}\\ \text{measures}\end{array}}{\underbrace{{\mathit{\alpha }}_{\mathbf{1}}^{\prime }E({\mathit{\theta }}_{\mathbf{1}}-{\mathit{\theta }}_{\mathbf{0}})}}-\underset{\begin{array}{c}\text{non}\text{invariant}\text{to}\text{affine}\\ \text{transformations}\text{of}\\ \text{measures}\end{array}}{\underbrace{(\mathrm{\Delta }\mathit{\alpha })E({\mathit{\theta }}_{\mathbf{0}})}}.\end{array}$$

For any α* that is an affine transformation of (α₀,α₁):

$$E(Y_1-Y_0)=({\mathit{\alpha }}^{\ast })E({\mathit{\theta }}_{\mathbf{1}}-{\mathit{\theta }}_{\mathbf{0}})+({\mathit{\alpha }}_{\mathbf{1}}-{\mathit{\alpha }}^{\ast })E({\mathit{\theta }}_{\mathbf{1}})-({\mathit{\alpha }}_{\mathbf{0}}-{\mathit{\alpha }}^{\ast })E({\mathit{\theta }}_{\mathbf{0}}).$$

For all three decompositions, the first set of terms associated with the mean change in skills due to treatment is invariant to affine transformations. The proof follows from the preceding reasoning. Any scaling of the factors is offset by the revised scaling of the factor loadings.

Notice, however that when α₁ ≠ α₀, in constructing decompositions of treatment effects we acquire terms in the level of the factors. For transformations to the first measure, the change in the location is shifted. Even though the scales of (Δα) and E(θ_d) offset, there is no compensating shift in the location of the factor. Thus the terms associated with the levels of the factor are not, in general invariant to affine transformations of first measures although the decompositions are invariant to monotonic transformations of any non-normalization measures. Obviously the point of evaluation against E(θ₁ − θ₀) is evaluated depends on the choice of α₀, α₁, and α* if they differ.

We now formally establish these results. It is enough to consider the transformation of one measure within group j for treatment category d. First, suppose that the transformation (28) is not applied to the first measure, that is, m^j ≠ 1. In this case, $E({\theta }_1^j-{\theta }_0^j)$; j ∈ 𝒥_p are invariant as they are identified through the first measure of each factor which is not changed. We can also show that the α^j, j ∈ 𝒥_p, are invariant. We identify α = [α^j; j ∈ 𝒥_p] through Cov(Y_d,M_1,d) = Σ_θdα. Therefore it suffices to show that covariance matrix Σ_θd is invariant under the linear transformation (28). But the covariance between the factors is identified through the first measure of each factor. The variance of factor j under transformation (28) is identified by:

$$\begin{array}{l}\frac{\text{Cov}(M_{1,d}^j,{\stackrel{\sim }{M}}_{m,d}^j)\text{Cov}(M_{1,d}^j,M_{m^{\prime },d}^j)}{\text{Cov}({\stackrel{\sim }{M}}_{m,d}^j,M_{m^{\prime },d}^j)}=\frac{\text{Cov}(M_{1,d}^j,a{M}_{m,d}^j)\text{Cov}(M_{1,d}^j,M_{m^{\prime },d}^j)}{\text{Cov}(a{M}_{m,d}^j,M_{m^{\prime },d}^j)}\text{by}\\ =\frac{a\text{Cov}(M_{1,d}^j,M_{m,d}^j)\text{Cov}(M_{1,d}^j,M_{m^{\prime },d}^j)}{a\text{Cov}(M_{m,d}^j,M_{m^{\prime },d}^j)}\\ =\frac{\text{Cov}(M_{1,d}^j,M_{m,d}^j)\text{Cov}(M_{1,d}^j,M_{m^{\prime },d}^j)}{\text{Cov}(M_{m,d}^j,M_{m^{\prime },d}^j)}\\ =\text{Var}({\theta }_d^j),\end{array}$$ (28)

so that the variance is unchanged. Hence α_d is unchanged.

Now suppose that transformation (28) is applied to the first measure, m^j = 1. In this case, the new variance of factor j is given by:

$$\begin{array}{l}\frac{\text{Cov}({\stackrel{\sim }{M}}_{1,d}^j,M_{m,d}^j)\text{Cov}({\stackrel{\sim }{M}}_{1,d}^j,M_{m^{\prime },d}^j)}{\text{Cov}(M_{m,d}^j,M_{m^{\prime },d}^j)}=\frac{a\text{Cov}(M_{1,d}^j,M_{m,d}^j)a\text{Cov}(M_{1,d}^j,M_{m^{\prime },d}^j)}{\text{Cov}(M_{m,d}^j,M_{m^{\prime },d}^j)}\\ =a^2\text{Var}({\theta }_d^j).\end{array}$$ (29)

The new covariance between factors j and j′ is given by:

$$\begin{array}{l}\text{Cov}({\stackrel{\sim }{M}}_{1,d}^j,M_{1,d}^{j^{\prime }})=a\text{Cov}(M_{1,d}^j,M_{1,d}^{j^{\prime }})\\ =a\text{Cov}({\theta }_d^j,{\theta }_d^{j^{\prime }})\end{array}$$ (30)

Let Σ̃_θd be the new factor covariance matrix obtained under transformation (28). According to equations (29)–(30), Σ̃_θd= I_aΣ_θdI_a, where, as before, I_a is a square diagonal matrix whose j-th diagonal element is a and has ones for the remaining diagonal elements. By the same type of reasoning, we have that the covariance matrix Cov(Y_d,M_1,d) computed under the transformation is given by: Cov(Y_d, M̃_1,d) = I_a Cov(Y_d,M_1,d). Let α̃ be the outcome factor loadings under transformation (28). Thus,

$${\mathit{I}}_a\text{Cov}(Y_d,{\mathit{M}}_{1,d})=\text{Cov}(Y_d,{\stackrel{\sim }{\mathit{M}}}_{1,d})={\mathbf{\sum }^{\sim }}_{{\mathit{\theta }}_d}\stackrel{\sim }{\mathit{\alpha }}={\mathit{I}}_a{\mathit{\sum }}_{{\mathit{\theta }}_d}{\mathit{I}}_a\stackrel{\sim }{\mathit{\alpha }}$$ (31)

and therefore $\stackrel{\sim }{\mathit{\alpha }}={\mathit{I}}_a^{-1}\mathit{\alpha }$. In other words, transformation (28) only modifies the j-th factor loading which is given by ${\stackrel{\sim }{\alpha }}^j=\frac{{\alpha }^j}{a}$.

Let the difference in factor means between treatment groups be ${\mathrm{\Delta }}^{j^{\prime }}=E({\theta }_1^{j^{\prime }}-{\theta }_0^{j^{\prime }})$, j′ ∈ 𝒥_p, and let Δ̃^j′ be the difference under transformation (28). Transformation (28) only modifies the j-th difference in means which is given by Δ̃^j = aΔ^j and thereby α̃^jΔ̃^j = α^jΔ^j. Thus α̃^j′ ${\stackrel{\sim }{\mathrm{\Delta }}}^{j^{\prime }}={\alpha }^{j^{\prime }}{\mathrm{\Delta }}^{j^{\prime }}={\alpha }^{j^{\prime }}E({\theta }_1^{j^{\prime }}-{\theta }_0^{j^{\prime }})$ for all j′ ∈ 𝒥_p, as claimed. It is straightforward to establish that if α₁ ≠ α₀, the decomposition is, in general, not invariant to affine transformations, although the term associated with E(θ₁ − θ₀) is.

6.2 A Sketch of More General Invariance Results

We next briefly consider a more general framework. We draw on the analysis of Cunha et al. (2010) to extend the discussion of the preceding subsection to a nonlinear nonparametric setting. We present two basic results: (1) outcome decomposition terms that are locally linear in θ are invariant to monotonic transformations of θ; and (2) terms associated with shifts in the technology due to the experimental manipulation are not. In this section we allow inputs to be measured with error but assume that unmeasured inputs are independent of the proxied ones. We focus only on invariance results and only sketch the main ideas.

Here we sketch the main results. Following the previous notation, we use D for the binary treatment status indicator, D = 1 for treated and D = 0 for control. We denote Y_d; d ∈ {0, 1} to denote the output Y when treatment D is fixed at value d. In the fashion, θ_d; d ∈ {0, 1} denotes the input θ when treatment D is fixed at value d. For sake of simplicity, let the production function be given by f: supp(θ) → supp(Y ) where supp means support. Thus Y_d = f(θ_d); d ∈ {0, 1}.

We analyze both the invariant and noninvariant case. We relax the the invariance assumption for the production function by indexing it by treatment status. We use f_d: supp(θ) → supp(Y ) to denote the production function that governs the data generating process associated with treatment status D = d.

In this notation, the average treatment effect is given by:

$$E(Y_1-Y_0)=E(f_1({\mathit{\theta }}_1)-f_0({\mathit{\theta }}_0)).$$ (32)

Equation (32) repeats the discussion in Section 2 that there are two sources of treatment effects exist: (1) treatment might shift the map between θ and the outcomes from f₀ to f₁ (i.e. it might violate invariance); and (2) treatment might also change the inputs from θ₀ to θ₁.

Assume the existence of multiple measures of θ that are generated through an unknown function M: supp(θ) → supp(M) that is monotonic in θ. Then, under conditions specified in Cunha, Heckman, and Schennach (2010), the marginal distributions of θ₁ and θ₀ can be non-parametrically identified (although not necessarily the joint distribution of θ₁ and θ₀). We develop the scalar case.

Theorem T-1. The scalar case

Let the production function be a uniformly differentiable scalar function f_d: supp(θ) → supp(Y ); d ∈ {0, 1, }. If the production function is autonomous, i.e. f₁(t) = f₀(t) ∀ t ∈ supp(θ), then the effect attributable to changes in θ is invariant to monotonic transformations M of θ.

Proof

Without loss of generality, write the input for treated in terms of the input for untreated plus the difference across inputs. Thus θ₁ = θ₀ + Δ. Now, under structural invariance:

$$Y_1-Y_0=f(M({\theta }_1))-f(M({\theta }_0))=f(M({\theta }_0+\mathit{\Delta }))-f(M({\theta }_0)).$$

From uniform differentiability of M and f we have that:

$$\underset{\mathit{\Delta }\to 0}{lim}\frac{Y_1-Y_0}{\mathit{\Delta }}=\frac{\partial f}{\partial M}\frac{\partial M}{\partial \theta }.$$

Thus the infinitesimal contribution of a change in input to output can be decomposed as:

$$d(Y_1-Y_0)=\frac{\partial f}{\partial M}\frac{\partial M}{\partial \theta }d\theta .$$

If we use θ as the argument of the function, under conditions specified in Cunha et al. (2010) nonparametric regression identifies $\frac{\partial f}{\partial M}\frac{\partial M}{\partial \theta }$. If we use M(θ) as the argument, nonparametric regression identifies $\frac{\partial f}{\partial M}$ but the increment to input is now $\frac{\partial M}{\partial \theta }d\theta$. The combined terms for the output decomposition remain the same in either case. Thus the decomposition is invariant to monotonic transformations M of inputs θ. Extension to the vector case is straightforward.

Suppose that we relax autonomy. For sake of simplicity, take the scalar case and let the input for the treated input be written as θ₁ = θ₀+Δ. In this case, we can write the total change in output induced by treatment as:

$$\begin{array}{l}{Y}_1-Y_0=f_1(M({\theta }_1))-f_0(M({\theta }_0))\\ =f_1(M({\theta }_0+\mathit{\Delta }))-f_0(M({\theta }_0))\\ =\left(f_1(M({\theta }_0+\mathit{\Delta }))-f_1(M({\theta }_0))\right)+\left(f_1(M({\theta }_0))-f_0(M({\theta }_0))\right).\end{array}$$

If we rework the rationale of the proof for Theorem T-1 and apply the intermediate value theorem, we obtain the following expression:

$$Y_1-Y_0=\underset{\text{Invariant}}{\underbrace{{\frac{\partial f_1}{\partial M}\frac{\partial M}{\partial \theta }|}_{\theta ={\theta }_0^{\ast }}\mathit{\Delta }\theta }}+\underset{\text{Non}-\text{Invariant}}{\underbrace{f_1(M({\theta }_0))-f_0(M({\theta }_0))}}.$$ (33)

where ${\theta }_0^{\ast }$ is an intermediate value in the interval (θ₀, θ₀ + Δ). The first term is invariant for the same reasons stated in Theorem T-1 which concerns the autonomous case. Namely, the change in $\frac{\partial f}{\partial M}$ offsets the change in $\frac{\partial M}{\partial \theta }$.

The source of non-invariance of the second term in Equation (33) is attributed to the shift in production function f₀ to f₁ due to treatment. This shift implies that the output evaluation will differ when evaluated at the same input points θ₀. Under structural invariance or autonomy, f₁(·) = f₀(·) and regardless of the transformation M, we have that f₁(M(θ₀)) = f₀(M(θ₀)) and, therefore, the second term of Equation (33) vanishes.

7 Summary and Conclusions

Randomization identifies treatment effects for outputs and measured inputs. If there are unmeasured inputs that are statistically dependent on measured inputs, unaided experiments do not identify the causal effects of measured inputs on outputs.

This paper reviews the recent statistical mediation literature that attempts to identify the causal effect of measured changes in inputs on treatment effects. We relate it to conventional approaches in the econometric literature. We show that the statistical mediation literature achieves its goals under implausibly strong assumptions. For a linear model, we relax these assumptions maintaining exogeneity assumptions that can be partially relaxed if the analyst has access to experimental data. Linearity gives major simplifying benefits even in the case where ${\mathit{\theta }}_d^p$ is independent of ${\mathit{\theta }}_d^u$, where the point of evaluation of mean effects does not depends on the distribution of ${\mathit{\theta }}_d^u$. Extension of this analysis to the nonlinear case is a task left for future work.

We also present results for the case where there is measurement error in the proxied inputs, a case not considered in the statistical literature. When the analyst has multiple measurements on the mismeasured variables, it is sometimes possible to circumvent this problem. We establish invariance to the choice of monotonic transformations of the input measures for both linear and nonlinear technologies.