A Rapid Genome-wide Gene-based Association Test with Multivariate Traits

Abstract

Objectives:

A gene-based genome-wide association study (GWAS) provides a powerful alternative to the traditional single SNP association analysis due to its substantial reduction in the multiple testing burden and possible gain in power due to modeling multiple SNPs within a gene. A gene-based association analysis on multivariate traits is often of interest, but imposes substantial analytical as well as computational challenges to implement it at a genome-wide level.

Methods:

We have proposed a rapid implementation of multivariate multiple linear regression approach (RMMLR) in unrelated individuals as well as in families. Our approach allows for covariates. Moreover the asymptotic distribution of the test statistic is not heavily influenced by the linkage disequilibrium (LD) among the SNPs and hence can be used efficiently to perform a gene-based GWAS. We have developed corresponding R package to implement such multivariate gene-based GWAS with this RMMLR approach.

Results:

We compare through extensive simulation several approaches for both single and multivariate traits. Our RMMLR maintains correct type-I error level even for set of SNPs in strong LD. It also has substantial gain in power to detect a gene when it is associated with a subset of the traits. We have also studied their performance on Minnesota Center for Twin Family Research dataset.

Conclusions:

In our overall comparison, our RMMLR approach provides an efficient and powerful tool to perform a gene-based GWAS with single or multivariate traits and maintains the type I error appropriately.

1 Introduction

The rapid progress in genotyping technology has greatly facilitated our understanding of the genetic aspect of various diseases. Several genome-wide association studies (GWAS) have been published on various complex diseases, where genotype data on a large number of single nucleotide polymorphisms (SNPs) are collected to study the association between these SNPs and a disease (Visscher et al., 2012). Currently, most existing statistical methods of detecting genetic association focus on analyzing SNPs one-by-one (Roeder et al., 2005).

Although, new SNPs are found to be associated with these diseases, little of the genetic risk or heritability for these diseases is explained by the additive effects of these SNPs. Studying one SNP at a time may not be sufficient to understand complex diseases. Analyses focusing on individual SNPs may have several limitations: (a) A large number of comparisons increases the probability of false positives and a stringent correction could lead to loss of power. (b) each SNP alone may have very little effect on risk of disease (Lesnick et al., 2007), but multiple causal variants together may increase the risk substantially. A single-SNP analysis may not be optimal here; especially in presence of multi-SNP effects.

Hence, gene-based association analysis is often of interest in genome-wide association studies. These approaches substantially reduce the multiple testing burden at a GWAS scale. Moreover by pooling information on multiple SNPs within a gene, one could gain substantial power in detecting association. Current gene-based association approaches are mostly limited to combining single SNP association p-values to propose a gene-based test statistic (Neale and Sham, 2004; Ballard et al., 2010; Wang et al., 2007). One limitation of these gene-based statistics is that combining single SNP p-values ignores the potential joint effect of multiple SNPs within a gene. Joint modeling of the SNPs within a gene could have substantial gain in power over these existing gene-based tests. Moreover, the current approaches typically require permutation or simulation testing to account for the correlation between the SNPs as well as the gene size. VEGAS (Liu et al., 2010) and PLINK set-based test (Purcell et al., 2007) are two such available approaches for performing gene-based tests. They can be computationally very intensive to perform a gene-based GWAS, since they require a large number of permutations to correct for multiple testing. Hence their usefulness to conduct a gene-based GWAS is somewhat limited. Moreover, these approaches have been implemented for univariate phenotypes.

In the study of a complex disease, several correlated traits are often measured as risk factors for the disease. For example, in the study of thrombosis, the intermediate correlated phenotypes such as Factor VII, VIII, IX, XI, XII, and von Willebrand factor jointly predict the risk of developing thrombosis (Souto et al., 2000; Germain et al., 2011). There may be genetic variants affecting several of these traits. Analyzing multiple disease-related phenotypes could potentially increase power to detect association of SNPs/genes with a disease. Moreover this joint analysis could reveal some pleiotropic genes involved in the biological development of the disease. It has been shown that modeling multivariate phenotypes may increase the power over analyzing individual phenotypes separately in genetic association studies (Klei et al., 2008; Lange et al., 2004).

Few approaches have been developed to perform association analysis with multivariate traits at a GWAS level. O’Reilly et al. (2012) proposed MultiPhen to detect association between multivariate traits and a SNP with unrelated individuals. It uses ordinal regression to regress a SNP on a collection of phenotypes and tests whether all regression parameters corresponding to the phenotypes in the model are significantly different from zero. van der Sluis et al. (2013) proposed a method TATES for testing association between multiple traits and multiple SNPs using extended Simes procedure on the univariate p-values derived from univariate trait and single SNP association analysis. Recently, Maity et al. (2012) proposed a kernel machine method for joint analysis of multiple genetic variants, which treats the SNP effects as a random effect in the model. Their test for association between multiple SNPs and the phenotypes is equivalent to testing the variance components corresponding to the random effect in a multivariate linear mixed model. Implementation of this approach requires parametric bootstrapping to estimate the distribution of the test statistic and could be computationally intensive at a GWAS level. Also this method has been proposed for unrelated individuals.

Recently, the advantage of using canonical correlation analysis to perform gene-based tests on multivariate phenotypes has been elaborately discussed in Tang and Ferreira (2012). Previously, Ferreira and Purcell (2009) proposed a multivariate test of association based on canonical correlation analysis (CCA) to simultaneously test the association between a single SNP and multiple phenotypes. Their CCA approach is equivalent to multivariate analysis of variance (MANOVA) or more generally the Wilk’s lambda test in multivariate multiple linear regression (MMLR) approach (Muller et al., 1984). According to O’Reilly et al. (2012), MultiPhen and CCA performed very similarly in terms of power to detect causal variants except in case of low frequency SNPs and non-normal phenotypes. Both O’Reilly et al. (2012) and van der Sluis et al. (2013) found significantly high power of CCA in case of a subset of traits were associated with the causal variant or gene. One major advantage of CCA is that it can easily be extended to incorporate multiple phenotypes as well as multiple SNPs ( such as a gene). CCA provides the opportunity to study such multivariate phenotype-genotype association analysis. But CCA cannot accommodate covariates and one needs to perform the computationally intensive permutation testing to implement CCA in family data (Ferreira and Purcell, 2009).

In this paper, we have used the equivalence between the canonical correlation analysis and multivariate multiple linear regression (MMLR) approach to analyze multiple traits as well as multiple SNPs in families. In fact, our approach can be applied to samples involving both families as well as unrelated individuals.The advantage of MMLR approach is that one can easily incorporate the covariates in the model. Another advantage of MMLR approach is that it could provide a gene-based test of association without the need for permutation testing (Tang and Ferreira, 2012). We have proposed here a rapid MMLR (RMMLR) in families. We have developed related R package to perform a multivariate gene-based GWAS with this RMMLR approach. We have compared the performance of this RMMLR approach with several existing gene-based association analysis approaches, all of which require permutation or resampling techniques to estimate the null distribution of the test statistic in presence of correlated SNPs or correlated phenotypes.

2 Methods

2.1 Models

For a set of pedigrees each including one or more related individuals, let ylij denote the measured phenotype l on individual j in pedigree i (i = 1, … , m, j = 1 , … , n_i, ∑_i = n, and l = 1, … , L). Let X_ijk denote the additive genotype score of k-th SNP (k = 1, 2, … , K) with alleles ‘A’ and ‘a’ of individual j in pedigree i, and X_ijk can take values of 0, 1, or 2 depending on the number of minor allele ‘A’ for individual j in i th pedigree. Let vector Y_li = {yli1, … , ylin_i} denote the vector of l-th phenotype on individuals in i-th pedigree, and X_ik = {X_i1k, … , X_inik} denote the vector of genotypes of k-th SNP from pedigree i. Let C_i be a n_i × p matrix that contains the p covariates of pedigree i. We are interested in methods to conduct gene-based association analysis in pedigrees with one (unrelated individuals) or more related members with univariate or multivariate quantitative phenotypes.

For a quantitative phenotype l, we can do a single SNP association test for the k-th SNP using the following linear mixed effect model,

$${\mathit{Y}}_{li}={\alpha }_l+{\mathit{X}}_{ik}{\beta }_{lk}+{\mathit{C}}_i{\beta }_{lc}+{∊}_{li}$$ (1)

$$={\mathit{X}}_i{\beta }_l+{∊}_{li},i=1,\dots ,m,$$ (2)

where α_l is the population mean, β_lk is the additive fixed effect of the k-th SNP on l-th trait, β_lc is a size p vector of the covariate effects, and ε_li is the random residual term for l-th trait which is modeled as

$${∊}_{li}\stackrel{ind}{~}MVN(0,{\mathit{V}}_{li}),$$ (3)

assuming independent pedigrees. The n_i × n_i matrix V_li is the variance-covariance matrix for l-th trait. To simplify the notation as shown on the right hand side of equation (1), the observed data on the (p + 1) fixed predictors (1 SNP, p covariates) and the intercept corresponding to pedigree i are contained in the n_i × (p + 2) design matrix X_i, and the (p + 2) parameters are contained in the vector β_l for l-th trait.

A maximum likelihood estimator of V_li is calculated by ${\widehat{\mathit{V}}}_{li}$ by assuming multivariate normal distribution of the phenotype and certain parametric structure of V_li and considering the above model in Equation 2 but without the SNP term X_ikβ_lk. As shown in Li et al. (2011b), this approximation technique produces minimally biased estimates of V_li under the assumption that a single SNP explains a small part of the total phenotypic variance. Let ${\widehat{\mathit{V}}}_l$ be the block-diagonal matrix with ${\widehat{\mathit{V}}}_{li}$’s on its diagonal blocks, i =1,2, … , m. We used bdspackage() in R (Hornik, 2012) to compute the inverse of this block-diagonal matrix, denoted by ${\widehat{\mathit{V}}}_l^{-1}$ and a Cholesky decomposition of ${\widehat{\mathit{V}}}_l^{-1}$ as ${\widehat{\mathit{V}}}_l^{-1}=S_l{S}_l^T$ (Golub and Van Loan, 1996; Horn and Johnson, 1985; Trefethen and Bau, 1997). The Cholesky decomposition of the positive definite covariance matrix ${\widehat{\mathit{V}}}_l^{-1}$ yields a matrix S_l such that ${\widehat{\mathit{V}}}_l^{-1}=S_l{S}_l^T$, where S_l is lower triangular with positive diagonal elements. The matrix S_l is called the ‘Cholesky factor’ of ${\widehat{\mathit{V}}}_l^{-1}$ and is equivalent to the square-root of ${\widehat{\mathit{V}}}_l^{-1}$ , denoted by $V_l^{-1∕2}$. Hence $V_l^{-1∕2}{\mathit{Y}}_l$ would multivariate normal distribution with mean $V_l^{-1∕2}\left(\mathit{X}{\beta }_l\right)$ and covariance matrix $V_l^{-1∕2}{V}_l{V}_l^{-1∕2}=\mathit{I}$. In other words, the transformed data $V_l^{-1∕2}{\mathit{Y}}_l$ or S_lY_l would produce observations following multivariate normal distribution with mean S_lXβ_l and covariance matrix I.

Then a simple linear regression for these unrelated observations is carried out using the Cholesky-factor-transformed data,

$$Y_l^{\ast }=S_l{\mathit{Y}}_l=S_l\mathit{X}{\beta }_l+{∊}_l^{\ast },$$ (4)

where X is the n × (p + 2) matrix containing predictor values of all the m pedigrees, Y_l is the size n vector of phenotypes, β_l = (α_l, β_lk, β_lc) as defined in equation (2), and the residual term ${∊}_l^{\ast }$ is distributed as N(0, I). We make association calls based on the F-test statistics from the simple linear regressions in equation 4. Here we want to test the null hypothesis H₀ : β_lk = 0, for k = 1, 2, … , K and l = 1, 2, … , L.

2.2 Combination Methods

We used two combination methods to perform gene-based association analysis. The combination methods combine the single SNP association p-values to generate test statistics for the gene-based tests. At the first stage, p-values for all SNPs within a gene are obtained through single-SNP association tests based on standard regression models adjusting for other covariates. We used a rapid feasible generalized least square (RFGLS) approach (Li et al., 2011b) to perform the single SNP association analysis in pedigrees. The second stage requires the use of a single p-value to represent the significance of each gene. We applied two methods, the Fisher’s combination test and minP approach to calculate the significance of each gene.

• minP approach: Consider K SNPs within a gene. The minP test statistic is given by $p_{\text{min}}={\text{min}}_{i=1}^K\left\{K{p}_i\right\}$ for a single phenotype. We can extend it to consider testing association between genes and multiple phenotypes. For L phenotypes and K SNPs, the test statistic is given by $p_{\text{min}}={\text{min}}_{i=1}^{KL}\left\{KL{p}_i\right\}$. Under the assumption of independence among the SNPs as well as among the phenotypes, this test statistic has uniform distribution between [0,1] under null. For positively correlated tests, this test tends to be conservative. There are alternative approaches such as Simes method, Sidak method (Simes, 1986; Li et al., 2011a; Sidak, 1967) that improve the conservativeness of the test. Otherwise permutation procedure or parametric bootstrap could be used to get valid p-values.

• Fisher’s Combination Test: The test statistic is given by ${\chi }^2=-2{\sum }_{i=1}^K\text{log}{p}_i$ for SNPs and a single phenotype, which has a chi-square distribution with 2K degrees of freedom under the null hypothesis when the K tests are independent. We can extend this test for multiple phenotypes as well. The test statistic for testing no association between a gene and multiple phenotypes could be given by ${\chi }^{2^{\prime }}=-2{\sum }_{i=1}^{LK}\text{log}{p}_i$ for K SNPs and L phenotypes. Assuming we have independent tests here, this test statistic has a chi-square distribution with 2KL degrees of freedom under the null hypothesis H₀. The major issue with this test is that it becomes anti-conservative for positively correlated tests, which could be the situation for the SNPs in LD or for positively correlated multiple traits. Hence a permutation procedure or parametric bootstrap technique (equivalent to VEGAS-SUM approach) is needed if a valid p value is to be obtained. The Versatile Gene-Based Test for Genome-wide Association (VEGAS) (Liu et al., 2010) is a recent multivariate method that sums the association signal from all the SNPs within a gene and corrects the sum for LD to generate a p-value. One thing to note here is that VEGAS can only handle a single trait to perform a gene-based GWAS.

2.3 Direct modeling of multiple SNPs and multiple phenotypes

The combination methods provide a convenient way of proposing gene-based tests by utilizing the single SNP association p-values. However by directly modeling multiple correlated traits and multiple SNPs, one could detect pleiotropic effects and could gain power by jointly modeling the effects of multiple SNPs in a single model.

Multivariate multiple linear regression

Below we describe a multivariate multiple regression model (MMLR) with L traits and K SNPs for n unrelated individuals. Consider the following model for n individuals with outcome variable ${\mathit{Y}}^{\ast }=(Y_l^{\ast },l=1,\dots ,L)$ in Equation 4 of length L:

$${\mathit{Y}}_i^{\ast }={\mathit{Z}}_i\beta +{\mathit{e}}_i;i=1,\dots ,n,$$

where e_i = (e_i1, …e_iL) follows multivariate normal distribution; ${\mathit{Y}}_i^{\ast }=(Y_{i1},\dots Y_{iL})$ contains transformed data on L phenotypes; Z_i contains the transformed data S_lX_i on K predictors (SNPs) and intercept for the i-th individual. The vector β = (β₀, β₁, β₂, … , β_K) represents the parameters corresponding to the intercept and K SNPs. In this case the within-sample sum of squares (SS) matrix (W) is calculated as the covariance matrix of the residuals of the model, and the between-sample SS matrix is calculated as the covariance matrix of the fitted values (B). We use the Wilk’s λ test, $\lambda =\frac{\mid W\mid }{\mid T\mid }$, where T = W + B to test the null hypothesis β = 0. It has been shown that for unrelated individuals, this MMLR approach is equivalent to the CCA approach mentioned before (Muller et al., 1984).

Compared with CCA, MMLR is much easier to expand to family structure and adjust for covariates. To apply it to family data, we use the computationally efficient RFGLS approach (Li et al., 2011b). We calculate the within-cluster covariance matrix for each trait, and left-multiply both the traits and the predictors separately by the inverse-square-root of the estimated covariance matrix. This transformation gives us the traits individually as independently distributed. We then compute the residuals for each trait from a model with intercept and modified covariates as well as the SNPs. Let us denote the residuals as ${\mathit{e}}_1^{\ast },{\mathit{e}}_2^{\ast },\dots ,{\mathit{e}}_L^{\ast }$. We compute the covariance matrix of these residuals. This will be our W. In order to calculate T, we compute the residuals for each trait from a model with only intercept and the modified covariates. The covariance matrix of these residuals will give us T. We calculate our test statistic as $\lambda =\mid \frac{W}{T}\mid$, which will be approximately distributed as F with degrees of freedom df1 and df2, where df1 = KL and $df2=\left(n-3∕2-\frac{K+L}{2}\right)s-\frac{KL}{2}+1$. We refer to this approach as rapid multivariate multiple linear regression (RMMLR).

2.4 Simulations

To compare different methods, we investigated their type I error and power by simulating data on nuclear families with two parents and two offspring. For simulating genotype data on a gene, we used a simulation set-up very similar to that of Li et al. (2011a). First, we generated genotype data on 16 SNPs with different LD structures. We generated 3 independent blocks of SNPs; the first and the third block with 6 SNPs and the second block with 4 SNPs. For low linkage disequilibrium (LD) scenario, pairwise LDs (r²) were 0.5, 0.4, 0.5 for the 3 blocks respectively; while for high LD scenario, pairwise LDs (r²) were 0.9, 0.8, 0.9 respectively. The minor allele frequencies (MAFs) for 3 blocks were 0.2, 0.4, 0.25 respectively. Note that X_ijk denote the genotype of the k-th SNP for the j-th member in the i-th family. For j-th member in i-th family, we draw a vector (16 × 1) of latent variables U_ij, from multivariate normal with covariance matrix as (1) low LD structure as shown in appendix of Li et al. (2011a); (2) high LD structure as shown in appendix of Li et al. (2011a). Then by assuming HWE, we dichotomize U_ijk such that if $U_{ijk}<p_k^2$, then X_ijk=2; if U_ijk > 1 − (1 − p_k)², then X_ijk = 0; otherwise X_ijk=1, k = 1, … , 16 and p_k is the MAF of kth SNP. We repeat this procedure to simulate genotypes of parents for all the nuclear families. Then following Mendel’s Law, we generate genotypes of 2 offspring in each family. From each LD block of SNPs, the first SNP is selected as the causal SNP. We consider 2 different gene-lengths such that the gene (1) contains the first 3 SNPs (2) contains all the 16 SNPs.

We then simulate five correlated traits. The simulation model is

$${\mathit{Y}}_{li}={\mathit{G}}_i\beta +{\alpha }_{li}+e_{li},$$

where Y_li = (Y_li1, Y_li2, Y_li3, Y_li4) is the vector of phenotypes for l-th trait in i-th family. The parameter α_li is the polygenic random effect for i-th family and l-th trait. G_i is the matrix of genotypes of the causal SNPs, which is a 4× r matrix if we have r causal SNPs.

We allow correlation among different traits within each family. Suppose we have 5 traits, We then draw α_i = (α_1i1, α_1i2, α_1i3, α_1i4, …, α_5i1, α_5i2, α_5i3, α_5i4) from multivariate normal with mean 0 and covariance matrix ∑₁ as:

$$\left(\begin{array}{cccc}\hfill {\sigma }_{a1}^{2}2\Phi \hfill & \hfill {\rho }_{ab}{\sigma }_{a1}{\sigma }_{a2}\ast 2\Phi \hfill & \hfill \dots \hfill & \hfill {\rho }_{ab}{\sigma }_{a1}{\sigma }_{a5}2\Phi \hfill \\ \hfill {\rho }_{ab}{\sigma }_{a1}{\sigma }_{a2}\ast 2\Phi \hfill & \hfill {\sigma }_{a2}^{2}2\Phi \hfill & \hfill \dots \hfill & \hfill {\rho }_{ab}{\sigma }_{a2}{\sigma }_{a5}2\Phi \hfill \\ \hfill \hfill & \hfill \hfill & \hfill \dots \hfill & \hfill \hfill \\ \hfill {\rho }_{ab}{\sigma }_{a1}{\sigma }_{a5}2\Phi \hfill & \hfill {\rho }_{ab}{\sigma }_{a2}{\sigma }_{a5}2\Phi \hfill & \hfill \dots \hfill & \hfill {\sigma }_{a5}^{2}2\Phi \hfill \end{array}\right),$$

where Φ is the kinship matrix and ρ_ab is the genetic correlation between traits, which is assumed in the simulation to be the same for all traits. In our simulation, for nuclear families with two offspring, we use the kinship matrix for offspring 1, offspring 2, parent 1 and parent 2 as

$$2\Phi =\left(\begin{array}{cccc}\hfill 1\hfill & \hfill 0.5\hfill & \hfill 0.5\hfill & \hfill 0.5\hfill \\ \hfill 0.5\hfill & \hfill 1\hfill & \hfill 0.5\hfill & \hfill 0.5\hfill \\ \hfill 0.5\hfill & \hfill 0.5\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0.5\hfill & \hfill 0.5\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)$$

and ${\sigma }_{a1}^2={\sigma }_{a2}^2={\sigma }_{a3}^2={\sigma }_{a4}^2={\sigma }_{a5}^2=60$. We also simulate the environmental component e_i = (e_1i1, e_1i2, e_1i3, e_1i4, ….e_5i1, e_5i2, e_5i3, e_5i4) from multivariate normal with mean 0 and covariance matrix as:

$$\left(\begin{array}{cccc}\hfill {\sigma }_{e1}^{2}I\hfill & \hfill \mathit{W}\hfill & \hfill \dots \hfill & \hfill \mathit{W}\hfill \\ \hfill \mathit{w}\hfill & \hfill {\sigma }_{e2}^{2}I\hfill & \hfill \dots \hfill & \hfill \mathit{W}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \dots \hfill & \hfill \hfill \\ \hfill \mathit{W}\hfill & \hfill \mathit{W}\hfill & \hfill \dots \hfill & \hfill {\sigma }_{e5}^{2}I\hfill \end{array}\right)$$

where ${\sigma }_{el}^2$ represent the environmental variance of trait l, l = 1, … , 5. In majority of the simulations, we consider no environmental correlation between the trait values for the same individual, i.e W = I. Also we assume ${\sigma }_{e1}^2={\sigma }_{e2}^2={\sigma }_{e3}^2={\sigma }_{e4}^2={\sigma }_{e5}^2=40$. For a 3-snp gene, only the first block is used; while for the 16 snp gene, all 3 blocks are used. We simulate 5 traits with different genetic correlations between the traits: ρ_ab = 0.33, 0.67, 1, which corresponds to a phenotypic correlation between the traits of 0.2,0.4 and 0.6 respectively. The first SNP of every block is the causal SNP under the alternative, if the gene has covered that block.

This means that the correlations between different traits are entirely coming from the genetic effect rather than the environment effect. Lastly, we add the causal SNP(s) effect to the mean. The causal effect is obtained as ${\beta }_k=\sqrt{\frac{h_k^2}{2p_k(1-p_k)}}$, for the k-th causal SNP, where $h_k^2$ is the phenotypic variance explained by the k-th causal SNP. For ρ_ab = 0.33 and ρ_ab = 0.67, we also perform 5000 simulations to study the effect environmental correlation on power. We allow for environmental correlation of r = 0.25 and r = 0.5 between each pair of traits, i.e we consider W = rσ_elσ_elI, for each pair of traits l and k, l, k = 1, .., 5.

3 Results

We first simulated data under the null hypothesis to see the impact on type I error. We simulated 100000 datasets on 1000 nuclear families under the null hypothesis of no association between a gene and 5 traits. The type I error was estimated by calculating the proportion of times the asymptotic p-value of the test statistic for each method was 0≤001, 0≤0001 and 0≤00001. We considered situations where the SNPs were in low LD and in high LD and presented here only the results for the gene with 16 SNPs. The minP statistic in low LD situation (Table 1) was not that conservative, but did get conservative in high LD situation (Table 2). On the other hand, Fisher’s test was inflated due to the positive correlation among the traits as well as the SNPs. The type I error for Fisher’s test was substantially higher for the high LD situation (Table 2) as compared to the low LD (Table 1) condition due to the higher positive correlation among the SNPs. Moreover the type I error for Fisher’s test was increased as the correlation among the traits increased from 0.2 to 0.6. This are known issues with minP approach and Fisher’s test, but we still wanted to demonstrate the extent of the impact of correlation among traits as well as SNPs on these two popular approaches and the need to use approaches such as Liu et al. (2010), Li et al. (2011a) to correct for these issues with type-I error. On the other hand, the RMMLR approach maintained correct type-I error under both low LD and high LD situation and for different degrees of correlation among the traits.

Table 1.

Type I error for testing association between 5 traits and a gene of length of 16 SNPs. There is moderate LD among the set of SNPs.

	α = 0.001			α = 0.0001			α = 0.00001
Trait cor	minP	Fisher	RMMLR	minP	Fisher	RMMLR	minP	Fisher	RMMLR
0.2	0.0012	0.0071	0.00095	9.8e−5	0.0018	9.75e−5	9.4e−6	4.5e−4	9.9e−6
0.4	0.0011	0.026	0.00095	9.5e−5	0.0012	9.5e−5	9.7e−6	5.8e−3	9.9e−6
0.6	0.0011	0.035	0.00096	9.8e−5	0.0017	9.5e−5	9.6e−6	8.7e−3	9.7e−6

Table 2.

Type I error for testing association between 5 traits and a gene of length of 16 SNPs. There is high LD among the set of SNPs

	α = 0.001			α = 0.0001			α = 0.00001
Trait cor	minP	Fisher	RMMLR	minP	Fisher	RMMLR	minP	Fisher	RMMLR
0.2	0.0007	0.026	0.0011	8.03e−5	0.0016	9.97e−5	0.000	5.5e−3	1.004e−5
0.4	0.0008	0.048	0.00095	5.1e−5	0.026	1.02e−4	0.000	0.0015	1e−5
0.6	0.0008	0.076	0.001	0.000	0.048	9.5e−5	0.000	0.031	9.9e−6

We next simulated data under the alternative. We considered situations where the gene was associated with 1, 2, 3, 4 or all 5 traits. For each scenario, we simulated 5000 datasets on 500 nuclear families. We also considered 2 different gene-length and different LD patterns among the SNPs to see the impact of gene-length and LD on power. We reported the empirical power for the minP and Fisher’s test in order to correct for any inflatedness or conservativeness in the type I error. The empirical power was calculated by counting the proportion of times the trait SNP was called significant (p-value ≤ empirical 0.001-th cut-off) out of the 5, 000 simulations. Since RMMLR approach maintained correct type I error rate, we reported the asymptotic power for the approach.

We first simulated data on 500 nuclear families for a gene of size 3 SNPs with one causal SNP explaining .6% of the phenotype variance. Table 3 shows the empirical power of minP, Fisher’s test and asymptotic power of RMMLR at a type-I error level of .001. We reported here the situations where the causal SNP is associated with all the traits and the situation where 3 of the traits are associated with the SNP. In case of complete association, minP and Fisher’s test had comparable power (Table 3) for different inter-trait correlations. The power for RMMLR approach was relatively lower than the other two approaches. All of them lost power as we increased the inter-trait correlation among individuals. On the other hand, the RMMLR approach had significantly higher power than other approaches in case a subset of traits were associated with the gene ( Table 3). Moreover the power for gene detection generally went up for the RMMLR approach when the trait correlation was increased in case the gene was associated with a subset of the traits, but the other two approaches lost power as the trait correlation went higher. Especially, Fisher’s test performed very poorly when the trait correlation was high and a subset of traits were associated with the gene.

Table 3.

Power of different methods for 3-SNP gene (1 causal SNP): moderate LD

Trait cor	All 5 traits associated			3 traits associated
	minP	Fisher’s test	RMMLR	minP	Fisher’s test	RMMLR
0.2	0.687	0.815	0.653	0.574	0.425	0.596
0.4	0.596	0.535	0.463	0.536	0.247	0.639
0.6	0.476	0.475	0.285	0.406	0.149	0.801

We next considered a 16-SNP gene with 3 causal SNPs explaining a total of 0.9% variability for each of the associated traits and where the gene was associated with 1,2,3,4 or all 5 traits. Figure 1 shows the performance of the different approaches when the correlation among the traits was 0.2,0.4 and 0.6. The SNPs were in moderate LD. In general, the RMMLR approach had significantly better or equivalent power to the other approaches except for the situation when the gene was associated with all the traits. It also appeared to perform better when the residual trait correlation was moderate or high (0.4 or 0.6). Especially when the trait correlation was 0.6, the power was substantially higher in case the gene was associated with a subset of traits (Figure 1). On the other hand, the power for both minP and Fisher’s test decreased as the trait correlation was increased. Fisher’s test gained little power for the 16-SNP gene compared to the 3-SNP gene situation (Table 3) due to the fact that multiple SNPs were associated with the traits. On the other hand, minP lost significant power for a 16-SNP gene (Figure 1) as compared to the 3-SNP gene study for not accounting for multiSNP association. As expected, Fisher’s test had very good power when most or all the traits were associated with the gene, but its inflated type I error due to high correlation among traits or SNPs significantly limited its usefulness to perform gene-based association analysis.

Figure 1.

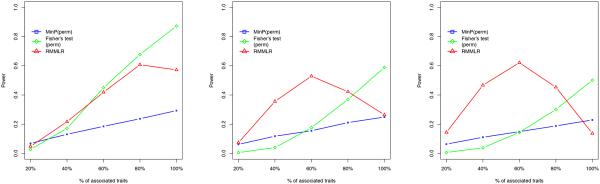
Figure shows the performance of the multivariate test of association. The powers for minP, Fisher’s test and RMMLR approach are shown for different number of traits being associated with a gene with 16 SNPs. The three figures (left to right) corresponds to the residual trait correlation of 0.2, 0.4 and 0.6 respectively.

We also checked the behavior of these approaches for a 16-SNP gene when the LD among the SNPs was high and the gene was associated with 3 out of the 5 traits. After correcting for type I error for minP and Fisher’s test, all the approaches maintained similar power for both the low LD (Table 4) and high LD situations (Figure 1). We also studied the effect of increasing environmental correlation for this 16-SNP gene with 3 causal SNPs and when the LD among the SNPs was high and the gene was associated with 3 out of the 5 traits. For a genetic correlation of ρ_ab =0.33 and 0.67, we considered environmental correlation (r) of 0.25 and 0.5. The overall residual trait correlation was 0.3 and 0.4 for ρ_ab = 0.33 and r= 0.25 and 0.5 respectively. The overall residual trait correlation was 0.5 and 0.6 for ρ_ab = 0.67 and r= 0.25 and 0.5 respectively. Our findings were very similar to Table 4. The power substantially went up for the RMMLR approach with the increase in residual trait correlation, but both minP and Fisher’s test lost power with the increase in residual trait correlation (results not shown).

Table 4.

Power of different methods for 16-SNP gene (3 causal SNPs): LD is high and 3 of these 5 traits are associated with the causal snps.

Trait cor	minP	Fisher’s test	RMMLR
0.2	0.171	0.450	0.419
0.4	0.170	0.250	0.523
0.6	0.152	0.144	0.675

In summary, the RMMLR approach performed really well when some but not all the correlated traits were associated with the gene. Moreover, the RMMLR approach maintained the correct type I error even for highly correlated traits and for markers in high LD. Hence this RMMLR approach provides a computationally efficient technique for gene-based GWA studies using unrelated individuals or families. Under complete association, Fisher’s test performed really well for detection of association, but we had to correct for the inflatedness in the type I error by simulating data under the null. The minP approach performed well for a 3 SNP gene, but the power of the minP approach was substantially lower than the other approaches for the 16-SNP gene.

3.1 Real Data Analysis

A genome-wide gene-association analysis was carried out using our proposed RMMLR approach and other existing tests on data from the Minnesota Center for Twin and Family Research (MCTFR), which consists of an interrelated series of longitudinal twin, family and adoption studies. The MCTFR sample and genotyping methods have been described by Miller et al. (2012); the MCTFR phenotypes have been described by Hicks et al. (2011); and an initial SNP-based GWAS analysis has been reported by McGue et al. (2013). Briefly, the sample used here includes 7188 individuals of European ancestry clustered in 2300 nuclear families. Included are 2072 mothers (mean [SD] age at assessment of 42.8 [5.3]), 1780 fathers (44.9 [5.7]), 1788 daughters (18.0 [0.8]) and 1548 sons (17.9 [0.7]). Families are distinguished by the relationship of the two participating offspring, which were either monozygotic twins, same-sex dizygotic twins, full biological siblings, adoptive siblings, or mixed adopted/biological siblings. The sample was genotyped using Illumina’s Human 660W-Quad Array (Illumina, Inc., San Diego, CA) and a description of the quality control (QC) procedures is given in Miller et al. (2012). Of the 561,490 SNP markers on the array, 527,829 (94.0%) passed all QC filters. QC filters on samples resulted in removal of fewer than 2% of genotyped participants. European ancestry was based on self-report and was confirmed through the principal component analysis of the covariance matrix of marker data as implemented in the Eigensoft package (Price et al., 2006).

The four quantitative clinical phenotypes used in this analysis are all indicators of a higher-order construct known as externalizing or disinhibitory psychopathology (Iacono et al., 2008). These phenotypes were derived using a higher-order factor analytic approach (Hicks et al., 2011) and included: 1) Nicotine factor (NIC_FAC), a measure of symptoms of nicotine dependence, 2) Alcohol Consumption factor (ALC_FAC), a measure of quantity and frequency indicators of alcohol consumption, 3) Illicit Drug Consumption factor (DRG_FAC), a measure of use of and symptoms of abuse and dependence on illicit substances, and 4) Behavioral Disinhibition factor (BD_FAC), a measure of indicators of non-substance use behavioral disinhibition. In the MCTFR, parents are typically assessed a single time, while offspring are assessed longitudinally, spanning adolescence through early adulthood. The factor scores here for the offspring are based on the assessment completed nearest their 17th birthday so long as that assessment was completed when they were between 16.5 and 21 years. The average (range) correlation among these four phenotypes was .56 (.46 to .68). We conducted both univariate and multivariate gene-based GWAS scans for these 4 phenotypes using our RMMLR approach. Covariates in these analyses included sex, age, generation (i.e., parent versus offspring) and the first 10 principal components of the genotype covariance matrix derived by the Eigensoft package (Price et al., 2006). For comparison, we also report findings from VEGAS-SUM gene-based GWAS findings. One important issue to note is that RMMLR is much more computationally efficient than the VEGAS-SUM approach. Moreover, RMMLR can perform multivariate gene-based GWAS, which could have more power to detect multi-SNP association within a gene.

We first used our RFGLS approach (Li et al., 2011b) to perform single SNP association tests. The stepparents in the sample were treated as unrelated individuals and the rest of the sample was classified into different family types. We assumed a 12 parameter structure for the residual covariance matrix to account for the difference in variances and correlation among the pedigree members in different family types. We then assumed normal distribution of the traits to estimate the covariance matrix through maximum likelihood estimation. The VEGAS-SUM approach was then used to perform a gene-based GWAS using the single SNP association test statistics. Next we used the same gene definition as used by VEGAS to implement the RMMLR approach. We estimated the pair-wise correlations among the SNPs within a gene and removed all except one of the SNPs in perfect LD with each other for our gene-based analysis.

The VEGAS-SUM approach is similar to the Fisher’s test we used in our Simulation study. The positive correlation in SNPs within a gene can cause inflatedness in the VEGAS test statistic. The bootstrapping in the VEGAS-SUM approach adjusts for such inflatedness. We performed a maximum of 10⁷ such bootstrap iterations to estimate the null distribution of the VEGAS test statistic. Note that it took us 6.02 hours of CPU time to do the 17,600 genes using 520,478 SNPs and it used up to 20 GB of RAM to conduct this gene-based GWAS.

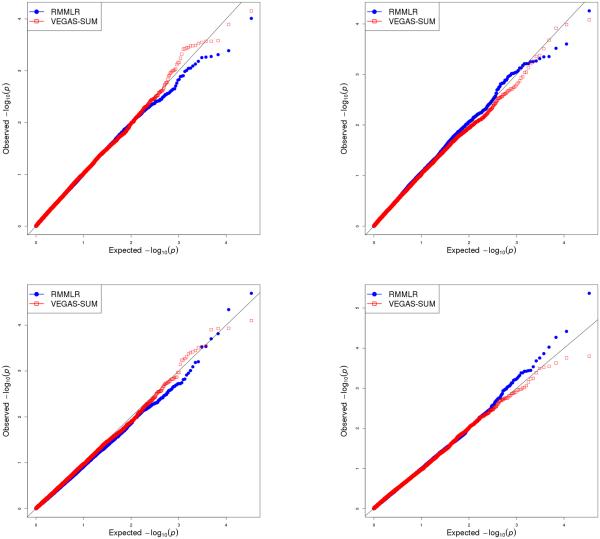
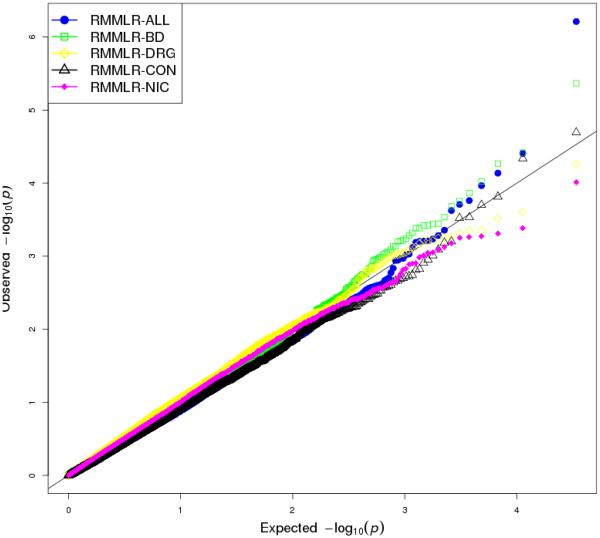
On the other hand, RMMLR was computationally very efficient and took us significantly less time (2.35 hours of CPU time) and memory (approximately 1.95 GB of RAM) to complete the analysis. Moreover, we were able to perform both univariate and multivariate gene-based GWAS with this approach (Figure 2 and Figure 3). The multi-trait multi-SNP association analysis did produce several more significant findings as compared to individual univariate multi-SNP association analysis, supporting our hypothesis of possible association between a subset of phenotypes and genes (Figure 3). Through our multivariate analysis, we found the gene RPL7 on Chromosome 8q21.11 to be genome-wide significant (p value 6.135530 × 10⁻⁷) even after applying Bonferroni correction for multiple testing (.05/17600 = 2.84 × 10⁻⁶). The corresponding univariate p values produced by the RMMLR approach were 0.007322907 for BD_FAC, 2.023403 ×10⁻⁵ for ALC_FAC, 0.001710981 for DRG_FAC and 0.004259516 for NIC_FAC. None of them were significant at the genome-wide level. Other than RPL7, we found gene MYL1 on Chromosome 2q33-q34 and RDH10 on 8q21.11 to have p-values <.00001 in the multivariate gene-based association analysis.

Figure 2.

Figure shows -log10(P-values) comparing the VEGAS-SUM and RMMLR approach for each of the 4 phenotypes NIC_FAC, DRG_FAC, ALC_FAC and BD_FAC respectively (top left, top right,bottom left, bottom right). There were 17600 genes. The filled squares show the qqplot of -log10(p-value)s for VEGAS-SUM approach. The filled circles show the qqplot of -log10(p-value)s from the RMMLR approach.

Figure 3.

Figure shows -log10(P-values) using RMMLR approach for each of the 4 phenotypes as well as for the 4 phenotypes analyzed together. The filled circles show the qqplot for -log10(p-value)s of RMMLR while analyzing the 4 phenotypes together.

4 Discussion

Very few methods are available to model association between multiple traits and multiple SNPs. In the study of a complex disease, several correlated traits are often measured as risk factors for the disease. Analyzing multiple disease-related phenotypes could potentially increase power to detect association of SNPs/genes with a disease. Moreover this joint analysis could reveal some pleiotropic genes involved in the biological development of the disease. Our flexible RMMLR approach could provide gene-based association analysis with univariate as well as multivariate traits. Our approach could be applied to secondary continuous traits collected as part of a case-control study using the retrospective likelihood method developed for mapping secondary phenotypes using regression models (SPREG) in case control studies (Lin and Zeng, 2009). One could also use this approach for interaction detection by adding higher order interaction terms in the regression model if there is any prior evidence or interest in modeling interaction between certain SNPs in a gene. The RMMLR approach is computationally efficient and simulation studies showed substantial power gain when the gene is associated with a subset of traits, especially in presence of moderate or high residual trait correlation. The method remains valid even when there is high LD among the SNPs and hence the asymptotic Wilk’s test can be used to assess the association. We have developed an R package to perform gene-based GWAS analyses with this RMMLR approach.

The CCA or MMLR approach has already been successfully implemented for unrelated individuals. Tang and Ferreira (2012) demonstrated the advantage of this CCA approach in multi-trait and multiSNP association analysis. Many genome-wide association studies involve family samples.

Ferreira and Purcell (2009) suggested technique for family data is computationally intensive and can only be implemented for single SNP association analysis. Here we propose a technique that can be implemented in families as well as in unrelated individuals. It is computationally efficient and captures the desirable features of the CCA algorithm. It has much higher power compared to the existing approaches, when a gene is associated with only a subset of traits.

It could get computationally intensive to compute the variance-covariance matrix in the MMLR approach (Equation 4) for every gene in the gene-based GWAS analysis. Our RMMLR approach is an approximation technique that avoids such intensive computation. The method works based on the principle that most of the genes in the GWAS study have very little or no effect on the traits. Hence estimating the variance matrix without including the gene effect does not cause much loss in power. On the other hand, if a gene is associated with the traits, our approximation technique can detect it. In our simulation studies, the RMMLR approach had more than 80% power to detect a gene explaining .6% of the phenotypic variance and in case the gene is associated with a subset of the traits with a sample size of 500 families with a familial correlation of 0.6.

Our univariate gene-based association testing with VEGAS was computationally intensive and it took us 6.02 hours of CPU time to test 17,600 genes using 520,478 SNPs and it used up to 20 GB of RAM to conduct this gene-based GWAS. On the other hand, RMMLR approach was easy to implement and we were able to use the the asymptotic p-values of the gene-based test statistic to assess the significance of the genes.

One disadvantage of this RMMLR approach over the combination methods is that it requires availability of genotype and phenotype data on individuals in order to perform the multivariate analysis. On the other hand, these combination methods require only the p-values from single SNP association analysis of univariate traits and hence might be more preferable to the user in some situations. We also need to remove SNPs in complete LD from the regression model to control for perfect multicollinearity for our RMMLR approach. Another issue is that the RMMLR approach assumes multivariate normality of the trait. Ferreira and Purcell (2009) found that the CCA approach remains valid even for non-normal trait. O’Reilly et al. (2012) found that in unrelated samples, CCA approach was sensitive to non-normality for low frequency SNPs. We expect similar behavior of the RMMLR approach in presence of non-normality, but intend to investigate it extensively through simulation studies in future.

In conclusion, our proposed RMMLR approach provides a useful framework for detection of gene-based association with single or multivariate traits, which could outperform the commonly-used permutation-based approaches, especially in case the gene is associated with a subset of traits. Our gene-based association analysis with multiple traits from the MCTFR dataset had some improved p-values as compared to the Univariate RMMLR tests, indicating evidence of association between the gene and a subset of these multiple correlated traits.