Human Scleral Structural Stiffness Increases More Rapidly With Age in Donors of African Descent Compared to Donors of European Descent

Abstract

Purpose.

We tested the hypothesis that the variation of peripapillary scleral structural stiffness with age is different in donors of European (ED) and African (AD) descent.

Methods.

Posterior scleral shells from normal eyes from donors of European (n = 20 pairs; previously reported) and African (n = 9 pairs) descent aged 0 and 90 years old were inflation tested within 48 hours post mortem. Scleral shells were pressurized from 5 to 45 mm Hg and the full-field, 3-dimensional (3D) deformation of the outer surface was recorded at submicrometric accuracy using speckle interferometry (ESPI). Mean maximum principal (tensile) strain of the peripapillary and midperipheral regions surrounding the optic nerve head (ONH) were fit using a functional mixed effects model that accounts for intradonor variability, same-race correlation, and spatial autocorrelation to estimate the effect of race on the age-related changes in mechanical scleral strain.

Results.

Mechanical tensile strain significantly decreased with age in the peripapillary sclera in the African and European descent groups (P < 0.001), but the age-related stiffening was significantly greater in the African descent group (P < 0.05). Maximum principal strain in the peripapillary sclera was significantly higher than in the midperipheral sclera for both ethnic groups.

Conclusions.

The sclera surrounding the ONH stiffens more rapidly with age in the African descent group compared to the European group. Stiffening of the peripapillary sclera with age may be related to the higher prevalence of glaucoma in the elderly and persons of African descent.

Scleral structural stiffness increases significantly with age in the peripapillary and midperipheral sclera in the African descent group, while only the peripapillary sclera significantly stiffened with age in the European descent group. Age-related scleral stiffening was significantly greater in African versus European descent donors.

Introduction

The results of several randomized prospective trials have identified risk factors associated with the development or progression of glaucoma. Across several studies, IOP, age, African ancestry, central corneal thickness (CCT), and increased optic disc cupping were independently associated with glaucomatous progression.^1–6 It is important to note that all of these risk factors have a biologically plausible association with either the level of IOP or the biomechanical behavior of the ocular coats and optic nerve head (ONH; age,^7–9 exposure to elevated IOP,¹⁰ African ancestry,^11,12 corneal thickness,¹³ and increased cupping¹⁴). Importantly, age is the only risk factors other than IOP that is independently associated with the onset and progression of glaucoma across all of the major prospective clinical trials conducted over the past 20 years. A significant association with African ancestry and the progression of glaucoma was seen in all studies that have included individuals of African descent. In addition to data from prospective trials in glaucoma and ocular hypertension, every population-based survey conducted to date has demonstrated a strong relationship between the prevalence of glaucoma with advancing age and African ancestry,¹⁵ despite almost all studies showing no changes in IOP with either risk factor.^16–22 While normal tension glaucoma is not uncommon within elderly populations,^23,24 it is not seen in children or young adults other than in a few isolated case reports.²⁵ Taken together, these findings indicate that the aging ONH becomes increasingly vulnerable to glaucomatous injury at similar levels of IOP, and that the eyes of individuals of African descent are more vulnerable to glaucomatous injury at similar levels of IOP than other racial groups.

We previously have couched glaucomatous etiology and pathophysiology in terms of a biomechanical framework,^26,27 because IOP is a mechanical insult, regardless of its mechanism of action. While the racial and age-related phenomena of glaucoma risk have been known for decades, few studies have been designed to test specific hypotheses about the common biomechanical mechanisms that may underlie these risks. As with any solid structure, the degree of mechanical deformation (strain) experienced by the ONH and sclera under a given level of IOP is dependent upon its 3-dimensional (3D) architecture and material properties, which combine to determine its structural stiffness, the tissue's inherent resistance to load.^27–36 Variation in ONH and scleral anatomy and material properties, either intrinsic or the result of remodeling that occurs with aging and/or between racial groups, may account for the increased susceptibility to IOP-induced injury as seen in the elderly and individuals of African ancestry. The lamina cribrosa is anchored into the peripapillary sclera at the scleral canal, and therefore deformations of the sclera are directly transmitted to the ONH. Hence, the biomechanics of the sclera and ONH are inseparably intertwined, and knowledge of scleral biomechanics informs ONH biomechanics.

Sigal et al.³³ determined that variations in scleral thickness, radius of the eye, laminar stiffness, and scleral thickness have the greatest influence on the biomechanical response of the ONH using computational models based on axisymmetric, idealized geometries, and a simplified material formulation (isotropic linear elastic). A follow-up study using more accurate estimates of the laminar and scleral material property values, although still isotropic and linear elastic, indicates that laminar structural stiffness also has a prominent role in determining laminar biomechanics.³⁷ In a computational study, Norman et al.³⁸ showed that the stiffness of the peripapillary sclera adjacent to the ONH is a particularly important factor in laminar biomechanics. Grytz et al.³⁹ suggested that the collagen architecture of the peripapillary sclera and lamina cribrosa can have a significant impact on the IOP-induced deformation response of the lamina cribrosa using computational modeling,³⁹ and recently Coudrillier et al.⁴⁰ showed that local anisotropic features in the peripapillary sclera produced significant changes in scleral canal expansion. These studies demonstrate that variation in the material properties and geometries of the sclera, which combine to govern the overall structural stiffness of the posterior sclera, are important determinants of the mechanical environment in the ONH.

In spite of the importance of the sclera in determining ONH biomechanics, surprisingly few studies have been designed to assess the sclera's mechanical behavior accurately in human eyes, especially as they change with age and/or differ with racial heritage. Studies have shown that the human sclera is hyperelastic^41–44 (stiffens as it stretches) and anisotropic^8,45,40 (resists deformation more in certain directions). We have shown recently that the sclera stiffens with age^8,46 in human donor eyes, and remodels in response to chronic elevated IOP exposure in a nonhuman primate model of glaucoma.^47,48 A recent study by Coudrillier et al.⁴⁹ also reported significant collagen stiffening in the human sclera with age. A computational study by Grytz et al.⁴⁵ offered a potential explanation of the mechanism that underlies the locally varying collagen fibril architecture in the sclera and its age-related remodeling, and it was hypothesized that the scleral collagen architecture evolves and remodels to maintain a homeostatic strain level in the collagen fibrils. Yan et al.⁵⁰ and Danford et al.⁵¹ observed that the local orientation of the collagen fibrils changes through the thickness of the sclera and was different between donors of African versus European descent, although no changes with age were observed.

The principal aim of this work was to test the hypothesis that the variation of the peripapillary scleral structural stiffness with age is different in donors of European (ED) and African (AD) descent. To accomplish this, we compared the peripapillary and midperipheral scleral strains measured in AD donors to those measured in a previous study of scleral shells from ED donors.⁵²

Materials and Methods

Human Eyes and Donor Demographics

Human eyes from ED and AD donors were procured from the Lions Eye Bank of Oregon (Portland, OR, USA) and the Alabama Eye Bank (Birmingham, AL, USA), and then preserved in isotonic saline solution at 4°C until testing. All eyes were deemed normal by next-of-kin questionnaire and were inflation tested within 48 hours post mortem. Eyes from donors with a history of glaucoma, diabetes, and high myopia (>6 diopters [D]) were excluded.

We collected 19 pairs of eyes from ED donors for a previous study⁵³ (mean age, 55 years; range, 20–90), combined with nine additional pairs eyes from AD donors (mean age, 51 years; range, 23–71), and used a statistical analysis to estimate the change in scleral strain with age. One additional pair of eyes from a newborn ED donor was included as a qualitative comparison to assess the appropriateness of our statistical estimate of sclera strain at the lowest age.

Inflation Testing and Mechanical Strain Calculations

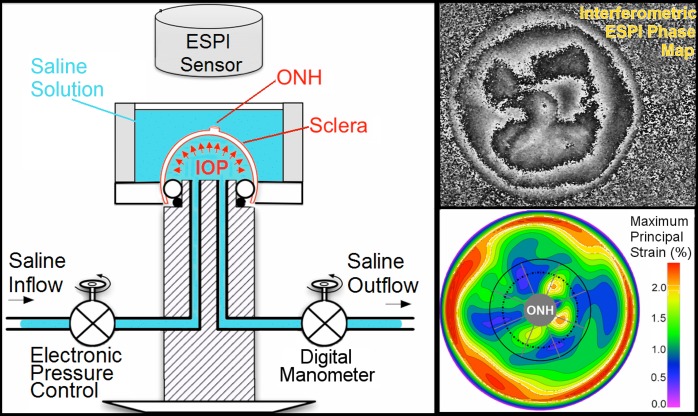
The apparatus and procedure used to inflation test the scleral shells have been described in detail in our previous studies (Fig. 1).^8,53 Briefly, each eye was clamped just posterior to the equator in a custom pressurization apparatus, preconditioned with 20 pressurization cycles from 5 to 30 mm Hg at a rate of 5 mm Hg per second, and then allowed to recover for 15 minutes. A starting pressure of zero could not be used because our experience indicates that the posterior scleral shell does not maintain its shape unless pressurized to at least 2 mm Hg. When increasing inflation pressure from 2 to 5 mm Hg, we consistently observed a large amount of deformation resulting from a change in scleral shell shape (geometry) rather than stretch (strain). As strain (mechanical stretch) is our outcome variable, 5 mm Hg was assumed to be the zero (or reference) load condition for the purposes of strain calculation. The scleral shells were inflated from 5 to 45 mm Hg in small steps of 0.01 to 0.2 mm Hg using an automated system with computer feedback control. Scleral surface displacements were recorded after the sclera had reached equilibrium at each pressure step using a commercial laser speckle interferometer (ESPI, Q-100; Dantec Dynamics A/S, Copenhagen, Denmark). The scleral shells were pressurized with PBS and measurements made while the tissue was fully immersed in PBS to ensure full tissue hydration throughout the experiment (Fig. 1, left). In a recent study, we assessed the displacement measurement uncertainty of this ESPI system in testing conditions similar to those used for scleral inflation; the ESPI average measurement uncertainty was ±16 nm at the 95% confidence level (CI). The ESPI technique's high spatial and displacement measurement resolution and ability to measure full-field, 3D displacements are ideal for quantifying the small localized deformations often observed in anisotropic and heterogeneous biological tissues, such the human sclera (Fig. 1, bottom right).⁵⁴ As in previous studies,^42,45,53 the inflation testing was performed at room temperature.

Figure 1.

Left: Diagram of the inflation testing apparatus. Right, top: A typical correlation fringe pattern representing the laser waveform phase variation measured by the ESPI. Right, bottom: A typical maximum principal strain map of the outer surface of the sclera. The boundaries of the peripapillary and midperipheral regions surrounding the ONH are shown by the solid and dashed lines on the lower right plot, respectively, and the boundaries of the 45°-wide sectors are shown with radial gray lines.

A customized B-spline fitting system⁵⁵ was used for obtaining continuous and differentiable analytical functions that define the 3D displacement field over the entire posterior third of the scleral surface as described previously.⁵³ The 3D deformation of the infinitesimally-thin outer layer of the sclera was obtained by analytical differentiation of the fitting system functions, which allows direct quantification of the mechanical strain without any intermediate finite element or analytical modeling. Furthermore, calculating mechanical strain directly from the differentiation of the experimental displacement yields a representation of scleral structural stiffness without the need for estimating material and geometric parameters, such as local scleral thickness, axial length, scleral canal opening size, collagen fibril orientation, and all other morphological and structural features that affect the peripapillary and midperipheral sclera's response to IOP. As such, the direct strain calculation technique used in this study has significant advantages over other approaches that require an interim computational or analytical modeling step (with all its explicit parameter requirements, and inherent assumptions and limitations) to estimate the strain. The strain formulation is reported in Equations 1 and 2, as described in our previous studies published in the biomechanics literature,^52,53 and the 3D strain tensor was computed in an approximated formulation as follows:

The ESPI displacements in Cartesian space were fit to continuous, differentiable, analytical functions 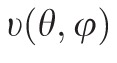= 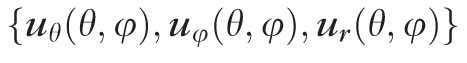for the meridional 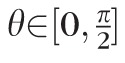, circumferential 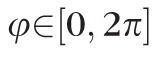, and radial directions, respectively. The analytical function defines the displacement field over the two-thirds of the outer surface of the posterior pole of the each eye. Five ( 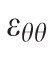, , 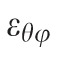, , 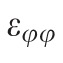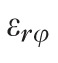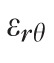) of nine components of the full strain tensor (Equation 1) were computed by direct mathematical differentiation of the analytical displacement functions, and by assuming zero variation in the radial direction of the displacement components tangent to the scleral surface. A recent study by Tang et al.⁵⁶ showed that strain varies through the thickness of the sclera, but the lateral displacements in the infinitesimally-thin outermost layer of the sclera do not appear to change quickly in the radial direction. So, meridional and circumferential displacement variations in the radial direction, 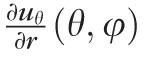and 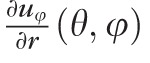in Equation 2, respectively, were assumed to be zero, and the sensitivity of the reported outcomes to this assumption was quantified as reported below.

Three components of the strain tensor, 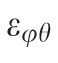, , 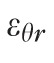and 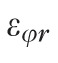, were computed by strain compatibility equations, and the final component, 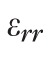, was numerically computed by assuming tissue incompressibility, thereby imposing 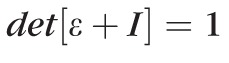(where I is the Identity Matrix).

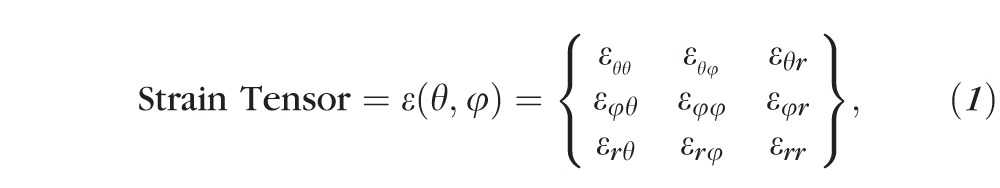where

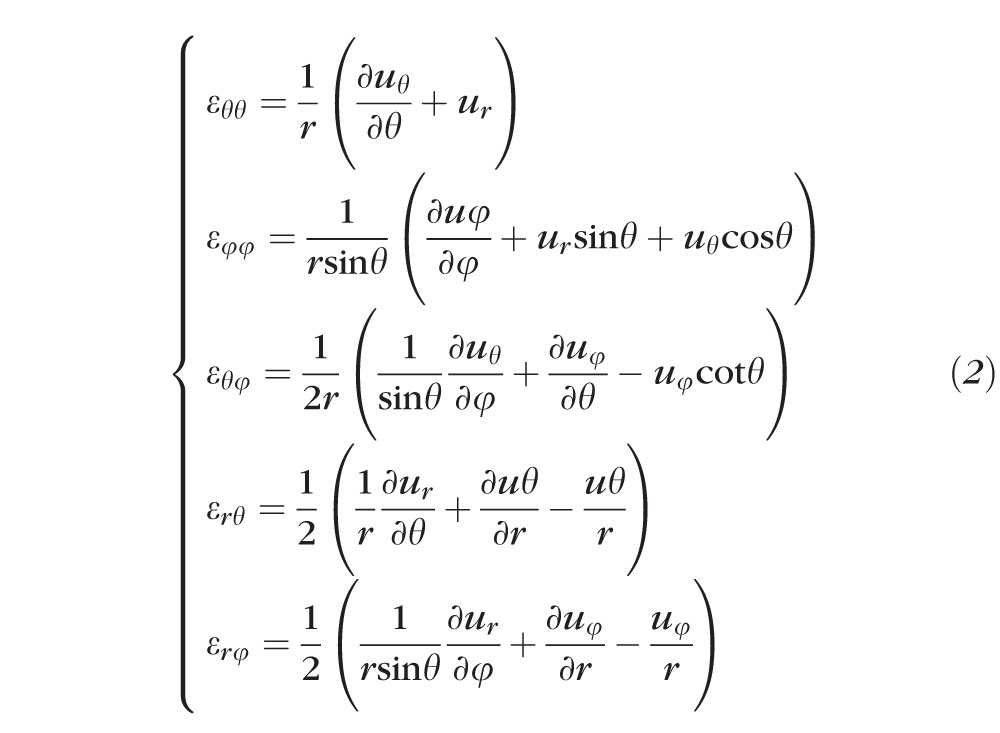The maximum principal tensile strain ( 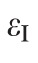, Equation 3) was computed over the entire scleral surface from the spectral decomposition of the full strain tensor:

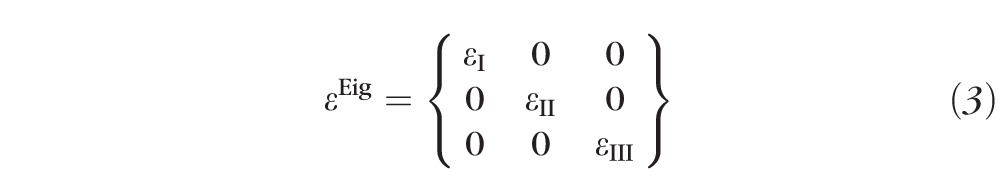The radius of the spherical coordinate system was computed by best-fitting the 3D coordinates of approximately 2500 points on the outer surface of the posterior sclera. These points were acquired using a 3D digitizer with a nominal resolution of approximately 200 μm (MicroScribe G2X; Immersion, San Jose, CA, USA), while the sclera was pressurized to 10 mm Hg with PBS. A pressure of 10 mm Hg was chosen to reduce the potential for penetration or deformation of the sclera with the digitizer tip so as to get the best possible scleral surface geometries. The difference in shape of the sclera when pressurized at 10 mm Hg compared to 5 mm Hg is negligible compared to the intrinsic error of the digitizer. Maximum principal strain is independent of the reference coordinate system, because it is the first invariant of the strain tensor. To compute the strain tensor, we assume that the meridional and circumferential displacement variations in the radial direction are zero in the infinitesimally-thin outermost layer of the sclera where the strain tensor is calculated (see above). Thus, the radial direction in the reference coordinate system should be coincident with the radial or through-thickness direction in the posterior scleral shell. Even large errors in the estimated sphere radius do not result in significant divergence of these two directions, and hence errors in the sphere radius estimate result in only negligible maximum principal strain errors. We also have analyzed the sensitivity of the maximum principal strain calculation to the aforementioned assumption, which is presented in full below.

Regionalization and Strain Sampling

The data analysis focused on measurements of the mean maximal principal (tensile) strain taken on a 200 × 200 equally-spaced grid of meridional (θ) and circumferential (φ) angles across a region of the scleral surface, including the peripapillary and midperipheral regions surrounding the ONH. The peripapillary region was defined as a 10° wide band adjacent to the ONH (approximately 2.2 mm wide) and the adjacent midperipheral region was defined for each eye such that it had the same surface area as the peripapillary region. For tabulation of mean sectorial strains with age within racial groups, mean maximum principal (tensile) strain was computed for eight circumferential sectors (45° wide) of equal surface area within the peripapillary and midperipheral regions surrounding the ONH.

Statistical Analysis

Strain values were modeled using Bayesian wavelet-based functional mixed models.⁵⁷ This method was used to model the maximum principal strain values as a continuous function of the scleral surface indexed by meridional (θ) and circumferential (φ) angles, and the age effect was modeled using an exponential function (see below). The Bayesian model was fit assuming noninformative vague prior distributions for the regression coefficients with a Markov Chain Monte Carlo procedure yielding posterior samples for all model parameters. Given these noninformative vague priors for the regression coefficients, the measured posterior probability (p) is approximately equivalent to the P value for a standard 2-sided t-test. For example, for parameter B the posterior probability p = 2*min[Probability(B > 0|data), Probability(B < 0|data)] is approximately the same as a P value for the 2-sided hypothesis test that B = 0. We chose the functional mixed modeling approach because it can model the maximum principal strain data on the entire meridional and circumferential grid while accounting for the correlations within each eye and among eyes from the same racial group, and accounting for the spatial autocorrelation of the strain data. Omission of, or improper accounting for the inherent spatial autocorrelation can potentially result in inefficient or even incorrect inferences; for example, higher type I errors, which is why we chose to use this Bayesian method that flexibly accounts for correlations within the sclera. Also, this method automatically accounts for sample size imbalance, such as that present in this study. Modeling and inferential details are given below, and additional detail concerning the statistical model can be found in our previous report.⁵²

We did not perform any a priori power calculations for this study, because it is difficult to compute statistical power for all of the comparisons considered, especially given the complexity of the model and the lack of a priori variance data upon which such a power calculation would rely. However, comparing the AD and ED groups' maximum principal strain using a simple independent t-test, 19 pairs of eyes in the ED group and nine pairs of eyes in the AD group would yield 80% power to detect an effect size of 0.82 SD units using a 2-sided test with 0.05 α level. Considering that we observed statistically significant age- and race-related differences in our data, the sample size was sufficient for detecting the effect by definition.

Error Assessments and Sensitivity Analysis

Two pairs of eyes (one from a young and one from an old donor) were used to assess the impact of our assumptions of tissue incompressibility and the zero variation of the in-plane displacement components in the radial direction at the outer surface of the sclera on the reported peripapillary sectorial strain. We also assessed the sensitivity of the reported strains to random displacement measurement noise. The analyses of these assumptions have been presented in detail in our prior study,⁵² so we present a brief summary of those findings here.

Tissue Incompressibility Assumption.

We assessed the impact of tissue compressibility by imposing a 15% decrease in 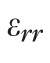(the only component in our method affected by this assumption) and quantified the absolute variation of the sectorial mean maximum principal strain. As a result we obtained a negligible 1.58% relative change in strain when assuming scleral incompressibility versus compressibility.

Assumption of Negligible Variation of In-Plane Displacement Components in the Radial Direction.

Maximum principal strain in a subpopulation of the tested eyes was computed using only the 2D, in-plane components of the strain tensor, 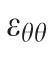, , 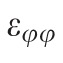, 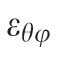whose computation doesn't require any underlying assumptions. While slightly different in magnitude, the strain change with age coefficients exhibited exactly the same sectorial pattern. Considering that the aim of the study is not to report actual strain values present in the peripapillary sclera at given pressure levels, but rather to report sectorial variability of strain levels and its variability with age and race, we preferred to base our strain computation on the approximated full strain tensor, in the belief that this formulation better represents the 3D strain in the peripapillary sclera.

Sensitivity of Strain to Random Displacement Measurement Noise.

To quantify the impact of random noise on the strain, we added random displacement noise from −5 to 5 μm to the raw displacement components at pressure levels from 10 to 45 mm Hg every 5 mm Hg. The resulting relative difference in sectorial mean maximum principal strain was 1.66%, which demonstrates the robustness of our customized B-spline fitting method to noise.

Interactions

The aforementioned estimates of potential error were calculated independently, but the highest total error can be achieved by combining all three potential sources of error. Considering the most stringent case of the summation of all possible sources of error, the maximum relative error in sectorial mean maximum principal strain was 3.77%, which is negligible given the differences we report in the Results section below.

Results

Regional Differences in Maximum Principal Strain With Age

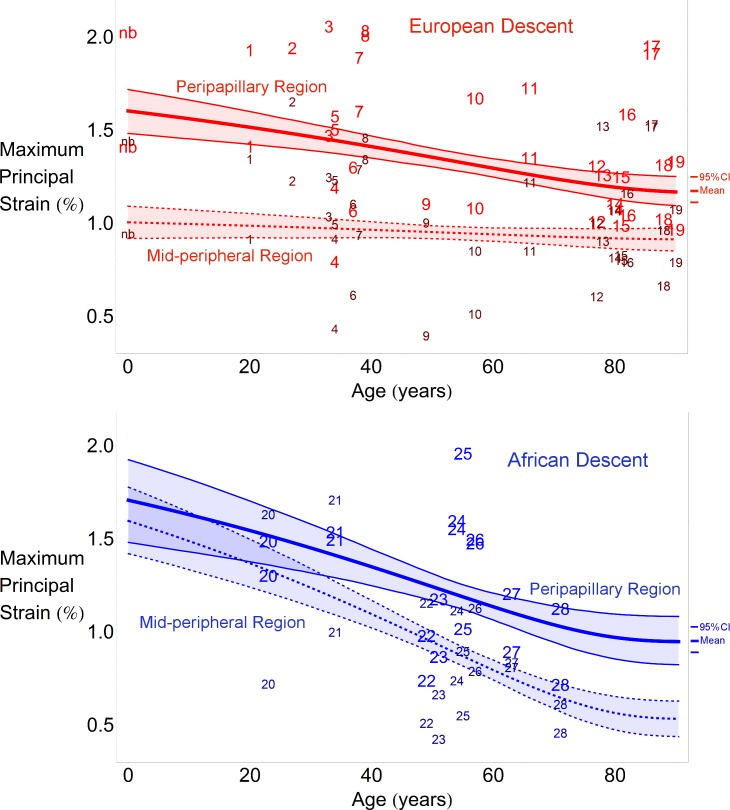
The average maximum principal strain was significantly larger in the peripapillary sclera compared to the midperipheral sclera within the ED and AD groups across all ages (P < 0.001, Fig. 2), with the exception of there being no significant differences between the two regions in the AD group at ages younger than 35 years. Peripapillary scleral strain significantly decreased with age in the AD and ED groups, but midperipheral strain decreased with age in only the AD group (P < 0.001, Fig. 2).

Figure 2.

Regional changes in maximum principal strain with age within racial groups. Scatterplots indicate the computed average strain values for the peripapillary (bigger font size) and midperipheral (smaller font size) paired by donor number. The thick lines denote the mean statistical estimate for each region and the thin lines denote the 95% point-wise CI of the estimated nonlinear regression line (not the data) in the ED group (red, upper) and AD group (blue, lower). Strain data from the newborn donor (nb) in the ED group were included in the upper plot, but not in the statistical analysis used to estimate the plotted curves, to provide a qualitative comparison of the statistical estimate a lower ages. Each regression plot shows the 95% CI of the curve representing the maximum principal strain variation with age for each region. In other words, the shaded regions show the 95% probability bound for the regression curve of the population.

Regional Differences in Maximum Principal Strain With Race

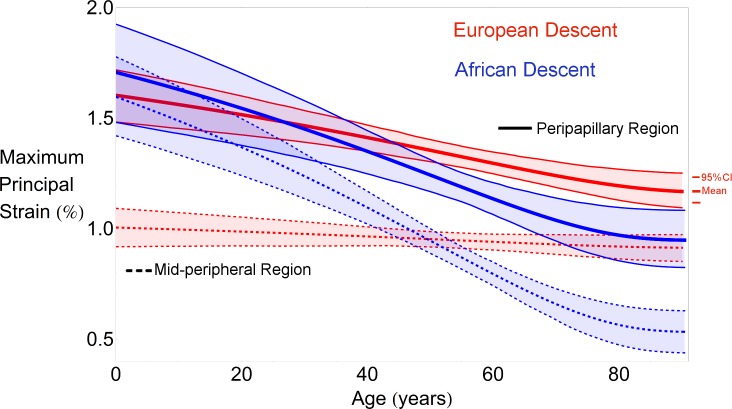
Differences in the average maximum principal strain in the peripapillary sclera of the ED and AD groups were not statistically significant at the lowest ages, as the 95% CI bands show in Figure 3. In fact, the average peripapillary scleral strain estimated at 20 years old is very similar in the two racial groups. The difference in average strain between the ED and AD groups becomes significant at 55 years of age due to the significantly greater age-related scleral stiffening of the AD group compared to the ED group (P < 0.001). The rate of change of scleral stiffening with age was different for the two groups for the peripapillary and midperipheral regions of the sclera (P < 0.001, Fig. 3).

Figure 3.

Regional changes in maximum principal strain with age and race. Overall regional mean maximum principal strain in the peripapillary region significantly decreases with age (P < 0.001) in European (red thick curves) and African (blue thick curves) descent groups; midperipheral strain did not exhibit a significant change with age in the ED group (red dashed), while this change was statistically significant in the AD group (blue dashed). Interestingly, the estimated average strain in the peripapillary sclera in the two groups is very similar at younger ages, but the average strain becomes significantly lower in the AD group at older ages due to the significantly higher rate of age-related stiffening in the AD group (P < 0.001). The thick lines denote the mean statistical estimate for each region and race. Each regression plot shows the 95% CI of the curve representing the maximum principal strain variation with age for each region (shaded region). In other words, the shaded regions show the 95% probability bound for the regression curve of the population.

Sectorial Differences in Tensile Strain by Age

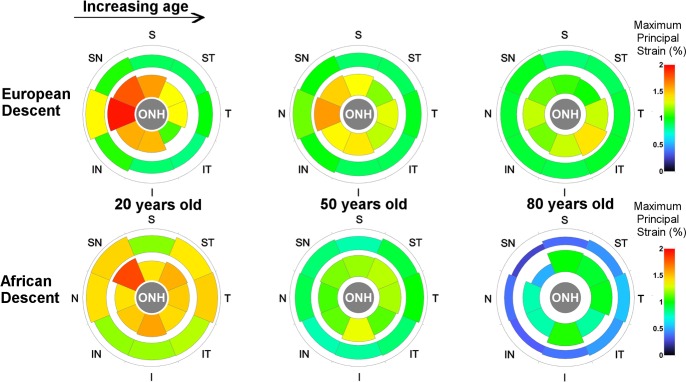
Average sectorial maximum principal strain for the peripapillary (inner sectors) and midperipheral regions of the sclera (outer sectors) are shown in Figure 4. As reported previously for the ED group,⁵² six of the eight sectors in the peripapillary region showed significant stiffening with age (P < 0.034 for all sectors, see Table), while the inferotemporal sector showed a significant softening with age (P < 0.001, see Table). In the midperipheral region further away from the ONH, only the nasal sector showed a significant stiffening (strain decrease) with age (P < 0.001, see Table). The Table lists the fitting function and estimates of the coefficients necessary to calculate the sectorial tensile strain in both regions as a function of age.

Figure 4.

Average sectorial strain estimated for three reference ages in the peripapillary (inner sectors) and midperipheral regions (outer sectors). The estimated strain patterns in the ED and AD groups are very similar at age 20, which continued up to age 50. At 80 years old, the estimated strain and strain pattern significantly differs in the two groups, with the AD group showing much lower strains compared to the ED group in the peripapillary and midperipheral regions. The peripapillary region was approximately 2.2 mm wide (10°-wide band), while the midperipheral was extended so as to have a surface area matching that of the corresponding peripapillary region. The ONH region varied by eye, and is represented in the figure as a region of generic size that includes the dissected edge of the dura mater at its scleral insertion.

Table.

Coefficient Estimates, SEs, and Posterior Probabilities (p) for the Age-Related Strain Change Coefficient b of the Nonlinear Regression Function for Maximum Principal (Tensile) Strain, Aggregated Within Sectors in the Peripapillary and Midperipheral Regions, for Both Racial Groups

	Predicted Maximum Principal Strain = a + b*e(age/[age-110]) Mean Values Over Sectors of the Peripapillary and Midperipheral Regions
	a				b
	European Descent		African Descent		European Descent			African Descent
Sector	Estimate	SE	Estimate	SE	Estimate	SE	p	Estimate	SE	p
Peripapillary region
Temporal	1.2523	0.09	0.9242	0.2134	0.1078	0.1892	0.57	0.6797	0.4403	0.116
Superotemporal	0.9825	0.0759	0.8839	0.1795	0.433	0.1628	0.004	0.8191	0.3725	0.024
Superior	1.0227	0.0885	0.9586	0.2085	0.71	0.1886	0.002	0.5533	0.4338	0.206
Superonasal	1.0765	0.0725	0.3877	0.1766	0.8697	0.153	<0.001	1.7796	0.3649	<0.001
Nasal	1.1884	0.0751	0.7128	0.1791	0.939	0.1574	<0.001	0.8662	0.371	0.022
Inferonasal	1.1125	0.0894	0.7121	0.2108	0.5452	0.1919	<0.001	0.947	0.447	0.046
Inferior	1.2357	0.0708	0.9883	0.1624	0.351	0.1518	0.034	0.7324	0.3456	0.042
Inferotemporal	1.4337	0.0682	0.7313	0.1569	−0.4357	0.1459	<0.001	0.8712	0.3256	0.01
Midperipheral region
Temporal	0.9286	0.0677	0.4662	0.1586	0.0771	0.1427	0.602	1.2359	0.3266	<0.001
Superotemporal	0.8849	0.0489	0.3677	0.1185	−0.0007	0.1069	0.976	1.2769	0.2492	<0.001
Superior	0.8472	0.0621	0.3003	0.1328	0.0464	0.1318	0.734	1.0927	0.2753	<0.001
Superonasal	0.9582	0.0575	0.1538	0.1267	0.0979	0.1234	0.438	1.6106	0.2601	<0.001
Nasal	0.8945	0.0601	0.294	0.1382	0.5673	0.1287	<0.001	1.3992	0.2865	<0.001
Inferonasal	0.9196	0.0703	0.2706	0.1654	0.1601	0.1489	0.304	1.1459	0.3473	<0.001
Inferior	0.9108	0.0526	0.3199	0.1218	−0.0611	0.1132	0.578	1.1013	0.2536	<0.001
Inferotemporal	0.9559	0.05	0.4008	0.1196	−0.1476	0.1088	0.17	1.0455	0.2465	<0.001

Due to the exponential formulation of the aging function, the coefficient a estimates the strain value in each sector at an age of 110 years old. Sectorial strains within each region by race can be estimated at any age using the function at the top of the table and the listed coefficient estimates. Note that given the noninformative vague priors for the regression coefficients, p is approximately equivalent to the P value for a 2-sided test of the null hypothesis that b = 0 using traditional frequentist statistics. Note that 110 years of age was chosen as the asymptotic value because it maximized the likelihood associated with the statistical model fit.

In the AD group, all the sectors in the peripapillary sclera showed a reduction in sectorial strain with age, but the Temporal and Superior sectors were not found to vary significantly. In the midperipheral sclera, all the sectors showed a significant stiffening with age in the AD group (P < 0.001, see Table).

Average sectorial maximum principal strains for the peripapillary and midperipheral regions are estimated for three discrete ages for both racial groups are shown in Figure 4. Several observations can be made: (first column) the regional and sectorial pattern was similar between the two groups at younger ages; (middle column) the sectorial pattern was similar, but the average strain values were lower in the AD group in middle age, indicating an increase in structural stiffness; (last column) at older ages, sectorial and regional patterns were markedly dissimilar with race, with the AD group showing a much stiffer sclera than the ED group.

Discussion

The main finding of this work is that mechanical strain in posterior human sclera significantly changed with age in ED and AD donor eyes, but the stiffening with age in the AD group was significantly greater than that estimated for the ED group. The sectorial pattern of peripapillary scleral strain was similar in the two groups at younger ages, but the peripapillary scleral strain was significantly lower in the AD group at higher ages due to the higher rate of age-related stiffening in the AD group. Mechanical strain was always higher in the peripapillary sclera than the midperipheral sclera in both ethnic groups, with the exception of the AD group at ages younger than 35 years.

To our knowledge, this study is the first to report differences in scleral strain between ED and AD donor eyes, and their sectorial age-related changes in the peripapillary and midperipheral sclera. Using PBS to pressurize the intact posterior scleral shell, coupled with noncontact, full-field displacement measurements made while the specimen was fully immersed in PBS, allowed inflation testing to be performed in physiologically mimetic conditions. The direct differentiation of analytical functions describing the continuous scleral displacement field allows direct calculation of the scleral strain tensor, which avoids the intermediate computational methods and their limiting assumptions that typically are required to estimate strain from experimental displacement data.

This work should be viewed with several limitations in mind, which have largely been described in detail in our previous reports.^52–54 Briefly, there is error in the displacement measurement at the outer edge of the specimen due to ESPI phase map reconstruction difficulties. We positioned the ONH and peripapillary sclera at the center (apex) of the posterior scleral specimen and analyzed strains in a relatively narrow band around the ONH to avoid these edge effects.

We assumed that the sclera is incompressible to calculate one of the nine strain tensor components necessary for our analyses, as described in our previous report.³⁵ This assumption affects only one of the nine strain tensor components used to calculate maximum principal strain; in fact, the sensitivity to this assumption has been proven to be minimal (see the “Error Assessments and Sensitivity Analysis” section in the Methods).

We computed the strain values assuming the zero strain state occurred at 5 mm Hg IOP; hence, the strain values we reported are lower than the actual strain. The rationale underlying this choice arises from our experimental experience that suggests that lower initial pressures would produce errors in the strain computation because the scleral shell is merely changing shape (geometric nonlinearity) at low IOPs. Unlike scleral inflation behavior at higher pressures, large changes in scleral shape can occur at low pressures with minimal associated scleral strain, which invalidates most analytical strain calculation methods. Also, the surface strains measured in the present study may not fully represent the range of strains that structural heterogeneities, collagen density and orientation, and/or morphological features may create through the thickness of the sclera.

We also performed scleral inflation testing at room temperature because the ESPI displacement measurement system we used in this study is so sensitive that thermal convection currents in heated PBS induce significant measurement errors. Testing temperature likely impacts the material properties of the sclera, but since all specimens were treated identically, our analysis of age- and race-related changes in the regional and sectorial strains that are the focus of this report should be unaffected.

The age span of human donors in the AD group is smaller than the ED group, in that the oldest AD donor was 74 years of age. The statistical model we used is appropriate for the analysis and yielded significant age-related differences with race, but our confidence in the strain estimates for AD individuals above 75 years of age is diminished by the lack of data at the high end of the age range.

Finally, we based our normality classification and exclusion assessment on next-of-kin questionnaire and hospital records, but did not confirm normality through an ophthalmic exam performed while the patient was living. This could prove crucial for studies on cellular activity or neural tissues, or those that are designed to detect differences due to treatments or disease states, such as glaucoma. However, conditions or diseases that are likely to significantly impact scleral biomechanics, such as glaucoma, diabetes, and high myopia, were excluded.

The detailed regional and sectorial distributions of scleral strain are important, as they inform us about the strains that scleral tissues and the resident cells actually experience when IOP is elevated, acutely and chronically. We measured scleral tensile strains that were significantly higher in the peripapillary sclera compared to the adjacent midperipheral sclera for both ethnic groups. A similar pattern of sectorial and regional variation in tensile strain was found in all eyes, but some eyes exhibited much higher strains overall than others. This wide range of strain between sectors of different eyes may relate to variations in scleral thickness and/or the distribution of collagen, elastin, or crosslink density.

Yan et al.⁵⁰ and Danford et al.⁵² reported that collagen fibril alignment in the temporal sector of the peripapillary sclera is more circumferential around the ONH in ED donors than AD donors, but these patterns do not change with age. Factors other than fibril alignment, such as collagen fibril crimp angle, scleral thickness, and/or nonfibrillar extracellular matrix stiffness, also likely are having significant roles in the strain differences we report with age and between the racial groups. All these factors could change with age and explain our findings, even if fibril alignment doesn't change with age as reported.^50,51

Mechanical tensile strain in the peripapillary sclera is a direct measure of the stretch to which the scleral fibroblasts, extracellular matrix, and penetrating vasculature are exposed. While we do not fully understand the extent to which peripapillary scleral strain is transmitted to the ONH and lamina cribrosa or how laminar strain induces axonal damage, it is plausible that high regional peripapillary strains induce high strains in the adjacent lamina cribrosa. Given that the sectorial pattern and age-related susceptibility to disk hemorrhages⁵⁸ and neuroretinal rim area loss⁵⁹ appears to closely match the age-related sectorial changes in peripapillary scleral strain in the ED group,⁴³ this certainly warrants investigation. Further work should be done to elucidate the mechanistic relationships between local peripapillary scleral strains, laminar strains, and focal retinal ganglion cell axon damage.

In conclusion, this study was designed to test the hypothesis that aging alters the regional and sectorial patterns of peripapillary and midperipheral scleral structural stiffness differently in persons of African heritage compared to persons of European heritage. The differences in age-related scleral strain change between persons of European and African heritage may be a direct or indirect factor related to the increased prevalence of glaucoma in the elderly of all races and individuals of African ancestry in particular.¹⁵ The results of these studies will serve as important inputs for future biomechanical modeling studies of the ONH and aging, while also accounting for racial differences, as well as providing accurate strain ranges for vitro studies of the response of scleral cells to mechanical deformation. In addition, quantification of scleral strain via postprocessing of clinical images may prove useful as an eye-specific assessment of biomechanical risk factors in glaucoma. Finally, it is important that future studies on the biomechanics of the posterior eye and ONH account for age and race in their experimental design.