POWERLIB: SAS/IML Software for Computing Power in Multivariate Linear Models

Abstract

The POWERLIB SAS/IML software provides convenient power calculations for a wide range of multivariate linear models with Gaussian errors. The software includes the Box, Geisser-Greenhouse, Huynh-Feldt, and uncorrected tests in the “univariate” approach to repeated measures (UNIREP), the Hotelling Lawley Trace, Pillai-Bartlett Trace, and Wilks Lambda tests in “multivariate” approach (MULTIREP), as well as a limited but useful range of mixed models. The familiar univariate linear model with Gaussian errors is an important special case. For estimated covariance, the software provides confidence limits for the resulting estimated power. All power and confidence limits values can be output to a SAS dataset, which can be used to easily produce plots and tables for manuscripts.

1. Description of POWERLIB

POWERLIB is a suite of SAS/IML modules which computes statistical power for hypothesis tests in a wide variety of univariate, multivariate, and repeated measures linear models with Gaussian errors and fixed predictors. This paper describes version 2.1 of POWERLIB. This version was developed using SAS version 9.1 and can be run on both Windows and UNIX systems. The code includes matrix names longer than 8 characters, a naming convention added in version 7; hence, the modules will not run in SAS versions 6.12 or earlier.

1.1. Available models and hypothesis tests

POWERLIB computes power for the four commonly used tests for the “univariate” approach to repeated measures: Box, Geisser-Greenhouse, Huynh-Feldt, and uncorrected. These four tests and associated methods will be collectively referred to as the UNIREP approach.

The program also computes power for the three most popular multivariate test statistics: Hotelling Lawley Trace, Pillai-Bartlett Trace, and Wilks Lambda. In this manual, these three tests and related methods are collectively referred to as the MULTIREP approach.

The UNIREP approach can be shown to be equivalent to a restricted class of linear mixed models with Gaussian errors which meet the following restrictions (Gurka et al. 2007):

1. No missing or mistimed observations (all subjects have the same number of observations at the same within-subject levels)

2. Factorial within-subject design

3. Common between-subject design for all responses

4. Homogeneity of covariance parameters for all subjects

5. Compound symmetric covariance structure.

The increasing popularity of mixed models for data analysis naturally motivates the need for reliable power analysis based on mixed models. Unfortunately, as Verbeke and Molenbergs (2000) noted, very little is known about non-null distributions in mixed models. Consequently, we know of no software that dependably calculates power for general mixed models. Use of the methods proposed by Gurka et al. (2007) within POWERLIB allows for power analysis for a restricted class of linear mixed models. Even though often in practice the required restrictions are not met, a power analysis based on this restricted class of mixed models may provide reasonable guidelines for sample size, even in more general scenarios (e.g, missing data). Thus, POWERLIB in this setting becomes a valuable tool for researchers who need to plan studies in which mixed models will be fit to the collected data.

The familiar univariate linear model with Gaussian errors is a special case of the multivariate and mixed model formulation. The program’s output and syntax simplifies for computation of power for this case.

1.2. Model and hypothesis notation

Power computations in POWERLIB are derived within the framework of the General Linear Multivariate Model (GLMM). Muller and Stewart (2006) and Timm (2002) provided detailed discussion of basic theory and practice for all models treated by POWERLIB, with the former focused more on theory and the latter more on practice. For N independent sampling units, p responses, and q predictors, the GLMM may be stated as:

$$\mathit{Y}=\mathit{X}\mathit{B}+\mathit{E},$$

with Y (N × p) containing information on random responses such as repeated measures, X (N × q) a fixed design matrix containing predictors, B (q × p) containing unknown parameters, and E (N × p) containing random errors. Rows of Y, X and E correspond to independent sampling units (such as subjects), columns of Y, B and E to level of the multivariate response (often time), and columns of X and rows of B to predictors. With r = rank(X), the methods used in this program assume N > r, row_i (E) ~ N_p (0, Σ), i ∈ {1, 2, …, N}, all rows independent, and no missing data in Y or X.

In the context of data analysis, values in B and Σ are estimated. In contrast, in the context of power analysis B and Σ are assumed known constants, although in practice, estimates of B and Σ from a previous study are often used. The software can compute confidence limits for power to reflect the uncertainty in the estimation of Σ, and in some cases, also in B.

The corresponding General Linear Hypothesis (GLH) involves Θ = CBU, with C an a × q matrix of known constants defining“between subject”contrasts, and U a p × b matrix of known constants defining “within subject” contrasts. The power program requires rank(C) = a ≤ q and rank(U) = b ≤ p. The GLH is

$$H_0:\mathbf{\Theta }={\mathbf{\Theta }}_0{H}_1:\mathbf{\Theta }\ne {\mathbf{\Theta }}_0.$$

Most often Θ₀ = 0.

1.3. Statistical theory

Detailed knowledge of the statistical theory behind power computations in multivariate linear models is not required to use this software; however, for more sophisticated users, POWERLIB provides options to choose distributional approximations. Defaults have been chosen to reflect methods the authors believe to be the best available, and should not be altered without explicit rationale. Muller et al. (1992) gives a review of the theory behind the power methods implemented. Muller and Benignus (1992) provides a brief introduction to the most basic ideas of power in the context of toxicology, while O’Brien and Muller (1993) provides a lengthy tutorial in linear models power. Additionally, sections 2.7 and 2.9 give several references for various distributional approximations for UNIREP and MULTIREP tests and their confidence limits.

1.4. Why use this software?

Commercial software for computing power in linear models with Gaussian errors are available, most notably NQuery, PASS, and PROC GLMPOWER from SAS. Ralph O’Brien¹ and Daniel Heitjan² also provide additional useful free software on their web sites. At this time, this software has the following advantages over these and other products:

1. POWERLIB implements the power approximations described in Muller et al. (2007), which has considerably better test size accuracy in some cases.

   1. PROC GLMPOWER from SAS does not compute power for multivariate Gaussian models, only univariate.
   2. PASS implements older multivariate power approximations from Muller and Barton (1989)

2. POWERLIB is easy to embed in other SAS/IML code for use in simulations.

3. POWERLIB is the only software that computes confidence limits for power in Gaussian linear models.

Program 1 Basic program skeleton

PROC IML SYMSIZE=2000; %INCLUDE "‥.\IML\POWERLIB21.IML"/NOSOURCE2; …programming statements to assign global matrices that describe model and choose options… RUN POWER; QUIT;

Program 2 Calling POWERLIB from within a module

START user_defined_module ( parm1, parm2, … parmn) GLOBAL (ESSENCEX, SIGMA, BETA, C, U, THETA0, REPN, BETASCAL, SIGSCAL, RHOSCAL, ALPHA, ROUND, TOLERANCE, TOLERANC, UCDF, UMETHOD, MMETHOD, LIMCASE, CLTYPE, N_EST, RANK_EST, ALPHA_CL, ALPHA_CU, DSNAME, OPT_ON, OPT_OFF); …your code here… …programming statements to assign POWERLIB global matrices… CALL POWER(_HOLDPOWER, _HOLDPOWERLBL, _POWERWARN, _POWERWARNLBL); …some more of your code here… FINISH user_defined_module;

2. How to Use POWERLIB

2.1. Execution

The POWERLIB21.IML file included in the distribution contains several modules and is the only file required to run POWERLIB. The POWER module performs all power calculations. All other modules included in the POWERLIB21.IML file, except for some independent utility modules discussed later in this paper, are called by the POWER module and are transparent to the user.

With basic knowledge of SAS/IML, POWERLIB is simple to use via the general program skeleton given in Program 1. The first two program statements are always required. They initialize IML, ask for extra symbol space, and make the power modules available for use. The RUN POWER statement executes the POWER module and is also required. Note that the directory listed in the %INCLUDE statement is the directory where POWERLIB21.IML has been copied; this most likely must be modified from this skeleton.

The software can also be run from within another module by using a CALL statement. This feature is particularly helpful when running simulations. Program 2 illustrates how to define a user module that calls the power software.

2.2. Inputs overview

User inputs to the POWERLIB modules are made through 25 global matrices listed in Table 1, grouped by application. Sections 2.4 – 2.11 discuss how to use these matrices in the order the groups are presented in Table 1. Because these matrices are global, use of these matrix names for reasons other than their intended purpose in POWERLIB will result in an error. When calling POWERLIB from within a module, these 25 matrices plus the matrix TOLERANC must be listed as global matrices in the module definition, as in the START statement in Program 2. In previous versions of POWERLIB, the current input matrix TOLERANCE was spelled as TOLERANC. We retained a matrix with this spelling in the CALL statement so that version 2.1 is compatible with programs written with previous versions of POWERLIB.

Table 1.

POWERLIB input matrices

Matrix Name	Description	Size	Default
ESSENCEX	Fixed effects design matrix	Varies	Required
BETA	Fixed effects matrix B	q × p	Required
C	Matrix C in GLH	a × q	Required
U	Matrix U in GLH	p × b, b ≤ p	Ip
SIGMA	Covariance matrix	p × p	Required
THETA0	Matrix Θ0	a × b	0
ALPHA	Type I error rates	1 row or col	0.05
REPN	List specifying # of times to duplicate each row of ESSENCEX	1 row or col	1
BETASCAL	List of multipliers for BETA	1 row or col	1
RHOSCAL	List of multipliers for correlation matrix RHO, created from SIGMA	1 row or col	1
SIGSCAL	List of multipliers for SIGMA	1 row or col	1
CLTYPE	Type of confidence interval to include in power calculations	1 × 1	−1
RANK_EST	Scalar giving design matrix rank in the analysis that yielded Σ and B estimates	1 × 1	None
N_EST	# of observations in the analysis that yielded Σ and/or B estimates	1 × 1	None
ALPHA_CL	Scalar specifying lower tail confidence limit probability	1 × 1	0.025
ALPHA_CU	Scalar specifying upper tail confidence limit probability	1 × 1	0.025
MMETHOD	List specifying HLT, PBT, WLK power approximation	3 × 1, 1 × 3, 1 × 1	[4 2 2]′
UCDF	List specifying CDF approximation for UNIREP (UN, HF, GG, BOX)	4 × 1, 1 × 4, 1 × 1	[2 2 2 2]′
UMETHOD	List specifying method for approximate Eε̃ and Eε̂	2 × 1, 1 × 2, 1 × 1	[2 2]′
ROUND	Scalar specifying how many decimal places to ROUND power values	1 × 1	3
TOLERANCE	Scalar specifying what the software considers numeric zero	1 × 1	1 × 10−12
OPT_ON	User options to turn on	1 row or col	See Table 2
OPT_OFF	User options to turn off	1 row or col	See Table 2
DSNAME	Specifies output SAS file name and location	1 × 2, 2 × 1, 1 × 3, 3 × 1	{WORK DODFAULT WORK}

2.3. Outputs overview

POWERLIB produces four output matrices:

          _HOLDPOWER  _HOLDPOWERLBL  _POWERWARN  _POWERWARNLBL

Unlike the input matrices listed in Table 1, these are not globally defined. As such, these four matrices must be listed if POWERLIB is executed with a CALL statement. As before, use of these four matrix names for reasons other than their intended purpose in POWERLIB may result in an error.

All power computations are saved to the matrix _HOLDPOWER with labels given in the vector _HOLDPOWERLBL. Sections 2.8.2 – 2.8.4 discuss options for choices of power computations to perform as well as elements to include in _HOLDPOWER.

By default, _HOLDPOWER is sent to the output window. Section 2.8.6 shows how to save the output matrix to a SAS dataset, which can be used, among other things, for graphing or simulation purposes. By default, several model matrices and warnings are sent to the output window prior to printing the output matrix. Section 2.8.5 discusses options that control matrix printing and warning notification.

Information about any numerical difficulties and approximation accuracies is stored in the global output matrix _POWERWARN with labels are given in the vector _POWERWARNLBL. These matrices are further documented in Section 2.12. Typical users will not need to inspect _POWERWARN.

2.4. Required matrices

Computing power for a GLH with fixed predictors requires knowing only seven variables: Σ, X, B, C, U, α and Θ₀. The user must always specify Σ, X, B, C, via the matrices SIGMA, ESSENCEX, BETA, and C, respectively. The power program assumes default values of U = I_p (which corresponds to a MANOVA hypothesis with multivariate responses), Θ₀ = 0, and α = 0.05, specified with the matrices U, THETA0, and ALPHA, respectively.

Note that for univariate models, SIGMA is the variance, not the standard deviation, because Σ = σ² is 1 × 1. POWERLIB gains substantial advantages from treating the univariate case as a special case of the multivariate, which requires the same variable name (SIGMA) for both settings, causing this potential source of confusion.

2.4.1 Input Checks

If a required input has not been given by the user or if any input matrix does not conform to the dimensions specified in Table 1, POWERLIB will stop with an error. POWERLIB also checks for many other possible errors in the user input matrices to assure they contain plausible values.

2.4.2 Specifying the design matrix X

The essence matrix (Helms 1988) contains one and only one copy of each unique row of the original matrix. We use this notation for X to ease choice of sample sizes for which to compute power. For example, the following shows the X matrix for an independent groups t-test with 10 observations, denoted as X₁, in terms of its essence matrix:

$${\mathit{X}}_1=\left[\begin{array}{cc}{\mathbf{1}}_{10}\hfill & {\mathbf{0}}_{10}\hfill \\ {\mathbf{0}}_{10}\hfill & {\mathbf{1}}_{10}\hfill \end{array}\right]=\left[\begin{array}{cc}1\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right]\otimes {\mathbf{1}}_{10}=\mathrm{E}\mathrm{s}({\mathit{X}}_1)\otimes {\mathbf{1}}_{10.}$$

In the above, 1₁₀ denotes a 10 × 1 vector of 1’s and 0₁₀ a 10 × 1 vector of 0’s. The ⊗ symbol denotes the Kronecker multiplication operator, where A ⊗ B = {a_ij · B} for any matrices A and B. See Muller and Fetterman (2002) for an introduction to ANOVA coding in one and two way designs.

The program assumes that X is specified in terms of its essence matrix and row replication factor. These are specified with the matrices ESSENCEX and REPN, respectively. In terms of these matrices, X₁ above is specified with:

ESSENCEX = I(2);
REPN     = 10;

The X matrix can also always be given as an essence matrix equal to the entire matrix and replication of one. In this way, X₁ can be specified with:

ESSENCEX = I(2) @ J(10,1,1)};
REPN     = 1;

In the above, X₁ had equal cell sizes. The program can tolerate unequal cell sizes through no special coding. As an example, consider:

$${\mathit{X}}_2=\left[\begin{array}{ccc}{\mathbf{1}}_{10}\hfill & {\mathbf{0}}_{10}\hfill & {\mathbf{0}}_{10}\hfill \\ {\mathbf{0}}_{15}\hfill & {\mathbf{1}}_{15}\hfill & {\mathbf{0}}_{15}\hfill \\ {\mathbf{0}}_{20}\hfill & {\mathbf{0}}_{20}\hfill & {\mathbf{1}}_{20}\hfill \end{array}\right].$$

Program 3 The simplest power program

Program code: PROC IML SYMSIZE=2000; %INCLUDE "‥\IML\POWERLIB203.IML"/NOSOURCE2; ESSENCEX = I(2) ; REPN = { 10 }; BETA = {0 1}‘; SIGMA = {1}; *=variance, because here covariance matrix is 1×1 ; C = {1 −1}; RUN POWER;

Output: ALPHA SIGSCAL BETASCAL TOTAL_N POWER 0.05 1 1 20 0.562

One way to specify this is:

ESSENCEX = {1 0 0, 1 0 0,
            0 1 0, 0 1 0, 0 1 0,
            0 0 1, 0 0 1, 0 0 1, 0 0 1};
REPN     =  5;

Alternately, as mentioned previously, X can be specified with ESSENCEX as the entire X matrix and REPN = 1. In this representation, X₂ is coded as:

ONE      = {1 0 0};
TWO      = {0 1 0};
THREE    = {0 0 1};
ESSENCEX = REPEAT(ONE, 10, 1) // REPEAT(TWO, 15, 1) // REPEAT(THREE, 20, 1);
REPN     = 1;

Finally, POWERLIB allows X to have fractional cell sizes, e.g, REPN = DO(1 TO 5 BY .5)′, by specifying the FRACREPN option. Section 2.8 discusses how to designate this and other options available with POWERLIB.

2.5. A simple power program - one power value from a two sample t-test

Program 3 gives the complete code needed to compute power for an independent groups t-test with ten observations per group and cell mean cell coding. This program computes one power value and is an example of the simplest program that can be written to call POWERLIB. Note that for univariate models, Σ = σ², a variance, not a standard deviation.

Program 4 Producing power for a range of scenarios

PROC IML SYMSIZE=2000; %INCLUDE "..\IML\POWERLIB203.IML"/NOSOURCE2; BETA = {0 1}‘; C = {1 −1}; SIGMA = {1}; *=variance, because covariance "matrix" is 1×1 ; ESSENCEX = I(2); REPN = {10 20}; BETASCAL = DO(0,.9,.1); SIGSCAL = {.5 1 2}; ALPHA = {.005 .01 .05}; RUN POWER;

2.6. Producing power for a range of scenarios

The program makes it easy to compute power for ranges of values of sample size, type I error, mean difference, variance, and correlation level among response variables, through the global matrices REPN, ALPHA, BETASCAL, SIGSCAL, and RHOSCAL, respectively.

REPN and ALPHA contain simple lists of desired sample size and significance levels. BETASCAL and SIGSCAL contain multipliers for the user-specified values of BETA and SIGMA, respectively. BETASCAL could be called THETASCAL because it also multiplies Θ by the same amount. RHOSCAL contains multipliers for the model correlation matrix created internally from SIGMA. REPN, ALPHA, BETASCAL, SIGSCAL, and RHOSCAL are always matrices which are 1 × n (a matrix with one row) or n × 1 (a vector). Each equals 1 by default, the equivalent of no change from the original model specification. When more than one of these matrices has been changed from the default, power is computed for all factorial combinations of inputs.

Program 4 generalizes the code in Program 3. The new inputs ask for:

1. 2 values of REPN

2. 10 values of BETASCAL

3. 3 values of SIGSCAL

4. 3 of ALPHA,

leading to power computed for, respectively:

1. Total sample sizes of 20 and 40

2. Mean differences of μ₁ − μ₂ = 0, μ₁ − μ₂ = 0.1, μ₁ − μ₂ = 0.2, …, μ₁ − μ₂ = 0.9

3. σ² = 0.5, σ² = 1.0, and σ² = 2.0

4. α = 0.005, α = 0.01, and α = 0.05,

for a total of 2*10*3*3 power values computed.

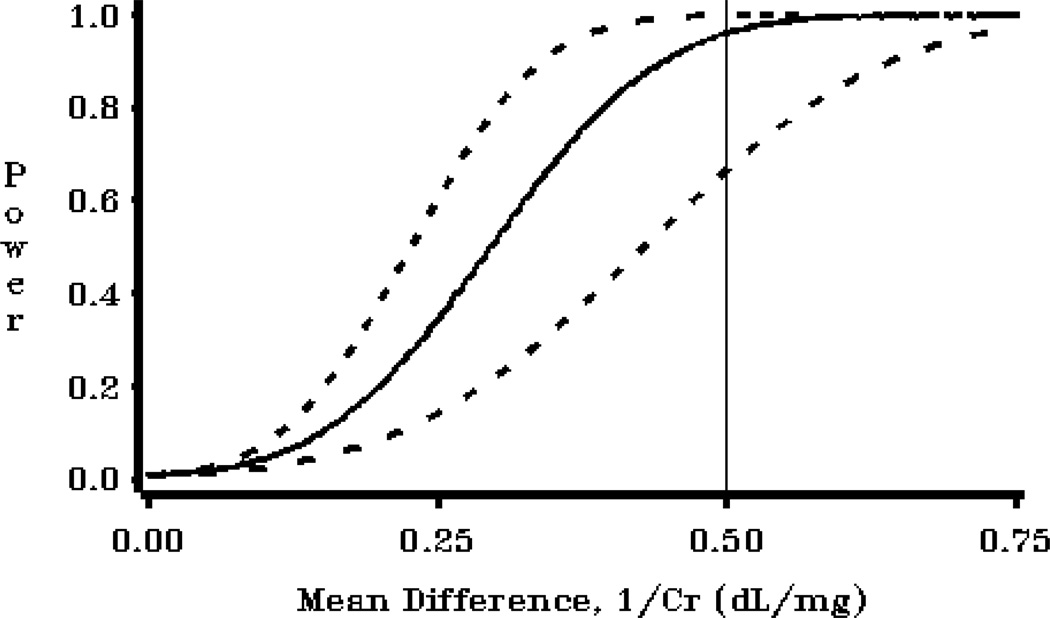
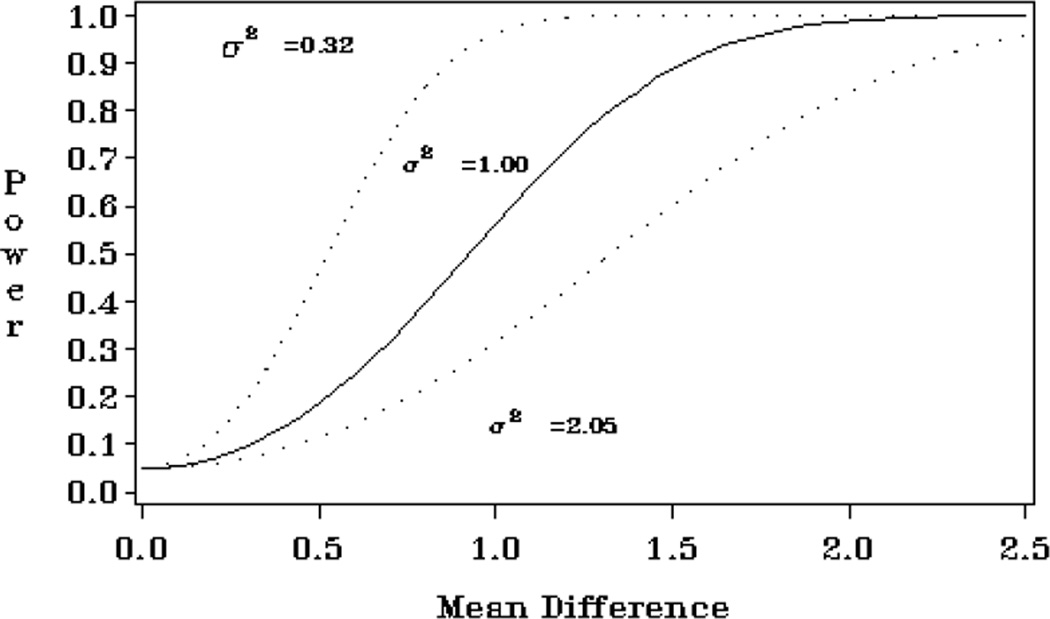
The matrices described in this section are especially useful for producing power curves. Such graphical displays of power over a wide range of study design parameters are far more helpful than computation of point estimates. Figure 1 gives the output of Example 1 in the Examples folder of software distribution. This program computes power over several values of mean difference (linear combination of elements of B).

Figure 1.

Power curve over several values of mean difference and sigma

2.7. Computing confidence limits for power

In the context of power analysis, B and Σ are assumed known constants. In practice, however, estimates of Σ only or of both B and Σ from a previous study are often used. The randomness of these estimates create randomness in resulting power values. Confidence intervals about power values, and confidence regions about power curves, greatly help in planning by accounting for the uncertainty due to using estimates. POWERLIB is the only current software which allows for computation of confidence intervals for power in Gaussian linear models.

Taylor and Muller (1995) and Taylor and Muller (1996) give theory for calculation of exact confidence intervals for univariate linear models with Gaussian errors. Gribbin (2007) and Park (2007) develop approximate confidence intervals for UNIREP and MULTIREP tests, respectively. These methods are exact for univariate models and for the MULTIREP tests when s = 1. For confidence limits for multivariate tests, we assume the user has given the (unbiased) REML estimate for Σ. Note that the current version of the program does not allow compensating for the bias of truncation discussed in Taylor and Muller (1996) and Muller and Pasour (1997).

The CLTYPE, RANK_EST, N_EST, ALPHA_CL, and ALPHA_CU input matrices specify how confidence limits are computed for all test powers.

CLTYPE specifies what type of confidence limits are computed and takes the following values:

• < 1 ⇒ No confidence limits are calculated; assumes B and Σ are known.

• = 1 ⇒ Confidence limits for B known and Σ estimated are calculated

• = 2 ⇒ Confidence limits for B estimated and Σ estimated are calculated

Program 5 Additional code to create confidence limits for power

CLTYPE = 1; N_EST = 21; *# Obs for variance estimate; RANK_EST = 1; *# model df for study giving variance estimate; ALPHA_CL = 0.025; *Lower confidence limit tail size; ALPHA_CU = 0.025; *Upper confidence limit tail size;

Confidence limits with Σ estimated and B known are available for all hypothesis tests available in POWERLIB. Currently, confidence limits where both B and Σ have been estimated are available only for univariate linear models (b = 1). Future research is needed to develop theory for confidence limits for multivariate tests in this case. We caution the reader that only very narrow conditions make using an estimate of B a defensible choice (Lenth 2001).

If CLTYPE ≥ 1, then RANK_EST and N_EST are required inputs. RANK_EST describes the rank of the design matrix from the previous study in which B and Σ were obtained. N_EST gives the total sample size of the previous study.

ALPHA_CL, and ALPHA_CU specify the desired lower and upper tail probabilities, respectively, for confidence limits computations. Both have default values equal to 0.025.

Program 5 gives an example of the additional code needed to create confidence limits for power. For the entire context of this code, see Example 4 in the Examples folder of the software distribution.

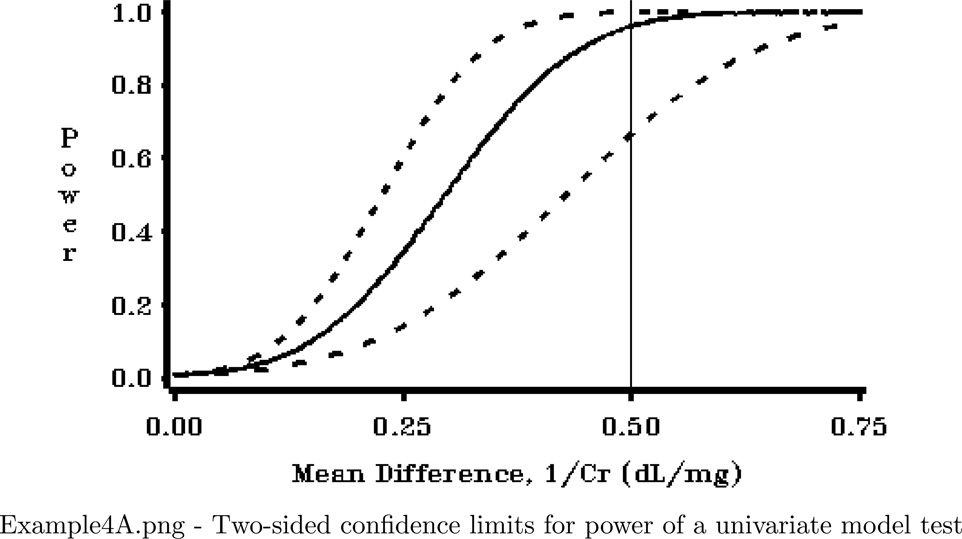
Figure 2, also produced by code in Example 4, shows an example of a useful plot for determining the impact of estimation of power parameters.

Figure 2.

Plot of confidence limits

2.8. Power computation, printing, and output options

2.8.1 Overview

Sections 2.8.2 – 2.8.6 describe the two global input matrices OPT_ON and OPT_OFF. Entries of these matrices are options which the user may specify to modify output produced by POWERLIB. These options allow the user to specify:

1. Options that choose which hypothesis test statistic(s) are computed

2. Additional model specification options

3. Options that specify which columns are included in the final output matrix _HOLDPOWER

4. Options that specify which matrices are printed to the screen by default

5. Overall printing and warning notification options

6. Options that control whether a SAS dataset is produced.

Table 2 gives a list of all possible entries (options) for OPT_ON and OPT_OFF. Assigning values to OPT_ON causes those options to be turned on; values in OPT_OFF are turned off. Both matrices must have only one row or have only one column. Order does not matter, nor does upper or lower case. The default selection of options corresponds to:

OPT_ON  = { GG HLT PBT WLK COLLAPSE ALPHA SIGSCAL BETASCAL TOTAL_N ESSENCEX
            BETA SIGMA RHO C U CBETAU WARN };
OPT_OFF = { UN HF BOX LTFR FRACREPN ORTHU POWERCASE RHOSCAL MAXRHOSQ N_EST
            RANK_EST UMETHOD MMETHOD FMETHOD UCDF RANKX RANKC RANKU
            NOPRINT DS };

Table 2.

Options specified in OPT_ON or OPT_OFF

Option Name	Description	Default ON?
UN	Compute power for UNIREP uncorrected
HF	Compute power for UNIREP Huynh-Feldt
GG	Compute power for UNIREP Geisser-Greenhouse	✓
BOX	Compute power for UNIREP Box
HLT	Compute power for Hotelling-Lawley Trace	✓
PBT	Compute power for Pillai-Bartlett Trace	✓
WLK	Compute power for Wilks’ Lambda	✓
COLLAPSE	s = 1 powers reduce to 1 column	✓
LTFR	Allow use of less than full rank X
FRACREPN	Allow use of fractional REPN values
ORTHU	Allow use of non-orthonormal U
POWERCASE	Include row #
ALPHA	Include ALPHA	✓
SIGSCAL	Include SIGSCAL	✓
RHOSCAL	Include RHOSCAL
BETASCAL	Include BETASCAL	✓
TOTAL_N	Include TOTAL_N	✓
MAXRHOSQ	Include max canonical correlation
CLTYPE	Include CLTYPE	if CLTYPE≥ 1
N_EST	Include N_EST
RANK_EST	Include RANK_EST
ALPHA_CL	Include ALPHA_CL	if CLTYPE≥ 1
ALPHA_CU	Include ALPHA_CU	if CLTYPE≥ 1
UMETHOD	Include UMETHOD
MMETHOD	Include MMETHOD
FMETHOD	Include FMETHOD
UCDF	Include UCDF
ESSENCEX	Print ESSENCEX matrix	✓
RANKX	Print the rank of the X matrix
BETA	Print B matrix	✓
SIGMA	Print Σ matrix	✓
RHO	Print RHO matrix	✓
C	Print C matrix	✓
RANKC	Print the rank of the C matrix
U	Print U matrix	✓
RANKU	Print the rank of the U matrix
THETA0	Print Θ0 matrix	if THETA0≠ 0
CBETAU	Print CBU matrix	✓
WARN	Print power program warnings	✓
NOPRINT	Suppress all printed output
DS	Write _HOLDPOWER to a SAS file with variable names _HOLDPOWERLBL

2.8.2 Choosing the hypothesis test statistic

POWERLIB can compute power for the Box, Geisser-Greenhouse, Huynh-Feldt, and uncorrected UNIREP tests, as well as the Hotelling Lawley Trace, Pillai-Bartlett Trace, and Wilks Lambda MULTIREP tests. To have power computed for each of these tests, specify the BOX, HF, GG, UN, HLT, PBT, or WLK options, respectively, in OPT_ON. The three MULTIREP tests and the Geisser-Greenhouse UNIREP test are computed by default. If power for these tests is not desired, specify the corresponding option in OPT_OFF. Power for each separate test statistic requested is given a separate column in the output dataset.

When b = 1 (and a ≥ 1), the UNIREP and MULTIREP tests coincide to give the familiar univariate linear model test. If the COLLAPSE option is on (as is the default), then if b = 1 (and a ≥ 1) all MULTIREP and UNIREP powers coincide, and so are combined into one output column labeled POWER. If the collapse option is on with b > 1 and a = 1 then all MULTIREP variable powers are combined into one column labeled POWER_MULT.

2.8.3 Additional model specification options

By default:

1. X must be full rank.

2. REPN must contain whole numbers.

3. U must be orthonormal.

The LTFR option allows choice of less than full rank X. The FRACREPN option allows choice of fractional values in REPN. To tolerate non-orthonormal U, specify the ORTHU option. Note that user utility modules UPOLY1, UPOLY2, and UPOLY3 (documented in section 2.13) may also be used to create orthonormal contrast matrices for 1–3 within or between factors.

2.8.4 Specifying columns included in the output matrix

Table 3 lists all possible columns included in the output matrix _HOLDPOWER. Most are not included by default. To add or remove columns, include the option of the same name from the third section Table 2 in OPT_ON or OPT_OFF. Note that asking the program to compute confidence limits for power values adds the columns with suffixes _L and _U to the output matrix.

Table 3.

All possible column labels for output matrix _HOLDPOWER

Column Label	Description
ALPHA	Type I error, α value for power calculation
ALPHA_CL	α value for power lower confidence limit
ALPHA_CU	α value for power upper confidence limit
BETASCAL	Multiplier for B that gave this power
EPSILON	Population Value of ε for UNIREP test power
EXEPS_GG	Approximate Eε̂ for the GG test
EXEPS_HF	Approximate Eε̃ for the HF test
FMETHOD	F probability calculation method with COLLAPSE option
FMETHOD_test	F probability calculation method for test
FMETHOD_L	F probability calculation method for lower confidence limit with COLLAPSE option
FMETHOD_test_L	F probability calculation method for lower confidence limit for test
FMETHOD_U	F probability calculation method for upper confidence limit with COLLAPSE option
FMETHOD_test_U	F probability calculation method for upper confidence limit for test
MAXRHOSQ	Maximum canonical correlation
N_EST	# of obs. which gave Σ and/or B estimates
POWER	Computed power with COLLAPSE option
POWER_test	Computed power for test
POWER_L	Lower confidence limit for power with COLLAPSE option
POWER_test_L	Lower confidence limit for power for test,
POWER_U	Upper confidence limit for power with COLLAPSE option
POWER_test_U	Upper confidence limit for power for test
POWERCASE	Row number of _HOLDPOWER matrix
RANK_EST	rank(X) in analysis providing Σ and/or B estimates
RHOSCAL	Multiplier for correlations from Σ
SIGSCAL	Multiplier for Σ
TOTAL_N	Total sample size
UCDF_test	CDF approximation used for power for UNIREP test
UMETHOD_HF	Method used for calculating E(ε̃)
UMETHOD_GG	Method used for calculating E(ε̂)

test ∈ UN, HF, GG, BOX, HLT, PBT, WLK

2.8.5 Options that control printing and warnings

POWERLIB prints several matrices to the screen by default after power computations are completed. The fourth section of Table 2 lists possible choices and defaults. User inspection of these matrices is important to verify that the model matrices specified to POWERLIB are those intended.

Specifying the NOPRINT option in OPT_ON ensures that no matrices are printed, including the final _HOLDPOWER output matrix. This option is especially useful when power values are output to a dataset and when many power values are computed in a simulation study.

By default, POWERLIB writes helpful warnings to the screen even when no fatal syntax error is present. To suppress printing of these, specify the WARN option in OPT_OFF.

2.8.6 Output to a dataset

To create a dataset, the user must specify the name of the dataset in the input matrix DSNAME as well as include the DS option in the matrix OPT_ON.

The user can name the data file by defining DSNAME as follows:

DSNAME = { libref membername };

For example, if DSNAME = {IN1 MYDATA}, the output file will be called IN1.MYDATA. Here IN1 refers to a library defined by a LIBNAME statement.

If DSNAME is not defined and the DS option is also selected or if “membername” already exists in the library specified by “libref”, a default file name is used. The default file names are numbered and of the form WORK.PWRDT### (where ### is a number). The program scans the library for the largest numbered data file and assigns the next number to the new data file. The maximum ### is 999. If PWRDT999 exists no more data files can be created. Note that the program uses the name _PWRDTMP as an intermediate file. If this file already exists in the specified library no files can be created. To use a library other than WORK as the default, define:

DSNAME = {libref membername defaultlib};

The software will not write over existing files. To continually write to the same file with multiple runs of the power software, the user must consciously delete the existing file. To delete a file IN1.MYDATA, for example, execute the statement:

CALL DELETE (IN, MYDATA);

prior to executing the software.

2.9. Choosing power approximations

2.9.1 Overview

All powers are approximated by noncentral F probabilities. Approximations are used for all tests whenever s = min (a, b) > 1, and for the UNIREP tests whenever b > 1 (whether or not a = 1). All MULTIREP tests’ powers (and test sizes) coincide whenever s = 1, while MULTIREP and UNIREP powers (and test sizes) all coincide if b = 1.

Naturally, the default approximation methods have been chosen, given the current state of knowledge, to be the best available; hence, most users will never need to change the approximation methods from the default. The information here is included to allow comparing to earlier versions of POWERLIB and other program output, and to allow for future developments.

Sections 2.9.2 and 2.9.3 discuss the input matrices UMETHOD, UCDF, and MMETHOD used to specify the distributional approximations used in computing power for the UNIREP and MULTIREP tests, respectively. Choices for these matrices are summarized in Table 4.

Table 4.

UNIREP and MULTIREP distributional approximation methods

Choice for CDF approximation for all UNIREP tests
UCDF [1]		→ Choice for Uncorrected test
UCDF [2]		→ Choice for Huynh-Feldt test
UCDF [3]		→ Choice for Geisser-Greenhouse test
UCDF [4]		→ Choice for Box test
UCDF [J]	= 1	→ Muller and Barton (1989) one moment approximation
	= 2	→ Muller, Edwards, and Taylor (2004) two moment approximation
	= 3	→ Exact via Davies (1980) method (This may fail; if it does a missing value is returned.)
	= 4	→ Exact via Davies (1980) Method, except if it fails, use Muller et al. (2007) approximation.
Choice for expectation of epsilon for Geisser-Greenhouse and Huynh-Feldt
UMETHOD [1]	= 1	→ Muller and Barton (1989) approximation for E(ε̃)
	= 2	→ Muller et al. (2007) approximation for E(ε̃)
UMETHOD [2]	= 1	→ Muller and Barton (1989) approximation for E(ε̂)
	= 2	→ Muller et al. (2007) approximation for E(ε̂)
Choice of CDF approximation for Hotelling-Lawley Trace
MMETHOD [1]	= 1	→ Pillai (1954, 1955) one moment null approximation
	= 2	→ McKeon (1974) two moment null approximation
	= 3	→ Pillai and Samson (1959) one moment null approximation + O’Brien and Shieh (1992) noncentrality multiplier
	= 4	→ McKeon (1974) two moment null approximation + O’Brien and Shieh (1992) noncentrality multiplier
Choices of CDF approximation for Pillai-Bartlett Trace
MMETHOD [2]	= 1	→ Pillai (1954, 1955) one moment null approximation
	= 2	→ Muller (1998) two moment null approximation
	= 3	→ Pillai and Samson (1959) one moment null approximation + O’Brien and Shieh (1992) noncentrality multiplier
	= 4	→ Muller (1998) two moment null approximation + O’Brien and Shieh (1992) noncentrality multiplier
Choices of CDF approximation for Wilks’ Lambda
MMETHOD [3]	= 1	→ Rao (1951) two moment null approximation
	= 2	→ Rao (1951) two moment null approximation
	= 3	→ Rao (1951) two moment null approximation + O’Brien and Shieh (1992) noncentrality multiplier
	= 4	→ Rao (1951) two moment null approximation + O’Brien and Shieh (1992) noncentrality multiplier

2.9.2 Choosing UNIREP approximations

The software allows choosing one of four approximations for the distribution of the UNIREP test statistic under the alternative via the values of UCDF given in Table 4.

The default is UCDF = {2, 2, 2, 2}, with all four UNIREP tests using the Muller et al. (2007) approximation for the distribution the test statistic under the alternative. Exact results may be achieved, at the cost of computing time, for the uncorrected (UN) and Box tests by specifying UCDF = {3, 2, 2, 3}.

UMETHOD specifies whether to use the Muller and Barton (1989) or Muller et al. (2007) approximations for E(ε̃) and E(ε̂). In turn, this option implies the approximate critical value used for the GG and HF tests. The default is UMETHOD = {2,2}.

2.9.3 Choosing MULTIREP approximations

For the MULTIREP tests, the Muller and Peterson (1984) approach requires specifying approximate degrees of freedom, which implies a critical value via the FINV() function, and an approximate noncentrality. By default, the program uses two moment approximations (Rao 1951; McKeon 1974; Muller 1998) for the null distributions, which imply degrees of freedom and critical values. Optionally, older and less accurate one moment methods are also available (Pillai 1954, 1955; Pillai and Samson 1959). By default, the MULTIREP tests use the Muller and Peterson (1984) noncentrality approximations. Optionally, each MULTIREP noncentrality may be multiplied by N/[N − rank(X)] as recommended by O’Brien and Shieh (1992). Using the O’Brien and Shieh (1992) multiplier gives slightly larger approximate powers. Especially for the Hotelling-Lawley test, the original Muller and Peterson (1984) noncentralities can be somewhat conservative in small samples.

Power approximations used for MULTIREP tests can be specified in the matrix MMETHOD. MMETHOD is a 3 × 1 vector whose elements correspond to one of four choices for the method used for the Hotelling Lawley Trace, Pillai-Bartlett Trace, and Wilks Lambda tests, respectively, as given in Table 4. The duplication of settings for Wilks’ test is merely for programming convenience.

The default setting is MMETHOD = {4,2,2}. Using the O’Brien and Shieh (1992) multiplier for all three multivariate tests may be chosen by setting MMETHOD = {4,4,4} or MMETHOD = 4 because MMETHOD can be specified as a 1 × 1 matrix, if all the entries are the same.

2.10. F distribution probability calculations

In all but the most extreme cases, POWERLIB computes the probabilities from an F distribution necessary for power computations using the SAS supplied CDF function. If a test evaluating extremeness of conditions indicates likelihood of the CDF function failing, then POWERLIB computes F probabilities using the Tiku approximation (Kotz et al. 2000). In situations where the Tiku approximations fails or will be inaccurate, POWERLIB uses a Gaussian approximation via the CDF function.

The user can see which method has been used by specifying the FMETHOD option in the OPT_ON matrix. This includes the FMETHOD columns listed in Table 3 into the output matrix _HOLDPOWER. Note that these columns merely describe which methods have been used; the user cannot modify the method chosen.

Values of FMETHOD are as follows:

• = 1 ⇒ CDF function (no approximation)

• = 2 ⇒ Tiku approximation (best approximation)

• = 3 ⇒ Normal approximation, |Z-score|< 6 (worst approximation)

• = 4 ⇒ Normal approximation, |Z-score|> 6 (approximation, but power is almost certainly zero or one)

• = 5 ⇒ Power missing

Difficulties with power calculation occur almost entirely occur when power approaches 0 or 1.

2.11. Numerical accuracy

The input matrices ROUND and TOLERANCE control the rounding of output values and the threshold for judging whether a numerical value is judged to be zero, respectively. The TOLERANCE variable is included to provide a user with sophistication in computing methods some flexibility when working with large models.

2.12. Error checking

Counts of certain numerical difficulties are stored in entries of the output vector _POWERWARN. Table 5 describes the elements of this matrix.

Table 5.

Error messages in _POWERWARN

Element	Description
1	A Tiku approximation was used in calculating power.
2	A Z approximation was used in calculating power.
3	A Z approximation was used in calculating power and |Z| > 6, so that the power returned is exactly 0 or 1.
4	Power is missing because the FINV function returned a missing value.
5	The lower confidence limit on power is conservative.
6	A Tiku approximation was used in calculating the lower confidence limit on power.
7	A Z approximation was used in calculating the lower confidence limit on power.
8	A Z approximation was used in calculating the lower confidence limit on power and |Z| > 6, so that the power returned is exactly 0 or 1.
9	The lower confidence limit on power is missing because the FINV function returned a missing value.
10	The upper confidence limit on power is conservative.
11	A Tiku approximation was used in calculating the upper confidence limit on power.
12	A Z approximation was used in calculating the upper confidence limit on power.
13	A Z approximation was used in calculating the upper confidence limit on power and |Z|> 6, so that the power returned was exactly 0 or 1.
14	The upper confidence limit on power is missing because the FINV function returned a missing value.
15	Power is missing because because the noncentrality could not be computed.
16	Confidence limits are missing because power is missing.
17	The approximate expected value of estimated epsilon was truncated up to 1/b.
18	The approximate expected value of estimated epsilon was truncated down to 1.
19	Power missing due to Davies’ algorithm fail.
20	Inputs give off-diagonal correlation = 1 in RHO.
21	(N - R) <= 5, so power approximations may be inaccurate, especially Huynh-Feldt.
22	Power values were rounded to 1 using the value contained in ROUND and should not be be reported as Power = 1. For example, if ROUND = 3 then report Power > 0.999.

2.13. User utilities

Four modules are included which are useful for creating U contrast matrices. These are:

     UMEAN  UPOLY1  UPOLY2  UPOLY3.

UMEAN is a function module which generates a p × 1 U matrix which computes the average response, p⁻¹ [1 1 … 1]′. For example, it could create the matrix:

$$\mathit{U}=[\begin{array}{ccccc}1/5\hfill & 1/5\hfill & 1/5\hfill & 1/5\hfill & 1/5]\prime .\hfill \end{array}$$

It has one input, p, which tells the size of the matrix to create. For any arbitrary value of p, the user may execute:

U = UMEAN(p);

For example, the previous matrix would be obtained with U = UMEAN(5).

UPOLY1, UPOLY2, and UPOLY3 each generate U contrast matrices with orthogonal polynomial coding for one, two, or three repeated factors, respectively, via the SAS ORPOL function.

UPOLY1 takes two inputs, VALUES and NAME. Here VALUES is a k × 1 vector or 1 × k matrix which gives the k levels of the single repeated factor. NAME is a 1 × 1 character matrix describing the repeated factor. The module outputs two matrices U and ULBL. Columns of U contains up to level k −1 polynomial contrasts; c contains labels for the order of the polynomial contrast each column represents. The UPOLY1 module may be called using the following syntax:

CALL UPOLY1 (VALUES, NAME, U, ULBL);

As an example, the following code creates a U matrix with orthogonal polynomial contrasts for four levels, 1, 10, 100, and 1000, of the factor DOSE:

LEVELS = {1, 10, 100, 1000};
FACTOR = {DOSE};
CALL UPOLY1 (LEVELS, FACTOR, U, ULBL);
PRINT U [COLNAME = ULBL];

The columns of U (as described by ULBL) are the linear, quadratic, and cubic polynomial trends for DOSE. This produces the matrix:

$$\mathit{U}=\left[\begin{array}{ccc}\hfill \mathtt{\text{DOSE}}1& \hfill \mathtt{\text{DOSE}}2& \hfill \mathtt{\text{DOSE}}3\\ \hfill -0.330& \hfill 0.442& \hfill -0.667\\ \hfill -0.320& \hfill 0.314& \hfill 0.741\\ \hfill -0.212& \hfill -0.836& \hfill -0.074\\ \hfill 0.862& \hfill 0.080& \hfill 0.001\end{array}\right].$$

UPOLY2 and UPOLY3, generate U contrast matrices with orthogonal polynomial coding for two and three repeated factors, respectively. Modules UPOLY2 and UPOLY3 work the same way as the UPOLY1 module except they require 4 or 6 input matrices, respectively, and produce 6 or 12 matrices, respectively, due to adding one or two more factors. These modules are called with the following syntax:

CALL UPOLY2 (VALUES1, NAME1, VALUES2, NAME2,
             U1, U1LBL, U2, U2LBL, U12, U12LBL);
CALL UPOLY3 (VALUES1, NAME1, VALUES2, NAME2, VALUES3, NAME3,
             U1, U1LBL, U2, U2LBL, U3, U3LBL,
             U12, U12LBL, U13, U12LBL, U23, U23LBL, U123,U123LBL);

Here VALUES1, VALUES2, and VALUES3 give the levels for factors 1, 2, and 3, respectively, and NAME1, NAME2, NAME3 describe factors 1, 2, and 3, respectively.

Also, U1, U2, and U3 give the main effect contrasts for factors 1, 2, and 3, respectively and U12, U13, and U23 give the two way interaction contrasts for factor 1 with 2, 1 with 3, and 2 with 3, respectively. U123 gives the three way interaction contrasts for factor 1 with 2 and 3.

U1LBL, U2LBL, U3LBL, U12LBL, U13LBL, U23LBL, and U123LBL give column labels for matrices U1, U2, U3, U12, U13, U23, and U123, respectively.

The following example code gives all orthogonal polynomial trends for three factors, AGE, DRUG, and TIME, with levels {2, 4, 6}, {1, 2, 3}, and {10, 30, 60}:

LEVELS1 = {2, 4, 6};
NAME1   = "AGE";
LEVELS2 = {1, 2, 3};
NAME2   = "DRUG";
LEVELS3 = {10, 30, 60};
NAME3   = "TIME";
CALL UPOLY3 (LEVELS1, NAME1, LEVELS2, NAME2, LEVELS3, NAME3,
             U1, U1LBL, U2, U2LBL, U3,U3LBL,
             U12, U12LBL, U13, U13LBL, U23, U23LBL, U123,U123LBL);
PRINT U1   [COLNAME = U1LBL];  PRINT U2   [COLNAME = U2LBL];
PRINT U3   [COLNAME = U3LBL];  PRINT U12  [COLNAME = U12LBL];
PRINT U13  [COLNAME = U13LBL]; PRINT U23  [COLNAME = U23LBL];
PRINT U123 [COLNAME = U123LBL];

Again, numbers in the column labels describe the degree of the polynomial trend corresponding to that column. Labels with one variable indicate a main effect; labels with two variable names indicate a two-way interaction; labels with three variables indicate a three-way interaction. The following statements create a U orthogonal polynomial trends matrix including all trends for main effects, two-way interactions, and the three-way interaction:

U   = U1 || U2 || U3 || U12 || U13 || U23 || U123;
LBL = U1LBL || U2LBL || U3LBL || U12LBL || U13LBL || U23LBL || U123LBL;

3. Concluding Remarks

For those familiar with SAS, POWERLIB substantially increases the power analysis capabilities related to univariate and multivariate linear models. With some simple manipulations of code in SAS/IML, one can calculate power for a wide range of tests and for a variety of approximation methods associated with them. At the same time, users who wish to use the best approximation methods available can simply use the default options in POWERLIB. POWERLIB offers cutting-edge power analysis capabilities, such as confidence intervals for power and power analysis for a special class of linear mixed models. For these reasons among others, POWERLIB is a capable tool for any SAS user who needs comprehensive sample size calculations when planning a study. Additionally, the ability to easily implement POWERLIB in simulation studies makes it a useful tool for those researching statistical power in general.

Appendix - Additional Examples

The code, log, and output listings for all the following power programs are found in the Examples folder included in the ZIP file available for download with this paper. They can be run in an interactive or a batch environment. Any necessary pre-existing files have been provided in the DATA folder. One change is needed for the user to run these programs. The folder where the POWERLIB files and folders have been copied must be specified in the macro variable ROOT with:

%LET ROOT = Your location here‥;

This variable is used when bringing in the POWERLIB21.IML code as in the statement:

%INCLUDE "&ROOT.\Iml\POWERLIB21.IML"/NOSOURCE2;

Additionally, the programs that produce plots will likely require changing the FILENAME statement, as well as a few GOPTIONS, such as DEVICE, to tailor the output to the particular computer. The DISPLAY (in GOPTIONS) may also need to be controlled.

Example 1: Power for a t-test with overlay plot

This example calculates power for a two-sample t-test. The hypothesis tested is whether the two group means are equal. Power is computed for three values of σ² and several values of mean difference (B). Powers for these values are then plotted on a power curve.

Example 1 Program Code:

*** Section that computes power values ***;

* Delete data set for power values if it exists *;

PROC DATASETS LIBRARY=WORK;
DELETE PWRDT1;
RUN; QUIT;

PROC IML SYMSIZE=1000 WORKSIZE=2000;
%INCLUDE "&ROOT.\Iml\POWERLIB21.IML"/NOSOURCE2;

* Define inputs to power program *;

SIGMA = {1};
SIGSCAL = {0.32 1.00 2.05};

ESSENCEX = I(2);
REPN = {10};

BETA = {0 1}‘;
BETASCAL = DO(0,2.5,0.05);
C = {1 −1};

OPT_OFF = {C U};
OPT_ON = {DS};
* The DS option creates a SAS file with the power calculation results.;
* Since no dataset name was specified, WORK.PWRDT1 is created.;

RUN POWER;

*** Section that creates plot ***;

PROC CONTENTS DATA=PWRDT1;
RUN;

PROC SORT DATA=PWRDT1 OUT=ONE;
BY BETASCAL SIGSCAL;
RUN;

* Create file for power curves of varying VARIANCE *;

PROC TRANSPOSE DATA=ONE OUT=TWO PREFIX=SIGPWR;
VAR POWER;
BY BETASCAL;
RUN;

* Create ANNOTATE dataset and assign symbols for labeling plots *;

DATA LABELS (KEEP= X Y XSYS YSYS TEXT STYLE SIZE);
LENGTH   TEXT $ 5  STYLE $ 8;
XSYS="2"; YSYS="2";
X=.26;  Y=.95; TEXT="s";     STYLE="CGREEK"; *SIZE=1.0; OUTPUT;
X=.31;  Y=.97; TEXT="2";     STYLE="TRIPLEX"; SIZE=.75; OUTPUT;
X=.50;  Y=.95; TEXT="=0.32"; STYLE="TRIPLEX"; SIZE=1.0; OUTPUT;
X=.76;  Y=.70; TEXT="s";     STYLE="CGREEK";  SIZE=1.0; OUTPUT;
X=.81;  Y=.72; TEXT="2";     STYLE="TRIPLEX"; SIZE=.75; OUTPUT;
X=1.00; Y=.70; TEXT="=1.00"; STYLE="TRIPLEX"; SIZE=1.0; OUTPUT;
X=1.01; Y=.15; TEXT="s";     STYLE="CGREEK";  SIZE=1.0; OUTPUT;
X=1.06; Y=.17; TEXT="2";     STYLE="TRIPLEX"; SIZE=.75; OUTPUT;
X=1.25; Y=.15; TEXT="=2.05"; STYLE="TRIPLEX"; SIZE=1.0; OUTPUT;
RUN;

* The plot will be saved to this file for future inclusion in a document.*;
FILENAME OUT01 "&ROOT.\Examples\EXAMPLE1.png";

GOPTIONS GSFNAME=OUT01 DEVICE=PNG
CBACK=WHITE COLORS=(BLACK) HORIGIN=0IN VORIGIN=0IN
HSIZE=5IN VSIZE=3IN HTEXT=12PT FTEXT=TRIPLEX;

SYMBOL1 I=JOIN V=NONE L=34 W=1.0;
SYMBOL2 I=JOIN V=NONE L=1  W=1.0;
SYMBOL3 I=JOIN V=NONE L=34 W=1.0;
AXIS1 ORDER=(0 TO 1 BY .1)  W=1.5 MINOR=NONE MAJOR=(W=1.5)
      LABEL=(ANGLE=−90 ROTATE=90);
AXIS2 ORDER=(0 TO 2.5 BY .5) W=1.5 MINOR=NONE MAJOR=(W=1.5);

* The plot overlays power curves for three different variances *;
TITLE1;
PROC GPLOT DATA=TWO;
PLOT SIGPWR1*BETASCAL=1
     SIGPWR2*BETASCAL=2
     SIGPWR3*BETASCAL=3/OVERLAY VAXIS=AXIS1 HAXIS=AXIS2 ANNOTATE=LABELS;
LABEL SIGPWR1="Power"  SIGPWR2="Power"  SIGPWR3="Power"
      BETASCAL="Mean Difference";
RUN;
QUIT;

Example 1 Listing Output:

The output below shows the first several lines of the calculated power values. Additional values were omitted to conserve space.

        ****POWER CALCULATIONS****
                  HOLDPOW
ALPHA   SIGSCAL  BETASCAL   TOTAL_N      POWER
0.05      0.32         0        20       0.05
0.05      0.32      0.05        20      0.054
0.05      0.32       0.1        20      0.066
0.05      0.32      0.15        20      0.087
0.05      0.32       0.2        20      0.116
0.05      0.32      0.25        20      0.155
0.05      0.32       0.3        20      0.202
0.05      0.32      0.35        20      0.258
0.05      0.32       0.4        20      0.322
0.05      0.32      0.45        20      0.391
0.05      0.32       0.5        20      0.465
0.05      0.32      0.55        20      0.539
0.05      0.32       0.6        20      0.612
0.05      0.32      0.65        20      0.681
… etc …

Example 1 Graphics Output:

Example 2: Power for a paired t-test

The following program performs power calculations for a simple paired t-test using a general linear hypothesis in a multivariate setting. The second section of code produces equivalent results as the first; however it uses difference scores to test the null hypothesis of no difference between group means.

Example 2 Program Code:

PROC IML SYMSIZE=2000;
%INCLUDE "&ROOT.\Iml\POWERLIB21.IML"/NOSOURCE2;

ESSENCEX = I(1);
SIGMA = {2 1, 1 2};
BETA = {0 1};
C = {1};
U = {1 −1}‘;
SIGSCAL = {1};
BETASCAL = DO(0,2.5,0.5);
REPN = { 10 };
OPT_ON = {COLLAPSE};
OPT_OFF= {C U};

RUN POWER;
QUIT;

*** Section with difference scores ***;
*** Is equivalent to the above ***;

PROC IML SYMSIZE=2000;
%INCLUDE "&ROOT.\Iml\POWERLIB21.IML"/NOSOURCE2;

ESSENCEX = I(1);
SIGMA = {2}; * Variance of Difference of Means *;
BETA = {1};
C = {1};
U = {1};

SIGSCAL= {1};
BETASCAL = DO(0,2.5,0.5);
REPN = { 10 };
OPT_ON = {COLLAPSE};
OPT_OFF= {C U};

RUN POWER;
QUIT;

Example 2 Listing Output:

Duplicate results have been omitted to conserve space.

        ****POWER CALCULATIONS****
                HOLDPOWER
ALPHA    SIGSCAL  BETASCAL   TOTAL_N      POWER
0.05           1         0        10       0.05
0.05           1       0.5        10      0.171
0.05           1         1        10      0.514
0.05           1       1.5        10      0.846
0.05           1         2        10      0.977
0.05           1       2.5        10      0.999

Example 3: Power for a t-test with 3 dimensional plot

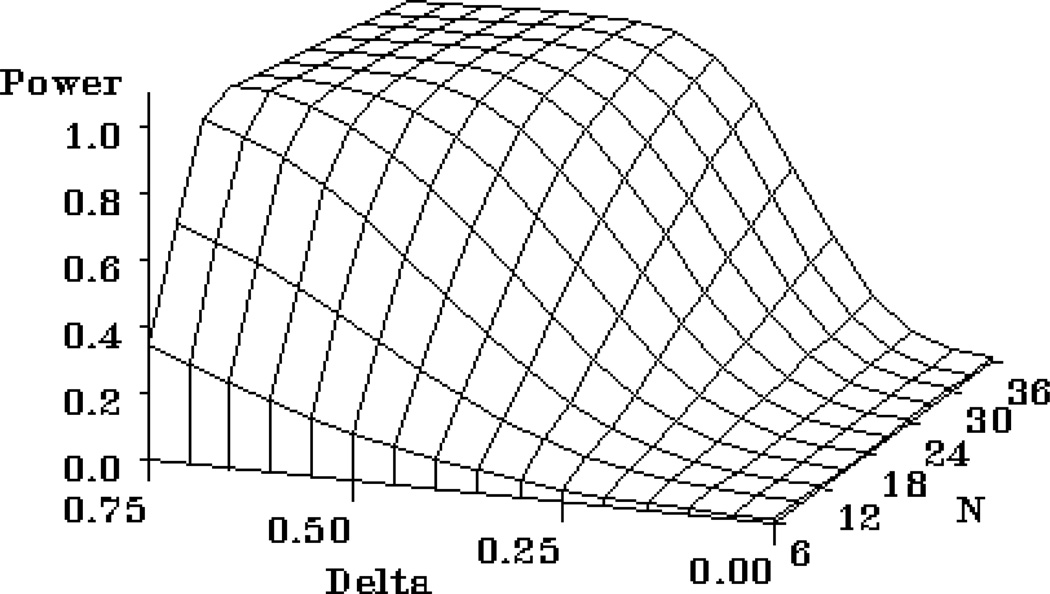
This program produces a 3-dimensional graph that illustrates power trade offs among total sample size and the hypothesized difference between the two group means. The analysis in this particular example is for an independent groups t-test.

Example 3 Program Code:

*** Section that computes power values ***;

* Delete data set for power values if it exists *;

PROC DATASETS LIBRARY=WORK;
DELETE PWRDT1;
RUN; QUIT;

PROC IML WORKSIZE=1000 SYMSIZE=2000;
%INCLUDE "&ROOT.\Iml\POWERLIB21.IML"/NOSOURCE2;

OPT_OFF = {WARN ALPHA};
OPT_ON = {NOPRINT DS};
* Output not printed to screen since NOPRINT option ON *;

ROUND = 6;
ALPHA = {.01};
SIGMA = {.068};
SIGSCAL = {1} ;
BETA = {0 1}‘;
C = {−1 1};
ESSENCEX = I(2);
REPN = DO(3,18,3);
BETASCAL = DO(0,.75,.05);
RUN POWER;

QUIT;

*** Section that creates plot ***;

FILENAME OUT01 "&ROOT.\Examples\EXAMPLE3.png";

%MACRO GRAPH(TILT,ROTATE);
TITLE1;
PROC G3D DATA=ONE GOUT=OUT01;
PLOT BETASCAL*TOTAL_N=POWER/
     ZMIN=0 ZMAX=1.0 ZTICKNUM=6   YTICKNUM=4   XTICKNUM=6   SIDE;
LABEL TOTAL_N ="N"    BETASCAL="Delta"     POWER   ="Power" ;
RUN;
%MEND;

PROC G3GRID DATA=PWRDT1 OUT=ONE;
      GRID  BETASCAL*TOTAL_N=POWER /SPLINE NAXIS1=16 NAXIS2=11 ;

GOPTIONS GSFNAME=OUT01 DEVICE=PNG
CBACK=WHITE COLORS=(BLACK) HORIGIN=0IN VORIGIN=0IN
HSIZE=5IN VSIZE=3IN HTEXT=12PT FTEXT=TRIPLEX;

%GRAPH(90, 300);

Example 3 Graphics Output:

Example 4: Confidence limits for a univariate model test

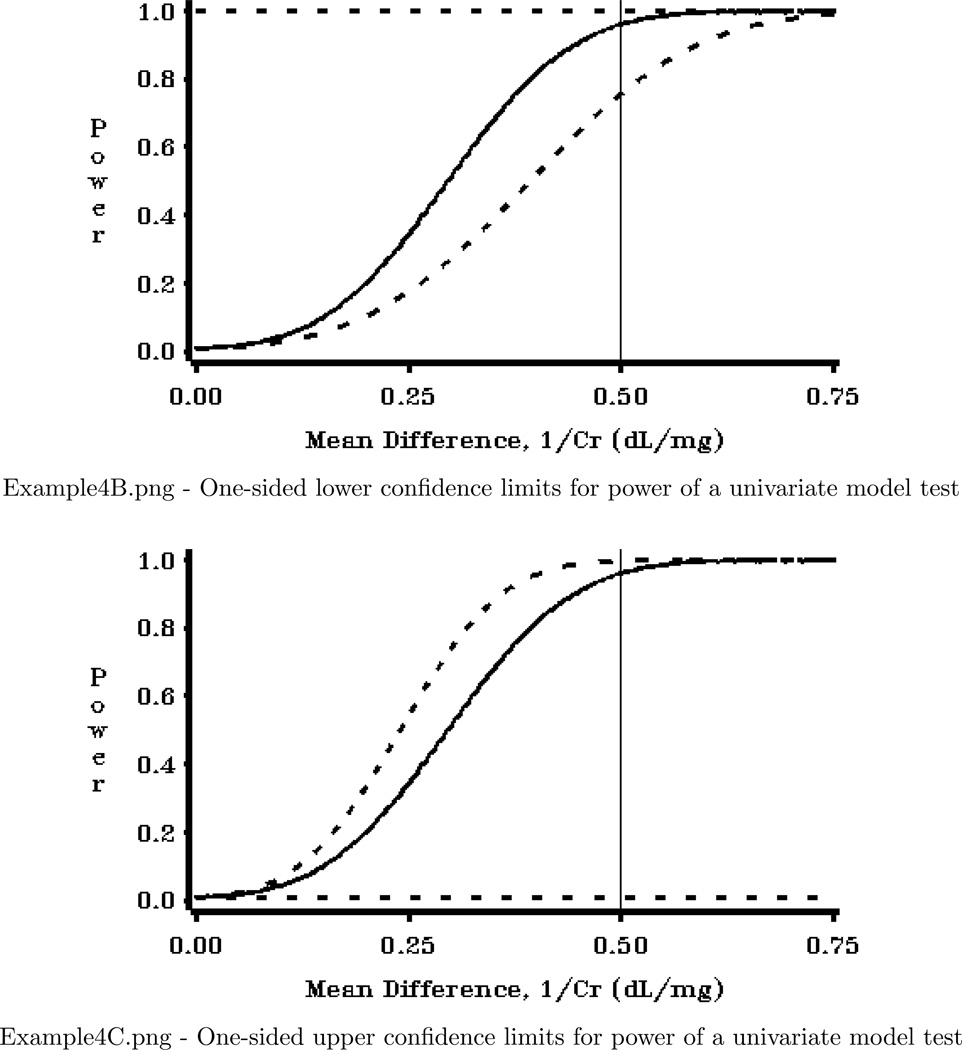
This program produces three very useful graphs for a power analysis. The graphs show confidence limits for power, which reflect uncertainty in power calculations due to use of estimated variance parameters. The program utilizes the power confidence limit calculations available in POWERLIB, and replicates the figures seen in Taylor and Muller (1995).

Example 4 Program Code:

*** Section that computes power values ***;

* Delete data sets for power values if they exist *;

PROC DATASETS LIBRARY=WORK;
DELETE PWRDT1 PWRDT2 PWRDT3;
RUN; QUIT;

PROC IML WORKSIZE=1000 SYMSIZE=2000;
%INCLUDE "&ROOT.\Iml\POWERLIB21.IML"/NOSOURCE2;

OPT_OFF = {ALPHA};
OPT_ON  = {NOPRINT DS};

ESSENCEX = I(2);  *Balanced two group t test, cell mean coding;
REPN = {12};

BETA = {0 1}‘;
BETASCAL = DO(0,.75,.01);

ALPHA={.01};
C    ={1 −1};

SIGMA  = {.068};
SIGSCAL = {1}   ;

* Statements to create two-sided confidence limits *;

CLTYPE = 1;
N_EST = 21;        *# Obs for variance estimate;
RANK_EST = 1;      *# model df for study giving variance estimate;
ALPHA_CL = .025;   *Lower confidence limit tail size;
ALPHA_CU = .025;   *Upper confidence limit tail size;
*Since no dataset name was specified, WORK.PWRDT1 is created.;

RUN POWER;

* Statements to create one-sided lower confidence limits *;

CLTYPE = 1;
N_EST = 24;        *# Obs for variance estimate;
RANK_EST = 1;      *# model df for study giving variance estimate;
*Above three statements could have been omitted here since they duplicate
those for two sided confidence limits*;

ALPHA_CL = 0.05;   *Lower confidence limit tail size;
ALPHA_CU =   0;    *Upper confidence limit tail size;
*Since WORK.PWRDT1 already exists, WORK.PWRDT2 is created.;

RUN POWER;

* Statements to create one-sided upper confidence limits *;

ALPHA_CL = 0;      *Lower confidence limit tail size;
ALPHA_CU = 0.05;   *Upper confidence limit tail size;
*Since WORK.PWRDT1 and WORK.PWDT2 already exist, WORK.PWRDT3 is created.;

RUN POWER;

QUIT;

*** Section that creates plot for two-sided confidence limits ***;

FILENAME OUT01 "&ROOT.\Examples\EXAMPLE4A.png";

GOPTIONS GSFNAME=OUT01 DEVICE=PNG
CBACK=WHITE COLORS=(BLACK) HORIGIN=0IN VORIGIN=0IN
HSIZE=5IN VSIZE=3IN HTEXT=12PT FTEXT=TRIPLEX;

SYMBOL1 I=SPLINE V=NONE L=34 W=2;
SYMBOL2 I=SPLINE V=NONE L= 1 W=2;
SYMBOL3 I=SPLINE V=NONE L=34 W=2;
AXIS1 ORDER=(0 TO 1 BY .2)    W=3 MINOR=NONE MAJOR=(W=2)
      LABEL=(ANGLE=−90 ROTATE=90);
AXIS2 ORDER=(0 TO .75 BY .25) W=3 MINOR=NONE MAJOR=(W=2)
      LABEL=("Mean Difference, 1/Cr (dL/mg)");

TITLE1;
PROC GPLOT DATA=PWRDT1;
PLOT (POWER_L POWER POWER_U)*BETASCAL/ OVERLAY NOFRAME HREF=.5
       VZERO VAXIS=AXIS1 HZERO HAXIS=AXIS2 NOLEGEND;
LABEL POWER_L="Power"  POWER  ="Power"  POWER_U="Power" ;
RUN; QUIT;

*** Section that creates plot for one-sided lower confidence limits ***;

FILENAME OUT01 "&ROOT.\Examples\EXAMPLE4B.png";

GOPTIONS GSFNAME=OUT01 DEVICE=PNG
CBACK=WHITE COLORS=(BLACK) HORIGIN=0IN VORIGIN=0IN
HSIZE=5IN VSIZE=3IN HTEXT=12PT FTEXT=TRIPLEX;

SYMBOL1 I=SPLINE V=NONE L=34 W=2;
SYMBOL2 I=SPLINE V=NONE L= 1 W=2;
SYMBOL3 I=SPLINE V=NONE L=34 W=2;
AXIS1 ORDER=(0 TO 1 BY .2)    W=3 MINOR=NONE MAJOR=(W=2)
      LABEL=(ANGLE=−90 ROTATE=90);
AXIS2 ORDER=(0 TO .75 BY .25) W=3 MINOR=NONE MAJOR=(W=2)
      LABEL=("Mean Difference, 1/Cr (dL/mg)");

PROC GPLOT DATA=PWRDT2;
PLOT (POWER_L POWER POWER_U)*BETASCAL/ OVERLAY NOFRAME HREF=.5
       VZERO VAXIS=AXIS1 HZERO HAXIS=AXIS2 NOLEGEND;
LABEL POWER_L="Power"  POWER  ="Power"  POWER_U="Power";
RUN; QUIT;

*** Section that creates plot for one-sided lower confidence limits ***;

FILENAME OUT01 "&ROOT.\Examples\EXAMPLE4C.png";

GOPTIONS GSFNAME=OUT01 DEVICE=PNG
CBACK=WHITE COLORS=(BLACK) HORIGIN=0IN VORIGIN=0IN
HSIZE=5IN VSIZE=3IN HTEXT=12PT FTEXT=TRIPLEX;

SYMBOL1 I=SPLINE V=NONE L=34 W=2;
SYMBOL2 I=SPLINE V=NONE L= 1 W=2;
SYMBOL3 I=SPLINE V=NONE L=34 W=2;
AXIS1 ORDER=(0 TO 1 BY .2)    W=3 MINOR=NONE MAJOR=(W=2)
      LABEL=(ANGLE=−90 ROTATE=90);
AXIS2 ORDER=(0 TO .75 BY .25) W=3 MINOR=NONE MAJOR=(W=2)
      LABEL=("Mean Difference, 1/Cr (dL/mg)");

TITLE1;
PROC GPLOT DATA=PWRDT3;
PLOT (POWER_L POWER POWER_U)*BETASCAL/ OVERLAY NOFRAME HREF=.5
       VZERO VAXIS=AXIS1 HZERO HAXIS=AXIS2 NOLEGEND;
LABEL POWER_L="Power"  POWER  ="Power"  POWER_U="Power" ;
RUN; QUIT;

Example 4 Graphics Output:

Example 5: Power for a test of the interaction of between and within factors in a multivariate model

This program performs a more complicated set of power calculations for a test of the hypothesis of no time by treatment interaction in a multivariate model.

Example 5 Program Code:

PROC IML SYMSIZE=1000 WORKSIZE=2000;
%INCLUDE "&ROOT.\Iml\POWERLIB21.IML"/NOSOURCE2;

OPT_OFF={ALPHA};
OPT_ON = {ORTHU UN HF GG BOX HLT PBT WLK MMETHOD UMETHOD MMETHOD};
* Specifying the option ORTHU in OPT_ON allows the program to provide;
* an orthonormal U matrix if one is not given by the user;
* This is the case for the following code;

* Create contrast matrices C and U (non-orthonormal) *;
P = 3;
Q = 4;
C = J(Q−1,1,1)||(−I(Q−1));
U = ( J(P−1,1,1)||(−I(P−1)) )‘;

ALPHA = .01;

VARIANCE = 1;
RHO = 0.4;
SIGMA = VARIANCE#(I(P)#(1-RHO) + J(P,P,RHO)); *Compound symmetry;
SIGSCAL = {1, 2};

ESSENCEX = I(Q);
REPN = {5,10};
BETA = J(Q,P,0);
BETA[1,1] = 1;
BETASCAL = DO(0, 2.0 , 0.50);

MMETHOD = {4,4,4}; * Two moment null approximations + OBrien and Shieh (1992)
                     noncentrality multiplier ON;

UCDF = {4,2,2,4};  * UN and Box (4):
                     Exact via Davies’ algorithm (1980), as in Muller,
                     Edwards, Simpson, and Taylor (2007). If exact fails,
                     then switch to approximation 2, MEST (2007);
                   * HF and GG (2):
                     Muller, Edwards, Simpson, and Taylor (2007)
                     approximation;

RUN POWER;

QUIT;

Example 5 Listing Output:

                             ****POWER CALCULATIONS****
                                     HOLDPOWER
SIGSCAL  BETASCAL   TOTAL_N POWER_HLT POWER_PBT POWER_WLK   EPSILON  EXEPS_UN  POWER_UN

   1         0        20      0.01      0.01      0.01         1         1      0.01
   1         0        40      0.01      0.01      0.01         1         1      0.01
   1       0.5        20     0.019      0.02     0.021         1         1     0.021
   1       0.5        40     0.039      0.04     0.041         1         1     0.042
   1         1        20     0.066     0.068     0.075         1         1     0.081
   1         1        40     0.242     0.224     0.247         1         1     0.266
   1       1.5        20     0.202      0.18     0.218         1         1     0.259
   1       1.5        40     0.683      0.58      0.66         1         1     0.727
   1         2        20     0.451     0.344      0.45         1         1      0.56
   1         2        40     0.955     0.849     0.929         1         1      0.97
   2         0        20      0.01      0.01      0.01         1         1      0.01
   2         0        40      0.01      0.01      0.01         1         1      0.01
   2       0.5        20     0.014     0.015     0.015         1         1     0.015
   2       0.5        40     0.022     0.022     0.023         1         1     0.023
   2         1        20     0.032     0.033     0.035         1         1     0.037
   2         1        40     0.089     0.088     0.094         1         1     0.097
   2       1.5        20     0.077     0.078     0.087         1         1     0.095
   2       1.5        40     0.287     0.262     0.291         1         1     0.316
   2         2        20      0.17     0.156     0.186         1         1     0.218
   2         2        40     0.607     0.518      0.59         1         1     0.651

                                     HOLDPOWER
  EXEPS_HF UMETHOD_HF  POWER_HF  EXEPS_GG UMETHOD_GG POWER_GG  EXEPS_BOX POWER_BOX

     1.189          2       0.01     0.895         2    0.007        0.5     0.001
     1.083          2       0.01     0.949         2    0.009        0.5     0.001
     1.189          2      0.021     0.895         2    0.016        0.5     0.002
     1.083          2      0.042     0.949         2    0.037        0.5     0.006
     1.189          2      0.081     0.895         2    0.065        0.5     0.011
     1.083          2      0.266     0.949         2    0.249        0.5     0.076
     1.189          2      0.259     0.895         2    0.221        0.5      0.06
     1.083          2      0.727     0.949         2    0.709        0.5     0.413
     1.189          2       0.56     0.895         2    0.509        0.5     0.215
     1.083          2       0.97     0.949         2    0.966        0.5     0.849
     1.189          2       0.01     0.895         2    0.007        0.5     0.001
     1.083          2       0.01     0.949         2    0.009        0.5     0.001
     1.189          2      0.015     0.895         2    0.011        0.5     0.001
     1.083          2      0.023     0.949         2     0.02        0.5     0.003
     1.189          2      0.037     0.895         2    0.028        0.5     0.004
     1.083          2      0.097     0.949         2    0.089        0.5     0.018
     1.189          2      0.095     0.895         2    0.076        0.5     0.014
     1.083          2      0.316     0.949         2    0.298        0.5     0.099
     1.189          2      0.218     0.895         2    0.184        0.5     0.047
     1.083          2      0.651     0.949         2    0.631        0.5     0.333

Example 6: Confidence limits for a UNIREP test in a multivariate model with plots

This program utilizes a dataset that contains cerebral vessel tortuosity measures for subjects in four regions of the brain. A set of power calculations is performed for the test of the hypothesis of no gender by region interaction with five age groups. Confidence limits are computed for these power values.

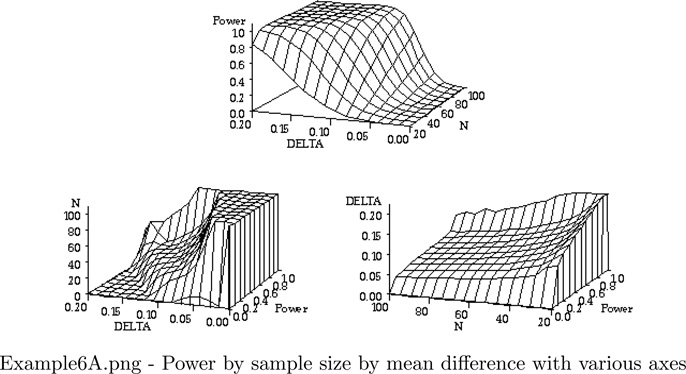
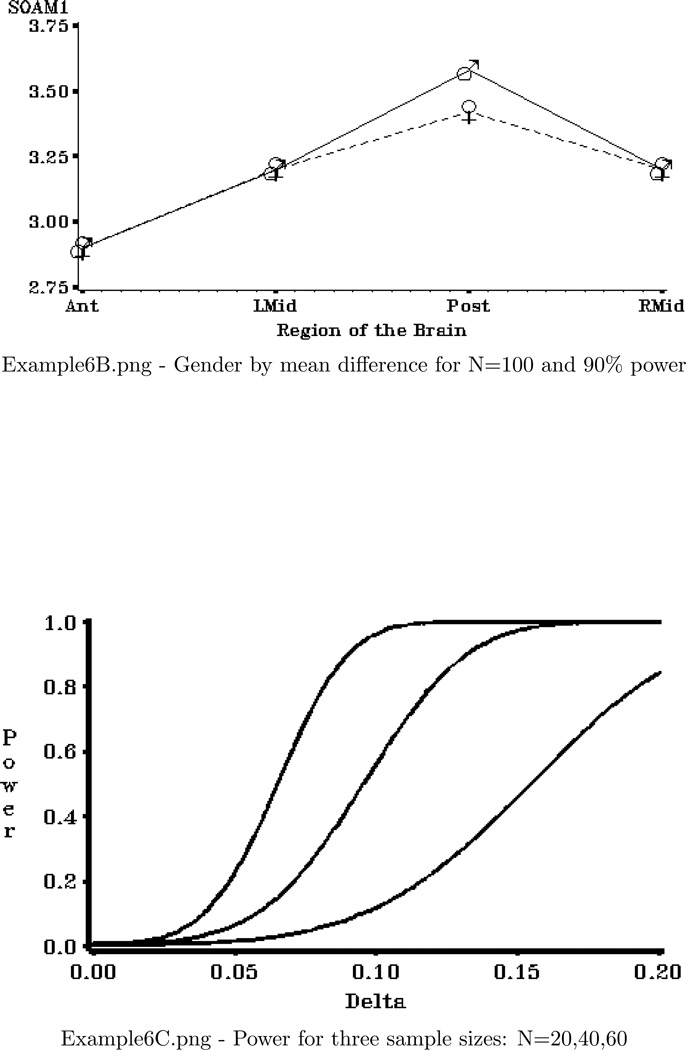
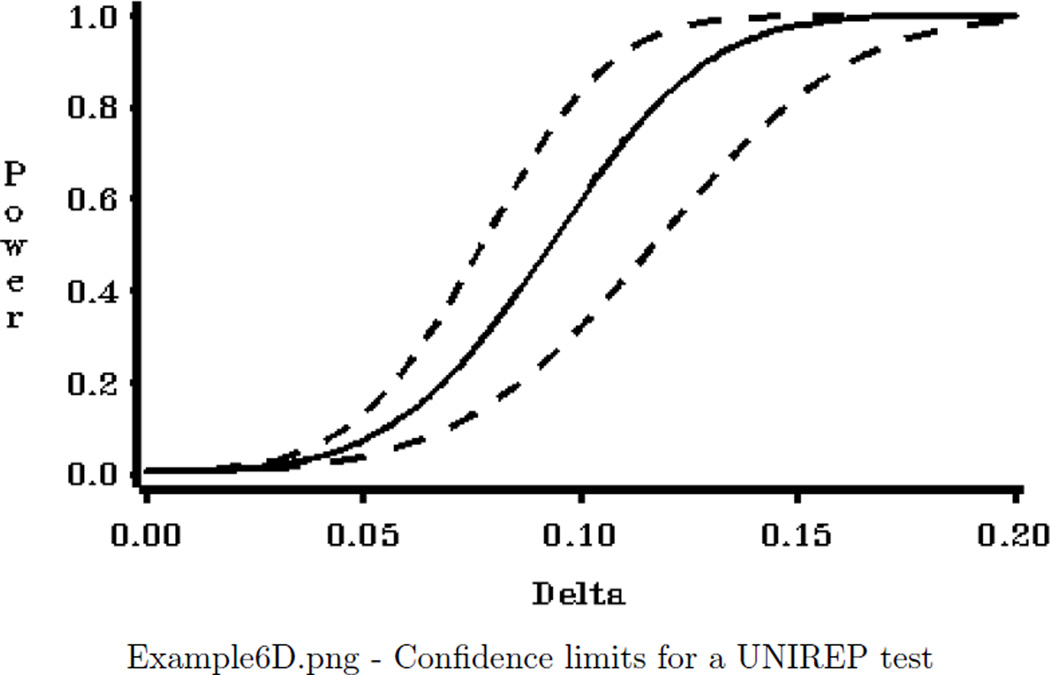
Four graphical displays are produced:

1. Three 3 dimensional plots of power by sample size by mean difference, displayed on different axes

2. A plot of the hypothesized gender by region interaction with a sample size of 100 and an approximate Geisser-Greenhouse power of 0.90.

3. A plot of Geisser-Greenhouse power curves for sample sizes of 20, 40, and 80 for the gender by region interaction.

4. A plot with confidence limits for power with N=40 from the third plot.

Example 6 Program Code:

LIBNAME IN01 V612 "&ROOT.\Data\";

*** Section that computes power values ***;

* Delete data sets for power values if they exist *;

PROC DATASETS LIBRARY=WORK;
DELETE ONE ONECL ;
RUN; QUIT;

PROC IML SYMSIZE=2000 WORKSIZE=2000;
%INCLUDE "&ROOT.\Iml\POWERLIB21.IML"/NOSOURCE2;

OPT_ON = {GG HF BOX UN TOTAL_N ORTHU NOPRINT};
OPT_OFF={WARN ALPHA};

USE IN01.P0104;
*Importing covariance matrix of data*;
READ ALL VAR {ANT LEFT POST RIGHT} WHERE(_TYPE_ = "COV") INTO INSIGMA;

* Rounding and viewing covariance matrix *;

RNM={ANT LEFT POST RIGHT};
ALPHA = .05/6;
SIGMA = ROUND(INSIGMA,.0001);
PRINT SIGMA[FORMAT=11.5 COLNAME=RNM];

* Define input matrices for power calculations *;

ESSENCEX = I(10);
REPN =DO(1,10,1);

P = 4;
Q = 2;

* Pattern of means for Gender by Region *;
BETARG= J(2,4, 3.2) + {.30}#({ −1  0 1  0,
                               −1  0 1  0}) ;
PRINT BETARG[COLNAME=RNM];
BETASCAL={1};

C = {1 −1} @ J(1,5,1);

REGION = {1,2,3,4};
RUN UPOLY1(REGION,"REGION",U1,REGU);
U=U1;

DO DELTA=0 TO .20 BY .0008;
  * Creation of Beta matrix based on varying Gender differences *;
  BETARGD = BETARG + (J(2,2,0)||(DELTA//(-DELTA))||J(2,1,0));
  * Final Beta matrix with age groups added *;
  BETA = BETARGD @ J(5,1,1) ;
  RUN POWER;
  HOLDALL=HOLDALL//( _HOLDPOWER||J(NROW(_HOLDPOWER),1,DELTA) );
END;

* Create dataset without confidence limits *;
* Create dataset manually so can appropriately label columns *;

NAMES = {"SIGSC" "BETASC" "N" "P_MULT" "EPS" "EXEPS_UN" "P_UN"
         "EXEPS_HF" "P_HF" "EXEPS_GG" "P_GG" "EXEPS_BOX" "P_BOX" "DELTA"};
CREATE ONE FROM HOLDALL [COLNAME = NAMES];
APPEND FROM HOLDALL;
CLOSE ONE;

OPT_OFF = {UN BOX HF WLK PBT HLT WARN ALPHA CLTYPE BETASCAL
           SIGSCAL ALPHA_CL ALPHA_CU};
OPT_ON = {GG ORTHU NOPRINT};

REPN = {2,4,8};

* Create dataset with values for confidence limits *;

CLTYPE = 1;     *Estimated variance only, with fixed means*;
N_EST = 21;     *# Obs for variance estimate*;
RANK_EST = 1;   *# Model DF for study giving variance estimate*;
ALPHA_CL = .025;           *Lower confidence limit tail size*;
ALPHA_CU = .025;           *Upper confidence limit tail size*;

FREE HOLDALL;
DO DELTA=0 TO .20 BY .0008;
  * Creation of Beta matrix based on varying Gender differences *;
  BETARGD = BETARG + (J(2,2,0)||(DELTA//(-DELTA))||J(2,1,0));
  * Final Beta matrix with age groups added *;
  BETA = BETARGD @ J(5,1,1) ;
  RUN POWER;
  HOLDALL=HOLDALL//( _HOLDPOWER||J(NROW(_HOLDPOWER),1,DELTA) );
END;

NAMES = _HOLDPOWERLBL || "DELTA";
CREATE ONECL FROM HOLDALL [COLNAME = NAMES];
APPEND FROM HOLDALL;
CLOSE ONECL;

QUIT;

*** Section that creates 3D plot ***;

DATA TWO;
N = 100; DELTA = 0; P_GG = 0; * Create ’dummy’ entry for graph *;
RUN;

DATA THREE;
SET ONE TWO;
KEEP N P_GG DELTA;
RUN;

* Delete any existing graphs *;

PROC DATASETS LIBRARY=WORK MEMTYPE=CATALOG;
DELETE GSEG ;
RUN; QUIT;

* Create 3D Power curves *;

FILENAME OUT01 "&ROOT.\Examples\EXAMPLE6A.png";
TITLE1;

%MACRO GRAPH(TILT,ROTATE);
PROC G3D DATA = FOUR GOUT = FIVE;
        PLOT DELTA*N = P_GG/
           ZMIN=0 ZMAX=1.0 ZTICKNUM=6 YTICKNUM=5 XTICKNUM=5;
        LABEL P_GG = "Power";
RUN;
%MEND;

* Each PROC G3GRID call takes a few minutes to run *;
PROC G3GRID DATA = THREE OUT = FOUR;
GRID DELTA*N = P_GG/SPLINE NAXIS1=16 NAXIS2=11;

GOPTIONS GSFNAME=OUT01 DEVICE=PNG
CBACK=WHITE COLORS=(BLACK) HORIGIN=0IN VORIGIN=0IN
HSIZE=7IN VSIZE=5IN HTEXT=16PT FTEXT=ZAPF;

%GRAPH(90,300);
RUN;QUIT;RUN;

%MACRO GRAPH(TILT,ROTATE);
PROC G3D DATA = FOUR GOUT = FIVE;
        PLOT DELTA*P_GG = N/
                ZMIN=0 ZMAX=100 ZTICKNUM=6 YTICKNUM=5 XTICKNUM=6 SIDE;
        LABEL P_GG = "Power";
RUN;
%MEND;

* Each PROC G3GRID call takes a few minutes to run *;
PROC G3GRID DATA = THREE OUT = FOUR;
        GRID DELTA*P_GG = N/SPLINE NAXIS1=16 NAXIS2=11;

GOPTIONS GSFNAME=OUT01 DEVICE=PNG
CBACK=WHITE COLORS=(BLACK) HORIGIN=0IN VORIGIN=0IN
HSIZE=7IN VSIZE=5IN HTEXT=16PT FTEXT=ZAPF;

%GRAPH(90,300);
RUN;QUIT;RUN;

%MACRO GRAPH(TILT,ROTATE);
PROC G3D DATA = FOUR GOUT = FIVE;
        PLOT N*P_GG = DELTA/
                ZMIN=0 ZMAX=0.2 ZTICKNUM=5 YTICKNUM=5 XTICKNUM=6 SIDE;
        LABEL P_GG = "Power";
RUN;
%MEND;

* Each PROC G3GRID call takes a few minutes to run *;
PROC G3GRID DATA = THREE OUT = FOUR;
        GRID N*P_GG = DELTA/SPLINE NAXIS1=16 NAXIS2=11;

GOPTIONS GSFNAME=OUT01 DEVICE=PNG
CBACK=WHITE COLORS=(BLACK) HORIGIN=0IN VORIGIN=0IN
HSIZE=7IN VSIZE=5IN HTEXT=16PT FTEXT=ZAPF;

%GRAPH(90,300);
RUN;QUIT;RUN;

PROC GREPLAY IGOUT=FIVE TC=TEMPCAT NOFS;
TDEF TEMP2BY2 DES="2 rows, 2 columns (3 plots)"
 1/LLX= 25 ULX= 25 LRX= 75 URX= 75   LLY=50 ULY=100 LRY=50 URY=100
 2/LLX= 0 ULX= 0 LRX= 50 URX= 50   LLY=0 ULY=50 LRY=0 URY=50
 3/LLX= 50 ULX= 50 LRX= 100 URX= 100   LLY=0 ULY=50 LRY=0 URY=50;
TEMPLATE TEMP2BY2;
TREPLAY 1:G3D  2:G3D1 3:G3D2;
RUN;QUIT; RUN;

*** Section that creates plot of values of gender*region
    differences that achieve 90% power ***;

FILENAME OUT01 "&ROOT.\Examples\EXAMPLE6B.png";

* Extracts data with GG power >= 0.89 *;

DATA SIX;
SET THREE;
IF N = 100 AND P_GG >= 0.89;
KEEP N P_GG DELTA;
RUN;

* Creates dataset for Beta plot *;

PROC IML SYMSIZE=2000 WORKSIZE=2000;

USE SIX;
READ ALL VAR {DELTA} INTO INDELTA;

BETARG= J(2,4, 3.2) + {.30}#({ −1  0 1  0,
                               −1  0 1  0});

RESET PRINT;
DELTA = INDELTA[1,1]; * Value of delta for which power is approx. 90% *;
BETARGD=(BETARG + (J(2,2,0)||(DELTA//(-DELTA))||J(2,1,0)))‘;
HOLD1= BETARGD[,1]//BETARGD[,2];
HOLD2=((DO(1,4,1))‘) // ((DO(1,4,1))‘) ;
HOLD3=J(4,1,1)//J(4,1,2);
HOLD=HOLD1||HOLD2||HOLD3;
HNAMES={"SOAM1" "IREGION" "GENDER"};
CREATE SEVEN FROM HOLD [COLNAME = HNAMES];
APPEND FROM HOLD;
CLOSE SEVEN;
QUIT;

GOPTIONS GSFMODE=REPLACE GACCESS=SASGASTD GSFNAME=OUT01
         CBACK=WHITE COLORS=(BLACK) DEVICE=PNG
         HTITLE=.1666 IN HTEXT=.1666 IN HBY=.1666 IN
         HPOS=80 VPOS=60 HSIZE=6.0 IN VSIZE=3.0 IN
         FTEXT=TRIPLEX FTITLE=TRIPLEX FBY=TRIPLEX;

AXIS1 LABEL=("SOAM1") ORDER=(2.75 TO 3.75 BY 0.25)   MAJOR=(W=3) MINOR=NONE;
AXIS2 LABEL=("Region of the Brain") MAJOR=(W=3)
      VALUE=("Ant" "LMid" "Post" "RMid");

SYMBOL1 I=JOIN L=1 VALUE=e H=6 FONT=SPECIAL;
SYMBOL2 I=JOIN L=2 VALUE=c H=6  FONT=SPECIAL;

TITLE1;
PROC GPLOT DATA=SEVEN;
  PLOT SOAM1*IREGION=GENDER / NOLEGEND NOFRAME VAXIS=AXIS1 HAXIS=AXIS2;
RUN;
QUIT;

*** Section that creates overlay plot of power for three sample sizes ****;

FILENAME OUT01 "&ROOT.\Examples\EXAMPLE6C.png";

PROC SORT DATA=ONE OUT=EIGHT;
BY N DELTA;
RUN;

DATA NINE;
MERGE EIGHT( WHERE=(N=20) RENAME=(P_GG=P20) )
        EIGHT( WHERE=(N=40) RENAME=(P_GG=P40) )
        EIGHT( WHERE=(N=80) RENAME=(P_GG=P80) );
RUN;

* Power curves for N = 20,40,80 *;

GOPTIONS GSFNAME=OUT01 DEVICE=PNG
CBACK=WHITE COLORS=(BLACK) HORIGIN=0IN VORIGIN=0IN
HSIZE=5IN VSIZE=3IN HTEXT=12PT FTEXT=TRIPLEX;

SYMBOL1 I=SPLINE V=NONE L=1 W=2 R=3;

AXIS1 ORDER=(0 TO 1.0 BY .20)    W=3 MINOR=NONE MAJOR=(W=2)
      LABEL=(ANGLE=−90 ROTATE=90);
AXIS2 LABEL=("Delta") ORDER=(0 TO .20 BY .05) W=3 MINOR=NONE MAJOR=(W=2);

PROC GPLOT DATA=NINE;
PLOT (P20 P40 P80)*DELTA/ OVERLAY NOFRAME
       VZERO VAXIS=AXIS1 HZERO HAXIS=AXIS2 NOLEGEND;
LABEL P20 ="Power" P40 ="Power" P80 ="Power";
RUN; QUIT;

*** Section that creates plot with confidence limits for power for N=40***;

FILENAME OUT01 "&ROOT.\Examples\EXAMPLE6D.png";

GOPTIONS RESET=ALL GSFNAME=OUT01 DEVICE=PNG
CBACK=WHITE COLORS=(BLACK) HORIGIN=0IN VORIGIN=0IN
HSIZE=5IN VSIZE=3IN HTEXT=12PT FTEXT=TRIPLEX;

SYMBOL1 L=1 I=SPLINE V=NONE W=2;
SYMBOL2 L=20 I=SPLINE V=NONE W=2 R=2;

AXIS1 ORDER=(0 TO 1.0 BY .20)    W=3 MINOR=NONE MAJOR=(W=2)
      LABEL=(ANGLE=-90 ROTATE=90);
AXIS2 LABEL=("Delta") ORDER=(0 TO .20 BY .05) W=3 MINOR=NONE MAJOR=(W=2);

PROC GPLOT DATA=ONECL;
WHERE TOTAL_N=40;
PLOT (POWER_GG POWER_GG_L POWER_GG_U )*DELTA/ OVERLAY NOFRAME
       VZERO VAXIS=AXIS1 HZERO HAXIS=AXIS2 NOLEGEND;
LABEL POWER_GG ="Power" POWER_GG_L ="Power" POWER_GG_U ="Power";
RUN; QUIT;

Example 6 Graphics Output:

Example 7: Illustrate use of the UPOLY1 module

This program demonstrates the use of the UPOLY1 module when performing power calculations for a time by treatment interaction.

Example 7 Program Code:

PROC IML WORKSIZE=1000 SYMSIZE=2000;
%INCLUDE "&ROOT.\Iml\POWERLIB21.IML"/NOSOURCE2;

OPT_ON  = {GG HF HLT PBT TOTAL_N};
OPT_OFF = {WARN WLK UN COLLAPSE ALPHA SIGSCAL BETASCAL};

ALPHA = .05;
VARIANCE = 1.5;
RHO = 0.25;
* Create compound symmetric covariance structure *;
SIGMA = VARIANCE#(I(5)#(1-RHO) + J(5,5,RHO));

ESSENCEX = I(2);
REPN = {10,20,40};

BETASCAL = 1;
BETA = {0 0 0 0 1,
        1 0 0 0 0};
C = {1 -1};

TIMES ={2 4 6 8 10};
RUN UPOLY1(TIMES  ,"Time", USCORE , SCORENM );
U = USCORE;

RUN POWER;
QUIT;

Example 7 Listing Output:

                        ****POWER CALCULATIONS****
                                HOLDPOWER
TOTAL_N POWER_HLT POWER_PBT   EPSILON  EXEPS_HF  POWER_HF  EXEPS_GG  POWER_GG
     20      0.51      0.51         1     1.054     0.625     0.804     0.574
     40     0.902     0.902         1     1.026     0.933     0.895     0.924
     80     0.999     0.999         1     1.013     0.999     0.946     0.999

Example 8: Illustrate use of the UPOLY3 module

This first part of this program demonstrates the direct creation of three way contrast matrices of two types, orthonormal polynomials, and pair-wise differences to a reference level. As long as cell mean coding is used for a factorial design (including the special case of a one-way design), the approach taken to create U matrices may be applied to C matrices, and vice versa, with the obvious change of transposing matrices. Although we recommend using UPOLY3, this example is intended to provide a basis for creating contrasts for more unusual designs. The second part of this program demonstrates creation of the same contrast matrices using the UPOLY3 module.

Example 8 Program Code:

*** Section that creates contrast matrices without UPOLY3 module***;

TITLE3 "UPOLY3 module not used";
PROC IML SYMSIZE=1000 WORKSIZE=2000;
RESET FUZZ NOAUTONAME FW=6 LINESIZE=80;
%INCLUDE "&ROOT.\Iml\POWERLIB21.IML"/NOSOURCE2;

ALPHA = .05;

* Choose dimensions of design *;
GA = 3; * =# groups for between factor A *;
GB = 3; * =# groups for between factor B *;
GC = 3; * =# groups for between factor C *;
TD = 3; * =#Times for within factor D *;
TE = 3; * =#Times for within factor E *;
TF = 3; * =#Times for within factor F *;

P = TD#TE#TF;
Q = GA#GB#GC;
ESSENCEX = I(Q);
BETA = J(Q,P,0);
BETA[1,1] = 1;

SIGMA=DIAG(DO(1,P,1));* Variances are 1,2,3,…p *;

* Get orthonormal sub matrices for U matrices *;
POLYD = ORPOL(1:TD);
UD1 = POLYD[,2:NCOL(POLYD)]‘;
POLYE = ORPOL(1:TE);
UE1 = POLYE[,2:NCOL(POLYE)]‘;
POLYF = ORPOL(1:TF);
UF1 = POLYF[,2:NCOL(POLYF)]‘;

* U matrix for Main effect D *;
UD = (UD1 @ J(1,TE,1) @ J(1,TF,1))‘;

* U matrix for Main effect E *;
UE = (J(1,TD,1) @ UE1 @ J(1,TF,1))‘;

* U matrix for Main effect F *;
UF = (J(1,TD,1) @ J(1,TE,1) @ UF1)‘;

* U matrix for DxE interaction *;
UDE = HDIR(UD,UE);

* U matrix for DxExF interaction *;
UDEF = HDIR(UDE,UF);

* Get sub matrices for between factors *;
CA1 = J(GA−1,1, −1)||I(GA−1);
CB1 = J(GB−1,1, −1)||I(GB−1);
CC1 = J(GC−1,1, −1)||I(GC−1);

* Main effect A *;
CA = CA1 @ J(1,GB,1) @ J(1,GC,1);

* Main effect B *;
CB = J(1,GA,1) @ CB1 @ J(1,GC,1);

* Main effect C[FORMAT=2.] *;
CC = J(1,GA,1) @ J(1,GB,1) @ CC1;

* AxB interaction *;
CAB = (HDIR(CA‘,CB‘))‘;

* AxBxC interaction *;
CABC = (HDIR(CAB‘,CC‘))‘;

BETASCAL = {9 18 27};
ROUND = 4;
OPT_ON = {NOPRINT GG HF UN PBT HLT WLK};
OPT_OFF = {WARN SIGSCAL ALPHA};
BUG = " ";

C = CA;
U = UD;
  DO REPN = 2 TO 12 BY 2;
  RUN POWER;
  HOLDA=HOLDA//_HOLDPOWER;
  END;
PRINT / "A×D";
PRINT HOLDA[COLNAME=_HOLDPOWERLBL ROWNAME=BUG];

C = CAB;
U = UDE;
  DO REPN=2 TO 12 BY 2;
  RUN POWER;
  HOLDABDE=HOLDABDE//_HOLDPOWER;
  END;
PRINT / "A×B × D×E Interaction";
PRINT HOLDABDE[COLNAME=_HOLDPOWERLBL ROWNAME=BUG];

C = CABC;
U = UDEF;
  DO REPN=2 TO 12 BY 2;
  RUN POWER;
  HABCDEF=HABCDEF//_HOLDPOWER;
  END;
PRINT / "A×B×C × D×E×F Interaction";
PRINT HABCDEF[COLNAME=_HOLDPOWERLBL ROWNAME=BUG];

QUIT;

*** Section that creates contrast matrices with UPOLY3 module ***;

TITLE3 "UPOLY3 module used to create contrast matrices";

PROC IML SYMSIZE=1000 WORKSIZE=2000;
RESET FUZZ NOAUTONAME FW=6 LINESIZE=80;
%INCLUDE "&ROOT.\Iml\POWERLIB21.IML"/NOSOURCE2;

ALPHA = .05;

* Choose dimensions of design *;
GA = 3; * =# groups for between factor A *;
GB = 3; * =# groups for between factor B *;
GC = 3; * =# groups for between factor C *;
TD = 3; * =#Times for within factor D *;
TE = 3; * =#Times for within factor E *;
TF = 3; * =#Times for within factor F *;

P = TD#TE#TF;
Q = GA#GB#GC;
ESSENCEX = I(Q);
BETA = J(Q,P,0);
BETA[1,1] = 1;

SIGMA = DIAG(DO(1,P,1)); * Variances are 1,2,3,…p *;

* Get orthonormal U matrices *;
CALL UPOLY3 ( (1:TD),"D", (1:TE),"E",  (1:TF),"F",
                          UD,UDLBL,   UE,UELBL,    UF,UFLBL,
                 UDE,UDELBL, UDF,UDFLBL,  UEF,UEFLBL,  UDEF,UDEFLBL );

* Get orthonormal C matrices *;
CALL UPOLY3 ((1:GA),"A" , (1:GB),"B" , (1:GC),"C",
                         U1,CALBL,    U2,CBLBL,    U3,CCLBL,
                U12,CABLBL, U13,CACLBL,   U23,CBCLBL,  U123,CABCLBL);

BETASCAL = {9 18 27};
ROUND = 4;
OPT_ON = {NOPRINT  GG HF UN  PBT HLT WLK};
OPT_OFF = {WARN SIGSCAL ALPHA};
BUG=" ";

C = U1‘;
U = UD;
  DO REPN = 2 TO 12 BY 2;
  RUN POWER;
  HOLDA=HOLDA//_HOLDPOWER;
  END;
PRINT / "A×D";
PRINT HOLDA[COLNAME=_HOLDPOWERLBL ROWNAME=BUG];

C = U12‘;
U = UDE;
  DO REPN = 2 TO 12 BY 2;
  RUN POWER;
  HOLDABDE = HOLDABDE//_HOLDPOWER;
  END;
PRINT / "A×B × D×E Interaction";
PRINT HOLDABDE[COLNAME=_HOLDPOWERLBL ROWNAME=BUG];

C = U123‘;
U = UDEF;
  DO REPN = 2 TO 12 BY 2;
  RUN POWER;
  HABCDEF = HABCDEF//_HOLDPOWER;
  END;
PRINT / "A×B×C × D×E×F Interaction";
PRINT HABCDEF[COLNAME=_HOLDPOWERLBL ROWNAME=BUG];

QUIT;

Example 8 Listing Output:

Duplicate results have been omitted to conserve space.

                        A×D

                       HOLDA
BETASCAL TOTAL_N POWER_HLT POWER_PBT POWER_WLK EPSILON

       9      54    0.0542    0.0546    0.0544  0.8789
      18      54    0.0672    0.0689    0.0683  0.8789
      27      54    0.0907    0.0945    0.0933  0.8789
       9     108    0.0593    0.0596    0.0595  0.8789
      18     108      0.09    0.0911    0.0907  0.8789
      27     108    0.1486    0.1511    0.1504  0.8789
       9     162    0.0644    0.0647    0.0646  0.8789
      18     162    0.1138    0.1148    0.1145  0.8789
      27     162    0.2109    0.2128    0.2124  0.8789
       9     216    0.0697    0.0699    0.0698  0.8789
      18     216     0.139      0.14    0.1397  0.8789
      27     216    0.2766     0.278    0.2778  0.8789
       9     270     0.075    0.0753    0.0752  0.8789
      18     270    0.1655    0.1664    0.1661  0.8789
      27     270    0.3436    0.3444    0.3444  0.8789
       9     324    0.0805    0.0807    0.0806  0.8789
      18     324    0.1931    0.1939    0.1936  0.8789
      27     324    0.4101    0.4103    0.4106  0.8789

                      HOLDA
EXEPS_UN POWER_UN EXEPS_HF POWER_HF EXEPS_GG POWER_GG

       1    0.061   1.7317    0.061   0.8311   0.0484
       1   0.0684   1.7317   0.0684   0.8311   0.0545
       1   0.0817   1.7317   0.0817   0.8311   0.0657
       1   0.0632   1.1616   0.0632   0.8619   0.0531
       1   0.0795   1.1616   0.0795   0.8619   0.0672
       1    0.111   1.1616    0.111   0.8619    0.095
       1   0.0658   1.0484   0.0658   0.8686   0.0559
       1   0.0916   1.0484   0.0916   0.8686   0.0787
       1   0.1447   1.0484   0.1447   0.8686   0.1262
       1   0.0684   0.9999   0.0684   0.8715   0.0585
       1   0.1048   0.9999   0.1048   0.8715   0.0907
       1   0.1825   0.9999   0.1825   0.8715   0.1613
       1   0.0712    0.973   0.0691   0.8731    0.061
       1   0.1188    0.973   0.1157   0.8731   0.1036
       1   0.2239    0.973    0.219   0.8731   0.1999
       1   0.0739   0.9559   0.0704   0.8742   0.0636
       1   0.1338   0.9559   0.1281   0.8742   0.1172
       1   0.2679   0.9559   0.2591   0.8742   0.2415

               A×B × D×E Interaction
                      HOLDABDE
BETASCAL TOTAL_N POWER_HLT POWER_PBT POWER_WLK EPSILON

       9      54    0.0582    0.0601    0.0591  0.8673
      18      54    0.0864    0.0947    0.0905  0.8673
      27      54    0.1455    0.1614    0.1555  0.8673
       9     108    0.0706     0.072    0.0713  0.8673
      18     108    0.1537    0.1587    0.1562  0.8673
      27     108    0.3425     0.342    0.3442  0.8673
       9     162    0.0836    0.0849    0.0842  0.8673
      18     162    0.2317    0.2345    0.2331  0.8673
      27     162    0.5439    0.5314    0.5396  0.8673
       9     216    0.0975    0.0988    0.0981  0.8673
      18     216    0.3179    0.3184    0.3182  0.8673
      27     216    0.7133    0.6948    0.7059  0.8673
       9     270    0.1125    0.1136     0.113  0.8673
      18     270    0.4077    0.4058    0.4069  0.8673
      27     270    0.8348    0.8164    0.8271  0.8673
       9     324    0.1284    0.1295    0.1288  0.8673
      18     324    0.4966    0.4924    0.4946  0.8673
      27     324    0.9117     0.897    0.9055  0.8673

                     HOLDABDE
EXEPS_UN POWER_UN EXEPS_HF POWER_HF EXEPS_GG POWER_GG

       1   0.0657   1.6919   0.0657     0.76   0.0437
       1   0.0804   1.6919   0.0804     0.76   0.0542
       1   0.1093   1.6919   0.1093     0.76   0.0755
       1   0.0706   1.1443   0.0706   0.8278   0.0544
       1   0.1057   1.1443   0.1057   0.8278   0.0831
       1   0.1859   1.1443   0.1859   0.8278   0.1513
       1   0.0759   1.0338   0.0759   0.8431   0.0603
       1   0.1357   1.0338   0.1357   0.8431   0.1109
       1   0.2837   1.0338   0.2837   0.8431   0.2428
       1   0.0815   0.9863   0.0801   0.8498   0.0658
       1   0.1703   0.9863   0.1679   0.8498   0.1425
       1   0.3965   0.9863   0.3926   0.8498   0.3508
       1   0.0874   0.9599   0.0831   0.8536   0.0712
       1   0.2095   0.9599   0.2014   0.8536   0.1783
       1   0.5143   0.9599   0.5024   0.8536   0.4672
       1   0.0936   0.9431   0.0871   0.8561   0.0768
       1   0.2529   0.9431   0.2398   0.8561   0.2183
       1    0.627   0.9431   0.6106   0.8561   0.5821

             A×B×C × D×E×F Interaction

                      HABCDEF
BETASCAL TOTAL_N POWER_HLT POWER_PBT POWER_WLK EPSILON

       9      54    0.0635    0.0708    0.0667   0.866
      18      54     0.117    0.1402    0.1317   0.866
      27      54    0.2467    0.2497    0.2742   0.866
       9     108    0.0939    0.0987    0.0958   0.866
      18     108    0.3236    0.3135    0.3209   0.866
      27     108    0.7676    0.6473    0.7239   0.866
       9     162    0.1281     0.132    0.1295   0.866
      18     162    0.5532    0.5141    0.5356   0.866
      27     162    0.9646    0.8948    0.9405   0.866
       9     216    0.1679    0.1706    0.1686   0.866
      18     216    0.7474     0.696    0.7237   0.866
      27     216     0.997    0.9788    0.9921   0.866
       9     270    0.2128    0.2142    0.2128   0.866
      18     270    0.8767    0.8309    0.8559   0.866
      27     270    0.9998    0.9969    0.9993   0.866
       9     324    0.2622     0.262    0.2613   0.866
      18     324    0.9473    0.9157    0.9334   0.866
      27     324         1    0.9997         1   0.866

                      HABCDEF
EXEPS_UN POWER_UN EXEPS_HF POWER_HF EXEPS_GG POWER_GG

       1   0.0712   1.6809   0.0712   0.6766   0.0372
       1   0.1031   1.6809   0.1031   0.6766   0.0566
       1   0.1754   1.6809   0.1754   0.6766   0.1041
       1   0.0826   1.1416   0.0826   0.7916   0.0586
       1   0.1722   1.1416   0.1722   0.7916   0.1297
       1   0.4082   1.1416   0.4082   0.7916   0.3374
       1   0.0953   1.0319   0.0953   0.8197   0.0722
       1   0.2619   1.0319   0.2619   0.8197   0.2141
       1   0.6665   1.0319   0.6665   0.8197   0.6065
       1   0.1092   0.9847   0.1071   0.8324   0.0855
       1   0.3689   0.9847   0.3645   0.8324   0.3163
       1   0.8572   0.9847   0.8544   0.8324   0.8209
       1   0.1246   0.9584   0.1183   0.8396   0.0995
       1   0.4853   0.9584   0.4724   0.8396   0.4309
       1   0.9538   0.9584   0.9504   0.8396   0.9382
       1   0.1413   0.9416   0.1316   0.8443   0.1145
       1   0.6013   0.9416   0.5833   0.8443   0.5489
       1   0.9886   0.9416   0.9871   0.8443   0.9837

Example 9: Test in a multivariate model with two within factors

This program illustrates using UPOLY2 and for two within and no between subject factor. It uses SIGSCAL and combines results from multiple runs of the power module. The results reproduce, except for some rounding differences, the predicted GG and HF powers in Table III in Coffey and Muller (2003), which used version 1 of POWERLIB, based on Muller and Barton (1989) methods. The example program also produces predicted Huynh-Feldt and Geisser-Greenhouse powers using the methods from Muller et al. (2007), which are the default in POWERLIB version 2.1. The new methods are far more accurate, especially for very small (near 1/b) or very large (near 1) values of ε.

Example 9 Program Code:

PROC IML SYMSIZE=1000 WORKSIZE=2000;
%INCLUDE "&ROOT.\Iml\POWERLIB21.IML"/NOSOURCE2;

ALPHA = .04;
OPT_ON = {NOPRINT GG HF BOX TOTAL_N UCDF UMETHOD};
OPT_OFF = {WARN ALPHA BETASCAL HLT PBT WLK };
ROUND = 2;

BETASCAL = 1;
THETA = {.25}#{.5 1 -1 .5}; * =Theta(cr) from 1st sentence *after*
                            * equation 7,  Coffey and Muller (2003);

* Following from Table II in Coffey and Muller (2003) *;
VARSTARE = {.47960 .01000 .01000 .01000}; * epsilon ~ .28 *;
VARSTARF = {.34555 .06123 .05561 .04721}; * epsilon ~ .50 *;
VARSTARG = {.23555 .17123 .05561 .04721}; * epsilon ~ .72 *;
VARSTARH = {.12740 .12740 .12740 .12740}; * epsilon = 1 *;
VARSTAR = VARSTARE//VARSTARF//VARSTARG//VARSTARH;
SIGSCAL = {0.50 1.00 2.00}; * <=> gamma in Coffey and Muller (2003) *;

* Log base 2 spacing Clip (2,4,16) and Region(2,8,32) *;
* Get orthonormal U matrices *;
RUN UPOLY2({1 2 4},"A", {1 3 5},"B",
            UA,NMA, UB,NMB, UAB,NMAB);
U = UAB;
C = 1;

ESSENCEX = {1};
REPN = {20};

  DO IVAR = 1 TO 4 BY 1;
  SIGSTAR = DIAG(VARSTAR[IVAR,*]);

  SIGMA = U*SIGSTAR*U‘;
  * 1st paragraph in section 2.4, Coffey and Muller 2003 *;
  BETA = THETA*U‘;
  * 1st paragraph in section 2.4, Coffey and Muller 2003 *;

    DO VERSION = 1 TO 2 BY 1;  *POWERLIB version;
    UCDF = J(4,1,VERSION);
    UMETHOD = J(2,1,VERSION);
    RUN POWER;
    HOLDALL = HOLDALL//_HOLDPOWER;
    END;
  END;

CREATE ONE VAR _HOLDPOWERLBL;
APPEND FROM HOLDALL;

QUIT;

PROC SORT DATA=ONE OUT=TWO;
BY UCDF_GG UMETHOD_GG SIGSCAL EPSILON;
RUN;

PROC PRINT DATA=TWO UNIFORM NOOBS;
BY UCDF_GG UMETHOD_GG  UCDF_HF UMETHOD_HF UCDF_BOX TOTAL_N;
PAGEBY UCDF_GG;
TITLE5 "All data in file";
RUN;

PROC PRINT DATA=TWO(RENAME=(SIGSCAL=GAMMA)) UNIFORM NOOBS;
VAR EPSILON GAMMA  POWER_GG POWER_HF ;
BY UCDF_GG UMETHOD_GG  UCDF_HF UMETHOD_HF UCDF_BOX TOTAL_N;
PAGEBY UCDF_GG;
TITLE5 "Version 2 far more accurate for Table III, Coffey and Muller (2003)";
RUN;

Example 9 Listing Output:

                                                               EXEPS_  POWER_
SIGSCAL   EPSILON   EXEPS_HF   POWER_HF   EXEPS_GG   POWER_GG    BOX     BOX

  0.5       0.28      0.29       0.92       0.28       0.92     0.25    0.91
  0.5       0.51      0.56       0.99       0.50       0.99     0.25    0.97
  0.5       0.72      0.73       1.00       0.63       1.00     0.25    0.99
  0.5       1.00      1.17       1.00       0.92       1.00     0.25    1.00
  1.0       0.28      0.29       0.66       0.28       0.65     0.25    0.63
  1.0       0.51      0.56       0.86       0.50       0.84     0.25    0.70
  1.0       0.72      0.73       0.93       0.63       0.92     0.25    0.75
  1.0       1.00      1.17       0.98       0.92       0.97     0.25    0.80
  2.0       0.28      0.29       0.37       0.28       0.37     0.25    0.35
  2.0       0.51      0.56       0.55       0.50       0.52     0.25    0.34
  2.0       0.72      0.73       0.64       0.63       0.61     0.25    0.33
  2.0       1.00      1.17       0.75       0.92       0.74     0.25    0.32