Abstract
Although many tools of cellular and molecular biology have been used to characterize single intracellular cycles of virus growth, few culture methods exist to study the dynamics of spatially spreading viruses over multiple generations. We have previously developed a method that addresses this need by tracking the spread of focal infections using immunocytochemical labeling and digital imaging. Here we build reaction-diffusion models to account for spatio-temporal patterns formed by the spreading viral infection front as well as data from a single cycle of virus growth (one-step growth). Systems with and without the interferon-mediated antiviral response of the host cells are considered. Dynamic images of the spreading infections guide iterative model refinement steps that lead to reproduction of all of the salient features contained in the images, not just the velocity of the infection front. The optimal fits provide estimates for key parameters such as virus-host binding and the production rate of interferon. For the examined data, highly-lumped infection models that ignore the one-step growth dynamics provide a comparable fit to models that more accurately account for these dynamics, highlighting the fact that increased model complexity does not necessarily translate to improved fit. This work demonstrates how model building can facilitate the interpretation of experiments by highlighting contributions from both biological and methodological factors.
1 Introduction
We consider using dynamic models to obtain a better quantitative and integrative understanding of both viral infections and cellular antiviral mechanisms. We expect this approach to provide key insights into mechanisms of viral pathogenesis and host immune responses, as well as facilitate development of effective anti-viral strategies. Our focus, however, is not to incorporate all the wealth of information already known about either of these topics. Rather, we seek to identify the critical biological and experimental phenomena that give rise to the experimental observations. We employ two experimental techniques: a one-step growth experiment which captures the dynamics of a single cycle of virus growth, and a focal-infection system, which permits quantification of multiple rounds of viral infection. The focal-infection system, which was described by Duca et al. (1), provides a unique platform for studying multiple rounds of the virus replication cycle as well as the innate ability of host cells to combat the invading virus.
We consider the example virus/host system of vesicular stomatitis virus (VSV) propagating on either baby hamster kidney (BHK) cells or murine astrocytoma (delayed brain tumor or DBT) cells. VSV is a member of the Rhabdoviridae family consisting of enveloped RNA viruses (2). Its compact genome is only approximately 12 kb in length, and encodes genetic information for five proteins. VSV is highly infective and grows to high titer in cell culture. It is used as a model system for studying viral replication (3,4). Also, VSV infection can elicit an interferon-mediated antiviral response from host cells (2). Thus the studied experimental system provides a platform for further probing the quantitative dynamics of this antiviral response. A great wealth of information is known about the interferon antiviral response (see, for example, Samuel (5) and Grandvaux et al. (6)), and several excellent models have already been built to study how the interferon response contributes to the human immune response (7–9). We seek to elucidate what level of complexity is requisite to explain the experimental data of the focal-infection system.
Yin and McCaskill (10) first proposed a reaction-diffusion model to describe the dynamics of bacteriophage (viruses that infect bacteria) as they spread in expanding plaques. The authors derived model solutions for this formulation in several limiting cases. You and Yin (11) later refined this model and used a finite difference method to numerically solve the time progression of the resulting model. Fort (12), Fort and Mendez (13), and Ortega-Cejas, Fort, Mendez, and Campos (14) revised the model of You and Yin (11) to account for the delay associated with intracellular events required to replicate virus, and derived expressions for the velocity of the propagating front. These works, however, focused on explaining the velocity of the infection front, a quantity derived from experimentally-obtained images of the infection spread. Our goal in this paper is to explain the infection dynamics contained within the entire images.
In this paper, we first present the experimental system of interest. Next, we outline the steps taken to analyze the experimental measurements (images of the infection spread) and propose a measurement model. We then formulate, fit, and refine models using the analyzed images, first for VSV infection of BHK cells, then for DBT cells. Finally, we analyze the results of the parameter fitting and present conclusions.
2 Materials and Methods
Cell and virus culture
Murine delayed brain tumor (DBT) cells were obtained from Dr. J. Fleming (U. of Wisconsin - Madison) and grown as monolayers at 37°C in a humidified atmosphere containing 5% CO2. DBT growth medium was Dulbeccos Modified Eagle Medium (Celgro, Fisher Scientific, Pittsburgh, PA) containing 10% newborn calf serum (NCS, Hyclone, Logan, UT), 4 mM Glutamax I (Glu, Gibco, Invitrogen Corporation, Carlsbad, CA), and 15 mM HEPES (Sigma-Aldrich, St. Louis, MO). Baby hamster kidney (BHK) cells were obtained from Dr. I. Novella (Medical College of Ohio) and grown under the same environment as the DBT cells. BHK growth medium was Minimal Essential Medium with Earles salts (Celgro, Fisher) containing 10% fetal bovine serum (FBS, Hyclone) and 2 mM Glutamax I (Glu, Gibco). Both BHK and DBT cells were sub-cultured approximately every third day. For sub-culture, monolayers were rinsed with Hanks Balanced Salt Solution (HBSS, Fisher), incubated in 0.025% trypsin/26 mM EDTA (Fisher) for 5 min, dispersed through mixing, and then re-plated in fresh growth medium at 1:15 (DBT) or 1:30 (BHK) dilution. No antibiotics were used and cells were sub-cultured no more than four months to minimize the effects of cell senescence. Viability of cell populations, as determined by trypan blue exclusion, at the time of experiments always approached 100%. N1 strain of vesicular stomatitis virus (VSV) was obtained from Dr. G. Wertz (University of Virginia). Mudd-Summers strain of VSV was obtained from Dr. I. Novella (Medical College of Ohio). The viruses were grown on BHK cells at multiplicity of infection (MOI) of 0.01 plaque forming units (PFU) per cell. Infected BHK cells were incubated in infection medium (MEM/Glu/2% FBS) for 20 hours. At the end of the incubation period, the medium was harvested and passed through a 0.2 μm filter. The filtered solution was aliquoted and stored at -90°C until use.
One-step growth infection of cell monolayers
One-step growth infection of cell monolayers were performed as described in Lam, Duca, and Yin (15).
Focal infection of cell monolayers
Cells were harvested and plated into six-well plates at 5×105 cells per well (in 2 ml of culture medium). Plated cells were returned to the incubator for overnight growth. The next day, the culture medium was suctioned from each well and replaced with 4 ml of agar overlay. The agar overlay was prepared by first combining agar powder (Agar Nobel, Difco) at 0.6% (w/v) with nanopure water (approximately 10% of the final volume), autoclaving the mixture at 121°C for 20 min, and then combining it with infection medium (90% of the final volume) that had been heated to 42°C. After agar addition, the plates were left at room temperature for 30 min to allow the overlay to solidify. They were then returned to the incubator for at least 60 min of recovery time before inoculation. To focally inoculate the cell monolayer under the agar overlay, a virus deposition reservoir was made by punching a hole in the center of the overlay using the tip of a Pasteur pipette. The plug of agar inside the tip of the pipette was subsequently removed by applying gentle suction through the pipette. Five microliters of virus inoculum at 1.6×107 infectious particles per ml was added to this reservoir to infect the exposed cells, giving an estimated MOI of 20. The inoculated plates were returned to the incubator until the predetermined fixation times. Goat anti-interferon antibodies were obtained from Fitzgerald (20-IS63, Fitzgerald Industries International, Concord, MA) and diluted to stock solutions of 4 × 104 and 2 × 104 units per milliliter. For infection, where indicated, these solutions were diluted with VSV stock solutions to yield concentrations of 100 units of antibodies per 5 μl of inoculum.
Fixation and immunocytochemistry
Representative focal-infected monolayers were fixed at selected time points with 3 ml of fixative per monolayer. The fixative consisted of 4% (w/v) paraformaldehyde (VWR International, West Chester, PA) and 5% (w/v) sucrose (Sigma) in 10 mM phosphate buffered saline (PBS, Sigma) at pH 7.4. After three hours of fixative exposure, the agar overlay was removed and the monolayers were rinsed twice with 2 ml/well of PBS. They were stored in PBS at 4°C until immunofluorescence labeling. Virus distributions were visualized by indirect immunofluorescence labeling of VSV-glycoprotein. Fixed monolayers were washed once with 1 ml of PBS/0.1% (w/v) saponin (PBS/SAP) and once with 1 ml PBS /SAP/5% (w/v) natal calf serum (NCS) for 10 min each. Monolayers were then blocked for 20 min with 1 ml of PBS/SAP/NCS/0.2% (w/v) bovine serum albumin (PBS/SAP/NCS/BSA). A primary monoclonal murine antibody against VSV-G (V5507, Sigma) was diluted 1:1000 in PBS/SAP/NCS, added at 0.5 ml to each monolayer, and incubated overnight at 4°C. The following day the monolayers were washed twice with PBS/SAP, once with PBS/SAP/NCS, and then blocked for 20 min with PBS/SAP/NCS/BSA. Cy3-conjugated donkey anti-mouse F(ab)2 secondary antibody (Jackson ImmunoResearch Laboratories, West Grove, PA) was diluted 1:300 in PBS/SAP/NCS and added to the monolayers at 0.5 ml each and incubated for 60 min at room temperature. Each monolayer were then washed twice with PBS/SAP to remove unbound antibody, put under 2 ml of PBS, and stored at 4°C until imaging.
Image collection, processing, and quantification
Images of the labeled monolayers were acquired using a Nikon TE300 inverted epifluorescent microscope equipped with a Nikon mercury light source, a Prior XYZ translation stage driven by Metamorph 6.0 software (Universal Imaging Corporation, Downingtown, PA), and a monochrome SensSys 4.0 cooled CCD camera. The excitation filter passed wavelengths from 530 to 550 nm. The dichroic mirror was at 565 nm and the emission filter passed wavelengths from 590 to 650 nm. The location and extent of infection was manually identified in each well and the number of microscope fields necessary to fully image the infected area at 4× magnification was estimated (4 to 120 fields). The system was then programmed to move the stage consecutively across the entire infected area, acquire an image at each position, and finally, combine the individual images into a single montage. The mean exposure time of the samples was approximately 15 minutes. However, the largest infections required up to 45 minutes. During this time, the samples were kept under 2 ml of PBS at room temperature, approximately 17 C. All images from an experiment were processed, using the same scaling factors, to map the captured intensities into the full range of 256 gray scales. The relative intensities of individual pixels within the images were not otherwise altered. Adobe Photoshop 7.0 (Adobe, San Jose, CA) was used to perform this initial image processing.
3 Modeling of the Experimental System
In this section, we discuss the assumptions made in modeling the focal-infection system. We first examine modeling of the experiment, presenting relevant parameters and initial conditions. Then we consider how to model the measurement process. Finally, we discuss the methods used to analyze and model the image measurements.
3.1 Modeling the Experiment
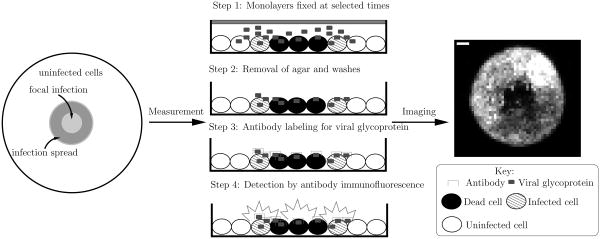
Figure 1 presents a general schematic of this experimental system along with a digital image acquired during such an infection. Table I presents parameters used to model the experimental conditions. We assume that cells are spherical objects, with the height of the cell monolayer equal to the resulting cell diameter. Concentrations for all species are calculated assuming that the volume of the monolayer is cylindrical. The dimensions of this cylinder are given by the height of the cell monolayer and the radius of the plate. We model the concentration of the initial virus inoculum using the piecewise linear continuous function
Figure 1.
Overview of the experimental system. Initially, host cells are grown in a confluent monolayer on a plate. The cells are then covered by a layer of agar. To initiate the infection, a pipette (one mm radius) is used to carefully remove a small portion of the agar in the center of the plate. An initial inoculum of virus is then placed in the resulting hole in the agar, initiating the infection. The agar overlay serves to restrict virus propagation to nearby cells. To monitor the infection spread, monolayers are fixed at various times post-infection. The agar overlay is removed and the cells are rinsed several times, the last time with a labeled antibody that binds specifically to the viral glycoprotein. Images of the monolayers are then acquired using an inverted epifluorescent microscope.
Table I.
Parameters used to describe the experimental conditions.
| Parameter | Symbol | Value |
|---|---|---|
| Cell volume | Vc | 3.4 × 10−9 ml |
| Initial number of uninfected cells | nunc,0 | 106 cells |
| Number of viruses in the initial inoculum | nvir,0 | 8.0 × 104 viruses |
| Radius of the plate | rplate | 1.75 cm |
| Initial concentration of uninfected cells | cunc,0 | 3.80 × 107 cells/cm3 |
| (1) |
Figure S8 in the supporting information plots this profile.
3.2 Analyzing and Modeling the Images
We assume that the measurement process (steps one through four in Figure 1) detects viral glycoprotein contained on and in infected and dead cells in the monolayer. Thus we model the total fluorescence intensity as the sum of a scaling constant times the sum of the infected and dead cell concentrations plus a constant background intensity. Linearity of the fluorescence signal response of these cell concentrations is the simplest physically reasonable assumption. Future studies may provide a more precise calibration of the transient response of these fluorescing cells. If available, any such measurement calibration function can be employed with the framework presented in this study. Additionally, we assume that the signal from dead cells decomposes as a first-order process over time.
We have reduced the amount of information in each image by partitioning the images into blocks of 20 pixels by 20 pixels, then averaging the pixels contained in each block. This averaging technique has the primary benefit of drastically reducing the total number of pixels that must be analyzed (in the case of the largest image, from roughly two million to five thousand pixels) while retaining the prominent features of the infection spread.
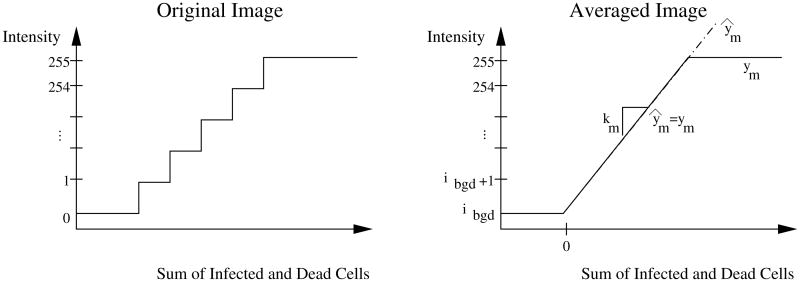
The CCD camera quantizes the continuous fluorescence intensity signal into a step-wise, discontinuous signal (integer valued from 0 to the saturating value of 255). For the averaged images, the intensity information is step-wise, discontinuous with increments of 1/400 over the range [0, 255] (i.e., 0, 0.0025, 0.005, …, 255). We approximate this signal using a piece-wise continuous function. The measurement model is then:
| (2) |
in which ym is the intensity measurement, ibgd is the background fluorescence (in intensity), km is the measurement constant, and cinfc and cdc refer to the concentrations of infected cells and dead cells, respectively. The background intensity for each image is estimated by averaging pixels along the edge of the image, none of which contain signal due to infection spread. Figure 2 shows the measurement model for the original images and depicts the measurement model given by equation (2).
Figure 2.
Measurement model. The original images quantize the sum of the infected and dead cell concentrations, a continuous variable, onto the integer-valued intensity. Each pixel in the averaged images is the mean of 400 pixels from the original image. We approximate the step-wise discontinuous intensity (incremented by 1/400 over the range [0, 255]) as a piece-wise, continuous function given by equation (2).
Figures S1 and S4 of the supporting information and Figure 6 contain all of the images examined in this work. For all experimental images presented in this work, we subtracted the estimated background intensity from each image and then rescaled the fluorescence by the same constant factor using the software package Octave. We assume that the infection propagation is radially symmetric even though some of these images demonstrate radial asymmetry. We expect that these regions of asymmetry are stochastic events that would average out given a sufficient number of experimental observations. The variance of the images at each time point was obtained by compiling statistics for the radial distributions; these distributions are presented in Figures S2 and S5 of the supporting information.
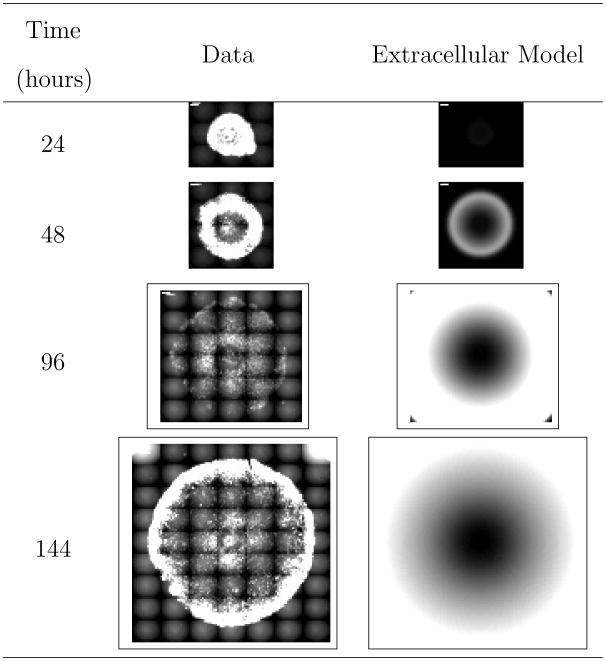
Figure 6.
Comparison of representative experimental images to model predictions for VSV propagation on DBT cells in the presence of interferon inhibitors. “Extracellular Model” refers to the derived reaction-diffusion model accounting for solely extracellular species. The white scale bar in the upper left-hand corner of the experimental images is one millimeter.
4 Propagation of VSV on BHK Cells
We first consider propagation of the VSV N1 strain on baby hamster kidney (BHK) cells. For this virus/host system, we incorporate information from two types of experiments: a one-step growth shown in Figure 3 (a), and time-course images from a focal infection (representative images are shown in the the first column of Figure 4). The full set of experimental images and the average radial profiles are presented in Figures S1 and S2 of the supporting information. For this virus/host system, the focal-infection images demonstrate two prominent features: (1) the infection propagates unimpeded outward radially and (2) the band of intensity amplifies from the first to the third measurement. We now consider models to quantitatively capture both of these features.
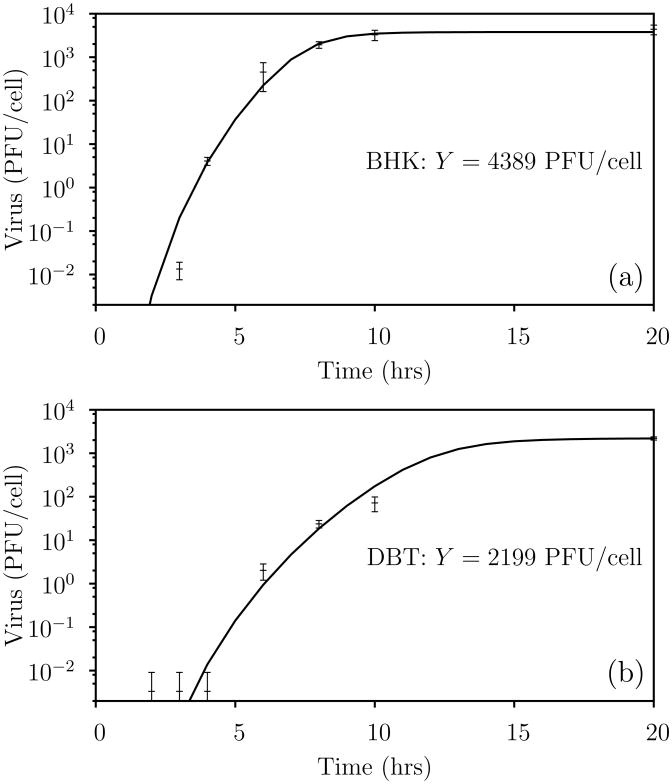
Figure 3.
One-step growth fits. Hill functions capture the dynamics contained in the one-step growth curves for VSV infection of (a) BHK and (b) DBT cells. Points and error bars are the means and standard deviations, respectively, from three independent experiments. The estimated yield of virus per infected cell Y is estimated as the mean of the final data point in each experiment.
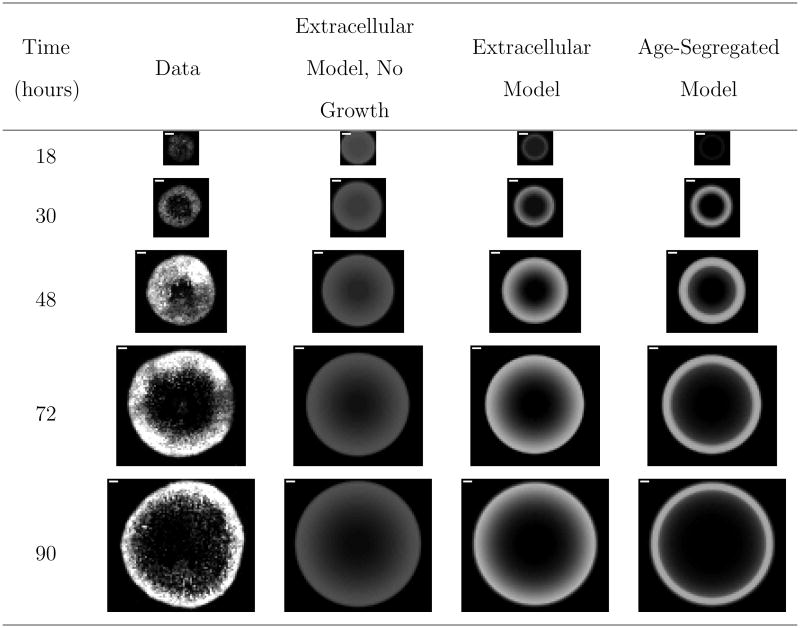
Figure 4.
Comparison of representative experimental images to model fits for VSV propagation on BHK cells. The full set of experimental images are available in Figure S1 of the supporting information. “Extracellular Model, No Growth” refers to the derived reaction-diffusion model in which the infected cells are not segregated by age and uninfected cells are not permitted to grow. “Extracellular Model.” is the same as the “Extracellular Model, No Growth” with the addition that uninfected cells are assumed to grow over the course of the experiment. “Age-Segregated Model” segregates the infected cell population by the age of infection. The white scale bar in the upper left-hand corner of the experimental images is one millimeter.
4.1 Development of a Reaction-Diffusion Model
We consider two types of reaction-diffusion models for describing this infection: an extracellular model in which all infected cells are assumed to behave identically the same, and an age-segregated model in which viral production from infected cells is a function of the infected cell age. These two models differ primarily in the way the one-step growth data is used. For the extracellular model, we assume that each infected cell yields Y viral progeny. We estimate Y by averaging the data from the last time point in the one-step growth curve of Figure 3 (a). In the age-segregated model, we fit the same one-step growth curve using the Hill function
| (3) |
Fitting of the data results in the prediction presented in Figure 3 (a) and parameters given in Table II.
Table II.
Parameters for the Hill-function fit of the VSV/BHK one-step growth data.
| Parameter | Value | 95% Confidence Interval |
|---|---|---|
| k̄1 | 3784. | ±1855. |
| k̄2 | 7.863 | ±0.9748 |
| k̄3 | 10.21 | ±1.497 |
The extracellular model is an extension of the model first proposed by Yin and Mc-Caskill (10) and later refined by You and Yin (11). We consider only extracellular species, namely virus, uninfected cells, infected cells, dead cells, and the limiting substrate. In this context, only the virus is allowed to diffuse, and we model the following reactions:
| (4a) |
| (4b) |
| (4c) |
| (4d) |
in which Y is the yield of virus per infected cell and all reactions are elementary as written. This description provides a highly lumped, minimal representation of viral infections. We assume growth of uninfected cells is controlled by a single limiting substrate; similar models are discussed in Bailey and Ollis (16, Ch. 7). The initial amount of this substrate permits growth to a dense monolayer (1/Vc, in which Vc is the volume of a single cell) if no virus is present. Also, dead cells are assumed to decay over time as noted in Section 3.2 to account for the decrease in signal intensity observed in the middle of the focal-infection images.
The concentrations of all species are segregated by both time and radial distance, giving rise to the following governing equations for the model:
| (5a) |
| (5b) |
| (5c) |
| (5d) |
| (5e) |
| (5f) |
in which the reaction terms are dictated by the stoichiometry of reaction 4 assuming that the reactions are elementary as written. We solve equation (5) by discretizing the spatial dimension using central differences with an increment of 0.025 cm, then solving the resulting set of differential-algebraic equations using the package DASKR, a variant of the predictor-corrector solver DASPK (17), with the banded solver option.
To better quantitatively capture the temporal nature of the one-step growth curve, we incorporate the life cycle of infected cells by segregating the infected cell population by the age of infection τ. We assume that infected cells cannot live longer than age τd, at which point these cells die. The considered reactions now become:
| (6a) |
| (6b) |
| (6c) |
| (6d) |
| (6e) |
in which all reactions are elementary as written except for equation (6b). The age-dependent virus production of this equation is given by the derivative of equation (3), i.e.,
| (7) |
noting the interchange of t in the one-step growth data to τ, the age of an infected cell. The model equations are then the following set of coupled integro-partial differential equations
| (8a) |
| (8b) |
| (8c) |
| (8d) |
| (8e) |
| (8f) |
| (8g) |
These equations bear remarkable similarity to the extracellular model in equation (5), but with several primary differences. First, the infected cell concentration has been segregated by the cell age in equation (8b). This segregation accounts for the fact that infected cells of different ages produce different amounts of virus. The boundary condition in equation (8f) specifies the generation rate of newly infected cells (τ = 0) from uninfected cells. Second, the virus production at any given time is a function of how many infected cells are of a given age and how much virus these cells are producing, giving rise to the first part of the integral term in equation (8a). The second part of this integral term results from super-infection of infected cells. Finally, when infected cells reach the maximum cell age τd, they die and become dead cells, giving rise to the f(τd) term in equation (8e). For derivation of age-segregated models without the spatial segregation, we refer the interested reader to Haseltine, Rawlings and Yin (18). We discretize the age dimension using orthogonal collocation on Lagrange polynomials (19) with seventeen points, and use the same spatial discretization scheme as in the reaction-diffusion model.
We determine optimal parameter estimates by solving the following least squares optimization
| (9a) |
| (9b) |
| (9c) |
| (9d) |
which minimizes the sum of squared residuals between the vectorized images yk and the model-predicted images h(xk;θ) in a pixel by pixel comparison by manipulating the model parameters θ. Here we use a log10 transformation of the parameters for the optimization. Also, the covariance matrix R is estimated from the experimental images as discussed in section 3.2.
4.2 Analysis of the Model Fit
Figure 4 presents the fitted results, and the fitted parameters are presented in Table III. Comparing the extracellular model results readily reveals that allowing for growth of uninfected cells greatly improves the fitting of the data. When such growth is included in the model, both the extracellular and age-segregated models fit the data well, with the extracellular model providing a slightly superior fit. We note that the maximal fluorescence of the model fits appears to be less than that contained within the experimental images. However, the model fits compare quite well to the averaged experimental data as demonstrated in Figure S3 of the supporting information. Finally, all parameters are estimated with good confidence.
Table III.
Parameter estimates for the VSV/BHK focal-infection models. Parameters are estimated for the log10 transformation of the parameters. NA denotes that the parameter is not applicable for the given model. “Extracellular Model, No Growth” refers to the derived reaction-diffusion model in which the infected cells are not segregated and uninfected cells are not permitted to grow. “Extracellular Model.” is the same as the “Extracellular Model, No Growth” with the addition that uninfected cells are assumed to grow over the course of the experiment. “Age-Segregated Model” segregates the infected cell population by the age of infections.
| Parameter | Units | Extracellular Model, No Growth | Extracellular Model | Age-Segregated Model | ||||
|---|---|---|---|---|---|---|---|---|
| k1 | Hr−1 | 1.40e − 10 | ±4.55e − 12 | 2.67e − 11 | ±3.30e − 13 | 5.35e − 10 | ±1.56e − 11 | |
| k2 | cm3/hr | 5.91e − 02 | ±5.14e − 03 | 6.73e − 02 | ±2.39e − 03 | NA | ||
| k3 | cm3/hr | NA | 4.00e − 10 | ±3.00e − 11 | 1.27e − 09 | ±6.83e − 11 | ||
| k4 | cm3/hr | 2.63e − 02 | ±3.94e − 03 | 8.72e − 02 | ±9.84e − 03 | 6.36e − 02 | ±7.65e − 03 | |
|
|
cm3/hr | NA | 3.45e + 07 | ±3.53e + 06 | 1.67e + 06 | ±4.63e + 05 | ||
| Dvir | cm2/hr | 2.38e − 06 | ±5.93e − 07 | 1.24e − 06 | ±1.66e − 07 | 1.17e − 05 | ±1.72e − 07 | |
| τd | hr | NA | NA | 1.74e + 01 | ±8.91e − 02 | |||
| km | cm−3 | 3.42e − 07 | ±7.44e − 15 | 9.31e − 08 | ±2.24e − 15 | 8.67e − 08 | ±6.39e − 16 | |
| Φ | 6.50 × 104 | 4.22 × 104 | 4.35 × 104 | |||||
Ware et al. (20) use laser light-scattering spectroscopy to estimate the diffusivity of the VSV virion to be 2.326 × 10−8 cm2/sec. Converting this value to cm2/hr yields a value of 8.37 × 10−5. This value is larger than the estimated values of 1.24 × 10−6 and 1.17 × 10−5 cm2/hr for the extracellular and age-segregated models, respectively (see Table III), which may be attributable to the fact that diffusion occurs through the agar.
The modeling process gives insight into how key biological and experimental phenomena contribute to the observable features of spreading focal infections. First, allowing for growth of the uninfected cells accounts for the amplification of the intensity in the first three images of the time-series data. Second, the infection spread is best characterized by considering only extracellular species in the model development. This result is somewhat surprising because the age-segregated model more accurately captures the dynamics of a single round of infection. However, note that the first time point in the data series is greater than the estimated maximum cell age (τd = 17.4 hrs < 18 hrs). Consequently, it appears that lumping infection events into a purely extracellular description as done in the extracellular model provides a reasonable approximation of the focal-infection system.
5 Propagation of VSV on DBT Cells
We now consider propagation of the VSV N1 strain on murine astrocytoma (DBT) cells. The first column of images in Figure 5 presents a representative time course for the experiment; the full set of experimental images and the average radial profiles are presented in Figures S4 and S5 of the supporting information. For this virus/host system, the images demonstrate three prominent features: (1) the infection propagates unimpeded outward radially for the first three images, (2) the intensity of the measurement amplifies from the first to the third measurement, and (3) the infection spread is halted after the third image and the intensity of the measurement diminishes. This particular cell line is known to have an antiviral strategy, namely the interferon signaling pathway (15, 21). We now build a model to quantitatively capture all of these features.
Figure 5.
Comparison of representative experimental images to model fits for VSV propagation on DBT cells. The full set of experimental images are available in Figure S4 of the supporting information. “Extracellular Model” refers to the derived reaction-diffusion model accounting for solely extracellular species. The white scale bar in the upper left-hand corner of the experimental images is one millimeter.
5.1 Refinement of the Reaction-Diffusion Model
We refine the extracellular reaction-diffusion model proposed in the previous section to model this infection. In addition to the extracellular species considered previously (virus, uninfected cells, infected cells, and dead cells), we also model interferon (without any distinction between the types α, β, and γ) and inoculated cells. Both virus and interferon are permitted to diffuse. The premise behind this mechanism is that interferon diffuses faster than the virus, but interferon is not produced as quickly initially as the virus. Hence we expect an initial propagation wave of virus to be overtaken by its inhibitor, interferon. This process leads to stagnation of the infection front.
We account for the following reactions:
| (10a) |
| (10b) |
| (10c) |
| (10d) |
| (10e) |
| (10f) |
| (10g) |
| (10h) |
| (10i) |
| (10j) |
in which all reactions are elementary as written. This reaction mechanism makes the following assumptions:
interferon binds to uninfected cells to form inoculated cells that are resistant to viral infection,
super-infection of infected cells does not alter the yield of virus per infected cell, and
virus binds indiscriminately to uninfected, infected, and inoculated cells.
We again assume that the infection propagation is radially symmetric. The concentrations of all species are then segregated by both time and radial distance, giving rise to the following governing equations for the model:
| (11a) |
| (11b) |
| (11c) |
| (11d) |
| (11e) |
| (11f) |
| (11g) |
| (11h) |
| (11i) |
in which the reaction terms are dictated by the stoichiometry of reaction 10 assuming that the reactions are elementary as written. Due to the large number of parameters for this system, we choose to use previously reported estimates of the viral and interferon diffusivities from Ware et al. (20) (Dvir = 8.37×10−5 cm2/hr) and Nichol and Deutsch (22) (Difn = 1.48× 10−3 cm2/hr). We estimate the remaining parameters using the same spatial discretization and nonlinear optimization as in the previous section.
5.2 Discussion
The second column of images in Figure 5 present the optimal fits for this model. This model quantitatively captures all features of the infection, and the model fits compare quite well to the averaged experimental data as demonstrated in Figure S6 of the supporting information. Table IV provides estimates for all of the model parameters. Note that the parameter k4 governing degradation of dead cells is not included. Hessian analysis revealed that the data provides no information on this parameter. Additionally, the parameter k5 governing the production of interferon from infected cells exhibits a large confidence interval.
Table IV.
Parameter estimates for the VSV/DBT focal-infection models. Parameters are estimated for the log10 transformation of the parameters.
| Parameter | Units | Extracellular Model | ||
|---|---|---|---|---|
| k1 | hr−1 | 7.60e − 11 | ±1.13e − 11 | |
| k2 | cm3/hr | 1.26e − 02 | ±5.75e − 04 | |
| k3 | cm3/hr | 2.85e − 10 | ±1.55e − 11 | |
| k5 | cm3/hr | 1.07e − 03 | ±3.99e − 03 | |
| k6 | cm3/hr | 8.22e − 09 | ±8.80e − 09 | |
| k7 | cm3/hr | 5.65e − 01 | ±6.54e − 02 | |
| km | 4.89e + 06 | ±8.25e + 05 | ||
|
|
cm−3 | 2.30e − 07 | ±2.07e − 13 | |
| Φ | 5.66 × 104 | |||
5.3 Model Prediction: Infection Propagation in the Presence of Interferon Inhibitors
To validate the model, we compare model predictions of the infection propagation in the presence of interferon inhibitors (antibody against interferon) to experimentally-obtained images. Here, we investigate the propagation of the VSV Mudd Summers strain on DBT cells. We assume that the dosing of interferon inhibitor is sufficiently large to completely inhibit production of interferon. Accordingly, we set the constant k5 corresponding to interferon production from infected cells to zero.
Figure 6 compares the results for the experimental data with the model predictions. Figure S7 of the supporting information compares the computed radial distributions from both the experimental data and the model prediction. The model over-predicts the radial propagation of the infection front for the latter two time points. Two phenomena most likely explain the deviations between the data and predictions. First, we suspect that the two VSV strains (Mudd Summers and N1) may have different rates of propagation and hence slightly different model parameters. Second, the dosing of the interferon inhibitor may not be large enough to completely eliminate the host antiviral response.
6 Conclusions
We have used quantitative models to investigate the dynamics of multiple rounds of viral infection and host antiviral response for the focal-infection system. We employed two types of experimental data for these studies: a one-step growth experiment in which all cells are infected simultaneously, and a focal-infection system in which the virus spreads spatially, leading to multiple generations of infection. We integrated the data from these two experiments using two types of models. The first model assumed a purely extracellular description of the system. Here, each infected cells was assumed to produce a yield of virus estimated by the final virus titer of the one-step growth experiment. The second model segregated infected cells by the age of infection. Here, infected cells produced virus as a function of their age as given by the dynamics of the one-step growth experiment. We then studied VSV infection of two different cell lines, BHK and DBT cells, the latter cell line being capable of eliciting an antiviral response.
For the VSV/BHK virus-host system, extracellular models capture the salient features contained in the measurements, namely unimpeded radial propagation of the infection front as well as amplification of the signal in the initial data points. Estimates of the viral diffusivity are smaller than the value obtained from an independent experiment, which may be attributable to the fact that occurs through the agar. Also, the model suggests that including growth of uninfected cells is critical for fitting the initial signal amplification. Interestingly, the extracellular model provides a slightly better fit of the data than the age-segregated model. This result was surprising because the age-segregated model captures the dynamics of the one-step growth experiments, while the extracellular model effectively ignores these dynamics. Consequently, we infer that highly-lumped infection models provide a reasonable approximation of the focal-infection system for the given data.
The finding that the simpler extracellular model predicts the experimental slightly better than the more complex age-segregated model deserves additional discussion. Cellular processes are inherently complex; even the relatively simple bacterium Escherichia coli has 4497 genes and 1133 enzymes (23). Deciding what level of complexity to include when examining experimental data thus invariably arises when any modeling effort is undertaken. Should one start from a minimal model representation and iteratively add complexity as needed to explain the experimental results, or should one start from a complex model in which all parameters simply cannot be tightly estimated from the data? A recent work by Gutenkunst et al. (24) suggests that modelers mostly opt for the latter case. Specifically, Gutenkunst et al. (24) found that parameters for sixteen systems-biology models could not be accurately estimated even with comprehensive simulated data, a feature of models that they termed “sloppiness”. While such “sloppy” models can still make well-constrained predictions (24), our work demonstrates that simply adding additional complexity to the model does not automatically increase the model fit even when the complexity is biologically or experimentally motivated. Rather, additional complexity may simply increase the number of unknown parameters without contributing to the fit whatsoever, thereby unnecessarily increasing the “sloppiness” of the model.
For the VSV/DBT virus-host system, the data initially behaves similarly to the VSV/BHK system (outward radial propagation of the infection front and amplification of the signal), but then the infection front stagnates and the signal strength diminishes. This stagnation occurs due to the host antiviral mechanism of interferon signaling. We only investigated the extracellular model on this system because the VSV/BHK results suggested that the age-segregated model did not provide a substantial benefit in fitting the data. Again, the proposed extracellular model is capable of quantitatively capturing the measurement dynamics. To further validate the model, we compared the model predictions with no interferon production to experiments of the VSV/DBT system dosed with interferon inhibitors. The model overestimated the radial propagation of the infection front. This over-prediction likely results from either incomplete inhibition of interferon production or differences due to the VSV strain (Mudd Summers versus N1), or even a combination of these two phenomena.
This work serves as a first step in providing a quantitative understanding of multiple rounds of both viral infection and host antiviral response. Comparing model predictions to experimental measurements requires modeling of both the underlying biology of the system and the experimental procedure. Additional experimental measurements such as microarray data or using reporter genes to detect interferon up-regulation should provide further constraints to the developed model and necessitate future model modification. We expect future iterations of additional experiments, measurements, and modeling to elucidate an even better comprehensive understanding of both viral infections and cell-cell signaling. For example, incorporating stochastic aspects (25, 26) (e.g., genetic bottlenecking, effects of finite population sizes, stochastic gene expression) of the virus growth and spread could help explain the degree of interferon induction and ultimately the dynamics of the spread. Also, as new intracellular measurements become available for this platform, we expect that more complicated models such as the age-segregated models examined here will prove instrumental in explaining the system behavior.
Supplementary Material
Figure S1: Experimental images obtained from the dynamic propagation of VSV on BHK cells. The white scale bar in the upper left-hand corner of the experimental images is one millimeter.
Figure S2: Radial infection profiles obtained by averaging the experimental images of the dynamic propagation of VSV on BHK cells. The color bar shows the standard deviation σ of each individual measurement from the mean value, and is saturated after σ > 3. Red lines show the average profile, and green lines show one standard deviation away from the mean. Note that the background fluorescence was estimated and subtracted from each image before calculating these radial profiles.
Figure S3: Comparison of the experimental and predicted radial infection profiles for the dynamic propagation of VSV on BHK cells: (a) extracellular model, no growth of uninfected cells; (b) extracellular model; and (c) age-segregated model. The thick and thin lines present the model predictions and the average experimental measurements, respectively.
Figure S4: Experimental images obtained from the dynamic propagation of VSV on DBT cells. The white scale bar in the upper left-hand corner of the experimental images is one millimeter.
Figure S5: Radial infection profiles obtained by averaging the experimental images of the dynamic propagation of VSV on DBT cells. The color bar shows the standard deviation σ of each individual measurement from the mean value, and is saturated after σ > 3. Red lines show the average profile, and green lines show one standard deviation away from the mean. Note that the background fluorescence was estimated and subtracted from each image before calculating these radial profiles.
Figure S6: Comparison of the experimental and predicted radial infection profiles for the dynamic propagation of VSV on DBT cells. A reaction-diffusion model accounting for solely extracellular species generated the predicted profiles. The thick and thin lines present the model predictions and the average experimental measurements, respectively.
Figure S7: Comparison of the experimental and predicted radial infection profiles for the dynamic propagation of VSV on DBT cells in the presence of interferon inhibitors. A reaction-diffusion model accounting for solely extracellular species generated the predicted profiles. The thick and thin lines present the model predictions and the average experimental measurements, respectively.
Figure S8: Profile of the initial virus concentration for the models. cvir,0 denotes the estimated initial concentration of virus in the inoculation radius.
Acknowledgments
We are grateful to Drs. Gail Wertz and Isabel Novella for providing the vesicular stomatitis viruses. The authors gratefully acknowledge the financial support of NSF through grant QSB EIA-0331337 and NIH through a Phased Innovation Award (R21 AI071197). ELH was supported by an NLM training grant to the Computation and Informatics in Biology and Medicine Training Program (NLM 5T15LM007359). ELH and JBR gratefully acknowledge the financial support of the industrial members of the Texas-Wisconsin Modeling and Control Consortium. VL was supported by a fellowship from the Biotechnology Training Program (NIH 5 T32 GM08349). All simulations were performed using Octave (http://www.octave.org). Octave is freely distributed under the terms of the GNU General Public License.
Notation
- cj
concentration of species j
- cunc,0
initial concentration of uninfected cells
- Difn
interferon diffusivity
- Dvir
virus diffusivity
- e
error vector
- h(xk; θ)
model prediction vector of the measurement
- ibgd
background fluorescence
- kj
rate constant for reaction j
- k̄j
jth constant for the Hill function fit
- km
conversion constant from infected cell concentration to intensity
- nunc,0
initial number of uninfected cells
- nvir,0
number of viruses in the initial inoculum
- R
weighting matrix for parameter estimation
- r
radial dimension
- rplate
radius of the plate
- t
time
- Vc
cell volume
- x
state vector
- Y
virus yield per infected cell
- y
measurement vector
- ym
intensity measurement
- λ
eigenvalue
- ∇θΦ
gradient of the objective function with respect to the model parameters for parameter estimation
- ∇θθΦ
Hessian of the objective function with respect to the model parameters for parameter estimation
- Φ
objective function value for parameter estimation
- ϕ
correction to the diffusivity for hindered diffusion
- τ
age of infection
- τd
maximum age of infection
- θ
vector of model parameters
Subscripts
- dc
dead cell
- ifn
interferon
- infc
infected cell
- inoc
inoculated cell
- unc
uninfected cell
- lsub
limiting substrate
- vir
virus
References
- 1.Duca KA, Lam V, Keren I, Endler EE, Letchworth GJ, Novella IS, Yin J. Quantifying viral propagation in vitro: Toward a method for characterization of complex phenotypes. Biotech Prog. 2001;17(6):1156–1165. doi: 10.1021/bp010115m. [DOI] [PubMed] [Google Scholar]
- 2.Rose JK, Whitt MA. Rhabdoviridae: The viruses and their replication. In: Knipe DM, Howley PM, editors. Fundamental Virology. fourth. Lippincott Williams & Wilkins; 2001. pp. 665–688. [Google Scholar]
- 3.Holland JJ, Villarreal LP, Breindl M. Factors involved in the generation and replication of rhabdovirus defective T particles. J Virol. 1976;17(3):805–815. doi: 10.1128/jvi.17.3.805-815.1976. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ball LA, Pringle CR, Flanagan B, Perepelitsa VP, Wertz GW. Phenotypic consequences of rearranging the P, M, and G genes of vesicular stomatitis virus. J Virol. 1999;73(6):4705–4712. doi: 10.1128/jvi.73.6.4705-4712.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Samuel CE. Antiviral actions of interferons. Clin Microbiol Rev. 2001;14(4):778–809. doi: 10.1128/CMR.14.4.778-809.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Grandvaux N, tenOever BR, Servant MJ, Hiscott J. The interferon antiviral response: from viral invasion to evasion. Curr Opin Infect Dis. 2002;15(3):259–267. doi: 10.1097/00001432-200206000-00008. [DOI] [PubMed] [Google Scholar]
- 7.Bocharov GA, Romanyukha AA. Mathematical model of antiviral immune response. III. Influenza A virus infection. J Theor Biol. 1994;167(4):323–360. doi: 10.1006/jtbi.1994.1074. [DOI] [PubMed] [Google Scholar]
- 8.Baccam P, Beauchemin C, Macken CA, Hayden FG, Perelson AS. Kinetics of influenza A virus infection in humans. J Virol. 2006;80(15):7590–7599. doi: 10.1128/JVI.01623-05. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hancioglu B, Swigon D, Clermont G. A dynamical model of human immune response to influenza a virus infection. J Theor Biol. 2007;246(1):70–86. doi: 10.1016/j.jtbi.2006.12.015. [DOI] [PubMed] [Google Scholar]
- 10.Yin J, McCaskill JS. Replication of viruses in a growing plaque: a reaction-diffusion model. Biophys J. 1992;61(6):1540–1549. doi: 10.1016/S0006-3495(92)81958-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.You L, Yin J. Amplification and spread of viruses in a growing plaque. J Theor Biol. 1999;200(4):365–373. doi: 10.1006/jtbi.1999.1001. [DOI] [PubMed] [Google Scholar]
- 12.Fort J. A comment on amplification and spread of viruses in a growing plaque. J Theor Biol. 2002;214(3):515–518. doi: 10.1006/jtbi.2001.2469. [DOI] [PubMed] [Google Scholar]
- 13.Fort J, Méndez V. Time-delayed spread of viruses in growing plaques. Phys Rev Lett. 2002;89(17):178101–1–178101–4. doi: 10.1103/PhysRevLett.89.178101. [DOI] [PubMed] [Google Scholar]
- 14.Ortega-Cejas V, Fort J, Méndez V, Campos D. Approximate solution to the speed of spreading viruses. Phys Rev E. 2004;69(3):031909. doi: 10.1103/PhysRevE.69.031909. [DOI] [PubMed] [Google Scholar]
- 15.Lam V, Duca KA, Yin J. Arrested spread of vesicular stomatitis virus infections in vitro depends on interferon-mediated antiviral activity. Biotech Bioeng. 2005;90(7):793–804. doi: 10.1002/bit.20467. [DOI] [PubMed] [Google Scholar]
- 16.Bailey JE, Ollis DF. Biochemical Engineering Fundamentals. McGraw-Hill; New York: 1986. [Google Scholar]
- 17.Brown PN, Hindmarsh AC, Petzold LR. Using Krylov methods in the solution of large-scale differential-algebraic systems. SIAM J Sci Comp. 1994;15(6):1467–1488. [Google Scholar]
- 18.Haseltine EL, Rawlings JB, Yin J. Dynamics of viral infections: Incorporating both the intracellular and extracellular levels. Comput Chem Eng. 2005;29(3):675–686. [Google Scholar]
- 19.Villadsen J, Michelsen ML. Solution of Differential Equation Models by Polynomial Approximation. Prentice-Hall; Englewood Cliffs New Jersey: 1978. [Google Scholar]
- 20.Ware BR, Raj T, Flygare WH, Lesnaw JA, Reichmann ME. Molecular weights of vesicular stomatitis virus and its defective particles by laser light-scattering spectroscopy. J Virol. 1973;11(1):141–145. doi: 10.1128/jvi.11.1.141-145.1973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Zerial A, Hovanessian A, Stefanos S, Huygen K, Werner GH, Falcoff E. Synergistic activities of type I (alpha, beta) and type II (gamma) murine interferons. Antiviral Res. 1982;2(4):227–239. doi: 10.1016/0166-3542(82)90045-6. [DOI] [PubMed] [Google Scholar]
- 22.Nichol JC, Deutsch HF. Biophysical studies of blood plasma proteins. VII. Separation of γ-globulin from the sera of various animals. J Am Chem Soc. 1948;70(1):80–83. doi: 10.1021/ja01181a025. [DOI] [PubMed] [Google Scholar]
- 23.Keseler IM, Collado-Vides J, Gama-Castro S, Ingraham J, Paley S, Paulsen IT, Peralta-Gil M, Karp PD. EcoCyc: a comprehensive database resource for Escherichia coli. Nucleic Acids Res. 2005;33:D334–D337. doi: 10.1093/nar/gki108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Gutenkunst RN, Waterfall JJ, Casey FP, Brown KS, Myers CR, Sethna JP. Universally sloppy parameter sensitivities in systems biology models. PLoS Comput Biol. 2007;3(10):1871–1878. doi: 10.1371/journal.pcbi.0030189. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Marcus PI, Rodriguez LL, Sekellick MJ. Interferon induction as a quasispecies marker of vesicular stomatitis virus populations. J Virol. 1998;72(1):542–549. doi: 10.1128/jvi.72.1.542-549.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hastings A, Arzberger P, Bolker B, Collins S, Ives AR, Johnson NA, Palmer MA. Quantitative bioscience for the 21st century. BioScience. 2005;55(6):511–517. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Figure S1: Experimental images obtained from the dynamic propagation of VSV on BHK cells. The white scale bar in the upper left-hand corner of the experimental images is one millimeter.
Figure S2: Radial infection profiles obtained by averaging the experimental images of the dynamic propagation of VSV on BHK cells. The color bar shows the standard deviation σ of each individual measurement from the mean value, and is saturated after σ > 3. Red lines show the average profile, and green lines show one standard deviation away from the mean. Note that the background fluorescence was estimated and subtracted from each image before calculating these radial profiles.
Figure S3: Comparison of the experimental and predicted radial infection profiles for the dynamic propagation of VSV on BHK cells: (a) extracellular model, no growth of uninfected cells; (b) extracellular model; and (c) age-segregated model. The thick and thin lines present the model predictions and the average experimental measurements, respectively.
Figure S4: Experimental images obtained from the dynamic propagation of VSV on DBT cells. The white scale bar in the upper left-hand corner of the experimental images is one millimeter.
Figure S5: Radial infection profiles obtained by averaging the experimental images of the dynamic propagation of VSV on DBT cells. The color bar shows the standard deviation σ of each individual measurement from the mean value, and is saturated after σ > 3. Red lines show the average profile, and green lines show one standard deviation away from the mean. Note that the background fluorescence was estimated and subtracted from each image before calculating these radial profiles.
Figure S6: Comparison of the experimental and predicted radial infection profiles for the dynamic propagation of VSV on DBT cells. A reaction-diffusion model accounting for solely extracellular species generated the predicted profiles. The thick and thin lines present the model predictions and the average experimental measurements, respectively.
Figure S7: Comparison of the experimental and predicted radial infection profiles for the dynamic propagation of VSV on DBT cells in the presence of interferon inhibitors. A reaction-diffusion model accounting for solely extracellular species generated the predicted profiles. The thick and thin lines present the model predictions and the average experimental measurements, respectively.
Figure S8: Profile of the initial virus concentration for the models. cvir,0 denotes the estimated initial concentration of virus in the inoculation radius.