Histidine in Continuum Electrostatics Protonation State Calculations

Abstract

A modification to the standard continuum electrostatics approach to calculate protein pK_as which allows for the decoupling of histidine tautomers within a two state model is presented. Histidine with four intrinsically coupled protonation states cannot be easily incorporated into a two state formalism because the interaction between the two protonatable sites of the imidazole ring is not purely electrostatic. The presented treatment, based on a single approximation of the interrelation between histidine’s charge states, allows for a natural separation of the two protonatable sites associated with the imidazole ring as well as the inclusion of all protonation states within the calculation.

INTRODUCTION

Histidine plays an essential role in protein chemistry where it is often found in the active site of enzymes. Much of histidine’s utility arises from the fact that histidine titrates near neutral pH. As such the quality of models used to describe the protonation of histidine is essential for the correct determination of pH dependent properties of proteins. The continuum electrostatics approach to protein pK_a calculations is a simple and practical method that has been developed over the past two decades^1–10. Work continues to improve the continuum electrostatics description while new models incorporating higher levels of detail from both the solvent and protein models have been developed^11–19. Here we describe a solution of one technical issue in continuum electrostatics calculations related to the specificity of interaction between the two protonatable sites of histidine. Several applications which demonstrate the utility of the current scheme are presented.

Histidine can bind a proton at the N^δ or N^ε atoms of the imidazole ring giving rise to four possible protonation states: the doubly deprotonated negative state, two neutral tautomers (N^δ and N^ε) with a single bound proton, and the doubly protonated positive state. The difficulty in treating histidine within standard continuum electrostatics approaches, such as the Full Finite Difference Poisson-Boltzmann (F/FDPB) formalism, arise from the fact that the partial atomic charges of the imidazole ring depend explicitly on the location of the bound proton(s) preventing the separation of the N^δ and N^ε titratable sites. The continuum electrostatics approach to pK_a calculations in proteins hinges on the fact that specific groups within a covalently bonded macromolecule can be treated as separate entities that interact classically. In order to separate two ionizable sites in the protein there should not be significant through bond charge transfer between the sites (i.e. they should be separated by many single bonds). Since the imidazole ring is conjugated, a proton bound to the N^δ site will significantly alter the charges at the N^ε site, and vice versa. This prevents the separation of the two imidazole sites within the standard approach.

To overcome theses problems a number of methods to treat histidine have been introduced. The simplest means to incorporate histidine into a two state model, where the protonation state of each titratable site is described by a binary variable n, is to fix one of the imidazole nitrogens in the protonated state, typically N^δ. The second imidazole nitrogen is then treated as the sole titratable site. This “single site” model¹ reduces the problem’s complexity, but also limits the chemistry of the histidine side chain that gives rise to its usefulness in proteins. The “pseudo independent site” model developed by Bashford and coworkers³ allows for the titration of both the N^δ and N^ε sites by essentially coupling two “single site” models for each histidine residue. In this model calculations are performed where each histidine is treated as titrating at the N^δ site. Subsequently, a complete set of calculations in which each histidine titrates at the N^ε sites is then performed. Finally, calculations are performed where each histidine is treated as N^ε except for one, which is treated as N^δ, in order to calculate the appropriate interactions between tautomers. These interaction energies are used to correct the free energy function to prevent sites from interacting with both the N^δ and N^ε forms of the same histidine. Furthermore, an arbitrarily large interaction energy between the tautomers of the same histidine is included to prevent the simultaneous deprotonation of both sites.

Each of the described methods has drawbacks; either the chemistry of histidine is oversimplified or the complexity of the calculation is increased. Here we describe a modification of the standard two state model for histidine that alleviates these issues. A simple binary representation of the protonation state is maintained, the computational complexity is only slightly increased compared to the single site model of histidine, and all protonation/charge states of the imidazole ring are modeled. Results are presented for several small proteins, superoxide dismutase, and respiratory complex I.

METHODS

Theory of Histidine in Continuum Electrostatics calculations

Continuum electrostatics methods attempt to calculate the shift in pK_a associated with transferring a model compound with known solution pK_a representing the given titratable amino acid from solution to the protein environment. This pK_a shift is typically considered to consist of three terms: the change in solvation energy (ΔΔG^Born), the interaction of charges in the titratable site with the fixed background charges of the protein (ΔΔG^Back), and the electrostatic interaction between titratable sites i and j (W_ij). Given the protonation state vector n⃑ with components n_i ∈ {0,1}, where a value of one indicates the site is protonated and zero deprotonated, the free energy associated with a given protonation state can be expressed as

$$G(\stackrel{\rightharpoonup }{n})=\sum _{i=1}^N{k}_{B}T\text{ln}(10)(pH-p{K}_{a,i}^{\text{int}r})(n_i-n_i^0)+\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{W}_{ij}(n_i-n_i^0)(n_j-n_j^0),$$ (1)

where n⁰ is the protonation state of the indicated site in the neutral charge (reference) state. The intrinsic pK_a is the pK_a associated with the given site in the protein when all other sites are in the reference state and is given by

$$p{K}_{a,i}^{\text{int}r}=p{K}_{a,i}^0+\frac{1}{k_{B}T\text{ln}(10)}[\mathrm{\Delta }\mathrm{\Delta }{G}_i^{\mathit{\text{Born}}}+\mathrm{\Delta }\mathrm{\Delta }{G}_i^{\mathit{\text{Back}}}],$$ (2)

where ΔΔG^Born, ΔΔG^Back, and W_ij can be expressed in terms of Green’s functions explicitly and have been given elsewhere^4,6. These expressions involve products over charges between sites and the appropriate Green’s function yielding interaction energies.

The charges of typical ionizable residues, with a single titratable site, can be expressed in terms of the protonation state as

$$\stackrel{\rightharpoonup }{q}(n)={\stackrel{\rightharpoonup }{q}}^{-}+n[{\stackrel{\rightharpoonup }{q}}^{+}-{\stackrel{\rightharpoonup }{q}}^{-}]={\stackrel{\rightharpoonup }{q}}^{-}+n\mathrm{\Delta }\stackrel{\rightharpoonup }{q},$$ (3)

where q⃑⁺ and q⃑⁻ are vectors comprised of the set of partial atomic charges for the site when protonated and deprotonated respectively. The constant term in Eq. (3) is subsumed into the protein background while the linear term determines the functional form of Eq. (1).

For histidine, we similarly define the set of charges q⃑⁺, q⃑^δ, q⃑^ε and q⃑⁻ corresponding to the set of charges associated with the positive doubly protonated, neutral N^δ and N^ε tautomers, and the negative doubly deprotonated states respectively. The charge state of a histidine residue can then be expressed as a function of its protonation state variables n^δ and n^ε as

$$\stackrel{\rightharpoonup }{q}(n^{\delta },n^{\epsilon })={\stackrel{\rightharpoonup }{q}}^{+}+(1-n^{\epsilon })({\stackrel{\rightharpoonup }{q}}^{\delta }-{\stackrel{\rightharpoonup }{q}}^{+})+(1-n^{\delta })({\stackrel{\rightharpoonup }{q}}^{\epsilon }-{\stackrel{\rightharpoonup }{q}}^{+}).$$ (4)

Clearly, if we substitute the values of (1, 0), (0, 1), and (1, 1) for (n^δ, n^ε) into Eq. (4) we obtain the charge distributions q⃑^δ, q⃑^ε, and q⃑⁺. However, q⃑⁻ does not appear in Eq. (4). When the values (0, 0) are encountered Eq. (4) yields

$$\stackrel{\rightharpoonup }{q}(0,0)={\stackrel{\rightharpoonup }{q}}^{\delta }+{\stackrel{\rightharpoonup }{q}}^{\epsilon }-{\stackrel{\rightharpoonup }{q}}^{+}\approx {\stackrel{\rightharpoonup }{q}}^{-}.$$ (5)

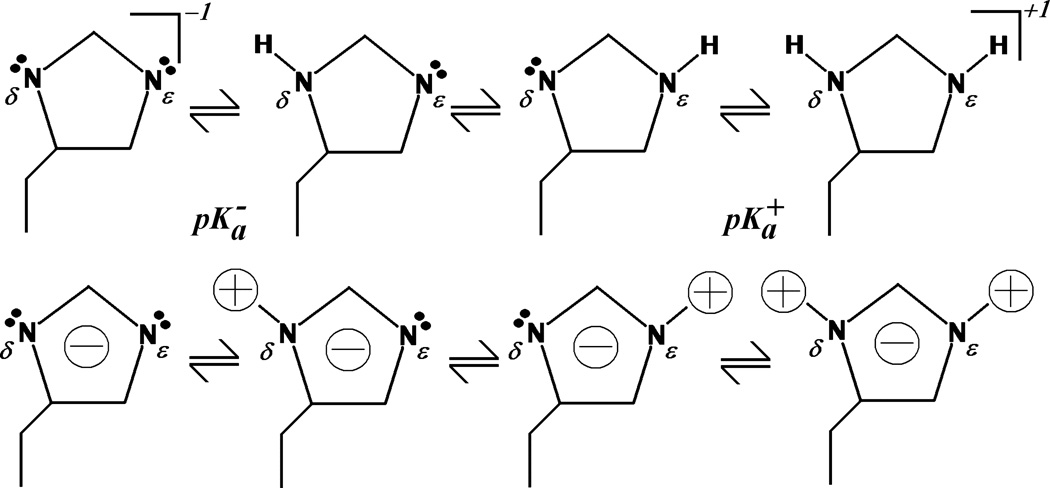
By examining Figure 1 it can be understood that Eq. (5) approximates the charge state of histidine when doubly deprotonated. In light of Eq. (5) we can rewrite Eq. (4) as

$$\stackrel{\rightharpoonup }{q}(n^{\delta },n^{\epsilon })={\stackrel{\rightharpoonup }{q}}^{-}+n^{\delta }\mathrm{\Delta }{\stackrel{\rightharpoonup }{q}}^{\epsilon }+n^{\epsilon }\mathrm{\Delta }{\stackrel{\rightharpoonup }{q}}^{\delta },$$ (6)

where Δq⃑^δ = (q⃑⁺ − q⃑^δ), etc. Eq. (6) has now essentially decoupled the N^δ and N^ε titratable sites via the approximation expressed in Eq. (5), since only the linear terms in Eq. (6) are of significance.

Figure 1.

Schematic diagram of the various charge states of histidine. Top, structural formulas for the deprotonated, neutral tautomers, and protonated forms of the histidine side chain. Bottom, cartoon representation of the approximate charge distribution in each charge state. The approximation of Eq. (5) can be understood qualitatively by superimposing the neutral tautomers. The result is a structure with two peripheral positive charges and two central negative charges. Subtraction of the doubly protonated state charges leaves a single negative charge centered on the imidazole ring.

To arrive at an expression analogous to Eq. (1) we must distinguish titratable sites from titratable residues (i.e. histidine is a single titratable residue, but consists of two titratable sites). The resulting expression has the same form as Eq. (1), but the sums are now over sites rather than residues. In deriving Eq. (1) from Eq. (6) the quadratic term, $n^{\delta }{n}^{\epsilon }(p{K}_a^{B-}-p{K}_a^{B+})$, arises which can be identified as the interaction energy between the n^δ and n^ε sites of the same histidine where $p{K}_a^{B-}$ and $p{K}_a^{B+}$ are the pK_as for the negative to neutral and neutral to positive reactions shifted by the desolvation energy respectively. Assuming the solvation energies are equal for the charged states, ΔG_solv (0,0) ≈ ΔG_solv (1,1), and for the neutral states, ΔG_solv (1,0) ≈ ΔG_solv (0,1), the pK_a values become

$$p{K}_a^{B-}=p{K}_a^{-}-\mathrm{\Delta }\mathrm{\Delta }{G}^{\mathit{\text{Born}}}p{K}_a^{B+}=p{K}_a^{+}+\mathrm{\Delta }\mathrm{\Delta }{G}^{\mathit{\text{Born}}},$$ (7)

and the interaction energy

$$W^{\delta \epsilon }=(p{K}_a^{-}-p{K}_a^{+})-2\mathrm{\Delta }\mathrm{\Delta }{G}^{\mathit{\text{Born}}},$$ (8)

where ΔΔG^Born is determined for the positive to neutral reaction. Note that ΔΔG^Born will reduce $p{K}_a^{+}$ and increase $p{K}_a^{-}$, since the lower dielectric protein environment will stabilize the neutral charge state. The difference $(p{K}_a^{-}-p{K}_a^{+})$ is the quantum mechanical (i.e. electronic) interaction energy between the N^δ and N^ε sites of the same histidine where $p{K}_a^{-}$ and $p{K}_a^{+}$ are the model pK_as associated with the negative to neutral and neutral to positive protonation reactions respectively. The interaction energy, Eq. (8), then serves to adjust between the appropriate pK_a value for the positive to neutral or neutral to negative reaction. In solution or if the desolvation term is neglected the interaction energy can be approximated as

$$W^{\delta \epsilon }=(p{K}_a^{-}-p{K}_a^{+})\approx 7.$$ (9)

The neutral charge state is typically chosen as the reference state, so either of the two neutral tautomers will suffice. Let us define n^δ0 ≡ 1 and n^ε0 ≡ 0; that is the reference state is the N^δ-tautomer. From this choice we see that the N^δ site is acidic while the N^ε site is basic. Model pK_as are then assigned according to

$$p{K}_a^{\delta }=p{K}_a^{-}-W^{\delta \epsilon }{n}^{\epsilon 0}=p{K}_a^{-}-(p{K}_a^{-}-p{K}_a^{+})(1)=p{K}_a^{-}\approx 14,p{K}_a^{\epsilon }=p{K}_a^{-}-W^{\delta \epsilon }{n}^{\delta 0}=p{K}_a^{-}-(p{K}_a^{-}-p{K}_a^{+})(0)=p{K}_a^{+}\approx 7.$$ (10)

The background term, ΔΔG^Back, in Eq. (2) is then calculated with all histidines as the N^δ-tautomer. From inspection of Eq. (6) it can be seen that the charge distributions q⃑⁺ and q⃑^ε are associated with n^δ while q⃑⁺ and q⃑^δ are associated with n^ε. It is important to note that the negative state charge distribution, q⃑⁻, is never encountered and is not utilized in the calculation explicitly. For simplicity we have assumed equivalent pK_as for the N^δ and N^ε sites. However, the method is not restricted to this case and the pK_as in Eqn. (10) can be adjusted as desired to reflect the difference in the titration behavior of the two sites.

The described modification allows for the inclusion of the variables (n^δ, n^ε) into a general state vector n⃑ = n₁,n₂…, and to treat these sites independently as with other sites. In fact any site with intrinsically linked protonatable sites, such as phosphate groups, for which an approximate charge distribution analogous to Eq. (5) can be constructed can be treated with this method.

Implementation: pKip

The method presented in the preceding section has been implemented as the standard model for histidine in the program “pKip: pK_as in proteins” currently under development. pKip is a general continuum electrostatics program designed for the calculation of pK_as in proteins. The program calculates all of the required terms in Eq. (1), and in turn relies on APBS²⁰ libraries to solve the linearized Poisson-Boltzmann equation (LPBE). The program features the inclusion of membranes, an arbitrary number of user specified dielectric constants, and membrane potentials. In the calculations described in the following sections pKip was used to calculate the electrostatic terms of Eq. (1) except where otherwise stated.

The average protonation state of each enzyme was determined by Metropolis Monte Carlo (MC) simulation as described by Beroza et al.²¹ and performed by our in house code “Monte” also under development in this lab.

Simulation Protocols

Protonation state calculations were performed on several small proteins (1MBC³, 2LZT²², 3RN3²³ and 1RNZ²⁴, 3BDC²⁵, 1BI6²⁶, 2RN2²⁷, 4PTI²⁸, 9RNT²⁹) for which some or all of the protonatable groups have experimentally determined apparent pK_as. Experimental pK_as were taken from³ for myoglobin, from²⁵ and³⁰ for SNase Δ+PHS variant, and³¹ for all others. Protonation state calculations were also performed on Human Cu/Zn Superoxide dismutase (accession code 1L3N)³² and the hydrophilic domain of NQO-oxidoreductase (respiratory complex I, structure 2FUG) from thermus themophilus³³.

In all cases a solvent dielectric of ε_s = 80 and ionic strength of I = 100 mM was employed. For all proteins an internal dielectric of ε_p = 20 was used, except for complex I and myoglobin where ε_p = 4 was used. CHARMM22³⁴ charges and radii were used throughout, except for myoglobin where the Amber/Bondi charges and radii were used as in³. The model pK_as were the same as those presented by Bashford and Karplus⁵ except for histidine which was assigned model pK_as of 14 and 7 for the doubly deprotonated to N^δ and the N^ε to doubly protonated reactions respectively except where otherwise noted. For each of the small test proteins and the PDB2PQR^35,36 program was used to add hydrogens and assign atomic charges and radii. For Complex I the Amber7³⁷ suite was used to add hydrogens and minimize their positions. The program “loopy”³⁸ included with the Jackal suite of programs was used to build in deleted residues and residues not resolved in the crystal structure of the hydrophilic domain of complex I. Various grid sizes and spacing were employed depending on the system. For all proteins studied the finest grid spacing was 0.2 Å or less. All MC simulations were performed at 300 K. The number of MC sweeps (MC steps per site) also varied depending on the system. For complex I 100,000 equilibration sweeps were performed followed by 50,000 production sweeps. MC simulations of the smaller proteins employed 10,000 to 20,000 production sweeps. Single and double MC moves were allowed to overcome poor sampling of highly correlated sites²¹. Parallel Tempering simulations performed on complex I did not show any significant differences from the single temperature simulations. Additional electrostatics calculations were also performed with the program MEAD^4,39 in order to compare the presented method to the “pseudo independent site” model of³.

Hartree-Fock ab initio calculations were performed on methylimidazole in the doubly protonated, singly protonated, and deprotonated states. All calculations were performed using the Gaussian 03⁴⁰ program at the 6–31G(d) level. Mulliken charges for each state were determined from the geometry optimized structures.

RESULTS AND DISCUSSION

Histidine Charges

To test the validity of the assumption expressed by Eq. (5) Mulliken partial atomic charges were calculated for the four possible protonation states of methylimidazole. The total charge for the doubly deprotonated state obtained from Eq. (5) is −1.00 e⁻ with a precision out to five significant figures. The per atom RMSD between the approximate and calculated charge distributions for the negative charge state was determined to be 0.037 e⁻, with the largest deviations occurring at the N^δ and N^ε protons. These protons are of course absent from the true negative protonation state, but are assigned a small charge in the approximate distribution. With per atom RMSD values below 4% this approximation should not introduce significant errors above the existing uncertainties in the F/FDPB method. Calculated charges for methylimidazole and derived charges for histidine from several force fields are provided in the Supporting Information.

Histidine Titration in Solution

To illustrate the method we first examine the titration of an isolated histidine side-chain in aqueous solution. Titration curves for the individual sites and the overall titration behavior is shown in Figure 2. Here we assume equivalent sites with intrinsic pK_as of 14 and 7 with interaction element W = 7 pK units. The energies of each protonation state are calculated from Eq. (1) as a function of pH, and the average protonation was calculated exactly from the Boltzmann distribution. There are four possible states specified by (n^δ, n^ε) with energies:

1. E(1,0) = (pH−14)(1−1)+(pH−7)(0−0)+7(1−1)(0−0)=0

2. E(0,1) = (pH−14)(0−1)+(pH−7)(1−0)+7(0−1)(1−0)=14−7−7 = 0

3. E(1,1) = (pH−14)(1−1)+(pH−7)(1−0)+7(1−1)(1−0)=(pH−7)

4. E(0,0) = (pH−14)(0−1)+(pH−7)(0−0)+7(0−1)(0−0)=−(pH−14)

For case 1 we obtain the expected result since this is the reference state, and is defined as the zero of energy. Case 2 is also correct, since we have assumed the sites are equivalent. Case 3 corresponds to the energy required to protonate a group with pK_a of 7, and case 4 corresponds to deprotonating a group with pK_a of 14. From the above analysis, we see that only for case 2 does the interaction energy enter the expression for the total energy (i.e. when the N^δ-tautomer is converted to the N^ε-tautomer).

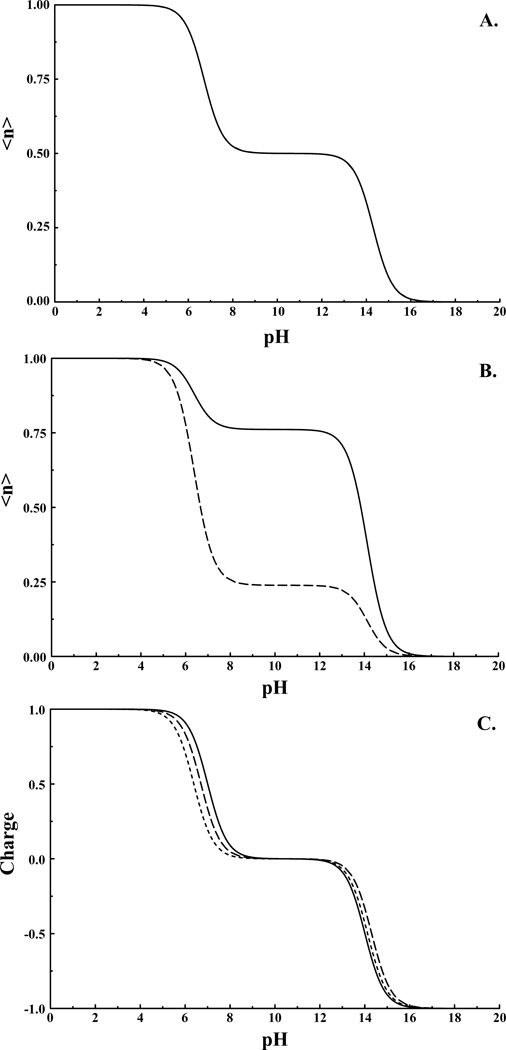
Figure 2.

Titration of histidine in solution with A) N^δ and N^ε treated as equivalent with a model pK_a of 7, and B) N^δ assigned model pK_a of 7 and N^ε assigned model pK_a of 6.6 (N^δ site solid line and N^ε site dashed line). Note in (A) curves are coincident. C) Overall titration behavior/charge for histidine models from (A) small dashed line, (B) large dashed line, and for two non-interacting sites with pK_as of 7 and 14.

From Figure 2A & 2C we observe apparent pK_as for the histidine side-chain of 6.7 and 14.3. The deviation from the expected values of 7 and 14 result from state splitting due to the interaction between states analogous to the splitting observed in coupled two level quantum systems. If we choose to differentiate the tautomers, say by assigning the N^ε site an intrinsic pK_a of 6.5, then cases 2 and 3 above would be adjusted to 0.5 and (pH-6.5) respectively, again as expected. Here we observe apparent pK_as of 6.4 and 14.1 (Figure 2B & 2C). The splitting is less than in the previous example because the two states are no longer in resonance. The apparent pK_as are very similar in both examples; however the titration behavior of the individual sites is quite different.

Histidine Titration in Proteins

Table I presents the RMSD deviation of the calculated and experimental apparent pK_as (pK_1/2) for a small set of eight test proteins. Table I includes comparisons between this work as well as the standard histidine treatments described in¹ and³, as well as with the fully empirical approach implemented in the popular PROPKA program³¹. Double entries in Table I indicate the RMSD of all ionizable residues (first value) and for histidines only (second value). As can be seen from Table I there are no significant deviations from the current method and the standard approach. Furthermore the accuracy of pK_as obtained from this method are comparable to those of PROPKA.

Table I.

RMSD for calculated and experimental pK_as by various methods.

Protein	PDB	RMSD (pKip)	RMSD (Standard)	RMSD (propka)c
Myoglobin	1MBC	1.66 (10), 1.20 (8)	1.74 (10), 1.33 (8)a	/
HEWL	2LZT	0.60 (19), 0.10 (1)	0.67 (19), 0.10 (1)a	0.66 (19)
RNase A	1RNZ	0.94 (15), 1.27 (4)	/	0.67 (14)
	3RN3	1.06 (16), 1.67 (4)	1.40 (16), 1.94 (4)b	0.94 (14)
SNased	3BDC	1.11 (16), 0.99 (2)	/	1.23 (16), 0.10 (2)
BI-VI	1BI6	0.65 (22)	/	0.68 (22)
RNase H	2RN2	1.02 (23), 0.55 (5)	/	0.72 (23)
BPTI	4PTI	0.46 (13)	0.70 (10)b	0.60 (14)
RNase T1	9RNT	0.96 (14), 0.66 (3)	/	1.51 (14)

Pairs of RMSD values are for all sites and for histidines only, respectively. Values in parenthesis give the number of sites included in the calculation of the RMSD.

^aMyoglobin results from³, HEWL results calculated with MEAD using the “pseudo independent site” model for histidine.

^bResults from¹ using a “single site” model of histidine.

^cpropka results from³¹.

^dSNase Δ+PHS variant³⁰.

HEWL contains only one histidine residue, HIS-15 (pK_1/2 = 5.6)³¹, which is modeled equally well by both the current (pK_a,calc. = 5.5) and “pseudo independent site” (pK_a,calc. = 5.7) models. Figure 3 illustrates the titration behavior of HIS-15. Figure 3A illustrates the behavior when the N^δ and N^ε sites are assigned the same pK_a of 7 for the neutral to positive reaction. Although it is still possible for the protein environment to differentiate the two protonation sites of histidine through either the background term or through site-site interactions it is clear that both sites are nearly equally populated over the entire pH range studied. Figure 3B illustrates the titration behavior of HIS-15 when the N^δ and N^ε sites are assigned model pK_as of 7.0 and 6.6 respectively for the neutral to positive protonation reaction. The RMSD for all pK_as is unchanged at 0.60, and the deviation for HIS-15 is 0.13 indicating no loss of accuracy. From Figure 3B it is clear that the N^δ and N^ε sites have differentiated with the N^δ site being preferentially protonated. Finally, Figure 3C presents the titration behavior of HIS-15 as determined with the model of³. The curves in Figures 3B and 3C are quite similar with significant deviations arising only beyond a pH of 10 for the individual sites while the total titration behavior of HIS-15 is nearly identical in the two figures to above pH 12. Around pH 13 our model of histidine begins to deprotonate as we approach the second pK_a.

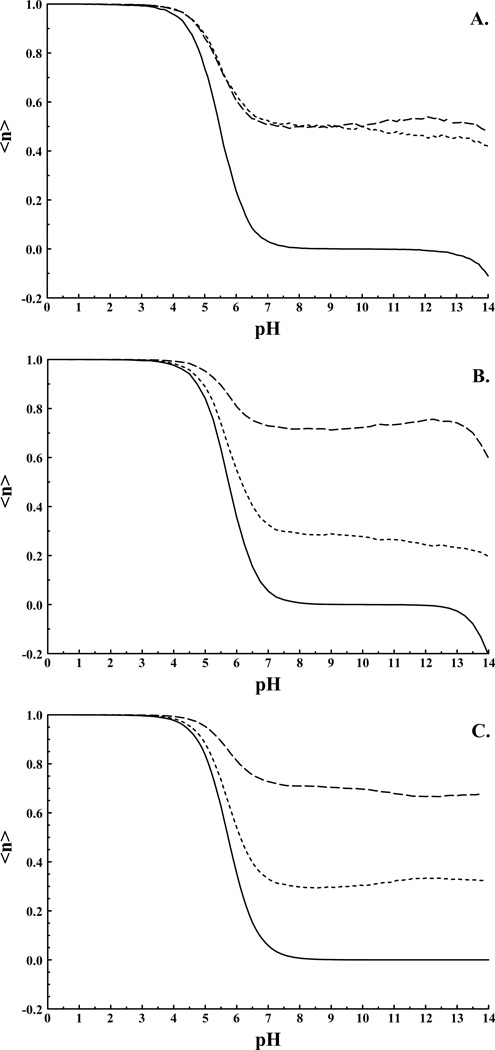
Figure 3.

HEWL HIS-15 titration curves. A) pKip result with $p{K}_a^{\delta }=14$ and $p{K}_a^{\epsilon }=7$ (N^δ and N^ε equivalent). B) pKip result with $p{K}_a^{\delta }=14$ and $p{K}_a^{\epsilon }=6.6$ (N^δ and N^ε non-equivalent). C) “pseudo independent site” result with $p{K}_a^{\delta }=7$ and $p{K}_a^{\epsilon }=6.6$ <n> is the average proton population of the indicated site; Large dashed line N^δ site, small dashed line N^ε site. Solid curves represent the total titration behavior/charge of the histidine residue.

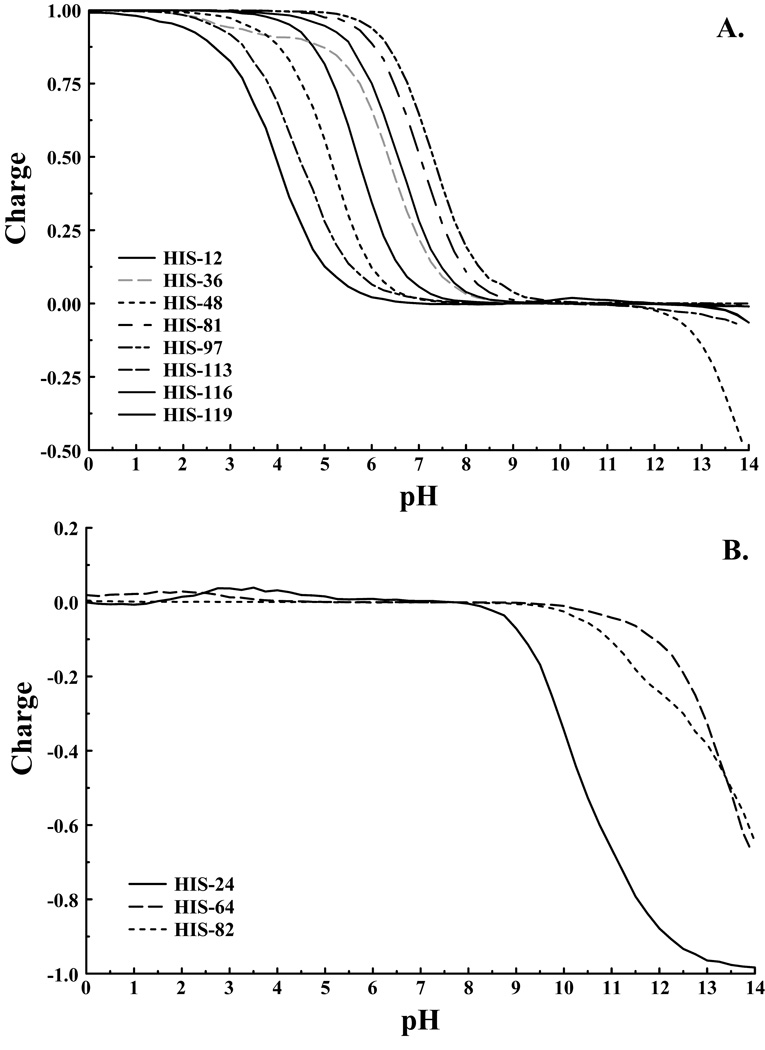
A perhaps better test case is that of myoglobin with eleven histidines exhibiting a range of behaviors. The RMSD values presented in Table I again show that the two representations of histidine both model the system with similar accuracy. The maximum deviation between experiment and the current model is 1.75 pK units for HIS-36, and is similar for both models. Figure 4 illustrates the titration behavior for the titrating and non-titrating histidines of myoglobin. Of the eight titrating histidines only HIS-48 exhibits any significant population of the fully deprotonated state. Again, deprotonation of the second proton is only observed above pH 12, well above biologically relevant pH values. For the remaining titrating histidines the second pK_a is up-shifted, and even at pH 14 these residues remain primarily in the neutral charge state. Of the three non-titrating histidines our method predicts pK_as below zero for the neutral to positive protonation reactions in agreement with previous calculations. Furthermore, these histidines were not observed to titrate above pH 4.7 experimentally³. Of these histidines HIS-24 is observed to deprotonate in the region between pH 9 and 13 while the remaining two histidines show apparent pK_as near 14. Experiments on proteins are rarely able to exceed a pH of 9, so none of the histidines of myoglobin should be observed in the negative charge state experimentally.

Figure 4.

A) Titrating and B) Non-titrating histidines of myoglobin as determined by the pKip program.

Imidazolate Ion and Cu/Zn Superoxide Dismutase

Superoxide dismutase (SOD) facilitates the dismutation of superoxide ions into oxygen and peroxide alleviating oxidative stress due to the presence of the reactive oxygen species. Superoxide dismutase is a unique example with which to test the described approach since it contains a bridging histidine ligand which is one of the very few examples of the imidazolate ion in biology. In Cu/ZnSOD HIS-63 bridges the Cu and Zn ions in the active site. Upon reduction of the Cu center HIS-63 dissociates from Cu and exhibits an apparent pK_a of 10.8 as determined from experiment⁴¹.

Six configurations out of thirty were chosen from the NMR solution structure of reduced Human Cu/ZnSOD³² to determine the pK_a of HIS-63. These configurations were chosen to represent the minimum, maximum, average and ideal (as determined from density functional theory⁴²) HIS-Cu distances. Since human Cu/ZnSOD is dimeric, a total of 12 pKa values were determined. pK_as were calculated using Eqns. (8) and (9) in order to asses the significance of the desolvation term in Eqn. (8). Use of Eqn. (8), with the desolvation term fully accounted for, resulted in a pK_a of 12.4 ± 1.1 while the pK_a calculated from Eqn. (9) was determined to be 9.3 ± 0.8 with RMSD values of 1.9 and 1.7 respectively. It has been shown that the Born solvation model, and hence solvation energies determined from solutions of the PBE, drastically overestimate the energetic cost of burying charged groups in the low dielectric protein environment^19,43,44. The above analysis indicates that the neglect of the desolvation term with respect to pK⁻ introduces errors that are roughly equal to the inaccuracies associated with solvation energies determined from the PBE with a protein dielectric of 20. It is apparent that to obtain consistent and accurate results from continuum electrostatics calculations improved solvation models that go beyond linear response theory are required.

Complex I: The Redox Bohr Effect

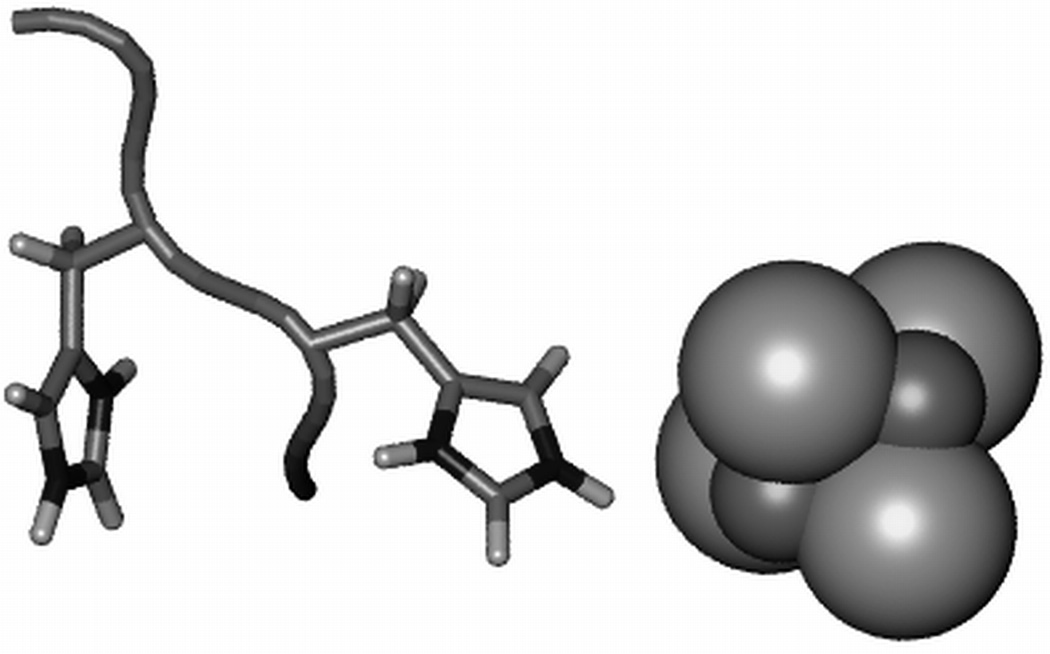
Respiratory complex I (NADH:Ubiquinone oxidoreductase) is a large (approximately 980kD in mitochondria and 550 kD in prokaryotes) membrane bound enzyme^45–49. The hydrophilic domain of complex I, which protrudes into the mitochondrial matrix, contains 832 ionizable residues, 65 of which are histidines, bringing the total number of ionizable sites to 897, since N_sites = N_non−HIS + 2N_HIS. Respiratory complex I is an oxidoreductase which couples the oxidation of NADH and the reduction of quinone to proton translocation across the mitochondrial membrane. Complex I utilizes a chain of seven iron-sulfur (FeS) clusters housed in the hydrophilic domain to effect this reaction over a distance of approximately 100 ų³. Here we focus on the last FeS cluster of the redox chain, N2. It has been known for some time that N2 is a redox Bohr active group⁵⁰. That is, the midpoint reduction potential of the cofactor varies with pH. It has been shown experimentally that the redox Bohr effect arises from the interaction of N2 with a nearby histidine, ₄HIS-169 (Thermus numbering, ₄HIS-226 in Y. lipolytica) of the 49 kDa subunit⁵¹. Figure 5 shows the configuration of FeS cluster N2, ₄HIS-169, and the adjacent histidine ₄HIS-170.

Figure 5.

The core of FeS cluster N2, CYS₄[Fe₄S₄]^2−/3−, shown as spheres and the adjacent histidines, ₄HIS-169 (center) and ₄HIS-170 (left), responsible for the redox Bohr effect.

The apparent midpoint reduction potential, $E_m^{\prime }$, of FeS cluster N2 can be measured experimentally via EPR experiments, and is the redox analogue to the apparent pK_a. $E_m^{\prime }$ is related to the shift in midpoint reduction potential, ΔE_m, according to the relation,

$$E_m^{\prime }=E_m+\mathrm{\Delta }{E}_m,$$ (11)

where E_m is the intrinsic midpoint reduction potential defined as the potential of the redox center when all other cofactors are oxidized⁵². E_m can be defined according to a known model reduction potential if available. To calculate ΔE_m we extend Eq. (1) to include redox centers in addition to protonatable sites^53,54. The redox state of the enzyme is fixed during each calculation, and the linear terms over redox sites involving (the unknown self energies) E_m can be dropped since they are constant. Thus the redox center, N2, only affects the titration calculations via the coulombic site-site interactions allowing us to calculate ΔE_m from the average protonation state,

$$\mathrm{\Delta }{E}_{m,\nu }=\sum _{I=1}^{N_s}{W}_{I\nu }(\langle n_I^{\mathrm{R}\mathrm{e}d}\rangle -\langle n_I^{Ox}\rangle ),$$ (12)

where $\langle n_I^{\mathrm{R}\mathrm{e}d}\rangle$ and $\langle n_I^{Ox}\rangle$ are the average protonation states of site I in the reduced and oxidized enzyme respectively. The subscript ν indicates the redox center.

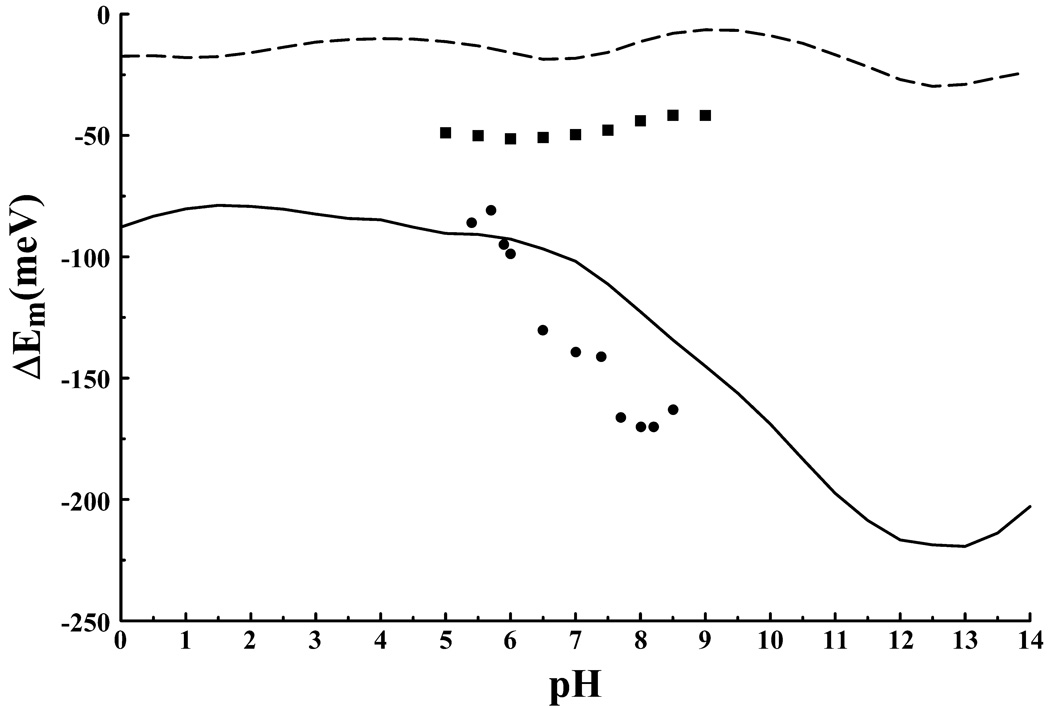
Figure 6 illustrates the results from the present calculations obtained using Eqn. (9). The solid line represents the calculated shift in midpoint reduction potential, ΔE_m, resulting from the interaction of N2 with the protonation state of the enzyme. Solid circles in Figure 6 represent the experimentally observed apparent midpoint reduction potential, $E_m^{\prime }$, of N2 from the Y. lipolytica derived enzyme⁵¹. It should be noted that the intrinsic midpoint reduction potential for the FeS cofactors of complex I varies among different species. Consequently complex I from T. thermophilus and from Y. lipolytica exhibit different $E_m^{\prime }$ values. Hence, it is coincidental that the calculated ΔE_m and the measured $E_m^{\prime }$ values fall in the same range of potential. Inclusion of the intrinsic redox potential, E_m, would simply shift the calculated ΔE_m vertically. A precise value of $E_m^{\prime }$ for N2 from thermus is not known^55,56. However, we are only interested in the variation in $E_m^{\prime }$ as a function of pH, and so a comparison between $E_m^{\prime }$ and ΔE_m is sufficient. As can be seen from Figure 6 the calculated and measured variations in the reduction potential of N2 are quite similar. The calculated values are shifted up in pH by approximately 2 pH units compared to the measured values, but otherwise reproduce the effect. It has been shown via mutagenesis studies that substitution of the conserved residue ₄HIS-169 by methionine eliminates the pH dependence of N2’s midpoint reduction potential in the pH range of 5 to 9⁵¹. Similarly, when the protonation state of the N^δ site of ₄HIS-169 is held fixed the calculated ΔE_m becomes pH independent (Figure 6, solid squares). These results suggest that ₄HIS-169 is the redox Bohr group associated with FeS cluster N2 in agreement with the experimental findings.

Figure 6.

The redox Bohr effect for FeS cluster N2 of complex I. The calculated shift in the midpoint reduction potential, ΔE_m, of N2 calculated with pKip (solid line) and with the “pseudo independent site” model (large-dashed line). The pKip result when the protonation state of ₄HIS-169 is fixed (solid squares) illustrates the loss of redox Bohr activity. Solid circles are the experimentally measured apparent midpoint reduction potentials for N2 from Y. Lipolytica²¹.

Of significant interest is the behavior of the adjacent histidine, ₄HIS-170. Our calculations predict this residue to significantly populate the doubly deprotonated negative charge state in both the oxidized and reduced enzyme. While ₄HIS-169 increases its protonation upon N2 reduction by 0.28 protons ₄HIS-170 becomes completely deprotonated with an associated decrease in protonation of 0.14 protons at pH 7 indicating some level of proton transfer from ₄HIS-170 to ₄HIS-169.

To investigate the appearance of the unexpected negative charge state of ₄HIS-170 calculations were performed with the model of³ where histidine can only populate the neutral or positive charge states. As can be seen from Figure 6 (large dashed line) this model fails to reproduce the redox Bohr effect. Furthermore fixing ₄HIS-170 in a neutral protonation state also eliminates the effect (data not shown). When the protein dielectric is increased from 4 to 10 the negative charge state of histidine is no longer populated, however the redox Bohr effect is again abolished. Use of Eqn. (8), rather than Eqn. (9), produces a large up shift in the pKa of ₄Hid-170 preventing deprotonation of the site and subsequently results in the observed pK_a of ₄HIS-169 increasing from ~9.5 to ~17.5. Redox Bohr activity is also lost.

The results are somewhat puzzling, but seem to indicate that the pK_a shift of ₄HIS-169 is being overestimated due to the inaccurate solvation model being used. Neglect of the desolvation term in Eqn. 8 results in an artificially lowered pK_a for ₄HIS-170 which in a fortuitous cancellation of errors reduces the pK_a of the redox Bohr group, ₄HIS-169. The fact that ₄HIS-169 is not conserved among species indicates that its role in the observed effect is most likely an artifact of the present calculation. However, nearby and highly conserved ₄TYR-87 which presumably suffers from the same overestimate in the desolvation contribution to the shift in pK_a could serve the same function as ₄HIS-170.

CONCLUSION

A convenient method to treat the two protonatable sites of histidine in protein electrostatics calculations has been presented and implemented in the program pKip. The method allows for the treatment of histidine’s protonatable sites as independent, and includes an accurate treatment of the negative charge state. We demonstrate the importance of the method in our calculations on the large protein respiratory complex I where the pH dependence of the midpoint reduction potential (redox Bohr effect) of the terminal FeS redox cofactor N2 is only reproduced when the negative charge state is included in the treatment. The primary drawbacks of the presented treatment of histidine lie within the formalism of the continuum electrostatics approach itself. The present study highlights the need for improved solvation models as suggested in^43,44,57,58 and for a more consistent application of continuum electrostatics principles as suggested by Krystalik^19,59.