Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Nov 13;4:7038. doi: 10.1038/srep07038

Acoustic rainbow trapping by coiling up space

Xu Ni 1, Ying Wu 2, Ze-Guo Chen 1, Li-Yang Zheng 1, Ye-Long Xu 1, Priyanka Nayar 1, Xiao-Ping Liu 1, Ming-Hui Lu 1,a, Yan-Feng Chen 1
PMCID: PMC4229664  PMID: 25392033

Abstract

We numerically realize the acoustic rainbow trapping effect by tapping an air waveguide with space-coiling metamaterials. Due to the high refractive-index of the space-coiling metamaterials, our device is more compact compared to the reported trapped-rainbow devices. A numerical model utilizing effective parameters is also calculated, whose results are consistent well with the direct numerical simulation of space-coiling structure. Moreover, such device with the capability of dropping different frequency components of a broadband incident temporal acoustic signal into different channels can function as an acoustic wavelength division de-multiplexer. These results may have potential applications in acoustic device design such as an acoustic filter and an artificial cochlea.

For several decades, slow light has attracted much research interest due to its promising applications in optical buffering, optical signal processing, and enhanced interactions between light and matter. The first demonstration of slow electromagnetic waves was carried out in a low-temperature coherent atomic system1. Then the effect of slow light was observed at room-temperature in solid-state medium such as photonic crystals2,3. However, limited by the constraint on the product of delay and bandwidth, high delay corresponds to narrow bandwidth. Thus, achieving wide bandwidth is a great challenge for traditional slow-light systems. Fortunately, researchers put forward the concept of rainbow trapping4,5,6, where wide bandwidth of electromagnetic waves can be trapped in a waveguide taper5 composed of negative-refractive-index (NRI) cores and dielectric claddings, and light of different frequencies can be slowed down at different positions of the waveguide. Moreover, various kinds of structures to realize rainbow trapping are designed including plasmonic grating structures4,6,7,8, insulator-NRI-insulator5,9, insulator-metal-insulator10, and metal-insulator-metal11,12 waveguide tapers. More recently, large-area rainbow trapping13,14 with broadband absorption is realized by using patterned hyperbolic metamaterial waveguide taper arrays15 consisted of multilayered metal/dielectric thin films.

In the acoustic counterpart, slow sound is also an interesting topic with potential applications16 in gas sensing, enhanced nonlinear effects, and applications requiring high sound intensity. Several structures have been suggested to obtain slow sound, including periodically corrugated rigid wire17, waveguide composed of alternatively-stacked cylindrical tubes18, phoxonic waveguide with air holes drilled on silicon membrane19. Recently, inspired by the concept of rainbow trapping, researchers20 experimentally demonstrated a novel anisotropic metamaterial that can effectively trap the broadband acoustic waves and spatially split different frequency components.

Miniaturization and integration are the developing trends of acoustic devices. To satisfy the needs of reducing the size of the device, high refractive-index acoustic medium is desired. But as to acoustic waves propagating in air, it is difficult to find a natural material with acoustic refractive-index higher than that of air. One solution is to use gases with optimized density and pressure, reducing the sound speed and increasing the acoustic refractive-index. However, this method adds complexity to the fabrication process because of the difficulty of the gas density manipulation and the gas diffusion. Therefore, it is more feasible by using artificial acoustic materials, including sonic crystals21,22,23 and acoustic metamaterials24,25,26,27 with exotic effective acoustic parameters28,29 and fantastic properties such as collimation30,31, subwavelength imaging32,33, one-way transmission34,35,36, and extraordinary transmission37,38,39. One promising candidate for high refractive-index acoustic metamaterials is space-coiling metamaterials40,41,42,43, which was first proposed theoretically by Liang and Li41. In the space-coiling metamaterials, acoustic waves are forced to travel in the channel system, obviously increasing the total propagation time, and therefore leading to a low sound velocity and a high refractive-index. Two-dimensional42,43 and three-dimensional44 versions of experiments were also carried out to verify the practical feasibility of this space-coiling metamaterials and are consistent well with the theoretical predictions.

In this work, we use space-coiling metamaterials to realize acoustic rainbow trapping, and to spatially distinguish different frequency components. Due to the high refractive-index of the space-coiling metamaterials, the size of this device is much more compact than the previous design without using subwavelength space-coiling units. A simplified model with effective refractive-index for the space-coiling structures is also developed. Results calculated from the model are consistent well with the space-coiling structures, which verify the validity of the high refractive-index model. Moreover, a time-dependent signal containing broadband multiple frequency components is incident onto this device. By comparing the pressure amplitude of the detected signal at the bottom of each channel of the device, we effectively analyzed the frequency components that are contained in the input signal. In addition, the calculated transmission spectrum suggests that this device can possibly be used as an acoustic filter for some special applications.

Results

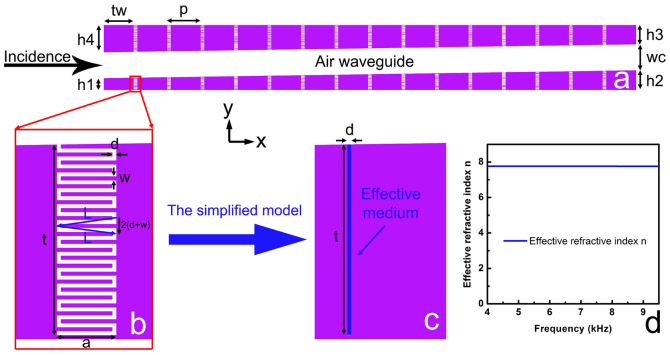
As shown in figure 1(a), the two-dimensional acoustic metamaterial to realize rainbow trapping is composed of a periodic array of space-coiling units with linearly increased depths attached to an oblique air waveguide. The oblique air waveguide is a parallelogram slit that cuts through a rectangular steel bar, whose structural parameters are h1 = 1.180 mm, h2 = 1.975 mm, h3 = 1.930 mm, h4 = 2.725 mm, wc = 2.620 mm. The distance between the adjacent space-coiling units is p = 3.375 mm, and the thickness of the steel wall between them is tw = 3.000 mm, both of which are much smaller than the operation wavelength ranging from 36.1 mm to 85.8 mm. An enlarged view of one space-coiling unit (width a = 0.375 mm and depth t = 1.200 mm) is shown in figure 1(b), with identical thin steel plate (width w = 0.025 mm) inserted in air, forming the coiling air channel (width d = 0.025 mm). The acoustic pressure waves can propagate freely in the air channel without a cut-off frequency due to the longitudinal property of acoustic waves. In other words, low-frequency acoustic waves approximately travel along the zigzag path denoted by the blue arrows shown in figure 1(b). It is foreseen that the effective refractive-index is relatively high, since the propagation time from the top inlet to the bottom is delayed by coiling up space. The effective refractive-index could be estimated by calculating the coiling factor determined by the following formula F = 2L/(2(d + w)) ≈ 7.57, i. e. the length of the zigzag path 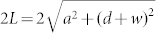Inline graphic divided by the corresponding depth 2(d + w) (figure 1(b)). With the coiling factor, we can model the space-coiling structure with an effective medium, shown in figure 1(c). The blue region represents the straight channel of the same width d and depth t, filled with an effective medium of high refractive-index n, and the purple region stands for steel. The effective refractive index n of the effective medium is nearly non-dispersive in the operation frequency range as shown in figure 1(d).

Figure 1.

Figure 1

Open in a new tab

(a) The illustration of the trapped-rainbow device, containing an oblique air waveguide attached with 30 space-coiling units of different depth. The acoustic wave is incident along x direction from the left side. (b) The zoomed-in illustration of the bottom-left space-coiling unit. The blue arrows show the effective propagation path of the acoustic waves inside the space-coiling unit. (c) The simplified model with effective medium, calculated to compare with the results obtained by the space-coiling structures. (d) The frequency dependence of the effective refractive index n of the effective medium.

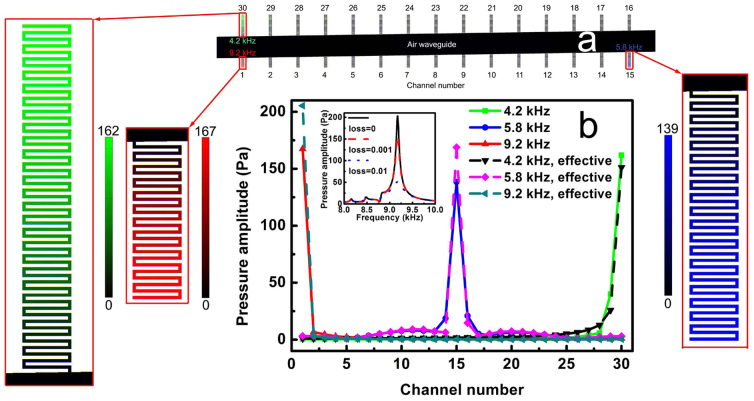
The field distributions for incident sound at three different frequencies (4.2 kHz, 5.8 kHz, 9.2 kHz) are shown in figure 2(a), where the wave at the highest frequency (9.2 kHz) is confined in the unit with the shortest channel depth, and the wave at middle frequency (5.8 kHz) propagates along the waveguide until it meets the 15th unit with longer channels. The wave at the lowest frequency (4.2 kHz) is trapped in the 30th unit, whose channel depth is the longest. The pressure amplitudes in each unit for incident waves at different frequencies are plotted in figure 2(b). Also plotted is the result for the same structure but the space-coiling units are replaced by their effective models (as shown in figure 1(c)) with the effective refractive index n = 7.74. Two groups of results overlap with each other. These results reveal that the different frequency components of a broadband incident acoustic wave can be spatially distinguished at different trapping positions, which is similar to the effect of optical “trapped rainbow”. To study how the thermo-viscous losses will influence the device performance, we introduce loss into the wave number 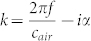Inline graphic, where f is the frequency, cair is the sound speed in air, and α is the attenuation coefficient of our concern. Without loss of the generality, we set the attenuation coefficient to be 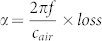Inline graphic, where loss is independent of the frequency. The inset of figure 2(b) shows the frequency dependence of the pressure amplitude at the bottom of channel 1 with different loss. It can be seen that loss will influence the pressure amplitude but the resonance frequency shift is not obvious.

Figure 2.

Figure 2

Open in a new tab

(a) The pressure amplitude distributions in the air region of the space-coiling structure when the acoustic waves of specific frequencies 4.2 kHz, 5.8 kHz, and 9.2 kHz are incident respectively. Color from green (blue, red) to black indicates pressure amplitude with unit of Pa from maximum value to zero for the frequency of 4.2 kHz (5.8 kHz, 9.2 kHz). Each of the 30 channels is labeled with a channel number. The insets show the zoomed-in field distributions inside the channels. (b) The pressure amplitude distribution at the bottom of each channel for the space-coiling structure and the effective structure (the structure shown in figure 1(c), denoted as “effective”). The inset shows the frequency dependence of the pressure amplitude at the bottom of channel 1 with different loss for sound propagation in air. The incident pressure amplitude is 1 Pa.

In order to illustrate the frequency-associated spatial dispersion effects, the position-dependent acoustic wave propagation along the waveguide is also demonstrated by the pressure amplitude distributions at the bottom of each channel shown in figure 3(a) with the excitation frequency ranging from 4 kHz to 9.5 kHz. The different frequency components gradually come to a stop, and are confined in the regions with different channel depth leading to enhanced pressure fields inside the channel. With the pressure amplitude of the incident sound to be 1 Pa, the maximum amplitude obtained at the bottom of the trapping channel is about 200 times larger than the incident amplitude. This result also agrees well with the effective model shown in figure 3(b).

Figure 3.

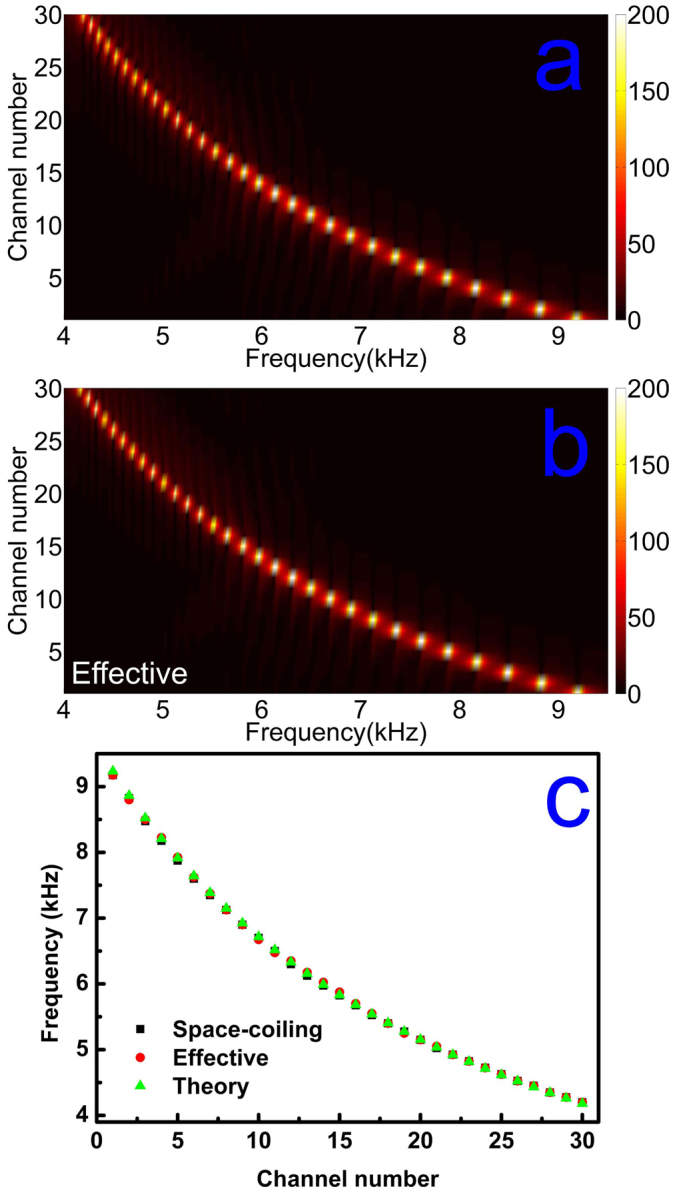
Figure 3

Open in a new tab

The pressure amplitude distributions at the bottom of each channel with changing frequencies of incident sound for (a) the space-coiling structure and (b) the effective structure. The incident pressure amplitude is 1 Pa. (c) The resonance frequency of each channel obtained by the simulation of the space-coiling structure (black square), the simulation of the effective structure (red circle), and the theoretical quarter-wavelength model (green triangle).

To explain the position-frequency relationship shown in figures 3(a) and 3(b), each channel with the channel number N can be effectively considered as a quarter-wavelength resonator, with tN = λ/4 describing the relationship between the channel depth tN and the sound wavelength λ. Since the channel depth tN and the channel number N satisfy the relation: tN = (N + 23) × (d + w), the trapping position can be expressed as a function of the sound frequency 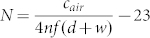Inline graphic, where f is the frequency of the incident sound. This equation can precisely predict the trapping position of the different frequency components, with detailed comparison illustrated in figure 3(c).

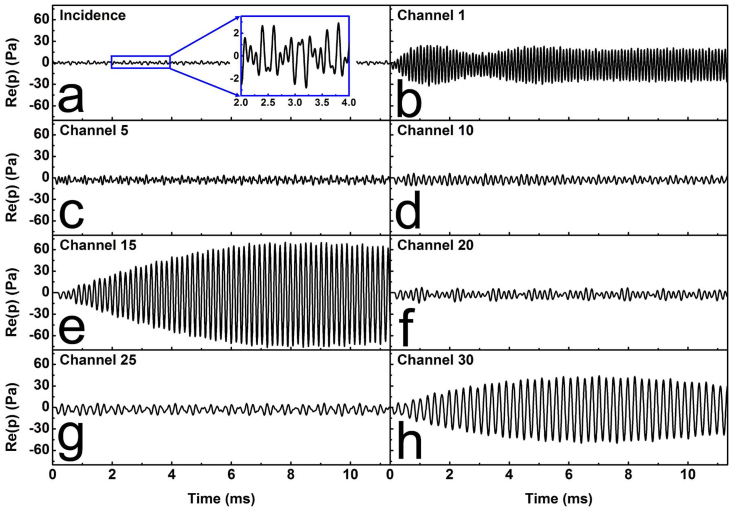
To demonstrate the working mechanism of this device for spatially distinguished frequency components, we use time-dependent signals to excite this device and observe the received signals at the bottom of each channel. The pressure signal is incident from the left entrance of the device. The time-dependent signal comprises three different frequency components and is expressed as ei 2πt × 4.2 kHz + ei 2πt × 5.8 kHz + ei 2πt × 9.2 kHz, whose real part is shown in figure 4(a). The received signal at the bottom of each channel is detected to demonstrate how the different frequency components are distinguished. Although there are 30 channels in this device, only 7 representative channels are selected to demonstrate the detected signal for the sake of concision and clarity of the figure. Figures 4(b) –4(h) represent channel 1, 5, 10, 15, 20, 25 and 30 respectively. It is discovered that, the detected signals are obviously enhanced in channels 1, 15 and 30, because the resonance frequencies of these channels (9.2 kHz, 5.8 kHz, and 4.2 kHz) are included in the incident signal. In contrast, the detected signals in the other channels (channel 5, 10, 20 and 25) are much weaker with the amplitudes only about one tenth of the enhanced ones. Therefore, by detecting the amplitudes of the received signals in different channels, the frequency components of the incident signal can be clearly estimated.

Figure 4.

Figure 4

Open in a new tab

(a) The time-dependent incident pressure signal containing simultaneously three specific frequencies 4.2 kHz, 5.8 kHz, and 9.2 kHz. The inset shows the zoomed-in incident signal. (b–h) The detected pressure signal at the bottom of seven representative channels for the space-coiling structure. The obvious enhancement of the pressure signal amplitude is noticed in channel 1, 15 and 30.

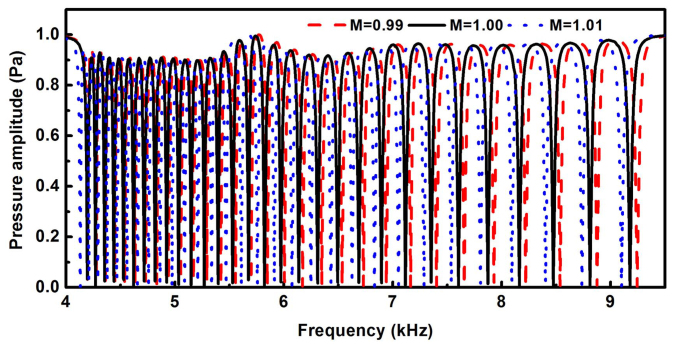
In addition to spatially distinguish different frequency components, this device can also be considered as an acoustic filter of some specific frequencies if the pressure transmission at the output end is concerned. After propagating along the waveguide attached with several resonance channels, certain parts of the incident acoustic wave are trapped in the resonating units and can be dropped from this trapping channel. Those trapped frequency components will disappear in the output acoustic waves. The filtering performance of the device studied earlier can be clearly demonstrated by calculating the transmission pressure amplitude at the outlet of the waveguide. The transmission spectrum in the frequency range from 4 kHz to 9.5 kHz is shown as the black solid line in figure 5, where 30 high-quality-factor resonance dips are clearly observed, in exact accordance with the trapped frequencies or the resonance frequencies of the 30 different channels. These channels with deep resonance dips could effectively prevent the propagation of specific-frequency sound waves. However, since there are also transmission windows between neighboring resonance dips, this device is designed to work at specific frequencies for real applications. In addition, several devices with the same mechanism but different structural parameters can be combined appropriately to provide resonance dips with slightly different frequencies, resulting in a much wider filtering frequency range. So this is the potential utilization of the acoustic trapped-rainbow device in the fields of the frequency-filtering application. Moreover, mechanically changing the device size may significantly modify the acoustic trapping and frequency multiplexing properties, which could make this device be implemented as an active metamaterial device. Therefore, the mechanical transformation coefficient M is introduced to represent that after the mechanical transformation all the dimensions in the x direction (such as a, p in figure 1) are multiplied by M and all the dimensions in the y direction (such as wc, t in figure 1) are divided by M to keep the volume constant. The transmission spectrum of the trapped-rainbow device with different mechanical transformation coefficient M is shown in figure 5. From this result it is found that in the case of M > 1 the frequency of the resonance dip is moved to the lower frequency due to longer air channels while in the case of M < 1 the resonance frequency shifts to the higher frequency because of shorter channels. The mechanical transformations enable such kind of devices to be tunable.

Figure 5. The transmission spectrum of the trapped-rainbow device with different mechanical transformation coefficient M.

Figure 5

Open in a new tab

The pressure amplitude is recorded at the output end of the device.The incident pressure amplitude is 1 Pa.

Discussion

In summary, we have realized the acoustic rainbow trapping effect by tapping an air waveguide with space-coiling units. The different resonant properties of the spatially distributed space-coiling units can exhibit an effective spatial dispersion similar to that of a meta-surface45. Unlike the reported design discussed in the reference20, using the high refractive-index space-coiling units reduces the physical depth of each channel of the device and makes the device much more compact. A numerical model utilizing the effective refractive-index instead of space-coiling structures is proposed to study such waveguide devices, and it is discovered that the results obtained from the model consist well with the direct numerical simulation of the space-coiling structures. Such device with the capability of dropping different frequency components of a broadband incident temporal acoustic signal into different channels can function as an acoustic wavelength division de-multiplexer. Our work might inspire unique acoustic device designs, such as artificial cochlea and acoustic filters.

Methods

Throughout this paper, numerical simulations are carried out by the finite element method supported by COMSOL Multiphysics. In the numerical simulations, the acoustic waves are incident from the left side along x direction shown in figure 1(a), with the pressure amplitude of 1 Pa. The material parameters used in the numerical simulations are mass density of air ρair = 1.25 kg/m3, sound velocity in air cair = 343 m/s, mass density of steel ρsteel = 7800 kg/m3, Young's modulus of steel Esteel = 209 GPa, and Poisson's ratio of steel vsteel = 0.292. In the air region, the frequency-domain Helmholtz equation for sound pressure is solved, while in the steel region the equation of structural mechanics for harmonic stresses and strains is solved. Since we are interested in the pressure field in the air region, the results of stresses and strains in the steel region are not demonstrated in the figures.

Author Contributions

X.N. carried out the numerical simulations and theoretical analysis. Z.G.C., L.Y.Z., Y.L.X. and X.P.L. contributed in the discussion of theoretical analysis. M.H.L. and Y.F.C. conceived and supervised the study. X.N., Y.W., P.N. and M.H.L. wrote the paper.

Acknowledgments

The work was jointly supported by the National Basic Research Program of China (Grant No. 2012CB921503 and No. 2013CB632702) and the National Nature Science Foundation of China (Grant No. 1134006, No. 11474158, and No. 11404164). We also acknowledge the support from Academic Program Development of Jiangsu Higher Education (PAPD) and the support from the Fundamental Research Funds for the Central Universities.

References

  1. Liu C., Dutton Z., Behroozi C. H. & Hau L. V. Observation of coherent optical information storage in an atomic medium using halted light pulses. Nature 409, 490–493 (2001). [DOI] [PubMed] [Google Scholar]
  2. Vlasov Y. A., O'Boyle M., Hamann H. F. & McNab S. J. Active control of slow light on a chip with photonic crystal waveguides. Nature 438, 65–69 (2005). [DOI] [PubMed] [Google Scholar]
  3. Gersen H. et al. Real-space observation of ultraslow light in photonic crystal waveguides. Phys. Rev. Lett. 94, 073903 (2005). [DOI] [PubMed] [Google Scholar]
  4. Gan Q., Ding Y. J. & Bartoli F. J. “Rainbow” trapping and releasing at telecommunication wavelengths. Phys. Rev. Lett. 102, 056801 (2009). [DOI] [PubMed] [Google Scholar]
  5. Tsakmakidis K. L., Boardman A. D. & Hess O. ‘Trapped rainbow' storage of light in metamaterials. Nature 450, 397–401 (2007). [DOI] [PubMed] [Google Scholar]
  6. Gan Q., Fu Z., Ding Y. J. & Bartoli F. J. Ultrawide-bandwidth slow-light system based on THz plasmonic graded metallic grating structures. Phys. Rev. Lett. 100, 256803 (2008). [DOI] [PubMed] [Google Scholar]
  7. Gan Q. et al. Experimental verification of the rainbow trapping effect in adiabatic plasmonic gratings. Proc. Natl. Acad. Sci. 108, 5169–5173 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Gan Q. & Bartoli F. J. Surface dispersion engineering of planar plasmonic chirped grating for complete visible rainbow trapping. Appl. Phys. Lett. 98, 251103 (2011). [Google Scholar]
  9. He S., He Y. & Jin Y. Revealing the truth about ‘trapped rainbow' storage of light in metamaterials. Sci. Rep. 2, 583; 10.1038/srep00583 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Park J. et al. Trapping light in plasmonic waveguides. Opt. Express 18, 598–623; 10.1364/OE.18.000598 (2010). [DOI] [PubMed] [Google Scholar]
  11. Jang M. S. & Atwater H. Plasmonic rainbow trapping structures for light localization and spectrum splitting. Phys. Rev. Lett. 107, 207401 (2011). [DOI] [PubMed] [Google Scholar]
  12. Chen Y., Gu J., Xie X. C. & Zhang W. Trapping and releasing light by mechanical implementation in metamaterial waveguides. J. Opt. Soc. Am. A 28, 272–277 (2011). [DOI] [PubMed] [Google Scholar]
  13. Hu H., Ji D., Zeng X., Liu K. & Gan Q. Rainbow trapping in hyperbolic metamaterial waveguide. Sci. Rep. 3, 1249; 10.1038/srep01249 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Ji D. et al. Broadband absorption engineering of hyperbolic metafilm patterns. Sci. Rep. 4, 4498; 10.1038/srep04498 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Cui Y. et al. Ultrabroadband light absorption by a sawtooth anisotropic metamaterial slab. Nano Lett. 12, 1443–1447 (2012). [DOI] [PubMed] [Google Scholar]
  16. Krauss T. F. Why do we need slow light? Nature Photon. 2, 448–450 (2008). [Google Scholar]
  17. Christensen J., Huidobro P. A., Martin-Moreno L. & Garcia-Vidal F. J. Confining and slowing airborne sound with a corrugated metawire. Appl. Phys. Lett. 93, 083502 (2008). [Google Scholar]
  18. Robertson W. M., Baker C. & Bennett C. B. Slow group velocity propagation of sound via defect coupling in a one-dimensional acoustic band gap array. Am. J. Phys. 72, 255–257 (2004). [Google Scholar]
  19. Laude V. et al. Simultaneous guidance of slow photons and slow acoustic phonons in silicon phoxonic crystal slabs. Opt. Express 19, 9690–9698; 10.1364/OE.19.009690 (2011). [DOI] [PubMed] [Google Scholar]
  20. Zhu J. et al. Acoustic rainbow trapping. Sci. Rep. 3, 1728; 10.1038/srep01728 (2013). [Google Scholar]
  21. Torrent D. & Sanchez-Dehesa J. Acoustic analogue of graphene: observation of Dirac cones in acoustic surface waves. Phys. Rev. Lett. 108, 174301 (2012). [DOI] [PubMed] [Google Scholar]
  22. Liu Z. et al. Locally resonant sonic materials. Science 289, 1734–1736 (2000). [DOI] [PubMed] [Google Scholar]
  23. Liu F., Huang X. & Chan C. T. Dirac cones at k = 0 in acoustic crystals and zero refractive index acoustic materials. Appl. Phys. Lett. 100, 071911 (2012). [Google Scholar]
  24. Christensen J. & Garcia de Abajo F. J. Anisotropic metamaterials for full control of acoustic waves. Phys. Rev. Lett. 108, 124301 (2012). [DOI] [PubMed] [Google Scholar]
  25. Zhang S., Xia C. & Fang N. Broadband acoustic cloak for ultrasound waves. Phys. Rev. Lett. 106, 024301 (2011). [DOI] [PubMed] [Google Scholar]
  26. Mei J. et al. Dark acoustic metamaterials as super absorbers for low-frequency sound. Nat. Commun. 3, 756; 10.1038/ncomms1758 (2012). [DOI] [PubMed] [Google Scholar]
  27. Lai Y., Wu Y., Sheng P. & Zhang Z. Q. Hybrid elastic solids. Nat. Mater. 10, 620–624 (2011). [DOI] [PubMed] [Google Scholar]
  28. Wu Y., Lai Y. & Zhang Z. Q. Elastic metamaterials with simultaneously negative effective shear modulus and mass density. Phys. Rev. Lett. 107, 105506 (2011). [DOI] [PubMed] [Google Scholar]
  29. Fang N. et al. Ultrasonic metamaterials with negative modulus. Nat. Mater. 5, 452–456 (2006). [DOI] [PubMed] [Google Scholar]
  30. Christensen J., Fernandez-Dominguez A. I., de Leon-Perez F., Martin-Moreno L. & Garcia-Vidal F. J. Collimation of sound assisted by acoustic surface waves. Nature Phys. 3, 851–852 (2007). [Google Scholar]
  31. Quan L., Zhong X., Liu X., Gong X. & Johnson P. A. Effective impedance boundary optimization and its contribution to dipole radiation and radiation pattern control. Nat. Commun. 5, 3188; 10.1038/ncomms4188 (2014). [DOI] [PubMed] [Google Scholar]
  32. Zhu J. et al. A holey-structured metamaterial for acoustic deep-subwavelength imaging. Nature Phys. 7, 52–55 (2011). [Google Scholar]
  33. Li J., Fok L., Yin X., Bartal G. & Zhang X. Experimental demonstration of an acoustic magnifying hyperlens. Nat. Mater. 8, 931–934 (2009). [DOI] [PubMed] [Google Scholar]
  34. Liang B., Guo X. S., Tu J., Zhang D. & Cheng J. C. An acoustic rectifier. Nat. Mater. 9, 989–992 (2010). [DOI] [PubMed] [Google Scholar]
  35. Fleury R., Sounas D. L., Sieck C. F., Haberman M. R. & Alu A. Sound isolation and giant linear nonreciprocity in a compact acoustic circulator. Science 343, 516–519 (2014). [DOI] [PubMed] [Google Scholar]
  36. Li X. F. et al. Tunable unidirectional sound propagation through a sonic-crystal-based acoustic diode. Phys. Rev. Lett. 106, 084301 (2011). [DOI] [PubMed] [Google Scholar]
  37. He Z. et al. Acoustic transmission enhancement through a periodically structured stiff plate without any opening. Phys. Rev. Lett. 105, 074301 (2010). [DOI] [PubMed] [Google Scholar]
  38. Estrada H. et al. Angle-dependent ultrasonic transmission through plates with subwavelength hole arrays. Phys. Rev. Lett. 102, 144301 (2009). [DOI] [PubMed] [Google Scholar]
  39. Park J. J., Lee K. J. B., Wright O. B., Jung M. K. & Lee S. H. Giant Acoustic Concentration by Extraordinary Transmission in Zero-Mass Metamaterials. Phys. Rev. Lett. 110, 244302 (2013). [DOI] [PubMed] [Google Scholar]
  40. Li Y., Liang B., Zou X. & Cheng J. Extraordinary acoustic transmission through ultrathin acoustic metamaterials by coiling up space. Appl. Phys. Lett. 103, 063509 (2013). [Google Scholar]
  41. Liang Z. & Li J. Extreme acoustic metamaterial by coiling up space. Phys. Rev. Lett. 108, 114301 (2012). [DOI] [PubMed] [Google Scholar]
  42. Xie Y., Popa B. I., Zigoneanu L. & Cummer S. A. Measurement of a broadband negative index with space-coiling acoustic metamaterials. Phys. Rev. Lett. 110, 175501 (2013). [DOI] [PubMed] [Google Scholar]
  43. Liang Z. et al. Space-coiling metamaterials with double negativity and conical dispersion. Sci. Rep. 3, 1614; 10.1038/srep01614 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Jones N. Three-dimensional printers are opening up new worlds to research. Nature 487, 22–23 (2012).22763531 [Google Scholar]
  45. Ma G., Yang M., Xiao S., Yang Z. & Sheng P. Acoustic metasurface with hybrid resonances. Nat. Mater. 13, 873–878 (2014). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES