Optimizing the Selectivity of Surface-Adsorbing Multivalent Polymers

Abstract

Multivalent polymers are macromolecules containing multiple chemical moieties designed to bind to complementary moieties on a target; for example, a protein with multiple ligands that have affinity for receptors on a cell surface. Though the individual ligand–receptor bonds are often weak, the combinatorial entropy associated with the different possible ligand–receptor pairs leads to a binding transition that can be very sharp with respect to control parameters, such as temperature or surface receptor concentration. We use mean-field self-consistent field theory to study the binding selectivity of multivalent polymers to receptor-coated surfaces. Polymers that have their ligands clustered into a contiguous domain, either located at the chain end or chain midsection, exhibit cooperative surface adsorption and superselectivity when the polymer concentration is low. On the other hand, when the ligands are uniformly spaced along the chain backbone, selectivity is substantially reduced due to the lack of binding cooperativity and due to crowding of the surface by the inert polymer segments in the chain backbone.

Introduction

Multivalent interactions between two objects are mediated by several moieties (henceforth referred to as “ligands” and “receptors”) that, individually, bind more weakly than a monovalent ligand–receptor pair with the same overall binding strength. Multivalent interactions are exquisitely sensitive to control parameters, such as the temperature, the strength of the ligand–receptor interactions that affect the binding free energy, and to the surface density of receptors: the number of multivalent species bound to a target may increase (much) faster than linearly with the surface density of receptors on the target.¹ We refer to this behavior as superselectivity. The existence of superselectivity makes multivalency a useful design tool to discriminate between target surfaces with different receptor densities.² In contrast, the selectivity of (monovalent) Langmuir surface adsorption can never exceed 1, as the number of bound (monovalent) particles can increase at most linearly with the density of surface binding sites.

Living organisms have evolved to exploit multivalency. For example, proteins are synthesized with multiple binding sites that enable superselective binding to receptors on cell surfaces, and viruses adhere to cell surfaces via multivalent interactions.² By comparison, the utilization of multivalency in the design of sensitive self-assembling materials is still in its infancy. One area where multivalency has been exploited is the design of DNA-coated colloids: over the past two decades a combination of experimental and theoretical work has yielded promising results for self-assembling DNA-coated colloids.³⁻⁸ In these systems, complementary single-stranded DNA is grafted to the surfaces of nanoparticles, resulting in a colloidal system that self-assembles over a narrow temperature range into aggregate structures “encoded” within the DNA ligands.

Polymers constitute another class of materials that can exhibit multivalency.⁹ Multivalent polymers play an active role in biological processes and have been considered for applications in therapeutics.^10,11 For example, recent experimental work has been done to examine the binding selectivity of hyaluronic acid, a primary (multivalent) component of the extracellular matrix of cells, to ferrocene ligands on a surface.¹² The experiment, complemented by an analytical theory, indicates selectivities larger than those obtained for multivalent nanoparticles.¹² Similar complementary ligand–receptor interactions have also been used to design a polymer material that exhibits selective surface interactions with a target substrate.¹³

The binding units on polymers, in contrast to those grafted to nanoparticles, have a greater degree of spatial freedom; a binding unit located on one portion of a long polymer may translate almost independently of another located at a different point on the chain simply by changes in the local conformation of the chain. Such mobility is not possible for binding units grafted onto the (solid) surfaces of nanoparticles. In addition, polymers may overlap and interpenetrate, thereby binding to essentially the same region of the receptor-coated surface. On the other hand, binding of a multivalent nanoparticle to a surface excludes that volume from binding by other entities above the surface. These two observations suggest a larger binding entropy for a multivalent polymer, compared to a solid multivalent particle.¹²

In an approximate sense, a multivalent polymer may be imagined as an A/B copolymer in which surface-active A segments are copolymerized into a particular chain sequence, or “architecture”, along with inactive B segments. A broad body of research has investigated the behavior of surface-segregating copolymers of a variety of different architectures; many of these studies suggest that the arrangement of surface-binding functional groups along a polymer chain backbone affects the binding enthalpy and entropy, leading to significant differences in adsorption statistics and local composition near an adsorbing surface.¹³⁻²⁸

In this paper, we examine how to optimize the surface binding selectivity of multivalent polymer chains by tuning the number of binding segments, or “linkers”, on the polymer, as well as their arrangement along the chain. Polymer self-consistent field theory (SCFT) is the primary tool used to perform this study. In the course of examining different chain architectures, we take a detailed microscopic look at the conformations of chains when they bind to a surface, and compare to existing studies on copolymer surface adsorption. From this, we elucidate the enthalpic and entropic ingredients that most strongly influence the adsorption selectivity of different chain architectures.

This paper is organized as follows. In the first section, we develop a mean-field self-consistent field lattice model by which we may study the equilibrium statistics of polymers adsorbed to a surface. Following that, we examine numerical SCFT results for chains with different ligand arrangements. In particular, we observe how binding selectivity changes as the number of segments per chain containing ligands increases, and as the polymer concentration changes. Moreover, we find that surface crowding leads to a reduction in binding selectivity. In the final section, we summarize our results and offer concluding remarks.

Self-Consistent Mean-Field Lattice Model

In this section, a statistical-mechanical model is developed to study the binding of polymers in solution to a surface via complementary ligand–receptor interactions. Of prime interest is how the conformations of the polymers change when their ligands bind to receptors on the surface. The model allows us to examine these conformational changes as a function of different spatial arrangements of ligands along the chain backbone, the number of receptors on the surface, and the ligand–receptor binding strength.

The polymer and solvent species may adopt different spatial configurations, each of which has a different Boltzmann weight determined by the number and arrangement of the polymer ligands bound to receptors on the surface. The self-consistent field theory (SCFT) lattice model for polymers originally developed by Scheutjens and Fleer provides a convenient framework in which the partition function for polymers in contact with an adsorbing surface may be numerically computed.^29,30 The model we develop here is similar to the mean-field SCFT lattice models employed to study copolymers and functionalized polymers at free and adsorbing surfaces.^{14,15,20,24,25,27}

An important approximation in the model is that multibody interactions between species in the system are decoupled into independent (one-body) interactions between the species and mean fields. The mean fields are computed self-consistently, in which case the (approximate) partition function of the system can be computed directly.

By decoupling interactions, each polymer chain interacts only with mean fields representing the sum of all interactions from adjacent polymers (and solvent) in the system. Thus, every chain in the system is statistically identical, and the problem of computing a partition function for polymers with multibody interactions reduces to the task of computing a single-chain partition function Q_pol in the presence of the mean fields. In the following two sections we describe the mathematical route to obtaining Q_pol in the context of the Scheutjens–Fleer lattice model.

Parameters

To describe the adsorption of polymers to a receptor-functionalized surface, we use a three-dimensional simple cubic lattice model, consisting of L layers, indexed by k = 1 to L. Each layer contains M lattice sites, and hence ML is equal to the total number of sites in the lattice. The system has two boundary conditions, located at k = 0 and k = L + 1. At k = 0, an “absorbing” boundary condition is implemented, which emulates a solid surface; this boundary is the adsorbing surface in the system. Conversely, an open, or “reflecting”, boundary condition is implemented at layer k = L + 1. The mathematical implementation of each boundary condition will be elaborated upon shortly. Note that the lattice is periodic in the two dimensions orthogonal to k.

The system is in contact with a reservoir at fixed polymer chemical potential, corresponding to a fixed polymer segment volume fraction of ϕ_pol^° in the reservoir. The system is defined as being in equilibrium with the reservoir when the polymer segment volume fraction far from the adsorbing surface is equal to ϕ_pol.

For a given choice of ϕ_pol^° in the reservoir, the system at equilibrium contains N_pol,eq polymer chains. Throughout, we will consider the case of identical polymer chains, comprised of N_t Kuhn segments (indexed by t = 1 to N_t). The linear dimensions of one lattice cell are taken to be equal to the length of one polymer Kuhn segment. The equilibrium average volume fraction ϕ_pol,eq of polymer segments in the system is related to N_pol,eq through

The remaining lattice sites not occupied by polymer segments are occupied by solvent segments.

Next we must specify: (1) the specific arrangement of ligands along the polymer chain, (2) the density of polymer-binding receptors on the system’s surface, and (3) the effective binding strength between the surface and the polymer-bound ligands.

To implement ligands along the polymer chain, we designate a subset of segments {t}_l along each of the chains as “linker” segments. In a given system, all chains have the same {t}_l distribution. A linker segment contains one ligand, capable of binding to receptors on the surface. The remaining “inert” (nonlinker) segments contain no ligands.

The surface onto which the polymers adsorb is assumed to be covered uniformly with N_rec receptors per lattice site. Each surface site can hold at most N_rec,max receptors; the quantity f = N_rec/N_rec,max thus describes the fraction of the surface occupied by receptors.

When a linker segment is located adjacent to the surface, i.e. located at layer k = 1, then its ligand may form a bond with any one of the N_rec receptors in that surface site. Details of the ligand–receptor binding statistics are presented in Appendix A. These binding statistics are collected into a single effective binding free energy βF̅ between a linker Kuhn segment and the surface. On the basis of the calculations in Appendix A, the effective linker-surface binding free energy is related to the pure ligand–receptor binding energy ε and the receptor fraction f by

1

The quantity

2

is similar to that used in Martinez et al.;¹ it is a convenient parameter containing both f and ε. As only γ appears in our theoretical description, there is no need to specify f and ε separately. We refer to γ as the “surface binding parameter”.

Mathematical Formulation

The parameters in our model then are the volume fraction ϕ_pol^° of polymer segments in the reservoir (i.e., in the bulk of the system, far from the surface); the distribution {t}_l of linker segments along the contour length of the polymer species; and the linker-surface binding parameter, γ. We now apply the standard tools of the Scheutjens–Fleer approach to compute the single-chain partition function, Q_pol, for a system with a given set of these parameters.

The Scheutjens–Fleer model employs chain propagators biased by mean fields in order to compute the Boltzmann weights for polymer configurations. The polymer species is represented by two independent propagators P_pol,1(k,i) and P_pol,2(k,i), each tracing the trajectory of the chain starting from one of its two termini. The quantity P_x(k,i) represents the probability that propagator x is located at layer k on step i. The propagator array P_x(k,i) is computed recursively by

3

where

is the mapping between propagator step i and chain segment t. We see two contributions to the probability P_x(k,i). The first is the probability that the propagator was located in an adjacent layer on the previous step P_x(k ± 1,i – 1) times the probability that it has diffused to layer k (which for a simple cubic lattice is 1/6 for the two layers adjacent to k). The second is the probability (4/6) × P_x(k,i – 1) that the propagator has remained in the current layer since the last step. The propagator equation for the solvent is simply

4

given that it is only one segment in length.

The Boltzmann weights exp(−V(k)), exp(−W_pol(k,t(i))), and exp(−W_sol(k)) in eqs 3 and 4 incorporate the interactions of the propagators with two mean fields in the system. The fields W_pol(k,t(i)) and W_sol(k) represent the surface interaction mean field, taking explicit forms for the polymer and solvent propagators of

5

where δ is the Kronecker delta. As shown here, W_pol(k,t(i)) and W_sol(k) only apply to segments located at layer k = 1. The field yields a Boltzmann weight of exp(−βF̅/2) for linker segments located at the surface layer, and a weight of exp(βF̅/2) for inert and solvent segments at that layer. Thus, the change in the free energy of the system when a linker segment swaps positions with an inert or solvent segment at the surface layer is βF̅, which is the binding free energy derived in Appendix A.

The field V(k) plays a role analogous to a hydrostatic pressure; it ensures that the volume fraction of polymer at each layer k is between zero and unity. An analytic form for V(k) is not available a priori, rather it is a function of the equilibrium ensemble of system states given the interaction field W_pol(k,t(i)) (and W_sol(k)), as well as the polymer volume fraction field ϕ_pol(k). Thus, V(k) is computed self-consistently via the method outlined in the next section.

In order to fully compute P_pol,1(k,i) and P_pol,2(k,i), boundary conditions for i = 1, k = 0, and k = L + 1 must be specified. The boundary condition at k = 0 is “absorbing”, where on each step i

The effect of this boundary condition is to remove (or “absorb”) all propagator trajectories that move to k = 0 on step i; that is, any trajectory that uses layer k = 0 as one of its steps i is not included in the equilibrium ensemble of trajectories. At the opposite side of the system, a “reflecting” boundary condition is implemented where

Here, the conditions of the system at layer L are “reflected” to the boundary layer L + 1 on step i, causing the system to see a mirror image of itself at that boundary on step i + 1. Note that we have incorporated a sufficient number of lattice layers (L = 50) such that chains adsorbed to the surface do not see their mirror images across the reflecting boundary, for the regime of surface binding strengths γ we study. The remaining boundary condition is

This condition specifies that propagators begin at each layer k with the Boltzmann weight for placement of segment t = 1 (for P_pol,1) and t = N_t (for P_pol,2) at layer k.

Given the propagator boundary conditions in conjunction with eq 3, the Boltzmann weights for all possible conformations of chains may be obtained by computing P_pol,1, P_pol,2, and P_sol across k for t = 1 through N_t. The composition rule³¹ is used to obtain the sum of Boltzmann weights q_pol(k,t) for conformations that have chain segment t at layer k:

6

The equivalent expression for the solvent is simply

As eq 6 yields the sum of Boltzmann weights for all chain conformations that have their segment t at layer k, then the sum of this quantity over k yields the single-chain partition function for the polymer species:

7

(Note that the value obtained for Q_pol does not depend on the segment t chosen to compute it.) The probability that segment t is located at layer k may then be conveniently obtained by

8

Self-Consistency and Grand-Canonical Equilibrium

Given an explicit choice for the overall polymer volume fraction ϕ_pol = N_polN_t/ML in the system, the canonical equilibrium fraction ϕ_pol(k) of polymer segments at each lattice layer must be computed by determining the bias field V(k). For the case of chains adsorbing to a surface in a solvent, V(k) ∝ ϕ_pol(k);^32,33 this serves as a convenient initial guess for the field. The final form of the field for a given system is obtained by computing ϕ_pol self-consistently. Beginning with an initial guess for the incompressibility field, V(k)_i, as well as an initial guess polymer volume fraction profile ϕ_pol(k)_i, the output volume fraction of polymer at each layer is obtained by an appropriately normalized sum of eq 6 over all segments t,

Similarly, the output volume fraction of solvent at layer k is

where N_sol = ML – N_tN_pol, and the solvent single-particle partition function is

The total volume fraction of material at a given lattice layer is then given by

The conditions for self-consistency of V(k) and ϕ_pol(k) are when

9

and

that is, when the input V(k)_i and ϕ_pol(k)_i yield an output total volume fraction ϕ(k) equal to unity at each k, and an output polymer volume fraction ϕ_pol(k) equal to the input ϕ_pol(k)_i (both to within a small margin of numerical error). When the self-consistent forms of V(k) and ϕ_pol(k) are obtained, then the single-chain partition function Q_pol represents the canonical equilibrium distribution of chain conformations for the given choice of system parameters, and statistics of the chain can be extracted via eq 8.

Grand-canonical equilibrium between the system, and the reservoir with polymer segment volume fraction ϕ_pol^°, is obtained by changing the number of chains N_pol in the system until the ϕ_pol(k) at layers far from the surface are equal to ϕ_pol. The choice of N_pol that yields ϕ_pol(k) = ϕ_pol^° far from the surface is N_pol,eq: the grand-canonical equilibrium number of chains in the system for a given fixed reservoir polymer concentration ϕ_pol. All numerical results presented in the following sections are at grand-canonical equilibrium with the reservoir; thus, we drop the “eq” subscript for readability.

Results and Discussion

To elucidate the effect of the density of surface binding sites on selectivity, we performed SCF calculations for polymers in the grand canonical ensemble. In particular, we study how polymers with different linker sequences bind to the surface, which linker sequences yield the highest selectivity, and how the selectivity is affected by changes in the polymer concentration.

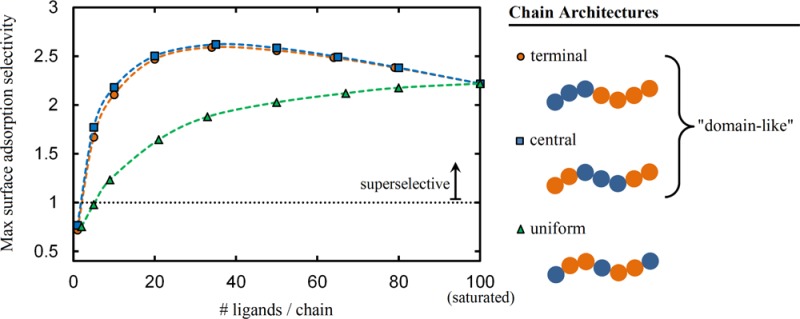
The three linker sequence architectures considered in this study are sketched in Figure 1. In the first architecture, some number of contiguous polymer segments beginning from one side of the chain are linker segments. Polymers of this nature will be referred to as “terminal linkers”. Similarly, the second architecture consists of polymer chains in which some number of contiguous segments in the center of the chain are linkers; these polymers shall be called “central linkers”. In both cases, we refer to the region of the chain containing the contiguous sequence of linker segments as the “linker domain”. The third architecture, “uniform linkers”, is a scenario in which some number of linker segments are placed uniformly along the chain. In all three cases, the number of linker segments in a given chain is given by the parameter N_l. A fourth architecture is also considered in which all polymer segments are linkers—this will be referred to as the “saturated linker”. It represents the limit of all three architectures in which N_l = N_t.

Figure 1.

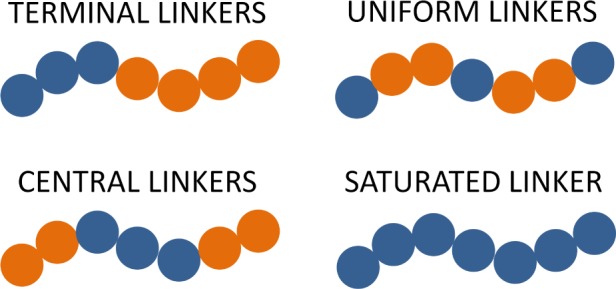
Schematic representations of the three types of linker architectures {t}_l examined in this study, along with the limiting-case “saturated” architecture. Blue (dark) circles represent linker segments, and orange (light) circles represent inert segments.

In all systems studied, polymer chains are comprised of N_t = 100 segments. The system is L = 50 layers in size, and each layer has M = 400 lattice sites, leading to a total system volume of ML = 20 000.

We performed calculations in the grand canonical ensemble, in which the volume fraction ϕ_pol^° of polymer segments in the reservoir is fixed, while that in the system depends on γ. Thus, as γ grows large and chains are drawn to bind to the surface, the effective concentration of chains in the system increases. The two reservoir values of polymer segment volume fraction we study here are ϕ_pol = 0.025 and 0.25.

In order to validate our approach, SCFT results are presented for surface adsorption of monomeric linkers in Appendix B. In that case we have analytical predictions for monomer binding statistics as a function of the mean-field model parameters. We find that the analytical predictions are in exact agreement with the numerical SCFT results.

The first part of our discussion examines the behavior of the surface adsorption profiles for polymers of terminal, central, and uniform linker architectures. The enthalpic and entropic factors driving adsorption of each chain architecture lend insight into their binding selectivities, which is the focus of the second half of the discussion. In particular, it is important to distinguish between the number of polymer chains bound to the surface, compared to the number of surface sites occupied by linkers. We focus on both quantities when evaluating selectivity, though the qualitative behavior of each architecture is the same across both measures.

Terminal and Central Linkers: Domain Cooperativity

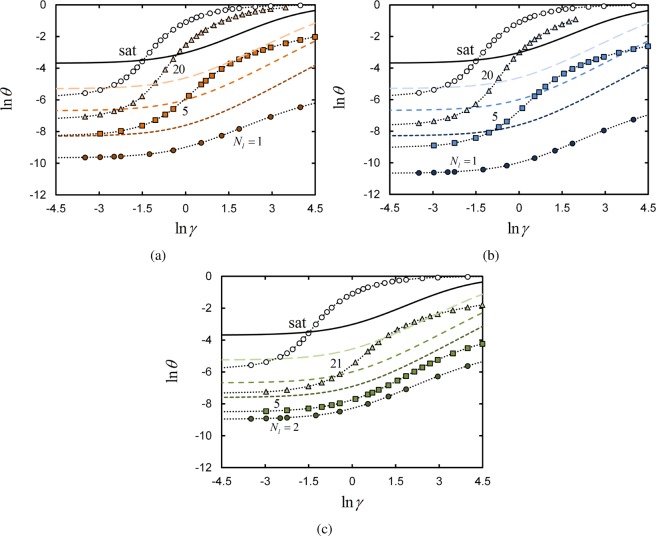
Figure 2a shows surface adsorption profiles of polymers as a function of the effective binding free-energy parameter γ for the terminal linker architecture with different numbers N_l of linker segments. The reservoir polymer segment concentration is ϕ_pol^° = 0.025. For comparison, analytically computed adsorption profiles of monomeric linker segments are shown, having reservoir concentrations of N_lϕ_pol/N_t These calculations represent the idealized scenario in which all linkers are a freely moving lattice gas undergoing Langmuir adsorption onto the surface. The adsorption profile of the saturated linker is also included in the figure.

Figure 2.

Log–log plot of the average fraction θ of occupied surface lattice sites, as a function of surface binding parameter γ for systems with ϕ_pol^° = 0.025. Numerical SCFT results (shaded points connected by dotted fit lines) are shown for the terminal linker (a), central linker (b), and uniform linker (c) architectures. In parts a and b, N_l = 1 (circles), 5 (squares), 20 (triangles), and 100 (open circles); in part c, N_l = 2 (circles), 5 (squares), 21 (triangles), and 100 (open circles). Profiles of monomeric linkers, with reservoir concentrations of N_lϕ_pol/N_t, are computed analytically via the mathematical result from Appendix B. In order of ascending N_l in each image, monomer profiles are plotted as short-dashed, medium-dashed, long-dashed, and solid lines.

We quantify the degree of adsorption by the fraction of lattice sites occupied by linkers at the surface layer (k = 1). The fraction of occupied surface sites is given by θ = M*/M, where M* is the number of surface sites occupied by linker segments. Note that M* is a statistical average over the distribution of conformations present in the system for a given γ.

For context, first consider the factors governing adsorption of monomeric linkers to the surface. The surface binding free energy F̅, determined by the choice of the parameter γ, defines the gain in enthalpy when a linker adsorbs to the surface; this competes with the loss in translational entropy when the segment is restricted to reside in that layer. The inflection point in γ for the adsorption profile occurs when the enthalpy gain upon surface binding (plus the surface translational entropy) is comparable to the chemical potential of the particles in the reservoir. The same observation applies to all subsequent polymeric cases.

Adsorption of polymer chains with one (i.e., N_l = 1) terminal linker can be viewed as a monomeric linker with a tail of N_t – 1 inert segments. A thorough discussion on the adsorption behavior of chains with one terminal binding segment is given by Theodorou.¹⁵ Here, we summarize the behavior of our own SCFT calculations relevant for understanding adsorption selectivity in a subsequent section, while also illustrating how the system self-assembles into a strongly stretched polymer brush as the surface binding free energy grows large.

Polymers with one terminal linker must undergo a conformational change upon binding to the surface; the inert segments reconfigure themselves from a random walk to a brush-like configuration in which the inert monomers extend away from the surface. Thus, there is a (conformational) entropic cost in order to bind the polymer’s lone linker to the surface, necessitating a larger binding free energy γ than required in the monomeric case to achieve the same fraction of bound species. In Figure 2a, this manifests itself as an adsorption profile that is shifted to the right, i.e., to larger γ values, compared to that of the monomeric linker. In addition, at low γ, the fraction of occupied surface sites is lower for the polymer than for the monomer; this is because the probability that the polymer linker segment is located at the surface is lower than that of a free monomer, as the latter does not have the steric constraint of an inert tail.

As the surface binding strength γ grows large, the chain’s terminal linker is drawn to bind to the surface regardless of the entropic cost involved. The result is the formation of a polymer brush, in which chains are “grafted” to the surface by the strong bonds between their linker segments and the surface. This is shown in Figure 3, where profiles of polymer volume fraction ϕ_pol(k) as a function of lattice layer k are given for systems with different γ. For increasing surface binding parameter γ, we find that the polymer segment volume fraction profile approaches the classical “parabolic brush” profile of strongly stretched polymer brushes.³⁴ Indeed, earlier studies of diblock copolymers with one surface-adsorbing block reveal the formation of tails of segments extending away from the surface due to the lack of one or more anchoring monomers on the nonbinding side of the chain.^15,16,18

Figure 3.

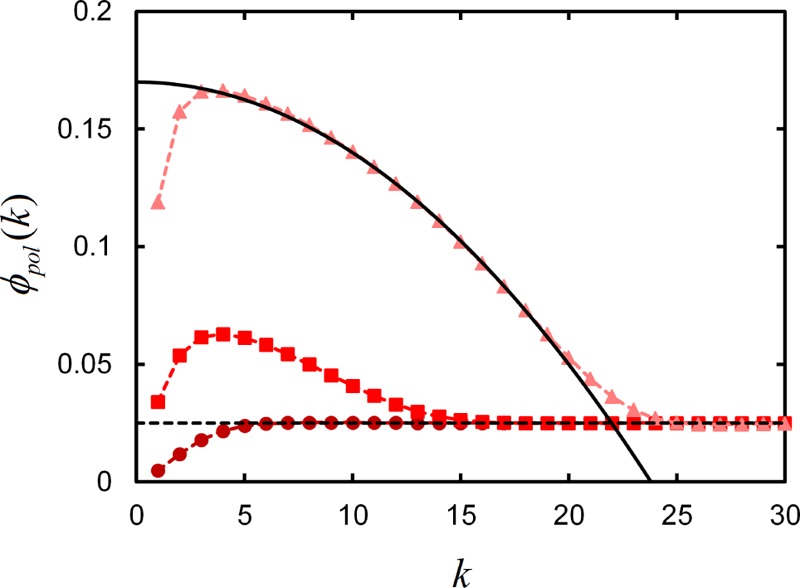
Local volume fraction of polymer segments ϕ_pol(k) at each lattice layer k, for terminal-linkers with N_l = 1 and ln γ = 1.85 (circles), 8 (squares), and 20 (triangles) in systems with ϕ_pol^° = 0.025. Solid black line is a parabola, showing parabolic curvature of grafted polymer segment density at large γ. Black dashed line is ϕ_pol.

Turning back to Figure 2a, we now consider the adsorption of chains with more than one terminal linker. The gain in free energy of a chain per surface-bound linker is F̅ = −k_BT ln(γ + 1).Therefore, chains with more linker segments are able to repay the entropic cost of the conformational change required for binding at smaller γ. The result of this entropy/enthalpy balance is the apparent horizontal shift of the adsorption profiles to smaller values of γ for chains with an increasing number of terminal linkers.

The profiles in Figure 2a for chains with more than one terminal linker are steeper near their inflection points, compared to the case with only one terminal linker. This illustrates cooperativity of linker adsorption; when one linker binds, the two directly connected adjacent linkers may very easily bind, and so on.

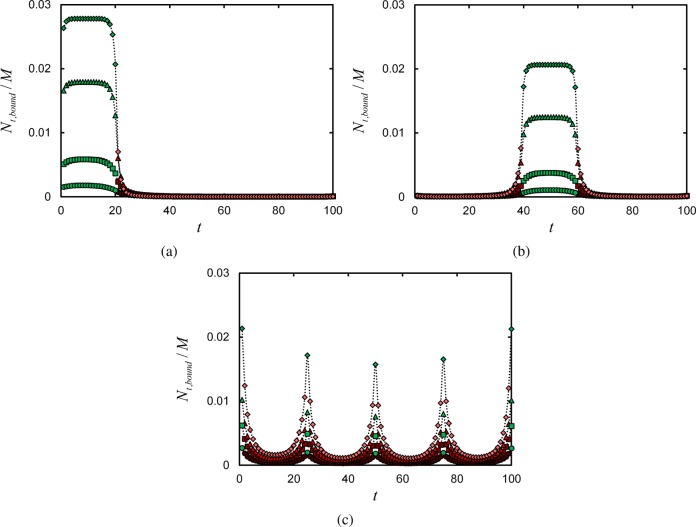
This effect is demonstrated in Figure 4a, where we show the number of segments N_t,bound with index t (along polymer chains) that are bound to the surface per unit surface area. This quantity is calculated via

10

Figure 4.

Number of segments with index t per unit surface area, N_t,bound/M, located at the surface lattice layer, k = 1, for various γ in terminal (a), central (b), and uniform (c) linker architecture systems with ϕ_pol^° = 0.025. In parts a and b, N_l = 20 and ln γ = −0.43 (circles), 0.20 (squares), 1.25 (triangles), and 1.97 (diamonds); in part c, N_l = 5 and ln γ = −3.98 (circles), 6.00 (squares), 8.00 (triangles), and 13.00 (diamonds). In all figures, points are numerical SCFT results, and dashed fit lines are included as guides to the eye; points colored green indicate which polymer segments t are linkers.

For increasing γ, there is evidently a uniform response in the probability that each linker is bound to the surface, i.e. all linker segments are approximately equally likely to be bound to the surface. This is evidence that the linker domain binds cooperatively. Note, however, that the binding probability is not entirely independent of the position of the linker segment in the chain: the binding probability is less on the extremities of the linker domain. This is not surprising because the entropy-energy balance favors detachment more at the extremities than in the middle of the linker domain.

The results in Figure 4a suggest a “molecular” adsorption/desorption process,¹⁸ in which the entire linker domain interacts with the surface as essentially a single contiguous entity (though noting the slight preference for linkers near the middle of the linking domain to bind to the surface earlier). This is in contrast to a “zipper” process, in which the linker domain binds (unbinds) to (from) the surface segment-by-segment as the binding free energy grows larger (smaller). Note, however, that our results represent a statistical average over all chain conformations in the system. Hence, while the average picture shown in Figure 4a indicates an all-or-nothing adsorption process, it is possible that some chains in the equilibrium ensemble exhibit zipper-like adsorption or desorption.

There is a limit to increasing the binding affinity of the polymers by adding linker segments. Depending on the concentration of polymers in the system, there is a threshold value of N_l at which linkers begin to compete for available binding sites on the surface. Adding more linker segments to each polymer beyond this threshold will thus not necessarily enhance the selectivity of polymer-surface binding.

The adsorption profile for the saturated-linker polymer shown in Figure 2a provides an example of this surface crowding effect. Recall that the saturated-linker architecture is one in which all N_t = 100 segments of each polymer chain in the system are linkers. We find in Figure 2a that the adsorption profile for this system initially increases steeply with γ, as the enthalpic term of the chain free energy is very strong (on the order of F̅N_t). However, the slope soon levels off due to the (entropic) competition for binding all linkers of all chains in the system onto the surface. A mean-field treatment of adsorbing polymers in semidilute solution is given by Johner,³⁵ considering the conformational structure of such systems in more detail and with scaling theory.

The adsorption profiles for chains with centrally located linkers are given in Figure 2b. These profiles qualitatively resemble those obtained for terminal linkers in Figure 2a. However, at low γ, the adsorption profiles have θ values that are smaller than those observed for the terminal linkers, particularly for small N_l. This is because segments at a chain terminus can access the surface more easily (entropically speaking) than segments in the middle of the chain; that is, there is a greater degree of chain reconfiguration that must occur for a central linker to expose its linker segments to the surface, compared to a chain where the linkers are located at one of the chain ends. Experiments that compare surface adsorption of polymers with terminally located and centrally located adsorbing functional groups also show a preference for the terminally located groups to bind to the surface.²⁷ For chains with centrally located linkers, reconfiguration allows for binding of the linker domain along with two tails of inert monomers extending away from the surface; this is consistent with the conformations of adsorbed triblock copolymers with a similar chain architecture.¹⁵

Figure 4b shows how the linker domain approaches the surface as γ increases, dragging the two adjacent tails of inert segments along. As in the case of the terminal linker domain, the centrally placed domain approaches the surface uniformly, illustrating the cooperativity of the binding process.

Uniform Linkers: Lack of Cooperativity and Loop/Train Crowding

Polymers which have their linkers uniformly placed along the chain backbone behave differently. Adsorption profiles for uniform linkers are shown in Figure 2c. They exhibit a more gradual adsorption transition compared to the terminal and central architectures, as well as comparatively less overall adsorbed material for a given γ. We can understand this behavior by observing the adsorption of individual segments of a uniform-linker chain in Figure 4c. Adsorption of the linkers onto the surface results in the formation of “loops”: strands of polymer segments extending away from the surface. Loops consist of the inert polymer segments between adjacent surface-bound linkers along a given chain. When the number of linkers per chain grows larger, the number of inert segments between linkers grows smaller, and the loops become short “trains” of monomers residing very near the surface. This is analogous to the behavior of polymers with adsorbing end groups, in which there is a transition from looplike to train-like behavior of the nonadsorbing chain segments when the number of segments between the adsorbing end groups decreases.¹⁷

This picture contrasts with adsorption of terminal and central linker chains in two ways. First, when linkers are grouped into domains, they exhibit cooperative binding due to their spatial proximity along the chain backbone. And second, the inert regions of terminal and central linker chains are not bounded on both ends, allowing them to extend away from the surface as tails in brush-like conformations. Both of these factors lead to a sharp response in the fraction of bound surface sites as a function of the binding strength γ as observed in Figure 2, parts a and b.

On the other hand, placing linkers uniformly along the chain backbone reduces or eliminates the possibility for cooperative binding, particularly when the number of linkers along the chain is low as in Figure 4c. In addition, adsorption of a chain requires the formation of loops and trains of inert segments at the surface, leading to crowding. These two factors give rise to the more gradual adsorption profiles of the uniform linker architecture.

For example, the adsorption profiles for uniform linker chains with 2 and 5 linkers in Figure 2c exhibit nearly identical inflection points. Apparently, adding additional linker segments does not induce cooperative binding when each linker is separated by many inert segments. This is in contrast to the dramatic shift in the adsorption profile inflection points and slopes for terminal and central architecture systems, e.g. when the number of linkers per chain is increased from 1 and 5 (see Figure 2, parts a and b).

Notably, an ellipsometric study of diblock copolymers, in which few surface-binding functional groups are randomly (rather than block-wise) distributed along one block, shows that the number of surface-bound polymers is statistically independent of the number of adsorbing functional groups.²² This is qualitatively consistent with our calculations for chains with few uniformly spaced linkers; adding additional linkers to the chain has little effect on the number of polymers adsorbed to the surface in Figure 2c.

As the number of linkers per chain grows larger, the number of inert segments between linkers decreases. This has the effect of decreasing the crowding of the surface by loops/trains of inert segments, as more segments per chain are now able to actively adsorb to the surface. In addition, the possibility of adsorption cooperativity is enhanced, as the topological distance between adjacent linkers grows smaller such that their positions become strongly correlated. Both factors cause the adsorption profiles of uniform linker chains to become steeper near their inflection points, as well as shifting the inflection points to smaller γ. The adsorption behavior then converges with the terminal and central chain architectures when the number of linkers approaches N_t; in this limit, the surface binding behavior is identical to that described by Johner.³⁵

Binding Selectivities

As the density of surface receptors increases, more linkers and more chains are bound to the surface. Binding selectivity quantifies how the extent of binding increases with receptor concentration. Adsorption is “superselective” when the extent of binding grows faster than the number of surface receptors.

There are two different kinds of selectivity. One expresses the surface receptor concentration dependence of the number of bound polymer chains—we refer to this as the “polymer-based” selectivity, α_pol. The other describes the dependence of the number of occupied surface sites—we denote this as the “surface-based” selectivity, α_sfc. The latter is equivalent to the measure of selectivity computed in Martinez et al.¹ The two selectivities are relevant under different experimental circumstances. Note that in both cases, a value greater than one indicates superselectivity.

Let us first consider the “surface-based” selectivity α_sfc, defined as

11

where N_rec is the number of receptors per lattice site on the surface. As γ ∝ N_rec as discussed in eq 2, then α_sfc may be written as

12

The “polymer-based” selectivity α_pol takes the form

13

where N_pol,b is the number of polymers bound to the surface, defined as the number of polymers having at least one linker located in a surface lattice site. This quantity is obtained by computing the single-chain partition function Q_pol,free for the subensemble of unbound chains in the system. Q_pol,free is calculated by first obtaining the (total) single-chain partition function Q_pol as well as the self-consistent mean fields V(k) and ϕ_pol(k) for the system, as explained in the Self-Consistent Mean-Field Lattice Model section, and then computing the sum of Boltzmann weights for propagator paths within those mean fields with the condition that none of their linker segments reside at the surface layer. The resulting sum of Boltzmann weights is Q_pol,free. This approach is equivalent to how Scheutjens and Fleer calculate the number of monomers belonging to surface-adsorbed chains in their formulation of polymer SCFT.²⁹

Having computed the single-chain partition function for the unbound chain subensemble, the number of chains bound to the surface is obtained by

14

where N_pol is the equilibrium number of polymer chains in the system for the given γ and ϕ_pol^°. (Normalizing N_pol,b by the surface area M, thereby obtaining the number of chains bound per unit area, does not affect the selectivities α_pol and α_sfc; both depend only on the derivative with γ of the logarithm of the adsorbed amount, in which the surface size M is held fixed.)

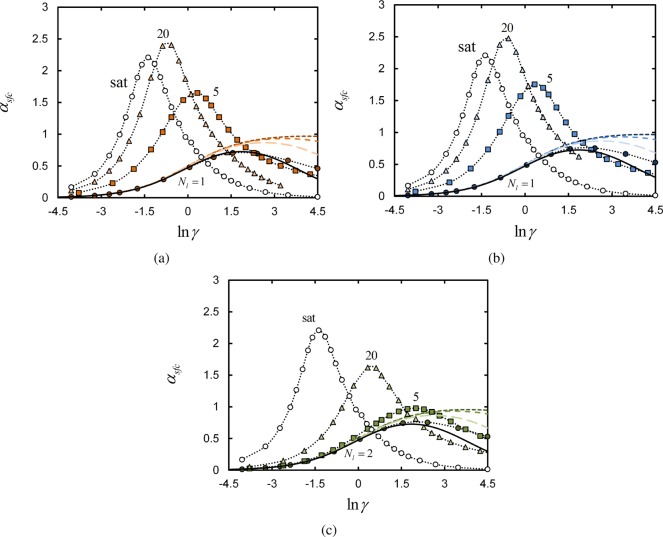
Figure 5 shows plots of the surface-based selectivity α_sfc as a function of γ for all systems contained in Figure 2. Obviously, the maximum of each α_sfc profile in Figure 5 coincides with the inflection point on the corresponding adsorption curve in Figure 2.

Figure 5.

Surface-based selectivity α_sfc vs ln γ for systems with ϕ_pol^° = 0.025. See Figure 2 caption for plot details.

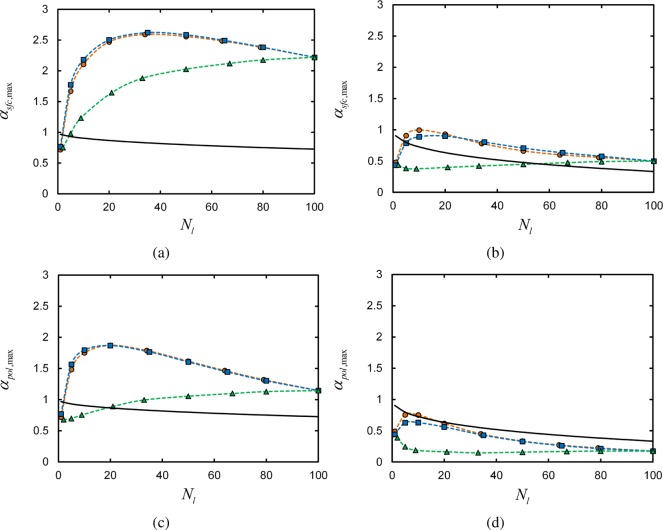
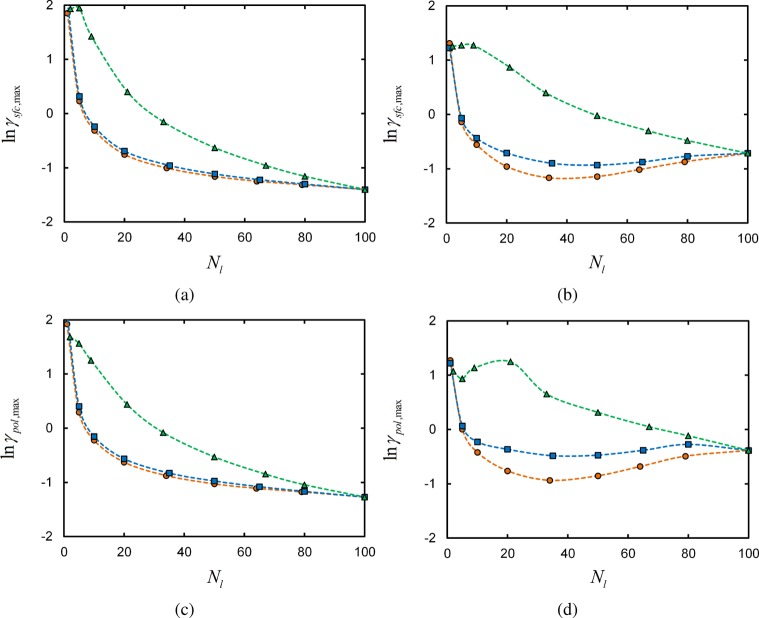
The maximum value of the selectivity, α_sfc,max, is plotted for each linker architecture as a function of the number of linkers per chain N_l in Figure 6, parts a and b. Results are provided for systems with reservoir polymer volume fractions of ϕ_pol^° = 0.025 (Figure 6a) and 0.25 (Figure 6b, to illustrate the effect of polymer concentration on the maximum selectivity. Parts a and b of Figure 6 and 7 show the value of ln γ at which α_sfc,max occurs. Similarly, parts c and d of Figure 6 and 7 show the maximum polymer-based selectivities α_pol,max and the ln γ at which they are found for the same architectures and N_l.

Figure 6.

Maximum surface-based selectivity α_pol,max (a, b) and polymer-based selectivity α_pol,max (c, d) for terminal (orange circles), central (blue squares), and uniform (green triangles) linker architectures as a function of the number of linkers per chain N_l. Results are shown for systems with ϕ_pol^° = 0.025 (a, c) and 0.25 (b, d). Points are numerical SCFT results, and dashed lines are guides to the eye. Solid line is maximum selectivity of monomer adsorption at concentrations of N_lϕ_pol/N_t.

Figure 7.

Surface binding parameter ln γ at which max surface-based selectivity α_sfc,max (a, b) and max polymer-based selectivity α_pol,max (c, d) is observed for terminal (orange circles), central (blue squares), and uniform (green triangles) linker architectures as a function of the number of linkers per chain N_l. Results are shown for systems with ϕ_pol^° = 0.025 (a, c) and 0.25 (b, d). Points are numerical SCFT results, and dashed lines are guides to the eye.

The selectivity trends observed for each chain architecture reflect the microscopic binding statistics discussed in the previous section. To start, consider the maximum selectivities computed in systems with ϕ_pol^° = 0.025 in Figure 6, parts a and c. Both the terminal- and central- linker α_max initially increase as the number of linkers per chain increases. This is consistent with the results examined in Figure 2, parts a and b, where we observed that increasing the number of linkers per chain results in a more cooperative—i.e., steeper—adsorption profile.

Adding too many linker segments to the chains results in competition for available surface sites at which to bind. Thus, the adsorption profile actually becomes less cooperative with increasing N_l. This results in a decrease in the maximum selectivity α_max for larger N_l in Figure 6, parts a and 6c.

The selectivities shown in Figure 6 indicate that a domain-type arrangement of linkers leads to adsorption behavior that does not depend strongly on the location of the domain, but rather the number of linkers within the domain. The maximum selectivities are similar for the terminal and central linker architectures for the two polymer concentrations considered, and agnostic of whether selectivity is evaluated in terms of the surface or the polymer. In addition, the values of γ at which the α_max occur for the two architectures closely coincide, as shown in Figure 7. This accords with the observation that the number of adsorbing segments in block copolymers, rather than the position(s) of the adsorbing block(s) along the chain, has the strongest influence on the amount of polymer that adsorbs to the surface.¹⁸

On the other hand, the selectivity of polymers with a uniform arrangement of linkers exhibit significantly different behavior in Figure 6. In particular, the binding selectivities are notably lower than those obtained for terminal and central linkers. This is because the linkers are not clustered into domains and thus cannot bind cooperatively; when one linker binds to the surface, it must carry with it neighboring domains of inert segments that do not yield additional adhesion to the surface. The inert segments crowd viable surface binding sites, reducing the ability for linkers on subsequent chains to bind to the surface. Enhanced adsorption of polymers with block-like, as opposed to randomly or uniformly distributed, arrangements of surface binding segments has been observed in both simulation and experiment.²⁸

Uniform linkers also differ from terminal and central linkers in γ_max—the values of γ at which α_max is observed for each N_l—in Figure 7. In all cases, for a given N_l, γ_max is larger for a uniform linker than that for a terminal or central linker. This implies that there is a weaker overall binding free energy for these systems, compared to a terminal/central linker architecture chain with the same N_l and at the same γ. As the energy per bound linker is the same in the two cases for the same γ, then it must be that there is a larger entropic penalty to adsorbing a uniform linker, compared to a central/terminal linker. The additional entropic penalty for adsorption of a uniform linker chain is the formation loops and trains, compared to simply having one or two free tails of inert segments for the terminal/central linker scenario.

As the number of linkers per chain grows in both cases, then the chain is increasingly restricted into a pseudo two-dimensional “pancake” conformation on the surface, such that the discrepancy in adsorption entropy loss between the two classes of architectures decreases. Thus, the difference between γ_max for uniform and terminal/central linker chains decreases for increasing N_l, ultimately converging at the same value when the chain is saturated with linkers.

Polymer concentration strongly affects the maximum binding selectivities α_max in Figure 6, and also influences the values γ_max at which the maxima are observed in Figure 7. Increasing the polymer segment concentration 10-fold, from ϕ_pol^° = 0.025 in Figure 6, parts a and c, to 0.25 in Figure 6, parts b and d, there is a notable decrease in selectivity for all architectures and N_l. The increase in polymer concentration particularly affects the systems at vanishing γ, as there is roughly speaking a 10-fold increase in the probability that a surface site is occupied by a linker polymer segment compared to the lower-concentration scenario. Thus, the adsorption profiles for all systems begin at larger baseline values of θ at low γ, leading to smaller growth in θ upon increasing γ.

The behavior of the selectivity based on the number of bound polymers (α_pol,max) is different than that depending on the number of occupied surface sites (α_sfc,max). Parts a and b of Figure 6 compared to parts c and d of Figure 6 show that α_pol,max is typically smaller than α_sfc,max for both reservoir polymer concentrations studied, as a “chain” entity has many more binding configurations than a single “linker” entity. For example, at vanishing γ, the probability that a chain is bound to the surface is obviously larger than that for individual linkers; the chain has N_l possible ways of binding per site, whereas a single linker has only 1.

As the number of linkers per chain grows, the probability that a chain is surface-bound at low γ increases even more. Hence, the adsorption profile of N_pol,b as a function of γ is more gradual for large N_l than the surface occupancy θ adsorption profile. The result is that α_pol,max decreases faster with N_l than α_sfc,max.

While the values of α_pol,max and α_sfc,max are different, the same qualitative relationship between the selectivities of terminal, central, and uniform linker architectures is observed; the terminal and central architectures fall into a single category due to their domain-like linker arrangement, while the uniform architecture exhibits generally lower selectivity and a different dependence on N_l. What is more, the values of γ at which the maximum selectivities α_pol,max are observed for each system, in Figure 7, parts c and d, are very near to that where the α_sfc,max occur in Figure 7, parts a and b. This indicates that the range of γ over which there is the most rapid (in γ-space) change in the number of bound chains is concurrent with the fastest increase in the number of occupied surface sites.

Receptor Occupancy and Efficiency

Here we examine the fraction of surface receptors (as opposed to entire surface lattice sites) that are bound to ligands as a function of γ. Recall that each linker segment contains only one ligand, while each surface lattice site contains N_rec = fN_rec,max receptors, where N_rec,max is the maximum number of receptors that a surface lattice site may hold. Drawing from the discussion in Appendix A, the probability that the ligand of a linker is bound to a receptor, given that the linker is located in a surface lattice site, is

15

Thus, the probability that a surface site holds a linker segment that has its ligand bound to one of the receptors in the site is pθ. The number of ligand-bound linker segments in the system is Mpθ. It then follows that the fraction ψ′ of all receptors MfN_rec,max on the surface occupied by ligands is

16

This can be rearranged into a quantity that does not depend on the (arbitrary) choices of N_rec,max and ε:

17

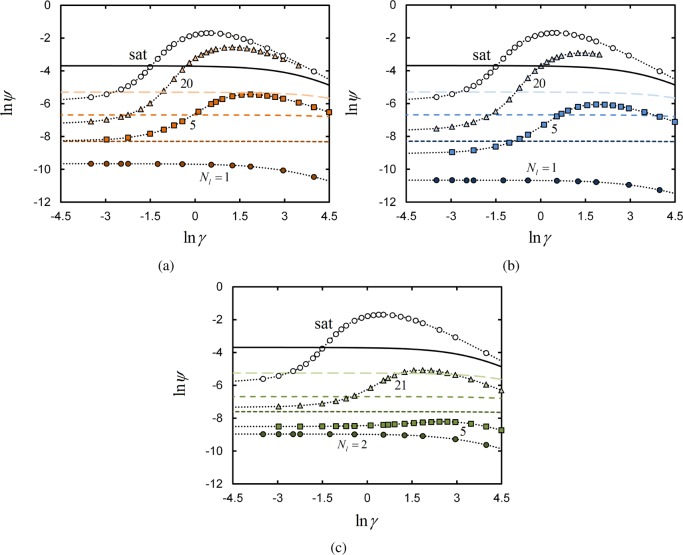
Plots of ln ψ as a function of ln γ for terminal-, central-, and uniform-linker architectures at ϕ_pol^° = 0.025 are shown in Figure 8. As a linker segment hosts only one ligand, then when a linker is located in a surface lattice site it blocks other linkers from binding to potentially available receptors within that site.

Figure 8.

Log–log plot of the average fraction ψ of occupied surface receptors, as a function of surface binding parameter γ for systems with ϕ_pol^° = 0.025. See Figure 2 caption for details.

At small γ, this exclusion effect is not significant; the fraction ψ of receptors bound to ligands initially increases with γ. As the number of receptors on the surface grows larger with γ, ψ begins to decrease. This reflects the fact that the number of surface receptors is increasing faster than the number of ligands that are sterically capable of binding. The value of γ at which lnψ is maximized indicates when receptors start to become unused, or “wasted”.

If we briefly imagine that these receptors are formed on a cell surface, then it is likely that each receptor costs the cell energy to synthesize. It would therefore seem that it is not in the cell’s interest to enter the regime in which it has created more receptors than may possibly be occupied by ligands. One way that the number of wasted receptors at the cell surface could be reduced is by increasing the number of ligands per linker segment.

However, comparing Figure 8 with the selectivities given in Figure 5, we find that the maximum binding selectivity occurs at values of γ prior to the point at which the fraction of bound receptors starts decreasing with γ. Thus, the cell is in principle able to exploit the selectivity maximum and then cease the expression of receptors before entering the regime where they become unused.

Conclusions

In this paper, we studied the surface adsorption of multivalent polymer chains with a variable number of ligands that can bind to a receptor-coated surface through ligand–receptor binding. We have applied a grand canonical formulation of polymer self-consistent field theory (SCFT) to study chain adsorption.

Our calculations allow us to estimate the adsorption isotherms and adsorption selectivity of polymers with different sequences of linker segments. The binding statistics between linker ligands and surface receptors is incorporated into the SCFT model by an effective binding strength per linker segment, γ; importantly, this quantity is proportional to the number N_rec of receptors per lattice site, such that changes in γ are interpreted as changes in the number of receptors per surface lattice site at fixed ligand–receptor binding strength.

A key result of our calculations is the binding “selectivity” of polymers with a particular sequence of linkers. Selectivity is a measure of the response in the number of bound polymers or occupied surface sites to a variation in the number of receptors on the surface. These polymer-based and surface-based measures of selectivity are explored by examining the binding statistics of systems as a function of γ, as well as the number of linker segments N_l per chain.

In our discussion, we consider polymers with “terminal”, “central”, and “uniform” linker sequences. The first two architectures are where linker segments of the polymer are placed into contiguous “linker domains” at one of the two chain termini, or at the chain midsection (respectively). In the third architecture the linkers are distributed uniformly along the chain.

Chains with clustered linkers tend to exhibit similar binding statistics. For terminal linker domains, increasing γ results in an enhanced tendency to binding the end domain of each chain to the surface. This adsorption results in the formation of a polymer brush. Chains with a domain of linkers placed at their midsections exhibit similar behavior, though there is a slightly larger entropic barrier to surface binding as a given chain must reconfigure itself such that the centrally located linkers bind to the surface while the two inert-segment tails of the chain extend away from the surface in a brush-like configuration. The extra entropic barrier for binding chains with a central arrangement of linkers results in those systems exhibiting slightly greater selectivities compared to the terminal-linker architecture.

Chains with a uniform arrangement of linkers along their backbone display poor selectivity compared to terminal and central linker architectures. The physical reason for this lower selectivity is that chains with a uniform distribution of linkers exhibit much less cooperativity upon binding, as well as the formation of loops of inert segments that crowd the surface from labile adsorption of new chains from the bulk.

In both architectures, there is a limit to the selectivity that can be achieved. Increasing the number of linkers per chain ultimately leads to competition for surface binding sites, such that polymer segment surface crowding—rather than binding cooperativity and multivalent degeneracy—dominates the binding statistics. Thus, there is an optimal number of linkers per chain that yields the largest binding selectivity. We show how this optimal value of selectivity occurs at larger N_l upon decreasing the chain concentration, thereby reducing the competition for free binding sites.

We also examine how the fraction of ligand-bound surface receptors (as opposed to surface lattice sites) changes as the number of bound polymer grows large. A critical value of γ (that depends on the chain architecture) is observed, after which the fraction of occupied receptors starts to decrease upon the addition of more surface receptors. This indicates that a fraction of the surface receptors beyond this point are unused, due to steric blocking by polymer segments that have already bound to the surface. However, the value of γ at which maximum selectivity occurs is well before this point in most cases; a cell or material could therefore exploit the selectivity maximum without entering the regime in which additional receptors are synthesized unnecessarily.

The results presented in this study indicate how the placement of ligands along a polymer chain can be used to tune their surface binding selectivity. This information is useful for designing surface adsorption in macromolecular systems. In fact, it is likely that evolution has already stumbled upon the design principles that we describe in this paper.

Appendix A. Mean-Field Linker-Surface Binding Parameter

In the SCFT lattice model outlined in section “Self-Consistent Mean-Field Lattice Model”, a linker segment represents a Kuhn segment of a polymer. One of the monomers comprising the Kuhn segment contains a ligand that can bind to any one of the receptors on the surface. We now derive the effective binding free energy F̅ for when a linker segment is located at a surface lattice site, i.e., a site at layer k = 1 in the model.

Let the number of receptors per surface lattice site by given by N_rec. When a linker segment is located in a surface site, then the ligand of that Kuhn segment may take on N_rec receptor-bound states, and N_rec,max – N_rec unbound states. Here, N_rec,max is the maximum number of receptors that can be grafted to a single surface site. The partition function for the Kuhn segment in the surface site is

where ε is the ligand–receptor binding energy. When the Kuhn segment is not in a surface site, then the partition function for the segment is simply

(In both cases, we ignore all the other possible positions of the ligand in a site, as they are identical in both surface and nonsurface sites.) The effective linker-surface binding free energy F̅ is then defined as

where f = N_rec/N_rec,max is the fractional coverage of receptors on the surface. The effective linker-surface binding free energy can be expressed in terms of the parameter

which conveniently contains both f and ε such that an arbitrary choice for one or the other needn’t be made; this is similar to the parameter utilized in Martinez et al.¹ Thus, we obtain

as the relationship between the effective binding free energy βF̅, and the parameter γ.

Appendix B. Monomer Adsorption Statistics

For purposes of validation, we present here the adsorption statistics of simple linker monomers in the grand canonical SCFT approach and compare to theory. The SCFT system contains L = 50 layers and M = 400 sites per layer. As described in section “Self-Consistent Mean-Field Lattice Model”, grand canonical equilibrium is achieved by specifying a fixed volume fraction ϕ° of polymer segments—here simply linker monomers—far from the adsorbing surface.

For a given reservoir linker monomer concentration ϕ°, the linker adsorption isotherm is given as a function of the surface binding free energy F̅ by the standard Langmuir form

18

where ⟨N⟩_sfc is the equilibrium number of linker monomers bound to the surface. Figure 9 presents the fraction of surface sites occupied by monomers as a function of the volume fraction of monomers in the reservoir. Results are given for several βF̅, revealing that the adsorption profiles numerically computed in the grand-canonical SCFT model exactly follow the analytical prediction, eq 18.

Figure 9.

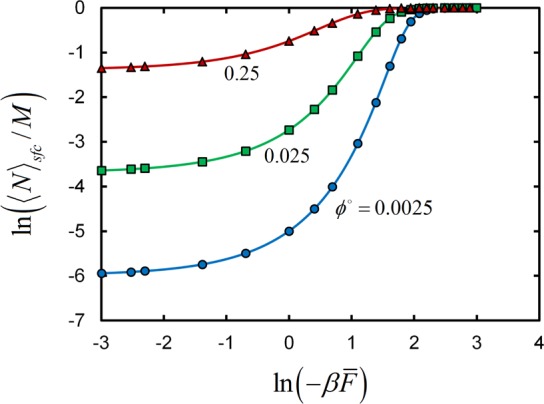
Log–log plot of the fraction of surface sites ⟨N⟩_sfc/M occupied by monomeric linkers as a function of the linker-surface binding free energy −βF̅. Points are numerical SCFT results, and solid lines are predictions from eq 18. Results are computed for three different concentrations of monomeric linkers in the reservoir, shown in the labels beside each curve.

The authors declare no competing financial interest.