Evaluation of accuracy of B-spline transformation-based deformable image registration with different parameter settings for thoracic images

Abstract

Deformable image registration (DIR) is fundamental technique for adaptive radiotherapy and image-guided radiotherapy. However, further improvement of DIR is still needed. We evaluated the accuracy of B-spline transformation-based DIR implemented in elastix. This registration package is largely based on the Insight Segmentation and Registration Toolkit (ITK), and several new functions were implemented to achieve high DIR accuracy. The purpose of this study was to clarify whether new functions implemented in elastix are useful for improving DIR accuracy. Thoracic 4D computed tomography images of ten patients with esophageal or lung cancer were studied. Datasets for these patients were provided by DIR-lab (dir-lab.com) and included a coordinate list of anatomical landmarks that had been manually identified. DIR between peak-inhale and peak-exhale images was performed with four types of parameter settings. The first one represents original ITK (Parameter 1). The second employs the new function of elastix (Parameter 2), and the third was created to verify whether new functions improve DIR accuracy while keeping computational time (Parameter 3). The last one partially employs a new function (Parameter 4). Registration errors for these parameter settings were calculated using the manually determined landmark pairs. 3D registration errors with standard deviation over all cases were 1.78 (1.57), 1.28 (1.10), 1.44 (1.09) and 1.36 (1.35) mm for Parameter 1, 2, 3 and 4, respectively, indicating that the new functions are useful for improving DIR accuracy, even while maintaining the computational time, and this B-spline-based DIR could be used clinically to achieve high-accuracy adaptive radiotherapy.

INTRODUCTION

Deformable image registration (DIR) is essential for linking the anatomy at one time to that at another time, while maintaining the desirable one-to-one geographic mapping, and it is thus fundamental for adaptive radiotherapy and image-guided radiotherapy. It has been increasingly applied to multimodality image fusion, automatic image segmentation, calculation of accumulated dose, 4D dose calculation and 4D computed tomography (CT)-derived ventilation [1–11]. Recently, several types of commercial DIR software have been developed and utilized in clinical settings. DIR algorithms implemented in commercial software have been evaluated by a number of researchers [4, 12–14]. Kirby et al. evaluated eleven DIR algorithms, including two commercial software programs: MIM (Software Inc., Cleveland, OH, USA) and Velocity AI (Velocity Medical, Atlanta, GA, USA). They concluded that different DIR algorithms yield very different results with potentially important clinical implications. Kadoya et al. evaluated four types of DIR algorithms, including one commercial software program (Velocity AI). These earlier studies showed reasonable accuracy of DIR overall, but large DIR errors were observed in some patients. Thus, further improvement of DIR accuracy is still needed.

In many cases, a registration algorithm is divided into a number of components. As mentioned above, it has been reported that some major differences in DIR algorithms cause differences in DIR accuracy [12]. However, the extent to which these components of DIR contribute to the accuracy is still unclear. One of the purposes of this study was to clarify this issue using a clinically meaningful metric.

Elastix, which is a publicly available DIR package, was developed by University Medical Center Utrecht, the Netherlands [15]. This registration package is partially derived from the Insight Segmentation and Registration Toolkit (ITK), which is an open source software package developed as an initiative of the US National Library of Medicine. In addition to the existing ITK image registration classes, several new functions are implemented in elastix. Some of these functions were experimentally examined by evaluating the dice similarity coefficient, the returned value of cost functions, and other values. Since these values depend on the size and shape of evaluated objects and metric functions, there is still a need for more reliable and comprehensive evaluation of DIR accuracy for its clinical application. Castillo et al. reported a method for evaluation of DIR accuracy using large landmark point sets [16]. It is a comprehensive evaluation method and is known as a standard method [17, 18]. Using large landmark point sets, we tested whether new functions implemented in elastix are useful for improving DIR accuracy.

MATERIALS AND METHODS

CT data and landmark point sets

A total of 10 patients with esophageal or lung cancer were studied. Datasets for the 10 patients were provided by DIR-lab (www.DIR-lab.com, 10 July 2014, date last accessed) and consisted of thoracic 4D CT images acquired as part of the standard treatment planning process at 2.5-mm slice spacing with a General Electric General Electric Discovery ST ET/CT scanner (GE Medical Systems, Waukesha, WI) and a coordinate list of anatomical landmarks that had been manually identified and registered by an expert in thoracic imaging. Extreme inhale and exhale phases of the 4D CT image sets were utilized in this study. Figure 1 shows inhale and exhale images and the distribution of 300 landmark pairs. Reference landmarks and 4D CT characteristics are given in Table 1. Although the original landmark points used in the study by Castillo et al. contained more than 1000 landmarks, the DIR-lab data were 300 landmarks from original landmarks for each patient. Expert landmark correspondence was used for evaluating DIR spatial accuracy.

Fig. 1.

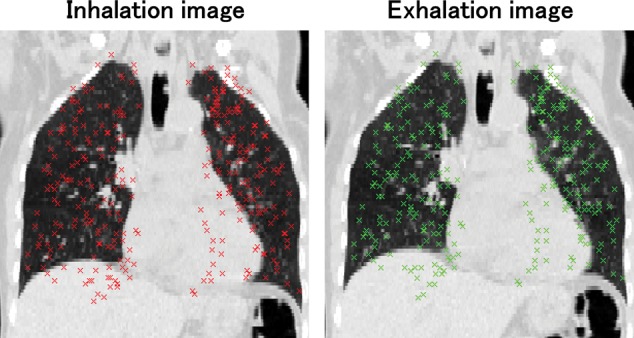
An example of maximum-inhale and -exhale images with 300 landmark pairs.

Table 1:

CT image and reference landmark characteristics

Case number	Displacement mean (mm)	Displacement SD (mm)	Image dimension	Voxel size (mm)
1	3.89	2.78	256 × 256 × 94	0.97 × 0.97 × 2.5
2	4.34	3.90	256 × 256 × 112	1.16 × 1.16 × 2.5
3	6.94	4.05	256 × 256 × 104	1.15 × 1.15 × 2.5
4	9.83	4.86	256 × 256 × 99	1.13 × 1.13 × 2.5
5	7.48	5.51	256 × 256 × 106	1.10 × 1.10 × 2.5
6	10.89	6.97	512 × 512 × 128	0.97 × 0.97 × 2.5
7	11.03	7.43	512 × 512 × 136	0.97 × 0.97 × 2.5
8	14.99	9.01	512 × 512 × 128	0.97 × 0.97 × 2.5
9	7.92	3.98	512 × 512 × 128	0.97 × 0.97 × 2.5
10	7.30	6.35	512 × 512 × 120	0.97 × 0.97 × 2.5

Additional information

All of the patient data used in this study were publicly available. Institutional review board (IRB) approval and further patient consent were thus unnecessary.

Lung parenchyma segmentation

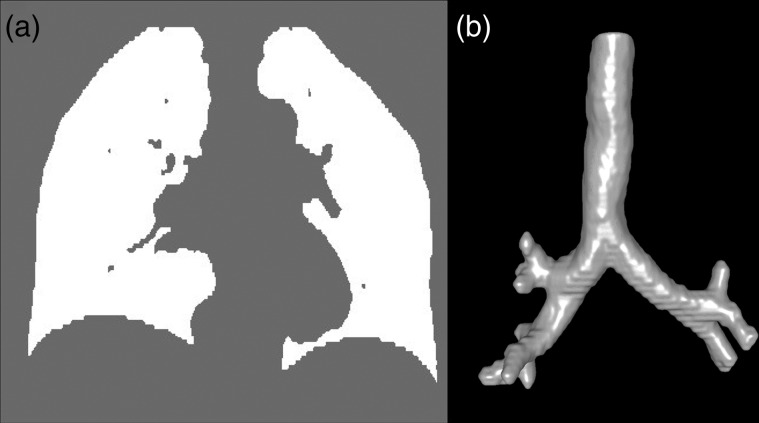
When using an intensity-based DIR algorithm, structures with strong contrast are more likely to be well aligned. Thus, high-contrast structures such as bones are likely to be well aligned, whereas low-contrast structures like lung parenchyma may not be. To circumvent misalignment of parenchymal structures, an intensity-based segmentation was applied to delineate lung voxels from the CT images. Voxels between −990 and −250 Hounsfield units (HU) were selected as representing pulmonary parenchyma [19, 20]. Each image was loaded and initial seed points were manually located in the trachea. Using the flood-fill algorithm [21] and a morphological filter, the trachea and main-stem bronchi were separately delineated and subsequently removed from the pulmonary parenchyma masks. Lung masks were checked and modified where necessary. In most cases, this modification required ∼5 min of manual effort per patient. Using lung masks, DIR was performed on the part of the image that was within the masks. Figure 2 shows an example of the lung masks and segmented airway trees.

Fig. 2.

CT airway and lung mask image. (a) A coronal section of lung mask is shown. (b) A volumetric rendering of the segmented trachea and main-stem bronchi is also shown.

B-spline-based DIR

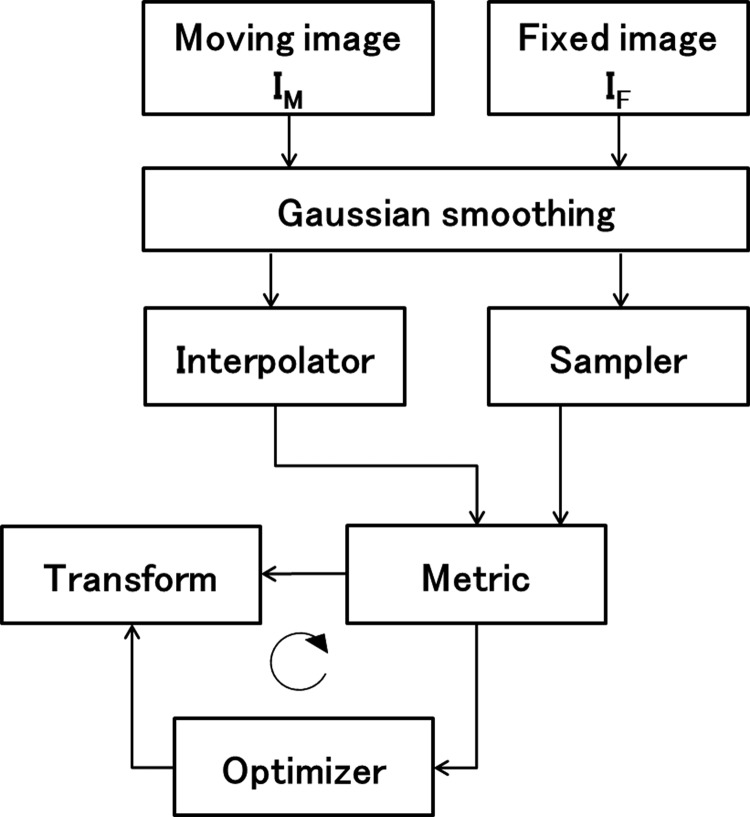
Elastix was used to deform peak inhale images to be aligned with peak exhale images. The framework of elastix is shown as a block scheme in Fig. 3. For each component (transform, similarity metric, etc.), several choices are available and the user can configure a registration algorithm. In addition to the existing ITK image registration classes, the following new functions are implemented in elastix [15]. New optimizers include Kiefer–Wolfowitz, Robbins–Monro and adaptive stochastic gradient descent (ASGD) [22], and new or more flexible cost functions include multi-feature α-mutual information, bending energy penalty term and rigidity penalty term [23]. To verify whether new functions in elastix are useful for improving DIR accuracy while keeping computational time, we performed DIR with four types of parameter settings. The first one represents original ITK (Parameter 1); this employs functions that are implemented in ITK. The second employs the new function of elastix (Parameter 2), and the third was created by modifying Parameter 2 in such as a way to keep the same computational time as that for Parameter 1. The last one is also a modified version of Parameter 2 (Parameter 4). Weight value of the bending energy penalty of Parameter 4 was set to zero. The following is details of these four parameters. Parameter 1 employed the standard gradient descent and normalized correlation coefficient as an optimizer and metric, respectively. These functions are standard components implemented in ITK. Parameters 2, 3 and 4 employed the ASGD as an optimizer and normalized correlation coefficient as a similarity metric. Parameters 2 and 3 employed a bending energy penalty term. Parameters 1 and 4 contained no constraint term. ASGD is based on the theoretical work by Plakhov [24]. It makes DIR more robust with little computation time per iteration required. The bending energy penalty term restricts undesired deformation and improves DIR accuracy. The functions that three parameters employed were as follows. Random 2000 coordinates sampling was used as a sampler. B-spline transform is among the most popular parametric methods to represent non-rigid deformations [25, 26], as it has recently been observed in a registration challenge. The cubic multi-dimensional B-spline polynomial was used for its flexibility. To perform DIR more efficiently, it is common to start the registration process using images that have lower complexity, e.g. images that are smoothed and possibly down-sampled. In elastix, after registration is completed in one stage, the result will be used as the initial condition for the next stage. Parameters for one stage, such as number of iterations, σ for Gaussian smoothing and control point grid spacing, can be different from those for the other stages. These values of Parameters 1, 2 and 4 were identical, and they are presented in Table 2. Parameter 3 was created by reducing the number of resolutions to six and changing the number of iterations to 320.

Fig. 3.

Basic registration components of elastix.

Table 2.

Parameter settings of each stage of DIR

Stage	Parameter 1, 2, 4			Parameter 3
	σ (voxel)	Iteration	Control point grid spacing (mm)	σ (voxel)	Iteration	Control point grid spacing (mm)
1	16	1000	80	32	320	160
2	8	1000	80	16	320	80
3	4	1000	40	8	320	80
4	2	1000	20	4	320	40
5	1	1000	10	2	320	20
6	4	2000	80	1	320	10
7	3	2000	40
8	2	2000	20
9	1	2000	10
10	1	2000	5

Evaluation of DIR accuracy

First, the manually measured displacement vector field (mDVF) was calculated by using the landmark coordinate list. Then the automatically calculated displacement vector field (aDVF) was calculated by using elastix. Registration errors between mDVF and aDVF were calculated. More detailed methodology is described in [16]. 3D registration errors were quantified. Additionally, registration errors were binned corresponding to the length of the mDVF. The computation times in the log files that elastix outputs were also evaluated. Additionally, we calculated the determinant of the Jacobian of a DVF at every voxel. The determinant of Jacobian implies local volume change. Local contraction and local expansion are implied where this value is <1 and >1, respectively. Singularity of the deformation (unrealistic deformation) is also implied with the Jacobian determinant being below zero. We calculated the volume of this value below zero. More details are given in [26].

RESULTS

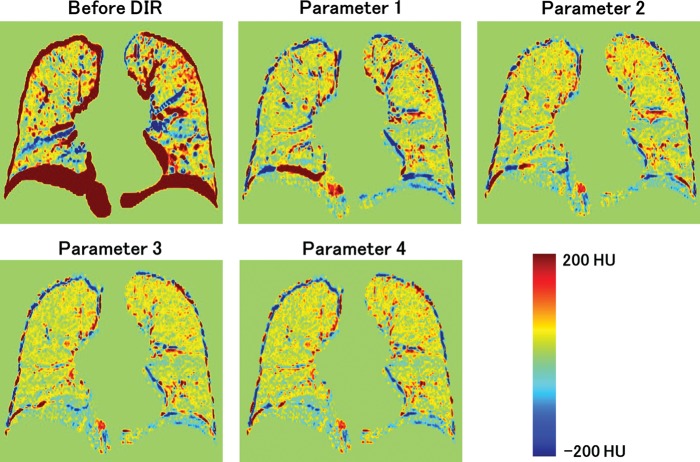
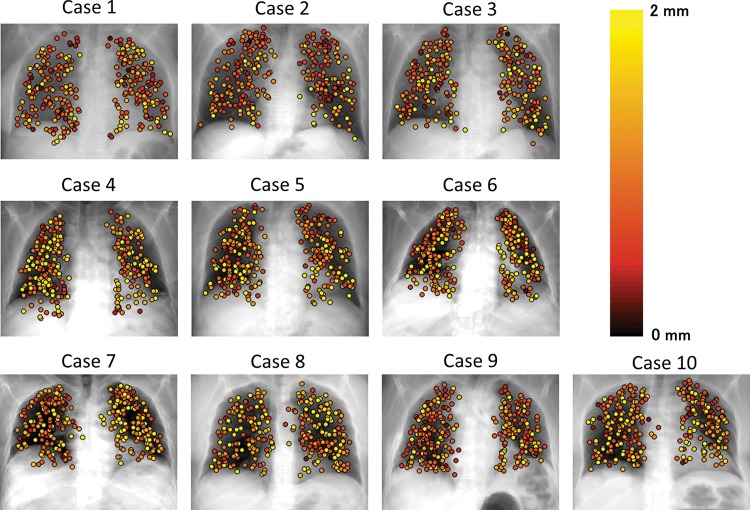
The differences between images for extreme inhale and exhale are shown in Fig. 4. Case 8 in Fig. 4 resulted in the largest registration error. Residual differences were dramatically reduced by performing DIR. A slightly larger difference was observed with Parameter 1 than with Parameters 2, 3 and 4. Registration errors for the cases are summarized in Table 3. The 3D registration errors in each case ranged from 1.08–2.99 for Parameter 1, 0.97–1.66 for Parameter 2, 1.02–1.78 for Parameter 3 and 0.99–2.04 for Parameter 4. The average registration errors with standard deviations for all cases were 1.78 (1.57), 1.28 (1.10), 1.44 (1.09) and 1.36 (1.35) mm for Parameters 1, 2, 3 and 4, respectively. Parameters 2, 3 and 4 resulted in a smaller DIR error than Parameter 1. Case 8 showed the largest improvement of DIR accuracy. This case also had the largest landmark displacement (the length of mDVF). The mean values of singularity (the volume of negative Jacobian) were 0.0, 0.5, 0.0 and 1.8 ml for Parameter 1, 2, 3 and 4, respectively. It should be noted that the unit of singularity is ml. Every parameter resulted in good singularity because only a small or no volume with negative Jacobian was generated in many cases. In summary, although ASGD contributed to a remarkable improvement in DIR accuracy, unrealistic deformation slightly increased (comparing Parameters 1 and 4). Using the bending energy penalty, both DIR accuracy and singularity were improved (comparing Parameters 2 and 4). Figure 5 shows 3D registration error binned corresponding to the length of mDVF. The point where displacement magnitude is 27.5 mm has a small sample size, hence its error bar is occasionally small. The registration error became larger according to the landmark displacement for all parameters. However, mean registration errors for Parameters 2, 3 and 4 were nearly equal to or less than 2.5 mm, which was the slice thickness of the CT images, representing reasonably high accuracy. On the other hand, Parameter 1 showed a larger registration error than Parameters 2, 3 and 4, especially where the displacement magnitude exceeded 15 mm. Figure 6 shows the local registration errors. Each landmark point was color-coded according to the 3D magnitude of registration error derived from Parameter 2. Since Parameter 2 showed high accuracy and low dependence on magnitude of landmark displacement, the local registration error did not greatly depend on its position in the lung. The mean computation times for all cases were 11.4, 87.6, 10.2 and 104.1 min for Parameters 1, 2, 3 and 4, respectively, with a workstation PC (2.40 GHz, eight cores). Parameter 3 showed reasonably high accuracy with no increase in computation time. It should be noted that the computation time of the DIR depends on the execution environment. Thus, computation time can always be changing.

Fig. 4.

Difference images of inhale and exhale images before and after DIR.

Table 3.

DIR spatial error and singularity summary

Case number	Parameter 1		Parameter 2		Parameter 3		Parameter 4
	Registration error	Singularity	Registration error	Singularity	Registration error	Singularity	Registration error	Singularity
1	1.08 (0.55)	0.0	1.01 (0.54)	0.0	1.02 (0.50)	0.0	1.04 (0.57)	0.9
2	1.21 (0.67)	0.0	0.97 (0.53)	0.0	1.03 (0.56)	0.0	0.99 (0.56)	0.0
3	1.57 (0.98)	0.0	1.14 (0.64)	2.3	1.25 (0.69)	0.0	1.23 (0.76)	2.4
4	1.76 (1.38)	0.0	1.47 (1.03)	0.0	1.52 (1.05)	0.0	1.50 (1.07)	0.0
5	1.84 (1.58)	0.0	1.40 (1.38)	0.6	1.71 (1.38)	0.0	1.40 (1.32)	1.2
6	1.55 (0.98)	0.0	1.41 (1.21)	0.1	1.45 (0.84)	0.0	1.56 (1.54)	5.4
7	2.42 (1.64)	0.0	1.32 (0.86)	0.1	1.79 (1.31)	0.0	1.36 (0.96)	1.8
8	2.99 (2.52)	0.0	1.66 (2.09)	1.4	1.78 (1.72)	0.0	2.04 (2.94)	4.3
9	1.40 (0.85)	0.0	1.11 (0.69)	0.0	1.36 (0.74)	0.0	1.13 (0.72)	0.0
10	1.94 (1.89)	0.0	1.28 (0.86)	0.5	1.47 (1.12)	0.0	1.31 (0.88)	1.5
Combined	1.78 (1.53)	0.0	1.28 (1.10)	0.5	1.44 (1.09)	0.0	1.36 (1.35)	1.8

3D mean (standard deviation) registration errors for each parameter are shown in units of mm. Singularity represents the volume with negative Jacobian in units of ml.

Fig. 5.

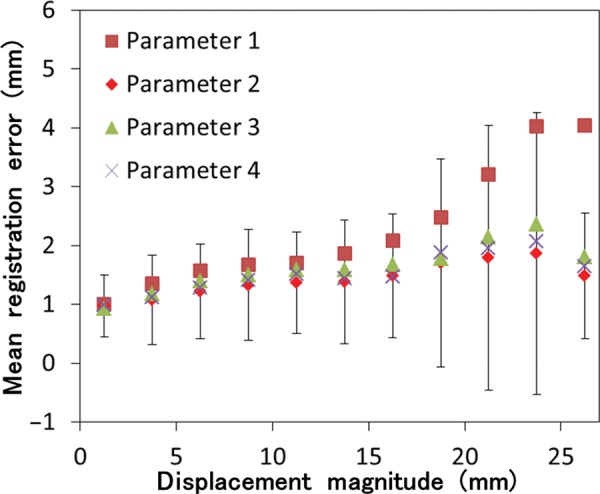
Registration error versus displacement magnitude of landmarks. Registration errors were binned corresponding to magnitude displacement of the landmarks in 2.5-mm increments. Only the error bar (standard deviation) of Parameter 2 is shown.

Fig. 6.

Local registration error. Each landmark point was color-coded corresponding to 3D magnitude of registration error, which derived from Parameter 2.

DISCUSSION

We evaluated the accuracy of B-spline transformation-based DIR implemented in elastix with three types of parameters. By using new functions in elastix, DIR accuracy was improved, even while keeping the same computation time. The improvement of accuracy was clear in cases that had large landmark displacement magnitude. We analyzed the relationship between landmark displacement and DIR accuracy and found that the improvement tended to be large where the lung was largely deformed. This improvement was achieved by modification of two DIR components. ASGD works with stochastic approximations of the cost function derivatives and, thus, requires little computation time to find robust deformation. The transform bending energy penalty term constrains unrealistic deformation and is likely to have contributed to the improvement. Salguero et al. [27] reported that uncertainty in DIR causes different mapped-doses. It is also obvious that DIR errors directly involve the accuracy of autocontouring. Yamamoto et al. [17] evaluated the variability of 4D CT ventilation with two types of registration algorithms. They reported that even less than a 1 mm difference of DVF can cause a significant difference in 4D CT-derived ventilation (<0.9 of Spearman's rank correlation coefficient). Therefore, the improvement of accuracy (0.34 mm improvement between Parameters 1 and 3) that we reported is clinically significant, and improved DIR would contribute to the higher performance of dose accumulation, 4D CT ventilation and autocontouring.

Castillo et al. reported that the mean 3D registration error of an in-house software-based optical-flow algorithm was 1.44 mm [28] using the same 10 sets of 4D CT images. In this study, the mean registration error from Cases 1–5 was 1.20 for Parameter 2. Gu et al. obtained the 3D registration error of in-house software based on Demons algorithms with these five sets of 4D CT and showed that the mean 3D registration error for all cases was 1.57 (1.54) mm [18]. Our result is comparable with the results of those earlier studies using optimized in-house DIR algorithms. Kadoya et al. also evaluated the accuracy of four types of DIR algorithms [12] including B-spline-based DIR implemented in Velocity AI, using these five sets of 4D CT images. The mean registration error with standard deviation of this B-spline-based DIR was 2.70 (2.24) mm. The registration error in our study was smaller than that obtained in their study with a commercial software-based B-spline algorithm. It should be noted that the registration accuracy and computation time are in a trade-off relationship. Commercial software is often designed to save calculation time and it might have caused the lower accuracy. Although elastix showed higher accuracy than that of the commercial software, further research is still needed to find parameters that can reduce computation time while maintaining acceptable accuracy for clinical use.

A number of reference standards have been utilized for validation of DIR software [29–31], including synthetically deformed images, high-contrast phantoms and expert-delineated landmark points. While synthetic images and phantoms might provide useful qualitative evaluation of DIR performance characteristics, they lack realism for clinical application. We utilized landmark-based validation of DIR algorithms with 4D CT images of real patients to achieve clinically meaningful validation of DIR. However, spatial intra-observer errors of landmark determination have been reported [16], and such errors may cause overestimation of the registration error, which is relatively large when DIR is performed well. Furthermore, if the distribution of reference landmarks is inclined to one side, the resulting registration error would be spatially weighted. It is necessary to confirm that the distribution of landmarks is not inclined. Therefore, care must be taken when registration errors are derived from different CT images or different landmark sets.

Wu et al. [19] divided 4D CT thoracic images into two regions (moving and less-moving subregions) and reported an improvement in DIR accuracy. The reported technique requires a long time and much manual effort. We divided thoracic images into ‘lung region’ and ‘others’. Our segmentation method is almost automatic, except for some manual modification, and requires less manual effort. Furthermore, improvement of DIR accuracy within the lung is obviously the same as that reported by Wu et al. Thus, our method is more appropriate for clinical use.

It has been reported that artifacts are observed in 4D CT images at an alarmingly high frequency (i.e. 90%) [32]. Some of the duplications, overlapping and incompleteness of the diaphragm found in [32] were also observed in the DIR-lab datasets we used. In this study, we utilized only maximum inhale and exhale images. The use of intermediate respiration phase images was reported [28], and this may reduce the influence of these artifacts. 4D CT acquisition with biofeedback or respiratory phase modeling [33, 34] was also reported, and this may reduce the artifacts themselves. Therefore, it may be possible to improve DIR accuracy with application of these techniques.

CONCLUSION

We evaluated the accuracy of B-spline-based DIR implemented in elastix using 4D CT images of 10 esophageal or lung cancer patients with 300 anatomical landmarks. Our results showed that the new functions implemented in elastix are useful for improving DIR accuracy while keeping the same computational time. This improvement was clear, especially where the lung moved a relatively large distance. This improved B-spline-based DIR could be used clinically to achieve high-accuracy adaptive radiotherapy.

FUNDING

This work was supported by Japan Society for the Promotion of Science-in-Aid for Young Scientists (B) (24791268) and a research grant of the Japan Radiological Society from Bayer.