Abstract
Motivation: Recently, a shift was made from using Gene Ontology (GO) to evaluate molecular network data to using these data to construct and evaluate GO. Dutkowski et al. provide the first evidence that a large part of GO can be reconstructed solely from topologies of molecular networks. Motivated by this work, we develop a novel data integration framework that integrates multiple types of molecular network data to reconstruct and update GO. We ask how much of GO can be recovered by integrating various molecular interaction data.
Results: We introduce a computational framework for integration of various biological networks using penalized non-negative matrix tri-factorization (PNMTF). It takes all network data in a matrix form and performs simultaneous clustering of genes and GO terms, inducing new relations between genes and GO terms (annotations) and between GO terms themselves. To improve the accuracy of our predicted relations, we extend the integration methodology to include additional topological information represented as the similarity in wiring around non-interacting genes. Surprisingly, by integrating topologies of bakers’ yeasts protein–protein interaction, genetic interaction (GI) and co-expression networks, our method reports as related 96% of GO terms that are directly related in GO. The inclusion of the wiring similarity of non-interacting genes contributes 6% to this large GO term association capture. Furthermore, we use our method to infer new relationships between GO terms solely from the topologies of these networks and validate 44% of our predictions in the literature. In addition, our integration method reproduces 48% of cellular component, 41% of molecular function and 41% of biological process GO terms, outperforming the previous method in the former two domains of GO. Finally, we predict new GO annotations of yeast genes and validate our predictions through GIs profiling.
Availability and implementation: Supplementary Tables of new GO term associations and predicted gene annotations are available at http://bio-nets.doc.ic.ac.uk/GO-Reconstruction/.
Contact: natasha@imperial.ac.uk
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
In many areas of biomedical research, ontologies play an important role in unification of knowledge as a hierarchy of terms and their mutual relationships. Among widely used ontologies is Gene Ontology (GO), which describes genes and gene products in terms of their associated biological process (BP), molecular function (MF) and cellular component (CC) (Ashburner et al., 2000). GO is a current major source of information for annotating genes and proteins across various species and providing tools for systematic assessment of experimental gene sets via enrichment analysis.
Since its foundation, GO has been growing in size and complexity containing today vast amounts of annotated biological data. Initially, GO was manually curated by domain experts and members of the research and annotation communities. However, because of their inconsistency in translation to GO terms and relations, manual curations have encountered many difficulties (Ashburner et al., 2001). Additionally, rapid development of technologies for biological data acquisition has resulted in an accumulation of biological data exceeding our ability to interpret (Chen and Xu, 2004).
To overcome these problems, many computational tools for automatic gene and protein annotation have been devised. Much effort has been invested in assessing the accuracy of such annotation predictions (Radivojac et al., 2013). Methods for gene annotation prediction have either followed approaches that transfer annotations from well-observed to partially observed genes based solely on sequence similarity (Loewenstein et al., 2009) or approaches that directly predict function of unknown genes using machine learning methods (Clare and King, 2003). Recent methodologies focus more on integration of distinct biological data sources, which contribute to more accurate predictions of gene annotation.
The availability of genomic-level information from high-throughput measurements of genetic and protein interactions, messenger RNA expression profiles and metabolic pathways has created new opportunities for function prediction. A major challenge is how to integrate all these diverse data to predict annotations of yet unannotated proteins. Among the widely used computational methods addressing this problem are Bayesian reasoning (Chen and Xu, 2004), network-based analysis (Mostafavi and Morris, 2010; Mostafavi et al., 2008), kernel-based statistical learning (Lanckriet et al., 2004) and matrix factorization-based data fusion (Žitnik and Blaz, 2014). All these methods have demonstrated that the integration of complementary biological data significantly improves accuracy of gene function annotation prediction.
Recent work incorporated large gene and protein interaction networks into a probabilistic clustering procedure to reconstruct the GO (Dutkowski et al., 2013). It identified new terms and relations that were missing from GO based solely on network topology. This work provides evidence that a large part of GO can be reconstructed using only topologies of molecular networks.
In this work, we propose a new data integration method for prediction of GO term annotations of unannotated genes and finding new relations between existing GO terms purely from network topology. The method is based on penalized non-negative matrix tri-factorization (PNMTF) for heterogeneous data clustering (Wang et al., 2008, 2011). PNMTF has been used for prediction of disease associations (Žitnik et al., 2013), identification of cancer subtypes (Liu et al., 2014), predicting protein–protein interactions (PPIs) (Wang et al., 2013) and detecting phenotype–gene associations (Hwang et al., 2012).
Here, we extend this method to take multiple types of molecular network data and use them to reconstruct and update GO with new information. We apply our method to Saccharomyces cerevisiae data used by Dutkowski et al. (2013): PPI network, genetic interaction (GI) network, gene co-expression (Co-Ex) network and integrated functional network known as YeastNet (Lee et al., 2007).
Our method takes all data in a matrix form and performs simultaneous clustering of genes and GO terms inducing new associations between genes and GO terms and between GO terms themselves. We extend the integration methodology to include similarity in wiring around non-interacting genes. We measure this by distance graphlet degree vectors (GDVs) (Pržulj, 2007). Graphlets and graphlet-based measures have bridged molecular network topology and biological function. For instance, simple homogeneous clustering of proteins in a PPI network based on the GDV similarity has revealed groups of proteins with a common biological function (Milenković and Pržulj, 2008; Milenković et al., 2010).
Therefore, we add these to incorporate more topology into the integration process and improve accuracy of predictions. Using various measures for assessing the quality of our prediction, we systematically examined the contribution of these additional topological constraints to GO prediction. Graphlet-based similarity has not been exploited in any of the previous network integration approaches.
Surprisingly, we find that our method can successfully reconstruct almost the entire GO by using solely topology of molecular interaction networks. Furthermore, we predict new GO term associations and gene annotations from integrated topologies of molecular interaction network and validate our predictions.
2 METHODS
2.1 Matrix tri-factorization for data integration
We use a co-clustering algorithm based on PNMTF to integrate multi-type biological data. The clustering analysis is used to infer new relations between data objects that were not previously present in the data. Such a technique makes use of all available information presented in the network form, including both inter-type relations and intra-type constraints (Ding et al., 2006; Wang et al., 2008). This algorithm aims to simultaneously cluster data using the interrelatedness between data types under the guidance of some prior knowledge given in the form of intra-type pairwise constraints. These constraints often indicate similarity or dissimilarity relationships between data objects of the same type. Constraints guide the clustering procedure so that similar objects can belong to the same cluster while dissimilar cannot.
The simplest co-clustering problem involves only two types of objects (e.g. genes and GO terms) with size n1 and n2. If there are n1 objects of the first type and n2 objects of the second type, then we have an inter-type relationship matrix with an entry representing the relationship between i-th data point in the first dataset and the j-th data point in the second dataset. Simultaneous clustering of these datasets can be seen as a solution of the non-negative matrix tri-factorization (NMTF) problem where a given relation matrix, can be approximated as the product of three low-rank matrix factors:
where non-negative and correspond to the cluster indicator matrix of the first and the second dataset, and corresponds to compressed low-dimensional version of the initial relation matrix. Rank factors, k1 and k2, are often chosen to be much smaller than the corresponding matrix dimensions (, ). NMTF algorithm minimizes the following objective function:
| (1) |
This objective function can be further used to incorporate intra-type constraints whose violation causes penalties. Constraints that relate data points, i and j, in two different datasets are represented via two constraint matrices, and . Entries of the constraint matrix are positive for dissimilar data objects because they impose penalties on the current approximation given in the Equation (1). Entries of the constraint matrix are negative for similar objects because they are rewords that reduce the objective function. Therefore, the constraint matrices can be included as additional penalty terms in the objective function in the following way:
| (2) |
where tr denotes the trace of a matrix. This optimization problem is known as PNMTF problem. Its solution produces two matrix factors, G1 and G2, that can be interpreted as the cluster indicator matrices for the first and the second dataset. Specifically, factor G1 is used to assign data objects from the first dataset to clusters so that data object j is placed in the cluster i if is the largest entry in column j (Brunet et al., 2004). This assignment procedure results in a binary connectivity matrix, C, of size with entry if objects p and q belong to the same cluster and otherwise. Hence, an integration of all data sources is achieved by clustering the first and the second datasets simultaneously using , and that encode the data.
Biological entities, such as genes and proteins engage in various molecular interactions, or are connected through GO relationships. We represent these as networks and integrate their network topology (also called structure) in the form of constraints of the objective function. These constraints are implemented into the objective function in the form of network Laplacians (Hwang et al., 2012; Wang et al., 2011). That is, we are now minimizing:
| (3) |
where represents network Laplacian of the molecular network of the α data type; is the network adjacency matrix, and is the diagonal degree matrix with entries being row summation of the matrix : . These additional, Laplacian-based terms encourage the connected or ontology-related genes (proteins) in the network to be assigned to the same cluster. To integrate the network data and predict GO term relationships from network topology, along with new gene annotations, the term imposes that interacting genes get placed into the same cluster and similarly imposes that linked GO terms get placed into the same cluster.
2.2 Integration of various constraints on the same objects
Most of the biological datasets include various types of interactions (i.e. constraints) over the same set of entities. For instance, genes might interact via GIs, and they also might be related based on the correlation of their expression profiles. The former is known as a GI network, and the latter as a gene Co-Ex network. To properly integrate this information into the clustering procedure, we make an improvement to the regularized PNMTF optimization problem. We extend it to take into account multiple constraints over the objects of the same type. Suppose we have a set of N adjacency matrices: , representing N data sources relating objects of the first type. By adding these constraints in the Laplacian form as penalty terms into our objective function (3), we end up with the following:
| (4) |
Integration of all available information about a particular data type has demonstrated to lead better predictions of new relations among data objects. For example, the integration of all available human molecular networks yields a successful reproduction of the existing and prediction of new associations between diseases (Žitnik et al., 2013).
Unlike previous works where only network connections are considered as constraints (Hwang et al., 2012; Liu et al., 2014; Wang et al., 2013; Zhang et al., 2011; Žitnik et al., 2013), our approach takes a step further by incorporating additional constraints in the form of topological similarity between nodes in a network that are not necessarily linked. Here, we use the topological similarity measure based on GDVs. Graphlets are small non-isomorphic-induced substructures of a large network (Pržulj et al., 2004). There are 29 graphlets containing 2–5 nodes. By taking into account the symmetries between nodes in a graphlet, we can distinguish between 73 automorphic orbits. Counting how many times a particular node touches any of 73 different orbits, we may define a 73-dimensional GDV (see Supplementary Fig. S1). For node u, i-th coordinate of its GDV vector, ui, denotes the number of times node u touches orbit i. GDV vector represents local structural properties of a node, and therefore, it can be used to compare topologies around nodes in a network. For that purpose, a measure of distance between nodes u and v is introduced as (Milenković and Pržulj, 2008):
| (5) |
where is defined as a logarithmic distance between nodes’ i-th orbits:
To take into account mutual dependencies between orbits, a weight is assigned to each orbit . The weight, wi, measures to which extent orbit i is affected by other orbits. Higher weights are assigned to orbits that are less affected by other orbits, whereas lower weights are assigned to orbits that are affected by many other orbits. The number of orbits that affect orbit i is given by oi.
Using the distance measure defined in Equation (5), GDV similarity between nodes u and v is measured as
GDV similarity measure has been used for predicting biological function of unclassified proteins (Milenković and Pržulj, 2008), classification of cancer and non-cancer genes (Milenković et al., 2010) and prediction of new cardiovascular disease genes (Sarajlić et al., 2013).
Here, we include GDV similarity measure into our objective function [Equation (4)] as followings. For each of the given data source β (i.e. biological network), we construct a similarity matrix . Then, by computing a statistically significant threshold for topological similarity of two nodes in each of the GDV similarity matrices, we consider only data objects (genes/proteins) with GDV similarity higher than the computed threshold (see Supplementary Fig. S2):
Topological similarity constraints are again implemented into the objective function through Laplacian regularization:
| (6) |
where, is a Laplacian of Σ matrix, and D is the diagonal matrix with entries equal to the row summation of Σ matrix.
2.3 Multiplicative update algorithm
We extend the original PNMTF algorithm (Wang et al., 2008) to handle the additional penalty terms and network regularizations in Equation (6). Solving the optimization problem results in the following multiplicative update rules for matrix factors G1, G2 and (Wang et al., 2008):
| (7) |
| (8) |
| (9) |
where we use + and − signs in superscripts to denote non-negative matrices and of a matrix M, respectively, defined as and . The algorithm starts by randomly initializing matrices G1 and G2, which are iteratively updated to minimize objective function in Equation (6). The rigorous proof of the correctness and convergence of these update rules can be found in (Wang et al., 2008). Under these update rules, the objective function J [Equation (6)] is guaranteed not to increase. Hence, we look at the change in the objective function between two consecutive iterations and define the stopping criterion as . In all our runs, parameter ϵ is set to , which was shown to be significant to minimize the objective function. Compared with the probabilistic clustering approach for GO reconstruction presented by Dutkowski et al. (2013), our approach is computationally more demanding because of slow convergence of multiplicative update rules. However, our approach is more general, as it can integrate any number and type of heterogeneous data that could lead to more accurate predictions.
2.4 Predicting associations between GO terms
Each factorization run produces matrix factors: G1 related to gene set, and G2 related to GO terms. We use G2 factor to construct connectivity matrix C as described in the Section 2.1. Clusters of mutually related GO terms are obtained from the connectivity matrix. To assess reliability and robustness of GO term associations prediction, we use the stochastic property of our algorithm. We perform multiple runs with the same rank parameters and different initial random initializations and construct a set of 20 different connectivity matrices: . Then, we compute the consensus matrix, , defined as the average over all connectivity matrices. Thereby entries in the consensus matrix range from 0 to 1, and they can be interpreted as probabilities that two GO terms, GOi and GOj, belong to the same cluster. To predict new GO term associations, we are only interested in values of probability equal to one because they correspond to the case of hard clustering, in which there is no overlap between clusters, and hence, there is no ambiguity in predicted GO term associations. The complete algorithm for prediction of new GO term association is summarized in Algorithm 1.
Algorithm 1 GO term associations prediction.
Input: Relation matrix: ; constraint matrices: , , for networks for Gene Ontology; rank parameters k1 and k2
Output: Consensus matrix
______________________________________________________________
for do
Initialize G1 and G2
while not do
Update using Equation (7) while keeping fixed G1 and G2
Update G1 using Equation (8) while keeping fixed G2 and
Update G2 using Equation (9) while keeping fixed G1 and
Compute connectivity matrix for GO terms using G2 for class assignment
Compute the average connectivity matrix as:
Extract new GO term relations:
To assess the statistical significance of GO term associations, we compute the P-value in the following way. First, we remove any prior knowledge on GO term relations (i.e. we remove matrix ). Then, we run our algorithm 100 times, each time with different relations matrix obtained by permuting the entries of the original relations matrix, . In total, we obtain different connectivity matrices. We define the P-value of a particular GO term association as the fraction of connectivity matrices in which that particular association is observed.
2.5 Rank parameters selection
Input parameters of our algorithm are factorization ranks, k1 and k2, which we systematically examine and choose to achieve a correct reduction of dimensionality of our data. These factorization ranks capture the meaningful information that can further be decomposed into clusters.
There is no agreed-upon procedure for choosing the right factorization ranks. The most common approach, widely used in many dimension reduction problems is cophenetic correlation coefficient, as a quantitative measure of stability for clustering (Brunet et al., 2004). For a given factorization rank, cophenetic correlation coefficient is computed over the values of the consensus matrix, . It is defined as the Pearson’s correlation coefficient between the distance matrix, , and the matrix of cophenetic distances obtained by the linkage used in hierarchical clustering for re-ordering . If the clustering is stable, i.e. the entries in are close to 0 or 1, then , otherwise, if the entries are scattered between 0 and 1, .
A simple generalization of this procedure applied to two types of our data (genes and GO terms) includes computation of cophenetic correlation coefficient for each of the consensus matrices, (for genes), (for GO terms), and then we define the average cophenetic correlation coefficient as
| (10) |
We search for the values of, k1 and k2, that maximize . We do this by running our algorithm for all pairs such that , so that we would capture the best dimensionality of our data (see below).
2.6 Datasets and preprocessing
To make our study directly comparable with the competing method for reconstructing GO from network data, we run our method on the same S.cerevisiae data as Dutkowski et al. (2013): PPI network from BioGRID (Chatr-Aryamontri et al., 2013), GI network from DRYGIN (Costanzo et al., 2010), gene Co-Ex network from SMD (Hubble et al., 2009) and integrated function network, YeastNet, from (Lee et al., 2007). For each of the these networks, we construct Laplacian constraint matrices, , respectively.
To apply multiplicative update rules, we make all data matrices of the same dimension: we construct them over the union of genes presented in all four data sources. The semantic structure of GO is also taken into account in our integration algorithm. We extract all GO terms for S.cerevisiae and create constraint matrix as follows. First, we construct a directed acyclic ontology graph using the four basic semantic types of GO relations: is_a, part_of, regulates and has_part. Then, we assign value 0.9l to each pair of GO terms as a measure of association strength, where l is the length of directed shortest path between terms in the ontology graph. This allows us to also take into account mutual influence of hierarchically distant non-adjacent GO terms (Zhu et al., 2005). The value of 0.9 is chosen from empirical observations, as described by Žitnik et al. (2013). Finally, we construct the Laplacian constraint matrix, , by using these values of association strengths.
Annotation files from GO are used to construct the binary relation matrix, , with entries if gene i is annotated by GO term j and 0 otherwise. For each of the aforementioned biological networks, we also compute GDV similarity constraint matrices: . As we describe in Section 2.2, we only consider gene pairs with statistically significant GDV similarity. All these network data are schematically represented in Figure 1.
Fig. 1.
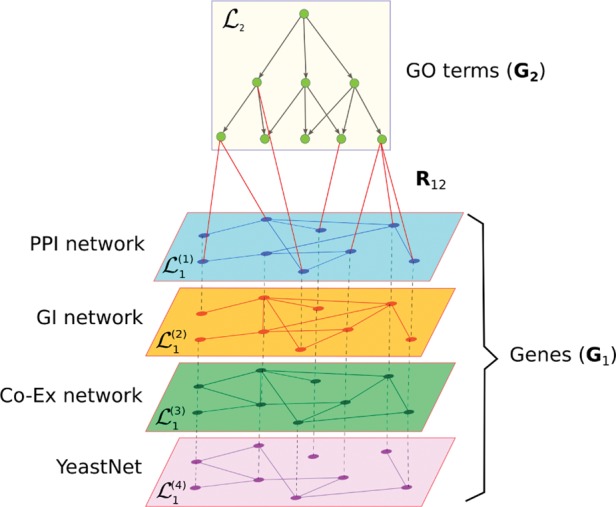
Schematic representation of datasets used in this study. Two types of objects are represented: genes interconnected via four types of interaction networks (PPI, GI, Co-Ex and YeastNet) and GO terms interconnected via directed semantic relations from GO hierarchy
3 RESULTS AND DISCUSSION
We apply our algorithm to identify new GO term relations and annotate proteins with existing GO terms by integrating multiple independent network sources given in the Table 1. We find that the optimal rank parameters k1 and k2 are 58 and 56, respectively (see Supplementary Fig. S3). We examine the contribution of each data source to the integration model.
Table 1.
All networks used in this study
| Data | Matrix representation | Matrix dimension | NNZa |
|---|---|---|---|
| PPI | 26 596 | ||
| GI | 22 480 | ||
| Co-Ex | 3410 | ||
| YeastNet | 21 146 | ||
| GDV similarity (PPI) | 93 536 | ||
| GDV similarity (GI) | 89 434 | ||
| GDV similarity (Co-Ex) | 2524 | ||
| GDV similarity (YeastNet) | 88 986 | ||
| GO semantic structure | 15 872 | ||
| Gene annotation | 45 782 | ||
Note: Matrix dimensions are given before unioning genes in all data to obtain the same dimension of matrices (see Section 2.6). GDV matrices are of different dimension than - matrices because they contain only genes that are statistically significantly similar (see Section 2.2).
aNumber of non-zero entries in a matrix.
3.1 Contribution of data to the integration model
We estimate the influence of each network on our integration model by comparing the quality of the initial model (consisting of four networks and their corresponding GDV similarity matrices) with the quality of the model with one data source removed from the initial set. Models are evaluated through residual sum of squares (RSS), , and explained variance (Evar), , that measure the performance of the matrix factorization algorithm and its ability to accurately reproduce the gene–GO term relation matrix. Low values of RSS and high values of Evar indicate better quality of the model (Hutchins et al., 2008).
We find that with the removal of each of the four data sources (a network along with its corresponding GDV similarity matrix) the value of RSS increases, while the value of Evar decreases, implying that each data source contributes to the quality of the model. Relative increase of RSS and relative decrease of Evar (with respect to the initial model containing all the data), computed by removing a particular network along with its corresponding GDV similarity matrix, are shown in the top panel of Figure 2. We find that the largest model degradation is achieved with the removal of GI network and its corresponding GDV similarity matrix. A similar result was reported by Žitnik et al. (2013): they found GIs to be the most informative data source in prediction of disease–disease associations. Exclusion of the gene Co-Ex network and its corresponding GDV similarity matrix results in the smallest changes in RSS and Evar indicating that Co-Ex data contribute the least to the quality of the model.
Fig. 2.
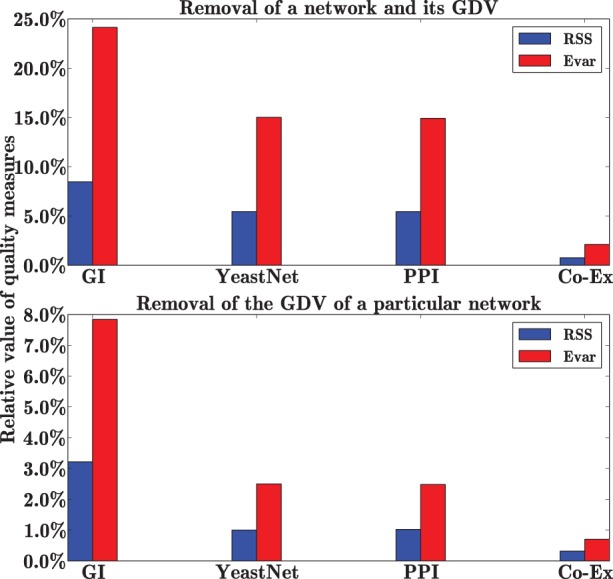
Relative contribution of each data source to the integration model measured by RSS, blue, and Evar, red. The top panel shows the relative changes in RSS and Evar with the removal of a particular network and its corresponding GDV similarity matrix. The bottom panel shows the same measures but only with removal of GDV similarity matrices
To examine the contribution of GDV similarities to our model, we conduct the same experiment by removing only the GDV similarity matrix of each of the biological networks from the initial dataset. The results are shown in the bottom panel of Figure 2.
We see that GDV similarities contribute to the quality of the models. The smallest contribution to the model, a relative increase of 0.32% in RSS, is that of the gene Co-Ex network. Also, we examine contributions of all pairs of the four networks. We confirm the observation of Dutkowski et al. (2013) that a combination of YeastNet and Co-Ex network contributes the least to the quality of the model ( %, %).
3.2 Recovering existing knowledge
Our integration of the biological networks and their corresponding GDV similarities results in a set of highly reliable GO term classes, represented as clusters in a block diagonal form of the consensus matrix. Size distribution of these clusters and the consensus matrix are shown in the Supplementary Figure S4. In addition to this experiment, we also perform the same analysis on the data consisting only of biological networks (excluding GDV similarities from our integration procedure). This allows us to compare the clustering results of different integration models and to estimate the importance of additional topological constraints.
To evaluate the performance of our methodology in reproducing GO term relations, we look at the overlap between cluster members and the existing GO hierarchy and find that on average 92% of cluster members are directly connected via semantic relations in GO. These cluster-induced GO term relations are confirmed to be statistically significant (, computed as explained in Section 2.4). A slightly lower score of 90% is achieved when considering only the network data without GDV similarity matrices, indicating that graphlet similarity matrices contribute to capturing relations, which would otherwise be missed.
Furthermore, we examine the robustness of this result to the removal of particular datasets. Surprisingly, we find that omission of GDV similarity matrix of gene Co-Ex network contributes the most to the predictive performance of our algorithm, leading to the maximum of 96% of recovered GO terms. Hence, inclusion of GDV similarity of gene Co-Ex network introduces noise into the integration procedure, wrongly guiding the clustering process, which in turn results in lower prediction performance. This is a consequence of the random GDV similarity distribution over all genes in the gene Co-Ex network (Supplementary Fig. S2C). Given that inclusion of GDV similarity matrix of the Co-Ex network impairs the predictive performance of our algorithm and because we have shown that its exclusion makes minimal effect on the quality of the model, we discard that data source from further analysis.
Surprisingly, recovering 96% of GO terms that are directly related in GO (this is not a percentage of recovered relations between GO terms) by is_a, part_of, regulates and has_part associations, indicates that entire GO could, in principle, be reconstructed solely from topologies of molecular interaction networks. Reporting this statistic is consistent with what previous studies using a similar methodology reported (Žitnik et al., 2013). When we say that ‘96% of GO terms is recovered’, we mean that our methodology correctly identifies a set of 96% of GO terms that contain relations between them. This does not mean that this set is fully connected (i.e. that each pair of GO terms in it is related). Our set of 96% of GO terms contains 78% of all relations currently present in GO. To our knowledge, because a large part of GO is sequence derived, this is the first conformation that network topology and sequence carry similar biological information.
To further validate the performance of our methodology in reconstruction of GO terms, we use the gene–GO term relation matrix, reconstructed from matrix factors . Its entries indicate the annotation strength of a gene, i, related to a GO term j, with denoting absence of annotation, while denoting the highest confidence of annotation. We define GO term j* as a candidate to annotate gene i if the association score is larger that the mean of association scores over all known annotations of gene i. To identify only high confidence gene-GO term predictions, we pick j* that are in the top 5% of largest association scores between GO term j* and all other genes. As before, we run our algorithm with and without GDV similarities (we exclude GDV similarities of Co-Ex network for reasons presented above).
We compute the percentage of reproduced, high confidence GO terms for CC, BP and MF separately. The results are shown in Figure 3a. Better results are achieved when GDV similarity matrices are included in the prediction model. Specifically, we capture 41% of BP terms, 41% of MF terms and 48% of CC terms. The BP and MF results outperform those of Dutkowski et al. (2013), whereas they achieve a higher percentage of reproduced GO terms in CC.
Fig. 3.
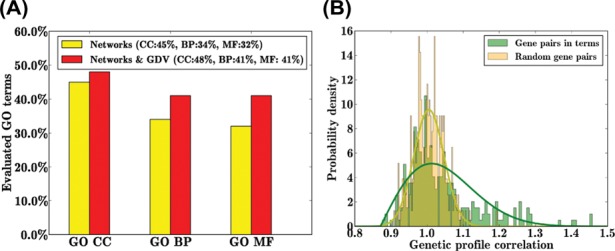
(a) The fraction of GO terms in each of CC, BP and MF obtained from entries of reconstructed gene–GO term relationship matrix obtained with and without GDV similarities (denoted in red and yellow colors, respectively). (b) Distribution of correlations of GI profiles among predicted genes associated to GO terms plotted against distributions of randomly selected gene pairs. Value of correlation, presented here, is shifted in the positive range: [0,2]
3.3 Validating predictions
Among all the statistically significant () GO term association predictions, we find 132 not presented in GO (see Supplementary Table S1). To further increase confidence, we extract these associations from clusters with fewer than three GO terms that are stable over multiple factorization runs. We find that 14 of the 132 associations are between GO terms that have high semantic similarity and also confirm that additional 31 associations agree with predictions of Dutkowski et al. (2013). For example, our approach predicts term GO:0035267 (NuA4 histone acetyltransferase complex) as a parent of GO:0032777 (Piccolo NuA4 histone acetyltransferase complex), which was also reported by Dutkowski et al. (2013) and submitted to the GO Consortium for inclusion into the ontology. We further perform literature curation to validate the remaining predicted GO associations. We find literature support for another 13 of them (Supplementary Table S1). Hence, we validate 58 of 132 of our predictions.
Our approach not only identifies novel GO term association but it also makes highly reliable predictions for new gene–GO term relations. We predict new functional annotation of 972 genes (see Supplementary Table S2). Highly reliable predictions are those with association strength in the top 5%, as described in Section 3.2. For instance, we predict three genes, YDR101C, YDR49C and YNL132W, to be involved in ribosomal subunit biogenesis (GO:0042273) and find that the same functional prediction was previously reported through different approaches by Chen and Xu (2004) and Joshi et al. (2004). To validate the 972 predicted annotations, we use the new unpublished full set of yeast’s GI profiles from Boone Lab (Boone, 2014). The data consist of Pearson’s correlation coefficients of genetic profiles between gene pairs. We create the distribution of these correlations between newly annotated gene pairs for which we predict GO annotations. We compare this distribution of genetic profile correlations between the same number randomly sampled pairs of genes (we sampled multiple times and got consistent results). We observe higher correlations for predicted gene pairs than for random pairs (Fig. 3b). Moreover, using two-sample Kolmogorov–Smirnov (KS) test, we show that these two distributions significantly differ (KS statistics, D = 0.2 and P-value, ). Thus, these results are highly consistent with our predictions of new annotations. This validates our predicted GO annotations. Even though GI profiling analysis provides evidence that our algorithm is able to successfully predict new gene functions, additional biological validation would be needed for better understanding of these newly assigned functions.
4 CONCLUSIONS
We introduce a method for reconstruction of GO that is based on integrating solely the topology of biological networks. It captures 96% of the existing GO term relations and is capable of successfully identifying additional GO term associations as well as predicting gene annotations. Our method is general in the sense that it can integrate any heterogeneous systems-level interaction data. Therefore, it can easily be extended with new data that could consequently enhance the model’s predictive performance. This work suggests that the entire GO could be reconstructed from molecular interaction networks.
Supplementary Material
ACKNOWLEDGMENT
We thank Professor Charlie Boone for giving us his unpublished complete set of genetic interactions in baker’s yeast.
Funding: This work was supported by the European Research Council (ERC) Starting Independent Researcher Grant 278212, the National Science Foundation (NSF) Cyber-Enabled Discovery and Innovation (CDI) OIA-1028394, the Serbian Ministry of Education and Science Project III44006 and ARRS project J1-5454.
Conflict of interest: none declared.
REFERENCES
- Ashburner M, et al. Gene ontology: tool for the unification of biology. Nat. Genet. 2000;25:25–29. doi: 10.1038/75556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner M, et al. Creating the gene ontology resource: design and implementation. Genome Res. 2001;11:1425–1433. doi: 10.1101/gr.180801. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brunet JP, et al. Metagenes and molecular pattern discovery using matrix factorization. Proc. Natl Acad. Sci. USA. 2004;101:4164–4169. doi: 10.1073/pnas.0308531101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chatr-Aryamontri A, et al. The BioGRID interaction database. Nucleic Acids Res. 2013;41:D816–D823. doi: 10.1093/nar/gks1158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y, Xu D. Global protein function annotation through mining genome-scale data in yeast Saccharomyces cerevisiae. Nucleic Acids Res. 2004;32:6414–6424. doi: 10.1093/nar/gkh978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clare A, King RD. Predicting gene function in Saccharomyces cerevisiae. Bioinformatics. 2003;19:ii42–ii49. doi: 10.1093/bioinformatics/btg1058. [DOI] [PubMed] [Google Scholar]
- Costanzo M, et al. The genetic landscape of a cell. Science. 2010;327:425–431. doi: 10.1126/science.1180823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding C, et al. Proceedings of the 12th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. 2006. Orthogonal nonnegative matrix t-factorizations for clustering. KDD ’06, New York, NY, ACM, pp. 126–135. [Google Scholar]
- Dutkowski J, et al. A gene ontology inferred from molecular networks. Nat. Biotech. 2013;31:38–45. doi: 10.1038/nbt.2463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubble J, et al. Implementation of genepattern within the stanford microarray database. Nucleic Acids Res. 2009;37:D898–D901. doi: 10.1093/nar/gkn786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hutchins LN, et al. Position-dependent motif characterization using non-negative matrix factorization. Bioinformatics. 2008;24:2684–2690. doi: 10.1093/bioinformatics/btn526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang T, et al. Co-clustering phenomegenome for phenotype classification and disease gene discovery. Nucleic Acids Res. 2012;40:e146. doi: 10.1093/nar/gks615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joshi T, et al. Genome-scale gene function prediction using multiple sources of high-throughput data in yeast Saccharomyces cerevisiae. OMICS. 2004;8:322–333. doi: 10.1089/omi.2004.8.322. [DOI] [PubMed] [Google Scholar]
- Lanckriet GRG, et al. A statistical framework for genomic data fusion. Bioinformatics. 2004;20:2626–2635. doi: 10.1093/bioinformatics/bth294. [DOI] [PubMed] [Google Scholar]
- Lee I, et al. An improved, bias-reduced probabilistic functional gene network of baker’s yeast, Saccharomyces cerevisiae. PLoS One. 2007;2:e988. doi: 10.1371/journal.pone.0000988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu Y, et al. A network-assisted co-clustering algorithm to discover cancer subtypes based on gene expression. BMC Bioinformatics. 2014;15:37. doi: 10.1186/1471-2105-15-37. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loewenstein Y, et al. Protein function annotation by homology-based inference. Genome Biol. 2009;10:207. doi: 10.1186/gb-2009-10-2-207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milenković T, Pržulj N. Uncovering biological network function via graphlet degree signatures. Cancer Inform. 2008;6:257–273. [PMC free article] [PubMed] [Google Scholar]
- Milenković T, et al. Systems-level cancer gene identification from protein interaction network topology applied to melanogenesis-related functional genomics data. J. R. Soc. Interface. 2010;7:423–437. doi: 10.1098/rsif.2009.0192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mostafavi S, Morris Q. Fast integration of heterogeneous data sources for predicting gene function with limited annotation. Bioinformatics. 2010;26:1759–1765. doi: 10.1093/bioinformatics/btq262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mostafavi S, et al. Genemania: a real-time multiple association network integration algorithm for predicting gene function. Genome Biol. 2008;9:S4. doi: 10.1186/gb-2008-9-s1-s4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pržulj N. Biological network comparison using graphlet degree distribution. Bioinformatics. 2007;23:e177–e183. doi: 10.1093/bioinformatics/btl301. [DOI] [PubMed] [Google Scholar]
- Pržulj N, et al. Modeling interactome: scale-free or geometric? Bioinformatics. 2004;20:3508–3515. doi: 10.1093/bioinformatics/bth436. [DOI] [PubMed] [Google Scholar]
- Radivojac P, et al. A large-scale evaluation of computational protein function prediction. Nat. Meth. 2013;10:221–227. doi: 10.1038/nmeth.2340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarajlić A, et al. Network topology reveals key cardiovascular disease genes. PLoS One. 2013;8:e71537. doi: 10.1371/journal.pone.0071537. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang F, et al. SDM. 2008. Semi-supervised clustering via matrix factorization. SIAM, pp. 1–12. [Google Scholar]
- Wang H, et al. Proceedings of the 20th ACM International Conference on Information and Knowledge Management. 2011. Simultaneous clustering of multi-type relational data via symmetric nonnegative matrix tri-factorization. CIKM ’11, New York, NY, ACM, pp. 279–284. [Google Scholar]
- Wang H, et al. Predicting protein-protein interactions from multimodal biological data sources via nonnegative matrix tri-factorization. J. Comput. Biol. 2013;20:344–358. doi: 10.1089/cmb.2012.0273. [DOI] [PubMed] [Google Scholar]
- Zhang S, et al. A novel computational framework for simultaneous integration of multiple types of genomic data to identify microrna-gene regulatory modules. Bioinformatics. 2011;27:i401–i409. doi: 10.1093/bioinformatics/btr206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu D, et al. Network constrained clustering for gene microarray data. Bioinformatics. 2005;21:4014–4020. doi: 10.1093/bioinformatics/bti655. [DOI] [PubMed] [Google Scholar]
- Žitnik M, Blaz Z. Matrix factorization-based data fusion for gene function prediction in baker's yeast and slime mold. Pac. Symp. Biocomput. 2014:400–411. [PMC free article] [PubMed] [Google Scholar]
- Žitnik M, et al. Discovering disease-disease associations by fusing systems-level molecular data. Sci. Rep. 2013;3:3202. doi: 10.1038/srep03202. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


