COFFDROP: A Coarse-Grained Nonbonded Force Field for Proteins Derived from All-Atom Explicit-Solvent Molecular Dynamics Simulations of Amino Acids

Abstract

We describe the derivation of a set of bonded and nonbonded coarse-grained (CG) potential functions for use in implicit-solvent Brownian dynamics (BD) simulations of proteins derived from all-atom explicit-solvent molecular dynamics (MD) simulations of amino acids. Bonded potential functions were derived from 1 μs MD simulations of each of the 20 canonical amino acids, with histidine modeled in both its protonated and neutral forms; nonbonded potential functions were derived from 1 μs MD simulations of every possible pairing of the amino acids (231 different systems). The angle and dihedral probability distributions and radial distribution functions sampled during MD were used to optimize a set of CG potential functions through use of the iterative Boltzmann inversion (IBI) method. The optimized set of potential functions—which we term COFFDROP (COarse-grained Force Field for Dynamic Representation Of Proteins)—quantitatively reproduced all of the “target” MD distributions. In a first test of the force field, it was used to predict the clustering behavior of concentrated amino acid solutions; the predictions were directly compared with the results of corresponding all-atom explicit-solvent MD simulations and found to be in excellent agreement. In a second test, BD simulations of the small protein villin headpiece were carried out at concentrations that have recently been studied in all-atom explicit-solvent MD simulations by Petrov and Zagrovic (PLoS Comput. Biol.2014, 5, e1003638). The anomalously strong intermolecular interactions seen in the MD study were reproduced in the COFFDROP simulations; a simple scaling of COFFDROP’s nonbonded parameters, however, produced results in better accordance with experiment. Overall, our results suggest that potential functions derived from simulations of pairwise amino acid interactions might be of quite broad applicability, with COFFDROP likely to be especially useful for modeling unfolded or intrinsically disordered proteins.

Introduction

Although advances in computational software and hardware have recently allowed for millisecond simulations of single proteins² and 100 ns simulations of the entire HIV-1 capsid³ using all-atom models, the extreme costs associated with large or long explicit-solvent biomolecular simulations continues to spur interest in the development of cheaper, coarse-grained (CG) simulation models: this interest is reflected in the large number of excellent review articles that have been written on this subject in recent years.⁴⁻¹⁹ One critical consideration in the development of CG models is how to map the detailed (usually all-atom) structural model to its more coarse, bead-level representation, that is, which degrees of freedom are to be factored out and which are to be left in. A second consideration, and the focus of the present work, is how to assign potential functions to the interactions of the CG beads so that they produce realistic or desired behavior.

One route to developing CG potential functions for use in simulations is by attempting to reproduce experimental data such as the free energies of transfer of model compounds (e.g., amino acids) between solvents,²⁰⁻²² or osmotic second virial coefficients.^23,24 This approach has the clear advantage of being grounded in reality but can, in some cases, leave the problem underdetermined as there may be several ways to reproduce the data. A second approach, feasible for proteins at least, is to use the statistics of interatomic or inter-residue distances observed in the Protein DataBank (http://www.rcsb.org) as a proxy for the thermodynamics of these interactions.²⁵⁻³¹ This approach has the advantage of being based on a very ready source of data, but there remain questions about how to define the reference state (i.e., the baseline against which the apparent interaction thermodynamics are to be computed) and the extent to which the resulting potential functions can be interpreted physically.³²⁻³⁴

A third approach, and the approach that is followed here, is to derive potential functions by attempting to reproduce the behavior seen in more detailed simulations (e.g., explicit-solvent, all-atom molecular dynamics (MD) simulations). One advantage with this approach is that, with current computational resources, it is now possible to obtain excellent statistics on both the thermodynamics and geometries of intra- and intermolecular interactions. For this reason, there have been a number of applications of this approach to biomolecular systems such as lipids,³⁵⁻⁴⁵ carbohydrates,⁴⁶⁻⁴⁹ and proteins;⁵⁰⁻⁵⁵ especially relevant to the present study is the work of the Betancourt group, who derived one-bead-per-residue nonbonded potential functions describing the mutual interactions of the 20 common amino acids by fitting to MD data.⁵⁶ The principal disadvantage with this approach is obviously the concern that the all-atom force fields are inaccurate, but in recent years, atomistic force fields for proteins have reached a sufficiently high level of sophistication and accuracy⁵⁷⁻⁶⁰ that this is likely to become a common route to deriving CG models.

We report here the optimization of a set of bonded and pairwise nonbonded potential functions for use in simulating protein systems by reproducing the thermodynamics of inter-residue interactions observed in corresponding all-atom, explicit-solvent MD simulations. Since one of our long-term interests is in simulating the behavior of proteins in the crowded conditions of biological cells, and given that such simulations will need to be conducted on very long time scales and length scales, our focus is on developing a CG protein model that is quite simple. Specifically, while there are many mapping schemes that might be imagined, we have chosen to use a model in which one pseudoatom is used to represent the backbone of each residue and 0–3 pseudoatoms are used to represent the side chains (see Methods).

There are a number of techniques that might be used to derive CG potential functions from all-atom simulation data, such as the inverse Monte Carlo method developed by Lyubartsev and Laaksonen^61,62 and the force matching approaches pioneered by Voth^37,63 and co-workers.⁶⁴ Here, however, we use the iterative Boltzmann inversion (IBI) method that was first introduced by Soper⁶⁵ to develop an atomistic water force field capable of reproducing radial distribution functions obtained from neutron scattering experiments, and later expanded by Reith, Pütz, and Müller–Plathe to refine a set of effective CG site–site pair potential functions for polyisoprene from atomic simulation data.⁶⁶ As the name implies, IBI uses an iterative approach, involving repeated rounds of CG simulation, to optimize potential functions so that distribution functions of interest observed in the more detailed simulations are reproduced to a desired level of accuracy in the CG simulations. The method has been successfully used by a number of different groups^{42,43,49,55,67−69} and has recently been implemented in a software package developed by the Lyubartsev group.⁷⁰

Here, we use the IBI methodology to (a) optimize bonded potential functions to reproduce the angle and dihedral distributions of single amino acids, and (b) optimize nonbonded potential functions to reproduce radial distribution functions of pairs of amino acids calculated from MD simulation. Using this methodology, we have created COFFDROP (COarse-grained Force Field for Dynamic Representation Of Proteins), a CG force field that captures the internal flexibility of single amino acids and the intermolecular interactions of every pairing of the amino acids as described by explicit-solvent MD simulation. We show that COFFDROP performs surprisingly well in simulations of high concentrations of amino acids and in very preliminary simulations of protein–protein interactions, both of which represent important steps toward the eventual goal of accurately simulating more complex, crowded biomolecular systems.

Methods

Systems Simulated

In this work, CG parameters are derived to describe the internal degrees of freedom of each of the 20 amino acids and their nonbonded interactions with each other; separate sets of parameters are derived for histidine’s neutral and protonated forms. In all of the simulations described here each amino acid was capped with an acetyl (Ace) group at the N-terminus and an N-methyl (Nme) group at the C-terminus in order to mimic the Cα atoms of adjacent residues that would be present in proteins. For the derivation of bonded parameters, each capped amino acid was simulated alone; for the derivation of nonbonded parameters, each possible pairing of the capped amino acids was simulated: since there are n(n – 1)/2 heterointeractions and n homointeractions, where n is the number of amino acid types, we simulated a total of 231 different amino acid-pair combinations. All MD simulations were performed using all-atom models in explicit solvent (see below). In order to test subsequently the ability of the derived nonbonded CG parameters to describe associations in more complex systems, additional MD simulations of systems comprising three or four molecules of alanine, asparagine, aspartate, cysteine, glycine, lysine, leucine, tryptophan, tyrosine, and valine were performed. To test the CG parameters at much higher amino acid concentrations, simulations of alanine, leucine, asparagine, and tryptophan were also performed at concentrations of 50, 100, 200, and 300 mg/mL. Finally, to test the CG parameters’ ability to describe a prototypical weak protein–protein interaction that has been the subject of recent MD work,¹ simulations of the small protein villin headpiece at a concentration of 9.2 mM were also performed.

Molecular Dynamics Simulations

All MD simulations were performed using GROMACS version 4.5.1.^71,72 In all simulations, the amino acid molecules were described with the Amber ff99SB-ILDN^73,74 force field and water molecules were modeled with the TIP4P-Ew model.⁷⁵ Simulations were performed within a 35 Å × 35 Å × 35 Å box to which periodic boundary conditions were applied. All simulations followed the same protocol: systems were first energy-minimized with a steepest descent algorithm for 1000 steps, gradually heated to 298 K over the course of 350 ps, and equilibrated for a further period of 1 ns. Following equilibration, a production simulation was carried out in the NPT ensemble, with the temperature maintained at 298 K using the Nosé–Hoover thermostat^76,77 and the pressure maintained at 1 atm using the Parrinello–Rahman barostat.⁷⁸ A cutoff of 10 Å was applied to short-range nonbonded interactions and the smooth particle mesh Ewald method⁷⁹ was used to calculate all long-range electrostatic interactions. A 2.5 fs time step was used with bonds being constrained to their equilibrium lengths using the LINCS algorithm.⁸⁰ Each production simulation was carried out for 1 μs with the atomic coordinates of the solutes being saved every 0.1 ps to give a total of 10 000 000 snapshots for each system. Each such simulation required approximately 10 days to complete on an 8-core server. Since our data may be of use for others interested in deriving CG force fields from all-atom explicit-solvent MD simulations, the trajectory files for all of our MD simulations have been made available for download from our group’s ftp server: ftp://128.255.119.154/pub/.

MD Analysis: Association Kinetics

To calculate the association rate constants for each amino acid pair, the protocol proposed by Zhang and McCammon⁸¹ was used. First, following our previous work,⁸² a radial distribution function, g(r), was calculated using only the closest distance between any pair of heavy atoms in each snapshot of the two solutes. Based on the plots of these 231 g(r) functions (see Results), and solely for the purposes of calculating association kinetics, we chose to define solutes as being in an associated state when the closest distance between any pair of heavy atoms was less than 3.9 Å, and being in a dissociated state when the closest distance was greater than 10.0 Å. Using these definitions, each simulation was analyzed to record—for every association event—the time elapsed between the system leaving the dissociated state and entering the associated state. The average number of such association events found in each simulation was 550; the highest number of events was 663 for the glycine–glycine system and the lowest number of events was 384 for the aspartate-glutamate system. Knowing the duration of each association event allowed a “survival function” for the dissociated state to be constructed and plotted versus time. Following Zhang and McCammon, this survival function was then fit to an exponential, y = A exp^(−Bt), where A is the value of the survival function at time, t = 0, and B is the (effectively unimolecular) association rate constant.

To determine whether the computed association rate constants were consistent with association occurring via a diffusion limited mechanism, the translational diffusion coefficients, D_trans, of the individual amino acids were calculated (from simulations of single amino acids) using Einstein’s equation:

1

where ⟨Δr²⟩ is the ensemble-average mean squared displacement of the center of mass of the amino acid and Δt is the observation interval over which the displacement is measured (in this case, 1 ns).

MD Analysis: Association Thermodynamics

The association constants, K_A, for each pair of amino acids were computed by integrating (using Simpson’s method) the g(r)s between 0 and 5.7 Å as outlined by Zhang and McCammon:⁸¹

2

Here, r is the distance expressed in units of 1600^1/3 Å, which allows K_A to be calculated corresponding to a standard state of 1 M. K_A was then converted into a binding free energy by using ΔG° = −RT ln K_A.

To determine the extent of similarities between amino acids in terms of their interactions with other amino acids, a dendrogram was created based on the Cα–Cα g(r) functions obtained from the all-atom MD simulations. First, a correlation coefficient was computed for each pair of amino acids by comparing their g(r) functions with all 21 amino acid types in the range 3–12 Å. For example, to determine how similar alanine and threonine are in terms of their interactions with amino acids, we computed the Spearman correlation coefficient for the entire set of 21 g(r)s for ala–ala, ala–arg, ala–asn, ..., with the set of 21 g(r)s for thr–ala, thr–arg, thr–asn, ... . Next, the resulting 231 correlation coefficients were converted into an effective “distance matrix” using the Canberra algorithm and converted into dendrogram form using agglomerative clustering implemented in the R function “hclust”. Both the creation of the distance matrix and the dendrogram were carried out using R version 2.14.10;⁸³ a related approach to clustering of amino acids according to their interaction preferences has been described by the Liang group.⁸⁴

COFFDROP Coarse Grained Mapping Scheme

The backbone mapping scheme used in COFFDROP places one pseudoatom at the Cα position, one pseudoatom on the methyl carbon of the Ace capping group and one pseudoatom on the methyl carbon of the Nme capping group. The side chains of the amino acids are represented by between 0 (for glycine) and 3 (for tryptophan) pseudoatoms (Supporting Information Figure S1 and Table S1). For the uncharged amino acids, all pseudoatoms carry a zero partial charge. For the amino acids that are typically charged at pH 7 (aspartate, glutamate, arginine, and lysine), and for the protonated form of histidine, a formal charge of either +1 or −1 was placed on the side chain pseudoatom that was closest to the true position of the charged functional group.

The mapping scheme described above was used to convert the 10 000 000 snapshots obtained from each MD simulation into their corresponding CG representations. The CG-converted MD simulations of the single amino acids were then used to generate “target” probability distributions of bond angles and dihedrals against which the bonded parameters of COFFDROP were parametrized. Similarly, the CG-converted MD simulations of pairs of amino acids were used to generate “target” g(r)s for all pseudoatom–pseudoatom interactions against which the nonbonded parameters of COFFDROP were parametrized.

Brownian Dynamics Simulations

All Brownian dynamics (BD) simulations were performed using the algorithm of Ermak and McCammon⁸⁵ with in-house software and using settings that corresponded as closely as possible to those used in the MD simulations. All amino acid simulations were performed within a 35 Å × 35 Å × 35 Å box to which periodic boundary conditions were applied. For systems that contained two or more charged amino acids, a grid-based Ewald method⁸⁶ was used to calculate the long-range electrostatic interactions; energies and forces computed with this method were identical to those obtained using the smooth PME method implemented in GROMACS. All simulations were performed at 298 K with a dielectric constant of 62.9 being applied to all electrostatic interactions as this is the reported value for the TIP4P-Ew water model⁷⁵ used in the MD simulations. All BD simulations were conducted for 5 μs, with a 50 fs time step being employed. As in our previous BD studies,^87,88 intramolecular hydrodynamic interactions were described at the Rotne–Prager–Yamakawa level of theory^89,90 with a hydrodynamic radius of 3.5 Å assigned to all pseudoatoms. The correlated random displacements required in order to satisfy the fluctuation–dissipation theorem were obtained by performing a Cholesky decomposition of each intramolecular diffusion tensor, with the latter being updated every 20 ps (i.e., every 400 simulation steps). Intermolecular hydrodynamic interactions, which are likely to be important only for larger systems than those studied here,^87,88 were not modeled; it is to be remembered that the inclusion or exclusion of hydrodynamic interactions does not affect the thermodynamics of interactions that are the principal focus of the present study. Each BD simulation required approximately 5 min to complete on one core of an 8-core server; relative to the corresponding MD simulation, therefore, the CG BD simulations are ∼3000 times faster.

COFFDROP Bonded Potential Functions

In COFFDROP, the potential functions used for the description of bonded pseudoatoms include terms for 1–2 (bonds), 1–3 (angles), 1–4 (dihedrals) interactions. To model the 1–2 interactions, a simple harmonic potential was used:

2

where ε^CG is the energy of a specific bond, K^bond is the spring constant of the bond, x is its current length, and x_o is its equilibrium length. The spring constant used for all bonds was 200 kcal/mol·Å². This value ensured that the bonds in the BD simulations retained most of the rigidity observed in the corresponding MD simulations (Supporting Information Figure S2) while still allowing a comparatively long time step of 50 fs to be used: smaller force constants allowed too much flexibility to the bonds and larger force constants resulted in occasional catastrophic simulation instabilities. Equilibrium bond lengths for each type of bond in each type of amino acid were calculated from the CG representations of the 10 000 000 snapshots obtained from the single amino acid MD simulations. As was anticipated by a reviewer, a few of the bonds in our CG scheme produce probability distributions that are not easily fit to harmonic potentials: these involve the flexible side chains of arg, lys, and met. We chose to retain a harmonic description for these bonds for two reasons: (1) use of a harmonic term will simplify inclusion (in the future) of the LINCS⁸⁰ bond-constraint algorithm in BD simulations and thereby allow considerably longer timesteps to be used and (2) the anharmonic bond probability distributions are significantly correlated with other angle and dihedral probability distributions and would therefore require multidimensional potential functions in order to be properly reproduced. While the development of higher-dimensional potential functions may be the subject of future work, we have focused here on the development of one-dimensional potential functions on the grounds that they are more likely to be easily incorporated into others’ simulation programs (see Discussion).

For the 1–3 and 1–4 interactions, the IBI method was used to optimize the potential functions. Since the IBI method has been described in detail elsewhere,⁶⁶ we outline only the basic procedure here. First, probability distributions for each type of angle and dihedral (binned in 5° intervals) were calculated from the CG representations of the 10 000 000 MD snapshots obtained for each amino acid; for all amino acids other than gly, these included two improper dihedrals (involving the Ace, Nme, Cα, and the first side chain pseudoatom) that were used to maintain correct chirality during CG simulations. Initial CG potential functions for use in BD simulations were generated by Boltzmann inversion of the CG probability distributions obtained from the MD simulations according to

3

Here, ε^CG(ξ) is the potential function of a specific angle or dihedral, ξ, R is the gas constant, T is the temperature in Kelvin, and prob^MD(ξ) is the “target” probability distribution obtained for the angle or dihedral from MD. A first BD simulation was then performed using these initial potential functions; forces and energies from each potential function were computed during the BD simulations using the method of cubic spline interpolation.⁹¹ Angle and dihedral probability distributions were then calculated from the BD simulation and compared to the corresponding distributions obtained from MD. The CG potential functions were then modified by amounts dictated by the differences between the MD and BD probability distributions according to

4

where the subscript j indicates the current iteration number and prob^BD(ξ) is the probability distribution obtained from BD of the corresponding degree of freedom. A scaling factor of 0.25 was applied in order to better control convergence of the procedure; in addition, to eliminate the possibility of uncontrolled drift in poorly sampled regions, the potential functions were only updated for bins in which the probability exceeded 1 × 10^–5 in both the BD and MD simulations. Having modified the potential functions, a new BD simulation was performed, and the potential functions were again updated according to the procedure outlined above. Convergence of the procedure was monitored by computing, following each new BD simulation, the absolute error between the “target” distribution function and the distribution function obtained from BD using

5

where N is the number of potential functions being optimized and the sum extends over each bin of the distribution. The IBI scheme was continued for 50 iterations for each type of amino acid in order to derive angle and dihedral energy functions capable of describing the conformational distributions observed in MD. Since the errors do not always diminish monotonically with increasing iterations (see Results), for all amino acids other than glycine the iteration that produced the lowest overall error for the dihedral probability distributions was selected for inclusion in COFFDROP; for glycine, the iteration that produced the lowest error for the angle probability distributions was selected.

COFFDROP Nonbonded Potential Functions

The IBI method was also used to optimize nonbonded potential functions using data obtained from simulations of pairs of capped amino acids. For each of the 231 MD simulations, “target” g(r)s were computed for all intermolecular pairs of pseudoatoms. As in our previous work,⁸² each g(r) was computed as the ratio of the distance distribution observed in MD to the corresponding distance distribution obtained from 100 000 000 random placements of two pseudoatoms in the same simulation box; g(r) values were computed for all distances from 0 to 20 Å with a bin size of 0.1 Å and were normalized to 1 between 18 and 20 Å.

For the first iteration of the IBI process, all nonbonded CG potential functions were assumed to follow a purely repulsive 1/r_ij¹² form (where r_ij is the distance between the two pseudoatoms). As was the case with the bonded potentials, the nonbonded potential functions were then modified by amounts dictated by the differences between the MD and BD g(r)s according to

6

where g(r)^BD(ξ) and g(r)^MD(ξ) are the g(r)s obtained for interaction ξ from the BD and MD simulations, respectively. Note that it was found that the scaling factor used to suppress oscillations in the optimization procedure needed to be smaller for the nonbonded potential functions than for the bonded potential functions. As with the bonded terms, potential functions were only adjusted for bins in which the probability exceeded 1 × 10^–5 in both the BD and MD simulations. In order to reduce noise in the nonbonded potential functions, they were all smoothed twice using a Savitzky–Golay procedure⁹² prior to being used in the next BD simulation. The IBI scheme was continued for 100 simulations for each amino acid pair and the nonbonded potential functions used in the iteration that produced the smallest error between the g(r) functions obtained from MD and BD were selected for use in COFFDROP.

It is to be noted that in all simulations involving pairs of charged pseudoatoms, the nonbonded potential functions to be optimized by IBI are supplemented by direct electrostatic interactions computed using Coulomb’s law with a dielectric constant set equal to that of the TIP4P-Ew water model (see above). Since these direct electrostatic interactions are not adjusted during the IBI procedure, the IBI-optimized nonbonded interaction terms are expected to describe all non-Coulombic components of the interaction between charged pseudoatoms.

Clustering Analysis

To assess the ability of COFFDROP’s nonbonded potential functions to describe interactions between more than two amino acids, additional all-atom MD and CG BD simulations were performed of systems containing between 3 and 54 amino acid molecules (again, in a 35 Å × 35 Å × 35 Å box). A clustering analysis was then performed on the MD and BD trajectory snapshots to determine whether the all-atom and CG simulation models predict similar degrees of solute–solute interactions. As before, the MD snapshots were first converted to their CG equivalents so that the MD and BD behavior could be directly compared. For all 10 000 000 snapshots generated in the MD and BD simulations, all intermolecular pseudoatom–pseudoatom distances were measured; any two solute molecules for which a pair of pseudoatoms was within 4.5 Å were considered to be in contact with each other. Then, as in our previous work,⁹³ clusters were constructed using in-house code to identify all solutes that shared one or more contacts with other solutes.

Villin Headpiece Simulation

To provide a preliminary test of whether COFFDROP’s nonbonded potential functions can accurately model the intermolecular interactions of proteins, CG BD simulations were performed for systems containing 8 copies of the villin headpiece protein (PDB ID: 1VII) in a 113 × 113 × 113 Å periodic box (a protein concentration of 9.2 mM). The simulation protocol used was identical to that used in simulations of amino acid pairs, with the exception that simulations were performed for periods of 50–200 ns in order to be consistent with the corresponding MD simulations recently reported by Petrov and Zagrovic.¹

Since the version of COFFDROP presented here has been derived from simulations that include only capped single amino acids, it does not contain parameters for the large number of bonded backbone terms (e.g., Cα–Cα–Cα–Cα dihedrals) that would be required in order to model polypeptide chains. In order to model the villin headpiece, therefore, we supplemented COFFDROP’s bonded potential functions for side chain angles and dihedrals with additional terms intended to maintain the native state conformation. Missing angle terms were modeled using harmonic potential functions with a force constant of 10 kcal/mol·rad and with the equilibrium angle taken from the native state structure. Missing dihedral terms were described with simple cosine potential functions used in our previous CG simulations of protein cotranslational folding events:⁹⁴

8

where V₁ is 0.5 kcal/mol·rad, V₃ is 0.25 kcal/mol·rad, φ is the value of the dihedral, and φ₁ and φ₃ are the phase angles defining the position of the energy maxima of the cosine terms.

Since our purpose here was to assess COFFDROP’s ability to model intermolecular interactions of proteins, we used simplified Go̅-like potential functions,⁹⁵ similar to those described in our previous work,⁹⁴ to model all intramolecular nonbonded interactions. To this end, all intramolecular nonbonded interactions were represented by one of two types of nonbonded potential functions depending on whether the two pseudoatoms are in contact with each other in the native state structure of the protein: contacts are defined here as any pair of (nonbonded) pseudoatoms that are within 5.5 Å of each other. Nonbonded interactions for those pseudoatom pairs that are in contact in the native state were modeled using a “12–10” Lennard-Jones-like potential:

7

where ε is the energy well depth assigned to the contact (1 kcal/mol·Å), r_ij is the distance between the pair of pseudoatoms during the simulation, and σ_ij is the distance between the pseudoatoms in the native structure. Nonbonded interactions for those pseudoatom pairs that are not in contact in the native state were treated with a purely repulsive term, E_ij = ε{(σ_ij¹²/r_ij)}, where σ_ij was set to 4 Å. The use of Go̅-like potential functions in this way ensures that the native state conformations of the proteins are retained in the simulations while still allowing COFFDROP to be used to describe their intermolecular interactions; the inclusion of potential functions specifically for the purpose of maintaining the native state structure has also been suggested by the developers of the MARTINI force field in applications of their force field to proteins.^22,96

Results

MD Simulation Analysis

Although the main focus of this work is on the derivation of CG potential functions for use in BD simulations, the MD trajectories generated in this study are interesting in their own right for investigating the behavior of amino acids through simulation. In particular, since all MD simulations have been performed without the imposition of any restraints to enforce interactions between the amino acids we can straightforwardly obtain both the thermodynamics and the kinetics of association for each type of amino acid-amino acid interaction.

We deal with kinetic aspects first. In previous work we showed that the effective association rate constants of small aliphatic hydrocarbons appear to be diffusion-limited.⁸² To determine if the same is true for the capped amino acids studied here, we first computed the translational diffusion coefficients of the isolated amino acids using the Einstein diffusion equation (see Methods). Encouragingly, for the 12 amino acids that were studied experimentally by Longsworth,⁹⁷ we obtain excellent agreement between the simulated and experimental values (r² = 0.97, Figure 1A). Despite this good agreement, it is noticeable that the MD values are uniformly lower than the corresponding experimental values (the slope of the regression line is 0.66). This is likely due to a combination of the following two factors: (a) the simulated amino acids possess capping groups (which double the molecular mass for glycine for example); (b) simulated translational diffusion coefficients are known to be subject to a system-size dependent slowdown when periodic boundary conditions are imposed.⁹⁸ These two factors appear to outweigh the compensating effect of the TIP4P-Ew water model’s viscosity being somewhat lower (0.742 mPa)⁹⁹ than the experimental value (0.899 mPa)¹⁰⁰ at 298 K. Having determined the translation diffusion coefficient of each amino acid, we could determine whether association of amino acid pairs is diffusion-limited by comparing the computed effective association rate constants (see Methods) with the sums of the translational diffusion coefficients of the two amino acids. Such a comparison is shown in Figure 1B; the linear regression gives r² = 0.69 with p < 0.001, which suggests that such associations are in general effectively diffusion-limited.

Figure 1.

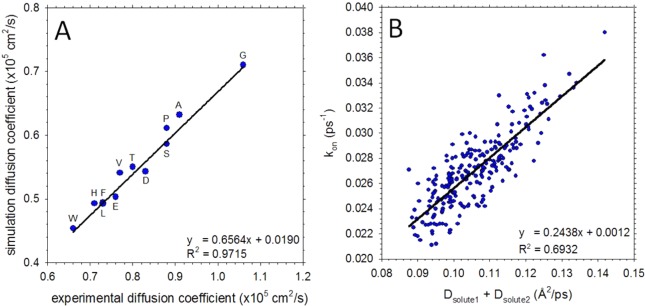
Translational diffusion coefficients and association kinetics of amino acids calculated from all-atom MD simulations. (A) Translational diffusion coefficients of 12 amino acids calculated from MD and compared to experimental data from Longsworth.⁹⁷ Each symbol is labeled using the one letter amino acid code. (B) Plot showing the correlation between the calculated effective association rate constant (k_on) and the sum of the individual amino acid translational diffusion coefficients. Each symbol represents a different amino acid pair.

Of more direct relevance to the remainder of the present work is the fact that the 231 × 1 μs MD simulations provide us with meaningful estimates of the association thermodynamics for all possible pairings of the amino acids. A simple way to gauge the interactions of different amino acid pairs is to compare their radial distribution functions (g(r)) computed using the Cα–Cα distance of each MD snapshot. Such a plot is shown in Figure 2A, from which it can be seen that significant interactions are apparent even at quite long Cα–Cα separation distances. More importantly, we can use these g(r)s to group amino acids according to the similarity of their interactions with other amino acids (see Methods); a dendrogram constructed on the basis of the computed Cα–Cα g(r) data is shown in Figure 2B. Encouragingly, it can be seen that amino acids that are known to share physicochemical similarities automatically group with one another in the dendrogram: in particular, the aliphatic, aromatic, acidic, and basic amino acids generally tend to form separate clusters. The groupings are not perfect, however, as gly surprisingly groups with the positively charged amino acids, thr is grouped with the aliphatic amino acids, and protonated his (hip) is more closely grouped with the negative amino acids than the positive amino acids. Overall, however, the dendrogram suggests that the g(r)s obtained from the MD simulations are sufficiently reliable—and contain sufficient information—to draw meaningful conclusions about the nature of amino acids’ interactions with other amino acids.

Figure 2.

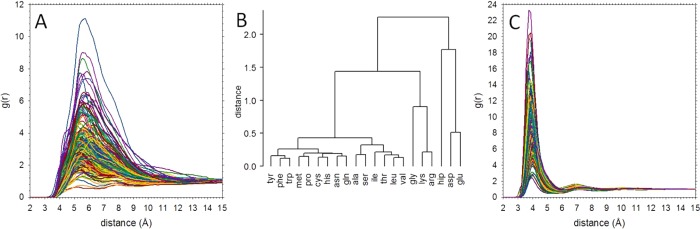
Radial distribution functions of amino acid pairs and amino acid dendrogram calculated from all-atom MD. (A) Plot showing 231 Cα–Cα g(r) functions. (B) Dendrogram created by performing agglomerative clustering on the calculated correlation coefficients of the 231 Cα–Cα g(r) functions shown in A. (C) Plot showing 231 g(r) functions calculated using only the closest distance between any pair of heavy atoms.

While g(r)s computed from the Cα–Cα distance provide a useful way of comparing the different natures of amino acid interactions, the fact that they appear to indicate that interactions occur over a considerable distance (up to ∼12 Å; see Figure 2A) means that they do not provide a particularly useful measure of when two amino acids are associated. An alternative and more intuitive way to represent the state of association is to compute g(r)s using the distance between the closest pair of (pseudo)atoms in each MD snapshot instead of the Cα–Cα distance.⁸² The g(r)s computed in this way for all 231 systems are shown in Figure 2C: these are much more in line with our intuition that significant intermolecular interactions are to be expected only at much shorter separation distances (<8 Å).

Bonded Potential Functions

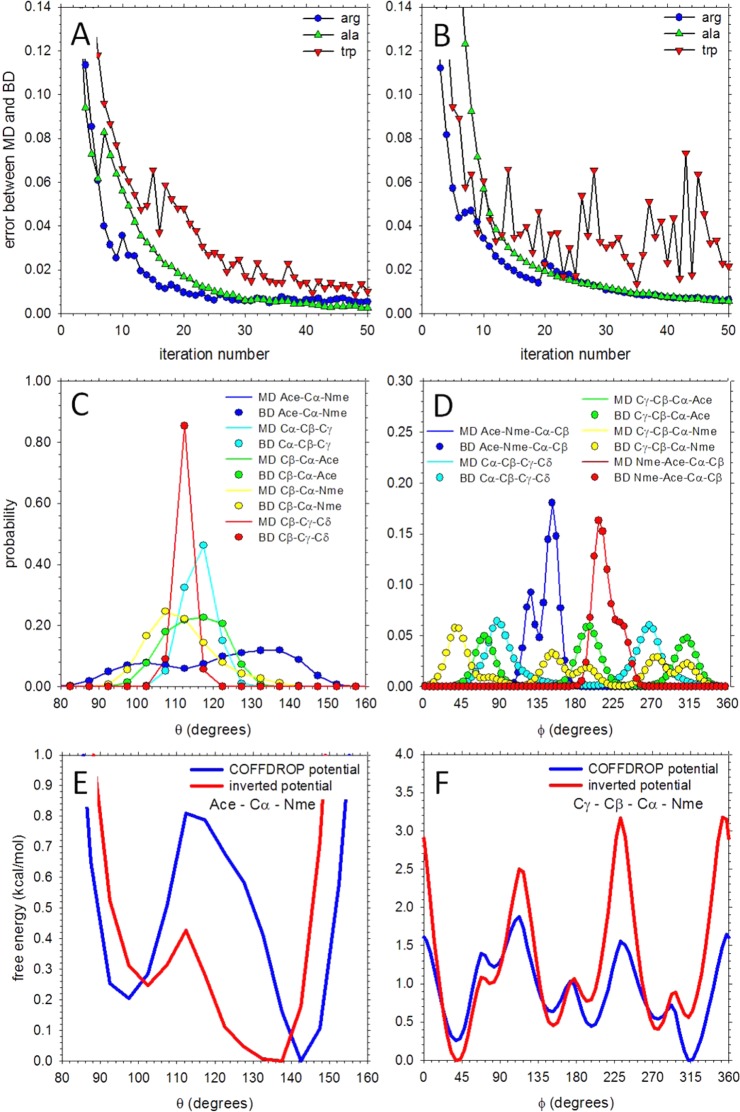
We next turned our attention to creating a CG force field capable of reproducing the behavior seen in the MD simulations focusing first on the conformational behavior of single amino acids. To establish the extent of convergence of the “target” MD simulation data, the 1 μs trajectories were first converted into their CG representations and then split into three 333 ns blocks from which the average and standard deviations of the angle and dihedral probability distributions were calculated. Supporting Information Figure S3 shows the results for tryptophan, which contains the most pseudoatoms of any amino acid; the standard deviations in all of the angle (Supporting Information Figure S3A) and dihedral (Supporting Information Figure S3B) probability distributions are small, indicating that 1 μs is a sufficient length to obtain convergence of these properties.

After determining that the MD simulations of the single amino acids were likely to be sufficiently converged, the iterative Boltzmann inversion (IBI) method was used to derive a set of bonded CG potential functions optimized to reproduce the angle and dihedral probability distributions obtained from MD. Figure 3A shows the combined error of the angle distributions sampled during the BD simulations as a function of the iteration number of the IBI protocol for three of the amino acids: arginine, alanine, and tryptophan; Figure 3B shows the same for the dihedral distributions. In all three systems the error in the angles and dihedrals decreases sharply during the first ∼10 iterations of the IBI procedure, before–in the case of alanine and arginine–undergoing a more gradual decrease over the succeeding 40 iterations. For tryptophan, significant fluctuations in the error continue to occur after the 10th iteration in both the angle and (especially) the dihedral distributions. The increased noise seen with tryptophan is likely a consequence of it containing the largest number of angle and dihedral potential functions–all of which have to be simultaneously optimized–and a result of it containing two internal nonbonded interactions that must also be optimized at the same time (see below). Even with the noise, however, the optimized bonded potential functions for tryptophan produce angle (Figure 3C) and dihedral (Figure 3D) probability distributions that match nearly perfectly with those measured in MD. A similarly high level of agreement between the angle and dihedral probability distributions from MD and from BD was obtained for all of the amino acids (Supporting Information Figure S4). Parts E and F of Figure 3 provide example comparisons of the optimized potential functions for angles and dihedrals, respectively, with those obtained by (noniterative) Boltzmann inversion of the MD data according to E(θ) = −RT ln f(θ), where f(θ) denotes the frequency with which a particular value of the angle or dihedral θ is sampled during MD. In general, the optimized COFFDROP potential functions (blue) are similar to the potential functions obtained by Boltzmann-inverting the MD data (red), but there are nevertheless cases where the optimized potential functions have quite different global minima from those obtained by Boltzmann inversion (see, e.g., Figure 3F).

Figure 3.

Derivation of COFFDROP bonded potential functions using the IBI method. (A) Plot showing the error in the angle probability distributions obtained from BD simulations as a function of IBI iteration number for the amino acids arginine, alanine and tryptophan. (B) Same as A but showing results for dihedral probability distributions. (C) Comparison of the angle probability distributions obtained from MD (lines) with those obtained from BD (circles) for tryptophan. Each color represents a different angle. (D) Same as C but showing results for dihedral probability distributions. (E) Comparison of an example angle potential function (Ace–Cα–Nme for tryptophan) obtained from using IBI (blue) with that obtained from noniterative Boltzmann inversion of the MD probability distribution (red). (F) Same as E but showing an example dihedral potential function (Cγ–Cβ–Cα–Nme for tryptophan).

It is to be noted that in addition to optimizing regular dihedral potential functions, we also optimized two improper dihedral functions for all amino acids other than glycine: both of these improper terms involved the Ace, Nme, Cα, and the first side chain pseudoatoms. Without including these improper dihedral functions, we found that amino acids could adopt incorrect chiralities during CG simulations. As an example, when the IBI procedure was carried out on alanine without placing potential functions on the improper dihedrals, the amino acid would freely interconvert between l- and d-like configurations even though all angle and dihedral probability distributions were accurately reproduced (Supporting Information Figure S5A). When, however, the IBI procedure was repeated with two additional potential functions placed on the improper dihedral terms, the amino acid was (correctly) restricted to the l-like configuration (Supporting Information Figure S5B); importantly, inclusion of these improper dihedral functions in the IBI process did not adversely affect the ability to reproduce the probability distributions for other angle and dihedral functions.

To explore if the IBI procedure would converge on the same final potential functions if different initial potential functions were used, example reoptimizations were performed for the bonded parameters of leu and lys. For leu, reoptimization was performed using as initial potential functions the final optimized potential functions obtained previously for lys; for lys, reoptimization was performed using as initial potential functions the final optimized potential functions obtained previously for leu. The results of the reoptimizations for leu are shown in Supporting Information Figure S6; those for lys are shown in Supporting Information Figure S7. In both cases, the initial probability distributions obtained using the “wrong” initial potential functions (green lines in rows B and D) are, predictably, in poor agreement with the “target” MD distributions (blue lines). After using the IBI procedure, however, all probability distributions obtained with the newly reoptimized potential functions are in good agreement with MD (compare blue lines with red symbols); this indicates that the choice of the initial potential functions need not be critical to the success of the IBI optimization. For the most part, the reoptimized potential functions are essentially identical to those obtained from the original IBI procedure (compare blue lines with red symbols in rows A and C). The few cases where they differ substantially (Supporting Information Figure S6 row C) involve low-probability (i.e., high energy) regions of the distributions; in all high-probability regions, however, the optimized and reoptimized potential functions are effectively identical.

Nonbonded Potential Functions

In addition to bond, angle, and dihedral potential functions, CG simulation of the single amino acid tryptophan in its capped form also required the introduction of two 1–5 (intramolecular) nonbonded functions: these occur between the distal side chain pseudoatom (which we call Cδ) and the Ace and Nme capping group pseudoatoms (Supporting Information Figure S8). Potential functions that capture these nonbonded interactions were again optimized using the IBI procedure at the same time that the angle and dihedral potential functions were optimized. In this case, the “target” functions to be matched were the probability distributions of the 1–5 pseudoatom interactions measured in the CG-converted MD trajectories, both of which are shown in Supporting Information Figure S9. The interesting shapes of these distributions reflect the peculiarities of the interactions within the capped tryptophan molecule. Both the Ace–Cδ and the Nme–Cδ distance distributions exhibit a broad peak centered at ∼5 Å and a sharp peak at ∼9 Å. The former is easy to explain since it corresponds to a favorable contact between the tryptophan phenyl ring and the methyl of each capping group. The latter is, at first sight, harder to explain since it is unusual to see sharp peaks indicating favorable interactions at long distances. Visual examination of the simulation trajectory, however, indicates that the internal structure of the capped tryptophan molecule dictates that when the Ace and Cδ pseudoatoms are in contact, the Nme and Cδ pseudoatoms must be at their furthest possible separation distance and vice versa (Supporting Information Figure S8); the sharp peak obtained at 9 Å in the Nme–Cδ distribution, therefore, is a consequence of (i.e., accompanies) the broader peak at ∼5 Å in the Ace–Cδ distribution. As with the angle and dihedral distributions, both the Ace–Cδ and the Nme–Cδ distance distributions can be well reproduced by IBI-optimized potential functions (Supporting Information Figure S9).

With the exception of the above interaction, all other types of nonbonded functions in the present version of COFFDROP have been derived from intermolecular interactions sampled during 1 μs MD simulations of all possible pairs of amino acids. To establish that the 1 μs duration of the MD simulations was sufficient to produce reasonably well converged thermodynamic estimates, the trp–trp and asp–glu systems, which respectively produced the most and least favorable binding affinities, were independently simulated twice more for 1 μs. Supporting Information Figure S10 row A compares the 3 independent estimates of the g(r) function for the trp-trp interaction calculated using the closest distance between any pair of heavy atoms in the two solutes; Supporting Information Figure S10 row B shows the 3 independent estimates of the g(r) function for the asp–glu interaction. Although there are differences between the independent simulations, the differences in the height of the first peak in the g(r) plots for both the trp–trp and asp–glu systems are comparatively small, which indicates that the use of equilibrium MD simulations to sample the amino acid systems studied here—at least with the force field that we have used—is not hugely hampered by the interactions being excessively favorable or unfavorable.

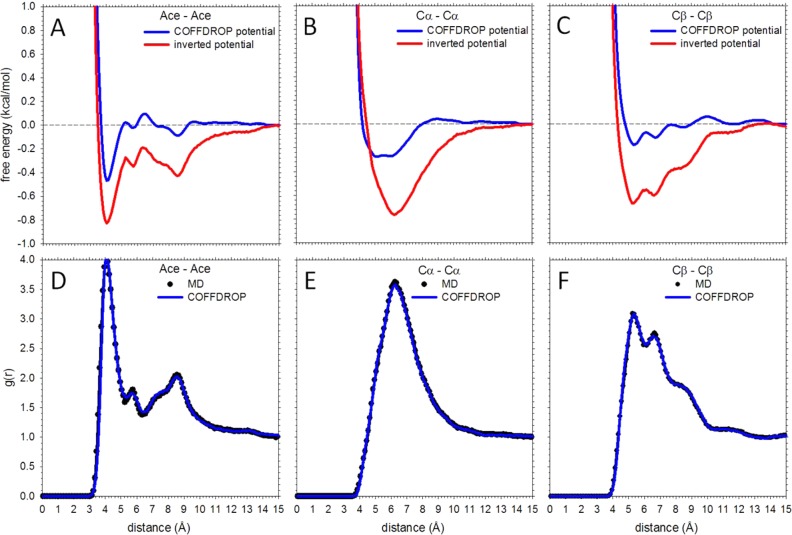
As was the case with the bonded interactions, the IBI procedure was used to optimize potential functions for all nonbonded interactions with the “target” distributions to reproduce in this case being the pseudoatom–pseudoatom g(r) functions obtained from the CG-converted MD simulations. During the IBI procedure, the bonded potential functions that were previously optimized to reproduce the behavior of single amino acids were not reoptimized; similarly, for tryptophan, the intramolecular nonbonded potential functions were not reoptimized. Shown in Figure 4A is the calculated average error in the g(r)s obtained from BD as a function of IBI iteration for three representative interactions: ile–leu, glu–arg, and tyr–trp. In each case, the errors rapidly decrease over the first ∼40 iterations. Following this point, the errors fluctuate in ways that depend on the particular system: the fluctuations are largest with the tyr–trp system which is likely a consequence of it having a larger number of interaction potentials to optimize. The IBI optimization was successful with all pairs of amino acids to the extent that binding affinities computed by integrating the Cα–Cα g(r)s obtained from BD simulations of each system were in excellent agreement with those obtained from MD (Figure 4B); all other pseudoatom–pseudoatom g(r)s were reproduced with similar accuracy.

Figure 4.

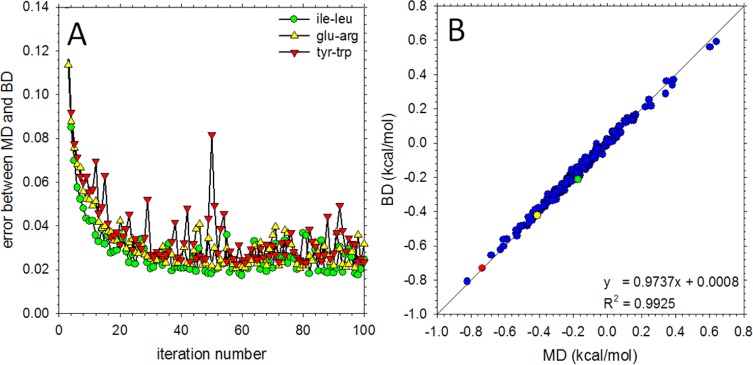
Derivation of COFFDROP nonbonded potential functions using the IBI method. (A) Plot showing the error in the nonbonded g(r) functions obtained from BD simulations as a function of IBI iteration number for the ile–leu (green circles), glu–arg (yellow upward triangles), and tyr–trp (red downward triangles) systems. (B) Comparison of binding affinities calculated from the Cα–Cα g(r) functions from MD (x-axis) and BD (y-axis). The green, yellow, and red symbols represent the ile–leu, glu–arg, and tyr–trp systems, respectively; the blue symbols represent the other 228 systems.

Some examples of the derived nonbonded potential functions are shown in Figure 5A–C for the val–val system. For the most part, the potential functions have shapes that are intuitively reasonable, with only a few small peaks and troughs at long distances that challenge easy interpretation. Most notably, however, the COFFDROP optimized potential functions (blue lines) are much less favorable and less long-ranged than the corresponding potential functions that are obtained by performing a Boltzmann inversion of the MD g(r)s according to E = −RT ln g(r) (red lines). The need for the iterative adjustment of the potential functions so that they properly reproduce the g(r)s (shown in Figure 5D–F) is therefore clear (see Discussion).

Figure 5.

Example nonbonded potential functions. (A) Plot comparing the Ace–Ace nonbonded potential function of the val–val system obtained from IBI (blue) with that obtained from noniterative Boltzmann inversion (red) of the MD g(r) function. (B) Same as A but for the Cα–Cα interaction; (C) same as A but for the Cβ–Cβ interaction. (D) Plot comparing the Ace–Ace g(r) of the val-val system obtained from MD (black circles) with that obtained from BD using COFFDROP (blue line). (E) Same as D but for for the Cα–Cα interaction; (F) same as D but for the Cβ–Cβ interaction.

The nonbonded potential functions that we have derived are pairwise terms that have been optimized to reproduce interactions between pairs of amino acids. The ultimate application of such potential functions, however, is to protein systems, which are obviously considerably more complicated than the systems studied above. One way to assess initially whether the pairwise interaction functions might work for more complicated systems is to carry out comparative (all-atom) MD and (coarse-grained) BD simulations of systems where three-body and higher interactions are unavoidable. To do this, we performed an additional series of 1 μs MD simulations of systems containing 3 or 4 copies of each of the following (capped) amino acids: ala, asn, asp, cys, gly, leu, lys, tyr, trp, and val; these systems were selected so as to provide a broad sampling of different physicochemical characteristics. The level of agreement between the MD and BD simulations was determined by performing a cluster analysis of the snapshots sampled during the simulations (see Methods); the results of such analyses are shown in Figure 6. The MD simulation data (blue symbols) show that populations of monomers, dimers, trimers and (in the case of 4-copy simulations) tetramers are observed in each simulation; the results for the tryptophan systems, for example, (far right of Figure 6), show that they are considerably more prone to forming higher-order clusters than more weakly interacting amino acids such as alanine (far left of Figure 6). More importantly, however, the distributions of the various cluster sizes obtained from the all-atom MD simulations are found to be well reproduced by the BD simulations using the CG nonbonded potential functions (green symbols): the (representative) results for the ala, leu, asn, and trp systems are shown in Figure 6, while the results for the other amino acids studied are shown in Supporting Information Figure S11. To verify that reproducing the clustering behavior seen in MD is not a trivial consequence of adding more amino acids to the simulation box, additional BD simulations were performed using purely steric nonbonded potentials (red symbols) and were found to be unable to reproduce the clustering behavior observed in MD.

Figure 6.

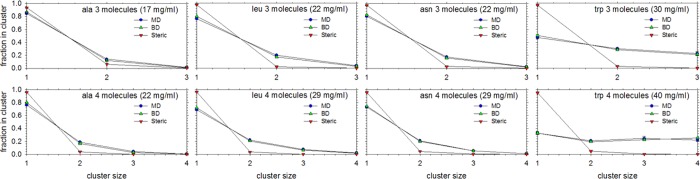
Clustering of alanine, leucine, asparagine, and tryptophan solutions in MD and BD. The plots show the fraction of solute molecules that are members of clusters of various sizes. Blue circles represent results from MD, green upward triangles represent results from BD using COFFDROP, and red downward triangles represent results from BD using steric nonbonded potentials.

To further test the transferability of our nonbonded potential functions to conditions that are even more different from those in which they were derived, additional 1 μs MD and BD simulations of systems containing 50, 100, 200, or 300 mg/mL of capped amino acids were also performed. To provide a range of interaction types and strengths for testing, these simulations were performed on ala, asn, leu and trp systems. Shown in Figure 7 are the results of cluster analyses for each of these systems at 200 and 300 mg/mL; the results for 50 and 100 mg/mL can be found in Supporting Information Figure S12. Again, the correspondence between the results obtained from the all-atom MD and the coarse-grained BD simulations is surprisingly good. For tryptophan at 200 and 300 mg/mL, the BD simulations successfully reproduce the prediction from MD that a single large cluster should form that traverses the width of the simulation box (for a visual comparison of the MD and BD snapshots of the 300 mg/mL trp system see Supporting Information Figure S13). At lower concentrations, the BD simulations predict a degree of clustering that is somewhat too high relative to MD (Supporting Information Figure S12); this suggests that the solubility predicted by the pairwise CG potential functions is somewhat lower than that predicted by the all-atom MD potential functions. For the other three amino acids studied, agreement with MD is again good, but, interestingly, the BD simulations in these cases predict a degree of clustering that is somewhat lower than that predicted by the MD simulations.

Figure 7.

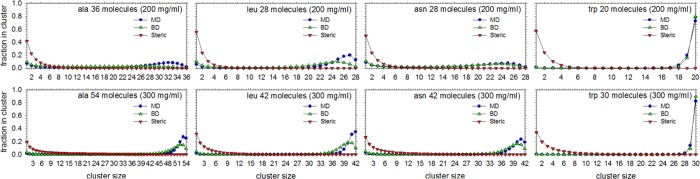
Clustering of alanine, leucine, asparagine, and tryptophan solutions at concentrations of 200 and 300 mg/mL in MD and BD. Same as Figure 6 but showing results for much higher concentrations.

After determining that COFFDROP’s nonbonded potential functions were able to reproduce the clustering behavior of concentrated amino acid solutions, we carried out a preliminary examination of their ability to describe a weak protein–protein interaction. The system we chose to simulate was a 9.2 mM solution of the villin headpiece protein that has been the subject of a recent comprehensive MD study by Petrov and Zagrovic.¹ These authors showed that with all tested MD force fields, aggregation of villin headpiece molecules occurs at a concentration of 9.2 mM during the course of a 50 ns MD simulation; experimentally, however, there is evidence to suggest that no significant aggregation occurs at this protein concentration.¹⁰¹ We found that when using COFFDROP’s nonbonded potential functions in our own simulations of the villin headpiece, significant aggregation occurred on the 50 ns time scale, just as it did using the Amber ff99SB-ILDN force field (and others) in Petrov and Zagrovic’s study (Figure 8A; blue circles); a view of the aggregated system is shown in Figure 8B. Continuing the COFFDROP simulation for an additional 150 ns did not reverse this aggregation.

Figure 8.

Clustering of villin headpiece solutions at a 9.2 mM concentration in BD. (A) Plot shows the fraction of villin headpiece molecules that are members of clusters of various sizes. Blue circles represent results using a 1.0 scaling factor with COFFDROP’s nonbonded potential functions, green upward triangles represent results using a 0.9 scaling factor, yellow downward triangles represent results using a 0.8 scaling factor, and red squares represent results using a 0.8 scaling factor and starting from a structure in which the villin molecules were already aggregated into a trimer and pentamer. (B) Image showing aggregated villin molecules obtained at the end of a 200 ns BD simulation using a 1.0 scaling factor. Each color represents a different villin molecule. (C) Image showing villin molecules at the end of a 200 ns BD simulation using a 0.8 scaling factor.

The fact that aggregation occurs suggests, on the one hand, that COFFDROP’s nonbonded potential functions do a good job of reproducing what the corresponding all-atom MD simulation force field predicts, but that on the other hand, they do a poor job of reproducing the experimental behavior. To explore whether simple alterations could be made to the nonbonded potential functions to better reproduce experiment, we performed two additional simulations in which all favorable regions of the nonbonded potential functions were scaled by factors of 0.8 and 0.9 respectively. With a scaling factor of 0.9, no large aggregates formed, but there remained a significant population of dimers (Figure 8A; green upward triangles); with a scaling factor of 0.8, however, the proteins remained monomeric with only transient formations of dimers (Figure 8A; yellow downward triangles); a view of this system is shown in Figure 8C. To determine if this scaling factor of 0.8 was sufficient to break up pre-existing aggregates, a final simulation was performed starting from the final snapshot obtained from the 1.0 scaling factor simulation: this snapshot had the eight villin molecules separated into two clusters: a trimer and a pentamer (Figure 8B). Encouragingly, these pre-existing aggregates rapidly dissociated when a simulation was started with a scaling factor of 0.8 (Figure 8A; red squares), suggesting that such a scaling factor appropriately shifts the thermodynamics of the model away from aggregates and toward monomers.

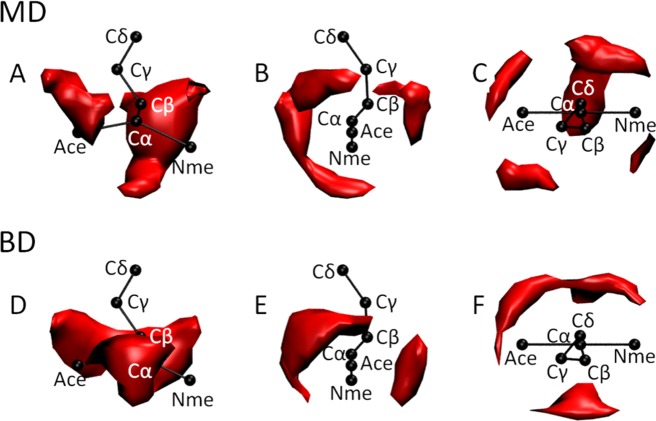
While the clustering behavior seen in both the concentrated amino acid and villin headpiece simulations indicate that COFFDROP’s nonbonded potential functions may be useful for modeling concentrated peptide and protein systems, it is important to note that there is one respect in which the functions perform quite disappointingly. To see this, we return to an analysis of the data obtained from simulations that contain only pairs of molecules. It will be recalled from above that convergence of the IBI procedure ensures that each of the individual pseudoatom–pseudoatom g(r)s are accurately captured by the CG simulations. However, each of the optimized nonbonded potential functions is assumed to be pairwise-additive, that is, independent of the other potential functions; it is therefore possible that important correlations between potential functions—if present—might not be properly described. A related issue is that each of the potential functions depends only on the distance between two pseudoatoms which means that orientational (angular) preferences might also not be correctly captured. It appears to be a disappointing consequence of these issues that even in simulations of two amino acid molecules the relative spatial dispositions of pseudoatoms can be quite poorly described by the CG potential functions. As one example of this we show in Figure 9 results for the tryptophan-tryptophan interaction. The contour plots in Figure 9 (A–C) show three different rotational views of one of the tryptophan molecules (black), highlighting (in red) the regions of nearby space that are most frequently occupied by the Cδ atom of the second tryptophan molecule during MD simulations. Figure 9 (D–F) shows corresponding results obtained from BD simulations using our CG potential functions. While there is some degree of similarity between the two sets of results, they are also clearly somewhat different, with some regions of space that are occupied during MD not being occupied during BD and vice versa; repeating the analysis with the two tryptophan molecules swapped indicates that these discrepancies are not due to poor sampling in either the MD or BD (Supporting Information Figure S14). This indicates that while it is possible to correctly reproduce all of the pseudoatom–pseudoatom g(r)s for CG models of the type developed here, this does not guarantee that the interaction geometries of the parent molecules will also be correctly reproduced.

Figure 9.

Spatial disposition of the Cδ pseudoatom of tryptophan in MD and BD. (A–C) Red contours show preferred locations of the Cδ pseudoatom of a tryptophan molecule interacting with a second tryptophan molecule (shown in black) sampled from MD; each of the panels A–C shows the same image viewed from a different orientation. (D–F) Same as panels A–C, respectively, but showing results from BD.

Discussion

We have described here the use of the IBI procedure to derive CG nonbonded potential functions for amino acid–based systems by matching pseudoatom–pseudoatom g(r)s sampled from 231 × 1 μs MD simulations of pairs of amino acids. The MD data themselves appear to be quite reliable–although one can probably never have too much sampling–and the patterns of interactions that the different types of amino acids exhibit match nicely with intuitive expectations (Figure 2B). For each system, the IBI procedure appears to have little trouble simultaneously optimizing all of the potential functions (a total of 30 independent functions in the case of the tryptophan–tyrosine system), and the derived potential functions make clear intuitive sense (Figure 5). Perhaps most surprisingly, while the resulting COFFDROP potential functions struggle to accurately describe the structural details of amino acid interactions (Figure 9), they do an excellent job of reproducing the thermodynamics of interactions in systems that are much more concentrated than those in which they were derived (Figure 7), and in reproducing the clustering seen with the same force field in recent MD simulations of the villin headpiece (Figure 8A).¹ The fact that the discrepancies with experiment seen in the latter application can be corrected by simply scaling the favorable nonbonded interactions highlights one of the potential advantages of using such CG potential functions, namely that they can often be adjusted in quite straightforward ways in order to better match experiment.²⁴ Further testing and refinement of COFFDROP for protein systems is the subject of ongoing work.

Our experiences with the use of the IBI procedure appear to mirror those of others.^{42,43,49,55,67−69} The bonded potential functions derived for single amino acids converge rapidly and are, at least in the cases studied here, often very similar to the potential functions that would be obtained by Boltzmann-inverting the angle and dihedral distributions obtained from MD (Figure 3E and F). Relative to the bonded functions, the nonbonded potential functions derived for interactions of pairs of amino acids have a little more trouble converging, with fluctuations in the errors remaining evident even at high iteration numbers (Figure 4A). Despite this, the IBI procedure still yields nonbonded potential functions that provide an excellent reproduction of all of the pseudoatom–pseudoatom g(r)s (Figure 4B). It is to be noted again that, in contrast to the bonded functions, the nonbonded potential functions that are derived by the IBI procedure are very different in strength and range from those obtained by Boltzmann-inverting the MD g(r)s (Figure 5A–C); this echoes the results shown by Reith et al. in their original publication of the IBI method.⁶⁶ It is also important to recall that while the Boltzmann-inverted potential functions have shapes that are reminiscent of those obtained from the IBI procedure they were not used as the initial functions for the IBI procedure: instead, to avoid any bias the IBI procedure was initialized with purely steric potential functions. The fact that the resulting potential functions automatically take on the same shapes as those derived by a noniterative Boltzmann-inversion of the MD data argues for the robustness of the iterative procedure.

One limitation of the nonbonded potential functions derived here is that they do not perform especially well in reproducing the interaction geometries of the amino acids (Figure 9). It is certainly possible to imagine that a better reproduction of these geometries could be obtained using potential functions that depend on more than just the distance between pairs of pseudoatoms. In this vein, the Betancourt group has already explored the use of MD-derived 4D potential functions that better incorporate orientational specificity in the interactions of amino acid side chains¹⁰² and the potential advantages of using 6D potential functions derived from molecular mechanics calculations for dramatically accelerating large-scale simulations have been highlighted by the Zuckerman group;¹⁰³ a number of other CG models of proteins^104,105 and nucleic acids^106−109 also incorporate multidimensional potential functions. We have not explored such approaches here for two reasons. First, while we think that equilibrium MD simulations of 1 μs duration are sufficient for us to derive 1D nonbonded potential functions (where the one dimension is the separation distance), we think it is unlikely that they will be sufficiently well sampled to allow the derivation of higher dimensional potential functions. Second, simple distance-dependent potential functions of the type developed here, presented in the form of look-up tables, are more easily incorporated by other users into their simulation programs; for this reason, all of our potential functions are provided in Supporting Information.

Despite the fact that our pairwise nonbonded potential functions struggle to fully reproduce the structural details of the interactions of amino acid pairs, they perform surprisingly well at predicting the thermodynamics of higher order interactions, including at total solute concentrations that approach those encountered in intracellular conditions.^93,110 In simulations of three or four amino acid molecules correct reproduction of the ratio of monomers and dimers is not a surprise as the potential functions were derived to match such distributions. But correct reproduction of the ratio of dimers to trimers or trimers to tetramers is not guaranteed. The fact that these ratios are successfully reproduced, therefore, and the observation that the potential functions also perform well at concentrations up to 300 mg/mL, suggests that pairwise nonbonded potential functions may be surprisingly transferable, at least in terms of capturing the effects predicted by corresponding all-atom MD simulations.

Interestingly, the behavior predicted by COFFDROP for the concentrated amino acid systems shows both similarities and differences with what we obtain when we perform corresponding simulations with two alternative CG parameter sets. Supporting Information Figure S15 compares the clustering obtained from COFFDROP with that obtained using the MARTINI version 2.2 force field^22,96 together with the MARTINI polarizable water model,¹¹¹ and with that obtained using the implicit-solvent, one-bead-per-residue potential functions derived by Betancourt and Omovie from fits to MD simulation data;⁵⁶ (the details of both of these latter sets of simulations are described in Supporting Information). In comparison with COFFDROP (blue symbols in Figure S15), MARTINI (red symbols) predicts somewhat weaker amino acid-amino acid interactions for the four amino acids studied here. The Betancourt and Omovie potential functions (green symbols), on the other hand, predict weaker amino acid-amino acid interactions for the ala and leu systems while predicting stronger amino acid-amino acid interactions for the asn and trp systems.

Regardless of these differences with other CG force fields, we think that our initial application of COFFDROP to simulations of the villin headpiece indicate that it is likely to be useful for modeling the intermolecular interactions of globular proteins. As noted above, we have shown that qualitative agreement with experiment for the villin headpiece requires the use of a scaling factor but simulations of a wider variety of protein–protein interactions will be required before the extent to which this approach works can be determined. To this end, we plan to match COFFDROP to experimental data that report more directly on the thermodynamics of protein–protein interactions. In this regard, obvious sources of data for parametrization are osmotic second virial coefficients,¹¹³ which a number of simulation studies have already attempted to model.^24,114−119 Since the current version of COFFDROP only contains bonded parameters for single amino acids, simulations of proteins will require Go̅-type⁹⁵ distance restraints such as those used here, or alternative approaches,^22,96 in order to maintain proteins in their native state structures. A more lasting solution to the problem will involve using the IBI procedure to derive bonded potential functions that describe the conformational preferences of the protein backbone and/or reward the formation of α-helical or β-sheet secondary structures. Potential functions derived in that way might be especially useful as a very rapid method for modeling the conformational dynamics of intrinsically disordered proteins (IDPs); this is the focus of ongoing work.

Supporting Information Available

Images of the CG amino acid models overlaid onto the all-atom models; CG bond length probability distributions obtained in BD using different K^bond values; average and standard deviations of tryptophan angle and dihedral probability distributions obtained from MD; angle and dihedral probability distributions obtained from MD and BD for every amino acid; improper dihedral probability distribution obtained from MD and BD for alanine; reoptimization of leu angle and dihedral potential functions using different (“wrong”) initial potentials; reoptimization of lys angle and dihedral potential functions using different (“wrong”) initial potentials; intramolecular nonbonded probability distribution obtained from MD and BD for tryptophan; snapshots showing the interaction of the Ace–Cδ and the Nme–Cδ pseudoatoms of tryptophan; three independent g(r) plots constructed using the closest distance between any pair of heavy atoms in the two solutes for the tryptophan–tryptophan and aspartate–glutamate systems; clustering of solutes in MD and BD for three and four molecules of aspartate, cysteine, glycine, lysine, tyrosine, and valine; clustering of solutes in MD and BD for 50 and 100 mg/mL solutions of alanine, leucine, asparagine, and tryptophan solutions; snapshot of 300 mg/mL typtophan solution obtained from MD and BD; spatial disposition of the Cδ pseudoatom of tryptophan obtained from MD and BD; COFFDROP average pseudoatom bond length; COFFDROP’s derived angle, dihedral, and nonbonded potential functions; clustering of solutes for 50, 100, 200, and 300 mg/mL solutions of alanine, leucine, asparagine, and tryptophan using COFFDROP, the Betancourt and Omovie force field, and the MARTINI version 2.2 force field; and table listing the heavy atoms that are used for the placement of pseudoatoms. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States