Quantum Electron Tunneling in Respiratory Complex I

Abstract

We have simulated the atomistic details of electronic wiring of all Fe/S clusters in complex I, a key enzyme in the respiratory electron transport chain. The tunneling current theory of many-electron systems is applied to the broken-symmetry (BS) states of the protein at the ZINDO level. One-electron tunneling approximation is found to hold in electron tunneling between the anti-ferromagnetic binuclear and tetranuclear Fe/S clusters with moderate induced polarization of the core electrons. Calculated tunneling energy is about 3 eV higher than Fermi level in the band gap of the protein, which supports that the mechanism of electron transfer is quantum mechanical tunneling, as in the rest of electron transport chain. Resulting electron tunneling pathways consist of up to three key contributing protein residues between neighboring Fe/S clusters. A distinct signature of the wave properties of electrons is observed as quantum interferences when multiple tunneling pathways exist. In N6a-N6b, electron tunnels along different pathways depending on the involved BS states, suggesting possible fluctuations of the tunneling pathways driven by the local protein environment. The calculated distance dependence of the electron transfer rates with internal water molecules included are in good agreement with a reported phenomenological relation.

Introduction

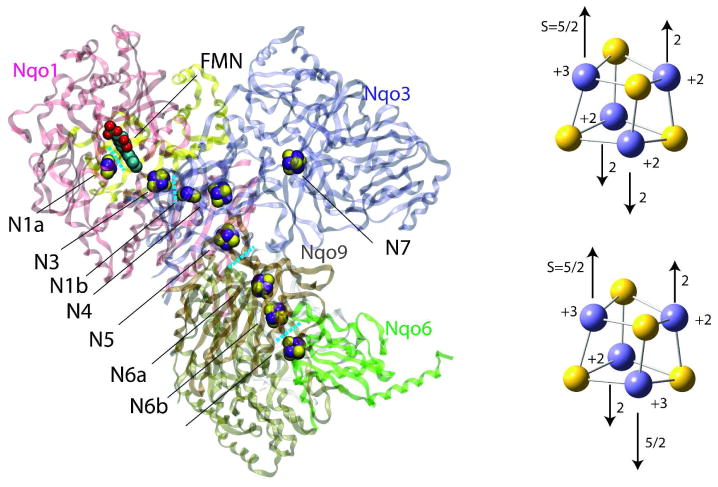
NADH:ubiquinone oxidoreductase (complex I) is a large L-shaped membrane-bound enzyme which plays a central role in electron transport chains of mitochondria and bacteria^1–4. Complex I transfer electrons over approximately 90 Å along flavin mononucleotide (FMN) and seven iron-sulfur (Fe/S) clusters (N3, N1b, N4, N5, N6a, N6b, N2) from NADH bound to the hydrophilic domain to ubiquinone in or near the hydrophobic membrane bound domain ⁵ (Figure 1). In turn, the reaction provides the driving force for creating the proton gradient across the membrane necessary for ATP synthesis ⁶. Complex I defects are the cause of several neurodegenerative diseases including Parkinson’s disease, Alzheimer’s disease and Huntington’s disease ⁷.

Figure 1.

Crystal structure of the hydrophilic domain of the respiratory complex I from the Thermus thermophilus ¹³ (left) and formal charges and schematic anti-ferromagnetic spin configurations of the reduced (right top) and oxidized (right bottom) 4Fe-4S clusters. In each electron transfer process between neighboring Fe/S clusters, the electron is passed from the reduced donor to the oxidized acceptor. Only core (4Fe and 4S) atoms are shown without cysteine ligands and electron delocalization is not considered for simplicity in the right panels.

Two Fe/S clusters (N1a and N1b) are binuclear (2Fe-2S), and six Fe/S clusters (N3, N4, N5, N6a, N6b, N2) are tetranuclear (4Fe-4S). Under physiological conditions, 2Fe-2S clusters have two redox states with formal iron valences (+3,+3) and (+3,+2), and 4Fe-4S clusters have two redox states with formal iron valences (+3,+3,+2,+2) and (+3,+2,+2,+2) to work as single electron carriers ⁸. The formal charges and schematic spin configurations of two redox states of 4Fe-4S clusters are shown in Figure 1 (right). Due to the anti-ferromagnetically coupled high-spin iron atoms, the Fe/S clusters have unique electronic properties ^9–12. The main feature of such clusters is the exceptionally high quasi-degeneracy of the electronic states, which has its origin in the 5-fold degeneracy of the d-orbitals of Fe ions. Theoretical studies of such anti-ferromagnetic systems had been performed by combining Heisenberg type Hamiltonian and the so-called broken-symmetry (BS) state ¹⁰, which resemble the pure spin ground state with some higher spin state contributions.

The crystal structure of hydrophilic domain of complex I from Thermus thermophilus was reported in 2006 ¹³, and the whole architecture of the enzyme was revealed in 2010 ¹⁴; however, the atomistic details of electron transfer along the chain of Fe/S metal clusters have remained unknown.

We have recently published the first report on the details of electron tunneling in complex I¹⁵. In this study, we extend our previous work to examine the quantum mechanical nature of electron tunneling, tunneling pathways and the strength of electronic coupling between Fe/S clusters in complex I with a semi-empirical electronic structure method ZINDO. The calculations are based on the analysis of BS states of the donor and acceptor quasi-continuum “bands” to obtain a dynamically averaged picture, which are found in good agreement with broken-symmetry DFT calculations.

ZINDO has been successfully applied to simulate the spin states and the electronic spectra of transition metal complexes with accuracy comparable to that of DFT (time-dependent DFT for spectra) ^16–18. The Heisenberg spin Hamiltonian and the resulting spin states of polynuclear transition metal complexes computed with ZINDO agree well with the experimental data ¹⁹. ZINDO also reproduce the electronic absorption spectra of mononuclear and binuclear Fe/S clusters ²⁰. ZINDO has also been extensively used for calculations of electron transfer in a variety of inorganic and organic systems ²¹; the method has an advantage in describing the through-space interactions of noncovalently bonded protein atoms due to its Slater-type orbitals ²².

The simulations of electron transfer between redox centers are based on the tunneling current theory ^23–24, which had been successfully applied to several systems previously. The theory treats many-electron wavefunctions explicitly by incorporating both the tunneling electron orbitals and the induced polarization of core electrons. Coarse-graining the transition flux between donor and acceptor gives the inter-atomic currents, which describe the tunneling flux at the atomic level ²⁴. Based on the tunneling flux theorem, the tunneling matrix element, the square of which is proportional to the electron transfer rate, is expressed as the total flux across the dividing plane between the donor and acceptor ^23–24 calculated.

Spin States of Fe/S clusters

In the reduced state [Fe₄S₄(SCH₃)₄]³⁻, three ferrous Fe²⁺ sites have spin S=2 with multiplicity 5, and one ferric Fe³⁺ site has spin S=5/2 with multiplicity 6; given the four possibilities of the ferric Fe site (Figure 1), the total number of states is 3000 (=5³ ×6 × 4 ). By dissecting the Fe/S cluster into two layers and applying appropriate Clebsch-Gordan series, the reduced [Fe₂S₂(SCH₃)₂]²⁻ and oxidized [Fe₂S₂(SCH₃)₂]¹⁻ layers have spin S₁₂=0,1, ···,4, and S₃₄=1/2,3/2, ···,9/2, respectively. Adding those two spins gives 380 irreducible spin representations of the 3000 states with the total spin S=1/2,3/2, ···,9/2. For example, states of total spin S=1/2 are generated by 9 different combination of (S_12,S₃₄)=(0,1/2), (1,1/2), (1,3/2), (2,3/2), (2,5/2), (3,5/2), (3,7/2), (4,7/2), and (4,9/2), which gives 36 representations by considering the four possible ferric Fe sites. The corresponding phenomenological Hamiltonian has been proposed as:

$$H=\sum _{i,j}{J}_{ij}{S}_i·S_j\pm B(S_{34}+1/2)\pm B^{\prime }(S+1/2)$$ (1)

where S_i and S_j are the atomic spins at the ith and jth iron sites, and S is the total system spin¹⁰. The first term is Heisenberg Hamiltonian, which describes the exchange couplings between the localized electrons with the spin coupling parameter J_ij. The second and third terms were introduced to describe the intra-layer and inter-layer resonance delocalization, respectively. Uniform J_ij are usually assumed for all Fe pairs. Here small variations of the spin couplings are introduced by assuming J₁₂ =J₀ + Δ and J₃₄ =J₀ − Δ. The solution thus becomes:

$$H=\frac{J_0}{2}S(S+1)+\frac{\mathrm{\Delta }}{2}[S_{12}(S_{12}+1)-S_{34}(S_{34}+1)]\pm B(S_{34}+1/2)\pm B^{\prime }(S+1/2).$$ (2)

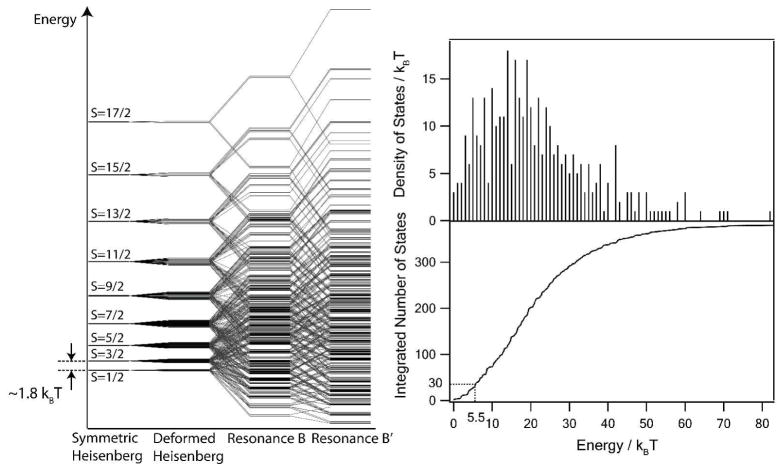
The resulting spin state energy diagram is shown in Figure 2 (left panel). The energies are calculated by employing calculated J₀, B, and B′ by BS-DFT ²⁵ and are scaled to match the experimentally observed J₀ of 250 cm^{−1 11}. Δ is set to be 5% of J₀.

Figure 2.

Spin state diagram (left panel), density of spin states and integrated number of spin states (right panel) of [Fe₄S₄(SCH₃)₄]³⁻ cluster. The total 3000 states are grouped by total spin S to 380 clusters overlapping in energy ¹⁰. The experimental value of the Heisenberg constant J is 250 cm⁻¹; a few tens of low-lying states contribute to the electron tunneling.

Estimated density of spin states and integrated number of states versus energy (in k_BT) are plotted in Figure 2 (right panel). 12 core atoms (4Fe + 8S) are expected to have significant vibronic couplings to the electronic states of the spin Hamiltonian. The fluctuation of the total vibrational energy associated with these atoms is estimated as $\sqrt{(12\times 3-6)}{k}_{B}T\approx 5.5k_{B}T$. As many as 30 states of spin S=2/1, 3/2, 5/2 and possibly 7/2 are present within the energy interval of 5.5 k_BT above the ground state, and can therefore be mixed through the vibronic coupling during the thermal dynamics. Spin-orbit coupling is also expected to be not too much smaller than k_BT in these systems, and will further lift the 2S+1 degeneracy of these states to give more than 100 different spin states. All relevant vibrations (Fe-S stretch, ring breathing, ring deformation, etc) of a Fe/S cluster calculated with BS-DFT have frequencies in 200–400 cm⁻¹, which corresponds to the time scale of 80–160 fs ^26–27, and therefore the time scale of the resulting mixing is expected to be 6 to 8 orders of magnitude faster than that of the slowest electron transfer.

Broken-Symmetry (BS) ground state of isolated [Fe₄S₄(SCH₃)₄]³⁻ are calculated at the ZINDO level with an optimized geometry by BS-DFT calculation ²⁸. The converged electronic structure reproduces the anti-ferromagnetic spin structure with two iron sites spin up and two iron sites spin down in agreement with BS-DFT calculations of Ref ¹⁰. The calculated BS HOMO, which contributes most to the electron tunneling, is a combination of Fe-Fe σ* and S-S σ*, in agreement with one of the two spin states coexisting at the room temperature ¹⁰. Figure 3 shows that both DFT and ZINDO produce similar results ²⁹, suggesting the reasonable accuracy of ZINDO comparable to that of DFT in the electron tunneling calculations.

Figure 3.

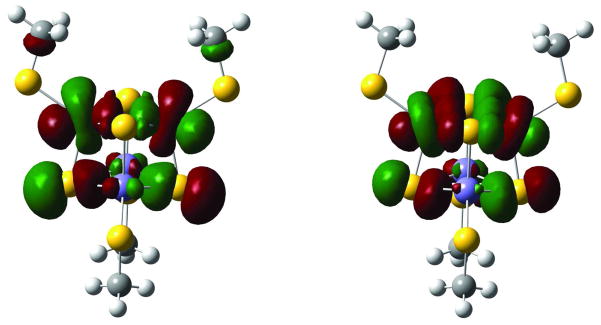
HOMO of the [Fe₄S₄(SCH₃)₄]³⁻ BS ground electronic states calculated at the DFT (B3LYP/6- 31G) (left) and ZINDO (right) levels. Both are in reasonable agreement.

Protein Pruning

Since the electron transfer reaction occurs locally between the neighboring iron-sulfur clusters, only the peptide close to the electron tunneling pathway significantly contributes to the reaction. We therefore perform calculations in two stages: first we identify the most important parts of whole protein with the approximate one-electron extended Hückel method using the procedure of protein pruning ³⁰; then we proceed with more accurate many-electron treatments using DFT and ZINDO semi-empirical method. In the pruning procedure, the tunneling matrix element is calculated at the extended Hückel level by using the perturbation theory Green’s functions, assuming a weak coupling of the donor and acceptor orbitals to the bridge orbitals. Here, we first include all the peptide residues located within a cylinder of radius R_cut with its axis connecting the donor and acceptor complexes; the cut-off radius R_cut is varied to find the minimum value which gives the tunneling matrix element within 5% error of the converged value. The tunneling matrix element is then calculated excluding residues one by one to identify the most essential ones. The peptide residues which change the tunneling matrix element by more than 1 % are retained. The x-ray crystal structure with optimized hydrogen atoms are used in all calculations. Since the protonation states of residues are unknown, neutral states of all residues are also assumed. The neutral hydroquinone state of riboflavin is employed as a model of the reduced FMN. Terminal dangling bonds are eliminated by capping C-terminals with –NHCH₃ groups and N-terminals with acetyl (-COCH₃) groups. The resulting pruned systems contain 200~500 atoms.

BS-ZINDO Calculations

BS donor and acceptor states of the pruned system at the ZINDO level are used for electron tunneling calculations. The BS-ZINDO calculations were performed as follows. First, the pruned peptide system, including the electron donor and acceptor, is dissected into several fragments with no covalent bonds between them. An electronic structure calculation is performed for each peptide fragment. The donor fragment has +1/2 and 0 spin and the acceptor fragment has 0 and +1/2 spin in the donor and acceptor electronic states, respectively. Due to the slight deformation of symmetric Fe/S clusters in the protein environment, several nearly degenerate BS ground states exist. In Eq. (2), the energy is lowest when each layer has the highest spin state, namely S₁₂=9/2 and S₃₄=9/2 for oxidized [Fe₄S₄R₄]²⁻ (R denotes ligands), or S₁₂=4 and S₃₄=9/2 for reduced [Fe₄S₄R₄]³⁻. BS-ZINDO calculations are carried out for such states of the oxidized donor and acceptor Fe/S fragments. 12 SCF initial guesses are employed by considering 6 possible choices of two oxidized Fe³⁺ and two reduced Fe²⁺ sites and 2 possible different spin alignments where a given pair of Fe²⁺ and Fe³⁺ sites can have parallel or anti-parallel spins. 2 to 10 different electronic spin states are obtained as converged SCF solutions, and 1 to 3BS states with the total energy less than 0.15 eV higher than the lowest one are considered in the subsequent calculations. The electronic spin states of the reduced [Fe₄S₄R₄]³⁻ are obtained by employing initial guesses from the converged electronic states of the oxidized [Fe₄S₄R₄]²⁻ clusters with N+1 electrons.

The resulting average 〈S²〉 values of the oxidized and reduced clusters are 8.9 and 8.6 in reasonable agreement with expected 9 and 8 by the Hamiltonian of Eq. (1) ¹⁰. The BS states consist mainly of S =1/ 2,3/ 2, and 5 / 2 pure spin states stabilized by B and B′ delocalization, which are in the range of thermal fluctuations (Figure 2).

BS-ZINDO calculations are performed for the total system with a set of different SCF initial guesses from the low-lying BS state pairs of the donor and acceptor fragments. The local electronic spin properties of each Fe/S cluster (namely, atomic spin densities, Mulliken charges, etc) are well preserved through the SCF procedure to the final converged solutions. The electron tunneling pathway and the tunneling matrix elements then calculated for different pairs of BS donor and acceptor states.

Electron Tunneling Calculation

Suppose the system is artificially “frozen” at the transition state of electron transfer reaction, where the energy of donor and acceptor electronic states are in resonance, the time-dependent wavefunction is described as a linear combination of the donor and acceptor diabatic states |Ψ_D〉 and |Ψ_A〉:

$$|\mathrm{\Psi }(t)\rangle =cos\left(\frac{T_{DA}}{\hslash }t\right)|{\mathrm{\Psi }}_D\rangle -isin\left(\frac{T_{DA}}{\hslash }t\right)|{\mathrm{\Psi }}_A\rangle ,$$ (3)

where T_DA is the tunneling matrix element. By combining Eq. (3) and a general expression of the probability current $\overrightarrow{j}(r,t)=\langle \mathrm{\Psi }(t)|\widehat{\overrightarrow{j}}(r)|\mathrm{\Psi }(t)\rangle$ where $\widehat{\overrightarrow{j}}(r)$ is the quantum-mechanical multi-electron flux operator, we have

$$\overrightarrow{j}(r,t)=-\overrightarrow{J}(r)sin\frac{2T_{DA}t}{\hslash }.$$ (4)

The spatial part of the probability current is called the transition flux described by ^23–24,31

$$\overrightarrow{J}(r)=-i<{\mathrm{\Psi }}_A\mid \widehat{\overrightarrow{j}}(r)\mid {\mathrm{\Psi }}_D>.$$ (5)

In the diabatic states, the tunneling electron is localized on their respective complexes. Assuming single Slater determinants for the donor and acceptor many-electron wavefunctions, the evaluation of the transition flux (Eq. (5)) becomes simplified by employing a set of corresponding (biorthogonal) orbitals^24,31. The corresponding donor and acceptor orbitals are obtained by appropriate rotations of the canonical MO’s of both states:

$$\begin{array}{l}|{\mathrm{\Psi }}_D\rangle =|{\phi }_{1\alpha }^D\cdots {\phi }_{m\alpha }^D{\phi }_{1\beta }^D\cdots {\phi }_{n\beta }^D\rangle \hfill \\ |{\mathrm{\Psi }}_A\rangle =|{\phi }_{1\alpha }^A\cdots {\phi }_{m\alpha }^A{\phi }_{1\beta }^A\cdots {\phi }_{n\beta }^A\rangle \hfill \end{array},$$ (6)

where the overlap matrix of |Ψ_D〉 and |Ψ_A〉 is diagonal: $\langle {\phi }_{i\sigma }^A|{\phi }_{j\sigma }^D\rangle ={\delta }_{ij}{s}_i^{\sigma }$^32–36.

For proteins the one-electron tunneling approximation holds ³¹, where a single pair of the corresponding orbitals with the smallest overlap $s_1^{\sigma }$ (denoted as tunneling orbitals) gives the largest and dominant contribution to the tunneling current, whereas the rest (core orbitals) undergo induced polarization and participate as an electronic Franck–Condon factor³⁷.

We have investigated the spatial extension of the tunneling tails of the tunneling orbitlas, which determines the tunneling pathways, by their atomic populations. For large systems, the population of the molecular orbital i on a given atom a can be evaluated as

$$P_{ia}=\sum _{\nu \in a}{C}_{i\nu }^2,$$ (7)

where C_iν is the contribution of the atomic orbital ν to the molecular orbital i. The scatter plots of the atomic population of the canonical and corresponding tunneling MO’s (Figure 4) shows the significance of the biorthogonalization procedure. Overall the scatter plots have slopes close to 1, in parallel to the diagonal lines with negative shifts in y-intercepts. The results show that the extension of the tails of the corresponding MO’s has similar distance dependence to those of canonical MO’s with significantly smaller amplitudes. That is consistent with that the corresponding donor and acceptor MO’s have dominant atomic population on single atoms of the core regions of the respective Fe/S clusters, as shown by the point in upper right corner of each panel. Significantly more localized corresponding MO’s suggest that the electron tunneling occurs primarily between a pair of donor and acceptor atoms in the corresponding orbital picture.

Figure 4.

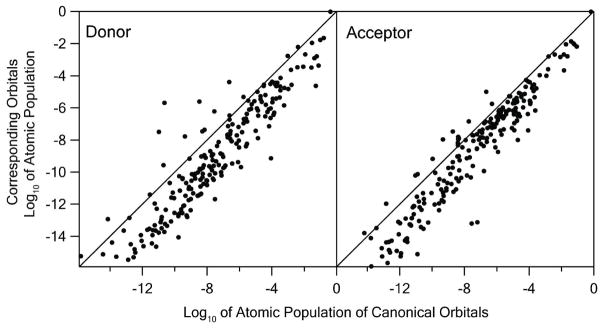
Scatter plots of the atomic population of the corresponding versus canonical tunneling donor (left) and acceptor (right) orbitals of N6a→N6b in base-10 logarithm. The diagonal lines represent the perfect correlation where both the canonical and corresponding MO’s have the same atomic populations on all atoms.

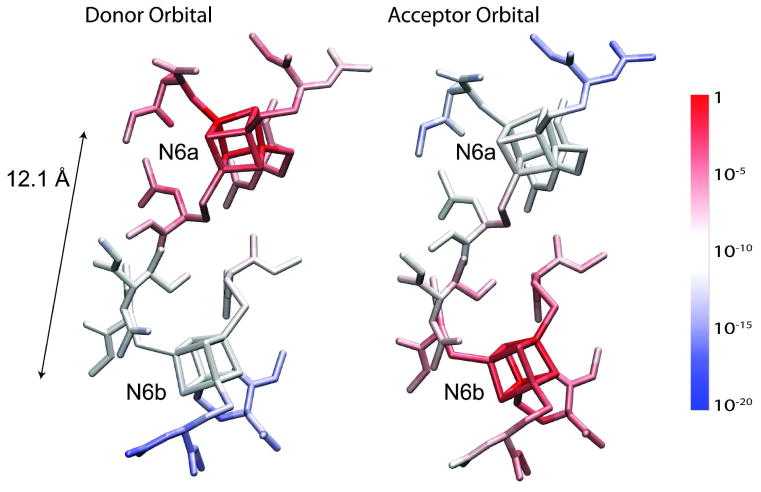
The atomic populations of the tunneling orbitals of the BS ground state of N6a→N6b are visualized in Figure 5. The donor orbital is localized on the donor complex (N6a) with a monotonically (close to exponentially) decaying tail toward the acceptor (N6b). The acceptor orbital is localized on the acceptor (N6b) with the similarly decaying tail to the donor (N6a). The overlap of the tunneling orbitals is calculated as $s_1^{\alpha }=5.0\times {10}^{-5}$. The next smallest overlap is 0.6 and all other overlaps are larger than 0.9, which suggests that core orbitals undergo only minor induced polarizations, maintaining their identities during the electron tunneling. The electronic Frank-Condon factors of all electron transfer processes tabulated in Table 1 are in the range between 0.44 and 0.75. The one tunneling electron approximation thus holds in the electron tunneling of complex I system where the donor and acceptor are multinuclear Fe/S clusters.

Figure 5.

Atomic population of the donor and acceptor tunneling orbitals of the BS ground state of N6→N6b. The atomic populations are indicated by blue-to-red color gradation in base-10 log scale. Hydrogen atoms are not shown to avoid complexity.

Table 1.

Distances, mediator residues, electronic Frank-Condon factor (FC), couplings <T_DA²>, and calculated rates k_ET of ET in Complex I. (C-to-C) and (G-to-G) are center-to-center and gateway-togateway atom distances. The gateway atoms are defined as core atoms of Fe/S clusters which give the largest contribution to the transition. When multiple G-to-G distances exist depending on the BS state pairs, the smallest one, which contributes most to ET, are shown. The mediator residues are the key residue, where majority of the flux passes along the main tunneling path, not including cysteine ligands. For couplings and rates, the numbers without parentheses are for the “dry” protein and the numbers in parentheses are for the protein with structural water included.

Pair	Distance [Å]		Mediator	FC	<TDA2> [cm−2]	kET [s−1]
	C-to-C	G-to-G
N3→N1b	14.0	11.0	3Ala63	0.50	4.6×10−4 (1.1)	1.3× 103 (2.9× 106)
N1b→N4	13.5	10.6	-	0.69	2.3×10−2	6.4 × 104
N4→N5	12.2	8.7	3Val232	0.67	9.8	2.8 × 107
N5→N6a	16.8	14.0	3Pro120	0.75	3.2×10−6 (2.3×10−3)	9.1 (7.3× 103)
N6a→N6b	12.1	9.3	-	0.60	0.98	2.8 × 106
N6b→N2	13.7	10.5	9Ile99	0.44	5.8×10−4 (5.3× 10−2)	1.9 × 104 (1.8× 106)

A total pruned system containing both donor and acceptor Fe/S clusters can be dissected into three, namely, the donor, acceptor, and the peptide bridge. The peptide bridge contains all peptide residues except for cysteine ligands and Fe/S clusters. The delocalization length of each molecular orbital L_i of the bridge peptides are evaluated by participation ration (PR) ³⁸:

$$L_i=1/\sum _n{\left(\sum _{a\in n}{P}_{ia}^2\right)}^2,$$ (8)

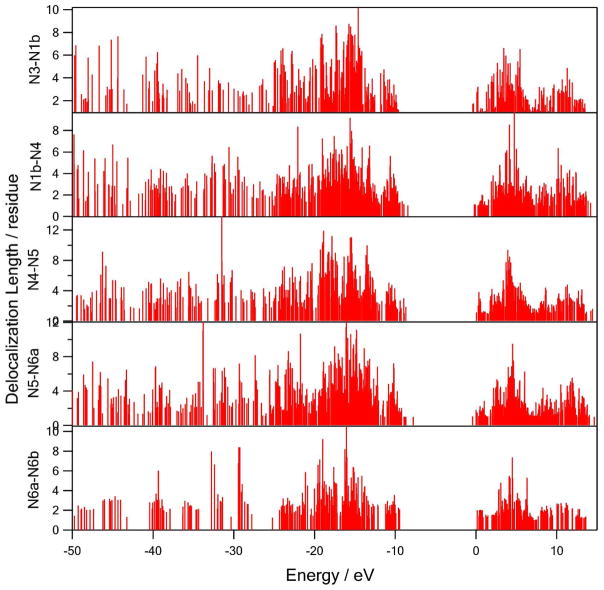
where n represents the index of protein residues. PR versus orbital energy is shown in Figure 6. The valence (occupied) band is up to the Fermi level of −10~−8 eV and the conduction (unoccupied) band starts at 0eV, which results in 8~10 eV energy gap between the two bands. While the unoccupied orbitals plotted are only the virtual orbitals, which do not necessarily correspond to actual electronic excitations, the calculated energy gap are in reasonable agreement with earlier studies. Occupied orbitals in the energy range −15 ± 3 eV are most delocalized over 9~12 residues. Unoccupied orbitals are less delocalized over 7~9 residues at about +4 eV. The bridges which contain aromatic residues (N5→N6a) have up to 2 eV higher Fermi level due to the aromatic π conjugations.

Figure 6.

The delocalization lengths of the molecular orbitals of the bridge peptide regions versus orbital energies.

The contributions of the donor, acceptor and bridge fragments to the donor and acceptor corresponding molecular orbitals of N6a→N6b are evaluated by:

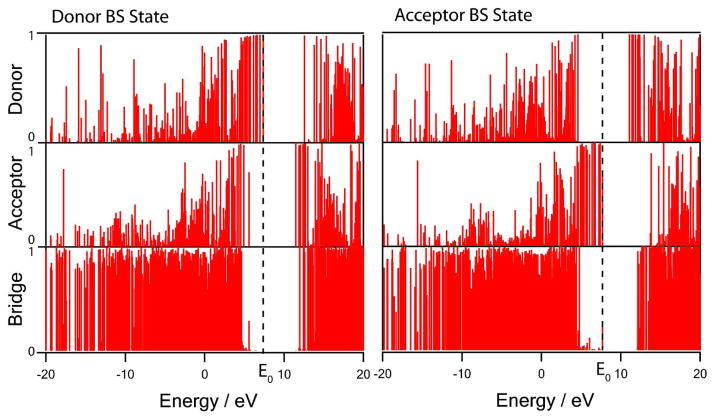
$$P_f=\sum _{\nu \in f}{C}_{i\nu }^2/\sum _{\nu }{C}_{i\nu }^2,$$ (9)

where f represents either donor, acceptor or bridge fragment. These contributions are plotted versus the orbital energy in Figure 7. The band gap of ~8 eV between the valence band and the conduction of the peptide bridge are blue shifted to +5 eV compared to the bridge only calculation due to the Coulombic repulsion with the additional 5 negative charges distributed over Fe/S clusters. In the donor electronic state (the initial state), the donor tunneling orbital is mostly localized on the donor with an energy at ~3 eV higher than the bridge valence band in the middle of the band gap together with other occupied d-orbitals of the donor. Similarly, in the acceptor state (the final state), the acceptor tunneling orbital is mainly localized on the acceptor with an energy at ~4 eV higher than the bridge valence band in the middle of the bridge band gap. Due to the increased electron-electron repulsions induced by an additional electron, all donor orbital energies are higher in the donor state and all acceptor energies are higher in the acceptor state. Both donor and acceptor orbitals are in resonance in energy. The result suggests that the tunneling orbitals are off-resonant from all molecular orbitals of the peptide bridge, which supports the direct electron tunneling mechanism between the donor and acceptor Fe/S clusters without any intermediate state involved where the electron is localized on some peptide residue.

Figure 7.

Normalized donor, acceptor and bridge contributions to the corresponding donor and acceptor BS molecular orbitals of N6a→N6b (Eq. (9)). Horizontal axis is orbital energy. The dashed lines represent the tunneling donor and acceptor orbitals in resonance at energy E₀.

By introducing the atomic basis set and the Mulliken type coarse-graining of the tunneling current, the transition flux (Eq. (5)) is expressed in terms of the interatomic currents, which has the following form in this paper ^31,39:

$$J_{ab}=\prod _{i\ne 0}{s}_i^{\alpha }\prod _i{s}_i^{\beta }\sum _{\nu \in a}\sum _{\mu \in b}\left(h_{\nu \mu }-E_0{S}_{\nu \mu }\right)\left(A_{\mu }{D}_{\nu }-D_{\mu }{A}_{\nu }\right).$$ (10)

Here ν and μ are the atomic orbitals of atom a and b; D_μ and A_ν are the expansion coefficients of the donor and acceptor tunneling orbitals, respectively; h_νμ and S_νμ are core Hamiltonian and overlap matrix, and E₀ is a tunneling orbital energy defined by

$$E_0=\sum _{\lambda ,\rho }{D}_{\lambda }{\overline{F}}_{\lambda \rho }{D}_{\rho }=\sum _{\lambda ,\rho }{A}_{\lambda }{\overline{F}}_{\lambda \rho }{A}_{\rho },$$ (11)

where F̄_λρ is the Fock matrix. The second equality in Eq. (11) corresponds to the resonance of the donor and acceptor redox potentials, and is achieved by applying a static electric field mimicking the solvation and the protonations of the protein residues in the in vivo environment.

Eq. (10) shows that the interatomic current is primarily determined by the overlap of the tails of the two tunneling orbitals. The electronic Frank-Condon factor ( ${\displaystyle \prod _{i\ne 0}}{s}_i^{\alpha }{\displaystyle \prod _i}{s}_i^{\beta }$) contributes as a uniform scaling factor for all inter-atomic currents, namely, larger induced polarization of the core electrons gives smaller tunneling currents. In case the electronic Frank-Condon factor is significantly smaller than 1 (for example, <0.1), the rearrangement of the core electrons is not negligible and the one-electron approximation no longer holds.

The total atomic current through a given atom a is expressed as

$$J_a^{\mathit{tot}}\equiv \frac{1}{2}\sum _b\left|J_{a,b}\right|,$$ (12)

which is proportional to the probability that a tunneling electron is passing through this atom in a tunneling transition. The tunneling matrix element, according to the total flux theorem ^23–24, is given by the surface integral of the tunneling flux across the dividing surface ∂Ω_D separating donor and acceptor complexes,

$$T_{DA}=-\hslash {\int }_{\partial {\mathrm{\Omega }}_D}(d\overrightarrow{s}·\overrightarrow{J}).$$ (13)

The tunneling matrix elements were calculated by Eqs. (10) and (13). In order to check that the total flux does not depend on dividing surface, the total flux is plotted with respect to the position of the dividing plane perpendicular to the line connecting donor and acceptor complexes in Figure 8. The flux is found conserved in sufficiently large range of the position of the dividing plane around the midpoint (0.5) between the donor and acceptor. For consistency, a midpoint position is chosen for the matrix element evaluation in all calculations.

Figure 8.

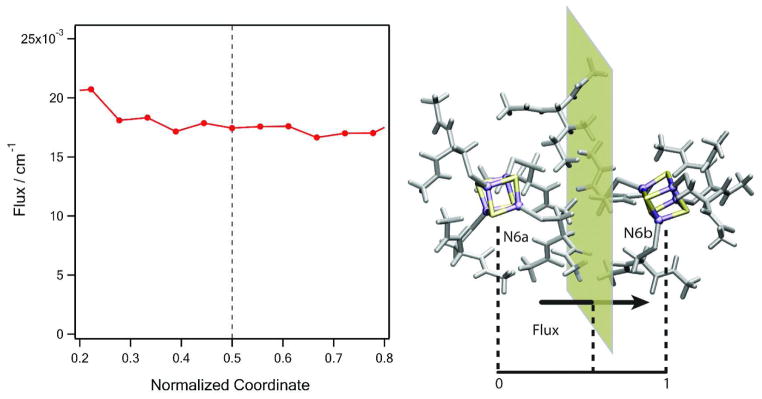
Calculated total flux of N6a→N6b across the dividing plane perpendicular to the line connecting the donor (N6a) and acceptor (N6b) complexes. The coordinate is normalized as 0 at the center of N6a and 1 at the center of N6b. The total flux is conserved in the vicinity of the transition (0.5), which gives the tunneling matrix element T_DA by the flux theorem (Eq. (13)).

Electron Tunneling Pathways

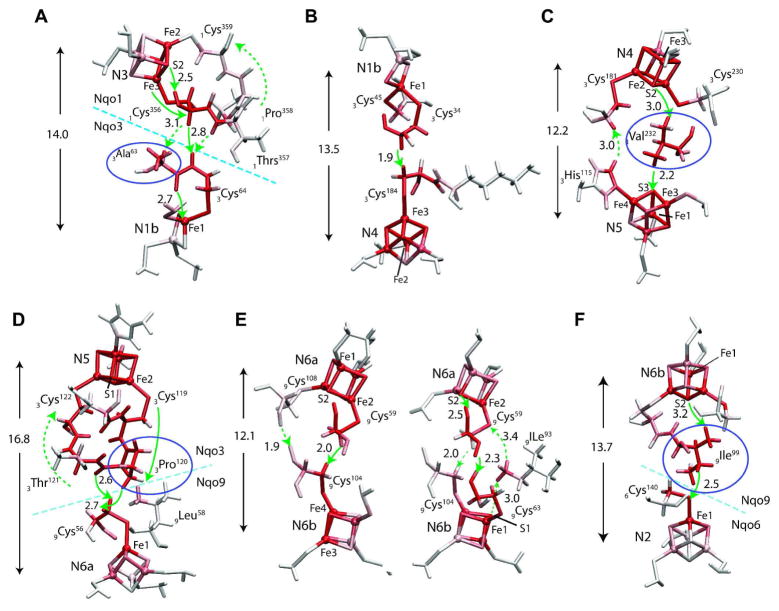
For different pairs of donor and acceptor BS states, the tunneling pathways are similar, except for some details at the Fe/S clusters themselves. Most typical tunneling pathways are shown in Figure 9. For shortest electron tunneling distances, the pathway runs either along the two cysteine wires of the donor and acceptor in direct van der Waals contact (N1b →N4 and N6a→N6b), or along a single mediator residue located in the middle of the two Fe/S complexes with two through-space jumps (N4→N5). For intermediate distances, e.g. N6b→N2, one cysteine ligand and one mediator residue participate. For longest distance tunneling (N3→N1b and N5→N6a), one neighboring residue of either exit or entrance cysteine also participates as an extended through-bond wire in addition to the two cysteine residues. One to three through-space jumps are involved, all over distances below 3.2 Å, which indicates that the tunneling electron avoids pathways with longer through-space jumps due to higher energy costs

Figure 9.

Electron tunneling pathways of (A) N3→N1b, (B) N1b→ N4, (C) N4→N5a, (D) N5→N6a, (E) N6a→N6b, (F) N6b→N2 Total atomic currents proportional to probability that the tunneling electron will pass through a given atom (Eq. (12)) is indicated by red color intensity. Only the residues with significant total atomic currents are shown. Through-space jumps are indicated by green arrows with distances in Å. When multiple paths present, directions of the electron flux in the primary and secondary paths are marked by solid and dashed arrows, respectively. The arrows and numbers in Å are center-to-center distances between the donor and acceptor clusters. Mediator residues are marked with violet circles.

Significant quantum interferences are observed between some Fe/S cluster pairs (N3→N1b, N4→N5 and N5→N6a). In N5→N6a process, clusters N5 has two cysteine (₃Cys¹¹⁹ and ₃Cys¹²²) wires connected by neighboring ₃Pro¹²⁰ and ₃Thr¹²¹ residues making the backbone loop (N5-₃Cys¹¹⁹-₃Pro¹²⁰-₃Thr¹²¹-₃Cys¹²²-N5) stabilized by a hydrogen bond and the ₃Pro¹²⁰ rigidity. The main electron tunneling flux from N5 is through ₃Cys¹¹⁹ and ₃Pro¹²⁰, part of which is reflected back to N5 through ₃Thr¹²¹ and ₃Cys¹²², the rest is transmitted to ₉Cys⁵⁶ with a 2.7 Å or 2.6 Å through-space jump across the subunit boundary of Nqo3 and Nqo9. The electron then tunnels through ₉Cys⁵⁶ ligand to reach N6a. In process N6a→N6b. the electron tunnels along two different pathways depending on the involved BS states, suggesting the sensitive nature of the pathways to the local protein environment.

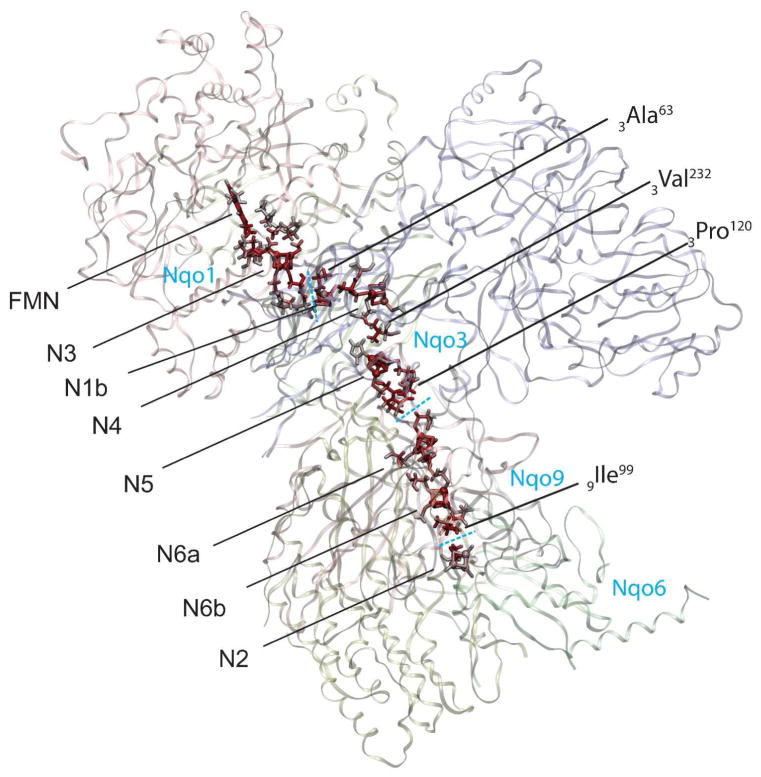
The whole electronic wiring of complex I is obtained by combining tunneling pathways of individual processes, as shown in Figure 10. It is clear that specific peptide residues serve as electronic wires connecting neighboring Fe/S clusters; individual electron tunneling paths involve up to three protein residues, including two cysteine ligands and one additional key residue. Notably, the clusters in the protein are oriented in a specific way – corner to corner – with Cys ligands mostly pointing toward each other, which is clearly the most efficient way to transfer electrons from one cluster to another. The protein subunit boundaries are clearly seen as significant gaps in the electronic wiring of complex I where internal water should exist.

Figure 10.

Calculated complete electron tunneling pathway from FMN to N2 of complex I. The atoms with significant electron tunneling probability are highlighted with red color intensity corresponding to their total current densities. The dashed lines indicate the subunit boundaries. Mediator residues of electron tunneling are marked with labels.

Electron Transfer Rates

The electron transfer rates between the clusters are calculated by using Marcus’ theory ⁴⁰

$$k_{ET}=\frac{2\pi }{\hslash }\frac{<{T_{DA}}^2>}{\sqrt{4\pi \lambda k_{B}T}}exp[-\frac{{(\mathrm{\Delta }{G}^0+\lambda )}^2}{4\lambda k_{B}T}].$$ (14)

Here we employ the generic reorganization energy λ = 0.5 eV ^41–42 and the experimental driving force ΔG = −0.15 eV for N6b→N2 and ΔG = 0 eV for all the other processes ^1,43 as computational values are expected to be sensitive to yet unknown electrostatic environment of the protein such as solvation and protonation states. The dynamical average of the electronic coupling matrix elements squared $\langle T_{DA}^2\rangle$ is evaluated based on the following observations. Different nearly degenerate electronic states are typically localized differently in the Fe/S cluster due to the anti-ferromagnetism, which means that the tunneling orbitals in the core regions are constantly changing in time, driven by the thermal dynamics of the protein environment. On the other hand, the tunneling tails of the different tunneling orbitals extending over the intervening protein space have similar spatial decay in shape, but depend strongly in absolute value on the orbital types with different localizations in the Fe/S clusters. The averaging procedure we introduced is as follows. For a given pair of donor and acceptor tunneling orbitals the tunneling matrix element is renormalized as: $T_{DA}^{\ast }=T_{DA}/\sqrt{P_D{P}_A}$, where P_D and P_A are the atomic populations on the respective gateway atoms defined as core atoms of Fe/S clusters which give the largest contribution to the transition. For different pairs of donor and acceptor orbitals, the renormalized matrix element $T_{DA}^{\ast }$ is about the same, and reflects the maximum possible coupling between redox centers, which occurs when donor and acceptor orbitals are localized on the respective gateway atoms. The dynamical and statistical average of the electronic coupling that determines the electron transfer rate is $<T_{DA}^2>={\gamma }_D{\gamma }_A{(T_{DA}^{\ast })}^2$, where γ = 1/ 8 for 4Fe-4S clusters and γ = 1/ 4 for 2Fe-2S clusters. Here we assume a statistically equal distribution of the tunneling orbitals over eight core atoms of 4Fe-4S cluster, and over four core atoms of 2Fe-2S cluster.

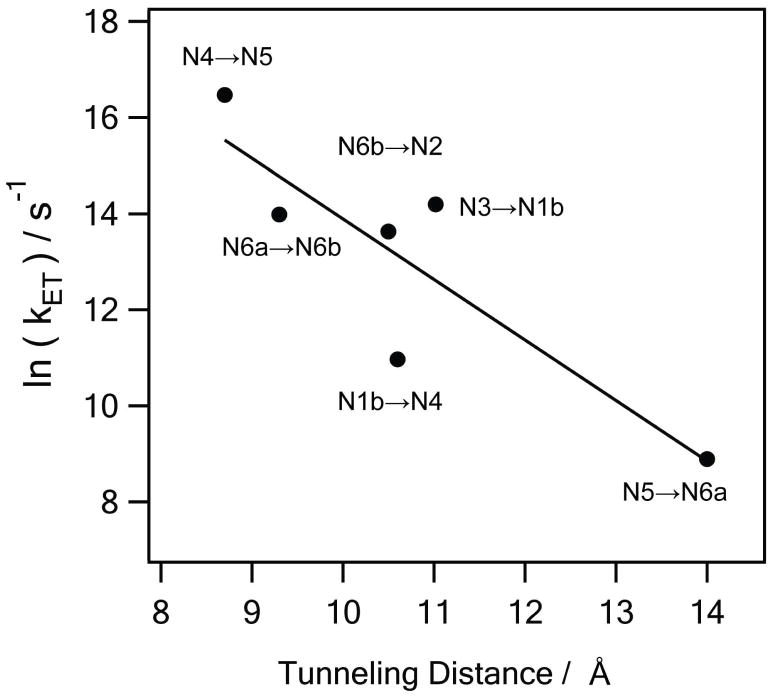
The calculated electronic couplings and the rates are shown in Table 1. Four electron transfer processes of N1b→N4, N4→N5, N6a→N6b, and N6b→N2 are faster than both the reported estimates of the total transfer rate: 170 s⁻¹ and10⁴ s⁻¹. However, the transfer rate of N3→N1b (~10³ s⁻¹) is slower than the highest estimate, and N5→N6a (~10 s⁻¹) is drastically slower than the reported rates. Both are the electron tunneling across the protein subunit boundaries, where internal water molecule should be present ⁴⁴, although the intervening water is not seen in the crystal structure due to its possible significant mobility.

We have thus performed the calculations of the electron tunneling processes of N3→N1b, N5→N6a, and N6b→N2 across the protein subunit boundaries with the internal water molecules included with their optimized structures. With water present between the subunits, the tunneling rates are dramatically increased by two to three orders of magnitude (Table 1). With this increase, the overall transfer rate now satisfies a typical physiological requirement ⁴¹, and is roughly equal to a typical electron transfer rate for such distance ⁴⁵. With the water included the negative slope of the distance dependence or ET rates in natural logarithm becomes 1.3, which agrees well with a typical 0.6 in base-10 log ⁴⁵. The internal water at the subunit boundaries is therefore an essential mediator for the efficient electron transfer along the redox chain of complex I. The calculated enhancement of the ET rate due to the internal water agrees well with a recent study on the bovine liver cytochrome b₅ ⁴⁶.

Discussions

Theoretical details and analysis of the atomistic simulation of the electron tunneling along Fe/S clusters in respiratory complex I are presented. The tunneling current theory is applied to the brokensymmetry (BS) donor and acceptor states of the pruned protein systems for individual electron transfer processes. The pruned protein system consists of anti-ferromagnetically coupled binuclear or tetranuclear Fe/S donor and acceptor clusters and a peptide bridge region connecting them.

While, the tunneling tails of the donor and acceptor orbitals contribute to the tunneling pathway, the induced polarization of the core electrons contributes as a scaling factor of the magnitude of the tunneling current through the electronic Frank-Condon (FC) factor. The calculated FC factors in the range of 0.44~0.75, and the small overlaps of the tunneling orbitals (<10⁻⁴) suggests that even in the case of the multinuclear (2Fe-2S or 4Fe-4S) anti-ferromagnetic donor and acceptor systems, the one tunneling electron approximation still holds. Only one electron primarily participates in tunneling and other electrons undergo induced polarized without any significant orbital and spin rearrangement. However the induced polarization effect is also significant and should be considered in the electron transfer rate calculations since the rates are scaled by the square of the FC factor (0.19~0.56).

Population analysis of the tunneling orbitals shows that the tunneling donor and acceptor orbitals are localized on donor and acceptor cluster, respectively with exponentially decaying tunneling tails extending toward each other through the peptide bridge region. The atomic populations of the donor orbital around the acceptor complex and the atomic population of the acceptor orbital around the donor complex are as small as 10⁻²⁰~10⁻¹⁵ depending on the tunneling distance. However, both donor and acceptor orbitals have much larger atomic populations of 10⁻¹⁰~10⁻⁷ in the vicinity of the midpoint between the donor and acceptor clusters where the tunneling matrix element is evaluated by the flux theorem. This result supports the advantage of the tunneling current theory in numerical stability of the computed tunneling matrix elements, as demonstrated in Fig. (8). The conventional direct evaluation requires the overlap integral of the two tunneling orbitals (Eq. (8a) of Ref. ³⁷), which can be more susceptible to numerical errors due to too small amplitude of the donor and acceptor orbitals at the acceptor and donor sites, respectively.

By analyzing the donor, acceptor and bridge contributions to the corresponding donor and acceptor orbitals of N6a→N6b, it is found that and the tunneling energy is ~3 eV higher than Fermi level in the middle of the energy gap between valence and conduction bands of the bridge peptide. This is reasonable since the tunneling orbitals are mainly from the d-orbitals of Fe atoms, which is off-resonant in energy with the any orbitals of protein bridge region, which typically consist of s and p orbitals of carbon, oxygen, nitrogen and hydrogen. This supports that the electron transport in complex I is achieved by the wave properties of electron via quantum tunneling.

A signature of the wave properties of electrons is observed when multiple electron tunneling pathways exist. Quantum interferences are pronounced in a characteristic peptide configuration where a peptide backbone loop connected to the donor is facing the cysteine ligand wire attached to acceptor in a few Å distance (N3→N1b and N5→N6a).

In N6a→N6b, electron tunnels along different pathways depending on the involved BS state pairs of Fe/S clusters. Considering that the spin states of the Fe/S clusters constantly change driven by the thermal fluctuations of the protein local environment, the result suggests that the electrons tunneling pathways also fluctuate accordingly. The tunneling pathways are mostly fixed and do not depend significantly on the BS state pairs for the other Fe/S pairs.

The averaging procedure of the coupling matrix element T_DA reflects the fact that many tunneling orbitals are statistically mixed in the course of protein dynamics. Different nearly degenerate electronic states are typically localized differently in the Fe/S cluster due to the anti-ferromagnetism; this means that the tunneling orbitals in the core regions are constantly changing in time, driven by the thermal dynamics of the protein environment. On the other hand, different tunneling orbitals, while having different structure at the cluster regions, are similar in the intervening protein space, where they extend their tunneling tails. It is the tail region of the wave functions that determines the efficiency of electron coupling between metal sites and the character of electron propagation in the protein matrix. Since the tunneling tails are more or less invariant in shape but depend strongly, in absolute value, on the orbital types, and since different orbitals with close energies are expected to be mixed in the course of thermal dynamics of the protein, a statistical renormalization of the tunneling orbitals and the corresponding tunneling matrix element is reasonable to evaluate the dynamical average of the coupling matrix element.

The internal water has been shown to accelerate the electron transfer kinetics so as to achieve the physiologically meaningful rate, and log of the electron transfer rate with internal water has a liner relationship with tunneling distance with the negative slope close to a typical value. Both results strongly suggest that the internal water play an essential role as a mediator of electron transfer in physiological conditions.

Since it is indicated that the dynamical mixing of the donor and acceptor BS electronic alters the electron tunneling pathways in intervening protein regions dynamically in N6a→N6b, the thermal fluctuations of the protein nuclear configurations and positions of the internal water can also dynamically change the instantaneous tunneling pathways, and can thus affect the resulting electron transfer rates, which should be investigated in future studies.

Figure 11.

Natural logarithms of the simulated electron transfer rates (in s⁻¹) versus the tunneling distance between gateway atoms (in Å). The negative slope of the least-squares line (solid line) is 1.3. The number is equivalent to 0.56 in base 10 logarithm, reproducing a typical value 0.6 in proteins ⁴⁵.