Skip to main content
PMC home page
Wiley Open Access Collection logoLink to Wiley Open Access Collection
. 2014 Mar 24;23(8):819–829. doi: 10.1002/pds.3607

Using fractional polynomials to model the effect of cumulative duration of exposure on outcomes: applications to cohort and nested case-control designs

Peter C Austin 1,2,3,*, Laura Y Park-Wyllie 4, David N Juurlink 1,2,5
PMCID: PMC4230473  PMID: 24664670

Abstract

Purpose

Determining the nature of the relationship between cumulative duration of exposure to an agent and the hazard of an adverse outcome is an important issue in environmental and occupational epidemiology, public health and clinical medicine. The Cox proportional hazards regression model can incorporate time-dependent covariates. An important class of continuous time-dependent covariates is that denoting cumulative duration of exposure.

Methods

We used fractional polynomial methods to describe the association between cumulative duration of exposure and adverse outcomes. We applied these methods in a cohort study to examine the relationship between cumulative duration of use of the antiarrhythmic drug amiodarone and the risk of thyroid dysfunction. We also used these methods with a conditional logistic regression model in a nested case-control study to examine the relationship between cumulative duration of use of bisphosphonate medication and the risk of atypical femur fracture.

Results

Using a cohort design and a Cox proportional hazards model, we found a non-linear relationship between cumulative duration of use of the antiarrhythmic drug amiodarone and the risk of thyroid dysfunction. The risk initially increased rapidly with increasing cumulative use. However, as cumulative duration of use increased, the rate of increase in risk attenuated and eventually levelled off. Using a nested case-control design and a conditional logistic regression model, we found evidence of a linear relationship between duration of use of bisphosphonate medication and risk of atypical femur fractures.

Conclusions

Fractional polynomials allow one to model the relationship between cumulative duration of medication use and adverse outcomes.

Keywords: Cox proportional hazards regression model, fractional polynomials, time-dependent covariates, survival analysis, pharmacoepidemiology, cohort study, nested case-control study

INTRODUCTION

Determining the functional form of the relationship between a variable that represents cumulative duration of past exposure to an agent and the hazard of an adverse outcome is an important issue in environmental and occupational epidemiology, public health, and clinical medicine. Important examples of cumulative duration of past exposure include tobacco smoke, industrial toxins, environmental pollutants, radiation, and medications taken for chronic medical conditions. Correctly describing the functional nature of the relationship between such exposures and the risk of an adverse event can inform regulators, public health officials, clinicians and patients and can identify whether or not cumulative toxicity is important. When it is, an accurate characterization of the relationship between cumulative duration of past exposure and toxicity can help to characterize safe levels of cumulative exposure, levels of cumulative duration of past exposure at which the risk becomes clinically important, and the level of total duration of exposure after which the risk of the outcome increases more rapidly.

Common study designs for the analysis of the effects of exposures on the risk of adverse events are the cohort design, the case-control design and nested case-control design. When using a cohort design, the Cox proportional hazards regression model is often used to describe the association between exposure and the hazard of an outcome. When using a case-control (or nested case control) design in which one or more controls have been individually matched to each case, conditional logistic regression can be used to determine the association between total cumulative duration of past exposure and the risk of the outcome.

The Cox proportional hazards regression model is frequently used in biomedical research to model the effect of explanatory variables on the hazard of the occurrence of a time-to-event outcome.1 A primary advantage of this model is that one is freed from making specific assumptions about the functional form of the hazard function or about the specific parametric family from which the distribution of event times arises. Two secondary advantages of this model are its abilities to incorporate time-varying covariate effects and time-dependent (or time varying) covariates.2 The former refers to a variable whose effect on the hazard of the outcome is allowed to change over the duration of follow-up. The latter refers to a variable whose value itself changes over the duration of follow-up.

Dichotomous or categorical time-dependent variables occur frequently in biomedical research. Each level of the variable represents a discrete state, and patients can move between different discrete states (e.g. receipt of an organ transplant, current use of chronic medication, and current use of different medications within the same therapeutic class). However, a time-dependent variable may also be a continuous variable. A particularly important type of continuous time-dependent variable is one denoting cumulative duration of past exposure. While incorporating categorical time-dependent variables into a Cox proportional hazards regression model is relatively straightforward, incorporating a continuous time-dependent variable is more complex. In particular, one must decide how to model what may be a non-linear relationship between a continuous time-dependent covariate and the log hazard of the outcome.

Different methods have been proposed for estimating the effect of cumulative duration of exposure on the risk of adverse outcomes. Hauptmann et al. used a B-spline to model the effect of incremental exposure on disease risk.3 The method was subsequently applied in a case-control study examining the effect of smoking on lung cancer. Richardson et al. used parametric latency functions to estimate the incremental effect of increasing exposure on disease risk.4 The method was subsequently illustrated by examining the association between radon exposure and lung cancer mortality in uranium miners. Richardson et al. describe that lagging exposure is often used to allow for a latency period in studies examining the effect of cumulative exposure on disease risk. They developed methods to allow for the joint estimation of parameters describing the association between exposure and outcome and the latency distribution.5 The method was illustrated by examining the association between cumulative asbestos exposure and lung cancer mortality in textile workers. Finally, both Abrahamowicz et al.6 and Sylvestre and Abrahamowicz7 developed a method for modelling the cumulative effects of time-dependent exposures in cohort studies, weighted by recency, represented by time-dependent covariates in a Cox proportional hazards model. In doing so, the function that assigns weights to previous doses was estimated using cubic regression splines. This method has been used to assess the cumulative effects of exposure to benzodiazepines on the risk of fall-related injuries in the elderly.8

When fitting regression models, analysts frequently categorize continuous explanatory variables, either out of convenience or in the interest of simplicity. However, several authors have criticized this practice.9–12 Drawbacks to categorization include difficulties in deciding how best to categorize the continuous variable, incorrect inferences, and the loss of information. However, assuming a linear relationship between the continuous variable and the outcome can also yield misleading analyses. Several different approaches have been proposed to account for non-linear relationships between fixed or time-invariant continuous explanatory variables and the outcome. These include the use of generalized additive models, restricted cubic smoothing splines, and fractional polynomials (FPs).12–14 Each of these approaches allows for flexible modelling of the relationship between a continuous fixed or time-invariant covariate and the outcome.

The objective of the current study was to examine the utility of FPs to model the relationship between cumulative duration of past exposure and the risk of an adverse outcome. We examine the use of these methods in two common study designs: the cohort design and the nested case-control design. We first provide a brief review of FPs for modelling the effects of continuous covariates. We then describe two case studies in which we examine the relationship between cumulative duration of past exposure to a specific medication and the risk of an adverse event.

FRACTIONAL POLYNOMIALS

Fractional polynomials were proposed by Royston and Altman as a restricted set of transformations of a single continuous variable.15,16 Given a continuous explanatory variable x > 0, a transformation of the form xp for p in S = {−2, −1, −0.5, 0, 0.5, 1, 2, 3} (with the convention that x0 denotes log(x)) is referred to as an FP transformation of degree 1. An FP1 function, defined as ϕ*(x,p) = β0 + β1xp = β0 + ϕ1(x;p), can be included in a regression model as an explanatory variable. There are eight FP transformations of degree 1.

Royston and Altman extended the definition of FP transformations to FPm transformations, where m is an integer ≥2. An FP2 transformation of x with powers p = (p1,p2) yields the vector 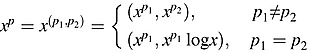Inline graphic. An FP2 function (for p1≠p2), defined as 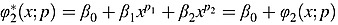Inline graphic, can be included in a regression model as an explanatory variable (for p1 = p2, the function would be modified as above). The powers p1 and p2 are taken from the same set S described in the previous paragraph. There are 28 FP2 transformations with distinct powers (p1 ≠ p2) and 8 FP2 transformations with equal powers (p1 = p2); consequently, there are a total of 44 FP1 and FP2 transformations. FP1 functions are always monotonic, while FP2 functions may be monotonic or unimodal. In medical applications, FP1 and FP2 transformations are used almost exclusively, with higher order transformations being used rarely. FP1 and FP2 functions allow representation of a wide range of non-linear relationships. For greater detail, the reader is referred to the comprehensive reference by Royston and Sauerbrei.14 Once a specific FP1 or FP2 function is incorporated into a regression model (for Cox proportional hazards models, the intercept is omitted from the FP function), the regression model can be estimated using conventional methods for the regression model at hand.

A closed test procedure, known as RA2, has been proposed for selecting the most appropriate FP function for inclusion in a regression model.17,18 In this procedure, which is described in greater detail in the references provided in this paragraph, a linear function is assumed as the default choice or selection. The test procedure preserves an overall family-wise type I error rate of α. One fits each of the 44 possible regression models, each containing a different FP function as an explanatory variable (possibly in addition to other covariates) and determines the deviance of each fitted model. We reproduce Royston and Sauerbrei's14 description of this selection procedure:

  1. Compare the best FP2 model for x against the null model using a test with 4 degrees of freedom. If the test is not significant, then one stops the process and concludes that the effect of x is not significant at the α level. Otherwise proceed.

  2. Test for the best FP2 for x against a linear relationship at the α level using a test with 3 degrees of freedom. If the test is not statistically significant, then one stops, with the final model being a straight line. Otherwise continue.

  3. Test for the best FP2 for x against the best FP1 at the α level using a test with 2 degrees of freedom. If the test is not significant, the final model is FP1; otherwise, the final model is FP2. At this point the procedure terminates.

The previous discussion of FPs and the procedure for selecting the best FP transformation for settings in which there is a single continuous variable one is seeking to model using FPs. It is also possible to use FPs to simultaneously model the effects of several continuous variables on the outcome. However, we do not consider this approach here, as the focus of the current study considers only a single continuous variable denoting cumulative duration of past exposure.

CASE STUDIES

We present two case studies to illustrate the use of FPs for modelling the relationship between cumulative duration of past exposure to a given medication and the risk of an adverse event. In the first, we use a cohort design, while in the second, we use a nested case-control design. In the former, cumulative duration of past exposure was modelled as a time-dependent covariate in a Cox proportional hazards model.

Cumulative duration of previous amiodarone use and thyroid dysfunction in elderly patients

Motivation

Amiodarone is an antiarrhythmic agent that is considered the most effective drug for controlling rhythm in atrial fibrillation.19,20 However, it has various effects on the thyroid.21,22 We examined the relationship between cumulative duration of previous use of amiodarone and the hazard of thyroid dysfunction in a cohort of subjects initiating treatment with amiodarone. Cumulative duration of previous use of amiodarone was treated as a continuous time-dependent covariate.

Methods

The Ontario Drug Benefit (ODB) database documents prescriptions filled under Ontario's drug benefit programme, which provides universal access to prescription medications to all Ontario residents over the age of 65 years old. We identified all Ontario residents over the age of 66 years old who filled a prescription for amiodarone in 2005 and who had not filled a prescription in the previous 365 days (the decision to exclude subjects who had filled a prescription for amiodarone in the previous year was based on an earlier study comparing brand name versus generic formulations of amiodarone in patients with atrial fibrillation23). We excluded subjects who had evidence of thyroid dysfunction in the year prior to the initial prescription for amiodarone, using methods similar to those described in a study comparing the effect of amiodarone formulations on thyroid dysfunction.23 The cohort consisted of 4839 patients. The date of cohort entry was defined to be the date on which the initial prescription of amiodarone was filled. The age and sex of each cohort member were determined by linking each subject to the Registered Persons Database (RPDB) using encrypted health card numbers. Each cohort member was followed up for the occurrence of thyroid dysfunction, using methods similar to those described in an earlier publication.23 For each subject, the time from cohort entry to the occurrence of thyroid dysfunction was determined. Subjects were followed until 31 December 2010 and were censored at death (as denoted in the RPDB) or if the event of interest had not occurred by the end of the study period. The median length of observed follow-up time was 1564 days (25th percentile: 390 days and 75th percentile: 1991 days). Twenty-two percent of the subjects experienced the occurrence of thyroid dysfunction.

For each subject, we used the ODB database to identify all prescriptions for amiodarone that were filled between the date of cohort entry and the end of follow-up. The duration of each prescription was determined from the mandatory days supply field of the prescription record. Using the date that each prescription was filled and the duration of each prescription, we were able to determine the cumulative duration of daily exposure to amiodarone during follow-up. For each new prescription, the cumulative duration of daily exposure was increased by one for each day supplied by that prescription. During periods of non-use (lapses in use of amiodarone), the cumulative duration of daily exposure remained unchanged from the value at the time the previous prescription expired. We were thereby able to determine, for each day of follow-up, a subject's cumulative duration of past exposure to amiodarone. In using this method, we are using prescription duration (number of days supplied) as a surrogate for duration of medication use. In reality, if a patient did not use some of the dispensed tablets, the actual duration of use would be less than the duration of the prescription (the number of days supplied). Using administrative data, it is not possible to determine with certainty whether patients actually take all the provided medication; however, in the presence of successive refills, it is sensible to assume that the total prescription duration is a good clinical proxy for the total duration of use.

The data set was structured so that there was one record per day of follow-up per subject. One variable denoted the cumulative duration of daily use of amiodarone for the day and subject to which the record pertained. The counting process style of model formulation was used for specifying the Cox proportional hazards model.

Each of the 44 FP1 and FP2 transformations was applied to the variable denoting current cumulative duration of daily use of amiodarone. We fit a Cox proportional hazards model in which the time to thyroid dysfunction was regressed on cumulative duration of amiodarone exposure (transformed using the corresponding FP transformation) and the patient's sex and age at cohort entry. The RA2 selection procedure was applied to select the most appropriate transformation of cumulative duration of drug exposure.

All statistical analyses were performed using SAS version 9.2 (SAS Institute Inc., Cary, North Carolina).

Results

The empirical cumulative distribution function describing the distribution of cumulative duration of amiodarone exposure at the end of follow-up for each subject is described in the left panel of Figure 1.

Figure 1.

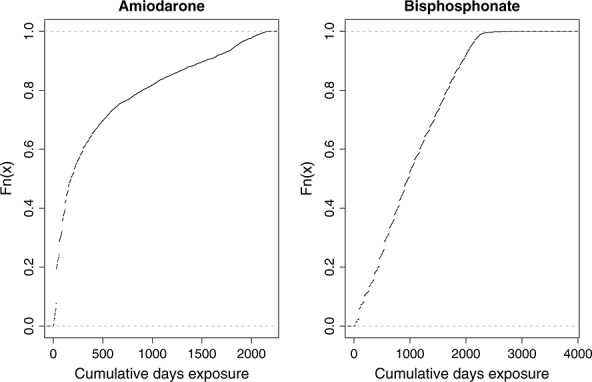
Figure 1

Open in a new tab

Cumulative days of medication use at the end of follow-up

The distributions of the deviance across the 8 FP1 models and the 36 FP2 models, along with that of the null model, are depicted in the left panel of Figure 2. The deviance of the best-fitting FP2 model, the best-fitting FP1 model, the linear model and the null model is reported in Table 1, along with the results of the test comparing different FP models. Using the RA2 selection algorithm, the FP2 transformation with P = (1, 1) was selected as the best-fitting FP transformation. The FP model that best described the relationship between cumulative duration of use of amiodarone and the log hazard of thyroid dysfunction was of the form β1x + β2x log(x), where x denotes cumulative use of amiodarone. The point estimates and associated 95% confidence intervals for β1 and β2 were 0.0216 (0.0176, 0.0256) and −0.0027 (−0.0032, −0.0022), respectively. Four other FP2 ((0.5, 2), (0.5, 1), (0.5, 3), and (0.5, 0.5)) transformations resulted in models with deviance within four of that of the best-fitting FP2 transformation. None of the FP1 transformations resulted in models whose deviance was within four of that of the best-fitting FP2 transformation.

Figure 2.

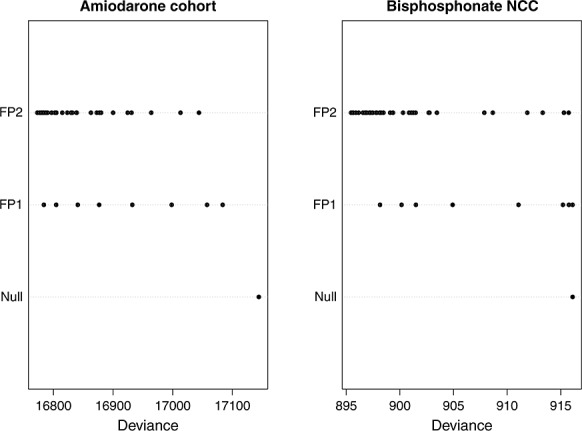
Figure 2

Open in a new tab

Deviances of all 44 fractional polynomial models

Table 1.

Fractional polynomial models for effect of cumulative duration of past amiodarone use on the risk of thyroid dysfunction

Model Deviance D P Step Comparison Deviance difference p-value
FP2 16 772.87 1, 1 1 FP2 versus null 371.72 <0.0001 (4 d.f.)
FP1 16 783.91 0 2 FP2 versus linear 103.80 <0.0001 (3 d.f.)
Linear 16 876.67 1 3 FP2 versus FP1 11.04 0.0040 (2 d.f.)
Null 17 144.59
Open in a new tab

The relationship between cumulative duration of daily use of amiodarone and the log-hazard ratio of thyroid dysfunction (relative to a subject with 1 day of amiodarone use) is described in the left panel of Figure 3. The vertical axis denotes the log-hazard ratio comparing the hazard for thyroid dysfunction for a subject with a given cumulative duration of use with that of a subject whose cumulative duration of use was equal to one (i.e. with that of a subject who had used amiodarone for one single day). On the horizontal axis is a rug plot describing the distribution of cumulative duration of amiodarone use at the end of follow-up. We describe the relationship between cumulative duration of amiodarone use and the risk of the outcome as described by the best-fitting FP1 and FP2 transformations and by the identity transformation (i.e. assuming a linear relationship). The FP2 (1, 1) transformation shows the risk of thyroid dysfunction increasing rapidly with increasing cumulative duration of amiodarone use. However, once cumulative duration of use exceeded approximately 700 days, the rate of increase in the risk of thyroid dysfunction begins to attenuate. The risk of thyroid dysfunction eventually begins to decrease with increasing duration of cumulative duration of amiodarone use. This attenuation and decrease may reflect depletion of susceptibles—those subjects who had higher risk for thyroid dysfunction experience an early failure. Alternatively, it may be because of exposure having occurred entirely in the distant past (i.e. subjects have discontinued treatment), and distant exposure may have little impact on the current risk of thyroid dysfunction.

Figure 3.

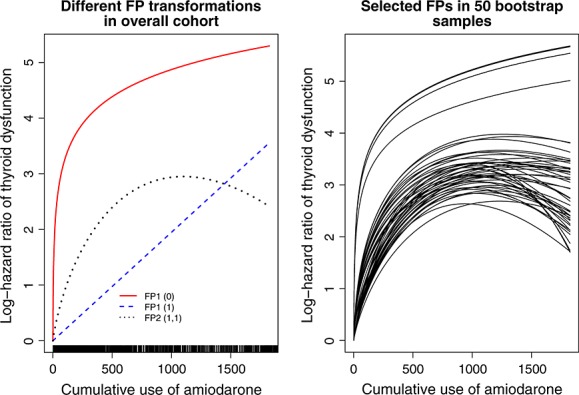
Figure 3

Open in a new tab

Relationship between cumulative duration of past amiodarone use and thyroid dysfunction

To examine uncertainty in the selection process, we drew 50 bootstrap samples from the original cohort (i.e. samples of the same size as that of the original sample drawn with replacement from the original sample). In each of these bootstrap samples, we used the RA2 algorithm to select the best-fitting FP transformation for cumulative duration of past exposure in each of the bootstrap samples. The relationship between cumulative duration of amiodarone use and the log-hazard ratio (relative to a subject with 1 day of amiodarone use) for thyroid dysfunction for each of these 50 models is described in the right panel of Figure 3. The FP2 (1, 1) transformation was selected for cumulative duration of amiodarone use in 17 of the 50 bootstrap samples, the FP2 (0.5, 1) transformation was selected in 22 of the 50 samples, and the FP2 (0.5, 2) and FP2 (0.5, 3) transformations were each selected in 3 of the 50 samples, while the logarithmic transformation was selected in the remaining 5 bootstrap samples. We do not advocate bootstrap sampling to guide model selection. Rather, this process was used to examine the stability of the selection algorithm to minor, random perturbations in the data set. We suggest that the transformation selected in the overall sample is the one that should be used.

Oral bisphosphonates and atypical fractures of the femur in elderly women

Motivation

Osteoporosis is associated with significant morbidity and mortality in the ageing population. Oral bisphosphonates have become a mainstay in the treatment of osteoporosis. Randomized trials have shown that bisphosphonates reduce the risk of osteoporotic fractures. However, concerns have emerged that bisphosphonate-related suppression of bone remodelling may adversely influence bone strength. A recent nested case-control study found that long-term bisphosphonate use was associated with an increased risk of atypical femur fractures in postmenopausal women.24 These are fractures involving the subtrochanteric or shaft region of the femur, generally after minimal trauma. Fractures at these sites are considered atypical because they are not characteristic of osteoporotic fractures. We used data from this published nested case-control study to describe the functional form of the relationship between cumulative duration of bisphosphonate exposure and the risk of an atypical femur fracture.

Methods

We used data from a previously published population-based nested case-control study that explored the association between bisphosphonate use and atypical fractures in a cohort of Ontario women 68 years of age and older who commenced treatment with an oral bisphosphonate between 1 April 2002 and 31 March 2008. The date of the first prescription for bisphosphonate therapy served as the cohort entry date. Women in the cohort were followed until the first atypical femur fracture, death or the end of the study period (31 March 2009). The reader is referred to the prior publication for greater details on the study cohort.24

Cases were defined as women who experienced an atypical femur fracture, identified by a hospitalization for a subtrochanteric or femoral shaft fracture between cohort entry and 31 March 2009. For each case, the index date was defined as the date of fracture. Each case was matched to five controls that at the case's index date were still at risk for an atypical fracture. The base cohort consisted of 205 466 women, while the nested case-control study consisted of 716 cases and 3580 matched controls.

For each patient in the matched sample, all prescriptions that were filled for oral bisphosphonate between the cohort entry date and the end index date were identified. The duration of each prescription was determined from the mandatory days supply field of the prescription record. Using the data on the duration of each prescription, we were able to determine for each subject in the matched sample the total cumulative duration of past exposure to bisphosphonate between cohort entry and the index data.

For each of the 44 FP1 and FP2 transformations, we fit a conditional logistic regression model in which the occurrence of an atypical femur fracture was regressed on cumulative duration of bisphosphonate exposure (transformed using the corresponding FP transformation) and the other covariates described in the prior publication. The RA2 selection procedure was applied to select the most appropriate transformation of cumulative duration of drug exposure.

For comparative purposes, we used restricted cubic regression splines (which are constrained to be linear in the tails) with four knots to model the relationship between cumulative duration of use of bisphosponate and the risk of atypical femur fracture.12 The knots were placed at the 5th, 35th, 65th, and 95th percentiles of the cumulative duration of bisphosponate use, as suggested by Harrell.12 The values of these percentiles were 90, 688, 1290, and 2092 days, respectively.

Results

The empirical cumulative distribution function describing the distribution of total bisphosphonate exposure on the index date for each subject is described in the right panel of Figure 1.

The distributions of the deviances across the 8 FP1 models and the 44 FP2 models, along with that of the null model, are depicted in the right panel of Figure 2. The deviance of the best-fitting FP2 model, the best-fitting FP1 model, the linear model, and the null model is reported in Table 2, along with the results of the test comparing different FP models. Using the RA2 selection algorithm, the FP1 transformation with P = (1) (i.e. the linear or identity transformation) was selected as the best-fitting FP transformation. Thus, the linear transformation resulted in the best description of the relationship between total cumulative duration of bisphosphonate use and the risk of atypical fracture of the femur. The regression coefficient for duration of cumulative duration of past exposure from the linear transformation was 0.0006146 (95% confidence interval: 0.0003049 to 0.0009243). Thus, every additional year of total cumulative duration of past exposure increases the odds of an atypical femur fracture by 25%.

Table 2.

Fractional polynomial models for effect of cumulative duration of bisphosphonate use on the risk of atypical femur fracture

Model Deviance D P Step Comparison Deviance difference p-value
FP2 895.453 −0.5, 1 1 FP2 versus null 20.656 0.0004 (4 d.f.)
FP1 898.156 2 2 FP2 versus linear 4.712 0.1941 (3 d.f.)
Linear 900.165 1 3 FP2 versus FP1 2.703 0.2589 (2 d.f.)
Null 916.109
Open in a new tab

The relationship between cumulative duration of bisphosphonate use and the log-odds ratio of atypical femur fracture (relative to a woman with a single day of bisphosphonate use) is described in the left panel of Figure 4 (a rug plot describing the distribution of cumulative duration of drug use is presented on the horizontal axis). We describe the relationship between cumulative duration of use and risk of atypical femur fracture for the best-fitting FP1 and FP2 transformations, the identity transformation (i.e. assuming a linear relationship), and the relationship described using restricted cubic regression splines. The vertical axis denotes the log-odds ratio comparing the odds of atypical femur fracture for a woman with a given cumulative duration of use of bisphosphonate relative to that of a woman whose cumulative duration of use was equal to one (i.e. with that of a woman who had used bisphosphonate for one single day).The FP2 (−0.5, 1) transformation described a clinical implausible relationship between duration of exposure and risk of atypical fracture. This transformation described a log-odds ratio that initially decreases with increasing duration of cumulative use. It then reaches a nadir. The log-odds ratio then increases with increasing duration of exposure.

Figure 4.

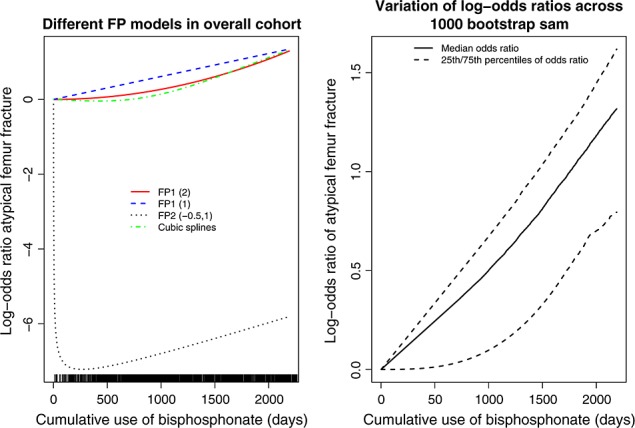
Figure 4

Open in a new tab

Relationship between cumulative use of bisphosphonate and atypical fracture of the femur

The RA2 algorithm selected the linear transformation as the best-fitting transformation. However, several other transformations were closer competitors. Two FP1 transformations (FP1 (2) and FP1 (3)) had deviances that were within four of that of the FP1 (1) transformation. Similarly, 24 of the FP2 transformations resulted in models whose deviance was within four of that of the FP1 (1) transformation. To examine the stability of the RA2 selection algorithm, we drew 1000 bootstrap samples of cases and their matched controls. In each bootstrap sample, we used the RA2 algorithm to select the most appropriate FP transformation of cumulative duration of use. In 37 (3.7%) of the 1000 bootstrap samples, the null model was selected as the best-fitting model. An FP1 transformation was selected as the best-fitting transformation in 728 (72.8%) of the bootstrap samples (with the linear transformation being selected as the best-fitting model in 591 of the bootstrap samples), while an FP2 transformation was selected in the remaining 235 (23.5%) bootstrap samples. We then determined, for each level of cumulative duration of past exposure, the log-odds ratio for an atypical fracture relative to a subject with only a single day of bisphosphonate use. We determined the 25th, 50th, and 75th percentiles of the distribution of these log-odds ratios. These values are described in the right panel of Figure 4. Moderate variability in the log-odds ratio is evident across the bootstrap samples, illustrating the variability that is inherent in the selection procedure. We examined different percentiles for summarizing the distribution of log-odds ratios. In a minority of bootstrap samples, a relationship that was more extreme than that of the FP2 (−0.5, 1) depicted in the left panel of Figure 4 was selected, resulting in negative log-odds ratios of very large magnitude. Thus, in a small number of bootstrap samples, the RA2 algorithm selected a model that was not clinically plausible.

DISCUSSION

We demonstrated that FPs can be used to model the relationship between cumulative duration of past exposure to a pharmaceutical agent and the risk of an adverse outcome. These methods can be used in cohort studies in which cumulative duration of past exposure is treated as a continuous time-dependent covariate. The methods are also applicable in case-control designs in which total cumulative duration of past exposure is treated as a continuous variable. Our focus was on modelling the relationship between current cumulative duration of medication use (in days) and the risk of an adverse event. However, the methods can be applied to more general problems. The methods could also be applied to model the relationship between cumulative dose exposure (e.g. in milligram of active ingredient) and the risk of an adverse outcome. Furthermore, in cohort designs, the use of FPs may allow one to model the relationship between any continuous time-dependent covariate (which takes on strictly positive values) and the hazard of an outcome.

We illustrated the applications of our methods in both a cohort design and a nested case-control design. There are advantages to each of these two designs. The use of a cohort design will, in general, result in greater statistical power and efficiency because information from all of the cohort members is being used, while a nested case-control design will result in greater computational efficiency.25,26 Conducting the FP analyses in the cohort of amiodarone users required over 400 times as much processor time than did conducting these analyses in the nested case-control study of bisphosphonate users. The substantial increase in process time for the cohort design arises from the fact that for these analyses, the data set must be structured so that there is one row of data for each day of follow-up, so that the cumulative duration of past exposure can be calculated separately for each day. Thus, for a cohort with 1000 subjects, each of who is followed for an average of 1000 days, the resultant data set will have 1 000 000 records. A further advantage of the nested case-control design is that when necessary data on all subjects in the cohort are not readily available, this design will be more economical than the cohort design because extra data will need to be collected for only the cases and the matched controls.27

In our second case study, which used a nested case-control design, we compared the use of FPs with the use of restricted regression splines. However, we did not conduct a similar comparison in our first case study that used a cohort design. The rationale for this omission highlights an advantage to the use of FPs to model the effects of continuous time-dependent covariates. The use of (restricted) cubic regression splines requires that the locations of knots be specified. Frequently, these knots are placed at specified quantiles of the distribution of the continuous variable.12 However, when the value of the continuous variable changes over the duration of follow-up, it is unclear how these quantiles should be determined. When the continuous variable denotes cumulative duration of past exposure, the distribution of that variable will shift to the right (or shift upwards) over time. If one decides to base the quantiles of the distribution of cumulative duration of past exposure at the end of follow-up, then the large majority of the values of the variable during the early phases of follow-up will lie to the left of the first or second knots, limiting the flexibility of the estimate. In contrast to this, the use of FPs does not rely on computing any such quantiles. Instead, the use of this method simply requires that one apply the appropriate FP1 or FP2 transformation to the value of the continuous time-dependent covariate at each follow-up time. In contrast to this, in a retrospective design such as the nested case-control study, the cumulative duration of past exposure is fixed at the index date (the event date for the cases). Therefore, the requisite quantiles can be specified, allowing one to use (restricted) cubic regression splines to model the non-linear relationship between cumulative duration of past exposure and the risk of the outcome.

In the current study, we explored the use of FPs for modelling the effect of time-dependent covariates on the log hazard of an outcome. An advantage to the use of FPs in the current context is that, for negative powers, they can model curves that tend to a horizontal asymptote as the explanatory variable tends to infinity (i.e. the curve becomes increasingly flat as the explanatory variable becomes very large). This may be useful in examining the effects of cumulative duration of past exposure if there are settings in which there is some ‘saturation’ level of cumulative duration of past use, above which the risk of an event does not change. Such a setting could not be modelled using cubic regression splines (which do not permit accurate approximation of curves in which there is a horizontal asymptote—cubic regression splines would result in the curve tending to either negative or positive infinity as the explanatory variable becomes arbitrarily large). While we believe our use of FPs to model the effects of time-dependent covariates to be original, it bears noting that FPs have been proposed for modelling time-varying covariate effects.14,28

The primary limitation of the method, as currently described, is that it does not take into account the recency of the exposure. Thus, a given duration of cumulative past exposure that occurred entirely in the distant past has the same effect on the current hazard of the occurrence of the outcome as the same duration of cumulative exposure that occurred recently. As noted in the INTRODUCTIONIntroduction, Hauptmann et al.,3 Richardson et al.,5 Abrahamowicz et al.6 and Sylvestre and Abrahamowicz7 have developed methods to allow one to account for recency of exposure or latency. In future work, the methods described in this paper need to be expanded to allow one to incorporate the timing of cumulative duration of past exposure when using FPs to model the exposure–outcome relationship.

In conclusion, FPs can be used to model the nature of the relationship between cumulative duration of past exposure to an agent and the risk of the occurrence of an outcome. These methods can be employed in cohort designs when cumulative duration of past exposure is treated as a time-dependent covariate in a Cox proportional hazards model. The methods can also be applied in case-control designs in which total cumulative duration of past exposure is assessed for each case and control. Increased use of these methods will provide investigators in clinical medicine, public health, and epidemiology with tools to examine the form of the relationship between cumulative duration of past exposure and the risk of an outcome.

CONFLICT OF INTEREST

The authors declare no conflict of interest.

KEY POINTS

  • Researchers may be interested in determining the effect of the cumulative duration of exposure or of cumulative dosage of a given agent on the risk of adverse outcomes.

  • The Cox proportional hazards regression model allows analysts to incorporate time-dependent or time-varying covariates. A class of time-dependent covariates is that denoting current cumulative duration of exposure to a given agent.

  • FPs are a regression method that allows analysts to determine the functional form of the relationship between a continuous covariate and an outcome variable.

  • In cohort studies, FPs can be used with Cox proportional hazards regression models to determine the functional form of the relationship between a time-dependent variable denoting cumulative duration of exposure to an agent and the risk of subsequent adverse outcomes.

  • In (nested) case-control studies, FPs can be used with conditional logistic regression models to determine the functional form of the relationship between a variable denoting cumulative duration of past exposure to an agent and the risk of an adverse outcome.

ETHICS STATEMENT

This study was approved by the Research Ethics Board of Sunnybrook Health Sciences Centre.

Acknowledgments

The authors gratefully acknowledge Dr Patrick Royston for providing comments on a draft of the manuscript.

This study was supported by the Institute for Clinical Evaluative Sciences (ICES), which is funded by an annual grant from the Ontario Ministry of Health and Long-Term Care (MOHLTC). The opinions, results and conclusions reported in this paper are those of the authors and are independent from the funding sources. No endorsement by ICES or the Ontario MOHLTC is intended or should be inferred. Dr Austin is supported in part by a Career Investigator award from the Heart and Stroke Foundation. This study was supported in part by an operating grant from the Canadian Institutes of Health Research (Funding number: MOP 86508). The opinions, results and conclusions reported in this paper are those of the authors and are independent from the funding sources. The data used in the reported analyses were held securely in a linked, de-identified form and analysed at ICES.

REFERENCES

  1. Cox D. Regression models and life tables (with discussion) J Roy Stat Soc B. 1972;34:187–220. [Google Scholar]
  2. Therneau TM, Grambsch PM. Modeling Survival Data: Extending the Cox Model. New York: Springer-Verlag; 2000. [Google Scholar]
  3. Hauptmann M, Wellmann J, Lubin JH, Rosenberg PS, Kreienbrock L. Analysis of exposure-time-response relationships using a spline weight function. Biometrics. 2000;56(4):1105–1108. doi: 10.1111/j.0006-341x.2000.01105.x. [DOI] [PubMed] [Google Scholar]
  4. Richardson DB. Latency models for analyses of protracted exposures. Epidemiology. 2009;20(3):395–399. doi: 10.1097/EDE.0b013e318194646d. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Richardson DB, Cole SR, Chu H, Langholz B. Lagging exposure information in cumulative exposure-response analyses. Am J Epidemiol. 2011;174(12):1416–1422. doi: 10.1093/aje/kwr260. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Abrahamowicz M, Bartlett G, Tamblyn R, du Berger R. Modeling cumulative dose and exposure duration provided insights regarding the association between benzodiazepines and injuries. J Clin Epidemiol. 2006;59(4):393–403. doi: 10.1016/j.jclinepi.2005.01.021. [DOI] [PubMed] [Google Scholar]
  7. Sylvestre M-P, Abrahamowicz M. Flexible modeling of the cumulative effects of time-dependent exposure on the hazard. Stat Med. 2009;28(27):3437–3453. doi: 10.1002/sim.3701. [DOI] [PubMed] [Google Scholar]
  8. Sylvestre M-P, Abrahamowicz M, Capek R, Tamblyn R. Assessing the cumulative effects of exposure to selected benodiazepines on the risk of fall-related injuries in the elderly. Int Psychogeriatr. 2012;24:577–586. doi: 10.1017/S1041610211002031. [DOI] [PubMed] [Google Scholar]
  9. Royston P, Altman DG, Sauerbrei W. Dichotomizing continuous predictors in multiple regression: a bad idea. Stat Med. 2006;25:127–141. doi: 10.1002/sim.2331. [DOI] [PubMed] [Google Scholar]
  10. Austin PC, Brunner LJ. Inflation of the type I error rate when a continuous confounding variable is categorized in logistic regression analyses. Stat Med. 2004;23(7):1159–1178. doi: 10.1002/sim.1687. [DOI] [PubMed] [Google Scholar]
  11. Steyerberg EW. Clinical Prediction Models. New York: Springer-Verlag; 2009. [Google Scholar]
  12. Harrell FE., Jr . Regression modeling strategies. New York, NY: Springer-Verlag; 2001. [Google Scholar]
  13. Hastie TJ, Tibshirani RJ. Generalized Additive Models. London: Chapman & Hall; 1990. [Google Scholar]
  14. Royston P, Sauerbrei W. Multivariable Model-Building. West Sussex: John Wiley & Sons, Ltd; 2008. [Google Scholar]
  15. Royston P, Altman DG. Regression using fractional polynomials of continuous covariates: parsimonious parametric modelling (with discussion) Appl Stat. 1994;43(3):429–467. [Google Scholar]
  16. Royston P, Altman DG. Approximating statistical functions by using fractional polynomial regression. Statistician. 1997;46:411–422. [Google Scholar]
  17. Ambler G, Royston P. Fractional polynomial model selection procedures: investigation of type I error rate. J Stat Comput Simulat. 2001;69:89–108. [Google Scholar]
  18. Sauerbrei W, Royston P. Corrigendum: Building multivariable prognostic and diagnostic models: transformation of the predictors using fractional polynomials. J Roy Stat Soc A. 2002;165:399–400. [Google Scholar]
  19. Roy D, Talajic M, Dorian P, et al. For the Canadian Trial of Atrial Fibrillation Investigators. Amiodarone to prevent recurence of atrial fibrillation. New Engl J Med. 2000;342:913–920. doi: 10.1056/NEJM200003303421302. [DOI] [PubMed] [Google Scholar]
  20. Zarembski DG, Nolen PEJ, Slack MK, Caruso AC. Treatment of resistant atrial fibrillation. A meta-analysis comparing amiodarone and flecainide. Arch Intern Med. 1995;155:1885–1891. [PubMed] [Google Scholar]
  21. Taylor CJ, Hodgkinson J, Hobbs FD. Rhythm control agents and adverse events in patients with atrial fibrillation. Int J Clin Pract. 2010;64(8):1069–1075. doi: 10.1111/j.1742-1241.2010.02426.x. [DOI] [PubMed] [Google Scholar]
  22. Martino E, Bartalena L, Bogazzi F, Braverman LE. The effects of amiodarone on the thyroid. Endocr Rev. 2001;22(2):240–254. doi: 10.1210/edrv.22.2.0427. [DOI] [PubMed] [Google Scholar]
  23. Tsadok MA, Jackevicius CA, Rahme E, et al. CMAJ. 2011;183(12):E817–E823. doi: 10.1503/cmaj.101800. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Park-Wyllie LY, Mamdani MM, Hawker GA, et al. Bisphosphonate Use and the Risk of Subtrochanteric or Femoral Shaft Fractures in Older Women. JAMA. 2011;305(8):783–789. doi: 10.1001/jama.2011.190. [DOI] [PubMed] [Google Scholar]
  25. Austin PC, Anderson GM, Cigsar C, Gruneir A. Comparing the cohort design and the nested case-control design in the presence of both time-invariant and time-dependent treatment and competing risks: bias and precision. Pharmacoepidemiol Drug Saf. 2012;21(7):714–724. doi: 10.1002/pds.3299. doi: 10.1002/pds.3299. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Essebag V, Platt RW, Abrahamowicz M, Pilote L. Comparison of nested case-control and survival analysis methodologies for analysis of time-dependent exposure. BMC Med Res Methodol. 2005;5:5. doi: 10.1186/1471-2288-5-5. doi: 10.1186/1471-2288-5-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Rothman KJ, Greenland S. Modern Epidemiology. Philadelphia, PA: Lippincott Williams & Wilkins; 1998. [Google Scholar]
  28. Sauerbrei W, Royston P, Look M. A new proposal for multivariable modelling of time-varying effects in survival data based on fractional polynomial time-transformation. Biom J. 2007;49:453–473. doi: 10.1002/bimj.200610328. [DOI] [PubMed] [Google Scholar]

Articles from Pharmacoepidemiology and Drug Safety are provided here courtesy of Wiley

RESOURCES