Actin cable distribution and dynamics arising from cross-linking, motor pulling, and filament turnover

A computational model of actin cables in fission yeast is presented that includes polymerization, severing, cross-linking, and motor pulling. Results reproduce observations in wild-type cells and cells lacking myosin V and are compared to images of cells overexpressing α-actinin. Formin clustering at cell tips is predicted to promote cable formation.

Abstract

The growth of fission yeast relies on the polymerization of actin filaments nucleated by formin For3p, which localizes at tip cortical sites. These actin filaments bundle to form actin cables that span the cell and guide the movement of vesicles toward the cell tips. A big challenge is to develop a quantitative understanding of these cellular actin structures. We used computer simulations to study the spatial and dynamical properties of actin cables. We simulated individual actin filaments as semiflexible polymers in three dimensions composed of beads connected with springs. Polymerization out of For3p cortical sites, bundling by cross-linkers, pulling by type V myosin, and severing by cofilin are simulated as growth, cross-linking, pulling, and turnover of the semiflexible polymers. With the foregoing mechanisms, the model generates actin cable structures and dynamics similar to those observed in live-cell experiments. Our simulations reproduce the particular actin cable structures in myoVΔ cells and predict the effect of increased myosin V pulling. Increasing cross-linking parameters generates thicker actin cables. It also leads to antiparallel and parallel phases with straight or curved cables, consistent with observations of cells overexpressing α-actinin. Finally, the model predicts that clustering of formins at cell tips promotes actin cable formation.

INTRODUCTION

The cellular actin cytoskeleton is crucial for numerous cell functions, such as cell motility, cytokinesis, and cell division (Blanchoin et al., 2014). Actin filaments organize into polymerizing and contractile networks and bundles with the help of nucleating, severing, side-binding, and cross-linking proteins (Blanchoin et al., 2014). A large body of work has studied how these molecular-level processes contribute to mesoscopic organization at the micrometer scale, using controlled in vitro experiments with purified proteins (Gardel et al., 2004; Reymann et al., 2010; Alvarado et al., 2013) and mathematical modeling (Kim et al., 2009; Wang and Wolynes, 2012; Cyron et al., 2013). A big challenge is to develop a similar quantitative understanding of actin structures in cellular systems. Mathematical models have been very useful in providing insight into the mechanisms of cellular actin networks nucleated by the Arp2/3 complex (Carlsson et al., 2010). However, very few modeling studies have examined cell structures nucleated by formin proteins, which generate bundles of antiparallel or parallel filaments (Wang and Vavylonis, 2008; Laporte et al., 2012).

Budding and fission yeast cells are ideal for quantitative studies of actin organization because they are amenable to genetic modifications and microscopic imaging. Their interphase actin cytoskeleton is organized into two distinct components (Figure 1A): actin patches (nucleated by the Arp2/3 complex) and actin cables (nucleated by formins) (Drake and Vavylonis, 2010; Kovar et al., 2011). The actin cables are bundles of ∼10 actin filaments (Kamasaki et al., 2005) that help cells establish polarized growth by providing tracks to transport secretory vesicles and organelles toward the growing part of the cell in both yeasts and plants (Vidali et al., 2009; Wu et al., 2010). In this work, we develop a model of actin cables in fission yeast that has a simple tube-like shape and a single actin cable nucleator, formin For3p. In fission yeast, actin cables growing from either tip can meet and cross-link with one another and form different morphologies, depending on the cross-linking dynamics. Of importance, actin cables are critical for polarized growth by supporting myosin cargo directional motility.

FIGURE 1:

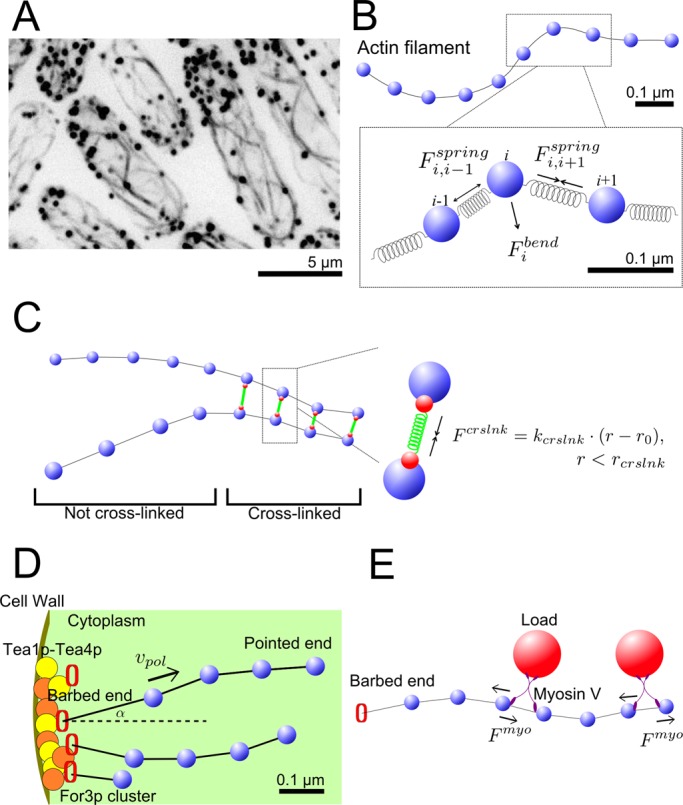
Model mechanism. (A) Images of actin cables in fission yeast (inverted black and white). GFP-CHD–tagged actin showing structures of actin cables (black lines) and actin patches (black dots). (B) A single actin filament is described by a bead-spring model. (C) The effect of cross-linking proteins that link neighboring actin filaments into bundles is represented as finite-range spring interactions. (D) Tea1p/Tea4p landmark proteins at the cell tip recruit For3p molecules to form clusters, which polymerize actin subunits into actin filaments. This is represented by growth of semiflexible polymers from fixed positions at cell tips. (E) Myosin V pulls actin filaments by carrying or anchoring on heavy loads. This is represented by tangential forces along actin filaments.

Several actin-associated proteins are known to be involved in actin cable dynamics in fission yeast (Win et al., 2001; Moseley and Goode, 2006; Goode and Eck, 2007; Skau and Kovar, 2010; Lo Presti et al., 2012; Miao et al., 2013). Formin protein For3p localizes at the cell tips and nucleates actin filaments by associating with transient cortical landmarks (Feierbach and Chang, 2001; Kovar, 2005; Martin et al., 2005). Severing protein cofilin (Cof1p) binds to the sides of actin filaments (Nakano and Mabuchi, 2006; Chen and Pollard, 2011) and, with the help of Aip1p (Moseley and Goode, 2006), severs them, thus allowing constant actin turnover. Actin filament cross-linking proteins likely keep the filaments together in bundles. Cross-linking protein fimbrin Sac6p is found in budding yeast cables (Moseley and Goode, 2006) but not fission yeast fimbrin Fim1p (Nakano et al., 2001; Wu et al., 2001; Skau et al., 2011), likely because of its low concentration. α-Actinin (Ain1p) is another cross-linker in fission yeast that may contribute to actin cable bundling. Both Fim1p and Ain1p can bundle filaments in parallel or antiparallel orientations (Skau and Kovar, 2010; Skau et al., 2011; Falzone et al., 2012; Laporte et al., 2012). Myosin V motor proteins (Myo51p, Myo52p), carrying secretory vesicles or anchoring on organelles, walk along actin filament toward the barbed end (Lo Presti et al., 2012). Some of these myosin V molecules associate with the cortical endoplasmic reticulum that is tightly attached to the plasma membrane while the two heads remain bound to actin cables (Zhang et al., 2012).

Here we develop a three-dimensional (3D) coarse-grained computational model to explore how the foregoing molecular mechanisms contribute to the large-scale actin cable organization in Figure 1A. We address the following questions: 1) Can a model that uses simple mechanisms such as polymerization, severing, and cross-linking explain important features of actin cables such as their thickness and network topology? 2) How is cable organization related to how motor proteins like myosin V anchor on cargoes or endoplasmic reticulum? 3) How do formin clustering, cross-linker strength, and concentration influence actin cable structure, orientation, dynamics, and polarity?

We use the model to quantify actin cable distributions and predict the effects of myosin V pulling, cross-linker concentration and strength, and formin clustering at cell tips. The model reproduces prior experimental results in myoVΔ fission yeast cells, for which actin cables curl up close to the tips and fail to span the entire cell (Lo Presti et al., 2012). We predict that overexpression of myosin V may result in unbundling of actin cables into individual stretched filaments. We show that increasing concentration and strength of cross-linkers, as well as increased clustering of formin nucleation sites, promotes actin filament bundling. At high cross-linking strength, actin filaments get cross-linked in mostly parallel orientations, whereas antiparallel bundles bulge or break up. Analysis of experiments of cells overexpressing Ain1p supports these predictions. Our work provides a framework for further quantitative understanding of actin structures in cellular systems.

RESULTS

Model description

In our 3D actin cable model, actin filaments are semiflexible polymers, simulated as beads connected by springs (Pasquali et al., 2001; Nédélec and Foethke, 2007; Alberts, 2009; Kim et al., 2009; Cruz et al., 2012; Materials and Methods and Supplemental Material). Each segment is 0.1 μm, representing ∼37 subunits, a scale small enough to allow us to include molecular-level processes and also smaller than the typical filament and cell size (Figure 1B). We use a coarse-grained description for actin filament cross-linking by proteins such as α-actinin and fimbrin (Nakano et al., 2001; Wu et al., 2001; Skau et al., 2011; Figure 1C). We simulate cross-linking as an effective isotropic attraction between filament beads that approach closer than a cross-linking range, as in an earlier two-dimensional model (Laporte et al., 2012; Figure 1C).

Formin-mediated polymerization of actin filaments is simulated as elongation of the first segment of the semiflexible chain at a fixed angle from a few cortical sites at the cell tips (Figure 1D and Table 1). These sites represent For3p bound to Tea1p-Tea4p clusters (Martin et al., 2005). We do not explicitly simulate the dissociation and recycling of formin For3p at the tips, which was previously studied (Wang and Vavylonis, 2008). Both For3p dissociation from cell tips and cofilin severing contribute to actin filament turnover. Because the precise mechanism is unknown, we include the simplest mechanism for turnover: we remove whole filaments with a rate that gives an average filament lifetime of 15 s (Vavylonis et al., 2008).

TABLE 1:

Model parameters.

Parameter	Description	Value	Unit
N	Number of formins at one tip (total 2N)	72
Ncluster	Number of clusters at one tip	12, 4→72
υpol	Polymerization rate (barbed end growth)	0.3	μm/s
τsever	Average turnover time	15	s
ιp	Persistence length of actin filaments	10	μm
κcrslnk	Cross-linking spring constant	2, 0→15	pN/μm
r0	Cross-linking gap distance	0.03	μm
rcrslnk	Cross-linking interaction range	0.09, 0→0.16	μm
ρmyo	Myosin motor linear density along actin filament	1, 0→10	#/μm
τmyo	Myosin lifetime on actin filament	5	s

For a complete list see Supplemental Table S1

Myosin V (Myo51p and Myo52p), which carries secretory vesicles or anchors on stationary organelles, can exert a stochastic force on the actin cables when walking toward the barbed end (Grallert et al., 2007; Clayton et al., 2010; Lo Presti et al., 2012; Zhang et al., 2012). Myosin V clusters move along cables with speeds of 0.5–2.5 μm/s over a few micrometers (Grallert et al., 2007; Clayton et al., 2010). We simulate the effects of myosin V on cables as a transient tangential force applied on the filament, toward the barbed end (Figure 1E). We assume 0.5 pN of force per myosin V (Mehta et al., 1999) and a 5-s association time and vary the linear density of motors along the filament to observe the effects of myosin V pulling.

We use a cylinder capped with two hemispheres to represent fission yeast. Excluded volume in fission yeast, such as vacuoles (Bone et al., 1998; Mulvihill et al., 2001) and nucleus, are simulated as immobile spheres that prevent actin filaments from going through them.

Simulation results using the parameter set in Table 1 reproduce actin cable structures similar to those observed in cells. Figure 2A shows simulations of actin filaments that grow out of 12 cortical sites per tip, with blue and red colors marking filaments that grow from either tip. After 180 s, which is long enough to reach steady state (see Materials and Methods), the filaments organize into a few bundles that contain filaments in both parallel and antiparallel orientation (Figure 2B). Filaments grow through the gaps among vacuoles and the nucleus, reaching filaments that polymerize from the opposite tip, generating bundles that span the cell length as in experimental images (Figure 1A).

FIGURE 2:

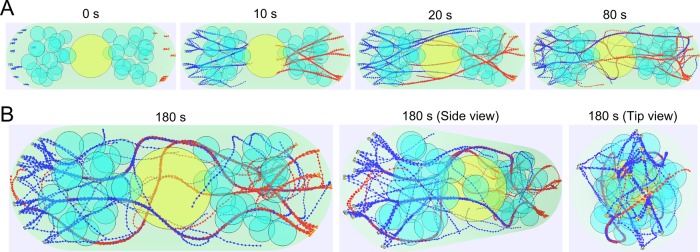
Simulated actin cables using parameter values from Table 1. (A) Time evolution of the simulation. Nucleus (yellow) and vacuoles/organelles (cyan) are simulated as impenetrable immobile spheres. The cytoplasmic region is marked in light green. Actin filaments growing from the left (right) side tip are marked in blue (red). Formin For3p clusters localized at the cell tip are marked in orange. (B) Simulated steady-state actin cables viewed from different perspectives (front, 45°, and 90°) showing a complete 3D cable structure.

Myosin V pulling effect on cable distribution

Prior experiments show that deletion of both copies of myosin V, Myo51p and Myo52p, leads to short, curved, and misoriented cables in interphase fission yeast cells (Lo Presti et al., 2012; Figure 3A). By eliminating the simulated myosin V pulling, actin filaments converge into thicker and less straight bundles near the cell tips that do not span the entire cell, in agreement with experimental observations (Figure 3B and Supplemental Video S1). Simulations predict that excessive myosin V pulling unbundles the cables (Figure 3B): as the number of myosin V per unit length along the filament, ρ_myo, increases from 0 to 10/μm, the percentage of bundled actin filaments decreases from 75 to 58% (Figure 3C). Increase in ρ_myo also leads to a more uniform distribution of filaments across the cell (Figure 3D and Supplemental Figure S3D). Enhanced myosin pulling affects the number of filaments in the largest linked cable, increases the total number of cables, and straightens them (Supplemental Figure S3, A–C). This highlights the critical role of motors in actin cable organization.

FIGURE 3:

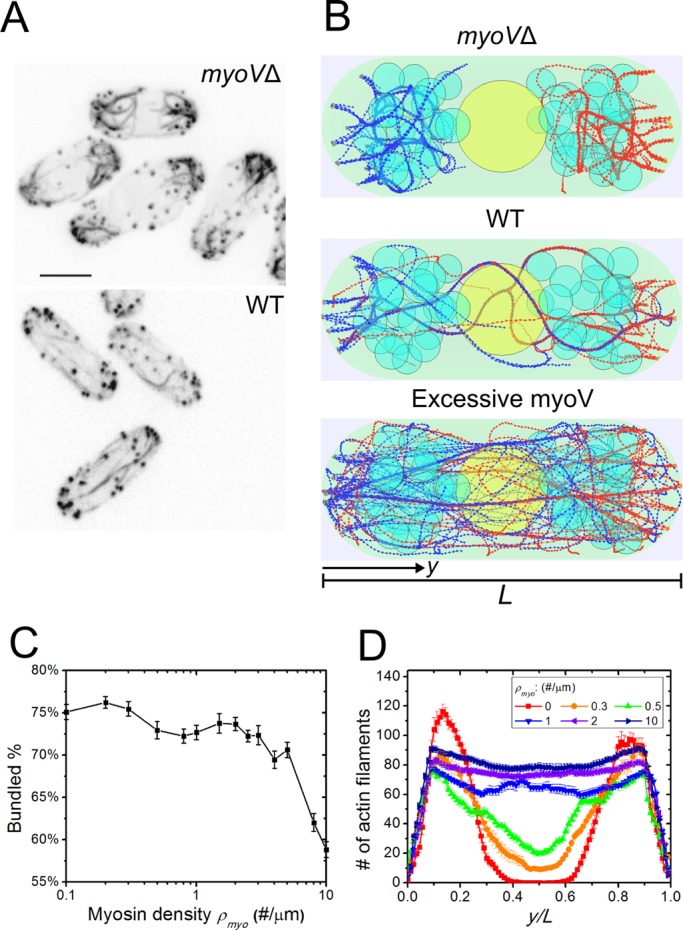
Simulations of myosin V force straightening actin cables (Supplemental Video S1). (A) Experimental images of actin cables in myoVΔ cells in which >95% of the cells showed misoriented and thick cables and >70% of the cells showed an extension defect (reproduced with permission from Lo Presti et al., 2012). (B) Simulated steady-state configurations of myosin density ρ_myo = 0, 1, and 10 μm⁻¹, showing misoriented cables at the tip, normal actin cables, and straightened but thin actin cables. (C) Bundled actin filament percentage as a function of myosin V density ρ_myo. Fewer actin filaments are bundled for high ρ_myo. Error bars are SEM from five runs. (D) Graph of actin filament bead concentration along the long axis of the cell (average of three simulations). More actin filaments are able to span the cell as ρ_myo increases.

Cross-linking strength and dynamics influence cable morphology

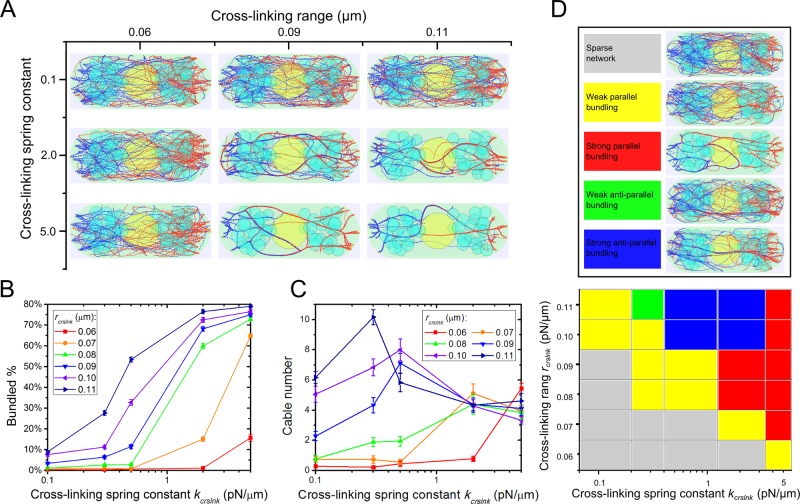
In our simulations, the kinetics of cross-link formation and breakage are described by two parameters: cross-linking range, r_crslnk, and spring constant, k_crslnk, which determines the depth of the interaction potential between cross-linked filament beads (for given r_crslnk). These parameters determine the rates of cross-link formation/breakage and reflect the type and concentration of cross-linker proteins in cells, with larger values representing stronger cross-linking. The simulated actin cable configurations at steady state vary depending on the values of r_crslnk and k_crslnk (Figure 4A and Supplemental Videos S2 and S3). We found that larger r_crslnk and k_crslnk promote actin filament bundling (Figure 4B). At k_crslnk = 2 pN/μm, the standard parameter, the actin filament bundled percentage increases from 2 to 77% as r_crslnk changes from 0.06 to 0.11 μm (Figure 4B). Conversely, the bundled percentage increases from 4 to 74% as k_crslnk increases from 0.1 to 5.0 pN/μm when r_crslnk = 0.09 μm (Figure 4B). Similar trends to Figure 4B are observed when measuring the number of filaments in the largest linked cable (Supplemental Figure S4A). Moreover, we show that r_crslnk and k_crslnk together regulate the number of cables (Figure 4C). For a given r_crslnk, there exists a k*_crslnk value giving the maximum number of cables (the cables at the peak value have average three to six filaments each; see Supplemental Figure S4B). For k_crslnk < k*_crslnk, the system has mostly unbundled filaments, and so the number of cables increases with increasing r_crslnk. For k_crslnk > k*_crslnk, most filaments become bundled. In this range, the dependence of the number of cables on k_crslnk and r_crslnk is weak, reflecting the maximum filament bundling that can be achieved within the filament turnover time with the given geometry and polymerization rate.

FIGURE 4:

Stronger cross-linking interactions promote actin cable formation in simulations (Supplemental Videos S2 and S3). (A) Steady-state configurations under different cross-linking spring constant (k_crslnk) and cross-linking interaction range (r_crslnk). (B) Bundled actin filament percentage increases with increasing r_crslnk and k_crslnk. (C) Cable number as a function of r_crslnk and k_crslnk. In B and C, error bars are SEM from five runs. (D) Polarity of actin filaments in cables varies with cross-linking parameters. In “weak” regions, most actin filaments are unbundled. In “strong” regions, most filaments are bundled in either primarily parallel or antiparallel orientations. Antiparallel orientations occur due to bundling of filaments that grow from different cell tips.

Polarity of filaments in simulated actin cables

Another feature of actin cables that changes with cross-linker parameters is the orientation of filaments within the cables, which is critical for cargo transport along cables. By measuring the filament orientation and degree of bundling as a function of k_crslnk and r_crslnk, we find different regimes in parameter space (Figure 4D) that include “weak” parallel and antiparallel regimes when <30% of the filaments are bundled and “strong” parallel and antiparallel regimes when >30% are bundled.

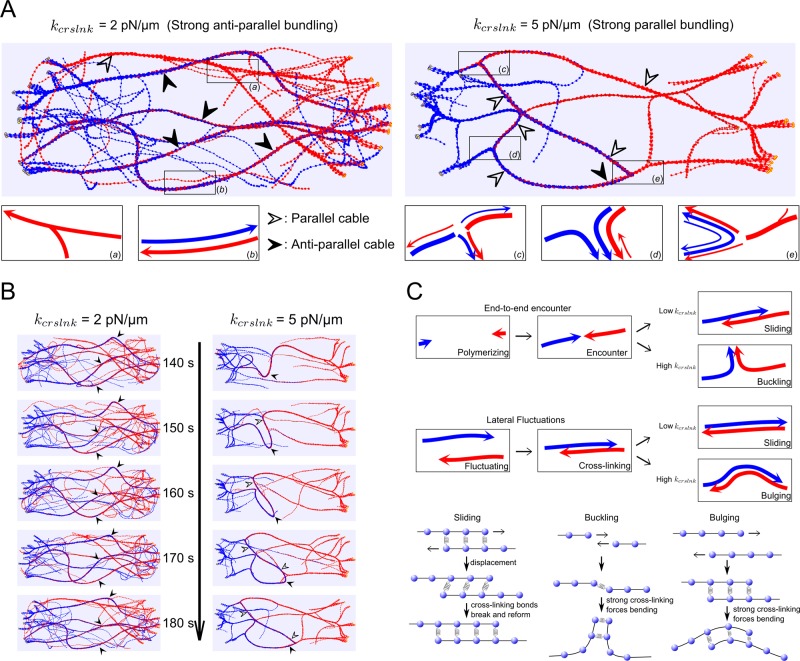
Figure 5A shows enlarged snapshots of cells at steady state in the strong antiparallel (left) and strong parallel (right) regimes. In the standard condition (k_crslnk = 2 pN/μm), actin filaments that grow out of the opposite tips form mostly cables with antiparallel filaments (solid arrowheads) and a few with parallel filaments (hollow arrowheads). In this condition, cross-linking is sufficiently weak to allow filaments polymerizing from opposite tips to slide past one another when they meet by end-to-end encounter or by lateral fluctuations, leading to steady cables with minor undulations (Figure 5, B and C, and Supplemental Video S4). In the high-cross-linking condition (k_crslnk = 5 pN/μm), we find mostly cables with parallel filaments and only few with antiparallel filaments. In this condition, cross-links are long lived, which induces buckling and bulging of filaments that meet by end-to-end encounter or lateral fluctuations (Figure 5, B and C, Supplemental Video S4). This results in formation of junctions at which filaments change direction to bundle in parallel (Figure 5A, c–e). The outcome of end-to-end encounters also depends on the angle of encounter, with a higher probability of parallel bundle formation for larger angle, similar to prior in vitro experiments (Reymann et al., 2010). These results further highlight how cross-linking dynamics combines with actin filament mechanics and nucleation geometry to regulate the polarity of actin filaments in bundles (Reymann et al., 2010).

FIGURE 5:

Cross-linking strength and dynamics influence the dynamics of actin cables (Supplemental Video S4). (A) Actin cable structures with cross-linking spring constant k_crslnk = 2 pN/μm (corresponding to the strong-antiparallel case of Figure 4), compared with k_crslnk = 5 pN/μm (strong-parallel case in Figure 4). Solid arrows point to antiparallel cables (blue and red filaments, the barbed ends of which are toward opposite directions). Open arrows point to parallel cables. (B) Time evolution of actin cable structures under high k_crslnk = 5 pN/μm in comparison with 2 pN/μm. For high k_crslnk, antiparallel cables are not stable: the cables bulge and sometimes even break to form parallel cables, whereas for low k_crslnk, antiparallel cables remain stable. (C) Schematic representation of sliding, buckling, and bulging mechanisms. In the low-k_crslnk case, filaments can slide through each other as they polymerize to form antiparallel bundles. In the high-k_crslnk case, cross-linking forces overcome mechanical forces to bend the cables, resulting in buckling and bulging and formation of mostly parallel bundles. The outcome of an encounter also depends on the angle of encounter and the thickness of the bundles.

Overexpression of α-actinin changes actin cable morphology, consistent with simulations

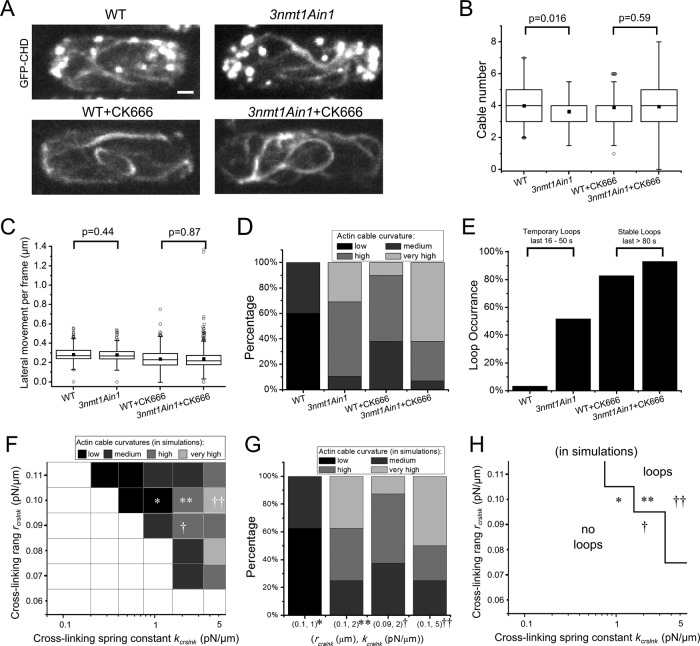
To further investigate the predicted effect of cross-linkers, we analyzed actin cables in wild-type cells and cells overexpressing α-actinin, using the 3nmt1Ain1 promoter (Figure 6A). We chose α-actinin because the effect of overexpression of the other cross-linker in fission yeast, fimbrin, is very drastic, with overexpression mutants having significantly modified cable morphologies (Wu et al., 2001; Laporte et al., 2012; Burke et al., 2014; see also Discussion). To better visualize actin cables, we also treated cells with CK666, an inhibitor of the Arp2/3 complex that depolymerizes actin patches (Nolen et al., 2009). This treatment causes an increase in the amount of actin in the cables, which also become longer and more curved (Burke et al., 2014). Treatment by CK666 may also release fimbrin from actin patches, resulting in an increase in cable cross-linking (Burke et al., 2014).

FIGURE 6:

Actin cable morphology changes due to increasing Ain1p concentration in live cells. (A) Fluorescence microscopy shows GFP-CHD–labeled actin of both wild-type and 3nmt1Ain1 fission yeasts. CK666 is added to the cells to depolymerize actin patches (bottom). (B) Measurement of cable number in different cells. (C) Measurement of lateral cable movement per frame, 8 s for WT and 10 s for other cases (see Supplemental Figure S5). In B and C, black square dot indicates average value; boxes contain 50% of data; whiskers, 1.5 interquartile range. (D) Curvature of the actin cables in different cells. (E) Loop occurrence in difference cells. For non–CK666-treated cells, loops occur rarely and last 16–50 s before disappearing. For CK666-treated cells, loops are stable and last >80 s. (F) Predominant cable curvature as function of cross-linking range and spring constant (n = 3 simulations/square). Symbols show one possible mapping of simulation parameters to experiments (*WT; **3nmt1Ain1; ^†WT+CK666; ^††3nmt1Ain1+CK666). Cables cannot be clearly distinguished in the blank area. (G) Cable curvature distribution for the corresponding parameter sets of F (n = 8 per parameter set) matches experiments of D. (H) Loop occurrences as a function of cross-linking range and spring constant for the same simulations as in F.

First we compared changes in cable numbers. Because cables do not have a clear beginning and end in either experiment or simulations, we counted the minimum number of distinct continuous cable segments that are required to generate the observed network structure in maximum intensity projections. Although some statistically significant differences were observed, there was no big variation in average cable number among the four experiments (Figure 6B). The resulting cable number is of the same order as in simulations of the strong-bundling cases (parallel and antiparallel) in Figure 4D. The weak dependence on cross-linker concentration is also consistent with the weak dependence of cable number on cross-linking parameters within the strong-bundled regimes described in our model (Figure 4C and Supplemental Figure S4B).

Second, we measured the lateral movement of the cables in time-lapse movies (see method in Supplemental Figure S5) and found that the average movement ranges from 0.24 to 0.28 μm in 8 (WT) or 10 s (other cases; Figure 6C). Simulations predict that the average movement ranges from 0.17 to 0.3 μm/10 s for parameter values in the strong-antiparallel and strong-parallel regimes, respectively (Supplemental Figure S6B). These numbers are similar in magnitude to the experimental data (see also Discussion).

A more sensitive measure of a shift of the system through the strong-parallel and strong-antiparallel regions is a change in cable curvature and formation of loops and curved structures with junctions (Figure 4D and Supplemental Figure S6A). Thus we also quantified the curvature distribution of the cables. We categorized the morphology into four types (Figure 6D and Supplemental Figure S7). Actin cables are more curved in the Ain1p-overexpression mutants than with WT for both untreated and CK666-treated cells. There are also more loop occurrences in untreated 3nmt1Ain1 cells than with WT (53% vs. 3%; Figure 6E). Of interest, loops occur in >80% of WT and 3nmt1Ain1 cells in CK666 and remain stable for at least 80 s. By contrast, in untreated cells, loops last only 20–30 s.

The experimental results of Figure 6, D and E, are in agreement with simulations, in which we commonly see loops in the high-cross-linking regimes, in which cables tend to bundle in parallel, generating junctions and loops. Figure 6F shows the predominant simulated actin cable curvature as function of r_crslnk and k_crslnk. The symbols in Figure 6F suggest a possible mapping of the model to experiment. The distribution of actin cable curvature at these points matches the experimental curvature distribution (Figure 6, D and G). We also looked at loop occurrences in simulations (Figure 6H). Loops are present for high r_crslnk and k_crslnk and remain stable for at least 60 s, a trend that qualitatively agrees with experimental observations in Figure 6E. Overall our analysis supports that WT cells are near the boundary of the model's strong-parallel and strong-antiparallel regimes and that Ain1p overexpression and CK666 treatment both push the system toward the strong parallel regime.

Formin clustering and cable structure

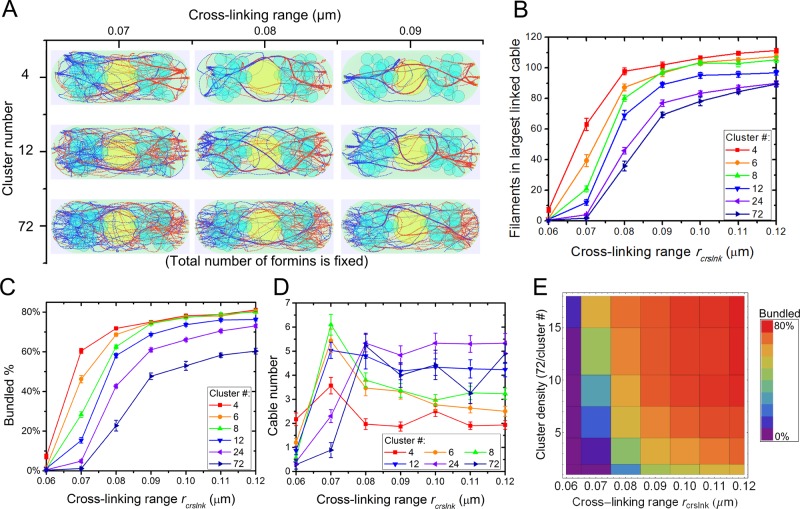
For3p generates cables from tip cortical sites containing ∼10 For3p dimers/site (Martin and Chang, 2006). This For3p clustering may help the generation of actin bundles and control of their thickness. It is also possible that For3p clustering is not required for cable formation, since filaments growing from For3p at distant tip sites can form bundles by cross-linking in the cytoplasm. We examined how actin cable distribution depends on the degree of clustering of For3p at cell tips and cross-linking among filaments. In Figure 7 we vary the number of cortical tip sites and distribute a fixed number of filament nuclei randomly among these sites. The cortical cluster sites are randomly distributed on the semispherical cell tip. Formins within the same cortical site are distributed randomly over a small area around the center of the site. We also study the interplay with cross-linking by varying the effective cross-linking range parameter r_crslnk.

FIGURE 7:

Clustering of For3p and increase in cross-linking strength promote actin cable formation in simulations. (A) Steady-state configurations under different cluster densities and cross-linking interaction range r_crslnk with 72 formin nucleation sites per cell tip partitioned in the indicated number of clusters. High For3p clustering (cluster number, 4) and large r_crslnk show fewer and thicker actin cables. (B) Number of actin filaments in largest linked cable increases with increasing r_crslnk and cluster density. (C) Bundled actin filament percentage increases with increasing r_crslnk and cluster density. (D) Cable number as a function of r_crslnk and cluster density. (E) Bundled percentage landscape as function of cluster density and r_crslnk corresponding to C. In B–D, error bars are SEM from five runs.

The steady-state configurations in Figure 7A indicate that formin clustering promotes bundling of actin filaments. The number of filaments in the largest linked cable and the percentage of actin filaments found in bundles increase with increasing clustering and cross-linking range r_crslnk (Figure 7, B and C). For example, for r_crslnk = 0.07 μm, the number of filaments in the largest linked cable grows from a composition of ∼3 filaments to >60, and the bundled percentage of actin filaments grows from nearly 0 to 60% as clustering is increased. The number of cables in the system has a more complex dependence on the varied parameters (Figure 7D). At low cross-linking, r_crslnk = 0.06 μm, higher formin clustering generates more cables, whereas for high cross-linking, r_crslnk > 0.08 μm, the effect is reversed. The reason is that for r_crslnk = 0.06 μm most filaments are unbundled (Figure 7C), and the clustering catalyzes the formation of a few bundles among many unbundled filaments. For r_crslnk > 0.08 μm, by contrast, most filaments (Figure 7C) get bundled through cross-linking interactions even when formins are unclustered; increasing formin clustering promotes the merging of these cables into thicker ones, leading to fewer cables.

DISCUSSION

We developed simulations of fission yeast actin cables that incorporate the function of the major actin-filament regulators and take into account the excluded volume of cell organelles. Our model reproduces actin cable structures and dynamics observed in live cells. The simulations show how lack of directional myosin V pulling and obstruction by organelles lead to misoriented and curly cable structure as observed in myoVΔ cells (Lo Presti et al., 2012). Two cross-linking parameters (r_crslnk and k_crslnk) affect the bundling of filaments into cables but have different effects on cable morphology. We also predict that formin clustering at the tips assists the bundling of actin filaments.

Our experimental analysis of wild-type cells and cells overexpressing α-actinin (with or without CK666) show that the cable number, lateral cable movement, cable curvature, and appearance of cable loops support the model predictions. The results of Figure 6, D and E, and the fact that fluctuations in lateral movement are larger in CK666 cells, as predicted in the strong-parallel regime (Supplemental Figure S6B), suggest that Ain1p overexpression and CK666 treatment both push the system toward the strong-parallel regime.

Electron microscopy images of actin cables (Kamasaki et al., 2005) suggest that short segments of actin filaments exist in cables, which may be the result of severing by cofilin or occur during the extraction process. Given these uncertainties, we implemented an approximate description of actin turnover and did not attempt to predict filament length distributions along actin cables. The latter, however, might have implications for the mechanical properties of actin cables (Heussinger et al., 2007) and relative filament sliding.

Some additional factors that might affect the structure of actin cables should be explored in future work. We focused on cells in the G2 phase, which are bipolar and 9 μm long on average. We did not explore the dependence on cell length or monopolar actin cable growth. Our model assumed filament polymerization exclusively at cell tips. Additional nucleation of actin filaments in the cytoplasm or binding of severed actin filament from patches to cables might help align cables over long distances across the cell, as observed in long cdc25-22 cells (Huang et al., 2012). Cross-linking was assumed to be isotropic, consistent with the measured cross-linking of filaments in both parallel and antiparallel orientations by fimbrin (Skau et al., 2011) and α-actinin (Meyer and Aebi, 1990; Courson and Rock, 2010). Addition of cross-link orientation bias might shift the boundaries of the antiparallel and parallel bundle formations in Figure 4D. We also assumed that the number of For3p nucleators at the cell tip is approximately constant. Formin For3p detaches from the cell tips and recycles back to the cell tips through diffusion (Martin and Chang, 2006; Wang and Vavylonis, 2008). Its activity might change in time as its Cdc42 activator tip concentration oscillates over 5 min (Das et al., 2012). These mechanisms could contribute to larger fluctuations in cable thickness and movement. Tropomyosin, which regulates myosin motor activity and filament stability, is another important regulator of actin cables in fission yeast (Skau and Kovar, 2010; Cranz-Mileva et al., 2013; Clayton et al., 2014). In our model, these effects of tropomyosin are collapsed into the myosin V parameters and filament turnover time.

Actin filament cross-linker fimbrin might also play a role in regulating actin cable thickness as described in Figure 4. In vitro experiments show that full-length Fim1p bundles actin filaments, whereas truncated Fim1p binds actin filaments but does not bundle them (Nakano et al., 2001; Skau et al., 2011). Overexpression of truncated Fim1A2 (containing only one actin-binding domain, ABD2) generates thick cables in fatter and shorter fission yeast (Nakano et al., 2001), and overexpression of the full-length Fim1p results in disorganization of the actin patches and actin cables and morphological cell defects (Nakano et al., 2001; Laporte et al., 2012). Deletion of fission yeast fim1 causes a small change in cable orientation and mild polarity defects (Wu et al., 2001; Skau et al., 2011). It is likely that the role of fimbrin Fim1p is more complex than a simple tuning of cross-linking interactions in actin cables. Fim1p has not been detected on actin cables, perhaps due to its low concentration there, but is highly concentrated at the actin patches, regulating their turnover and limiting the effect of tropomyosin (Nakano et al., 2001; Wu et al., 2001; Skau and Kovar, 2010; Skau et al., 2011). Models accounting for the effects of Fim1p concentration would involve considering its effect on the whole actin cytoskeleton, which includes actin patches.

In our model the filament cross-link formation rate depends on r_crslnk (thus larger cross-linker concentration corresponds to larger r_crslnk), whereas the rate of cross-link breakage depends on both r_crslnk and k_crslnk (breakage rate decreases as either parameter increases). These are effective parameters representing the combined action of multiple cross-linkers present in yeast cells. Changing these parameters (Figure 4) helps us to interpret and predict actin cable structures in cross-linker overexpression or deletion mutants. We note, however, that a more detailed model would be needed to calculate a more accurate dependence of our effective parameters on the properties and concentrations of multiple molecules that can cross-link actin filaments in different orientations and with different strength. Although in many cases actin-filament cross-linkers have redundant function, the properties of a system with two types of cross-linkers can be complex. For example, networks cross-linked by α-actinin and fascin stiffen under shear (Tseng et al., 2002). In actin networks cross-linked by fascin and filamin, structural and viscoelastic properties are modified independently (Schmoller et al., 2008). The viscoelasticity of composite actin networks with α-actinin and palladin is modified by the two types of cross-linkers cooperatively (Grooman et al., 2012). Cross-linking can also influence actin filament turnover (Schmoller et al., 2011); however, we find that our model predictions are robust to such an effect even when the turnover rate changes by a factor of 2 (Supplemental Materials and Supplemental Figure S8).

Budding yeast is another model organism in which actin cable organization principles similar to the ones described here for fission yeast might apply. Fimbrin Sac6p cross-links actin filaments to bundles (Adams et al., 1995; Cheng et al., 1999; Sandrock et al., 1999; Miao et al., 2013). Similar to Fim1p in fission yeast, overexpression of Sac6p strongly influences the distribution of both actin patches and actin cables (Sandrock et al., 1999), whereas deletion of Sac6p disrupts actin cables (Karpova et al., 1995) and changes bud morphology (Watanabe et al., 2009). Unlike cables in fission yeast, which can grow from both tips, budding yeast cables grow from the bud into the mother, and antiparallel cross-linking might be less important. In budding yeast, formins Bni1p at the bud tip and Bnr1p at the bud neck nucleate actin filaments at different polymerization rates (Huckaba et al., 2006; Moseley and Goode, 2006). The difference in the rates of polymerization might be another factor regulating cable morphology, along with the fact that Bnr1p not only polymerizes actin filaments, but also serves as a bundling factor (Moseley and Goode, 2005). Another layer of complexity is that two types of myosin pull on actin cables in budding yeast. Type V myosin Myo2p moves processively along actin cables in the presence of tropomyosin (Hodges et al., 2012), whereas type II myosin Myo1p bound to the bud neck regulates actin cable retrograde flow (Huckaba et al., 2006). A future model of actin cable morphology in budding yeast would have to account for the foregoing differences, as well as the different bud–mother geometry. The present work provides a framework for such studies.

MATERIALS AND METHODS

Simulation methods

We use Langevin dynamics to update the positions r_i of the ith filament bead in simulation time dt (Figure 1B):

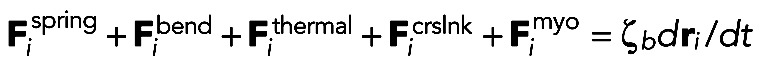(1)

where ζ_b is an effective drag coefficient of the filament segment. This approximation neglects possible long-range hydrodynamic interactions. The spring force is calculated from the stretching/compression of the springs:

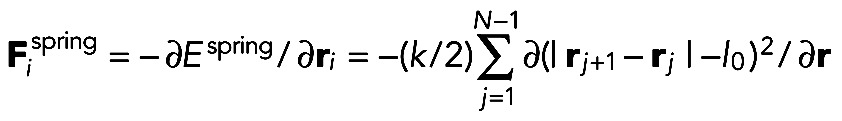where l₀ is the equilibrium spring length. We used k = 100 pN/μm, less than the stiffness of 437 pN/nm for a 0.1-μm-long actin filament segment (estimated using the measured stiffness of 1-μm-long filaments and the fact that stiffness is inversely proportional to length; Kojima et al., 1994). This value allows a large dt = 10⁻⁴ s, which maintains approximately constant segment lengths. The bending force is calculated from the deformation of neighboring beads:

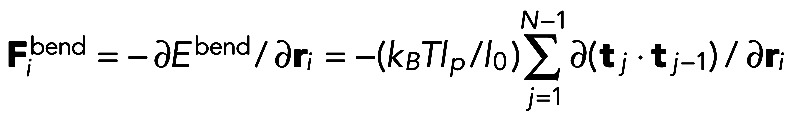where 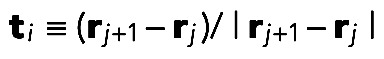, and l_p = 10 μm is the filament persistence length (Gittes et al., 1993). The thermal force obeys

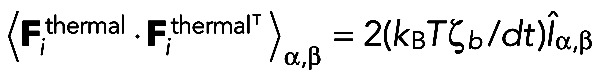where 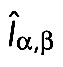is the second-order unit tensor (Pasquali et al., 2001). To implement polymerization, a new bead is introduced to the elongating polymer chain as soon as the elongating first segment reaches twice the size of spring equilibrium length, l₀.

We implement an effective isotropic attraction between filament beads: when bead i is within r_crslnk to bead j, an interaction force

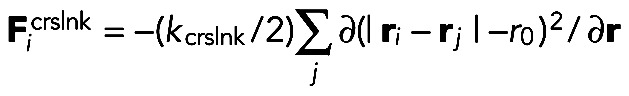is added to Eq. 1. Here r_crslnk and k_crslnk characterize the binding/unbinding kinetics of the cross-linkers and their concentration. Parameter r₀ = 0.03 μm is the average distance between two cross-linked filament segments, a number somewhat larger than the size of α-actinin and fimbrin (Klein et al., 2004; Sjoblom et al., 2008).

We tested that our simulations reproduce properties of individual filaments, including persistence length, relaxation time, and energy equipartition theorem (see Supplemental Materials and Supplemental Figures S1 and S2). Simulations were run for 180 s, a time longer than the filament turnover time and the longest relaxation time of 3-μm-long filaments, which is 23 s.

Strains, growing conditions, and cellular methods

The S. pombe strains used in this study are JW1349-2 (41nmt1-GFP-CHD (rng2)-leu1+ rlc1-tdTomato-natMX6 ade6-M210 leu1-32 ura4-D18) and JW3764 (kanMX6-3nmt1-ain1 41nmt1-GFP-CHD (rng2)-leu1+ rlc1-tdTomato-natMX6 ade6-M210 leu1-32 ura4-D18). In JW3764, AIN1 was under the control 3nmt1 promoters integrated at its native chromosomal loci (Bähler et al., 1998). To induce nmt1 promoters, cells were first grown at 25°C in YE5S (yeast extract medium containing adenine, histidine, leucine, uracil, and lysine) for 24 h at exponential phase, washed four times in EMM5S (Edinburgh minimal medium containing adenine, histidine, leucine, uracil, and lysine), and then grown for 18 h in EMM5S before microscopy.

Microscopy and data analysis

Live-cell microscopy was performed as described previously (Laporte et al., 2013) at 24–25°C, using a thin layer of EMM5S liquid medium with 20% gelatin (Sigma-Aldrich, St. Louis, MO) and 0.1 mM n-propyl-gallate. For imaging, we used a 100×/1.4 numerical aperture Plan-Apo Nikon objective lens on a spinning disk confocal microscope (UltraVIEW ERS; PerkinElmer Life and Analytical Sciences, Waltham, MA) with 440-, 488-, 514-, and 568-nm lasers and an ORCA-AG camera (Hamamatsu, Bridgewater, NJ). No binning was used for strains expressing GFP-CHD. Images were analyzed using ImageJ (National Institutes of Health, Bethesda, MD). Images in figures are maximum-intensity projections of z-sections spaced at 0.2–0.4 μm.

Experiments with drugs

For CK-666 treatment, exponentially growing cells were washed in EMM5S with 0.1 mM n-propyl-gallate and preincubated with 100 μM Arp2/3 inhibitor CK-666 (Chemdiv, San Diego, CA; Nolen et al., 2009) for 5 min to reduce the interference of actin patches for analysis. Then, cells were imaged immediately on bare slides, with the start of the observation defined as time 0. GFP-CHD images were collected in 8-s intervals for the wild-type strain and 10-s intervals for the overexpressing Ain1 strain over 10 min.

Abbreviations used:

CHD

calponin homology domain

GFP

green fluorescent protein

WT

wild type