Nucleosomes, transcription, and probability

Abstract

Speaking of current measurements on single ion channel molecules, David Colquhoun wrote in 2006, “Individual molecules behave randomly, so suddenly we had to learn how to deal with stochastic processes.” Here I describe theoretical efforts to understand recent experimental observations on the chromatin structure of single gene molecules, a molecular biologist's path toward probabilistic theories.

INTRODUCTION

The primary focus of my research has been the chromatin structure of transcriptionally active promoters. This has been a longstanding problem in molecular biology. Over the course of our studies, the notion eventually emerged that a solution to this problem required both a novel conceptual framework and befitting methods that are different from those commonly used for the analysis of in vivo chromatin structure. In short, chromatin structure had to be studied at the level of single gene molecules rather than ensemble averages, and the results of such analyses required probabilistic, that is, quantitative, theories.

This conclusion, whose evolution I outline here, stands in contrast to the paradigmatic determinism of molecular biology, whose central theory—the genetic code—makes qualitative and not quantitative predictions, namely, amino acids from codons. Like any code, it is a prime example of determinism. Determinism appears to be a requirement for biological function, and in light of the genetic code's success, it is understandable that ever since, many biological problems have been seen as decoding problems; codes abound in the molecular biological literature, including codes for the regulation of transcription. This qualitative emphasis may also explain, at least in part, why molecular biologists, inculcated by their discipline's paradigm (Kuhn, 1962), by and large tend to view quantitative theories as idle play and with suspicion.

However, not all problems in molecular biology resemble the transmission of sequence information between polymers. In contrast to the remarkable specificity of biomolecular polymerization reactions, brought about at the expense of free energy for proofreading (Hopfield, 1974), gene expression, when viewed at the single-cell level, exhibits a surprising degree of variation in the number of expressed molecules, which appears to defy deterministic expectations.

It is often said that this variation, or “noise,” results from the randomness of molecular behavior. However, justification of this “randomness assumption” remains an unsolved problem in statistical mechanics (van Kampen, 1991); probabilistic theories may be justified only on philosophical grounds.

Here I argue that assumptions of stochastic behavior can be imposed by the epistemological requirement that our theories be refutable or testable (Popper, 1963). This situation is met, in particular, in the theoretical treatment of microscopic molecular behavior, where elimination of the variables that describe the motions of the surrounding bath molecules allows for treatment of the individual molecule in isolation, by probabilistic means (van Kampen, 2007). Molecules behave randomly in this sense.

Whatever our justification, if molecular behavior is random, then probabilistic theories are inevitable if we want to understand how molecules engender physiology; after all, I suppose, this is the fundamental aim of molecular biology.

DNase-HYPERSENSITIVE SITES

Beginning with Carl Wu's seminal work (Wu, 1980), in vivo chromatin structure has been analyzed mostly by variations of one method: the endonucleolytic digestion of DNA in isolated nuclei. A critical finding of such studies has been that promoter sequences (including enhancers) tend to be more susceptible to DNase I and other endonucleases than sequences of the gene body, especially when transcriptionally active. It is generally believed that the observed differences in endonuclease sensitivity are largely attributable to differences in the spooling of DNA in nucleosomes (Kornberg, 1974), a shared trait of eukaryotic organisms. The spooling inhibits access of the DNA to transcription factors and RNA polymerase, but also to endonucleases.

THE PHO5 PROMOTER

The PHO5 promoter of Baker's yeast has been a classical model for analyzing the structure of transcriptionally active promoter chromatin (Almer et al., 1986). Mild digestion of yeast chromatin with DNase I reveals a periodic accessibility pattern at the transcriptionally repressed PHO5 promoter, indicative of translationally well positioned nucleosomes (Kornberg, 1981). In contrast, the transcriptionally induced, or “activated,” promoter DNA appears more or less uniformly accessible. This finding was initially explained by the hypothesis that the promoter converts from a fully nucleosomal into a nucleosome-free state upon transcriptional induction (Almer et al., 1986). However, closer examination demonstrated the existence of particles at all nucleosome positions of the activated promoter that were indistinguishable from nucleosomes at the repressed promoter by micrococcal nuclease digestion and sedimentation analysis (Boeger et al., 2003).

ERGODIC HYPOTHESIS

This apparent paradox could be resolved by the conjecture that some, but not all, promoter nucleosomes unspool completely upon transcriptional activation, whereas the remaining nucleosomes are statistically distributed over the nucleosome positions of the promoter (Boeger et al., 2003). The essential implication of this hypothesis is that promoter chromatin represents an ensemble of distinct nucleosome configurations. It explained both the existence of nucleosomes at all nucleosome positions across a population of cells and the apparent absence of structure by DNase I digestion, which now could be understood as the result of averaging over a structurally heterogeneous population. This latter point warrants special emphasis: Averaging over a heterogeneous population erases all structural information.

The assumption of structural heterogeneity invokes a yet-more-interesting “ergodic hypothesis”: At steady state, each promoter molecule visits each of the configurational states over time, in some sequence; that is, promoter chromatin is dynamic rather than static.

A fair amount of independent experimental observations has been accumulated to support the notion that activated promoter chromatin represents an ensemble of distinct nucleosome configurations (Boeger et al., 2008; Mao et al., 2010). However, alternatives could not be refuted as long as the existence of distinct nucleosome configurations could not be “directly” observed. This required the analysis of chromatin structure at the level of single gene molecules. Methods for the isolation of single gene molecules (Hamperl et al., 2014) now allow us to look at the nucleosome configurations of single molecules in the electron microscope (Brown et al., 2013).

NUCLEOSOME CONFIGURATIONS

Our analysis has focused on three nucleosome positions of the PHO5 promoter. There are 2³ or 8 combinatorial possibilities for occupying these positions: the nucleosome-free configuration, the fully nucleosomal configuration, three configurations with one nucleosome, and three configurations with two nucleosomes or one unoccupied position. Remarkably, all of these possibilities, including the fully nucleosomal promoter—the predominant configuration under repressing conditions—could be observed microscopically in a population of transcriptionally induced PHO5 molecules (Brown et al., 2013). How can this structural variation be explained?

GRAPHS

We may think about the underlying nucleosome dynamics in terms of a directed graph; it consists of labeled nodes, representing the eight nucleosome configurations, and directed edges joining pairs of nodes (Figure 1). Edges represent possible transitions between configurations and are thus directed (directed edges may be represented by arrows; Figure 1), An outgoing edge to node i is an edge that points away from i. For our purposes it is suitable to call such graphs transition graphs (however, since no other graphs will be considered, I may occasionally simply say “graph”).

FIGURE 1:

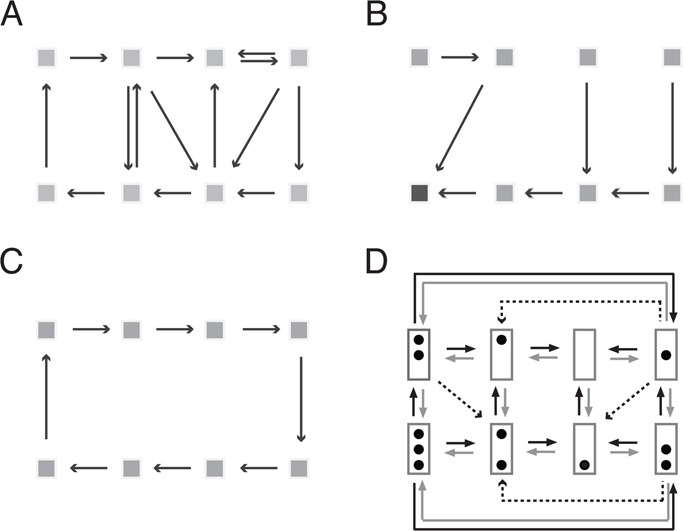
Transition graphs. (A) Strongly connected, branched graph. Nodes are indicated as squares. (B) Not strongly connected, unbranched (deterministic) graph. The darker gray square represents an absorbing state. (C) Cyclical graph. (D) Transition graph for simple process model of PHO5 promoter nucleosome dynamics (Brown et al., 2013). The promoter is represented by a box and occupied nucleosome positions as dots. Black, gray, and dashed arrows indicate assembly, disassembly, and sliding transitions, respectively.

What is the total number of transition graphs on eight nodes? A simple consideration shows that this number is 2^8×7 = 7.2 × 10¹⁶; it enumerates all theoretical possibilities within our (limited) theoretical framework (see later discussion).

A directed graph is called strongly connected if any node can be reached from any other node by a chain of (directed) edges (Figure 1, A and C), and not strongly connected otherwise (Figure 1B). The ergodic hypothesis implies that the transition graph is strongly connected. This limitation excludes ∼10% of all possible transition graphs.

BRANCHED AND UNBRANCHED TRANSITION GRAPHS

We may further distinguish between graphs on the number of outgoing edges per node. I call transition graphs with more than one outgoing edge for at least some nodes branched (Figure 1A). Thus, given the current configuration, the next configuration can be predicted only statistically. In contrast, graphs with no more than one outgoing edge per node are called unbranched or deterministic (Figure 1, B and C), for the next configuration (in time) is known if the present configuration is known.

Strongly connected unbranched graphs are called cyclical (Figure 1C). The observation of all eight possible nucleosome configurations excludes all transition graphs that are not strongly connected, conditional on the truth of the ergodic hypothesis. In other words, our experimental observations tell us this: either the ergodic hypothesis or all theories based on not-strongly connected transition graphs are false.

MARKOV ASSUMPTION AND MASTER EQUATION

The dynamics of promoter nucleosomes may be envisioned as the flow of probability mass between the nodes of the transition graph along its edges (stochastic process). To describe this flow mathematically, it is assumed that the current of probability mass along the edge from node i into node j linearly depends on the probability mass at node i, p_i, and that its rate constant, w_ji, is constant in time for all i and j (assumption of a homogeneous Markov process). The Markov assumption implies that (probabilistic) predictions of the future depend only on the present state and not past states. On this assumption, the following differential matrix equation, the master equation, is obtained from the Chapman–Kolmogorov equation of stochastic process theory (van Kampen, 2007):

where p is the column vector (p₁,…,p₈) and W is the 8 × 8 matrix (w_ij); its diagonal elements are the negative sums of the other column elements:

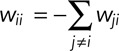W is called the generator of the process (Cinlar, 2013).

THE STATIONARY DISTRIBUTION

At steady state, probability currents into and out of each node are balanced, and the master equation becomes

The solution to this equation, p, is called the steady-state or stationary distribution. Algebraically, it is an element of the kernel of W, that is, the set of vectors mapped by W onto the zero vector, 0. Whether the process has a unique stationary distribution depends on its transition graph. It can be proved that processes on strongly connected transition graphs have a uniquely defined stationary distribution (Mirzaev and Gunawardena, 2013).

The formal theoretical task then consists in finding a generator W whose kernel is spanned by the microscopically observed configurational frequency distribution f or a vector satisfyingly similar to it (f ≈ p). There is no algorithm to solve this problem, nor are potential solutions necessarily unique. The following simplifying assumption limits investigations to a subclass of conceivable solutions—processes that I call simple.

“SIMPLE” PROCESSES

Transitions may be classified according to their kind. I distinguish three kinds: transitions that add nucleosomes, remove nucleosomes, or rearrange nucleosomes between positions. I refer to these as assembly, disassembly, and sliding transitions, respectively. I make the simplifying assumption that the value of the generator elements, w_ji, depends only on the kind of transition and call such processes simple.

Thus there are at most three numerically distinct generator elements, and since we may set one of them equal to 1—for example, the rate constant for nucleosome assembly—on some appropriate time scale, there are only two degrees of freedom or model parameters. Their values are determined by application of the likelihood axiom (Edwards, 1992), that is, we maximize the probability of our experimental data, given the transition graph.

Competing transition graphs are likewise evaluated. We (tentatively) adopt that graph under which the experimental observations enjoy greater probability and refute its competitor. This provides a coherent approach to the problem of assessing the relative merits of competing probabilistic theories and hypotheses, that is, of transition graphs and their parameter values.

Of note, the refutation of a probabilistic theory is always relative to a competitor that better corresponds to the data, for no observation is considered impossible; data are only more or less likely. (Thus corroboration and refutation are closely linked. It may be argued that this principle is not limited to probabilistic theories. In general, scientific arguments should proceed, wherever possible, by critical evaluation of pairs or families of competing hypotheses.)

On the assumption of a simple stationary process, the theoretical problem of reconstructing the promoter nucleosome dynamics reduces to the purely topological problem of finding the “correct” transition graph.

A “STOCHASTIC” SOLUTION

Remarkably, there exists a transition graph for a simple stationary process whose theoretical predictions closely correspond to electron microscopic observations (Brown et al., 2013). The defining features of this graph are that assembly and disassembly transitions occur only between configurations that differ by exactly one nucleosome—that is, nucleosomes are removed and added to the promoter one by one—and nucleosomes are slid out of, but not into, the central promoter position (Figure 1D).

The most essential property of this graph, however, is that it is branched; every one of its nodes has at least three outgoing edges. Thus knowledge of the current nucleosome configuration does not determine the future configuration. The promoter passes through a random sequence of nucleosome configurations. In this sense the promoter nucleosome dynamics is stochastic. (The Markov assumption furthermore implies that sojourn times are statistically distributed; Cinlar, 2013.)

Relative frequency distributions observed in mutants that either lack the transcriptional activator of PHO5 or bear deletion mutations in its activation domain were all explained by the assumption of a simple stochastic process on the same transition graph (Figure 1D) but with different values for the model parameters (Brown et al., 2013). In contrast, the earlier theory—that active and repressed promoter chromatin are singular states, fully nucleosomal and nucleosome free, respectively—required two distinct transition graphs with distinct absorbing states (states that lack outgoing edges; Figure 1B).

REFUTATION OF SIMPLE CYCLICAL PROCESSES

Relative to this solution, many alternative processes can be refuted. Of importance, it can be shown that all simple processes on cyclical transition graphs, of which there are 7!, or 5040, account for our microscopic observations less well than the graph of Figure 1D. On the ergodic hypothesis, all deterministic graphs are cyclical graphs. Thus, provided the process is simple and the ergodic hypothesis is true, the microscopic observations allow us to refute all deterministic transition graphs.

TRANSCRIPTIONAL BURSTING

The most essential aspect of the present result is that the transition graph that solves the problem is branched. The structural variation between molecules is thus understood as the result of random choice between alternative nucleosome configurations. On the well-corroborated theory that not all promoter nucleosome configurations are equally conducive to transcription (Mao et al., 2011), this result predicts that periods of transcriptional activity randomly alternate with periods of inactivity, when the promoter is structurally unresponsive to regulatory signals. Thus transcription should occur in the form of random bursts. This notion has its origin in attempts to understand the variation in gene product abundances, or “noise,” of gene expression.

It is widely believed that transcription indeed occurs in random bursts (Sanchez and Golding, 2013). Its molecular basis, however, is unknown. The structural analysis of single molecules demonstrated that the nucleosomal variation between promoter molecules may provide such a basis, a mechanism for the generation of transcription noise (Brown et al., 2013). Of importance, on the basis of this assumption and expression noise measurements, it could be inferred that nucleosome loss upon promoter activation occurs by acceleration of removal rather than inhibition of reformation, that is, nucleosome removal is rate limiting to transcription (Mao et al., 2010; Brown et al., 2013).

However, the nucleosomal variation between promoter molecules may be the result of the promoter's deterministic response to compositional variation of its intracellular environment, a symptom of transcriptional bursting, rather than its origin. This possibility has not been ruled out (Brown et al., 2013). The hypothesis that promoter nucleosome dynamics generates transcription noise awaits critical testing.

SIMPLICITY AND TESTABILITY

It may be asked whether the assumption of a branched transition graph is inevitable for explaining the structural heterogeneity of promoter chromatin. The answer is no. It can be proved that any process on a cyclical, that is, deterministic, graph can account perfectly for any conceivable microscopic observation if the rate constants (generator elements) of all eight edges are allowed to be chosen freely. This would contravene the simple process hypothesis—but who says that biology is simple?

Of course biology is not simple. However, our theories, in a sense, have to be. The cyclical process example shows that the introduction of sufficiently many model parameters, or auxiliary hypotheses, insulates a theory against refutation; it no longer can clash with observation and thus has lost contact with reality. The uncertainty of choice between future nucleosome configurations implied by a branched transition graph can be eliminated. However, the prize for the assumption of a deterministic graph is irrefutability or loss of “empirical content” (Popper, 1959). Thus theories must be simple enough that our empirical observations “matter.”

SUMMARY

It has been believed that active and repressed promoter chromatin are singular states, fully nucleosomal and nucleosome free, respectively (Almer et al., 1986; Reinke and Horz, 2003). Thus the structural dynamics that connects the experimentally distinguishable structures of transcriptionally “active” and “inactive” promoter chromatin has a predetermined end point; the fully nucleosomal and nucleosome-free configurations are absorbing states; the steady state is static. In contrast with this deterministic hypothesis stands the probabilistic dynamical theory that single promoter molecules continually pass through all possible nucleosome configurations in random sequence (although not all sequences are possible). The transition from repressed to induced “state” is explained by a shift in probability of configuration with more to those with fewer nucleosomes rather than a transition between structurally distinct singular states.

This probabilistic theory accounts both for the findings that were explained by its predecessor and the findings that refuted it. It has suggested new independent experimental tests and novel corroborating observations—for example, electron micrographs of single gene molecules—and it raises new, deeper, problems. Of importance, it links chromatin to transcription fluctuations, which the earlier theory did not. (Nor would any code theory foster such a connection.) This conjectured link, together with noise measurements, has provided a critical argument in support of the hypothesis that promoter nucleosome removal is rate limiting to transcription (Mao et al., 2010; Brown et al., 2013). However, whether promoter nucleosome dynamics indeed generates transcription noise, as the argument assumed, must still be independently tested.

CONCLUDING REMARKS

Theoretical possibilities were represented as graphs. Many other problems in biology may be formalized in this way, providing possibly a common formal language and hence common formal problems and solutions for otherwise disparate biological fields (Gunawardena, 2012).

I argued here, specifically, in defense of quantitative theories because they can be imposed by the nature of the problem. As shown, assumptions of uncertainty, or probabilistic theories, can become inevitable when the empirical content of deterministic alternatives tends to zero, that is, when there are no conceivable experimental results that could contradict them.

More fundamentally, however, I plead for theory, quantitative or not. The age of “big data” has led some to herald the end of theory (Glass and Hall, 2008). However, data, no matter how big, do not explain anything; theories do, namely the data. Experiments contribute to the growth of knowledge only by refutation of theoretical possibilities. All knowledge, therefore, is conjectural, especially empirical knowledge. Data have meaning only when viewed in light of competing theories. This insight, the solution of Hume's problem of induction (Popper, 1972), remains a challenging notion to many. Yet, “biology is more theoretical than physics” (Gunawardena, 2013).