Emergent mechanics of biological structures

Abstract

Mechanical force organizes life at all scales, from molecules to cells and tissues. Although we have made remarkable progress unraveling the mechanics of life's individual building blocks, our understanding of how they give rise to the mechanics of larger-scale biological structures is still poor. Unlike the engineered macroscopic structures that we commonly build, biological structures are dynamic and self-organize: they sculpt themselves and change their own architecture, and they have structural building blocks that generate force and constantly come on and off. A description of such structures defies current traditional mechanical frameworks. It requires approaches that account for active force-generating parts and for the formation of spatial and temporal patterns utilizing a diverse array of building blocks. In this Perspective, we term this framework “emergent mechanics.” Through examples at molecular, cellular, and tissue scales, we highlight challenges and opportunities in quantitatively understanding the emergent mechanics of biological structures and the need for new conceptual frameworks and experimental tools on the way ahead.

INTRODUCTION

Although no individual molecule can be said to be alive, molecules come to life as part of larger macromolecular machines to give rise to cells and organisms. Life is not only a chemical process, but also a mechanical one: mechanoenzymes push and yank, cells spatially organize their contents, change shape, and move, and organisms develop, swim, and run. To understand the inner workings of life's machines, we must unravel their mechanics: how they generate and respond to mechanical force across scales, and how mechanical forces are transmitted across them. Having characterized the mechanics of many of life's fundamental building blocks over the past few decades, we now ask: How do the mechanics of larger-scale structures emerge from those of their constituent parts? For example, how do the mechanics of macromolecular structures emerge from those of molecules, and how do the mechanics of tissues emerge from those of cells? This hierarchical thread, in which mole­cules make cells that make organisms, interlaces mechanics at all length scales. Remarkably, new mechanical features that are dramatically different from those of the smaller-scale com­ponents can emerge in multicomponent, dynamic living structures. Understanding how these mechanical attributes emerge from first principles—a dream for quantitative scientists—remains a frontier.

The central challenge in understanding the mechanics of biological structures is that they are dynamic and constantly sculpt themselves: their building blocks consume energy and generate force, they come on and off on their own, and whole structures morph to take new shapes and functions. These structures thus have “emergent mechanics,” which we define as mechanics that arise from the above complex dynamics and the interplay (feedback loops) between them. We contrast these to the mechanics of static structures that are frozen in space and time. The emergent mechanics of biological structures can be dramatically different from the mechanics of their constituent parts, and they often defy current mechanics frameworks and intuition. In this Perspective, we discuss the attributes of living biological architectures that determine their mechanical properties and the challenges that biology presents for understanding and predicting the mechanics that emerge. Throughout, we draw on simple examples across scales, from molecules to tissues, to highlight specific challenges and possible ways ahead. We view the integration of active force-generating parts, dynamics in space and time, and mechanics as an opportunity for quantitative and physical thinking to impact our understanding of biological structures.

From structure to mechanics

What are the key parameters that regulate the mechanics of multicomponent structures across biological length scales? First, let us look from a traditional viewpoint of mechanics. 1) Perhaps most simply, the material properties of the individual building blocks can impact those of the bigger structure. For example, titin's molecular-scale stiffness ultimately defines that of muscle tissue (Wang et al., 1991). 2) Similarly, the basic architecture of a structure—how different building blocks are oriented and connected to each other—will influence its mechanics. As a striking example, the parallel orientation of microtubules in the spindle (the machine that segregates chromosomes at cell division) results in a mechanically anisotropic structure (Shimamoto et al., 2011) supporting different mechanical functions along different axes. 3) Similarly, the density of building blocks and cross-links between them can determine the viscosity of the assembled structure. For example, this is displayed in cytoskeletal filament networks cross-linked to different extents (Gardel et al., 2004). 4) Moreover, the shape of a structure and its internal cross-linking geometry can regulate the spatial patterns of mechanical stresses across it. For instance, the shape of a tissue can determine the propagation of mechanical forces across cells and dictate where stress is felt and thus where cells proliferate (Nelson et al., 2005). 5) Finally, the affinity of interactions between building blocks will influence larger-scale mechanics. For example, the binding affinity between different building blocks can specify how deformable a structure is, and thus cell–cell junction affinities can regulate a tissue's mechanical integrity (Takeichi, 2014). Notably, the above structural parameters all have analogies in everyday life: structural engineers consider the elastic moduli of materials (1), support beam orientations (2) and densities (3), and anchor point geometrical distributions (4) and strengths (5).

Mechanics of dynamically changing structures

Despite knowing much about their building blocks and architecture, we are (for the most part) unable to predict the mechanics of living structures in the most rudimentary sense. For instance, given an infinite choice of building blocks, we cannot a priori design a new, higher-order structure of a desired compliance or viscosity or of a given force generation capability. Even predicting whether a biological structure will be more liquid-like or solid-like can be a challenge. Why? Because biological structures are wildly dynamic: their structural components themselves can consume energy and can rapidly turnover while the whole structure persists and changes architecture (MacKintosh and Schmidt, 2010). Subtle variations in parameters (energy expenditure, architecture, and temporal dynamics) can dramatically change the mechanics of the resulting structure in ways we do not understand. In contrast, structural engineers design macroscopic structures (such as houses and bridges) that are built once and for all, with fixed architectures and components that are there to stay. They understand—and can model and predict—how subtle parameter variations can fine-tune mechanics, such as earthquake resistance.

Biological structures can arise from a concoction of parts through self-assembly or self-organization. In self-assembly, order arises from local interactions between “passive” building blocks: no energy is consumed, and structures typically reach a steady state (Brangwynne, 2011). In self-organization, order arises from self-driven “active” parts that consume (dissipate) energy (Nédélec et al., 1997; Karsenti, 2008). This energy comes from metabolism, bringing biological processes out of equilibrium: this empowers living structures to transform themselves again and again, to generate autonomous motion, and to organize life. As a classic example, cytoskeletal structures constantly build, unbuild, and rebuild themselves to match changing needs (Kirschner and Mitchison, 1986) and their dynamics themselves generate force (Dogterom et al., 2005). This raises a simple paradox: how can biological structures be so dynamic and yet persistently generate force and maintain their mechanical integrity? The answer lies in understanding the emergent mechanics of these structures, and we lack both the conceptual framework and tools needed to understand them. Here are a few reasons why.

Challenges

A first key challenge to understanding the mechanics of living structures is time: how does one describe the mechanics of a structure whose components constantly turn over and evolve and whose mechanically relevant time scales range from milliseconds (molecular motor stepping) to days (organism developing)? Here we must simultaneously take into account the finite lifetime of building blocks and the time scale of their structural parameters and interactions. On-and-off rates provide one natural time scale in the system. For example, a structure whose components come on and off every second will be mechanically unlike another whose components turn over every hour. Indeed, the rate of repair and dynamic remodeling of structures can inherently regulate responses to mechanical force. A second key challenge is space: how does one describe the mechanics of a structure whose architecture and force transmission (load-bearing) paths evolve over time? Most biological structures are spatially nonuniform, and their mechanically interconnected length scales (Fletcher and Geissler, 2009; Fletcher and Mullins, 2010) range from nanometers (molecular motors) to meters (organisms). Thus the mechanical responses of individual elements depend on where they are located in the structure and the structure's local and global architecture. Knowledge of both these local- and global-scale parameters is required to describe such structures, but probing architecture across a wide length scale range is difficult. A third key challenge is that self-organizing structures can consume energy and actively generate force. How does one describe the mechanics of a biological structure whose responses to (internal and external) force include changes in the production of force itself?

Complexity

Although these three challenges are significant, it is their combination that presents the grandest challenge to understanding emergent mechanics (Figure 1): temporal, architectural, and active force-generation dynamics all affect each other (feedback loops), raising the structure's complexity to a level that defies traditional frameworks and everyday intuition.

FIGURE 1:

Challenges in emergent mechanics. Biological structures are dynamic and self-organize: their building blocks come on and off on their own, whole structures transform to take new shapes and functions, and their building blocks can consume energy and generate force. Not only do these structures interweave 1) temporal, 2) architectural, and 3) active force-generation dynamics, but they do so across length scales (from nanometers to meters) and time scales (from milliseconds to days). New theoretical frameworks and experimental approaches that integrate these three aspects will provide headway in understanding the emergent mechanics of biological structures.

In some cases, the biological structures formed by self-organization may even be “emergent” themselves, an extreme class of highly dynamic structures. In the physical world, tornados and sand dunes are examples of emergent structures, with matter, energy, and information coherently interacting to build a dynamic structure that evolves over time and across scales, in this case from molecules to tens of meters. Emergent structures exhibit properties that their smaller building blocks (air molecules or sand grains) do not, and these arise from the collective behavior of building blocks. In the living world, such structures include the mitotic spindle, active membranes in endocytic pits, and intricate self-repairing tissue and organ systems. In contrast to tornados and sand dunes, these living structures are spatially heterogeneous, have a great diversity of building blocks and interactions, and include building blocks that themselves actively consume energy.

How can we understand—and ultimately model and predict—the mechanics of these biological structures? Progress will require mapping mechanical interactions across all relevant scales. Building such a spatiotemporal force map that will mechanically link individual molecules (piconewton forces), large cellular machines (nanonewton forces), and cells and tissues (micronewton forces) is a grand challenge in active dynamic structures. This highlights the growing need for new theoretical and experimental tools and represents a great opportunity for biologists, physicists, and engineers to work together.

From molecules to cells

To illustrate the challenges of understanding how constituent molecules give rise to the emergent mechanics of cellular-scale structures, we turn to the spindle. The spindle's size, dynamics, and mechanics are dramatically different from those of its parts. Indeed, the spindle is a striking example of emergent mechanics: how do the spindle's simple parts come together to make a machine that coordinates an intricate dance of chromosomes and ultimately their segregation? Individual tubulin blocks, a few nanometers across, come together to form the spindle, which is ten or more microns across in mammals. To segregate chromosomes, the spindle must be able to deform, change size, and generate force, which require a flexible, dynamic, and active structure. As a first challenge to understanding its emergent mechanics, the spindle persists for one hour, whereas most of its components turn over in seconds or minutes (Saxton et al., 1984) as its thousands of microtubules grow and shrink via dynamic instability (Mitchison and Kirschner, 1984). Our understanding of spindle mechanics must inherently take into account the time scale of components and their interactions, which can be linked to the time scale of the spindle's response to force—for example, its viscosity (Shimamoto et al., 2011). Second, the spindle's architecture changes dramatically as its function changes throughout mitosis, for example, from metaphase to anaphase; in addition, large fluxes and movements of microtubules can take place in structures that at first glance appear static (Mitchison, 1989). Quantifying spindle architecture has been challenging, in part because of how large the spindle is compared with its densely packed small building blocks, and new strategies to interrogate spindle architecture are being designed to meet these challenges (Brugués et al., 2012). Third, both walking motors and microtubule dynamics actively generate force in the spindle. We are beginning to understand how these active processes generate and respond to force at the molecular level, a basic requirement for understanding how the spindle generates and responds to force to segregate chromosomes.

Understanding the emergent mechanics of complex macromolecular assemblies will require us to quantify temporal dynamics, precise architectural parameters, and active force generation processes and the relationship between all of them and mechanics across scales (Cai and Sheetz, 2009; Mayer, Depken, et al., 2010; Kasza and Zallen, 2011; Shimamoto et al., 2011; Forth et al., 2014; Figure 1). In part because macromolecular assemblies have so many dynamic parts, it has been hard to reconstitute or purify many of them outside cells. In turn, probing their mechanics inside cells has been challenging due to the physical access needed for mechanical probes. In this regard, in vivo force measurement probes are an exciting new development (Grashoff, Hoffman, et al., 2010; Krieg et al., 2014). To bridge our understanding across length scales, it will be important to measure how forces generated by individual molecules affect larger-scale structures and how stresses across the whole structure flow through individual molecules. Toward this goal, it would be empowering to be able to externally control and tune the on-and-off kinetics, architecture, and active force-generation ability of the structure's building blocks: for example, these could be controlled via small molecules, mechanical confinement, and light (Nakamura et al., 2014), respectively. Such strategies would allow us to test simple predictions of our current understanding and may pave the way to designing structures with new mechanics.

From cells to organisms

Moving to a larger length scale, that of multicellular organisms, how can we comprehend the physical properties of a large cluster of homogeneous or heterogeneous cells? From the outset, calling an aggregate of cells or a tissue “dynamic” may seem paradoxical. After all, our common macroscopic perception of a tissue is static and fixed—a structure that resists stress and maintains the mechanical integrity of organs. However, at the microscopic scale of individual cells, a very different (and dynamic) story emerges, as is readily seen during development and tissue maintenance and homeostasis (Guillot and Lecuit, 2013). From the early proposals of differential adhesion theory, cellular ensembles have been described as being like a fluid with specific surface tension associated with cellular interfaces (Foty and Steinberg, 2005). For decades, we have known that macroscopic cellular rearrangements play a critical role in morphogenesis at developmental time scales. Mature tissue has also been uncovered to have the plasticity to recover from injury and trauma and to maintain homeostasis, for example, in the kidney (Rabelink and Little, 2013). Thus the conceptual challenges described above for understanding the mechanics of macromolecular assemblies are similar at multicellular scales (Figure 2).

FIGURE 2:

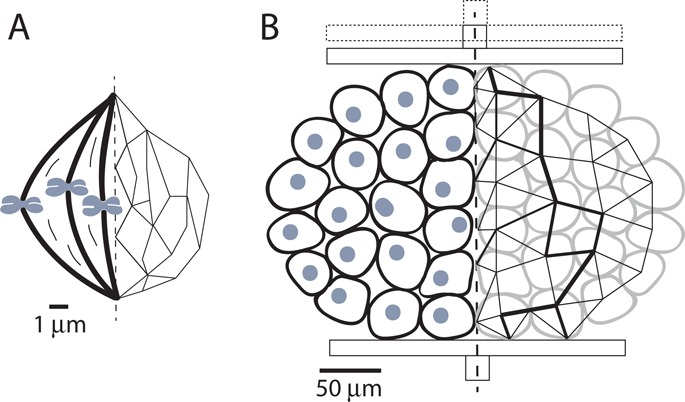
Macromolecular structures and cellular ensembles show conceptual similarities in how forces flow through them, although at different length scales. (A) The spindle is one example of a macromolecular structure with changing force propagation paths (Elting, Hueschen, et al., 2014; Sikirzhytski, Magidson, et al., 2014). Dynamic restructuring of these paths under internal and external perturbations is crucial to the robustness of chromosome segregation. (B) Similarly, an ensemble of cells under internal and external forces deforms and restructures itself, rerouting forces (see line path thickness) passing through individual cells. Owing to the dynamic nature of cell–cell interactions, cellular ensembles can show surprising behaviors: they can flow like a fluid and yet sustain forces like a solid.

Cells in a tissue connect with each other via a multitude of common junctions: desmosomes and adherens, tight, and gap junctions, which enable the flow of information (both forces and signaling molecules) and materials locally between cells. In organisms ranging from the largest (whale) to the smallest (tardigrade) animals, a basal membrane keeps cellular ensembles together in place. These cellular ensembles depict measurable emergent mechanical properties such as surface tension, viscosity, elasticity, and plasticity (Lecuit and Lenne, 2007). What dynamic cellular-scale processes bring about these emergent mechanical properties of this tissue? How do these emergent mechanics change over time as the tissue responds to external signals—for example, an infection or developmental cue? Candidate parameters controlling these emergent mechanics include the turnover rate of cellular junctions (Nishimura and Takeichi, 2009), the active migration of a single cell or cell cluster (Weijer, 2009), and the rate of cell birth and death (Sancho, Battle, et al., 2003). Comparing cellular ensembles to active fluid models (Ramaswamy, 2010) instead of traditional passive viscoelastic fluids provides renewed hope in building a continuum theory to explain the myriad set of behaviors of aggregates in which each cell can actively generate force. Although approaches focused on minimization of energy of the whole ensemble have already resulted in a number of fascinating biological discoveries for cellular ensembles (Hayashi and Carthew, 2004), future work should begin to incorporate the complexity and dynamic activity of a single cell into the aforementioned models. To understand emergent mechanics at this scale, a more appropriate analogy might, for example, borrow ideas from the physical theory of active granular matter (Kumar et al., 2014).

Outlook

With so many moving pieces (literally and figuratively) that constitute dynamic biological systems, we need to ask ourselves: How do we know when we have understood the fundamental essence of a biological phenomenon? This task lies squarely in how we frame our questions. In the specific context of mechanics, our goal should be focused on extracting the general mechanical design principles (Rafelski and Marshall, 2008) used by biological systems and not only on exact individual interactions. It is very likely the case that these mechanical design principles will be fundamentally new and as such may not have a known analogue in nonliving physical systems. More conceptually, some of the mechanical design principles could potentially cut across scales and thus describe examples from the smallest to the largest relevant scale in biology. To probe these design principles, we would further need to develop new theoretical and experimental tools to uniquely quantify the mechanics of dynamic, ever-changing structures in biology. Theoretical tools will need to modify continuum models of active systems (Marchetti et al., 2013) to incorporate heterogeneous building blocks that vary over both space and time. Experimental measurements will require reconstitution of basic biological functionality from minimum components (Sanchez, Chen, DeCamp, et al., 2012) and the capability to mechanically perturb, control, and tune building blocks at will (Nakamura et al., 2014). Potential discoveries of fundamentally new mechanical design principles should not only be exciting to those chasing the mysteries of biological systems, but also to physicists looking for new laws governing states of active matter—something of a win-win situation.