Abstract
Trigger waves are a recurring biological phenomenon involved in transmitting information quickly and reliably over large distances. Well-characterized examples include action potentials propagating along the axon of a neuron, calcium waves in various tissues, and mitotic waves in Xenopus eggs. Here we use the FitzHugh-Nagumo model, a simple model inspired by the action potential that is widely used in physics and theoretical biology, to examine different types of trigger waves—spatial switches, pulses, and oscillations—and to show how they arise.
INTRODUCTION
Multicellular organisms are at times required to quickly coordinate behavior over large distances. For example, a human experiencing the fight-or-flight response elevates heart rate, dilates pupils, and constricts peripheral blood vessels within seconds. Diffusion alone could not distribute signaling molecules at significant concentrations throughout even millimeter- or centimeter-scale organisms fast enough to account for the coordinated behaviors of physiology. Although the diffusion of a small molecule (with a typical diffusion coefficient D in cytoplasm of 300 μm2/s; Allbritton et al., 1992) over the distance scale of a cell (d = 10 μm) is extremely fast (t = d2/2D ≈ 0.2 s), diffusion across a centimeter-scale animal like a bumble bee would take ∼2 days, and diffusion across a meter-scale animal like a human would take ∼5000 years.
One way in which animals have solved this problem is through microtubule-based transport, which, unlike diffusion, does not slow down as distance increases. Typical rates of microtubule-based transport are ∼1 μm/s (Prahlad et al., 1998, 2000; Fletcher and Theriot, 2004), which would make transport over 1 cm take just <3 h and transport over 1 m take ∼12 days.
Flow can allow for even quicker communication over long distances. For example, when the adrenal gland releases epinephrine, it can exert its full effect on systems throughout the human body in ∼1 min, which is the average time it takes for blood to make one circulation (Hall, 2010). This is equivalent to a propagation speed of ∼30 mm/s. Similarly, fungi and plants use flow to distribute biological molecules throughout the cytoplasm of some large cells. Actomyosin-driven cytoplasmic streaming mixes the contents of Chara corallina cells as large as 10 cm in length at speeds of up to 100 μm/s (Verchot-Lubicz and Goldstein, 2010).
Still, fluid flow is too slow to coordinate the most rapid behaviors observed in multicellular life. Placing one's hand on a hot stove elicits muscle action in tens of milliseconds (Malcolm, 1951). In this case, action potentials travel to the spinal cord and back at speeds of up to ∼100 m/s to accomplish the rapid reflex response (Hursh, 1939; Swadlow and Waxman, 2012). Waves of calcium ions spread across and sometimes between cells at speeds of ∼5–30 μm/s (Cornell-Bell et al., 1990; Stricker, 1999). This is slow compared with an action potential, but it is still faster than diffusion for large cells and tissues, and, like the action potential, a calcium wave spreads without slowing down or losing amplitude. Recently the mitotic state has been shown to spread at a constant speed of ∼1 μm/s through Xenopus cytoplasm in the absence of flow (Chang and Ferrell, 2013). This propagation of the mitotic state is believed to help spatially coordinate cell division. Finally, in various migrating eukaryotic cells in culture, one often sees waves of membrane protrusion and actin polymerization that spread from the front of the cell toward the back of the cell at speeds of ∼0.1 μm/s (Machacek and Danuser, 2006; Weiner et al., 2007; Bretschneider et al., 2009; Barnhart et al., 2011; Allard and Mogilner, 2013).
Each of these phenomena is an example of what are termed trigger waves (Winfree, 1972; Tyson and Keener, 1988). Trigger waves do not slow down or lose amplitude as they travel, eliminating two problems that come with relying solely on diffusion to move molecules across large distances. Even though the proteins that generate action potentials, calcium waves, mitotic waves, and actin waves are different, and even though the time scales of the various waves range over nine orders of magnitude, the underlying dynamical processes are similar.
Here we review the topic of how trigger waves are generated, with the goal of explaining in a self-contained way the mechanistic basis of these beautiful and important phenomena. For readers interested in more detail on the physics of trigger waves, the classic review by Tyson and Keener (1988) and the analysis of propagating fronts presented by Rinzel and Terman (1982), Elphick et al. (1997), and Hagberg and Meron (1994) are recommended.
We use a set of equations well known to physicists, the FitzHugh–Nagumo (FHN) model (FitzHugh, 1961; Nagumo et al., 1964). Originally proposed as a simplification of the Hodgkin–Huxley model of action potentials (Hodgkin and Huxley, 1952), the FHN equations can be viewed as a simple and general model of interlinked positive and negative feedback loops that can produce various types of dynamical responses, including switches, pulses, and oscillations. Moreover, by adding diffusion to the FHN model, one can produce trigger waves that rapidly propagate these switches, pulses, and oscillations over large distances. Before beginning with the analysis of the FHN model, it is helpful to examine some of the circuits that generate biological trigger waves in greater detail. We begin with the most venerable biological trigger wave, the action potential.
Action potentials
Action potentials originate at the axon hillock (Figure 1A) and propagate down the axon at an undiminishing speed and amplitude (Figure 1B). Typically, action potentials occur at irregular time intervals, but in some cases, circuits of neurons fire with a regular period.
FIGURE 1:
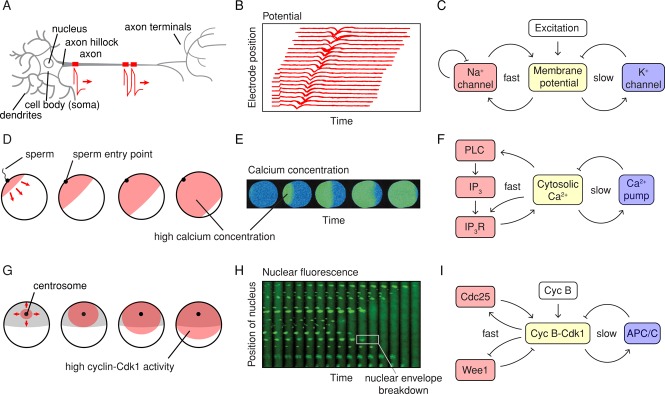
Examples of biological trigger waves. (A–C) Action potentials. (A) Action potentials are generated at the axon hillock and propagate distally down the axon. (B) Recordings of an action potential traveling down an axon, measured by an array of extracellular electrodes. The inward flux of Na+ during an action potential registers as a negative deflection of the potential registered by the extracellular electrodes. (Adapted from Bakkum et al., 2013.) (C) Schematic view of the circuit that generates the action potential. (D–F) Calcium waves in fertilized eggs. (D) Calcium waves are generated at the sperm entry point and spread across the egg. (E) Calcium concentrations as a function of time in a fertilized oocyte from the milky ribbon worm, Cerebratulus lacteus, as measured by ratiometric imaging after calcium green loading. (Taken from Stricker, 1999.) (F) Schematic view of the circuit that generates calcium waves. (G–I) Mitotic waves in Xenopus eggs. (G) About 1 h after fertilization and the postfertilization calcium wave, a wave of Cdk1 activation spreads from near the centrosome to the cortex of the cell. (H) Waves of mitosis in Xenopus egg extracts. Thin Teflon tubes were filled with cycling Xenopus egg extracts together with sperm chromatin and a nuclear localization signal–green fluorescent protein marker. Waves of nuclear envelope breakdown spread from the fastest regions of the cytoplasm, near the middle of this section of the tube, outward. (Taken from Chang and Ferrell, 2013.) (I) Schematic view of the circuit that generates waves of cyclin B-Cdk1 activation.
The key protein in the generation and propagation of the action potential is the voltage-sensitive sodium channel (Figure 1C). When the plasma membrane begins to depolarize, that is, the intracellular side of the membrane becomes less negative with respect to the extracellular side, stochastic opening of the voltage-sensitive sodium channels occurs more frequently. Channel opening allows sodium to rush inward down its concentration and potential gradients, depolarizing the membrane further. This constitutes a positive feedback loop (Figure 1C), and in principle the cycle of depolarization → channel opening → depolarization could continue until the inside of the cell is positive enough to keep more Na+ from flowing inward. The fact that the feedback loop is operating at the level of protein conformation changes and ion flows, both of which are very rapid processes, allows the peak of the action potential to be attained in <1 ms.
The action potential is terminated by two processes: the delayed opening of voltage-sensitive potassium channels, which allows K+ to flow out of the cell and restore the net negative charge of the inside, and the autoinactivation of the voltage-dependent sodium channel (Figure 1C). Taken together, the circuit is a system of interlinked positive and negative feedback loops.
Calcium waves
Calcium waves occur in many species and cell types (Gilkey et al., 1978; Busa and Nuccitelli, 1985; Cornell-Bell et al., 1990; Goldbeter et al., 1990; Stricker, 1999; Codazzi et al., 2001; Choi et al., 2014). One particularly striking example is the calcium wave that occurs when a sperm fertilizes an egg (Figure 1, D and E). Typically, the wave initiates at the sperm entry point, sweeps across the egg at ∼5–30 μm/s, and results in a filling of the whole egg with high (approximately micromolar) concentrations of free Ca2+ (Stricker, 1999). The high intracellular calcium helps prevent the refertilization of the egg by a second sperm. In some species, a single calcium wave occurs; in others, there is a succession of waves (Stricker, 1999). Calcium waves also occur in numerous other cells and tissues and can occur as solitary pulses, trains of pulses, or sustained pulsatile oscillations (Meyer and Stryer, 1988; Cornell-Bell et al., 1990; Goldbeter et al., 1990; De Young and Keizer, 1992; Straub et al., 2000; Lewis, 2003).
Like action potentials, calcium waves are generated by a circuit with positive feedback (Figure 1F). In this case, an increase in free intracellular Ca2+ activates phospholipase C (PLC), which cleaves the phosphatidylinositol 4,5 bisphosphate (PIP2) and generates the second messenger inositol trisphosphate (IP3). IP3 then binds to IP3 receptors (IP3R) on the calcium-filled endoplasmic reticulum (ER), allowing Ca2+ to flow into the cytoplasm and bringing about further activation of PLC (Figure 1F). Thus an increase in intracellular calcium brings about a further increase. In addition, cytosolic Ca2+ more directly stimulates the release of ER Ca2+ by regulating IP3 receptors and ryanodine receptors on the ER. There are therefore two interlinked positive feedback loops operating on similar time scales. The increase in cytosolic Ca2+ is limited by the finite capacity of the ER and then reversed by membrane-bound calcium pumps, constituting a negative feedback loop (Figure 1F).
Mitotic waves
About 1 h after the postfertilization calcium wave passes through a Xenopus egg, a wave of mitosis spreads through the cell (Hara, 1971, 1980), beginning in the vicinity of the centrosome and congressed pronuclei and progressing to the cell cortex at a constant speed of ∼1 μm/s (Figure 1G; Hara, 1971; Rankin and Kirschner, 1997; Perez-Mongiovi et al., 1998; Chang and Ferrell, 2013). This wave can be visualized by putting cycling Xenopus egg cytoplasm mixed with nuclei in a Teflon tube and watching the nuclei disappear as mitosis spreads through the cytoplasm (Figure 1H; Chang and Ferrell, 2013). Mitotic waves are believed to help spatially coordinate mitosis and cell division in the huge (1.2 mm) Xenopus egg.
The circuit that generates this wave of mitosis is shown in Figure 1I. It is centered on the cyclin B–cyclin-dependent kinase 1 (Cdk1) complex, the master regulator of mitosis. The protein kinase Cdk1 in turn is regulated by fast, interlinked positive and double-negative feedback loops (Cdk1 activates its activator Cdc25C and inactivates its inactivator Wee1), which constitutes a bistable switch (Pomerening et al., 2003; Sha et al., 2003). The switch is then turned back off by a time-delayed negative feedback loop (Yang and Ferrell, 2013); Cdk1 activates APC/CCdc20 complex, a ubiquitin E3 ligase that promotes cyclin B degradation and restores the system to a low-Cdk1-activity state.
Differences and commonalities
These three examples of spatiotemporal signaling are different in many respects. For one thing, the proteins involved are unrelated: sodium and potassium channels in the case of action potentials; phospholipases, IP3 receptors, and pumps in the case of calcium waves; and kinases, phosphatases, and ubiquitin ligases in the case of mitotic waves. The wave velocities and the distances over which the waves typically propagate are different as well. Finally, some of these waves recur in an oscillatory manner, and some are solitary pulses.
In all three cases, however, the outputs (membrane depolarization, intracellular Ca2+, or cyclin B-Cdk1 activity) spread through space and time via trigger waves. Trigger waves are made possible by the coexistence of two essential processes. The first is a local reaction process, which typically exhibits bistability, excitability, or relaxation oscillations. The FHN model is a particularly simple and well-studied ordinary differential equation model with interlinked positive and negative feedback loops that can exhibit, for the appropriate choice of parameters, all three of these behaviors. It is not necessarily the best or most realistic model of any of these processes, but it contains the basic ingredients needed for generating trigger waves, and for this reason, we will use this model for the reaction portion of our trigger wave model. The other essential process is some sort of spatial coupling mechanism. Here we assume that diffusion provides the spatial coupling and use Fick's second law to describe it.
The FHN model
Because of its simplicity, richness, and relevance to biology, the FHN model has been the subject of hundreds of papers (Rocsoreanu et al., 2000), including much work on waves and spatial propagation (Rinzel and Terman, 1982; Hagberg and Meron, 1994; Elphick et al., 1997; Neu et al., 1997). The model is a modification of the van der Pol oscillator model, which was originally inspired by vacuum tube circuits (van der Pol and van der Mark, 1928).
The FHN model consists of two ordinary differential equations in two time-dependent variables:
|
|
|
|
The first equation includes all of the fast reactions; the second, the slow ones (because the parameter ε is generally taken to be <<1).
In its original context as a model for the action potential, the variable u represents the membrane potential, and the three terms on the right-hand side of Eq. 1 represent three ways that the membrane potential is rapidly regulated. The first term, du/dt ∝ u, is the positive feedback, where depolarization linearly promotes more depolarization through the voltage-gated sodium channel. The second term, du/dt ∝ − u3, is a fast negative feedback loop, which roughly corresponds to the autoinactivation of the sodium channel. The third term represents a recovery process like the outward potassium currents that oppose depolarization. The functional forms and coefficients were chosen such that the u-nullcline is shaped like a backward S, which is critical to the model's behavior (see later discussion), and not because they correspond exactly to the situation in nerves or other biological oscillators.
The second variable, v, is related to the potassium gradient. The resting situation, where the extracellular concentration of K+ is lower than the intracellular concentration, corresponds to a negative value of v. The processes that regulate v are all assumed to occur on a slow time scale. The first term represents the activation of the voltage-gated potassium channel by the membrane potential u, which increases the value of v. The second term, –εbv, represents the pumping of K+ out of the neuron. The third term on the right-hand side, εa, roughly corresponds to a potassium leak current.
The FHN model is less directly related to calcium signaling and Cdk1 activation, but one can still draw analogies: for calcium signaling, u can represent the free cytosolic calcium, and v can represent the pumps and leaks that regulate calcium concentration more slowly. For mitosis, u can represent cyclin B-Cdk1 activity and v can represent the more slowly varying cyclin B concentration. Note, however, that the enduring significance of the FHN model for biologists does not come from a precise correspondence between the individual terms of the two equations and any particular biological process. Instead, it lies in the fact that the model is a simple way of generating bistability, excitability, and relaxation oscillations, three systems-level behaviors known to arise in a number of biological contexts.
Bistability in the FHN model
Here we assume a = 0.1 and e = 0.01 and change the behavior by varying the parameter b. Note that all parameters and variables are dimensionless throughout. When b is relatively large (b > 1.8), the system is bistable. Depending on the initial conditions, the system will settle down into one of two alternative stable steady states, one with a negative membrane potential (Figure 2A) and one with a positive membrane potential. For the initial value of v assumed here (v = −0.3), all trajectories that start with u > −0.3 (the threshold shown by the dashed line in Figure 2A) will approach the positive-potential steady state (Figure 2A, red curve), and all trajectories that start with u < −0.3 will end up at the negative-potential steady state (Figure 2A, blue curve). Thus a small perturbation that pushes the system across the threshold will be amplified into a large difference in the system's ultimate fate.
FIGURE 2:
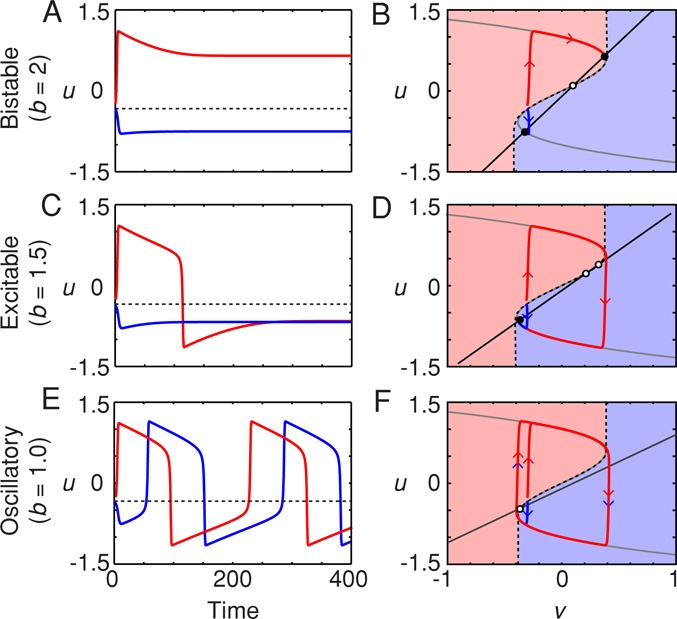
Different types of dynamics from the FHN model. (A, C, E) Time course; (B, D, F) phase plots. (A, B) Bistability. For b = 2, the system is bistable, with two stable steady states (B, filled circles) and one saddle point (B, open circle). For the value of v(t = 0) assumed here (v(t = 0) = –0.3), trajectories beginning above a threshold value of u (A, dashed line) go to the high-u stable steady state, whereas those beginning below the threshold go to the low-u stable steady state. In the phase plane, a separatrix (dashed curve) divides the starting points that approach the high-u stable steady state (pink area) from those that go to the low-u steady state. (C, D) Excitability. For b = 1.5, there is a single stable steady state plus a saddle point and an unstable steady state. Trajectories beginning above the threshold (C) or the separatrix (D) yield a pulse of u and circle the unstable steady state before settling down to a low steady-state value of u. Those beginning below the threshold do not yield a pulse of high u. (E, F) Oscillations. For b = 1.0, the single steady state is unstable. From all initial conditions (except starting right on the unstable steady state), the trajectories approach the same stable limit cycle, although from above the threshold, they go first to the upper limb of the u-nullcline, and below the threshold, they go first to the lower limb. A, C, and E are time courses; B, D, and F are phase plots. In each case, a = 0.1, ε = 0.01, v(t = 0) = −0.3, and u(t = 0) = −0.25 (red trajectories) or −0.35 (blue trajectories).
The origin of the bistability can be understood by examining a phase plot of the two-variable system, where the values of u and v (each of which is a function of time) are plotted in the uv-plane (Figure 2B). Stable steady states are attained when both du/dt and dv/dt are equal to zero:
|
|
|
|
Equation 3 defines a curve in the uv plane, the u-nullcline, and it can be thought of as the steady-state response of u to various constant levels of v (Figure 2B, gray curve). The positive feedback and cubic negative feedback terms give the nullcline a characteristic backward-S shape that is critical for the behavior of the model. Equation 4 is the v-nullcline, a straight line that describes the steady-state response of v to u (Figure 2B, black line). Wherever the two nullclines intersect, both time derivatives (Eqs. 1 and 2) are equal to zero and the system is in steady state. For the particular value of b chosen in Figure 2, A and B (b = 2), the two nullclines intersect at three points (Figure 2B). Two of the intersection points can be shown through linear stability analysis (Strogatz, 1994) to represent stable steady states (filled circles), and one is an unstable saddle point (open circle). This means that the system is bistable.
Some initial conditions produce trajectories that approach the negative-potential steady state (Figure 2, A and B, blue region) and others that approach the positive-potential steady state (Figure 2, A and B, pink region). A separatrix (dashed curve) divides the basins of attraction for the two stable steady states.
Excitability in the FHN model
As b is decreased, the slope of the v-nullcline decreases. This moves one of the stable steady states from the upper limb of the u-nullcline to the middle limb, and it changes from being stable to unstable. This leaves a single remaining stable steady state—the low-membrane-potential steady state (Figure 2D). The system is now monostable but excitable. For some initial conditions, u and v will proceed more or less directly to the remaining stable steady state (Figure 2D, blue curve), whereas for others, the trajectory first shoots to the u-nullcline, circles around the unstable steady state, and only then heads toward the stable steady state (Figure 2D, red curve). The result is that some initial conditions will result in pulses of depolarization (Figure 2C, red curve), whereas others will not (Figure 2C, blue curve). The separatrix dividing the trajectories that pulse from those that do not is similar in shape to that which divided the basins of attraction in the bistable case (Figure 2B).
Oscillations in the FHN model
When b is decreased below ∼1.2, so that the v-nullcline intersects the middle limb of the u-nullcline rather that the lower limb, there is only one steady state, and it is unstable (Figure 2F). The result is that the system is now oscillatory rather than excitable, and this type of oscillation in which the trajectory switches back and forth between the two limbs of the u-nullcline is termed a relaxation oscillation. From some initial conditions, the trajectories aim upward (Figure 2F, pink region), and from others, they aim downward (blue region), but they always approach the same stable limit cycle (Figure 2F). This yields an unending succession of alternations between high and low membrane potentials (Figure 2E), which are very similar to repeated trains of the pulses that were generated when the model was in its excitable regime (Figure 2C, red curve).
Thus the FHN model can exhibit three types of behavior: bistability, excitability, and oscillations. When combined with a spatial coupling mechanism like diffusion, each of these responses can be propagated as a trigger wave.
Reaction-diffusion dynamics in the FHN model
The ordinary differential equations of the FHN model describe either the behavior of a well-stirred, spatially homogeneous system or a spatially inhomogeneous system with no coupling between points in space. To generate trigger waves, we need the system to be both inhomogeneous and spatially coupled. Action potentials, calcium waves, and mitotic waves all arise out of spatial inhomogeneities in either the initial conditions of the system or the parameters of the system. Because they all occur within a shared cytoplasm, we will assume here that diffusion provides the spatial coupling.
In the absence of any local reaction process, a locally elevated concentration of molecules will spread through a cell and eventually approach a homogeneous spatial distribution. Fick's second law describes how the concentrations change in time through diffusion. For one spatial dimension (e.g., for diffusion in a thin tube like an axon) this is
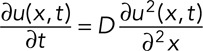 (5) (5)
|
where D is the diffusion coefficient, typically ∼300 μm2/s for a small molecule like IP3 and ∼10 μm2/s for a rapidly diffusing cytosolic protein or for Ca2+, which spends most of its time bound to proteins (Allbritton et al., 1992). We can add diffusion terms to the FHN model to yield a system of partial differential equations:
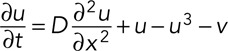 (6) (6)
|
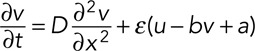 (7) (7)
|
These can be solved numerically for some choice of parameters and initial conditions. For each of the simulations shown in Figure 3, we assumed that we have a long, one-dimensional tube (like an axon) with the system in a low-u state (u(t = 0) ∼ –0.6, v(t = 0) ∼ –0.3) everywhere except for a small region in the middle of the tube, where the system has a higher membrane potential (u(t = 0) = 1). In Figure 3D, the oscillatory case, we also assumed that the frequency of the oscillations is higher in the middle of the tube than in the other regions. We then assumed that either there was no diffusive coupling (top, D = 0) or there was diffusive coupling (bottom, D = 1) and examined how the systems evolved with time. We represent the value of u at each point in space and time by a heat map color scale.
FIGURE 3:
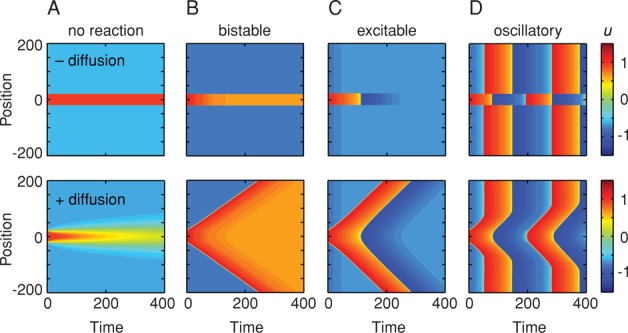
Three types of trigger waves from coupling the FHN reactions to diffusion. The system is assumed to have one spatial dimension (represented on the y-axis); it is essentially a long, thin tube. The values of u as a function of time and position are represented by a heat map color scale. In all cases we assumed that the system has a high initial value of u in the middle of the tube over a width of 40 units (u(t = 0) = 1) and a low initial value of u elsewhere (u(t = 0) = –0.6). The initial value for v is the same everywhere (v(t = 0) = –0.3). For the oscillatory case, we also assumed that the frequency of the oscillations is higher in the middle of the tube (b = 0.5) than in the rest of the tube (b = 1), acting as a pacemaker for the whole system. In the top panels there is no diffusive coupling (D = 0), while in the bottom panels diffusion is included (D = 1). The FHN parameters are the same as those shown in Figure 2.
If there is no reaction and no diffusion, then the middle region remains red and the outer regions remain blue indefinitely (Figure 3A, top). Adding diffusion makes the high-potential region both spread out and decrease in amplitude with time (Figure 3A, bottom), as would be expected intuitively. The high-u region has a significant effect only on the regions close to it and only for a limited period of time.
Bistable, excitable, and oscillatory trigger waves
The situation is very different when we assume that the reactions of u and v are described by the FHN model. If the system is bistable (b = 2), so that in the absence of diffusion the two regions settle into the two different stable steady states (Figure 3B, top), then adding diffusion of the appropriate strength allows the high-u state to propagate up and down the tube at constant speed (Figure 3B, bottom). Eventually the entire tube flips from the low-u state to the high-u state. If the system is excitable (Figure 3C), diffusion allows a pulse of high u to spread up and down the tube at constant speed (Figure 3C, bottom). If the tube is oscillatory, with the phase advanced and frequency higher in the center of the tube relative the rest of the tube, the fast oscillations spread up and down from the center at constant speed until they meet up with the delayed oscillations (Figure 3D, bottom). With each successive oscillation, the trigger wave of fast oscillations spreads further up and down the tube (Figure 3D, bottom). In each of these cases, a dynamical phenomenon—bistable switching, excitable spikes, or oscillations—propagates through space via trigger waves.
To get an idea of why the combination of FHN reactions and diffusion allows for the generation of trigger waves, first ignore diffusion and recall that there is a separatrix or threshold built into the reactions (Figure 2). For a given initial value of v, if you begin with a value of u above the threshold, the trajectory will have one sort of fate, and if you begin below it, another. In the bistable case (Figure 2, A and B), the threshold separates the trajectories that approach the high-u steady state from those that approach the low-u steady state; in the excitable case (Figure 2, C and D), it separates the trajectories that include an upward pulse of u from those that do not; and in the oscillatory case (Figure 2, E and F), it separates the oscillations that initially head toward the upper limb of the u-nullcline from those that head toward the lower limb.
Diffusion provides a mechanism for crossing the threshold. This is illustrated in Figure 4 for the case of the bistable FHN system. Diffusion mixes nearby values such that a point in space within the low-u region will have its value of u initially increase as the high-u region mixes with it and then eventually fall back down (Figure 4, A–C). The higher the diffusion coefficient, the faster is the initial increase, but the fall back down is faster as well (Figure 4, A–C). Diffusion can therefore allow the value of u to increase above the threshold (or, in phase space, to cross the separatrix) for some period of time. If the time is sufficient, the FHN reactions can convert that region of space into an even higher level of u (Figure 4, C and D). The entire process is repeated in the next region of space and then the next, resulting in a trigger wave of bistable switching that never slows down and never peters out (Figure 4C). Similar arguments can be made for the excitable and oscillatory cases.
FIGURE 4:
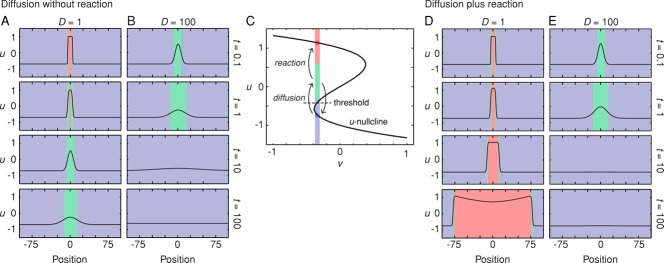
Diffusion can push the system across a threshold. (A, B) Diffusive spreading of a high-u state in the absence of reaction for two different diffusion coefficients. The values of u as a function of position and time are depicted both as curves and in a simplified red-green-blue heat map representation. Increasing the diffusion coefficient allows some regions within the low-u region to attain moderately high (green) levels of u more quickly, but for a shorter duration. (C) Phase plot for one point in space that is initially in the low-u region. Diffusion moves the value of u across the threshold into the green region, but in the absence of reaction, eventually returns it to the blue region. If the FHN reactions are fast enough, they can capture the suprathreshold trajectory and convert this point in space to a high-u (red) state. (D, E) Diffusion plus reaction allows self-regenerating trigger waves to propagate outward (D) unless the diffusion coefficient is too high (E).
We assumed here that the initial value of v in both the low- and high-u regions is negative, so that the low-u region is close to the threshold and the high-u region is far from it (Figure 4C). This makes it so that it is easier for diffusion and reaction to convert the low-u region to a high-u region than vice versa. If instead we had assumed that the initial value of v were positive, then we would obtain a trigger wave of the low-u state that would spread into, and eventually take over, the high-u region.
The time scales of reaction versus diffusion
As the FHN reactions speed up and the diffusion coefficient D increases, in general the speed of the trigger wave increases. The speed s is approximated by the equation
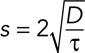 (8) (8)
|
where D is the diffusion coefficient and τ is related to the doubling time for the system's positive feedback, essentially the inverse of the speed of the reactions. This equation was first presented by Robert Luther in his 1906 analysis of chemical waves and then, independently in 1937, by R. A. Fisher in a classic paper on the spatial spread of an advantageous gene allele through a population (Luther, 1906; Fisher, 1937; Showalter and Tyson, 1987). As Showalter and Tyson (1987) pointed out, for action potentials, the equivalent of D is ∼0.034 m2/s and τ ≈ 0.3 ms in the giant squid axon, yielding a propagation speed of 20 m/s, in good agreement with experimental observation (Hodgkin and Huxley, 1952). For calcium-induced calcium release, D ≈ 10 μm2/s and τ ≈ 1 s, yielding a wave speed of ∼6 μm/s, in reasonable agreement with observation (Stricker, 1999). For the IP3-mediated positive feedback loop, the IP3 diffusion coefficient is higher (∼300 μm2/s), but the PIP2 hydrolysis-mediated feedback is probably slower, yielding a similar wave speed (Meyer, 1991; Allbritton et al., 1992). For mitotic waves, assuming that the diffusion coefficients for the proteins involved are ∼10 μm2/s and the flipping time for the bistable switch is ∼10–100 s, we obtain a wave speed of ∼0.6-2 μm/s (Novak and Tyson, 1993), again in good agreement with experimental observations (Chang and Ferrell, 2013).
Note that there is a limit to how much speed one can obtain by increasing the diffusion coefficient D; if the diffusion is too fast for the reactions, the activity will dissipate before the trigger wave can be initiated (Figure 4D). Thus, to generate a trigger wave, the time scale for diffusion cannot be too fast relative to the time scale of the reactions.
Trigger waves tend to self-organize
Figures 3 and 4 show trigger waves emerging out of a spatially inhomogeneous system, with a small central region that differs from the rest of the domain. Within each of these spatial domains, however, the systems are perfectly homogeneous. However, real biological systems tend to be less than perfectly homogeneous. What would happen if we assumed that the initial conditions and model parameters were noisy, varying over some reasonable range over space?
This question is addressed for an oscillatory FHN system in Figure 5A. Rather than starting with two discrete domains with different initial conditions, we assume that there are small, random variations in initial conditions and parameter values throughout the system. As the system begins to oscillate, the noise makes it unclear whether there are trigger waves or not (Figure 5A). Eventually, discrete foci from which oscillations emerge become apparent, and eventually a single focus, where the oscillation frequency happened to be highest, dominates the behavior of the whole tube. Similar behavior is seen in biological trigger waves. In the experiment shown in Figure 5B, mitotic waves become apparent after a couple of cell cycles and self-organize so that they emerge from three discrete foci by cycle 4, two foci by cycle 5, and 1 focus by cycle 6 (Figure 5B, arrows). Thus trigger waves do not just propagate information relatively quickly; they can also make noisy events become more orderly.
FIGURE 5:
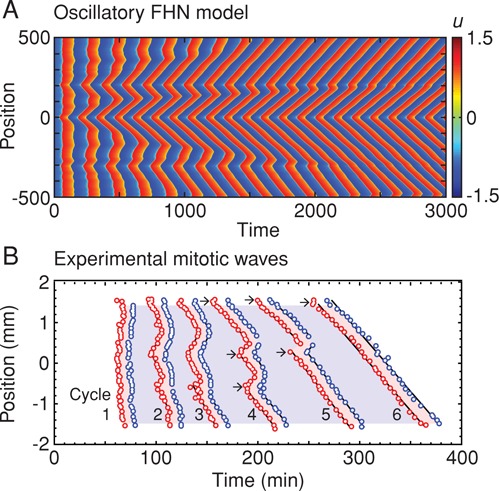
Trigger waves tend to self-organize. (A) Self-organizing trigger waves in an oscillatory FHN model with the model's parameters assumed to be inhomogeneous in space. A single focus of oscillations eventually dominates the whole system. (B) Self-organizing mitotic waves in Xenopus egg extracts in Teflon tubes. The red circles mean that a reporter nucleus at that position entered mitosis at that time. The blue circles denote mitotic exit. In cycle 1, there is no obvious relationship between position and time of mitotic entry or exit, but by cycle 6, a wave of mitosis starting near the top of the tube dominates the whole system. The arrows denote positions from which waves apparently originate. (Adapted from Chang and Ferrell, 2013.)
Concluding remarks
Here we examined the FitzHugh–Nagumo model with one-dimensional diffusion and showed how three types of trigger waves can be generated: waves of switching from one stable steady state to another, wave-like pulses, and oscillatory waves. These trigger waves propagate without slowing down or petering out and tend to be self-organizing. Pulsatile trigger waves (Figure 3C) can be thought of as models for solitary action potentials and calcium waves. Oscillatory trigger waves (Figure 3D) are relevant to mitotic waves and to repeated trains of action potentials and calcium waves.
The trigger waves examined here are made possible by the fact that the u-nullcline of the FHN model is shaped like a backward S, which makes it possible for diffusion to push the system across a threshold that separates qualitatively distinct dynamical responses. Other models whose reactions are different from those used in the FHN model (see, e.g., Novak and Tyson, 1993; Yang and Ferrell, 2013) can yield trigger waves as well, provided that one variable in the model is an S-shaped function of another.
So far we have only considered trigger waves operating within a single cell, with diffusion providing the spatial coupling mechanism. In principle, other mechanisms can provide this spatial coupling. For example, with actin waves, as Allard and Mogilner (2013) pointed out, diffusion, mechanical stress, and polymerization may all be involved in spatial coupling.
Moreover, if a system possesses an intercellular coupling mechanism, mediated, for example, by paracrine signaling or direct cell–cell interactions, then trigger waves can mediate and organize communication within multicellular tissues. The classic example is the pacemaker circuitry of the heart, where the fastest oscillators (in the sinoatrial node) keep the slower oscillators (in the rest of the myocardium) in step through trigger waves. Similarly, the slime mold Dictyostelium discoideum uses intercellular cAMP trigger waves to organize its aggregation into a multicellular organism (Palsson and Cox, 1996). We suspect that many other examples of intercellular trigger waves remain to be discovered. For example, Trusina and colleagues conjectured that inflammatory responses spread through tissues via trigger waves (Yde et al., 2011a, b). It seems likely that a number of wave-like developmental phenomena, like the propagation of the morphogenetic furrow during Drosophila eye development (Tomlinson and Ready, 1987; Sato et al., 2013), may also be mediated by trigger waves, here acting as an intercellularly propagating bistable switch.
The prerequisites for a trigger wave are 1) a system of reactions that includes strong positive feedback and nonlinearity, and 2) a spatial coupling mechanism. Given how commonplace these basic ingredients are in cell signaling and how important it is that cellular regulation be coordinated both spatially and temporally, we suspect that trigger waves will prove to be important in many other contexts as well.
Acknowledgments
We thank Daniel Berenson, Xianrui Cheng, Alisa Moskaleva, and Julie Theriot for helpful comments and discussions. This work was supported by grants from the National Institutes of Health (GM046383 and GM107615). L.G. acknowledges support by the Research Foundation–Flanders, the Belgian American Educational Foundation, and the Research Council of the Vrije Universiteit Brussel.
Abbreviations used:
- Cdk1
cyclin-dependent kinase 1
- ER
endoplasmic reticulum
- FHN
FitzHugh-Nagumo
- IP3
inositol trisphosphate
- IP3R
IP3 receptor
- PIP2
phosphatidylinositol 4,5 bisphosphate
- PLC
phospholipase C.
Footnotes
REFERENCES
- Allard J, Mogilner A. Traveling waves in actin dynamics and cell motility. Curr Opin Cell Biol. 2013;25:107–115. doi: 10.1016/j.ceb.2012.08.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allbritton NL, Meyer T, Stryer L. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science. 1992;258:1812–1815. doi: 10.1126/science.1465619. [DOI] [PubMed] [Google Scholar]
- Bakkum DJ, Frey U, Radivojevic M, Russell TL, Muller J, Fiscella M, Takahashi H, Hierlemann A. Tracking axonal action potential propagation on a high-density microelectrode array across hundreds of sites. Nat Commun. 2013;4:2181. doi: 10.1038/ncomms3181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barnhart EL, Lee KC, Keren K, Mogilner A, Theriot JA. An adhesion-dependent switch between mechanisms that determine motile cell shape. PLoS Biol. 2011;9:e1001059. doi: 10.1371/journal.pbio.1001059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bretschneider T, Anderson K, Ecke M, Muller-Taubenberger A, Schroth-Diez B, Ishikawa-Ankerhold HC, Gerisch G. The three-dimensional dynamics of actin waves, a model of cytoskeletal self-organization. Biophys J. 2009;96:2888–2900. doi: 10.1016/j.bpj.2008.12.3942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busa WB, Nuccitelli R. An elevated free cytosolic Ca2+ wave follows fertilization in eggs of the frog, Xenopus laevis. J Cell Biol. 1985;100:1325–1329. doi: 10.1083/jcb.100.4.1325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chang JB, Ferrell JE., Jr Mitotic trigger waves and the spatial coordination of the Xenopus cell cycle. Nature. 2013;500:603–607. doi: 10.1038/nature12321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Choi WG, Toyota M, Kim SH, Hilleary R, Gilroy S. Salt stress-induced Ca2+ waves are associated with rapid, long-distance root-to-shoot signaling in plants. Proc Natl Acad Sci USA. 2014;111:6497–6502. doi: 10.1073/pnas.1319955111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Codazzi F, Teruel MN, Meyer T. Control of astrocyte Ca(2+) oscillations and waves by oscillating translocation and activation of protein kinase C. Curr Biol. 2001;11:1089–1097. doi: 10.1016/s0960-9822(01)00326-8. [DOI] [PubMed] [Google Scholar]
- Cornell-Bell AH, Finkbeiner SM, Cooper MS, Smith SJ. Glutamate induces calcium waves in cultured astrocytes: long-range glial signaling. Science. 1990;247:470–473. doi: 10.1126/science.1967852. [DOI] [PubMed] [Google Scholar]
- De Young GW, Keizer J. A single-pool inositol 1,4,5-trisphosphate-receptor-based model for agonist-stimulated oscillations in Ca2+ concentration. Proc Natl Acad Sci USA. 1992;89:9895–9899. doi: 10.1073/pnas.89.20.9895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elphick C, Hagberg A, Maolmed B, Meron E. On the origin of traveling pulses in bistable systems. Phys Lett A. 1997;230:33–37. [Google Scholar]
- Fisher RA. The wave of advance of advantageous genes. Ann Eugen. 1937;7:353–369. [Google Scholar]
- FitzHugh R. Impulses and physiological states in theoretical models of nerve membrane. Biophys J. 1961;1:445–466. doi: 10.1016/s0006-3495(61)86902-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fletcher DA, Theriot JA. An introduction to cell motility for the physical scientist. Phys Biol. 2004;1:T1–10. doi: 10.1088/1478-3967/1/1/T01. [DOI] [PubMed] [Google Scholar]
- Gilkey JC, Jaffe LF, Ridgway EB, Reynolds GT. A free calcium wave traverses the activating egg of the medaka, Oryzias latipes. J Cell Biol. 1978;76:448–466. doi: 10.1083/jcb.76.2.448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldbeter A, Dupont G, Berridge MJ. Minimal model for signal-induced Ca2+ oscillations and for their frequency encoding through protein phosphorylation. Proc Natl Acad Sci USA. 1990;87:1461–1465. doi: 10.1073/pnas.87.4.1461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hagberg A, Meron E. Pattern formation in non-gradient reaction-diffusion systems: the effects of front bifurcations. Nonlinearity. 1994;7:805–835. [Google Scholar]
- Hall JE. Guyton and Hall Textbook of Medical Physiology. Maryland Heights, MO: WB Saunders; 2010. [Google Scholar]
- Hara K. Cinematographic observation of “surface contraction waves” (SCW) during the early cleavage of axolotl eggs. Wilhelm Roux' Archiv. 1971;167:183–186. doi: 10.1007/BF00577039. [DOI] [PubMed] [Google Scholar]
- Hara K, Tydeman P, Kirschner M. A cytoplasmic clock with the same period as the division cycle in Xenopus eggs. Proc Natl Acad Sci USA. 1980;77:462–466. doi: 10.1073/pnas.77.1.462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol. 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hursh JB. Conduction velocity and diameter of nerve fibers. Am J Physiol. 1939;127:131–139. [Google Scholar]
- Lewis RS. Calcium oscillations in T-cells: mechanisms and consequences for gene expression. Biochem Soc Trans. 2003;31:925–929. doi: 10.1042/bst0310925. [DOI] [PubMed] [Google Scholar]
- Luther R. Raumliche fortplanzung chimischer reaktionen. Z. Elektrochem. 1906;12:596–600. [Google Scholar]
- Machacek M, Danuser G. Morphodynamic profiling of protrusion phenotypes. Biophys J. 2006;90:1439–1452. doi: 10.1529/biophysj.105.070383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Malcolm DS. A method of measuring reflex times applied in sciatica and other conditions due to nerve-root compression. J Neurol Neurosurg Psychiatry. 1951;14:15–24. doi: 10.1136/jnnp.14.1.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meyer T. Cell signaling by second messenger waves. Cell. 1991;64:675–678. doi: 10.1016/0092-8674(91)90496-l. [DOI] [PubMed] [Google Scholar]
- Meyer T, Stryer L. Molecular model for receptor-stimulated calcium spiking. Proc Natl Acad Sci USA. 1988;85:5051–5055. doi: 10.1073/pnas.85.14.5051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagumo J, Arimoto S, Yoshizawa S. An active pulse transmission line simulating nerve axon. Proc IRE. 1964;50:2061–2070. [Google Scholar]
- Neu JC, Presissig RS, Krassowska W. Initiation of propagation in a one-dimensional excitable medium. Physica D. 1997;102:285–299. [Google Scholar]
- Novak B, Tyson JJ. Modeling the cell division cycle: M-phase trigger, oscillations, and size control. J Theor Biol. 1993;165:101–134. [Google Scholar]
- Palsson E, Cox EC. Origin and evolution of circular waves and spirals in Dictyostelium discoideum territories. Proc Natl Acad Sci USA. 1996;93:1151–1155. doi: 10.1073/pnas.93.3.1151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Perez-Mongiovi D, Chang P, Houliston E. A propagated wave of MPF activation accompanies surface contraction waves at first mitosis in Xenopus. J Cell Sci. 1998;111:385–393. doi: 10.1242/jcs.111.3.385. [DOI] [PubMed] [Google Scholar]
- Pomerening JR, Sontag ED, Ferrell JE., Jr Building a cell cycle oscillator: hysteresis and bistability in the activation of Cdc2. Nat Cell Biol. 2003;5:346–351. doi: 10.1038/ncb954. [DOI] [PubMed] [Google Scholar]
- Prahlad V, Helfand BT, Langford GM, Vale RD, Goldman RD. Fast transport of neurofilament protein along microtubules in squid axoplasm. J Cell Sci. 2000;113:3939–3946. doi: 10.1242/jcs.113.22.3939. [DOI] [PubMed] [Google Scholar]
- Prahlad V, Yoon M, Moir RD, Vale RD, Goldman RD. Rapid movements of vimentin on microtubule tracks: kinesin-dependent assembly of intermediate filament networks. J Cell Biol. 1998;143:159–170. doi: 10.1083/jcb.143.1.159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rankin S, Kirschner MW. The surface contraction waves of Xenopus eggs reflect the metachronous cell-cycle state of the cytoplasm. Curr Biol. 1997;7:451–454. doi: 10.1016/s0960-9822(06)00192-8. [DOI] [PubMed] [Google Scholar]
- Rinzel J, Terman D. Propagation phenomena in a bistable reaction-diffusion system. SIAM J Appl Math. 1982;42:1111–1137. [Google Scholar]
- Rocsoreanu C, Georgescu A, Giurgiteanu N. The Fitzhugh-Nagumo Model: Bifurcation and Dynamics. Dordrecht, Netherlands: Springer; 2000. [Google Scholar]
- Sato M, Suzuki T, Nakai Y. Waves of differentiation in the fly visual system. Dev Biol. 2013;380:1–11. doi: 10.1016/j.ydbio.2013.04.007. [DOI] [PubMed] [Google Scholar]
- Sha W, Moore J, Chen K, Lassaletta AD, Yi CS, Tyson JJ, Sible JC. Hysteresis drives cell-cycle transitions in Xenopus laevis egg extracts. Proc Natl Acad Sci USA. 2003;100:975–980. doi: 10.1073/pnas.0235349100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Showalter K, Tyson JJ. Luther's 1906 discovery and analysis of chemical waves. J Chem Educ. 1987;64:742–744. [Google Scholar]
- Straub SV, Giovannucci DR, Yule DI. Calcium wave propagation in pancreatic acinar cells: functional interaction of inositol 1,4,5-trisphosphate receptors, ryanodine receptors, and mitochondria. J Gen Physiol. 2000;116:547–560. doi: 10.1085/jgp.116.4.547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stricker SA. Comparative biology of calcium signaling during fertilization and egg activation in animals. Dev Biol. 1999;211:157–176. doi: 10.1006/dbio.1999.9340. [DOI] [PubMed] [Google Scholar]
- Strogatz SH. Nonlinear Dynamics and Chaos: With Applications to Physics, Biology, Chemistry, and Engineering. Cambridge, MA: Westview Press; 1994. [Google Scholar]
- Swadlow HA, Waxman SG. Axonal conduction delays. Scholarpedia. 2012;7:1451. [Google Scholar]
- Tomlinson A, Ready DF. Cell fate in the Drosophila ommatidium. Dev Biol. 1987;123:264–275. doi: 10.1016/0012-1606(87)90448-9. [DOI] [PubMed] [Google Scholar]
- Tyson JJ, Keener JP. Singular perturbation theory of traveling waves in excitable media (a review) Physica D. 1988;32:327–361. [Google Scholar]
- van der Pol B, van der Mark J. The heartbeat considered as a relaxation oscillator, and an electrical model of the heart. Phil Mag Supp. 1928;6:763–775. [Google Scholar]
- Verchot-Lubicz J, Goldstein RE. Cytoplasmic streaming enables the distribution of molecules and vesicles in large plant cells. Protoplasma. 2010;240:99–107. doi: 10.1007/s00709-009-0088-x. [DOI] [PubMed] [Google Scholar]
- Weiner OD, Marganski WA, Wu LF, Altschuler SJ, Kirschner MW. An actin-based wave generator organizes cell motility. PLoS Biol. 2007;5:e221. doi: 10.1371/journal.pbio.0050221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Winfree AT. Spiral waves of chemical activity. Science. 1972;175:634–636. doi: 10.1126/science.175.4022.634. [DOI] [PubMed] [Google Scholar]
- Yang Q, Ferrell JE., Jr The Cdk1-APC/C cell cycle oscillator circuit functions as a time-delayed, ultrasensitive switch. Nat Cell Biol. 2013;15:519–525. doi: 10.1038/ncb2737. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yde P, Jensen MH, Trusina A. Analyzing inflammatory response as excitable media. Phys Rev. E. 2011a;84:051913. doi: 10.1103/PhysRevE.84.051913. [DOI] [PubMed] [Google Scholar]
- Yde P, Mengel B, Jensen MH, Krishna S, Trusina A. Modeling the NF-kappaB mediated inflammatory response predicts cytokine waves in tissue. BMC Syst Biol. 2011b;5:115. doi: 10.1186/1752-0509-5-115. [DOI] [PMC free article] [PubMed] [Google Scholar]


