The double-helix point spread function microscope is used to track single pairs of fluorescently labeled chromosomal loci in live yeast cells in three dimensions. Enhanced velocity cross-correlations are observed between pairs of GAL loci in diploid cells under repressive conditions, and ubiquitous subdiffusive exponents are found to be near 0.6–0.75.
Abstract
Single-particle tracking has been applied to study chromatin motion in live cells, revealing a wealth of dynamical behavior of the genomic material once believed to be relatively static throughout most of the cell cycle. Here we used the dual-color three-dimensional (3D) double-helix point spread function microscope to study the correlations of movement between two fluorescently labeled gene loci on either the same or different budding yeast chromosomes. We performed fast (10 Hz) 3D tracking of the two copies of the GAL locus in diploid cells in both activating and repressive conditions. As controls, we tracked pairs of loci along the same chromosome at various separations, as well as transcriptionally orthogonal genes on different chromosomes. We found that under repressive conditions, the GAL loci exhibited significantly higher velocity cross-correlations than they did under activating conditions. This relative increase has potentially important biological implications, as it might suggest coupling via shared silencing factors or association with decoupled machinery upon activation. We also found that on the time scale studied (∼0.1–30 s), the loci moved with significantly higher subdiffusive mean square displacement exponents than previously reported, which has implications for the application of polymer theory to chromatin motion in eukaryotes.
INTRODUCTION
In recent decades, the application of fluorescence microscopy to the imaging and tracking of chromatin loci has revealed a wealth of dynamical information in both eukaryotic and prokaryotic cells. Although the importance of chromatin positioning and movement during cell division was documented long ago, the formerly static picture of chromatin during interphase has undergone extensive revision. Studies have consistently shown that chromosomal loci undergo constant random motion during interphase within some finite volume of confinement (Marshall et al., 1997; Heun et al., 2001; Vazquez et al., 2001; Albert et al., 2012). At the same time, there is increasing evidence that the positioning of eukaryotic genes and the chromosomes they comprise within the three-dimensional (3D) volume of the nucleus is in fact nonrandom. Chromosomes in higher-order eukaryotes are segregated into distinct subnuclear sections called chromosome territories (Cremer et al., 2006). Analogous units seem to persist even in the relatively small nucleus of the model organism budding yeast (Saccharomyces cerevisiae; Berger et al., 2008). Chromosome conformation capture techniques have shown that gene loci that are distantly positioned in linear genetic space can often be clustered in real 3D space (Lieberman-Aiden et al., 2009; Duan et al., 2010). Intergene proximity may in some cases be tied to the fact that certain sets of genes exhibit common transcriptional control. For instance, genes that are silenced together may be positioned near shared silencing factors (Gasser et al., 2004). Conversely, genes that are activated together may cluster near common “transcription factories,” that is, foci of active RNA polymerases (Sutherland and Bickmore, 2009). However, these aspects are not necessarily present in every case, and assessment of the generality of these observations is warranted.
In certain cases, the positioning and motion of certain loci have been reported to change in response to transcriptional status. One well-studied example is the cluster of GAL genes in budding yeast (i.e., the GAL locus), which consists of three genes (GAL7, GAL10, and GAL1). These GAL genes are located on chromosome II and code for enzymes necessary for the metabolism of galactose. When the preferred carbon source dextrose is present, the GAL genes are repressed, and the locus is more often found near the center of the nucleus, away from the nuclear envelope (in ∼60–80% of cells; Casolari et al., 2004; Green et al., 2012). When dextrose is absent and galactose is available, the genes become activated and are more often found at the nuclear periphery associated with factors of the nuclear pore complex (in ∼60% of cells; Casolari et al., 2004; Green et al., 2012). The character of the motion of the GAL locus changes dramatically in conjunction with this repositioning as its 3D subdiffusive movements convert to constrained sliding along the inner membrane of the nuclear envelope, effectively reducing the dimensionality of the motion (Cabal et al., 2006). Although on the surface these findings may suggest a gene-gating hypothesis (Blobel, 1985) as the basis of this repositioning, recent studies suggest a more nuanced relationship. For example, the tethering of the GAL locus to the periphery was shown to diminish initial induction of the genes and is required for rapid repression after gene inactivation, effectively establishing a negative feedback mechanism (Green et al., 2012). Furthermore, the interaction of the GAL gene locus with the SUMO protease Ulp1 at the nuclear pore is important for the proper regulation of its transcriptional induction (Texari et al., 2013).
Because association with common transcriptional regulators has been implicated in distant genomic correlations and in the colocalization of genomic loci in discrete transcriptional factories (Sutherland and Bickmore, 2009), we sought to examine whether the two copies of the GAL locus in the nucleus of a diploid yeast cell showed correlated movements or colocalization in either activating or repressive conditions. To simultaneously track two gene loci in live yeast cells, we applied precise, two-color, wide-field 3D fluorescence localization microscopy using the double-helix point spread function (DH-PSF) microscope (Pavani et al., 2009; Thompson et al., 2010). Details of how the DH-PSF works are given in the references and in Materials and Methods. Briefly, the DH-PSF microscope enables 3D position estimation from a single image by converting the light emitted from a single point into two closely spaced lobes in the image. The lobes assume different angles between the line connecting their center points and the vertical as a function of z-position relative to the focal plane (Figure 1A). Thus, as a tracked locus moves in z, the two lobes in its image revolve around one another, effectively tracing out a double-helix shape, without the need for any scanning or image stack recording. From a single snapshot, it is possible to fit a double-Gaussian function (i.e., the sum of two two-dimensional [2D] Gaussians plus a constant offset) to the two lobes using least squares. The midpoint between the positions of the Gaussians gives the lateral (x, y) position, and comparison of the angle of revolution to a calibration curve gives the z-position, all to within subdiffraction precision. Previous studies of 3D chromatin tracking in yeast often used confocal scanning methods (Gartenberg et al., 2004; Bystricky et al., 2005; Cabal et al., 2006; Neumann et al., 2012), which are excellent for time-lapse tracking over longer periods of time but limit the attainable temporal resolution, spatial resolution, and throughput. As compared with confocal scanning methods, our wide-field/nonscanning dual-color DH-PSF approach allows for improved temporal resolution (10-Hz imaging rate) and throughput (∼100 cells) over a 2-μm z-range without scanning, enabling the examination of aspects of the 3D organization and dynamics of chromatin in living cells with subdiffraction precision.
FIGURE 1:

(A) Behavior of the DH-PSF as a function of axial defocus (z). (B) Fluorescence images from the green (top) and red (bottom) channels at 10-s intervals of one example track pair. Scale bar, 1 μm. (C) The 2D projection of trajectories from B overlaid on white light image of whole cell. Scale bar, 1 μm.
RESULTS AND DISCUSSION
To conduct simultaneous tracking of the two GAL loci in diploid yeast, we labeled one copy with the LacO/LacI-GFP system and the other with the TetO/TetR-mCherry system (see Figure 2 for the labeling schematics described later). We collectively refer to this as a dual-label, dual-chromosome (DLDC) scheme. As one negative control, we also conducted experiments in which we simultaneously tracked only one copy of the GAL locus along with one copy of the gene PES4 located on chromosome VI, since both the nuclear positioning and transcriptional regulation of PES4 are unaffected by growth in galactose (Taddei et al., 2006). Although PES4 and the GAL locus can be considered transcriptionally independent, they are both located near the centromere of their respective chromosomes (∼50 and ∼40 kbp, respectively). Different pericentromeric genes have been shown to exhibit additional correlations during metaphase, related to their common association with the spindle pole body (Stephens et al., 2013). Although we attempted to exclude mitotic cells and include only cells in G1 interphase in our study, we still sought to exclude centromeric effects that could potentially arise due to the default Rabl-like conformation of budding yeast chromosomes. Therefore, as a second negative control, we examined correlations in a strain in which one copy of the GAL locus was labeled and one copy of the nonpericentromeric RPL9A gene on chromosome VII was labeled and studied this strain in both dextrose and galactose conditions.
FIGURE 2:
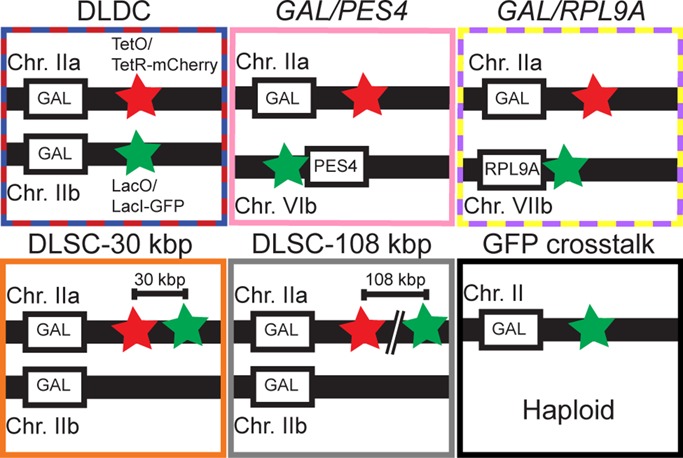
Labeling scheme for each condition imaged. Green star corresponds to LacO/LacI-GFP label, and red star corresponds to TetO/TetR-mCherry label. TetO repeats were integrated at the same position relative to the GAL locus (<3 kbp from GAL1) wherever present. LacO repeats were integrated in the same position (i.e., <3 kbp from GAL1) for the DLDC and GFP cross-talk experiments. LacO repeats are immediately adjacent to the 5′ end of PES4 for the GAL/PES4 experiment. The DLDC and GAL/RPL9A cases were imaged in galactose and dextrose, whereas all other (control) cases were imaged in dextrose. Distances between loci and labels in schematic are not necessarily to scale.
As a positive control, we simultaneously labeled two loci at different locations along the same copy of chromosome II, with TetO repeats integrated at the same region near GAL and LacO repeats integrated at some distance away. We imaged two such dual-label, single-chromosome (DLSC) strains with minimal label separations of ∼30 and ∼108 kbp, respectively, between the center of the TetO repeats and LacO repeats. Finally, as an ultimate positive control on the magnitude of estimated correlations we were capable of measuring in the presence of limiting factors such as localization noise and registration error, we imaged the single copy of the GAL locus in haploid cells labeled with LacO/LacI–green fluorescent protein (GFP) in both the green and red color channels. This was made possible by the observation that in the absence of red fluorescent protein to swamp the signal and upon removal of a 600-nm long-pass filter, the red tail of the GFP emission spectrum was significant enough to track the GFP-labeled locus in the red channel, given sufficiently increased pumping intensity. Under the other experimental conditions, the presence of GFP cross-talk could potentially lead to an artifactual increase in correlations if not treated properly. Thus care was taken to filter out obvious artifacts and to carefully bound the effects in more subtle cases (see Materials and Methods, Supplemental Figure S2, and accompanying Supplemental Material). All strains described here were grown and imaged in dextrose, except the explicitly noted DLDC-galactose and GAL/RPL9A-galactose cases.
Precision of the two-color DH-PSF microscope
Figure 1B depicts images from each fluorescence channel of a single example cell at different times during the trajectories. In each image, we see the two lobes of the DH-PSF on top of a slightly larger circular background, likely due to unbound fluorescent proteins dispersed throughout the nucleus. Once we fitted the two (x, y, z) trajectories of a pair, we registered the tracks in three dimensions by transforming the red channel data into the coordinates of the green channel using a recently published method (Gahlmann et al., 2013). Transformation of the red coordinates into the green coordinates is necessary to be able to enumerate accurately the distances between loci appearing in each channel and to compensate for the relative geometric transformations incurred between the two optical paths so that the x, y, and z components of velocities properly correspond with one another. The 3D target registration errors of the transformation were in the range of 10–20 nm, although an additional bias possibly due to refractive index mismatch also had to be treated (see Supplemental Figure S1 and accompanying text in the Supplemental Material). Figure 1C shows a 2D projection of the registered tracks from Figure 1B overlaid on the white light image of the cell.
After fitting and filtering as described in Materials and Methods, we obtained the following numbers of analyzed track pairs in each condition: NDLDC-dextrose = 110, NDLDC-galactose = 104, NGAL/PES4 = 40, NGAL/RPL9A-dextrose = 35, NGAL/RPL9A-galactose = 50, NDLSC-30 kbp = 35, NDLSC-108 kbp = 47, and Ncross-talk = 122. DLDC-dextrose data were collected in three separate sets (N1 = 53, N2 = 37, N3 = 20), and the DLDC-galactose data were recorded in two sets (N1 = 31, N2 = 73). The mean track pair length across all conditions was 302 frames (30.2 s), with SD = 145 frames (14.5 s). The track lengths were mostly limited by the bleaching of mCherry, which generally gave lower signal-to-background ratios than did the GFP labels. This fact is reflected in the estimated approximate values of localization precision we obtained: [σx, σy, σz] = [13, 12, 23 nm] for green and [24, 28, 44 nm] for red. These estimated averages were obtained by calculating the time-averaged mean square displacement (TAMSD) for each trajectory and finding the TAMSD-intercept b and slope m obtained by tracing the line connecting the first two points of the TAMSD. The following expression gives the localization precision in terms of b and m (Savin and Doyle, 2005):
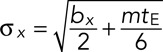 (1) (1)
|
where tE is the exposure time of one frame (0.1 s in our case) and analogous expressions exist for y and z. We stress that these values are only approximate, since the treatment in Savin and Doyle (2005) only holds for pure Brownian motion, which was not found to be the case here (see later discussion). Still, our simulations indicate that this method should only overestimate the localization precision by a few nanometers at most (see Supplemental Material). These reported values are the averages of the distributions of errors calculated from each individual TAMSD. Each condition studied had slightly different photophysics, and so we also estimated localization precision for each case separately (Supplemental Table S2).
Interlocus distances
Cis-acting regulatory elements were recently reported to induce clustering of distinct gene loci in yeast (Brickner et al., 2012). It was therefore of interest to investigate whether transcriptional activation of the GAL loci may induce a similar change in the 3D distance between the two loci in diploid yeast. To test this hypothesis, we computed the time average of the 3D interlocus distance over the first 10 frames (when signal is highest) of each track pair. These values were then binned to produce the distributions shown in Figure 3. Figure 3A shows the probability density functions (PDFs), and Figure 3B shows the associated cumulative distribution functions (CDFs) under each condition. The narrowly peaked PDF of the cross-talk experiment (black) gives the lower limit for our estimates of interlocus distance set by localization and registration errors. The mean of this distribution is <Rcross-talk> = 48 ± 2 nm (mean ± SEM determined from 100 bootstrapped samples), which is on the order of what is expected from the approximate localization errors given in the previous section. The two DLSC cases both peak to the right of this limit, in the expected order (mean and SEM rounded to nearest 10 nm): <RDLSC-30 kbp> = 300 ± 20 nm and <RDLSC-108 kbp> = 430 ± 40 nm. A previous study using fluorescence in situ hybridization (FISH) found results similar to our DLSC-108 kbp case for yeast loci separated by a similar genomic distance along chromosome VI (436 nm for 103-kbp separation; Bystricky et al., 2004). However, a pair of loci separated by 30 kbp in Bystricky et al. (2004) was reported to have an average Euclidean separation of ∼160–190 nm, somewhat smaller than the DLSC-30 kbp case we found here. Possible reasons for this discrepancy are several. First, the FISH portion of their study reported distances from a single 2D confocal section. This procedure could cause deflation of the true Euclidean value, since the z-extent of a confocal section (i.e., depth of focus, ∼500–700 nm) is nonzero due to diffraction. Second, the differences in labels may contribute, since the TetO and LacO inserts themselves have a nonnegligible length and could conceivably affect the compaction of the chromatin differently than the FISH probes used in Bystricky et al. (2004). Note that this finite label size and integration method also makes our estimates of minimal genomic distance approximate, which should discourage overinterpretation of this aspect of our results beyond a validation of the two-color DH-PSF microscope in exploring the flexibility of the chromatin fiber. We also note that residual registration and localization error will falsely inflate the computed distances and that this error will have a greater relative effect on more closely separated loci. Finally, the difference may be explained in part by heterogeneity of chromatin compaction. The relevant portion of Bystricky et al. (2004) only dealt with chromosomes V, VI, and XIV, whereas we looked at chromosome II. In any case, it is interesting that the distribution of RDLSC-108 kbp is noticeably broader than that of RDLSC-30 kbp. As the distance between loci on the same chromatin fiber becomes significantly larger than the persistence length of the polymer (170–220 nm according to Bystricky et al., 2004), the floppier section can access more conformations covering larger separations.
FIGURE 3:
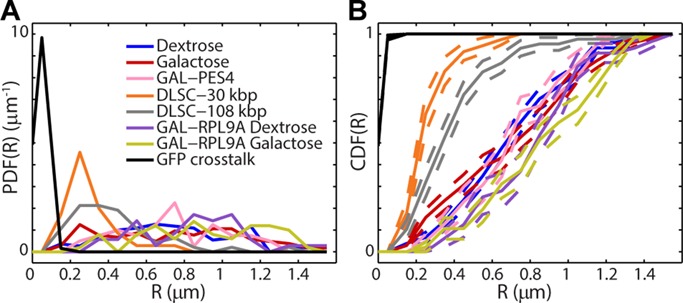
Distributions of interlocus distances for each condition. (A) PDFs with 100-nm binning. (B) CDFs with 100-nm binning. Dashed lines give ± SEM for each bin as determined from 100 bootstrapped samples.
In contrast to the DLSC strains, the interlocus distributions of the DLDC and GAL/PES4 cases are significantly broader over the range ∼200 nm to ∼1.5 μm (Figure 3A), the upper bound of which corresponds roughly to the average radius of the diploid nucleus (Marshall et al., 1997). The large widths of these PDFs are reflected in the linearity of the CDFs (Figure 3B). There does not appear to be a very clear difference among the three, and the average values of each distribution are remarkably similar: <RDLDC-dextrose> = 750 ± 30 nm, <RDLDC-galactose> = 750 ± 40 nm, and <RGAL/PES4> = 750 ± 40 nm. These results suggest that on average there is not a strong preference for the colocalization of both copies of the GAL locus, regardless of transcriptional status. However, the mean value of 750 nm is about half the mean separation one would expect from two uncorrelated points distributed uniformly throughout a sphere of radius 1.5 μm, indicating a propensity for the two copies of each of the GAL locus and PES4 to be within the same nuclear subvolume. This observation is not surprising, since chromatin is known not to be distributed uniformly throughout the nucleus (Berger et al., 2008). In fact, as previously mentioned, both the GAL locus and PES4 are fairly close to the centromeres of their chromosomes, and budding yeast centromeres are anchored to the spindle pole body throughout interphase. By contrast, the distributions corresponding to the GAL/RPL9A-dextrose and GAL/RPL9A-galactose cases give correspondingly larger interlocus distances between the GAL locus and a nonpericentromeric locus. Mean distances for these cases are <RGAL/RPL9A-dextrose> = 870 ± 50 nm and <RGAL/RPL9A-galactose> = 910 ± 50 nm.
Velocity cross-correlations
Although transcriptional activation of the GAL loci in galactose does not seem to augment the likelihood of colocalization on average, we examined whether transcriptional activation leads to an increase in correlated movements, perhaps through transient association with shared transcriptional machinery (Fraser and Bickmore, 2007). To address this, we first developed a robust methodology to analyze the correlated movements of the distinctly labeled loci in our various strains. When tracking with discrete time steps, one does not have access to the true instantaneous velocities of the particles but instead the average velocities over a given time interval. The smallest such time interval possible, δmin, is given by the inverse of the frame rate (δmin = tE = 0.1 s in our case). However, it is useful to define average velocity more generally, since more interesting information might emerge by looking at displacements over integer multiples of δmin. Thus we define velocity over time interval δ parametrically as follows:
|
|
where 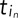 is the time of the inth frame of the nth track pair, and corresponding equations hold for the y and z dimensions. With this definition of velocity, we can define the components of the average velocity cross-correlation at time lag τ between the green (g) and red (r) channels as a time-dependent Pearson correlation coefficient as follows:
is the time of the inth frame of the nth track pair, and corresponding equations hold for the y and z dimensions. With this definition of velocity, we can define the components of the average velocity cross-correlation at time lag τ between the green (g) and red (r) channels as a time-dependent Pearson correlation coefficient as follows:
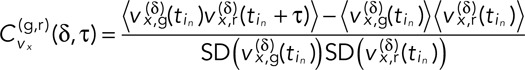 (3) (3)
|
where corresponding equations hold for y and z. We equate the total velocity cross-correlation, 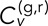 , to the average value of those of the three individual dimensions. Note that we have a choice in calculating the averages denoted by the angle brackets and implicit in the SDs of Eq. 2. If we simply average over in separately for each individual track pair n, then we obtain the full distribution of the ensemble of time-averaged velocity cross-correlations (TAVCCs). If we instead sum over all in and all n before dividing by the total number of terms, we get a time-ensemble-averaged velocity cross-correlation (T-EAVCC), which has superior statistics due to increased averaging but does not allow access to the full distribution. We address both the TAVCC and the T-EAVCC here. Note that given sufficient averaging, the subtracted term in the numerator of Eq. 3 should evaluate to 0. However, we chose to leave it in our calculation since for short tracks, a large random step in one channel could falsely inflate the correlation otherwise. Note also that the denominator of Eq. 3 is proportional to the geometric mean of the mean square displacements (MSDs) in the two channels. We include this factor in order to scale away any differences in the calculated cross-correlation between different conditions that might arise simply because the loci are more mobile in one condition than in another. For instance, since the MSD of the GAL locus in dextrose is larger than that in galactose (Cabal et al., 2006), not including the denominator in Eq. 3 would otherwise automatically inflate
, to the average value of those of the three individual dimensions. Note that we have a choice in calculating the averages denoted by the angle brackets and implicit in the SDs of Eq. 2. If we simply average over in separately for each individual track pair n, then we obtain the full distribution of the ensemble of time-averaged velocity cross-correlations (TAVCCs). If we instead sum over all in and all n before dividing by the total number of terms, we get a time-ensemble-averaged velocity cross-correlation (T-EAVCC), which has superior statistics due to increased averaging but does not allow access to the full distribution. We address both the TAVCC and the T-EAVCC here. Note that given sufficient averaging, the subtracted term in the numerator of Eq. 3 should evaluate to 0. However, we chose to leave it in our calculation since for short tracks, a large random step in one channel could falsely inflate the correlation otherwise. Note also that the denominator of Eq. 3 is proportional to the geometric mean of the mean square displacements (MSDs) in the two channels. We include this factor in order to scale away any differences in the calculated cross-correlation between different conditions that might arise simply because the loci are more mobile in one condition than in another. For instance, since the MSD of the GAL locus in dextrose is larger than that in galactose (Cabal et al., 2006), not including the denominator in Eq. 3 would otherwise automatically inflate 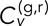 in dextrose relative to that in galactose. Whether or not to include this effect in our calculation of
in dextrose relative to that in galactose. Whether or not to include this effect in our calculation of 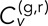 is somewhat subjective, and so we explored a different metric for velocity correlation in the Supplemental Material (Supplemental Figures S3 and S4 and accompanying text). Note that
is somewhat subjective, and so we explored a different metric for velocity correlation in the Supplemental Material (Supplemental Figures S3 and S4 and accompanying text). Note that 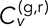 as defined in Eq. 3 lies in the interval [−1, 1]. However, the denominator of Eq. 3 contains extra terms due to finite localization error (see Mean-squared displacement and velocity autocorrelation section), and so the maximum
as defined in Eq. 3 lies in the interval [−1, 1]. However, the denominator of Eq. 3 contains extra terms due to finite localization error (see Mean-squared displacement and velocity autocorrelation section), and so the maximum 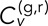 calculated will actually be <1.
calculated will actually be <1.
We first consider the T-EAVCC version and its time dependence. Figure 4, A and B, shows the time-ensemble-averaged version of 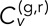 as a function of time lag τ for fixed values of δ = 1 and 5 s, respectively, for all conditions studied. Analogous plots for all δ produced by integral increments used between 1 and 10 s are shown in Supplemental Figure S5. Note that each plot consists of a positive peak at τ = 0 and decay to near zero on either side. Note that two objects undergoing uncorrelated random motion would have zero correlation at all τ. The positive peak at τ = 0 indicates that on average the velocity step occurring in the green channel at a given time is positively correlated with the velocity step occurring in the red channel at the same time. In other words, a kick of one locus is accompanied by a similar kick of the other locus around the same time, suggesting coupling between the two objects. Such behavior is not necessarily expected for two separate chromosomes; it is therefore somewhat surprising that we see a weak but significant correlation at τ = 0 even for our negative controls GAL/PES4 and GAL/RPL9A. The discernible negative-going peaks at τ = ±δ in the cross-talk data are most likely a consequence of the elasticity of the medium (see Mean-squared displacement and velocity autocorrelation section), which is a well-documented effect for bacterial chromosomal loci (Weber et al., 2010a). The deviations from zero at large |τ| for the other conditions in Figure 4B are due to diminished averaging at these points. Note that the |τ| at which the correlation curves decay to 0 is dependent on δ due to the inclusion of overlapping time intervals in our average.
as a function of time lag τ for fixed values of δ = 1 and 5 s, respectively, for all conditions studied. Analogous plots for all δ produced by integral increments used between 1 and 10 s are shown in Supplemental Figure S5. Note that each plot consists of a positive peak at τ = 0 and decay to near zero on either side. Note that two objects undergoing uncorrelated random motion would have zero correlation at all τ. The positive peak at τ = 0 indicates that on average the velocity step occurring in the green channel at a given time is positively correlated with the velocity step occurring in the red channel at the same time. In other words, a kick of one locus is accompanied by a similar kick of the other locus around the same time, suggesting coupling between the two objects. Such behavior is not necessarily expected for two separate chromosomes; it is therefore somewhat surprising that we see a weak but significant correlation at τ = 0 even for our negative controls GAL/PES4 and GAL/RPL9A. The discernible negative-going peaks at τ = ±δ in the cross-talk data are most likely a consequence of the elasticity of the medium (see Mean-squared displacement and velocity autocorrelation section), which is a well-documented effect for bacterial chromosomal loci (Weber et al., 2010a). The deviations from zero at large |τ| for the other conditions in Figure 4B are due to diminished averaging at these points. Note that the |τ| at which the correlation curves decay to 0 is dependent on δ due to the inclusion of overlapping time intervals in our average.
FIGURE 4:
Statistics of 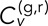 as calculated from both time-ensemble averaging (left of dividing line) and time averaging (right of dividing line). (A, B)
as calculated from both time-ensemble averaging (left of dividing line) and time averaging (right of dividing line). (A, B) 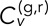 as a function of τ for fixed δ = 1 s (A) and δ = 5 s (B). (C)
as a function of τ for fixed δ = 1 s (A) and δ = 5 s (B). (C) 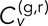 as a function of δ for fixed τ = 0, calculated at 1-s intervals. Error bars indicate ± SEM calculated from 10 bootstrapped samples of N track pairs. (D, E) CDFs of
as a function of δ for fixed τ = 0, calculated at 1-s intervals. Error bars indicate ± SEM calculated from 10 bootstrapped samples of N track pairs. (D, E) CDFs of 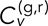 for each condition for δ = 1 s (D) and δ = 5 s (E). Dashed lines give ± SEM for each bin as determined from 100 bootstrapped samples. (F, G) Scatter plots depicting relationship between early-time-averaged interlocus distance and
for each condition for δ = 1 s (D) and δ = 5 s (E). Dashed lines give ± SEM for each bin as determined from 100 bootstrapped samples. (F, G) Scatter plots depicting relationship between early-time-averaged interlocus distance and 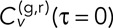 .
.
Thus the most interesting point to focus on is at τ = 0, and so we extract and display these points for various δ in Figure 4C. Note that the correlations become larger for increasing δ, in part because the magnitude of the correlated movements becomes sufficiently larger than the localization error (Supplemental Figure S8 and accompanying text). The first question to address is why each condition displays a positive peak at τ = 0, even in the cases of GAL/PES4 and GAL/RPL9A, despite the lack of evidence for high average colocalization. One could imagine a coupling mechanism that might allow for even noncolocalized loci to exhibit correlations due to entanglement of the chromosome polymers at points of contact located some distance away. In addition, force from the cytoskeleton (Koszul et al., 2008) acting on local chromatin regions could contribute to our observations. Consistent with these findings, positive correlations of chromatin movement have been shown to persist in mammalian nuclei across 4–5 μm over the course of several seconds (Zidovska et al., 2013) and between opposite telomeres of certain budding yeast chromosomes (Bystricky et al., 2005).
Although positive correlations seem explicable by the foregoing logic, we must also consider the possible effects of nuclear motion. During the time scale we studied (up to ∼30 s), a previous report concluded that nuclear rotation was insignificant based on fluorescence recovery after photobleaching (FRAP) data (Bystricky et al., 2005). However, many yeast chromatin- tracking studies account for nuclear translations by staining the whole nucleus or nuclear envelope and subtracting its movements (Marshall et al., 1997; Sage, 2005; Cabal et al., 2006). We did not do so here since our two color channels were occupied by signal from the loci themselves. Although we feel that nuclear translation should be less significant on our relatively short time scale than on the time scales typically used in time-lapse studies (>10 min), we cannot rule out its effects completely. Thus we emphasize that the main conclusions drawn from this study should rely on the differences between correlations across the conditions. In other words, even if nuclear translation produced some baseline level of positive correlations in all experiments, it is unlikely to account for the fact that, for example, we see significantly higher correlations in the DLDC-dextrose case than the GAL/PES4 case, despite their being in the same carbon source and having similar pericentromeric positioning. Furthermore, we think it is unlikely that nuclear motion can account for all of the positive correlations observed in even the GAL/PES4 case, for example, since we observe individual track pairs whose TAVCC curves peak away from τ = 0. This type of behavior seems to indicate a finite response time of the correlated movement that is not explicable by the global translation of the nucleus alone. We give an example of such behavior and explain the implications in more depth in the next section.
Another striking feature of the plots in Figure 4, A and B, is the large separation between the upper limit set by the cross-talk data and the DLSC-30 kbp case. This difference underscores the flexibility of the chromatin polymer. Biological implications of this observation include the fact that genes positioned in adjacent linear space may yet concurrently access distinct subnuclear domains, consistent with gene looping (de Laat and Grosveld, 2003; Fraser and Bickmore, 2007) and HiC data (Lieberman-Aiden et al., 2009; Duan et al., 2010). The same flexibility may also enhance or augment boundary activity by permitting genes to elude the spreading of proximal transcriptional activation or silencing (Ishii et al., 2002; Meneghini et al., 2003). The ordering of 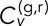 values makes sense in that between the DLSC cases, closer genomic and spatial separation means higher correlations, and both the DLSC cases display higher correlations than the cases in which the loci are on separate chromosomes.
values makes sense in that between the DLSC cases, closer genomic and spatial separation means higher correlations, and both the DLSC cases display higher correlations than the cases in which the loci are on separate chromosomes.
Parsing the DLDC, GAL/PES4, and GAL/RPL9A data more closely reveals interesting results. We see that the average DLDC-galactose correlations are essentially indistinguishable from our negative controls in dextrose, whereas the DLDC-dextrose correlations become more like those of the DLSC-108 kbp case at larger δ, thus demonstrating a significant difference between the DLDC-dextrose and DLDC-galactose cases. Pulling numbers from Figure 4, B and C, we see that indeed at δ = 5 s and τ = 0, 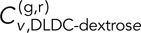 = 0.27 ± 0.02 is comparable to
= 0.27 ± 0.02 is comparable to 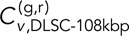 = 0.33 ± 0.04, and
= 0.33 ± 0.04, and 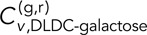 = 0.16 ± 0.02 is in turn more similar to
= 0.16 ± 0.02 is in turn more similar to 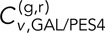 = 0.16 ± 0.03 and
= 0.16 ± 0.03 and  = 0.15 ± 0.02 (mean ± SEM calculated from 10 bootstrapped samples of N track pairs). To get an indication of the repeatability of these values, we can inspect the T-EAVCC values of the three sets of DLDC-dextrose and two sets of DLDC-galactose separately. For δ = 2 s and τ = 0, we have
= 0.15 ± 0.02 (mean ± SEM calculated from 10 bootstrapped samples of N track pairs). To get an indication of the repeatability of these values, we can inspect the T-EAVCC values of the three sets of DLDC-dextrose and two sets of DLDC-galactose separately. For δ = 2 s and τ = 0, we have 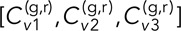 = [0.19 ± 0.04, 0.17 ± 0.02, 0.18 ± 0.02] for the DLDC-dextrose case and
= [0.19 ± 0.04, 0.17 ± 0.02, 0.18 ± 0.02] for the DLDC-dextrose case and 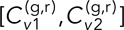 = [0.11 ± 0.02, 0.11 ± 0.02] for DLDC-galactose, indicating excellent repeatability despite only a modest disparity between the conditions for this smaller δ. For δ = 5 s and τ = 0, we have
= [0.11 ± 0.02, 0.11 ± 0.02] for DLDC-galactose, indicating excellent repeatability despite only a modest disparity between the conditions for this smaller δ. For δ = 5 s and τ = 0, we have 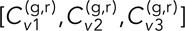 = [0.27 ± 0.03, 0.28 ± 0.03, 0.23 ± 0.07] for the DLDC-dextrose case and
= [0.27 ± 0.03, 0.28 ± 0.03, 0.23 ± 0.07] for the DLDC-dextrose case and 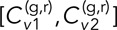 = [0.13 ± 0.04, 0.17 ± 0.02] for DLDC-galactose, indicating reasonable repeatability in each. Note that for δ = 5 s, the DLDC-dextrose set with the lowest
= [0.13 ± 0.04, 0.17 ± 0.02] for DLDC-galactose, indicating reasonable repeatability in each. Note that for δ = 5 s, the DLDC-dextrose set with the lowest 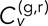 is also the set with the lowest N value (20) overall and thus the highest error in the mean. Figure 4C shows that the gap between DLDC-dextrose and DLDC-galactose widens as δ increases. However, the agreement among sets within each case becomes less convincing at larger δ due to insufficient averaging (Supplemental Figures S6 and S7).
is also the set with the lowest N value (20) overall and thus the highest error in the mean. Figure 4C shows that the gap between DLDC-dextrose and DLDC-galactose widens as δ increases. However, the agreement among sets within each case becomes less convincing at larger δ due to insufficient averaging (Supplemental Figures S6 and S7).
Consequently, although we originally hypothesized that transcriptional activation would confer heightened correlative motion, our data instead suggest, at least for the GAL locus, that repression (in dextrose) moderately yet significantly increases such movements relative to activating conditions (in galactose). This increase in correlative motion could be induced through shared factors responsible for transcriptional repression of the GAL loci, including Gal80 and Mig1 (Johnston et al., 1994). The fact that the increase in average correlations is not commensurate with an increase in average interlocus distance, however, indicates that the mechanism is likely more complex than simple association with the same concentrated focus of these factors. If the correlative motion in dextrose represents the actual baseline of such motion between the two GAL loci, this would indicate that activation in galactose impedes correlative movement. This would be supported, for instance, if the individual GAL loci associate with distinct nuclear pores upon transcriptional activation (Casolari et al., 2004; Cabal et al., 2006; Green et al., 2012). Association with a nuclear pore complex might be accompanied by disentanglement of chromosome II near the GAL locus from neighboring chromosomes, which could enable more independent motion.
The notion that the heightened correlations seen in DLDC-dextrose may be a result of a more generic combination of pericentromeric gene positioning (Stephens et al., 2013) and global motions in this carbon source is challenged by the fact that GAL/PES4 shows significantly lower correlations also in dextrose despite both of these loci also being located near centromeres. One might suspect that the residual positive correlation seen for GAL/PES4 may be in part due to centromeric proximity, but the fact that GAL/RPL9A-dextrose displays the same correlations for δ = 5 s suggests that this residue has an alternate main cause. Instead, these residual correlations could be due to nuclear motion, as already explained, and so we here reiterate that the relative values of the correlations are the important metrics. We do note, however, that the correlations for GAL/RPL9A-galactose are somewhat lower still (0.10 ± 0.02 for δ = 5 s), perhaps lowering the bound for the contribution of nuclear motion, although the carbon source could have an effect on the motion of the nucleus itself. Any such possible global effect of carbon source still does not discount our conclusion that GAL/GAL correlations are unique when taken with the results of our negative controls in dextrose. In any case, it is clear that more experiments are necessary to elucidate the true drivers and impediments of correlative motion.
Next, we consider the time-averaged version of 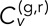 (TAVCC), which allows us to access the ensemble distributions of correlations for each condition. The resulting CDFs for δ = 1 s and 5 s are given in Figure 4, D and E, respectively. Again we see a gap between the cross-talk data and the DLSC data and between the DLSC data and the separate chromosome data. The difference between DLDC-dextrose and DLDC-galactose is less readily apparent than in the T-EAVCC. This is due to the fact that by only time averaging each track pair and then binning the results, we are placing equal weight on shorter, noisier tracks as we are on longer, less noisy tracks. Noisy tracks will tend to have lower
(TAVCC), which allows us to access the ensemble distributions of correlations for each condition. The resulting CDFs for δ = 1 s and 5 s are given in Figure 4, D and E, respectively. Again we see a gap between the cross-talk data and the DLSC data and between the DLSC data and the separate chromosome data. The difference between DLDC-dextrose and DLDC-galactose is less readily apparent than in the T-EAVCC. This is due to the fact that by only time averaging each track pair and then binning the results, we are placing equal weight on shorter, noisier tracks as we are on longer, less noisy tracks. Noisy tracks will tend to have lower 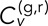 since the denominator in Eq. 3 is larger. Thus the center of these distributions is deflated, which condenses the gap between the conditions. Shorter tracks will broaden these distributions, which also diminishes the gap between conditions.
since the denominator in Eq. 3 is larger. Thus the center of these distributions is deflated, which condenses the gap between the conditions. Shorter tracks will broaden these distributions, which also diminishes the gap between conditions.
Calculating the TAVCC for each track pair also allows us to examine the relationship between 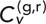 and interlocus distance, R. This is illustrated in the scatter plots in Figure 4, F and G, for δ = 1 s and 5 s, respectively. The relationship appears to be nontrivial, as interlocus distance seems to decrease with increasing TAVCC. We can quantify this apparent correlation by pooling the cases together (leaving out the cross-talk data that are bunched at low R) and calculating the Pearson correlation coefficient, ρ, between the variables
and interlocus distance, R. This is illustrated in the scatter plots in Figure 4, F and G, for δ = 1 s and 5 s, respectively. The relationship appears to be nontrivial, as interlocus distance seems to decrease with increasing TAVCC. We can quantify this apparent correlation by pooling the cases together (leaving out the cross-talk data that are bunched at low R) and calculating the Pearson correlation coefficient, ρ, between the variables 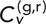 and R. Note that one would not expect a correlation of −1 even in the absence of statistical noise since the correlations should decay to 0 at large R, not continue along a straight line into negative values. For δ = 1 s, we get ρ = −0.58 ± 0.03 (mean ± SEM determined from 100 bootstrapped samples); for δ = 5 s, we get ρ = −0.44 ± 0.04. The presence of a negative correlation makes sense since we would expect that chromosome segments containing loci that are closer together are more likely to become entangled with one another and pull each other around. This further speaks to the fact that our main results are likely not artifacts of nuclear translation since a translation of the whole nucleus should translate all points within it by the same amount, at least by the same assumptions that allow one to subtract the motion of the nuclear center of mass as in other studies.
and R. Note that one would not expect a correlation of −1 even in the absence of statistical noise since the correlations should decay to 0 at large R, not continue along a straight line into negative values. For δ = 1 s, we get ρ = −0.58 ± 0.03 (mean ± SEM determined from 100 bootstrapped samples); for δ = 5 s, we get ρ = −0.44 ± 0.04. The presence of a negative correlation makes sense since we would expect that chromosome segments containing loci that are closer together are more likely to become entangled with one another and pull each other around. This further speaks to the fact that our main results are likely not artifacts of nuclear translation since a translation of the whole nucleus should translate all points within it by the same amount, at least by the same assumptions that allow one to subtract the motion of the nuclear center of mass as in other studies.
Interesting single-track-pair examples
During the course of our analysis, we observed individual instances of fascinating behavior between distinct chromosomal loci. Of importance, our single-particle tracking approach allows us to highlight prominent track pairs that exhibit either high or low 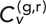 . Supplemental Movies S1–S4 show four such example track pairs that exhibit the range of correlations. Data from one such highly correlated DLDC-dextrose example are shown in Figure 5, A–D. Figure 5, A–C, shows the x-, y-, and z-projections of the velocity trajectories in the green and red channels as calculated for δ = 5 s. The x- and z-projections of both loci appear to exhibit notable pseudo-oscillatory behavior (Pliss et al., 2013). Of interest, however, there seems to be a phase lag between the pseudo-oscillations of the loci, as in this particular case the red-tagged locus leads the green-tagged locus. This fact is further demonstrated by calculating the TAVCC, which is plotted in Figure 5D. Here we see a large peak (>0.5) centered near τ = 2 s, indicating ∼2-s response time between the leading red locus and the lagging green locus. Of course, there is no biological reason why the red should always lead the green, and so the ensemble contains track pairs that show the reverse relation just as often, giving rise to the symmetric T-EAVCC shown in Figure 4, A and B. An example from the DLDC case that shows a significant positive peak for τ < 0 is given in Supplemental Figure S14.
. Supplemental Movies S1–S4 show four such example track pairs that exhibit the range of correlations. Data from one such highly correlated DLDC-dextrose example are shown in Figure 5, A–D. Figure 5, A–C, shows the x-, y-, and z-projections of the velocity trajectories in the green and red channels as calculated for δ = 5 s. The x- and z-projections of both loci appear to exhibit notable pseudo-oscillatory behavior (Pliss et al., 2013). Of interest, however, there seems to be a phase lag between the pseudo-oscillations of the loci, as in this particular case the red-tagged locus leads the green-tagged locus. This fact is further demonstrated by calculating the TAVCC, which is plotted in Figure 5D. Here we see a large peak (>0.5) centered near τ = 2 s, indicating ∼2-s response time between the leading red locus and the lagging green locus. Of course, there is no biological reason why the red should always lead the green, and so the ensemble contains track pairs that show the reverse relation just as often, giving rise to the symmetric T-EAVCC shown in Figure 4, A and B. An example from the DLDC case that shows a significant positive peak for τ < 0 is given in Supplemental Figure S14.
FIGURE 5:

Data from two example track pairs. (A–C) Velocity trajectories of a highly correlated example from the DLDC-dextrose case in each dimension, for δ = 5 s. Green lines correspond to the track from the green fluorescence channel, and red lines to the track from the red fluorescence channel. (D) The time-average velocity cross-correlation of the same track pair as in A–C. (E–G) Same as in A–C but for a different track pair from the DLDC-galactose case, which exhibits low correlations. (H) Same as in D but for the track pair addressed in E–G. (I) The 3D position trajectories of loci from E–H, color coded in time.
Figure 5, E–I, depicts an example track pair from the DLDC-galactose condition with particularly low correlations. No obvious qualitative relation between the velocity trajectories is apparent in Figure 5, E–G, in contrast to the previous example. This is quantified by the relatively flat TAVCC curve in Figure 5H. Figure 5I shows the 3D position trajectories traced by this locus pair color coded with time. The plot is rotated to a particularly suggestive view, from which the two loci appear as though they follow the curvature of the nuclear envelope, as reported previously when the GAL locus becomes associated with factors of the NPC (Cabal et al., 2006). The full 3D reconstruction is shown in Supplemental Figure S15, which can be rotated interactively. Strikingly, the two loci appear to be associated at distinct regions of the envelope. We also saw examples of locus pairs that qualitatively seemed to associate at overlapping regions of the envelope (Supplemental Figures S16 and S17), with TAVCC values >0.2. However, the identification of peripheral association by track curvature is admittedly subjective, and more careful quantitation must be done by labeling the periphery in a third color, for example, before any strong conclusions can be made on this observation.
Mean-squared displacement and velocity autocorrelation
Numerous chromatin-tracking studies in yeast and other organisms have examined the MSDs of tagged loci to identify characteristic motion. The MSD is defined by
|
|
where 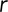 is the 3D position, and again we have a choice in how we compute the average denoted by the angle brackets; we chose to pool displacements from all tracks and compute a total time-ensemble average akin to the T-EAVCC described earlier in order to obtain sufficient averaging. Unsurprisingly, previous studies found these MSDs to increase initially before plateauing at longer times due to confinement of the loci within subregions of the nucleus (Marshall et al., 1997; Heun et al., 2001; Drubin et al., 2006; Neumann et al., 2012). At times before this confinement becomes apparent, loci appear to move subdiffusively, that is, their MSDs are proportional to δα for some
is the 3D position, and again we have a choice in how we compute the average denoted by the angle brackets; we chose to pool displacements from all tracks and compute a total time-ensemble average akin to the T-EAVCC described earlier in order to obtain sufficient averaging. Unsurprisingly, previous studies found these MSDs to increase initially before plateauing at longer times due to confinement of the loci within subregions of the nucleus (Marshall et al., 1997; Heun et al., 2001; Drubin et al., 2006; Neumann et al., 2012). At times before this confinement becomes apparent, loci appear to move subdiffusively, that is, their MSDs are proportional to δα for some 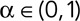 . Bacterial chromosomal loci tend to exhibit α ∼ 0.4 rather ubiquitously (Weber et al., 2010a; Javer et al., 2013). Previous studies in yeast determined α values around 0.5 for various loci (Hajjoul et al., 2013), and one early tracking study of the GAL locus reported α within the range 0.4–0.5 (Cabal et al., 2006). Thus we were surprised to find values of α = 0.75 for dextrose and α = 0.64 in galactose from analysis of the MSD (Figure 6, A and B) of the GAL locus in our study, indicating a higher degree of diffusivity than previously believed, at least on this time scale. Data shown here are taken only from the green channel since the signal-to-noise ratio (SNR) was markedly better. The values do not change significantly if we analyze the MSD averaged only with nonoverlapping frame intervals as well (Supplemental Figure S10 and Table S4). This finding also did not seem to be related to ploidy, as tracking in haploids gave α = 0.77 in dextrose (Table S3). Furthermore, all loci in the various strains tracked in this study showed α values between 0.6 and 0.75 (Supplemental Figure S9 and Supplemental Table S3), indicating that this behavior is more general than just applying to the GAL locus or pericentromeric loci alone. In light of this surprising result, we performed a control experiment in which we tracked freely diffusing fluorescent beads in 90% glycerol/water solution (Supplemental Figure S12) using the same experimental apparatus. With the same analysis software, we estimated α = 0.98, consistent with the expected result of α = 1. The larger α values also cannot be explained by the translation of the nucleus, since our dual-locus tracking scheme allowed us to bound the nuclear contribution to the MSD. Namely, we can set a bound for the contribution of nuclear translation to the apparent MSD by calculating the “cross MSD” (CMSD),
. Bacterial chromosomal loci tend to exhibit α ∼ 0.4 rather ubiquitously (Weber et al., 2010a; Javer et al., 2013). Previous studies in yeast determined α values around 0.5 for various loci (Hajjoul et al., 2013), and one early tracking study of the GAL locus reported α within the range 0.4–0.5 (Cabal et al., 2006). Thus we were surprised to find values of α = 0.75 for dextrose and α = 0.64 in galactose from analysis of the MSD (Figure 6, A and B) of the GAL locus in our study, indicating a higher degree of diffusivity than previously believed, at least on this time scale. Data shown here are taken only from the green channel since the signal-to-noise ratio (SNR) was markedly better. The values do not change significantly if we analyze the MSD averaged only with nonoverlapping frame intervals as well (Supplemental Figure S10 and Table S4). This finding also did not seem to be related to ploidy, as tracking in haploids gave α = 0.77 in dextrose (Table S3). Furthermore, all loci in the various strains tracked in this study showed α values between 0.6 and 0.75 (Supplemental Figure S9 and Supplemental Table S3), indicating that this behavior is more general than just applying to the GAL locus or pericentromeric loci alone. In light of this surprising result, we performed a control experiment in which we tracked freely diffusing fluorescent beads in 90% glycerol/water solution (Supplemental Figure S12) using the same experimental apparatus. With the same analysis software, we estimated α = 0.98, consistent with the expected result of α = 1. The larger α values also cannot be explained by the translation of the nucleus, since our dual-locus tracking scheme allowed us to bound the nuclear contribution to the MSD. Namely, we can set a bound for the contribution of nuclear translation to the apparent MSD by calculating the “cross MSD” (CMSD),
|
|
FIGURE 6:
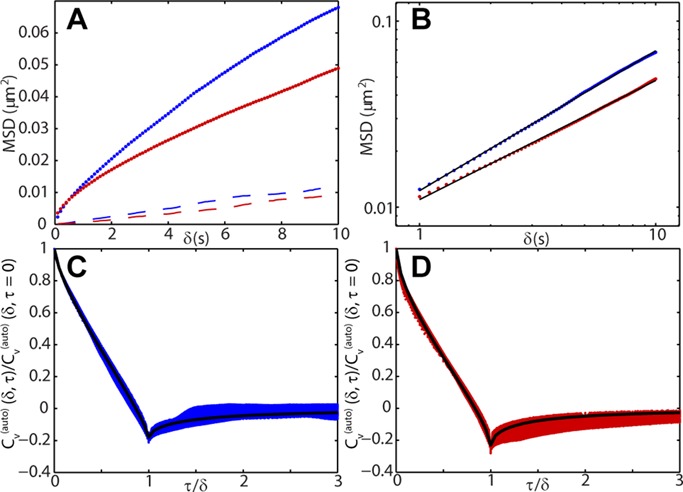
MSD and velocity autocorrelations for DLDC data. (A) Time-ensemble-averaged MSD for DLDC-dextrose (blue dots) and DLDC-galactose (red dots) plotted on linear scale. Upper bounds of contribution of nuclear translation to total MSD calculated as described in the Supplemental Material for dextrose (dashed blue line) and galactose (dashed red line). (B) Time-ensemble-averaged MSD for DLDC-dextrose (blue dots) and DLDC-galactose (red dots) plotted on log-log scale over the time scale used for subdiffusive parameter estimation. Fitted lines are overlaid in black, giving estimated parameters of D* = 0.0020 and α = 0.75 for dextrose and D* = 0.0018 and α = 0.64 for galactose. (C) Scaled velocity autocorrelation for DLDC-dextrose for δ on the interval [1, 10 s] at 0.1-s intervals. Curve fitting to Eq. 6 gives solid black line. (D) Same as in C but for DLDC-galactose.
where the subscripts g and r denote green and red channels, respectively. (CMSD is related to the mean-squared relative displacement between loci; see Supplemental Figure S11 and accompanying text.) In the Supplemental Material we give a complete derivation of the fact that the CMSD is an upper bound for MSDN, that is, the nuclear contribution to the apparent MSD. We also show in the Supplemental Material that the apparent MSD is the sum of the true locus MSD (i.e., corrected for nuclear translation) and MSDN. Therefore subtracting CMSD from our apparent MSDs gives a bound for the effect of nuclear translation on our estimation of α. Figure 6A shows clearly that the MSD of the GAL locus is well above the upper bound of the nuclear MSD (dashed lines) in both dextrose and galactose. The dashed lines in Figure 6A were found by calculating the CMSD for each strain/experimental condition and then ascribing the lowest curves occurring in dextrose (GAL/PES4) and galactose (GAL/RPL9A-galactose) as the limiting behavior. Subtracting this upper bound did not change the fundamental observation of higher estimated α values than previously reported. For instance, we still found α = 0.71 in dextrose after removing this bound. Although this treatment does not explicitly rule out a contribution from nuclear rotation, we note that previous studies that found lower α values also did not treat this, so it is unlikely to explain the difference.
Several factors can possibly account for the apparent discrepancy in α for the GAL locus in comparison to previous reports. First, and perhaps most important, it has been reported that finite localization error causes false deflation of α if not properly accounted for (Martin et al., 2002; Kepten et al., 2013). It is widely known that localization error produces a constant offset in the MSD for pure Brownian motion (i.e., α = 1; Savin and Doyle, 2005). However, it can easily be shown that this constant offset will also manifest itself for subdiffusive motion (see Supplemental Material), despite the fact that it is rarely addressed in biological applications. Thus fitting an MSD curve to the form 6D*δα (where D* is a constant) without allowing for a constant offset will cause an underestimation of α. A previous study over a comparable time scale in HeLa cells that did allow for a constant offset found a similar α = 0.71 (Zidovska et al., 2013). Typically, fitting is done on the log-log scale, in which case, the slope of the resulting line becomes the estimate for α. In such a plot, the effect of localization error is to bend the line toward lower slopes at early times (Martin et al., 2002). Such a bend is obvious if the tracking study takes place over multiple orders of magnitude relative to the frame interval and there is sufficient statistics available. However, if this is not the case, the manifestation of this problem may be difficult to discern. In our study, we fitted the MSD on a time range over which the curves were linear (1–10 s), after the bend due to finite localization error but before the nonlinearity that appears at longer times due to insufficient averaging (Figure 6B and Supplemental Figure S9).
The second factor that might contribute to the discrepancy with previous findings is the fact that we are tracking only the loci on shorter time scales, before they have a chance to sense their subnuclear confinement. Confinement will cause a kink in the log-log MSD curve that is easily detectable, given sufficient temporal sampling and statistics, but again can be harder to detect otherwise. To confirm that the combination of localization error and confinement could account for the lower values for α found in a previous, we simulated trajectories as fractional Brownian motions (fBm; see discussion below and Supplemental Material) with subdiffusive parameters informed by our findings (α = 0.75, D* = 0.0021) and the frame interval, time scale, and localization error used in Cabal et al. (2006; see Supplemental Material for simulation details). We applied a radius of confinement of 500 nm, consistent with the size of the GAL locus gene territory found in Berger et al. (2008). Indeed, we found that this produced an underestimation of α = 0.45. It should be made clear that this finding does not discount the main results of Cabal et al. (2006) since the thrust there was to compare behavior between activated and repressed loci, not to provide absolute estimates of α. However, it does suggest caution when interpreting these α values and, for instance, attempting to infer the polymeric characteristics of the chromosome from them.
A third factor that could contribute to the apparent α inconsistency is the possibility that some aspects of chromatin motion may show differences in different strain backgrounds. Preliminary data indicate that tracking of the GAL locus in a different S. cerevisiae strain, W303, consistently gives α = 0.6. This value is still higher than that previously reported (Cabal et al., 2006; Hajjoul et al., 2013; and still “super-Rousean”—see later discussion) but lower than most of the loci tracked in the present study with background strain S288c. This heritability effect is a topic of future investigation. We further note that the labeling scheme could have an effect on the character of motion, possibly by influencing the local state of chromatin compaction. However, the TetO and LacO schemes used here have also been the primary labeling methods in most other locus-tracking studies in yeast, including those that have reported lower α values (Cabal et al., 2006; Hajjoul et al., 2013). Finally, although our analysis only included cells identified as G1 in brightfield images, our study would have been strengthened by a third marker that clearly delineates the morphology of the nucleus for more robust cell cycle classification.
The seemingly universal α = 0.4 found for bacterial chromosomal loci is very likely a true description of the motion since time sampling and statistics have been excellent in these studies (Weber et al., 2010a; Javer et al., 2013). This does not necessarily mean that one should expect the yeast nucleus to exhibit the same scaling, since its organization is fundamentally different. Although a number of types of motion can produce subdiffusion, including the continuous-time random walk (in which a particle exhibits jumps punctuated by a broad distribution of waiting times due to, e.g., transient binding events) and obstructed diffusion (due to random encounters with obstacles), these bacterial loci have been shown to exhibit characteristics consistent with fractional Brownian motion (fBm). fBm is the mean-zero Gaussian process that is both self-similar and stationary, and a one-dimensional fBm trajectory x(t) is characterized by the covariance function defined as (Dieker, 2004)
|
|
Setting α = 1 in Eq. 6 recovers the familiar independent-increment pure Brownian motion, whereas setting α < 1 produces subdiffusive motion with correlated increments. Such motion can be produced when an object diffuses through a viscoelastic medium. From Eq. 6, one can derive the scaled velocity autocorrelation function,
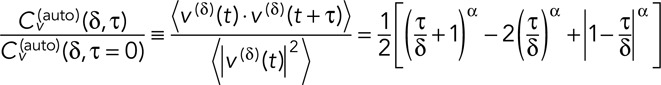 (7) (7)
|
Thus, by computing the scaled velocity autocorrelation function and fitting to Eq. 7 as described in Weber et al. (2012), we can assess whether the GAL locus in yeast exhibits fBm as bacterial loci do. The scaled velocity autocorrelation is plotted as a function of τ/δ for the dextrose case (Figure 6C) and the galactose case (Figure 6D; as calculated from data acquired in the green channel due to superior SNR) for all δ on the interval [1, 10 s] at 0.1-s increments (larger δ introduces artifacts due to poor averaging). We see reasonable fits to Eq. 7 with α as the only free parameter (Figure 6, C and D), producing estimates of α = 0.70 in dextrose and α = 0.62 in galactose, in decent agreement with the values determined from fitting the MSD (α = 0.75 and α = 0.64, respectively). Qualitatively, the persistent negative peak at τ/δ = 1 is a signature of the “push-back” of the elastic medium. A negative peak due to localization error would decay for increasing δ, whereas a negative peak due to confinement would grow with increasing δ to a constant −½ (Weber et al., 2012). Thus we conclude that the motion of the GAL locus is well described as an fBm process, in congruence with findings in bacteria. This has potentially interesting implications for the application of polymer theory to chromatin dynamics. The fBm of bacterial loci was found to be consistent with a simple Rouse polymer in a viscoelastic medium, which can give rise to α < 0.5 (Weber et al., 2010b). Such a model cannot explain α > 0.5 that we observed, however, and so future work must be carried out to explain such a “super-Rousean” result. A possible explanation for the observed behavior could come from a contribution from active (i.e., ATP-dependent) processes, which were observed in some previous chromatin dynamics studies (Marshall et al., 1997; Heun et al., 2001; Neumann et al., 2012; Javer et al., 2014). However, previous work in Escherichia coli and on the LEU2 locus in S. cerevisiae showed that the dominant effect of ATP depletion on chromosomal motion was to change D*, not α for these particular cases (Weber et al., 2012).
Conclusion
By using the DH-PSF microscope, we were able to simultaneously track pairs of fluorescently labeled chromosomal loci in diploid budding yeast with high precision in three dimensions on a time scale of ∼0.1–30 s. Application of this technique revealed a higher mobility for the GAL locus on this time scale than previously reported. This technique also gave access to the correlations in velocity arising from coupled motion of loci. The two copies of the GAL locus exhibited higher velocity correlations in a repressive environment than in an activating one. Under repressive conditions, the correlations between GAL loci resembled those of two loci separated by ∼108 kbp along the same chromosome, whereas under activating conditions, GAL loci correlations were equivalent to those evinced by distinct pericentromeric gene loci located on different chromosomes and by a pair of loci on separate chromosomes with vastly different genomic separations from centromeres. Inspection of individual track pairs suggests a wealth of interesting behavior, such as finite response times of correlative motion and the interplay between association with the nuclear envelope and the degree of correlations. However, more experiments are needed to fully elucidate these observations. Our results highlight the utility of single-pair tracking as a complementary tool to static imaging, conformation capture techniques, and single-particle tracking for the study of epigenetics. Pair tracking with concurrent colocalization to nuclear landmarks should be conducted in future studies since these might play a role in sequestering groups of genes and exerting forces on them. Future studies should also examine correlations between multitudes of pairs of loci spanning the full range of genomic distances. Although our wide-field technique did allow for a considerable improvement in throughput over confocal scanning methods (from tens to hundreds of cells), further automation of the analysis will allow for truly high-throughput studies.
MATERIALS AND METHODS
Strains and growth
All strains used in this study are based on the S288c (BY4743) background (Supplemental Table S1). Cells were grown at room temperature (∼22ºC) to early to mid log phase in synthetic complete (SC) medium containing 2% dextrose or 2% galactose as indicated. Care was taken to maintain the cells in early to mid log phase for an extended period before imaging.
Microscopy
Cells were spun down and mixed with a diluted solution (∼100× from stock into either dextrose or galactose/cell medium solution) of multicolor 0.1-μm fluorescent fiducial beads (TetraSpeck; Invitrogen, Carlsbad, CA) before being mounted on a 1% agarose (Sigma-Aldrich, St. Louis, MO) pad. The bead stock contained some amount of azide, a known decoupler (Heun et al., 2001). However, the final concentration of azide was ≤10−4%, roughly two orders of magnitude lower than typically administered lethal amounts. The cells appeared to grow normally overnight when left in the presence of this final dilution of bead solution. Once on the agarose pads, the cells were sandwiched with another coverslip, and the edges were sealed with wax. Slides were then mounted on a modified inverted microscope stand (Diaphot 200; Nikon, Melville, NY) in which the internally mounted tube lens had been removed and replaced with a lens just outside the body of the stand. Cells were illuminated with a 488-nm laser (CrystaLaser, Reno, NV) at ∼45 W/cm2 and a 561-nm laser (Sapphire, Coherent, Santa Clara, CA) at ∼25 W/cm2. Fluorescence was collected using one of two microscope objectives: a numerical aperture (NA) 1.40 oil-immersion objective (UPlanSApo 100×/1.40 NA oil; Olympus, Tokyo, Japan) or a supercorrected objective (PlanoApoN 60×/1.40 NA oil SC; Olympus). The supercorrected objective was used in some later data sets in an attempt to improve registration accuracy, but this did not produce a noticeable difference. To maintain the magnification of the original 100× system, the tube lens was replaced with a designed train of lenses once the supercorrected objective was installed. Collected fluorescence traveled through a multi-bandpass dichroic mirror (zt405/488/561rpc; Chroma Technology, Rockingham, VT) within the microscope stand. After the tube lens/lenses, the light was passed through a dual-channel 4f optical processing system that served to convolve the standard PSF with the DH-PSF as described in detail elsewhere (Gahlmann et al., 2013). In brief, the 4f system consists of two additional lenses: the first lens is placed one focal length (f) from the image plane formed by the standard microscope, and it produces the Fourier transform of the input field (i.e., the field at this intermediate image plane) a distance f behind the lens. Access to this Fourier plane allows for modulation of the field in such a way so as to convolve the standard PSF of the microscope with the DH-PSF shape. This modulation is achieved by placing specially engineered quartz transmission phase masks that encode the DH-PSF (DoubleHelix, Boulder, CO) at this Fourier plane. The second lens of the 4f optical system is then placed a distance f from the Fourier plane, which transforms the now-modulated field back into an image that is recorded on a camera placed a distance f behind this lens.
The fluorescence was filtered through a 561 notch filter (NF03-561E; Semrock, Rochester, NY) and a dual-bandpass filter (Brightline Multiband 523/610; Semrock) before being split into two color channels by a 560-nm dichroic beam splitter (FF560-FDi01, Semrock). The red channel was further filtered through a 600-nm long-pass filter (E600LP; Chroma Technology, Rockingham, VT) in order to reduce GFP cross-talk. This long-pass filter was removed for the haploid GFP cross-talk tracking experiments. The color channels were imaged simultaneously onto separate regions of an electron-multiplying charge-coupled device camera (Ixon DU-897E; Andor Technology, Belfast, Northern Ireland) operating at a maximal gain level of 300.
An appropriate field of view for dual-color tracking was found by searching for a region of cells in which the GFP-labeled loci were within the same depth of focus (∼2 μm) as the fiducial beads located at the coverslip. Then image stacks were recorded at 10 Hz according to the following procedure: record a few seconds with only the 488-nm laser on to assess the degree of GFP cross-talk before dual-color tracking, perform dual-color tracking with both lasers on until the red signal bleaches into the background, and then again record a few seconds with only the 488-nm laser on to assess the degree of GFP cross-talk after the bleaching of the red fluorophores. This procedure allowed us to throw out tracks for which GFP cross-talk might cause obvious artifacts and carefully bound the effect in more subtle cases (Supplemental Figure S2 and accompanying text). The lasers were then both turned off, and a white light image stack of the field was taken to make sure the cells were stationary on the relevant time scale and to identify cell cycle phase of each analyzed cell. Only loci from cells identified as being in G1 phase were included in the final analysis, as determined by cellular morphology.
Analysis
Each image stack was analyzed by identifying loci and fiducial beads by hand. Custom MATLAB (MathWorks, Natick, MA) tracking software was then used to estimate the position of each identified object in each frame by least-squares fitting to a sum of two 2D Gaussian functions plus a constant offset. The amplitudes and widths of each Gaussian and the constant offset were the parameters of the fit. Fiducial trajectories were smoothed by convolving with a 15-frame temporal boxcar function in order to suppress the propagation of bead localization error in later drift compensation. Locus trajectories were then filtered by having the user inspect each resulting position and velocity trajectory individually and reset thresholds and/or reject frames in which clear fitting artifacts were present. After this step, the user visually compared each fitted double Gaussian to the raw images of the locus through the first and last 50 frames in order to reject any persisting fitting artifacts (e.g., fitting of the background in cells with high nuclear background was avoided). We then transformed the locus trajectories from the red channel into the coordinates of the green channel. The transformation map was found by scanning a sample of 0.1-μm orange fluorescent beads (FluoSpheres; Invitrogen, Carlsbad, CA) immobilized at an interface in 1% polyvinyl alcohol (Polysciences, Warrington, PA) through a 3D volume and then using the algorithm detailed in Gahlmann et al. (2013). To best approximate the media of the cell imaging, the fluorescent bead sample for the registration measurement was covered with either water or an agarose pad. Still, since the beads could not be scanned away from the interface, the mimicry of the final imaging was only approximate, resulting in a small residual z-dependent registration error for which we compensated empirically (Supplemental Figure S1 and accompanying text). No additional compensation for index of refraction mismatch was applied since the subdiffusion parameters of the z-component of the MSDs did not differ from those of the x- and y-components in any repeatable, significant way, likely because the z-distance traversed during the time scale studied was not large enough on average to make any small apparent z-distortion very significant. After transformation, the locus trajectories were corrected for stage drift as inferred from fiducial tracks.
Supplementary Material
Acknowledgments
We thank Thomas Lampo and Andrew Spakowitz for helpful discussions and Nate Krefman, David Drubin, and Georjana Barnes for the TetR-3XmCherry construct. M.P.B. was supported by a Robert and Marvel Kirby Stanford Graduate Fellowship. This work was supported by National Institute of General Medical Sciences Grant 2R01GM085437 (to W.E.M.) and National Institutes of Health Grant R01GM058065 (to K.W.).
Abbreviations used:
- DH-PSF
double-helix point spread function
- DLDC
dual-label, dual-chromosome
- DLSC
dual-label, single-chromosome
- TAMSD
time-averaged mean square displacement
- TAVCC
time-averaged velocity cross-correlation
- T-EAVCC
time-ensemble–averaged velocity cross-correlation.
Footnotes
This article was published online ahead of print in MBoC in Press (http://www.molbiolcell.org/cgi/doi/10.1091/mbc.E14-06-1127) on October 13, 2014.
REFERENCES
- Albert B, Léger-Silvestre I, Normand C, Gadal O. Nuclear organization and chromatin dynamics in yeast: biophysical models or biologically driven interactions. Biochim Biophys Acta. 2012;1819:468–481. doi: 10.1016/j.bbagrm.2011.12.010. [DOI] [PubMed] [Google Scholar]
- Berger AB, Cabal GG, Fabre E, Duong T, Buc H, Nehrbass U, Olivo-Marin JC, Gadal O, Zimmer C. High-resolution statistical mapping reveals gene territories in live yeast. Nat Methods. 2008;5:1031–1037. doi: 10.1038/nmeth.1266. [DOI] [PubMed] [Google Scholar]
- Blobel G. Gene gating: a hypothesis. Proc Natl Acad Sci USA. 1985;82:8527–8529. doi: 10.1073/pnas.82.24.8527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brickner DG, Ahmed S, Meldi L, Thompson A, Light W, Young M, Hickman TL, Chu F, Fabre E, Brickner JH. Transcription factor binding to a DNA zip code controls interchromosomal clustering at the nuclear periphery. Dev Cell. 2012;22:1234–1246. doi: 10.1016/j.devcel.2012.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bystricky K, Heun P, Gehlen L, Langowski J, Gasser SM. Long-range compaction and flexibility of interphase chromatin in budding yeast analyzed by high-resolution imaging techniques. Proc Natl Acad Sci USA. 2004;101:16495–16500. doi: 10.1073/pnas.0402766101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bystricky K, Laroche T, van Houwe G, Blaszczyk M, Gasser SM. Chromosome looping in yeast: telomere pairing and coordinated movement reflect anchoring efficiency and territorial organization. J Cell Biol. 2005;168:375–387. doi: 10.1083/jcb.200409091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cabal GG, Genovesio A, Rodriguez-Navarro S, Zimmer C, Gadal O, Lesne A, Buc H, Feuerbach-Fournier F, Olivo-Marin J, Hurt ED. SAGA interacting factors confine sub-diffusion of transcribed genes to the nuclear envelope. Nature. 2006;441:770–773. doi: 10.1038/nature04752. [DOI] [PubMed] [Google Scholar]
- Casolari JM, Brown CR, Komili S, West J, Hieronymus H, Silver PA. Genome-wide localization of the nuclear transport machinery couples transcriptional status and nuclear organization. Cell. 2004;117:427–439. doi: 10.1016/s0092-8674(04)00448-9. [DOI] [PubMed] [Google Scholar]
- Cremer T, Cremer M, Dietzel S, Müller S, Solovei I, Fakan S. Chromosome territories—a functional nuclear landscape. Curr Opin Cell Biol. 2006;18:307–316. doi: 10.1016/j.ceb.2006.04.007. [DOI] [PubMed] [Google Scholar]
- de Laat W, Grosveld F. Spatial organization of gene expression: the active chromatin hub. Chromosome Res. 2003;11:447–459. doi: 10.1023/a:1024922626726. [DOI] [PubMed] [Google Scholar]
- Dieker T. MSc Thesis. Amsterdam, Netherlands: University of Twente; 2004. Simulation of Fractional Brownian Motion. [Google Scholar]
- Drubin DA, Garakani AM, Silver PA. Motion as a phenotype: the use of live-cell imaging and machine visual screening to characterize transcription-dependent chromosome dynamics. BMC Cell Biol. 2006;7:19. doi: 10.1186/1471-2121-7-19. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duan Z, Andronescu M, Schutz K, McIlwain S, Kim YJ, Lee C, Shendure J, Fields S, Blau CA, Noble WS. A three-dimensional model of the yeast genome. Nature. 2010;465:363–367. doi: 10.1038/nature08973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fraser P, Bickmore W. Nuclear organization of the genome and the potential for gene regulation. Nature. 2007;447:413–417. doi: 10.1038/nature05916. [DOI] [PubMed] [Google Scholar]
- Gahlmann A, Ptacin JL, Grover G, Quirin S, von Diezmann ARS, Lee MK, Backlund MP, Shapiro L, Piestun R, Moerner WE. Quantitative multicolor subdiffraction imaging of bacterial protein ultrastructures in 3D. Nano Lett. 2013;13:987–993. doi: 10.1021/nl304071h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gartenberg MR, Neumann FR, Laroche T, Blaszczyk M, Gasser SM. Sir-mediated repression can occur independently of chromosomal and subnuclear contexts. Cell. 2004;119:955–967. doi: 10.1016/j.cell.2004.11.008. [DOI] [PubMed] [Google Scholar]
- Gasser SM, Hediger F, Taddei A, Neumann FR, Gartenberg MR. The function of telomere clustering in yeast: the circe effect. Cold Spring Harb Symp Quant Biol. 2004;69:327–337. doi: 10.1101/sqb.2004.69.327. [DOI] [PubMed] [Google Scholar]
- Green EM, Jiang Y, Joyner R, Weis K. A negative feedback loop at the nuclear periphery regulates GAL gene expression. Mol Biol Cell. 2012;23:1367–1375. doi: 10.1091/mbc.E11-06-0547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hajjoul H, Mathon J, Ranchon H, Goiffon I, Mozziconacci J, Albert B, Carrivain P, Victor JM, Gadal O, Bystricky K, et al. High-throughput chromatin motion tracking in living yeast reveals the flexibility of the fiber throughout the genome. Genome Res. 2013;23:1829–1838. doi: 10.1101/gr.157008.113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Heun P, Laroche T, Shimada K, Furrer P, Gasser SM. Chromosome dynamics in the yeast interphase nucleus. Science. 2001;294:2181–2186. doi: 10.1126/science.1065366. [DOI] [PubMed] [Google Scholar]
- Ishii K, Arib G, Lin C, Van Houwe G, Laemmli UK. Chromatin boundaries in budding yeast: the nuclear pore connection. Cell. 2002;109:551–562. doi: 10.1016/s0092-8674(02)00756-0. [DOI] [PubMed] [Google Scholar]
- Javer A, Kuwada NJ, Long Z, Benza VG, Dorfman KD, Wiggins PA, Cicuta P, Lagomarsino MC. Persistent super-diffusive motion of Escherichia coli chromosomal loci. Nat Commun. 2014;5:3854. doi: 10.1038/ncomms4854. [DOI] [PubMed] [Google Scholar]
- Javer A, Long Z, Nugent E, Grisi M, Siriwatwetchakul K, Dorfman KD, Cicuta P, Lagomarsino MC. Short-time movement of E. coli chromosomal loci depends on coordinate and subcellular localization. Nat Commun. 2013;4:3003. doi: 10.1038/ncomms3003. [DOI] [PubMed] [Google Scholar]
- Johnston M, Flick JS, Pexton T. Multiple mechanisms provide rapid and stringent glucose repression of GAL gene expression in Saccharomyces cerevisiae. Mol Cell Biol. 1994;14:3834–3841. doi: 10.1128/mcb.14.6.3834. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kepten E, Bronshtein I, Garini Y. Improved estimation of anomalous diffusion exponents in single-particle tracking experiments. Phys Rev E. 2013;87:052713. doi: 10.1103/PhysRevE.87.052713. [DOI] [PubMed] [Google Scholar]
- Koszul R, Kim K, Prentiss M, Kleckner N, Kameoka S. Meiotic chromosomes move by linkage to dynamic actin cables with transduction of force through the nuclear envelope. Cell. 2008;133:1188–1201. doi: 10.1016/j.cell.2008.04.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman-Aiden E, van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, et al. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science. 2009;326:289–293. doi: 10.1126/science.1181369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marshall WF, Straight A, Marko JF, Swedlow J, Dernburg A, Belmont A, Murray AW, Agard DA, Sedat JW. Interphase chromosomes undergo constrained diffusional motion in living cells. Curr Biol. 1997;7:930–939. doi: 10.1016/s0960-9822(06)00412-x. [DOI] [PubMed] [Google Scholar]
- Martin DS, Forstner MB, Käs JA. Apparent subdiffusion inherent to single particle tracking. Biophys J. 2002;83:2109–2117. doi: 10.1016/S0006-3495(02)73971-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meneghini MD, Wu M, Madhani HD. Conserved histone variant H2A. Z protects euchromatin from the ectopic spread of silent heterochromatin. Cell. 2003;112:725–736. doi: 10.1016/s0092-8674(03)00123-5. [DOI] [PubMed] [Google Scholar]
- Neumann FR, Dion V, Gehlen LR, Tsai-Pflugfelder M, Schmid R, Taddei A, Gasser SM. Targeted INO80 enhances subnuclear chromatin movement and ectopic homologous recombination. Genes Dev. 2012;26:369–383. doi: 10.1101/gad.176156.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pavani SRP, Thompson MA, Biteen JS, Lord SJ, Liu N, Twieg RJ, Piestun R, Moerner WE. Three-dimensional, single-molecule fluorescence imaging beyond the diffraction limit by using a double-helix point spread function. Proc Natl Acad Sci USA. 2009;106:2995–2999. doi: 10.1073/pnas.0900245106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pliss A, Malyavantham KS, Bhattacharya S, Berezney R. Chromatin dynamics in living cells: identification of oscillatory motion. J Cell Physiol. 2013;228:609–616. doi: 10.1002/jcp.24169. [DOI] [PubMed] [Google Scholar]
- Sage D. Automatic tracking of individual fluorescence particles: application to the study of chromosome dynamics. IEEE Trans Image Processing. 2005;14:1372–1383. doi: 10.1109/tip.2005.852787. [DOI] [PubMed] [Google Scholar]
- Savin T, Doyle PS. Static and dynamic errors in particle tracking microrheology. Biophys J. 2005;88:623–638. doi: 10.1529/biophysj.104.042457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephens AD, Snider CE, Haase J, Haggerty RA, Vasquez PA, Forest MG, Bloom K. Individual pericentromeres display coordinated motion and stretching in the yeast spindle. J Cell Biol. 2013;203:407–416. doi: 10.1083/jcb.201307104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sutherland H, Bickmore WA. Transcription factories: gene expression in unions. Nat Rev Genet. 2009;10:457–466. doi: 10.1038/nrg2592. [DOI] [PubMed] [Google Scholar]
- Taddei A, Van Houwe G, Hediger F, Kalck V, Cubizolles F, Schober H, Gasser SM. Nuclear pore association confers optimal expression levels for an inducible yeast gene. Nature. 2006;441:774–778. doi: 10.1038/nature04845. [DOI] [PubMed] [Google Scholar]
- Texari L, Dieppois G, Vinciguerra P, Contreras MP, Groner A, Letourneau A, Stutz F. The nuclear pore regulates GAL1 gene transcription by controlling the localization of the SUMO protease Ulp1. Mol Cell. 2013;51:807–818. doi: 10.1016/j.molcel.2013.08.047. [DOI] [PubMed] [Google Scholar]
- Thompson MA, Casolari JM, Badieirostami M, Brown PO, Moerner WE. Three-dimensional tracking of single mRNA particles in Saccharomyces cerevisiae using a double-helix point spread function. Proc Natl Acad Sci USA. 2010;107:17864–17871. doi: 10.1073/pnas.1012868107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vazquez J, Belmont AS, Sedat JW. Multiple regimes of constrained chromosome motion are regulated in the interphase Drosophila nucleus. Curr Biol. 2001;11:1227–1239. doi: 10.1016/s0960-9822(01)00390-6. [DOI] [PubMed] [Google Scholar]
- Weber SC, Spakowitz AJ, Theriot JA. Bacterial chromosomal loci move subdiffusively through a viscoelastic cytoplasm. Phys Rev Lett. 2010a;104:238102. doi: 10.1103/PhysRevLett.104.238102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber SC, Spakowitz AJ, Theriot JA. Nonthermal ATP-dependent fluctuations contribute to the in vivo motion of chromosomal loci. Proc Natl Acad Sci USA. 2012;109:7338–7343. doi: 10.1073/pnas.1119505109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber SC, Theriot JA, Spakowitz AJ. Subdiffusive motion of a polymer composed of subdiffusive monomers. Phys Rev E. 2010b;82:011913. doi: 10.1103/PhysRevE.82.011913. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weber SC, Thompson MA, Moerner WE, Spakowitz AJ, Theriot JA. Analytical tools to distinguish the effects of localization error, confinement, and medium elasticity on the velocity autocorrelation function. Biophys J. 2012;102:2443–2450. doi: 10.1016/j.bpj.2012.03.062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zidovska A, Weitz DA, Mitchison TJ. Micron-scale coherence in interphase chromatin dynamics. Proc Natl Acad Sci USA. 2013;110:15555–15560. doi: 10.1073/pnas.1220313110. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


