Abstract
Eye motion is a major impediment to the efficient acquisition of high resolution retinal images with the adaptive optics (AO) scanning light ophthalmoscope (AOSLO). Here we demonstrate a solution to this problem by implementing both optical stabilization and digital image registration in an AOSLO. We replaced the slow scanning mirror with a two-axis tip/tilt mirror for the dual functions of slow scanning and optical stabilization. Closed-loop optical stabilization reduced the amplitude of eye-movement related-image motion by a factor of 10–15. The residual RMS error after optical stabilization alone was on the order of the size of foveal cones: ~1.66–2.56 μm or ~0.34–0.53 arcmin with typical fixational eye motion for normal observers. The full implementation, with real-time digital image registration, corrected the residual eye motion after optical stabilization with an accuracy of ~0.20–0.25 μm or ~0.04–0.05 arcmin RMS, which to our knowledge is more accurate than any method previously reported.
OCIS codes: (110.1080) Active or adaptive optics, (120.3890) Medical optics instrumentation, (170.3880) Medical and biological imaging, (170.4470) Ophthalmology, (330.2210) Vision - eye movements
1. Introduction
The adaptive optics scanning light ophthalmoscope (AOSLO) has become an important tool for the study of the human retina in both normal and diseased eyes [1–4]. The human eye is constantly in motion; even during careful fixation, normal, involuntary, microscopic eye movements [5,6], cause the scanned field of the AOSLO to move continuously across the retina in a pattern that corresponds exactly to the eye motion. Fixational eye motion causes unique distortions in each AOSLO frame due to the fact that each image is acquired over time. In the normal eye, these movements tend to be rather small in amplitude. However, in patients with retinal disease or poor vision, fixational eye movements can be amplified [7] and introduce distortions that are a major hindrance to efficient AOSLO imaging, in some cases precluding imaging altogether. Unfortunately, these patients are potentially some of the most interesting to study using this technology. It is therefore desirable, particularly for clinical imaging, to minimize or eliminate this motion altogether.
The velocity of the fast scanning mirror is the primary limitation to achieving very high frame rates that would effectively eliminate image distortion within individual frames [8,9]. The frame rate of current research AOSLOs is limited by the speed of appropriately-sized, commercially-available fast scanning mirrors, which achieve a maximum frequency of ~16 kHz. All clinical and most experimental uses of these instruments require that the AOSLO image be rectified (i.e. ‘desinusoided’) to remove the sinusoidal distortion caused by the resonant scanner, registered (to facilitate averaging) and averaged (to increase SNR) to generate an image for qualitative or quantitative analysis. Image registration works by recovering the eye motion and nullifying it, and is required to generate high SNR images from AO image sequences. Several methods for recovering eye motion from scanned imaging systems have been described in various reports [8–15].
Photographic techniques were first used to accurately measure eye movements over 100 years ago [16]. Over the last century, many different methods have been developed to accurately measure eye motion, including scleral search coils and many different types of external eye imaging systems [5]; many of these methods have been coupled with stimulus delivery systems to stabilize or manipulate the motion of the retinal image. One of the earliest attempts to precisely measure the two dimensional motion of the retinal image [17] employed the ‘optical-lever’ method to indirectly measure it by measuring the motion of the globe; this technique measures the light reflected from a plane mirror attached to the eye with a tightly fitting contact lens [18]. The optical lever method was used to both measure eye movements and deliver stabilized stimuli to the retina; this method has achieved very precise optical stabilization, with an error of 0.2–0.38 arcmin, or less than the diameter of a foveal cone (~0.5 arcmin) [19,20]. Despite its precision, the invasive nature of this method and its limitations for stimulus delivery caused it to be largely abandoned after dual-Purkinje image (DPI) eye trackers were developed [21–23]. As the name suggests, DPI eye trackers use the Purkinje images (ie. images of a light source reflected from the cornea and lens) to non-invasively measure eye position. This is another example of indirect measurement of retinal image motion as it uses a surrogate (in this case the motion of the Purkinje images) to the motion of the retina. Modern DPI eye trackers can measure eye motion and manipulate visual stimuli with a precision of ~1 arcmin [23]. Despite their precision, each of these methods can only indirectly infer the motion of the retinal image; here we report on recent advances to measure and stabilize eye motion by directly tracking the motion of the retina itself.
Ott and colleagues showed that a scanning laser ophthalmoscope (SLO) could be used to calculate eye motion by measuring the motion of the retinal image [10–12,24]. The first full implementation of offline recovery of eye movements from an AOSLO for the purpose of image registration, was described by Stevenson and Roorda [9]. This report also compared the AOSLO as an eye tracker to measurements simultaneously obtained from a DPI. The method was expanded and improved by Vogel and colleagues [8] and evolved into online digital stabilization for the purpose of stabilized stimulus delivery [25], and was used to guide the placement of a stimulus onto targeted retinal locations, ultimately achieving the capability to stimulate single cones in vivo in the normal human eye [26–28]. To improve the flexibility of stabilized stimulus delivery, the electronics for imaging and light source modulation were migrated to field-programmable gate array (FPGA) technology, enabling high-speed real-time eye tracking [29]. FPGA technology facilitated the implementation of open-loop SLO optical tracking [30] and achieved successful application to OCT [31,32].
During the same period that these advancements were occurring in the Roorda laboratory, the Burns laboratory and Physical Sciences Inc. developed a closed-loop optical eye tracking system for an AOSLO with an integrated wide field of view (FOV) line scan imaging system [14,33,34]. This device used a tracking beam reflectometer to measure displacements of the optic disc in real-time and provide stabilization signals to tip and tilt mirrors. However, this system required significant tuning of parameters and settings for each eye to achieve stable tracking and robust re-locking and an additional imaging subsystem [33]. This device achieved 10-15 μm tracking accuracy for the wide FOV scanning system [33], but residual AOSLO motion was not compensated for with real-time image registration.
To combine and improve upon the achievements of our colleagues at UC Berkeley, IU, and PSI, we have implemented a robust closed-loop optical stabilization system with digital registration in one of our AOSLO systems and report its performance here in normal eyes.
2. Methods
2.1 Optical Stabilization
To implement optical stabilization in one of our existing AOSLO systems (described in detail elsewhere [35]) we modified the system to utilize a 2-axis tip/tilt mirror (S-334.2SL, Physik Instrumente, Karlsruhe, Germany) for both slow scanning and optical stabilization. The tip/tilt mirror (TTM) replaced the slow galvanometric scanner (labeled as vertical scanner in the optical diagram of the system shown in Fig. 5 of [35]). The TTM provides the capability to steer the beam at the pupil plane. In our optical system, each mirror axis has ± 3 degrees of independent optical deflection. When the mirror is mounted at 0° or 90°, the two axes and are aligned at + 45° and –45°, as shown in Fig. 1.
Fig. 1.

Two axes of the PI TTM (dark shaded square) showing its full range of motion (lightly shaded diamond). The dashed rectangle encloses the area of the stabilization range that can be utilized in the optical system. The small dark square shows the size of a 1.5° × 1.5° AOSLO imaging field. Scale bar is one degree.
For convenience, we define,
| (1) |
| (2) |
| (3) |
where and are motions in individual directions of the mirror, is the combined motion, and (a, b) are amplitudes in the two axes. In our optical system, the slow scanner scans the retina in the vertical direction and the fast scanner scans in the horizontal direction. The slow scanner is driven with a periodic ramp signal. The vertical scan is generated on the TTM by applying the inverse ramp signal to each axis; this produces motion in the vertical direction. Each signal is reduced by a factor of to generate the desired amplitude. The frequency of this signal, which sets the frame rate of the system, is ~22 Hz; ideally, the retrace would be instantaneous, however, in practice this is not possible and the retrace time is ~2.3 ms. The combination of and gives the full range of the TTM(illustrated by the shaded diamond in Fig. 1); the size of the 1.5° × 1.5° AOSLO imaging field is shown as the dark square. Theoretically, as long as the imaging field does not move outside of this range, the mirror can stabilize the motion by dynamically updating the position of the imaging beam. However, due to constraints from implementing this within our existing optical system, the AOSLO beam is vignetted by mechanical parts when the tracking mirror steers the AOSLO imaging field out of the area enclosed by the dashed rectangle in Fig. 1. Therefore, it can be seen that the full stabilization range of the TTM cannot be utilized simply by replacing the slow scanner in the existing optical system. A redesign of the optical system is necessary to take advantage of the full range of the TTM.
The tracking algorithm demonstrated here is image-based and relies on matching subsequent data to an acquired ‘reference frame’; the user manually chooses a reference frame and the algorithm registers subsequent ‘target frames’ to the reference frame. This algorithm has been briefly mentioned in previous reports [29,30,32] and is described in detail here, in the appendix. A flow chart of the stabilization system is illustrated in Fig. 2, and consists of the following procedures:
Fig. 2.

Flow chart of optical stabilization system
-
1.
Light reflected/scattered from the retina is converted to an analog voltage by the light detection system (in this case a photomultiplier tube (PMT))
-
2.
Images are digitized with an analog-to-digital converter (A/D)
-
3.
The A/D sends data to the host PC
-
4.
The graphics processing unit (GPU), executes preprocessing and then the tracking algorithm (see Appendix for details)
-
5.
The host PC sends the calculated eye motion to a digital-to-analog converter (DAC).
-
6.
The DAC converts digital eye motion (xt, yt) to an analog voltage
-
7.
The analog voltage is sent to the drive electronics of the TTM
-
8.
The TTM moves to the position of (xt, yt) to negate the eye motion
A FPGA device (ML506, Xilinx Inc., San Jose, CA) is employed to control data acquisition [29] and to program the DAC for driving the TTM. The A/D chip is integrated on the FPGA for image acquisition, and the D/A is performed with a dedicated 125MSPS 14-bit DAC (DAC2904EVM, Texas Instruments Inc., Dallas, TX). The tracking algorithm runs on a consumer level GPU (GTX560, NVIDIA Corporation, Santa Clara, CA).
2.2 Strip-level data acquisition and eye motion tracking
In any real-time control system, it is important to reduce system latencies; these can be electronic or mechanical. The mechanical latencies are usually fixed and determined by the specifications of the components acquired from the manufacturers (e.g. the mechanical response time of the TTM). Here we focus on the latencies that we can control: the electronic latencies, and present solutions to reduce them.
Traditionally, in a video rate imaging system, data is sent to the host PC frame by frame. Due to its scanned acquisition method and small field of view distortions are introduced into each AOSLO frame because the eye often moves faster than the frame rate; these distortions are amplified as the FOV becomes smaller. With an image-based algorithm such as cross-correlation, these ‘within-frame’ distortions, which encode the motion of the eye during the frame, can be recovered by dividing a whole frame into multiple strips (consisting of several scan lines) where the motion of each individual strip is calculated separately. A single line is acquired extremely rapidly with respect to fixational eye motion and can often be considered to be effectively undistorted (aside from the sinusoidal distortion induced by the fast scanner). The amount of distortion encoded into each strip of data is directly proportional to the velocity of the eye during strip acquisition. Sheehy and colleagues [30] have reported on some aspects of the stabilization algorithm performance, however, the relationship between eye velocity and algorithm accuracy needs further study. Images can be registered by calculating and applying the motion from individual strips. The motion calculated from each strip is sent to the TTM to steer the imaging beam back to the location of that strip on the reference frame. Ideally, real-time images from the eye will not shift and will be ‘frozen’ completely when stabilization is engaged, however, this would require zero latencies and a perfect motion tracking algorithm. In reality, some residual eye motion will still be seen after optical stabilization is activated due to tracking algorithm errors and the mechanical and electronic latencies. As previously stated, the mechanical latencies are out of our control; our goal here was to reduce the electronic latencies as much as possible. The source and duration of each of the electronic latencies are listed in Table 1.
Table 1. Electronic latencies of the optical stabilization system.
| Duration (ms) | Source | Description | |
|---|---|---|---|
| T1 | ~1.2 | Data acquisition | Sampling time for one strip of data |
| T2 | ~0.07 | Data buffering | Transit time from A/D to GPU |
| T3 | ~0.25 | Preprocessing | Image rectification & denoising |
| T4 | ~0.25 | Large amplitude motion & blink detection | See section 6.3 |
| T5 | ~0.25 | Small amplitude motion | See section 6.2 |
| T6 | ~0.06 | Eye motion encoding | Converts digital motion (x,y) to voltage (X,Y) to drive TTM |
We applied a 2-D smoothing filter, either 3x3 (kernel and ) or 5x5 (kernel and ) in preprocessing (T3) to make the cross-correlation algorithm more robust to noise. In some very low contrast images, a 2-D Sobel filter (kernel Sx = T[1 0 −1] and Sy = [1 0 −1] T ) was applied after the smoothing filter, in the form of ∣Sxk∣ + ∣Syk∣, where k is the image strip. The edge artifacts from the convolution are set to 0 after filtering. We then threshold the filtered images and set to 0 those pixels whose gray level is less than 25% of the maximum gray level in the filtered image. In this way, we produce a sparse matrix for use with the tracking algorithm. T4 and T5 are the latencies associated with the main components of the tracking algorithm and are described in detail in the appendix. Of the six electronic latencies listed in Table 1, T2 and T6 are on the order of tens of microseconds each; these are difficult to reduce further and negligible compared to the other four.
To reduce the data acquisition latency (T1), we implemented strip-level data acquisition. Each frame was divided into multiple strips and the FPGA sent each strip to the host PC as soon as the analog signal was digitized. The host PC then activated the tracking algorithm on the GPU immediately after the new strip was received. If the images were sent to the host PC frame by frame, the averaged T1 would be at least half the time required to acquire a frame (i.e. ~23 ms for a 22 fps system). This case is equivalent to frame-level stabilization since the TTM is not updated until the end of a frame where motion of all strips are calculated all together. The best scenario is to use motion of the bottom strip of the current frame to drive the TTM to stabilize image of the next frame. This bottom strip has one strip sampling latency (e.g, t) to the first strip of the next frame, and one whole frame (e.g., T) plus one strip latency (t) to the last strip of the next frame. The averaged result for T1 will be T/2 + t. Apparently, a simple frame-level stabilization has a whole frame of sampling latency. After adding T2, T3, T4, T5, and T6 for all strips of a single frame, the total electronic latency would be tens of microseconds, far too long to realize real-time stabilization. Ideally, buffering line-by-line, or even pixel-by-pixel, could further reduce the latencies from data acquisition, but FFT based cross-correlation needs significantly more data than a pixel or a line for a robust result. Due to high noise and low contrast images, particularly in diseased eyes, we found in our particular system that tracking efficiency, defined as the ratio of successfully stabilized strips to the total number of strips after tracking, was ~50% greater for a 32-line strip than for a 16-line strip. This number will, of course, likely vary depending on the imaging system.
The transfer of image data from the device to the host PC is implemented by Bus-Master DMA technology. Strip-level data acquisition and buffering are balanced by two factors: 1) the capability of the host PC to handle hardware interrupts and 2) the minimum amount of data required for robust cross-correlation. Our benchmarking shows that at the rate of 1000 interrupts/second, the PC interrupt handler uses only ~3–5% of its CPU resources (e.g. on Intel i3, i5, and i7 CPUs); at the rate of 10,000 interrupts/second, it uses ~50–70% of its CPU resource, which causes serious reliability issues for smooth scheduling of the other PC threads, such as preprocessing and eye motion detection. In our system, the data acquisition strip height was set to 16 lines, this corresponds to ~852 interrupts/second for 576 × 576 pixel images acquired at ~22 Hz where ~30 lines are cropped out since they are in retrace and nonlinear zone of the slow scan.
Figure 3 illustrates the timing of strip-level data acquisition and eye motion detection with the six electronic latencies. In Fig. 3, each frame is divided into multiple strips, with strip indices k, k + 1, k + 2, k + 3, … and N lines per strip. To calculate eye motion at location L (red solid circle in Fig. 3), the algorithm uses 2N strips, one from the existing data (k) and the just acquired strip (k + 1). Therefore, the algorithm obtains the data after strip k + 1 is completely received. In our case, the time required to collect strip k + 1 with N = 16 lines is ~1.2 ms, therefore T1 = 1.2 ms. After strip k + 1 is acquired, data is buffered (T2), and the algorithm proceeds with preprocessing (T3), large amplitude motion & blink detection (T4), small amplitude eye motion calculation (T5) and mirror motion encoding (T6). The computations for T3, T4, and T5 are offloaded to the GPU; each step takes ~0.2–0.25 ms. It should be noted that all of these computations can conveniently be migrated to the CPU when future processors become powerful enough. Taking into account the event-driven operating system (Microsoft Windows 7, Microsoft Corporation, Redmond, WA), the total computational and buffering latency is Tc = T2 + T3 + T4 + T5 + T6 (~0.7–0.8 ms). From Fig. 3, it can be seen that to run in real-time, Tc must be less than T1, as all computation must be completed before the algorithm receives the next strip of data(i.e. strip k + 2), which is required to calculate the eye motion one strip below location L (yellow circle M in Fig. 3). With the current 16 lines per strip, the total electronic latency (T1 + T2 + T3 + T4 + T5 + T6) is ~1.9–2.0 ms. Thus the TTM will receive commands ~1.9–2.0 ms after the eye moves. The mechanical latency of the TTM (ie. the time required to reach the desired position after the drive voltage has been updated) is variable and depends upon the drive voltage increment, which is dependent upon the motion of the eye. Typically, during eye drift, the voltage increment is on the order of 15–20 mV and the TTM has a mechanical latency of ~2 ms. Therefore, the mirror will steer the beam back to its original (reference) location ~4 ms after the eye moves. We chose this relatively slow TTM because of its high mechanical stability.
Fig. 3.
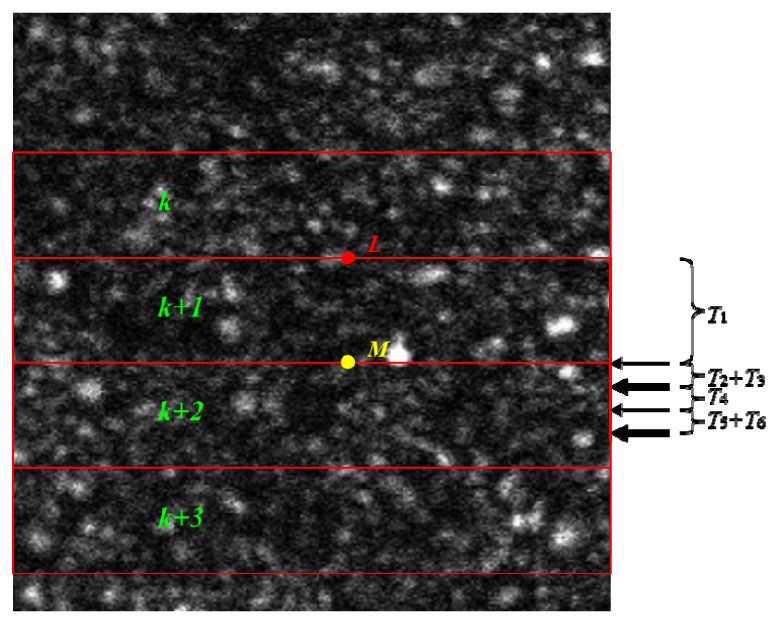
Strip-level data acquisition, buffering, and eye motion detection. The duration of the longest latencies (T1,T3,T4 & T5) are denoted by the brackets; arrows denote the end of each latency. Note that T2 and T6 are extremely short; their durations are denoted by the thickness of the labeled arrows.
2.3 Closed-loop optical stabilization
Optical stabilization is implemented using closed-loop control with,
| (4) |
where t and t + 1 denote the time sequence, are control gains in the horizontal and vertical directions, is the residual image motion in each direction, calculated from the tracking algorithm, is the current position of the stabilization mirror, and is the new position of the stabilization mirror. Units of are the same, in pixels or arcseconds. is dimensionless. As mentioned previously, the two axes of the stabilization mirror point to 45° and 135°, as shown in Fig. 1, thus needs to be rotated 45° before they are applied. As previously stated, the stabilization mirror is used simultaneously for slow scanning, so the net signals applied on the two axes of the stabilization mirror are,
| (5) |
where Θ is the operator of 45° rotation, and is the slow scanning ramp signals. Due to the relatively slow mechanical response of the stabilization mirror (~2 ms) and the fast eye motion update rate from the tracking algorithm (~1.2 ms), we set the gain to ~0.1–0.15 to achieve stability. This low gain also helps the system to smoothly re-lock eye motion after large amplitude motion or a blink (see Appendix), which usually occurs every few seconds.
2.4 Digital image registration
Theoretically, once optical stabilization is activated and the mirror dynamically compensates for the eye motion, it can be seen from Eq. (4), that the tracking algorithm calculates residual image motion only. Residual image motion is significantly smaller than the raw motion before optical stabilization. Digital image registration uses this small residual motion signal to create a registered image sequence. The computational accuracy of the digital registration is ± 0.5 pixels. Digital registration is executed during the period when the retrace period of the slow scanner (i.e., when it is moving backward after a full frame has been acquired but before the next frame begins). No additional cross correlation is required for digital registration because the motion of any strip from the current frame is calculated before it is used to drive the stabilization mirror. The motions from all strips are used directly for digital registration at the end of this frame.
2.5 Evaluation of system performance
To evaluate system performance, we tested both optical stabilization alone and optical stabilization combined with digital image registration on a model eye and several normal human eyes. The model eye consisted of an achromatic lens and a piece of paper. Motion was induced in the model eye image by removing the final flat mirror in the AOSLO system and placing a galvanometric scanner at a point conjugate with the exit pupil of the optical system before directing it into the model eye. The model eye was used to test the performance with sinusoidal motion at 1 and 2 Hz in the direction of the fast scan, with amplitudes of 0.21° and 0.17° and peak velocities of ~79 arcmin/sec and ~128 arcmin/sec, respectively. These peak velocities are faster than those reported in the literature for all fixational eye motion except for microsaccades [5]. To test system performance in the living eye, 2–3 image sequences (20 or 30-seconds in duration) were acquired at each of several locations in the central macula. The FOV was ~1.5° × 1.5°(~434 × 434 µm, on average); images were 576 × 576 pixels. Each image sequence was acquired in three stages: 1) no tracking (ie. normal eye motion), 2) optical stabilization only, and 3) both optical stabilization and digital registration. The frame when each epoch began was recorded digitally for later analysis. Reference frames were selected manually. For three participants (NOR011a, NOR025a, NOR037a), 15 retinal locations were imaged (shown in Fig. 4(a)). NOR047a was imaged at 21 retinal locations (shown in Fig. 4(b)), while NOR046a was imaged at 15 random locations within the central macula. For all participants but NOR046a, retinal locations were targeted using fundus guided fixation target control software [36]. This software (written in MATLAB (MathWorks, Natick, MA) using elements of the Psychophysics toolbox extensions [37–39]), controlled the position of a fixation target and mapped target displacements to the estimated location of the AOSLO imaging field on the retina. The estimated imaging location was displayed in the software GUI as a square overlaid on a wide field fundus image of the participants eye, which was acquired from a separate imaging system prior to AOSLO imaging. The fixation target was a small white circle (~30 arcmin in diameter)displayed on an LCD monitor and viewed off of a laser window placed in front of the eye. The laser window transmitted the AOSLO light but reflected a portion of the fixation target light into the eye. The fixation target for NOR046a was an array of blue LEDs.
Fig. 4.
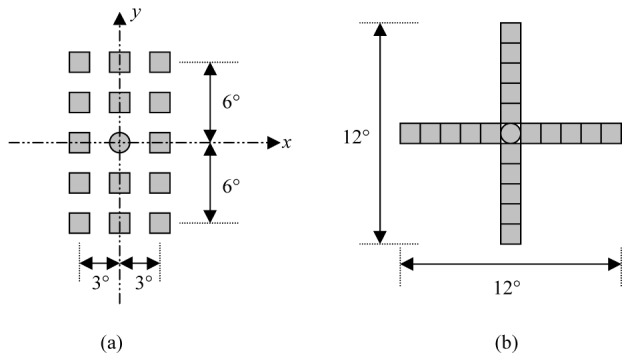
Human imaging locations. Subjects NOR011a, NOR025a, NOR037a, were imaged using the pattern of locations shown in (a), while subject NOR047a was imaged with the pattern shown in (b). The gray circle denotes the foveal center imaging location, while the gray squares denote eccentric imaging locations.
To evaluate system performance, we calculated the RMS separately for each condition. RMS was calculated using Eq. (6),
| (6) |
where, F is the number of frames, S is the number of strips in a single frame, ri are the locations of individual strips, and is the mean location of the strips. The RMS values we report here were calculated for all frames successfully tracked with the small amplitude motion component of the algorithm (see Appendix), thus they exclude all motion measurements greater than ½ the strip height, or 16 pixels.
2.6 Participants
Five participants with normal vision were recruited from the faculty and staff of the University of Rochester and the local community. Two of the authors participated; they were experienced observers and were aware of the purpose of the experiment (EAR & KN; NOR046a & NOR047a, respectively). The other three subjects were naïve as to the purposes of the experiments but each had participated in AOSLO imaging previously. Participants ranged in age from 25 to 65 years. All participants gave written informed consent after the nature of the experiments and any possible risks were explained both verbally and in writing. All experiments were approved by the Research Subjects Review Board of the University of Rochester and adhered to the Tenets of the Declaration of Helsinki.
3. Results
Media 1 (1.1MB, MPEG) illustrates the performance of optical stabilization for each condition of model eye motion. Residual motion after optical stabilization was ~1/12 of the original motion at 1 Hz and ~1/7 at 2 Hz, thus ~92% and ~85% of the motion was compensated for with optical stabilization in each of the model eye conditions, respectively.
Media 2 (2.4MB, MPEG) shows an image sequence from a human eye. The first 4 seconds demonstrate typical normal human fixational eye motion in AOSLO. After 4 seconds elapsed, optical stabilization was activated. As can be seen from the image sequence, there was still a small amount of residual motion. Shortly after 10 seconds have elapsed, digital image registration is activated to eliminate residual motion; the remaining frames are nearly ‘frozen’ completely. It should be noted that after optical stabilization was activated, the two non-naïve participants (NOR046a & NOR047a) reported that in many of the trials the imaging field appeared to fade away. This is the well-known phenomenon of Troxler fading [40], which occurs when an image is stabilized on the retina [41]. For these experienced observers, microsaccades often occurred shortly after they noticed the Troxler fading, as they made reflexive movements to reestablish the raster image. Troxler fading was usually noticed several seconds after optical tracking was activated.
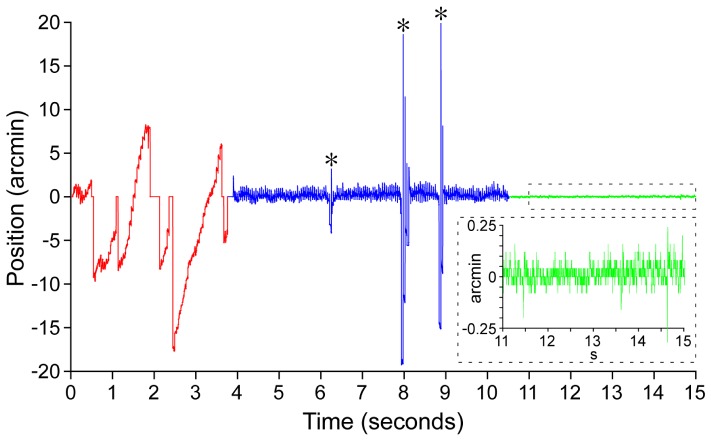
The motion trace calculated from Media 2 (2.4MB, MPEG) is shown in Fig. 5. Eye motion without optical stabilization was 5.4 arcmin (~26.9 µm) RMS; after optical stabilization it was 0.48 arcmin (~2.4 µm) RMS; after both optical stabilization and digital registration it was 0.034 arcmin (~0.17 µm) RMS. It should be reiterated that blinks and motion outside the range of the tracking algorithm (ie. frame out) are not counted in the RMS values reported here, as accurate measurements were outside the capability of this method. In Fig. 5, for example, after optical tracking is turned on, the position values for the three spikes denoted by the asterisks are not counted. This isimplemented by adding a second round of cross-correlation, where the stabilized images are correlated with the reference directly, with a correlation threshold of 0.85. This step is defined as ‘error-proofing’ which kicks out all spurious motions from the optically stabilized and digitally registered images. We found that the method also performed quite well on low contrast images; this is illustrated in Media 3 (580.5KB, MPEG) .
Fig. 5.
Eye motion trace computed from the image sequence shown in Media 2 (2.4MB, MPEG) , showing vertical (y) component of eye motion before (red) and after optical stabilization alone (blue) and optical stabilization combined with digital registration (green). Inset shows zoomed in trace for the region denoted by the dashed rectangle. Asterisks denote spurious motion measurements during blinks or large amplitude motion (see Appendix for details).
We acquired 184 image sequences from the five participants. Optical stabilization failed completely in only one trial (location: 3°, –6°) in one participant (NOR037a); in this case, the eye moved too fast at large amplitude (i.e. microsaccades were too frequent) for the operator to manually select a good reference frame. Table 2 lists the performance of optical stabilization for the remaining 183 trials. Residual RMS ranged from 0.34 to 0.53 arcmin (~1.65–2.50 µm). Tracking efficiency, defined as the ratio of successfully stabilized frames to the total number of frames after tracking, was 85%, on average, and ranged from 76 to 92%, depending upon the observer. Tracking efficiency was correlated with the occurrence rate of blinks and microsaccades. The residual RMS after digital registration from all five subjects ranged from 0.04 to 0.05 arcmin (~0.20–0.25 μm).
Table 2. Optical stabilization system performance for each participant.
| Subject ID | Total Trials | Failed Trials | Tracked Frames | Failed Frames | Tracking Efficiency | Residual RMS (arcmin) |
||
|---|---|---|---|---|---|---|---|---|
| (x) | (y) | (r) | ||||||
| NOR011a | 31 | 0 | 11,357 | 2686 | 76% | 0.38 | 0.57 | 0.42 |
| NOR025a | 39 | 0 | 11,729 | 2039 | 83% | 0.27 | 0.37 | 0.34 |
| NOR037a | 36 | 1 | 14,154 | 2090 | 85% | 0.38 | 0.54 | 0.53 |
| NOR046a | 40 | 0 | 13,585 | 1044 | 92% | 0.30 | 0.42 | 0.39 |
| NOR047a | 37 | 0 | 7,645 | 952 | 88% | 0.29 | 0.40 | 0.35 |
4. Discussion
Our method is compared to previous methods in Table 3. To our knowledge, the combination of optical stabilization and digital registration reported here is more accurate than any other method reported in the literature. The performance of optical stabilization alone is comparable only to the optical lever technique [19,20] and is nearly 10 times better than the optical tracking performance previously reported by Hammer and colleagues in AOSLO [34]. The combined performance from optical stabilization and digital registration is ~3–4 times better than digital tracking alone, as reported by two of the authors in an earlier paper [29]. Moreover, the success rate of tracking (183/184) and tracking efficiency (85%, on average) is significantly higher than that reported previously for digital stabilization alone [29].
Table 3. Comparison to other stabilization and registration methods.
| Method | Optical stabilization (arcmin) | Digital registration (arcmin) | Description |
|---|---|---|---|
| Rochester AOSLO (this report) | 0.34–0.53 | 0.04–0.05 | Optical stabilization with digital registration |
| Berkeley AOSLO [29] | N/A | 0.15 | Digital image registration only |
| PSI-IU WF-SLO [34] | 3–4 | N/A | Utilized optic disk reflectometer for optical stabilization |
| Optical lever [19,20] | 0.2–0.38 | N/A | Direct optical coupling via rigid contact lens |
| Dual Purkinje (DPI) eye tracker with optical deflector [21,22] | 1 | N/A | Measures displacements of Purkinje reflexes from cornea and lens; coupled to optical deflector |
| EyeRis™ [23] | 1 | N/A | DPI with gaze contingent display |
Interestingly, tracking efficiency (reported in Table 2) appeared to be directly related to imaging duration. Tracking efficiency appeared to gradually decrease as imaging duration increased. As noted above, tracking efficiency is directly correlated with the number of frames that can be tracked; we are unable to track blinks and large amplitude motion, such as microsaccades. It appears that this may be related to increased fatigue, as microsaccade frequency appears to decrease after participants take a short break. This phenomenon was consistent across all five subjects and warrants further investigation.
There are several changes that can be implemented to the current system to improve performance, including: increasing the accuracy of digital registration by employing sub-pixel cross-correlation, implementing real-time ‘error-proofing’ and incorporating automatic reference frame selection. One possible solution for sub-pixel cross correlation is to implement either the approach of Guizar-Sicairos and colleagues [42] or Mulligan [43]. The ‘error proofing’ step is currently implemented offline, but it will be implemented in real-time by placing this computation during the retrace period of the slow scanner. Algorithmic automatic reference frame selection may be able to solve the problem for the one failed trial in which the algorithm could not be locked manually. Future work is needed to determine appropriate image metrics to use for reference frame selection. In addition, a method is needed for removing intraframe distortion from the reference frame, as these distortions will be encoded into the registered images. A solution to this problem may be possible by using multiple frames to synthesize a reference image that is free of intraframe distortions. It should be noted that torsional eye movements (rotations about the line of sight) are not corrected; this is perhaps the greatest limitation of this approach. We have calculated the image rotation for the 1.5° × 1.5° AOSLO imaging field at the gaze locations used here, and found that it was <0.05° for the 20-second video sequences we acquired. After Stevenson and Roorda [9], we calculated image rotation by dividing each long horizontal strip equally into two strips and measured the displacement of these image patches on consecutive frames. Cross-correlation was used to calculate the translation between the two strips on the left and right side of each image, defined as (xL, yL) and (xR, yR). The difference of (yL - yR) was ~0.1–0.2 pixels, on average; the distance between left and right strips was 256 pixels. Therefore, the maximum torsion in a single 20-second video was: 0.2/256 × 180/π = 0.045° (~2.7 arcmin). We occasionally saw larger torsion (e.g. ≥1°). In these cases the tracking algorithm simply fails, requiring either 1) a new reference frame, or 2) a delay until the eye rotates back sufficiently so that the algorithm may re-lock.
Further system improvement can be attained with the use of faster mirrors. The mechanical performance of the TTM we used decreases with increased input frequency, so stabilization performance decreases as the frequency of the motion increases. The Nyquist frequency of the tracking algorithm is equal to ½ of the strip rate, which in this implementation is 426 Hz. However, there are potential aliasing problems from the implementation of the imaging system and the no-data gap during retrace interval which have not been fully characterized and merit further study.
Additionally, it is worthwhile to implement a faster frame rate, e.g., by increasing the speed of the resonant scanner. It should be noted that we could increase the frame rate without increasing the resonant scanner speed but this would reduce the number of lines per frame, increasing the frequency of ‘frame out’ errors. Increasing the resonant scanner rate could substantially reduce the within frame distortions that are a major problem for clinical imaging, particularly longitudinal studies of eye disease. We are exploring the possibility of using different mirror technologies, such as polygonal or MEMS-based scanning mirrors in future systems. A polygonal mirror would obviate the need for image rectification as it would produce a linear image but we have not determined whether the mechanical stability will be sufficient for our purposes. MEMS-based mirrors are available that scan at high rates, but the small size of these mirrors pose challenges for optical design and implementation.
From Fig. 5 it can be seen that despite the improved performance demonstrated here, this tracking system still has several disadvantages: 1) it does not take full advantage of the tracking range of the tip/tilt mirror, 2) it has difficulty stabilizing fast relatively large amplitude motion (ie. microsaccades), 3) it still suffers from ‘frame-out’ (when the motion is greater than can be covered by the current reference frame or strip, see Appendix for details on this issue), and 4) it has difficulty resetting the position of the tracking mirror after microsaccades, blinks, and/or frame-out.
5. Conclusions
-
1)
Optical stabilization can be accomplished in an AOSLO by replacing the existing 1-D slow scanner with a 2-axis tip/tilt mirror
-
2)
Optical stabilization was successful in all but one of 183 trials. On average, 85% of all frames were successfully stabilized.
-
3)
Optical stabilization reduced eye motion from several to tens of arcmin to ~0.34-0.53 arcmin (~1.66–2.56 µm).
-
4)
Digital registration of residual RMS eye motion after optical stabilization was accurate to ~0.04-0.05 arcmin (~0.20–0.25µm)
-
5)
Tracking efficiency decreased as imaging duration increased, likely reflecting an increase in the microsaccade and blink rate with fatigue.
Acknowledgments
The authors wish to thank our collaborators on our Bioengineering Research Partnership: David W. Arathorn, Steven A. Burns, Alf Dubra, Daniel R. Ferguson, Daniel X. Hammer, Scott B. Stevenson, Pavan Tiruveedhula, and Curtis R. Vogel, whose work formed the foundation of the advances presented here. The authors also wish to thank Mina M. Chung and Lisa R. Latchney for their assistance with recruiting and coordinating participants. Research reported in this publication was supported by the National Eye Institute of the National Institutes of Health under grants EY014375 and EY001319. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. This research was also supported by a research grant from Canon, Inc. and by unrestricted departmental grants from Research to Prevent Blindness.
6. Appendix
6.1 FFT cross-correlation
To implement image-based eye motion calculation, we employed the widely used FFT-based cross-correlation. FFT-based cross-correlation was chosen for motion tracking because it has been proven to be robust and successful [34–36], and can be implemented for fast execution on specialized processors such as GPUs, Digital Signal Processors (DSP), or FPGAs. For convenience of coding and maintenance, we offloaded all computation intensive eye motion calculations to the GPU and utilized NVIDIA Compute Unified Device Architecture (CUDA) technologies such as CFFT, shared memory and textures to speed up data processing.
For the motion tracking algorithm to run efficiently in real-time, an appropriate balance must be found between computational speed and robustness. Our goal is to make the algorithm sufficiently fast to run in real-time while still generating accurate measurements of retinal image motion. The computational cost of FFT cross-correlation can be analyzed by examining each step of a single calculation, shown in Eqs. (7)-(11),
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
where r(x,y) is the reference image, t(x,y) is the target image, FFTR2C() is the forward 2D real-to-complex FFT operator this is implemented with the CUDA function cufftExecR2C, FFT−1C2R() is the inverse 2D complex-to-real FFT operator (also implemented with cufftExecR2C),, A(u,v), R(u,v), and T(u,v) are images in frequency domain. (x,y)max is the translation between the reference image r(x,y) and the target image t(x,y). The most costly computations are the FFT operations (ie. Eqs. (7), (8) and (10)). In a serial processor, Eq. (9) involves 4N floating-point multiplication and 2N floating-point addition where N is the number of pixels in an image, but the computation is substantially accelerated on a multi-core GPU. Computation time for Eq. (11) is trivial compared to the other four. Therefore, a typical cycle of one motion measurement involves three FFT operations from Eqs. (7), (8) and (10) and one dot product from Eq. (9).
To minimize computational cost for cross-correlation, we reduce both the number of FFT operations per iteration and the size of the image. Each time we perform a new cross-correlation, we only perform two FFT operations instead of three. This is accomplished by storing in memory all FFTs that are required for future computations, such as all of the FFTs from the reference image (which are computed and stored only once, just before the tracking algorithm is activated). In addition, we utilize the smallest image size (N) possible for each stage of the algorithm (as described below).
6.2 Small amplitude motion tracking
Fig. 6.

Small amplitude motion is calculated by comparing strips of data between consecutive frames. This works well when the motion between frames is small (such as between frame Fr and Fn. However, this fails when the between frame motion is large (such as between frame Fr and frame Fn + 1).
shows three frames from an AOSLO image sequence illustrating typical small amplitude eye motion for a healthy normal observer. To obtain motion measurements at a frequency greater than the frame rate, which is required for real-time optical stabilization and digital image registration, we divide each frame into multiple strips along the orientation of the slow AOSLO scan. In the example shown in Fig. 6, the fast scan is horizontal and the slow scan is vertical. Individual strips are denoted as the red rectangles: k, k+1, k+2, and k+3. When the motion between frames is small, such as between frames Fr and Fn in Fig. 6, cross-correlation between two strips with the same index (e.g. strips k+1) returns the translation of that strip. However, when the amplitude of the motion is large, there are cases when there is no overlap between any pair of strips with the same index from the reference frame Fr and frame Fn+1. In practice, we have found that the tracking algorithm requires ~32 lines (ie. two data acquisition strips of 16 pixels each) for a robust cross-correlation result for our typical AOSLO images. It should be noted that the minimum image size for robust cross-correlation is highly application dependent; we have found that this height is sufficient for images of the photoreceptor mosaic from multiple AOSLO instruments. More work is needed to determine the absolute minimum size as well as the appropriate size for images of other retinal layers.
Due to the nature of the scanning system and the strip level data acquisition scheme, the tracking algorithm is more susceptible to ‘frame-out’ when motion is orthogonal to the fast scan axis. Frame-out occurs when an acquired strip falls outside of the reference frame. Each strip is much smaller in the slow direction (ie. 32 pixels high vs. 512 pixels wide); therefore a much smaller amount of motion will bring a strip outside the range of the corresponding comparison strip on the reference frame.
To increase the probability of having sufficient overlap when using a small strip size, we first calculate the full frame motion between the previously acquired frame and the reference frame. This is illustrated in Fig. 7
Fig. 7.
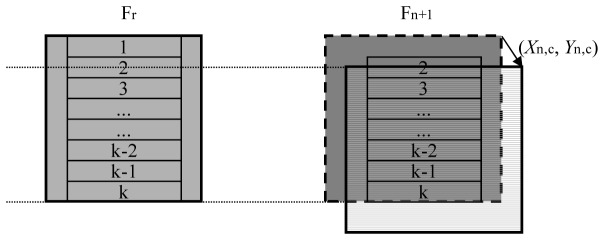
A frame offset (Xn,c,Yn,c) is applied before calculating strip motion to increase the probability that strips on the current frame will be compared with the appropriate overlapping strips on the reference frame (Fr)
, where Fr is the reference frame, Fn is the frame whose eye motion has just been detected, and Frame Fn+1 is the target frame for strip motion calculation. The frame motion (Xn,c, Yn,c) between frames Fr and Fn is computed after all of frame Fn has been acquired but before the first strip of frame Fn+1 is received. In the AOSLO system, this computation is conveniently placed during the retrace period of the slow scanner.
Computational cost is reduced for calculating the frame motion (Xn,c, Yn,c) by using only the central portion of the frame for cross-correlation. We typically use a portion of the frame that is twice the height of a single strip, as illustrated by the shaded region of the reference frame (Fr) shown in Fig. 8
Fig. 8.
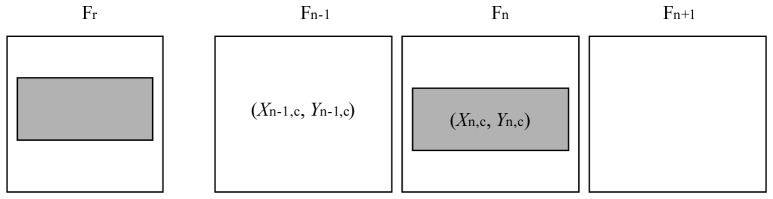
The computational cost of the frame offset (Xn,c,Yn,c) calculation is reduced by using only the central portion of the frame (denoted by the shaded region).
. As mentioned previously, the cross-correlation calculation is also reduced to only 2 FFT calculations here, as the FFT for this sub region of the reference frame was calculated when it was selected as the reference frame. To calculate the frame motion of the current target frame (Fn), the algorithm crops a patch of the same size from frame Fn, but with the offset between the previous frame and the reference frame applied (Xn-1,c, Yn-1,c). Frame motion is measured differently for large amplitude motion detection, as described in section 6.3, below.
6.3 Large amplitude motion and blink detection
Large amplitude motion and blinks are detected using the same FFT-based cross-correlation algorithm. However, in this case we calculate the motion (dXn,dYn) between consecutive frames and use strips from the same image location (ie. strip k is always compared to strip k, etc.), as illustrated in Fig. 9
Fig. 9.
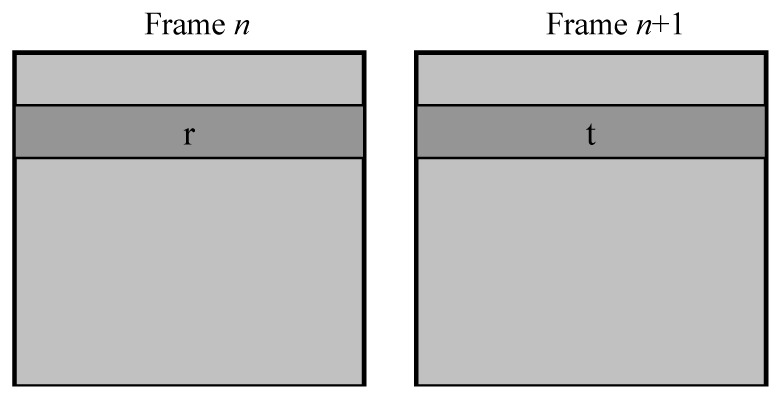
Large amplitude motion and blink detection computes motion between consecutive frames using strips from the same frame position (denoted by the darker shading).
. Large amplitude motion is considered to be detected when the relative motion is greater than a user-specified threshold and a blink is considered to be detected when the correlation coefficient drops below a user specified threshold. The user-defined thresholds may vary from subject to subject, and from system to system, but for the purposes of this study we used thresholds of: motion greater than 30 pixels and correlation coefficients less than 0.2–0.3. We use this low correlation coefficient threshold for two reasons: 1) in many clinical imaging situations, particularly with diseased eyes, images have very low contrast and high noise and do not produce correlation coefficients greater than 0.5–0.6, even between two consecutive frames, and 2) as discussed before, we use sparse matrices instead of full matrices for cross correlation. The image size used for this stage is typically the same as that used for the frame motion calculation described previously (ie. twice the small amplitude motion strip size, or 64 pixels in this case). These values can be adjusted to tolerate more or less error as required for the particular experiment or application. To reduce computational cost in our real-time system, the algorithm only looks at the first four pairs of strips from the two consecutive frames. These four pairs of strips usually cover about the first half of each frame (e.g. here we use 4 strips of 64 lines each, so 256/576 or ~44% of the frame). As stated in section 2.2 above, the PC threads for detecting large and small amplitude motion run simultaneously. When any strip pair reports large amplitude motion or a blink, the algorithm immediately stops calculating small amplitude motion for the rest of the strips from the current target frame and starts the ‘re-locking’ procedure (outlined in section 6.4, below). It should be noted that this approach may exclude some ‘good’ data strips from the current target frame, but it was implemented in this way so as to free up sufficient processing power for the computationally costly re-locking procedure.
6.4 Re-locking after large amplitude motion and blinks
In order to re-lock eye position after large amplitude motion or a blink, the algorithm increases the cross-correlation image size to the entire frame. This allows it to cover the largest eye motion possible with FFT based cross-correlation, thus increasing the probability that it will re-lock, but it comes at a huge computational cost due to the increased image size. To reduce the image size in this implementation, we downsample the image to half its size, either by sampling alternative pixels or binning 2×2 pixels to 1 pixel. This reduces computational complexity, but also reduces computational accuracy to 2 pixels. Downsampling could be 3×3 or more depending upon the particular application but will further reduce accuracy.
The algorithm will continue to cross-correlate downsampled full frames until the cross-correlation coefficient rises back above a user specified threshold. When this happens, the algorithm returns a frame motion (Xn,Yn) between the current frame, Fn, and the reference frame, Fr. However, this alone is insufficient to consider the tracking algorithm to be re-locked. The algorithm will then use (Xn,Yn) as an offset to calculate the motion (Xn+1,Yn+1) between the reference frame and the next frame (Fn+1). Simultaneously, the algorithm re-enters the large amplitude & blink detection stage of processing to calculate the motion (dXn+1, dYn+1) of the central patch between consecutive frames Fn and Fn+1. The algorithm then computes the difference between ((Xn+1,Yn+1)-(Xn,Yn)) and (dXn+1, dYn+1). If this value is less than a user-defined threshold (typically 50% of the small amplitude motion strip height or 32 pixels, in this case) then the algorithm has successfully re-locked. Otherwise it will continue calculating full frame cross-correlations until it re-locks, is stopped, or a new reference frame is selected. After re-locking, the frame motion (Xn,c, Yn,c) is used to coarsely orient the frames so that small amplitude, fine motion calculations can resume.
References and links
- 1.Liang J., Williams D. R., Miller D. T., “Supernormal vision and high-resolution retinal imaging through adaptive optics,” J. Opt. Soc. Am. A 14(11), 2884–2892 (1997). 10.1364/JOSAA.14.002884 [DOI] [PubMed] [Google Scholar]
- 2.Roorda A., Romero-Borja F., Donnelly Iii W., Queener H., Hebert T., Campbell M., “Adaptive optics scanning laser ophthalmoscopy,” Opt. Express 10(9), 405–412 (2002). 10.1364/OE.10.000405 [DOI] [PubMed] [Google Scholar]
- 3.Williams D. R., “Imaging single cells in the living retina,” Vision Res. 51(13), 1379–1396 (2011). 10.1016/j.visres.2011.05.002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Rossi E. A., Chung M., Dubra A., Hunter J. J., Merigan W. H., Williams D. R., “Imaging retinal mosaics in the living eye,” Eye (Lond.) 25(3), 301–308 (2011). 10.1038/eye.2010.221 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Martinez-Conde S., Macknik S. L., Hubel D. H., “The role of fixational eye movements in visual perception,” Nat. Rev. Neurosci. 5(3), 229–240 (2004). 10.1038/nrn1348 [DOI] [PubMed] [Google Scholar]
- 6.Rolfs M., “Microsaccades: Small steps on a long way,” Vision Res. 49(20), 2415–2441 (2009). 10.1016/j.visres.2009.08.010 [DOI] [PubMed] [Google Scholar]
- 7.Rossi E. A., Achtman R. L., Guidon A., Williams D. R., Roorda A., Bavelier D., Carroll J., “Visual Function and Cortical Organization in Carriers of Blue Cone Monochromacy,” PLoS ONE 8(2), e57956 (2013). 10.1371/journal.pone.0057956 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Vogel C. R., Arathorn D. W., Roorda A., Parker A., “Retinal motion estimation in adaptive optics scanning laser ophthalmoscopy,” Opt. Express 14(2), 487–497 (2006). 10.1364/OPEX.14.000487 [DOI] [PubMed] [Google Scholar]
- 9.S. B. Stevenson and A. RoordaF. Manns, P. G. Söderberg, A. Ho, B. E. Stuck, and M. Belkin, eds., “Correcting for miniature eye movements in high resolution scanning laser ophthalmoscopy,” in Ophthalmic Technologies XV,Proceedings of SPIE, F. Manns, P. G. Söderberg, A. Ho, B. E. Stuck, and M. Belkin, eds. (SPIE, Bellingham, WA, 2005), Vol. 5688, pp. 145–151. 10.1117/12.591190 [DOI] [Google Scholar]
- 10.Ott D., Eckmiller R., “Ocular torsion measured by TV- and scanning laser ophthalmoscopy during horizontal pursuit in humans and monkeys,” Invest. Ophthalmol. Vis. Sci. 30(12), 2512–2520 (1989). [PubMed] [Google Scholar]
- 11.Ott D., Lades M., “Measurement of eye rotations in three dimensions and the retinal stimulus projection using scanning laser ophthalmoscopy,” Ophthalmic Physiol. Opt. 10(1), 67–71 (1990). 10.1111/j.1475-1313.1990.tb01109.x [DOI] [PubMed] [Google Scholar]
- 12.Ott D., Daunicht W. J., “Eye-Movement Measurement with the scanning laser ophthalmoscope,” Clin. Vis. Sci. 7, 551–556 (1992). [Google Scholar]
- 13.Stetter M., Sendtner R. A., Timberlake G. T., “A novel method for measuring saccade profiles using the scanning laser ophthalmoscope,” Vision Res. 36(13), 1987–1994 (1996). 10.1016/0042-6989(95)00276-6 [DOI] [PubMed] [Google Scholar]
- 14.Burns S. A., Tumbar R., Elsner A. E., Ferguson D., Hammer D. X., “Large-field-of-view, modular, stabilized, adaptive-optics-based scanning laser ophthalmoscope,” J. Opt. Soc. Am. A 24(5), 1313–1326 (2007). 10.1364/JOSAA.24.001313 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Harvey Z., Dubra A., “Registration of 2D Images from Fast Scanning Ophthalmic Instruments,” in Biomedical Image Registration, Fischer B., Dawant B. M., Lorenz C., eds., Lecture Notes in Computer Science No. 6204 (Springer Berlin Heidelberg, 2010), pp. 60–71. [Google Scholar]
- 16.Dodge R., Cline T. S., “The angle velocity of eye movements,” Psychol. Rev. 8(2), 145–157 (1901). 10.1037/h0076100 [DOI] [Google Scholar]
- 17.Nachmias J., “Two-Dimensional Motion of the Retinal Image during Monocular Fixation,” J. Opt. Soc. Am. 49(9), 901–908 (1959). 10.1364/JOSA.49.000901 [DOI] [PubMed] [Google Scholar]
- 18.Riggs L. A., Armington J. C., Ratliff F., “Motions of the Retinal Image during Fixation,” J. Opt. Soc. Am. 44(4), 315–321 (1954). 10.1364/JOSA.44.000315 [DOI] [PubMed] [Google Scholar]
- 19.Riggs L. A., Schick A. M., “Accuracy of retinal image stabilization achieved with a plane mirror on a tightly fitting contact lens,” Vision Res. 8(2), 159–169 (1968). 10.1016/0042-6989(68)90004-7 [DOI] [PubMed] [Google Scholar]
- 20.Jones R. M., Tulunay-Keesey T., “Accuracy of image stabilization by an optical-electronic feedback system,” Vision Res. 15(1), 57–61 (1975). 10.1016/0042-6989(75)90059-0 [DOI] [PubMed] [Google Scholar]
- 21.Cornsweet T. N., Crane H. D., “Accurate two-dimensional eye tracker using first and fourth Purkinje images,” J. Opt. Soc. Am. 63(8), 921–928 (1973). 10.1364/JOSA.63.000921 [DOI] [PubMed] [Google Scholar]
- 22.Crane H. D., Steele C. M., “Generation-V dual-Purkinje-image eyetracker,” Appl. Opt. 24(4), 527 (1985). 10.1364/AO.24.000527 [DOI] [PubMed] [Google Scholar]
- 23.Santini F., Redner G., Iovin R., Rucci M., “EyeRIS: a general-purpose system for eye-movement-contingent display control,” Behav. Res. Methods 39(3), 350–364 (2007). 10.3758/BF03193003 [DOI] [PubMed] [Google Scholar]
- 24.Mulligan J. B., in Recovery of Motion Parameters from Distortions in Scanned Images, Le Moigne J., ed. (NASA Goddard Space Flight Center, 1997), pp. 281–292. [Google Scholar]
- 25.Arathorn D. W., Yang Q., Vogel C. R., Zhang Y., Tiruveedhula P., Roorda A., “Retinally stabilized cone-targeted stimulus delivery,” Opt. Express 15(21), 13731–13744 (2007). 10.1364/OE.15.013731 [DOI] [PubMed] [Google Scholar]
- 26.Sincich L. C., Zhang Y., Tiruveedhula P., Horton J. C., Roorda A., “Resolving single cone inputs to visual receptive fields,” Nat. Neurosci. 12(8), 967–969 (2009). 10.1038/nn.2352 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Arathorn D. W., Stevenson S. B., Yang Q., Tiruveedhula P., Roorda A., “How the unstable eye sees a stable and moving world,” J. Vis. 13(10), 22 (2013). 10.1167/13.10.22 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Harmening W. M., Tuten W. S., Roorda A., Sincich L. C., “Mapping the Perceptual Grain of the Human Retina,” J. Neurosci. 34(16), 5667–5677 (2014). 10.1523/JNEUROSCI.5191-13.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Yang Q., Arathorn D. W., Tiruveedhula P., Vogel C. R., Roorda A., “Design of an integrated hardware interface for AOSLO image capture and cone-targeted stimulus delivery,” Opt. Express 18(17), 17841–17858 (2010). 10.1364/OE.18.017841 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Sheehy C. K., Yang Q., Arathorn D. W., Tiruveedhula P., de Boer J. F., Roorda A., “High-speed, image-based eye tracking with a scanning laser ophthalmoscope,” Biomed. Opt. Express 3(10), 2611–2622 (2012). 10.1364/BOE.3.002611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Vienola K. V., Braaf B., Sheehy C. K., Yang Q., Tiruveedhula P., Arathorn D. W., de Boer J. F., Roorda A., “Real-time eye motion compensation for OCT imaging with tracking SLO,” Biomed. Opt. Express 3(11), 2950–2963 (2012). 10.1364/BOE.3.002950 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Braaf B., Vienola K. V., Sheehy C. K., Yang Q., Vermeer K. A., Tiruveedhula P., Arathorn D. W., Roorda A., de Boer J. F., “Real-time eye motion correction in phase-resolved OCT angiography with tracking SLO,” Biomed. Opt. Express 4(1), 51–65 (2013). 10.1364/BOE.4.000051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ferguson R. D., Zhong Z., Hammer D. X., Mujat M., Patel A. H., Deng C., Zou W., Burns S. A., “Adaptive optics scanning laser ophthalmoscope with integrated wide-field retinal imaging and tracking,” J. Opt. Soc. Am. A 27(11), A265–A277 (2010). 10.1364/JOSAA.27.00A265 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hammer D. X., Ferguson R. D., Bigelow C. E., Iftimia N. V., Ustun T. E., Burns S. A., “Adaptive optics scanning laser ophthalmoscope for stabilized retinal imaging,” Opt. Express 14(8), 3354–3367 (2006). 10.1364/OE.14.003354 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dubra A., Sulai Y., “Reflective afocal broadband adaptive optics scanning ophthalmoscope,” Biomed. Opt. Express 2(6), 1757–1768 (2011). 10.1364/BOE.2.001757 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Rossi E. A., Rangel-Fonseca P., Parkins K., Fischer W., Latchney L. R., Folwell M. A., Williams D. R., Dubra A., Chung M. M., “In vivo imaging of retinal pigment epithelium cells in age related macular degeneration,” Biomed. Opt. Express 4(11), 2527–2539 (2013). 10.1364/BOE.4.002527 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Brainard D. H., “The psychophysics toolbox,” Spat. Vis. 10(4), 433–436 (1997). 10.1163/156856897X00357 [DOI] [PubMed] [Google Scholar]
- 38.Kleiner M., Brainard D., Pelli D. G., “What’s new in Psychtoolbox-3?” Perception 36, 1 (2007). [Google Scholar]
- 39.Pelli D. G., “The VideoToolbox software for visual psychophysics: Transforming numbers into movies,” Spat. Vis. 10(4), 437–442 (1997). 10.1163/156856897X00366 [DOI] [PubMed] [Google Scholar]
- 40.D. (I.P.V.) Troxler , “Über das Verschwinden gegebener Gegenstände innerhalb unseres Gesichtskreises. [On the disappearance of given objects from our visual field],” Ophthalmol. Bibl. Ger. 2, 1–53 (1804). [Google Scholar]
- 41.Riggs L. A., Ratliff F., Cornsweet J. C., Cornsweet T. N., “The Disappearance of Steadily Fixated Visual Test Objects,” J. Opt. Soc. Am. 43(6), 495–501 (1953). 10.1364/JOSA.43.000495 [DOI] [PubMed] [Google Scholar]
- 42.Guizar-Sicairos M., Thurman S. T., Fienup J. R., “Efficient subpixel image registration algorithms,” Opt. Lett. 33(2), 156–158 (2008). 10.1364/OL.33.000156 [DOI] [PubMed] [Google Scholar]
- 43.Mulligan J. B., “Image processing for improved eye-tracking accuracy,” Behav. Res. Methods Instrum. Comput. 29(1), 54–65 (1997). 10.3758/BF03200567 [DOI] [PubMed] [Google Scholar]