Optical coherence Doppler tomography for quantitative cerebral blood flow imaging

Abstract

Optical coherence Doppler tomography (ODT) is a promising neurotechnique that permits 3D imaging of the cerebral blood flow (CBF) network; however, quantitative CBF velocity (CBFv) imaging remains challenging. Here we present a simple phase summation method to enhance slow capillary flow detection sensitivity without sacrificing dynamic range for fast flow and vessel tracking to improve angle correction for absolute CBFv quantification. Flow phantom validation indicated that the CBFv quantification accuracy increased from 15% to 91% and the coefficient of variation (CV) decreased 9.3-fold; in vivo mouse brain validation showed that CV decreased 4.4-/10.8- fold for venular/arteriolar flows. ODT was able to identify cocaine-elicited microischemia and quantify CBFv disruption in branch vessels and capillaries that otherwise would have not been possible.

1. Introduction

Cerebral blood flow (CBF) plays a crucial role in brain physiology, metabolism and function. For example, to uncover the temporal-spatial patterns of neurovascular coupling during neural activity is of great importance for understanding functional variations in cerebral cortical activity [1–4], which serves as the fundamental principle of many imaging technologies for brain functional studies. Intravital two-photon microscopy has been widely utilized to explore the velocity change of red blood cells (RBCs) in a microvascular vessel in response to brain stimulation by tracking the time-lapse shadowgraph of fluorescently labeled RBCs flowing through an individual micro-vessel [5]. Despite high resolution and sensitivity, this method suffers from a small field of view (FOV), allowing to only measure a few vessels and thus is unable to quantitatively map the heterogeneity of cerebral vascular flow networks and their dynamics. On the other hand, the blood-oxygenation level dependent (BOLD) signal of fMRI provides hemodynamic information of the entire brain by sensing paramagnetic deoxy-haemoglobin in venous blood [6], but its limited spatial resolution does not allow for resolving vessel compartments and cannot distinguish flow changes from individual vessels, which can be important to understand the mechanisms of downstream responses to specific brain activations and brain dysfunction. Therefore, there is a need to bridge the gap between these two groups of image modalities.

In recently years, new imaging modalities such as optical coherence Doppler tomography (ODT) have demonstrated the potential for 3D imaging of the cerebral blood flow velocity (CBFv) network on the brain cortex [5, 7–11]. Unlike two-photon microscopy that requires fluorescence tracker, ODT detects blood flow velocity based on the intrinsic Doppler effect of moving scatterers (mostly of RBCs) in the blood stream [12], thus circumventing the need for fluorescence labeling which may induce potential side effects. A major difficulty for Doppler flow imaging is to separate Doppler flow signal from background noise, e.g., induced by tissue micromotion and heterogeneity. Several methods have been reported to tackle the challenge. For instance, Wang et al. reported optical angiography (OAG) by separating moving and static scattering elements within tissue [13]. Mariampillai et al. utilized speckle variance across multiple frames to visualize blood flow in the mouse dorsal skinfold [14, 15]. These methods have dramatically improved detection for measuring the subsurface microvasculature though they do not necessarily provide directional flow detection [16]. However, in many biomedical applications, e.g., brain functional studies, quantitative CBFv imaging is demanding, which can provide important insights of brain hemodynamics and function/dysfunction. The common approach for phase-based OCT flowmetry [12, 17, 18] was based on the phase subtraction method (PSM) derived by Chen, et al., which reconstructs flow images by measuring the phase difference between successive A-scans [12]. Like any phase-based interference methodology, this method is confronted with two main problems. One is the limited dynamic range due to the 2π periodicity of phase (i.e., ambiguity) or phase ramping [19, 20]. To extend the dynamic range, we showed in our previous work that high flow rate can be retrieved by summing up the number of phase wrapped rings owing to high signal to noise ratio (SNR) of digital frequency ramping method (DFRM) [21]. Importantly, this was the first report of quantitative CBFv imaging from original OCT scan data by solely digital image processing (i.e., no additional phase modulation. e.g., by scanning reference mirror or dense A-scan scheme). Mathematically, the similarity of wrapped and true phase gradient modulo 2π was reported to solve the 1-D phase wrapping issue [22]. However, those approaches were developed to extend dynamic range “upwards” to recover faster flow, whereas the recovery of slow flow (e.g. capillary flow) was neglected, which plays a critical role in neurovascular coupling. Another remaining problem for quantitative CBFv imaging is the Doppler angle coupling that profoundly affects the accuracy of true velocity measurement, especially, when the vessels are oriented horizontally along the cortical surface, resulting in serious underestimation of the flow rates. Therefore, it is of great importance to trace the Doppler angle accurately for retrieving absolute flow velocity.

Several approaches estimated full velocity by introducing transverse velocity based on the Doppler spectrum broadening instead of calculating the phase shift only [23–26]. However, the limited sensitivity for numerical aperture dependent spectrum broadness may restrict the detection of minimal transverse velocity for common low-NA optical systems or may require focal tracking of flows from different depths, i.e., additional imaging time. In addition, more sophisticated ODT systems have been developed with dual or multi-axis detections to potentially improve the estimate of Doppler angles [27, 28].

Ultrahigh-resolution OCT has been comprehensively investigated [29, 30], based on which ultrahigh-resolution optical coherence Doppler tomography (µODT) was developed in our lab to quantify cerebral blood flow disruption elicited by repeated cocaine injections and other manipulations [31]. In this paper, we present methods to improve the quantification of cocaine’s neurotoxic effects on the cortical CBFv network in both acute and chronic animals. A phase summation method was introduced to extend the ODT dynamic range downwards (e.g., enhancing the detection of minimal flow, ν_min) without sacrificing the upper flow detection range. Continuous vessel tracking was applied to improve the angle (cosθ) correction and thus the retrieval of true flow velocity. These methods were validated first in an intralipid flow phantom study and then applied to quantify the flow disruption to the rat brain secondary to acute cocaine challenge and to chronic cocaine exposures. It was also found that the newly upgraded imaging setup using new graphic and parallel computing features allowed for on-site, instantaneous image processing and display of 3D CBFv images and thus allows for the immediate selection of ROIs for tracking the dynamic changes triggered by acute cocaine challenge. However the same methodology could be applied to other types of stimulations (e.g., physiological, other pharmacological agents).

2. Methods

2.1 Animal preparations

CD2 mice (Charles River, Kingston, NY; male, 25-30g/each) were used to conduct the CBFv imaging studies. All of the animal experiments were approved by the Institutional Animal Care and Use Committee of Stony Brook University. Animals were anesthetized with inhalation of 2% isoflurane (in 100% O₂) and mounted on a custom stereotaxic frame to eliminate motion artifacts. A 3 × 3mm² cranial window was created on the right side of the somatosensory motor cortex. The exposed cortical surface was immediately covered with 2% agarose gel and affixed with a 100-µm-thick glass coverslip using biocompatible cyanocrylic glue. The physiological state of the mice, including electrocardiography, respiration rate and body temperature, was continuously monitored (SA Instruments, Stony Brook, NY).

2.2 Optical instrumentation

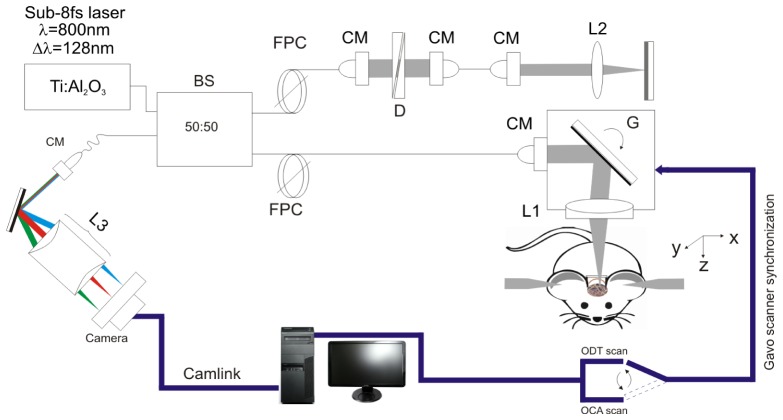
As illustrated in Fig. 1, a custom spectral domain ultrahigh-resolution optical coherence tomography (µOCT) [31, 32] system was used for simultaneous imaging of cortical brain vasculature with ultra-high resolution optical coherence angiography (µOCA) and of 3D quantitative CBFv network with ultrahigh-resolution optical Doppler tomography image (µODT) over a large field of view of 3 × 3 × 1mm³. The µOCT system was illuminated by a sub-8fs Ti:Sapphire laser (λ = 800nm, Δλ≈128nm) and was optimized by spectral reshaping (Δλ_FWHM≈154nm - bandwidth of cross-spectrum [32]) to provide a short coherence length (L_c = 2ln(2)λ²/(πΔλ_FWHM)) of ~2.4μm in free space and ~1.8μm in brain tissue. In the sample arm, a microscopic objective (f16mm/NA0.25) was used to focus the beam on brain cortex and collect backscattered light from brain cortex, providing a transverse resolution of ~3µm. The recombined sample and reference beams that carry spectral interference fringes (i.e., A-scan) were detected by a high-speed linescan camera (2048 pixels; AViiVASM2, Atmel) running at 10kHz. Synchronizing with the servo mirrors (6210H, GSI) for lateral scans, the acquired sequential 3D data set were streamlined to a PCIe SSD for simultaneous µODT and µOCA image processing.

Fig. 1.

A schematic of spectral-domain μOCT system for simultaneous 3D μODT and μOCA imaging. CM: collimator, D: dispersion compensator; FPC: fiber polarization controller, L1, L2, L3: achromatic lenses, G: servo mirrors. BS: beam splitter.

2.3 Cross-platform GUI for instantaneous 3D OCA/ODT image display

In our previous studies, post-image processing was implemented to reconstruct ODT (i.e., CBFv) and OCA images. However, for many neuroimaging studies, instantaneous CBFv image display is crucial to allow for selecting proper ROIs within the heterogeneous CBF networks for dynamic imaging observation, e.g., to track the spontaneous microischemic events elicited by acute cocaine and its recovery process. To tackle the challenge, we developed a graphical user interface (GUI) for real-time ODT image reconstruction. As illustrated in Fig. 2(a), multi-threading processing was implemented to boost computation-intensive image reconstruction tasks, including 6 sub-thread parallel computing: 1) Data acquisition and discrete streaming, 2) K-space linearization [33], 3) FFT or Hilbert transform, 4. amplitude image (OCT) reconstruction, 5) ODT reconstruction, and 6) en face maximum-intensity-projection (MIP) image display of the reconstructed 3D CBFv network. Figure 2(b) shows the GUI module and status during image acquisition, including the displays of 2D OCT image of current scan and instantaneously updating MIP display of 3D CBFv image while the dashed line (A-A') points to the 2D cross-sectional OCT or ODT image (switchable) on the left.

Fig. 2.

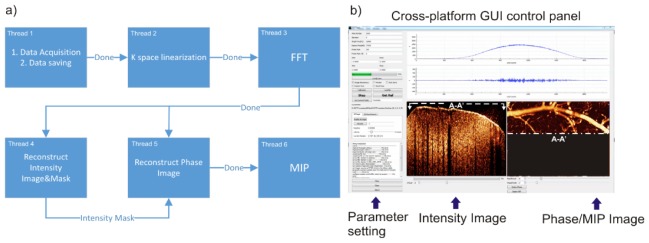
A sketch of new image acquisition and processing GUI to enable instantaneous display of 3D ODT of the quantitative CBFv network. a) Diagram of multi-threading structure with 6 sub-threads running separately with inter-thread data synchronization. b) Screen capture of GUI control panel during scanning CBFv network in vivo.

For reconstruction and display of the en-face CBFv image, both phase subtraction method (PSM, faster) and phase-intensity mapping (PIM, slower but at higher SNR) [31] modules have been included in the GUI platform and many other image processing tools (e.g., median and Gauss filtering) are developed and embedded, among which a unique function that has been found very useful in our studies is a mouse click selection of a smaller ROI to allow for immediate new time-lapse 3D ODT imaging to track the CBFv dynamics responding to cocaine challenge. It is noted that discrete streaming splits large data set (>64MB) into multiple sub blocks (<8MB) to speed up data transfer rate, and full data set has thus been reduced by binning every 2 A-scans to optimize the processing time.

2.4 Phase summation and angle correction to improve CBFv network imaging

As the phase shift (Δϕ: [-π, π]) measured by Doppler flowmetry is a product of flow velocity (ν) and time duration (T) [12], i.e.,

$$v=\frac{{\lambda }_0\Delta \varphi }{4\pi nTcos\theta }$$ (1)

where λ₀ is central wavelength, n is refractive index, and θ is the angle between light propagation and the flow direction. The flow detection sensitivity and the dynamic range contradicts to each other (e.g., phase wrapping artifacts). In the previous study, we reported frequency binning (upward, i.e., T→2T, 3T, ...) [31] to effectively enhance the sensitivity for slow capillary flow detection, but this method restrains its dynamic range (causing faster flows to saturate). Here, we present a new downward binning method that enhances the detection sensitivity of minimum detectable flow (ν_min) without degrading the dynamic range (e.g., reducing phase wrapping threshold). Because of oversampling (commonly used in ODT to improve the phase stability), the spatial separation between two adjacent A-lines is likely as small as a fraction of the lateral resolution, and thus the phase difference (decorrelation) between 2 stationary spots is negligible. Then, the phase shift Δϕ_2T,z(i) between double spaced A-line lines (2T) can be calculated by a summation of phase shifts of 2 adjacent single-spaced A-lines (T), Δϕ_T,z(i), Δϕ_T,z(i + 1), using the autocorrelation algorithm [34],

$$\Delta {\varphi }_{T,z}(\mathrm{i})=\mathrm{arc} \tan \left\{\frac{\mathrm{Im}(A_{i+1,z})\mathrm{Re}(A_{i,z})-\mathrm{Im}(A_{i,z})\mathrm{Re}(A_{i,+1z})}{\mathrm{Im}(A_{i+1,z})\mathrm{Re}(A_{i,z})+\mathrm{Im}(A_{i,z})\mathrm{Re}(A_{i+1,z})}\right\},-\pi \le \Delta {\varphi }_{T,z}(\mathrm{i})\le \pi$$ (2)

where Re(A_i,z) and Im(A_i,z) refer to the real and imaginary parts of the i-th A-scan signal after FFT, and

$$\Delta {\varphi }_{2T,z}(\mathrm{i})=\Delta {\varphi }_{T,z}(\mathrm{i})+\Delta {\varphi }_{T,z}(\mathrm{i}+1),-2\pi \le \Delta {\varphi }_{2T,z}(\mathrm{i})\le 2\pi$$ (3)

This implies that by summing up the successive phase shift Δϕ_T(i) and Δϕ_T(i + 1), the detectable phase range can be extended to [-2π, 2π] because each A-line pair Δϕ_T,z contributes a phase range of [-π,π]. The extension of Doppler velocity dynamic range(VDR) results in preserved phase wrapping threshold (ν_wrap) and a lower (1/2) minimal detectable flow (ν_min→ν_min/2), where ν_wrap and ν_min are defined by the following equations [18, 19],

$$v_{\mathit{wrap}}=\frac{{\lambda }_0\Delta {\varphi }_{\max }}{4\pi nTcos\theta }$$ (4)

$$v_{\min }=\frac{{\lambda }_0{\sigma }_{\Delta \varphi }}{4\pi nT}=\frac{{\lambda }_0{(\mathrm{SNR})}^{-1/2}}{4\pi nT}$$ (5)

$$VDR[\text{dB}]=20\text{log}\left(\frac{V_{\mathit{wrap}}}{v_{\min }}\right)$$ (6)

where σ_Δϕ refers to system phase instability [35]. Also, the decrease of ν_min to half is a result of the doubled time interval (T→2T), and importantly the SNR is preserved by this linear summation algorithm. It is noteworthy to point out the difference of this method from previously reported phase binning method [32] by which, without phase summation Eq. (3), the system dynamic range is still limited within [-π,π] even though the time interval used for phase shift calculation is doubled from T to 2T. Thus limited dynamic range due to doubled time interval could easily cause phase wrapping for high speed flows in the binning method.

2.5 Angle correction

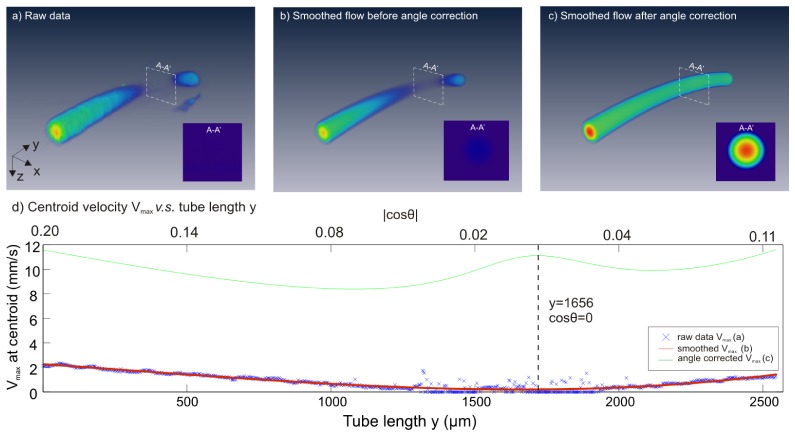
Since vessels in the cortical brain can be horizontally oriented, angle correction is needed to correct measurement errors. Previously θ correction was implemented by using the upper edge or centroid positions of the flow profile across 2-3 adjacent B-scans (cross-sectional images), this method works reasonably well except for flat vessels where θ≈90°, which may lead to severe correction errors (i.e., cosθ→0, 1/cosθ→∞ in Eq. (1) for ν computation). Here, we apply vessel tracking to numerically approach the flow gradient cosθ_z. Vessel skeleton is extracted by tracking the centroid of flow cross-section frame by frame which can be discontinuous due to flat angle of flow direction (Fig. 3(a), 3(b)).

Fig. 3.

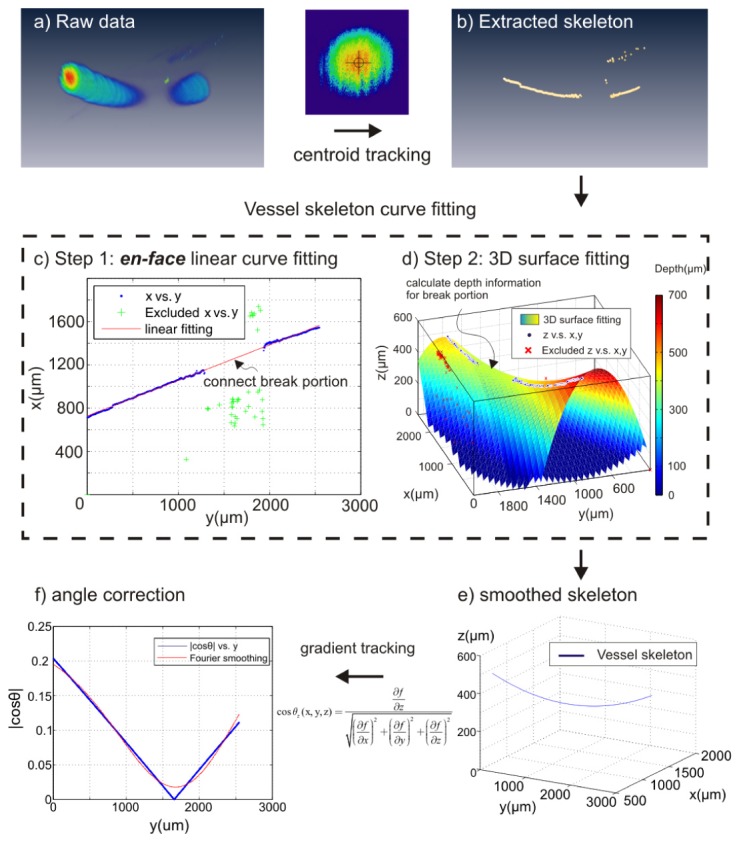
Numerical method for vessel tracking and least-squares fitted angle correction. Vessel skeleton (b) was generated by centroid tracking of the raw data (a). 2D (c) and 3D (d) curve fitting was applied to smoothen raw vessel skeleton extracted by centroid tracking technique, i.e., blue dots in (d). As result of two-step fitting, a vessel skeleton f(x,y,z) was obtained in (e). (f): Doppler angle |cosθ_z(x,y,z)| was calculated by Eq. (9) and further smoothened by Fourier curve (red line) to avoid extreme case when cosθ_z = 0.

It is aimed to obtain a clean and smooth vessel skeleton without a break segment, which can be accomplished by different algorithms. Here we used simple 2-step curve fitting to connect the break segment and further smoothen the vessel skeleton:

• 1. 2D curve fitting fills the skeleton blank on en-face projection image (x-y plane) (Fig. 3(c))

  $$x=a\cdot y+b$$ (7)
• 2, Combing a polynomial 3D surface fitting (Fig. 3(d)) and result of step 1,

  $$z(x,y)=p_{00}+p_{10}\cdot y+p_{01}\cdot x+p_{20}\cdot y^2+p_{11}\cdot \mathit{xy}+p_{02}\cdot x^2$$ (8)

  where p_ij (i, j = 0, 1, 2) are polynomial coefficient. one can obtain the continuous skeleton function f(x,y,z) in 3D (Fig. 3(e)). Thus the cosine of Doppler angle cosθ(x,y,z) can be easily calculated as:

  $$\cos {\theta }_z(\mathrm{x},\mathrm{y},\mathrm{z})=\frac{\frac{\partial f}{\partial z}}{\sqrt{{\left(\frac{\partial f}{\partial x}\right)}^2+{\left(\frac{\partial f}{\partial y}\right)}^2+{\left(\frac{\partial f}{\partial z}\right)}^2}}$$ (9)

  where f(x, y, z) is a 3D skeleton curve and ∂f/∂x, ∂f/∂y, ∂f/∂z are the gradients with respect to the corresponding axes. At θ≈90°, the evaluated ∣cosθ_z(x,y,z)∣ is further smoothened to avoid cosθ = 0 by Fourier curve (Fig. 3(f)). Doppler velocity (v_z) was also tracked by averaging a disk area of radius equal to 10µm at flow centroid, and the true velocity(v_T) was obtained by dividing cosine of Doppler angle, i.e.,

  $$v_z=\frac{{\lambda }_0\Delta \varphi }{4\pi nT}$$ (10)

  $$v_T=\frac{v_z}{\cos {\theta }_z}$$ (11)

3. Results

3.1 Multi-threading GUI to permit instantaneous 3D ODT image processing and display

The ability to instantaneously visualize 3D CBFv network and dynamics is an important feature for neuroimaging studies, e.g., to identify cocaine elicited microischemic events and track its dynamic changes. To facilitate instantaneous en-face image processing, it is required that the image processing time is shorter than the image acquisition time per B-scan to ensure continuously updating of the 3D ODT display (MIP). Additionally, a fast data streaming rate for large data set (>64MB) is highly desirable to meet this requirement. Figure 4 shows that at 10kHz sampling rate (16ks/B-scan) commonly used for CBFv studies, data acquisition using discrete data streaming (1882.3MB/s) is 8.3-fold faster than previously continuous streaming (223.3MB/s) and is only 7.9% longer than the theoretical rate (1.6s). Combined with multi-threading processing and optimized discrete data set allocation, the total time partitioned for en-face reconstruction is 38.4% shorter than that for data acquisition; therefore, the platform has reached the goal for continuous 3D ODT display (MIP) without frame dropping.

Fig. 4.

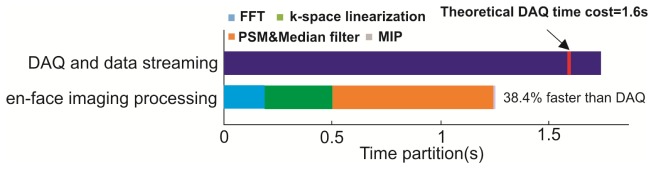
Comparison of time partition between data acquisition thread and phase reconstruction threads.

3.2 Phase summation to enhance CBFv quantification

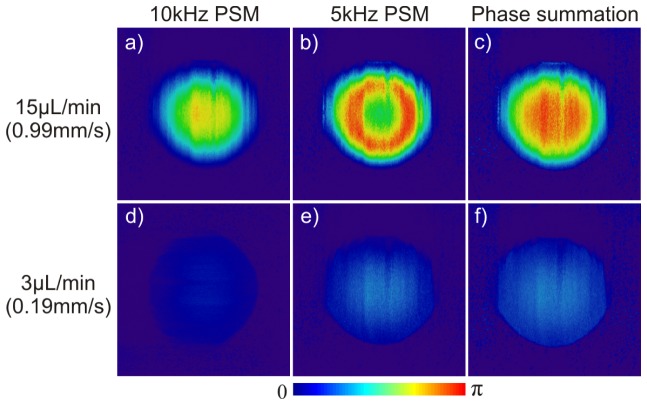
A flow phantom study using 1% intralipid solution pumped through PE10 tubing (CMA400, Microdialysis) was performed to validate the performance improvement of the phase summation method. Figure 5 shows the comparative results of the phase images reconstructed using 3 different methods for fast flow (15µL/min, or line axial velocity of v_max/f = 0.99mm/s) and slow (3µL/min, v_max/s = 0.19mm/s) flow rates at Doppler angle of θ≈83°. PSM at 10kHz provides the best flow velocity profile and accuracy (0.96mm/s, 96.5% of v_max/f) for fast flow showing no phase wrapping artifact (a) but suffers poor sensitivity for slow flow (46.9µm/s) (d), even though the system sensitivity is v_min = 10.3µm/s (SNR = 33.2dB) according to Eq. (5). As a result, only 12% of full dynamic range (π) is detected and the flow profile is barely distinguishable from the background (d). By applying frequency binning to 5kHz as previously reported [31], the detection sensitivity for slow flow increases to 22.1µm/s (e) and the detected phase is doubled to 24.2% of the full range (π), yielding a measured velocity of 0.18mm/s to 93.1% of v_max/s = 0.19mm/s. However, it fails to retrieve the full velocity profile for fast flow (b) because of reduced phase wrapping threshold v_wrap Eq. (4) that leads to phase wrapping artifacts. The detected flow rate (0.34mm/s) is severely underestimated, i.e., only to 33.8% of v_max/f = 0.99mm/s. Interestingly, phase summation method preserves the parabolic velocity profile of the fast flow (c) and the measured maximum velocity of 0.91mm/s is 92.5% of v_max/f = 0.99mm/s; meanwhile, it increases the sensitivity for slow flow (f) to the 26.5µm/s (equivalent to that by frequency binning (e)), yielding a measured velocity of 0.20mm/s and phase shift over 27% of the full range (π). Interestingly, its dynamic range as defined by 20log(v_max/f/v_max/s) is enhanced by 17.5% in method 3 (30.7dB) compared to method 1 (26dB). More dramatic enhancement (i.e., 30.4%) is found in comparison between method 2 (23.5dB) and method 3 (30.7dB) because of no phase wrapping. It should be noted that nonlinear pseudocolor map was applied in method 3 to project the extended phase range [0, 2π] onto [0, π] for comparison purpose.

Fig. 5.

Phantom flow study (1% intralipid, ϕ280µm tubing) to demonstrate that phase summation method enhances the sensitivity for slow flow detection and increases the dynamic range for fast flow detection. All images are projected onto same phase scale [0, π] for comparison.

3.3 Angle correction to enhance absolute flow speed quantification

Gradient vessel tracking method improves the accuracy of ODT for CBFv quantification. A phantom flow study was performed with 1% intralipid pumped at a constant flow rate of 20µL/min or equivalently ν_max = 10.8mm/s in ϕ280µm micro tube. Assume that the phantom follows laminar flow phenomena, then its velocity distribution is characteristic of a parabolic profile that obeys [36]:

$$v(\mathrm{r})={\mathrm{v}}_{\max }(1-\frac{r^2}{R^2})=\frac{2F}{\pi R^2}(1-\frac{r^2}{R^2})$$ (12)

where F is the instantaneous flow rate of the cross-section, R is radius of the inner surface of the micro tube and r is distance away from flow centroid. Figure 6 compares the images of the raw flow profile reconstruction by PSM (a), velocity-smoothened flow profile before (b) and after (c) angle correction using our vessel tracking method. The corresponding cross-sectional flow velocity profile at cosθ = 0 was plotted in the inset of each image. The corresponding maximal velocity (ν_max) profiles on flow centroid are plotted in panels (d). The ν_max measurement accuracy after angle correction using gradient vessel tracking approach is dramatically increased by ~11.5 fold from 8.0% (0.86 ± 0.60 mm/s) to 91.3% (9.86 ± 0.94 mm/s) of the theoretical ν_max = 10.8mm/s (note that the underestimation could be induced by ν_max itself which sis theoretically derived rather than measured). It is noteworthy that gradient vessel tracking method shows superior performance over previous 2- or 3- point correction method with 6.1-fold improved accuracy from 14.9% (1.60 ± 1.43mm/s, 3-point correction) of ν_max. This method also yields much improved measurement precision, i.e., the coefficient of variation (i.e., CV = standard deviation/mean) of the measured velocity was 9.3-fold smaller, from CV = 0.89 (3-point method) down to CV = 0.096 (gradient vessel tracking).

Fig. 6.

Results of flow phantom study (1% intralipid, ϕ280µm tubing) to show that angle correction using gradient vessel tracking dramatically ~9.3-fold reduces the error in flow rate quantification.

In addition to phantom validation, gradient vessel tracking was used to retrieve the absolute CBFv within individual branch vessel along a vascular tree by continuously correcting cosθ_z of vessel mesh function f(x, y, z). Figure 7 shows a 3D µODT image of a mouse somatosensory motor cortex (1.9 × 1.5 × 1mm³) acquired at 10kHz A-scan rate, which included artifacts because of no angle correction. A vein (highlighted by dashed blue lines) and an artery (highlighted by dashed red lines) showing flow discontinuity due to angle-velocity coupling were corrected by our gradient tracking method. After correction, CBFv of the vein increased by ~31-fold from ν_VF = 0.35 ± 0.25mm/s to ν_VF = 11.07 ± 3.12mm/s, whose measurement precision evaluated by its standard deviation (CV = 0.28) was 4.4-fold smaller than its counterpart (CV = 1.24) using 3-point correction method (ν_VF = 6.90 ± 8.54mm/s). CBFv of the artery also increased dramatically (66.3-fold) from un-corrected velocity ν_AF = 0.36 ± 0.13mm/s to ν_AF = 23.92 ± 2.88mm/s, whose CV = 0.12 was 10.8-fold smaller than CV = 1.30 by 3-point method (ν_AF = 6.14 ± 7.96mm/s). Both corrected AF and VF flow rates are close to the physiological parameters for the mouse cerebral cortex [37, 38].

Fig. 7.

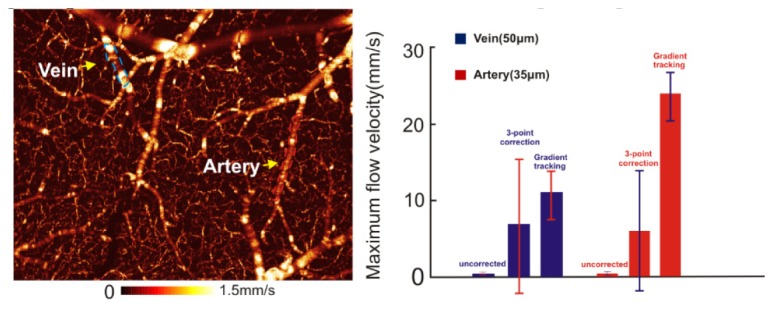
3D ODT image of quantitative CBFv network on a mouse somatosensory motor cortex (1.9 × 1.5 × 1mm3). Left panel: 3D CBFv image without angle correction; Right panel: comparison of flow rate correction for a vein and an artery.

3.4 Quantification of CBFv changes elicited by chronic cocaine administration

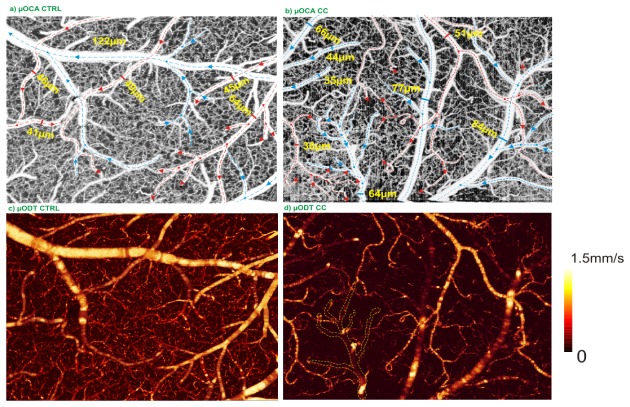
With the improvements of angle correction for fast branch vessels and the phase summation method for detection of minute slow flows (e.g., in capillaries), we can better quantify the CBFv changes elicited by cocaine challenge. For instance, we documented that repeated acute cocaine induced microischemia [31]; it would be equally important if not more to study how chronic cocaine affects brain physiology and function, e.g., the CBFv network. In vivo µODT imaging was performed on the somatosensory motor cortex of a mouse on day 30 after daily intraperitoneal injection of cocaine (1mg/kg). Figure 8 compares the µOCA and µODT images between a normal mouse and a mouse exposed to chronic cocaine. The dashed red and blue lines in the upper µOCA panels indicate the flow directions in arterial and venular vessel compartments; separation of veins and arteries was based on flow directions detected by µODT combined with vascular physiology (i.e., arterial flows spread out into smaller branches whereas venular flows merge from smaller tree branches). Figure 8(c), 8(d) shows dramatic flow decrease in chronic cocaine treated mice. Analytic results show that CBFv in arterial vessels decreased 22.49% ± 8.71% (p<0.05, n = 3 vessels) from 19.07 ± 3.53mm/s to 14.77 ± 5.17mm/s, whereas CBFv in veinal vessels decreased 68.47% ± 6.00% (p<0.05, n = 3 vessels) from 16.76 ± 2.27mm/s to 5.29 ± 1.04mm/s. Not only did CBFv of pial veins and arteries decrease dramatically, but also the capillary CBFv network was disrupted, resulting in a 49.06% ± 17.88% flow decrease from 0.31 ± 0.06mm/s in control mouse to 0.15 ± 0.05mm/s in the chronic cocaine mouse even though there were no significant changes in capillary density.

Fig. 8.

3D OCA images (upper panels) and 3D ODT images (lower panels) of the somatosensory motor cortex (2 × 1.5 × 1mm³) from a control mouse (left) and a chronic cocaine treated mouse (right), showing significant decreases in the entire CBFv network. Dashed circles show examples of vasoconstriction.

3.5 CBFv disruption imaged by en-face ratio ODT

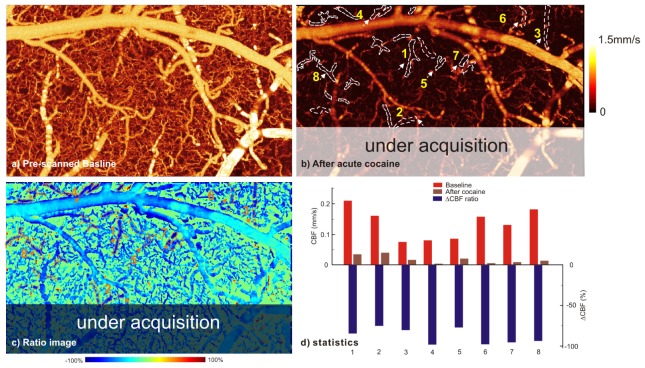
Instantaneous display of the CBFv network during in vivo imaging is valuable when tracking dynamic features in the neurovascular network, which are often heterogeneous and sometimes short lasting. Moreover, the ratio image between current image under acquisition (e.g., after cocaine injection or brain stimulation) and the baseline image can be an important feature to immediately identify the relevant ROIs in which to monitor the hemodynamic changes (e.g., ischemia) (e.g., Fig. 8). Figure 9 shows instantaneous µODT image tracking of CBFv disruption resulting from repeated acute cocaine administration (2.5mg/kg/ea, intravenously). Compared with regular µODT images (a - baseline period, b - after 2 doses of cocaine injections), ratio image (c) clearly shows those vessels vulnerable to flow disruption. Panel (d) indicates cocaine elicited heterogeneous CBFv disruption: flow shutdown occurring in vessels 4,6,7,8 (over 90% decrease) and major flow decrease in vessels 2, 5 (~75%). The partial transparent mask indicates the part of cortex that was scanned during image acquisition.

Fig. 9.

Ratio image to quickly track the ROIs, e.g., vessels with drastic flow decrease after repeated cocaine administration (2.5mg/kg/ea, iv). a) baseline CBFv image, b) currently updating CBFv image, c) ratio image of (b)/(a) to identify flow disruptions, d) statistical analysis of CBFv decrease. White dashed lines: ROIs with diminishing flows.

4. Conclusion and discussion

Neuroimaging techniques that enable high spatiotemporal resolution and quantitative imaging of the cerebral blood flow network and dynamics are of high clinical relevance and may provide important insight into brain physiology (hemodynamics, metabolism), brain function and to understand the mechanisms underlying neurovascular dysfunction of disease progression. Unlike conventional brain imaging techniques such as PET or MRI that allow for noninvasive whole brain diagnosis, intravital optical imaging may be restricted for deep brain imaging due to limited penetration depth, but it has many unique merits such as high sensitivity, superior spatiotemporal resolutions that compliment fMRI and PET modalities. For example, the high spatiotemporal resolutions can be used to help delineate the different vessel compartments that contribute to fMRI BOLD signals, and assess whether the BOLD changes are due to flow rate (CBFv) and/or changes in vessel diameters (dilation or contraction). In recent years, intravital TPM has been widely used to visualize the cerebral microcirculatory distribution and to assess cellular vascular interactions. By tracking fluorescently labeled RBC movement, TPM is capable of accurately measuring the RBC velocity within individual microvessels. Alternatively, optical coherence Doppler tomography is a relatively new high-resolution imaging technique that can provide tracker- or label- free quantitative imaging of CBFv (i.e., RBC velocity) based on Doppler frequency shift generated by moving scattering particles (presumably RBCs in the bloodstream). Recent studies of our labs and from others show that quantitative ODT can be uniquely useful for imaging the highly heterogeneous CBFv network responses to brain activations, such as cocaine elicited vasoconstriction and microischemic events. Despite recent technologic advances and some preclinical imaging studies, several remaining technical problems may hinder its applications in brain functional imaging studies, among which limited dynamic range for Doppler phase detection and Doppler angle correction may prevent it for simultaneous imaging of vastly different flow rates in the cerebrovascular network (e.g., fast flows over 30mm/s in large AF and VF vs. slow flows under 0.05mm/s in minute capillaries) and accurately measuring absolute flow values. Methods such as dual-beam ODT and frequency binning algorithms have been reported to tackle the problems. Here, we apply two relatively simple but effective methods, i.e., phase summation algorithm and gradient vessel tracking method to address the problems and validate the effectiveness of these methods in both flow phantom studies and in vivo 3D mouse CBFv imaging studies. Phase summation method enhanced the detection of the minimal detectable flow while preserving the dynamic range, i.e., the upper threshold for fast flow (causing phase wrapping). Gradient vessel tracking technique continuously traced the Doppler angle cosθ_z(x,y,z) of a vessel by tracking the gradients of the extracted vessel skeleton f(x,y,z). In the phantom study, we showed that it improved the accuracy for true flow velocity measurement by 11.5-fold over uncorrected flow value and 6.1-fold over conventional 3-point correction method. Although not shown here, the over-correction around θ_z≈90° can be further suppressed by removal of background noise. For in-vivo validation studies, we showed the neurotoxic effects of acute and chronic cocaine on the CBFv network on the mouse somatosensory motor cortex, clearly documenting drastic vasoconstriction and microischemia elicited by chronic cocaine administration or by repeated acute cocaine challenges. For instance, the results showed 22.49 ± 8.71% (p<0.05; n = 3 vessels) decrease in arterial CBFv, 68.47 ± 6.00% decrease (p<0.05, n = 3 vessels) in veinal CBFv, and an overall 49.06% ± 17.88% (p<0.05, n = 20 capillaries) decrease in capillary CBFv networks. Finally, results in Fig. 8 illustrate that quantitative ODT (c, d) provided accurate imaging diagnosis of CBFv network disruption by chronic cocaine, which OCA (a, b) failed.

Additionally, our new GUI platform features multi-threading structure with simultaneous data processing (38.4% faster than acquisition) to permit instantaneous CBFv image display, which is useful for brain functional studies such as those that assess cocaine effects on the highly heterogeneous cerebral microvascular network. It should also be noted that angle correction was performed on some branch vessels. Correction of all of the vessels, especially capillary beds is computation intensive and may need more advanced image process approaches for vessel tracking and angle correction. From the imaging acquisition point of view, more optimization work is needed to improve the accuracy of fast flow correction (that needs fast scanning to reduce phase wrapping) and detection sensitivity for slow capillary flows (that needs slow scanning).