Abstract
Polarization sensitive optical coherence tomography (PS-OCT) is a functional extension of conventional OCT and can assess depth-resolved tissue birefringence in addition to intensity. Most existing PS-OCT systems are relatively complex and their clinical translation remains difficult. We present a simple and robust all-fiber PS-OCT system based on swept source technology and polarization depth-encoding. Polarization multiplexing was achieved using a polarization maintaining fiber. Polarization sensitive signals were detected using fiber based polarization beam splitters and polarization controllers were used to remove the polarization ambiguity. A simplified post-processing algorithm was proposed for speckle noise reduction relaxing the demand for phase stability. We demonstrated systems design for both ophthalmic and catheter-based PS-OCT. For ophthalmic imaging, we used an optical clock frequency doubling method to extend the imaging range of a commercially available short cavity light source to improve polarization depth-encoding. For catheter based imaging, we demonstrated 200 kHz PS-OCT imaging using a MEMS-tunable vertical cavity surface emitting laser (VCSEL) and a high speed micromotor imaging catheter. The system was demonstrated in human retina, finger and lip imaging, as well as ex vivo swine esophagus and cardiovascular imaging. The all-fiber PS-OCT is easier to implement and maintain compared to previous PS-OCT systems and can be more easily translated to clinical applications due to its robust design.
OCIS codes: (170.4500) Optical coherence tomography, (230.5440) Polarization-selective devices, (170.4580) Optical diagnostics for medicine
1. Introduction
Optical coherence tomography (OCT) [1] is a well-established imaging modality for diagnosis of ocular disease. In addition to ophthalmic OCT, catheter-based OCT [2], using fiber-optic probes, is also rapidly becoming a useful tool in cardiovascular imaging for diagnosis of coronary artery disease [3, 4] and in endoscopic imaging for assessment of gastrointestinal pathology [2, 5, 6]. Conventional OCT generates intensity images and therefore has limited capability to directly differentiate tissue types. Polarization sensitive OCT (PS-OCT) [7] is a functional extension of OCT and can assess the depth-resolved polarization properties of light to provide additional tissue contrast. The corneal stroma, sclera and retinal nerve fiber layer (RNFL) as well as muscle, tendons, nerve, bones, cartilage and teeth are known to exhibit birefringence. Alteration of tissue birefringence is often associated with disease progression. For example, loss of RNFL birefringence is observed during early stages of glaucoma, a leading cause of blindness in the developed world [8, 9]. PS-OCT has found many applications, including anterior [10–13] and posterior eye imaging [13–16], skin imaging [17–20], burn depth and thermal damage assessment [21–24], dental imaging [25, 26] and atherosclerotic plaque characterization [27–29].
Since the first demonstration of PS-OCT in 1992 [30], many different PS-OCT systems have been developed. PS-OCT systems can be generally divided into two categories based on whether the exact polarization state of the incident light on the sample is known. Type I PS-OCT precisely controls the polarization state of light incident on the sample. The most commonly used setup is to illuminate the sample with circularly polarized light [30–33]. By using polarization sensitive detection, tissue birefringence information can be extracted from the intensity ratio between the detected vertical and horizontal polarization channels. Type I PS-OCT is suitable for free space implementation because it is easy to control the polarization states. However, for fiber-based systems, the input and output polarization states are generally unknown due to birefringence in the single-mode (SM) fibers, and may vary during the imaging procedure. One solution is to use polarization-maintaining (PM) fibers and PM couplers to preserve the polarization states of the incident and output light [34–37]. However, PM fibers introduce a polarization mode dispersion (PMD) delay between the polarization components along the slow and fast axis. Connections between PM fibers must be spliced carefully to avoid cross-coupling of polarization states [35, 38]. In addition, unmatched PM fiber length between the reference and sample arms may degrade the interferometric intensity measurement and completely obscure the phase (if optic axis measurement is desired). Compensation must be very carefully performed either in hardware [35] or post-processing [36]. Other Type I PS-OCT methods which use more than one known polarization states of light to probe the sample have also been demonstrated [39]. In summary, Type I PS-OCT has the advantage that polarization information can be retrieved in a single A-scan and only signal intensity is required for birefringence calculation. However, it is mainly suitable for free-space OCT or fiber-based OCT with a bulk-optics scanner. Type I PS-OCT systems have not been reported for catheter-based systems, since there is no easy way to control and maintain the polarization states of light transmitted through the fiber-optic probe [40].
In comparison, Type II PS-OCT illuminates the sample with two or more polarization states without knowing the exact polarization state of the incident light, and is particularly suitable for fiber-based OCT systems. Saxer et al [41] reported the first fiber-based PS-OCT using an electro-optic modulator (EOM) to modulate the input light into four polarization states on the Poincare sphere. Stokes vector analysis was used to calculate sample birefringence. A Jones matrix analysis method was developed by Park et al [42] as an alternative method for birefringence calculation. For type II PS-OCT, at least two different input polarization states are needed if polarization sensitive detection is employed. Additional input states are required if a single detector is used [43]. Multiple polarization states can be probed sequentially [41, 42] or simultaneously by polarization multiplexing using electro optic modulators [44, 45] or acousto-optic frequency shifters [46]. Sequential probing sacrifices imaging speed, and requires birefringence stability of the system between successive A-lines, which is difficult to achieve in catheter-based imaging. Simultaneous measurement of polarization multiplexed signals overcomes these limitations, although there is a tradeoff in imaging range and signal-to-noise ratio (SNR). Recently, passive polarization multiplexing, by encoding different polarization states into different depths within a single A-scan, has been demonstrated [47, 48]. Passive multiplexing does not require expensive active modulation components or sophisticated synchronization control, and is simpler to implement. A related method has also been demonstrated in free space Type I PS-OCT [49].
OCT commercialization and clinical translation have been a great success during the past ~20 years, especially in the fields of ophthalmic and cardiovascular imaging. However, despite tremendous technological advancement and clinical interest, clinical translation of PS-OCT has been difficult and commercialization of PS-OCT is rare. One reason is the high complexity of existing PS-OCT systems. For example, free space PS-OCT is susceptible to misalignment making it difficult to operate in the clinical environment. Type II PS-OCT systems typically require sophisticated synchronization control, and have high requirements for system SNR and phase stability. These factors limited the clinical translation of PS-OCT.
In this paper, we present a simple, compact and robust swept source PS-OCT system that is suitable for clinical translation. The system utilizes a Type II PS-OCT scheme and is based on passive polarization multiplexing [47]. The system is implemented with all-fiber components, and requires minimal alignment, which promises easier operation and maintenance. We demonstrated this PS-OCT design for both ophthalmic imaging and catheter-based imaging. We also developed a simplified post-processing algorithm for speckle noise reduction. For ophthalmic imaging, to overcome the imaging range limitation from passive polarization multiplexing [47], we used clock frequency multiplication to double the imaging range for a commercially available short cavity light source. For catheter-based OCT, we demonstrated PS-OCT imaging with a MEMS-tunable vertical cavity surface emitting laser (VCSEL) [50–52] and a high speed micromotor probe [53] in human finger and lip, as well as ex vivo swine esophagus and arteries.
The paper is organized as follows. We first describe a generic implementation of depth-encoded all-fiber PS-OCT. We present theory governing PS-OCT, and discuss operation and processing algorithms to extract the tissue birefringence information. We next demonstrate an ophthalmic PS-OCT system with an extended imaging range and present examples of human retinal imaging. Then, we describe a catheter-based PS-OCT system and present human finger and lip imaging in vivo and swine esophagus and cardiovascular imaging ex vivo. Finally, we discuss the limitations and future work.
2. Methods
2.1 PS-OCT generic implementation
2.1.1 System overview
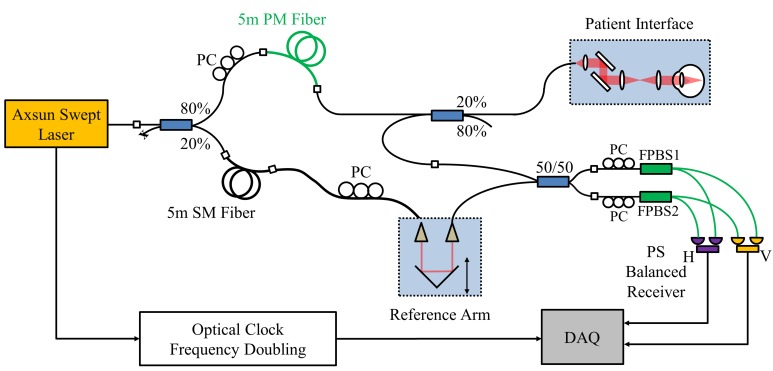
A generic implementation of PS-OCT based on swept-source OCT (SSOCT) technology is illustrated in Fig. 1. Compared to spectral domain OCT (SDOCT), SSOCT provides longer imaging range with less signal roll-off, and is more suitable for passive polarization multiplexing. Polarization multiplexing is achieved using a PM fiber in the sample arm path. Light entering the PM fiber will be decomposed into two orthogonal polarization states, which will be separated by λL/2LB (in air) after traveling the PM fiber of length L, where λ is the wavelength of the light and LB is the PM fiber beat length. By selecting a proper length of PM fiber, signals from the two orthogonal polarization states of the input light can be acquired in a single A-scan, but separated at different depths. A polarization controller (PC1) is used to balance the power between the two orthogonal polarization states. In the reference arm, a SM fiber with the same length is used to match the PM fiber. A polarization controller (PC2) is used to balance the power between the two detection channels. Fiber-optic coupler 2 is used to deliver and re-couple the light to and from the sample, avoiding the use of circulators, which can generate significant PMD and create erroneous birefringence [54, 55]. Light from the reference and sample arms are recombined and interfere at coupler 3. For polarization sensitive detection, two fiber-based polarization beam splitters (FPBS) are used, rather than free-space PBS as in our previous publication [47] and in most other PS-OCT systems [46, 48]. FPBS eliminate free space to fiber coupling, improve SNR, and significantly simplify alignment. However, the FPBS must be used carefully to ensure the sample phase retardation calculation is correct. We will discuss the theory and method in detail below.
Fig. 1.

Schematic of the depth-encoded PS-OCT system. PM fibers are shown in green. A length of PM fiber is used to generate two orthogonal polarization states separated by a given delay in a single A-scan. Two fiber-based polarization beam splitters (FPBS) are used for dual balanced polarization sensitive detection.
2.1.2 Use of fiber-based polarization beam splitters (FPBS)
FPBS with SM fiber input are used, avoiding the deleterious effect of PMD caused by PM fibers. However, the polarization states of the light from the SM fibers are in general unknown. In particular, the polarization states at the input ports of the two FPBS may be different, making the detection unbalanced. We describe a simple calibration procedure using two polarization controllers to adjust the input light polarization to the FPBS to achieve balanced detection for arbitrary input polarization states and obtain a correct phase retardation calculation.
The calibration procedure is as follows. One free port of coupler 2 can be used as the calibration port, as shown in Fig. 1. Before calibration, the reference and sample arms are blocked. We input linearly polarized light from the calibration port and maximize one output of FPBS 1 (without loss of generality, we assume the port is connected to the horizontal channel) by manipulating PC3. We then maximize the corresponding output of FPBS 2 connected to the same channel by adjusting PC4. We have the following lemma:
Lemma 1: After the above calibration procedure, the two detection channels are both balanced. Moreover, the sample phase retardation can be determined correctly.
Proof: We employ Jones matrix analysis here to prove lemma 1. We denote the Jones matrix from the calibration port to the FPBS as, from the calibration port to coupler 3 as, and from coupler 3 to the two FPBS as and, respectively. Since these paths only consist of short SM fibers and an SM fiber coupler, by neglecting any polarization-dependent gain or loss, their Jones matrix can be represented as a unitary matrix [56]:
| (1) |
Where,,, and * denotes complex conjugate. Given linearly polarized light as the input, the output of FPBS1 and 2 areandrespectively. When we adjust PC3, the intensity of the vertical channel is minimized and. Therefore, becomes a pure wave retarder with horizontal optic axis. The same is true for. We can represent them as
| (2) |
Where. We then separate the common pathfrom
| (3) |
Now for light out of coupler 3 with arbitrary polarization states, the input light to the two FPBS will be
| (4) |
Note that the detectors can only detect intensities of the post-interference light, and since
| (5) |
The horizontal and vertical channels are balanced for any given input polarization states after the calibration. We next prove that the sample phase retardation can be determined correctly. The input light coming from the PM fiber can be represented as
| (6) |
Where and are the depth-multiplexed orthogonal polarization states. Following the Jones matrix formalism proposed by Park et al. [42], we denote the Jones matrix from the PM fiber to the sample surface by , the round trip matrix of the sample by, and from the sample surface back to the coupler 3 as , respectively. Since the two detectors are now balanced for any given polarization state, we can treat, where means equivalent. We define an equivalent Jones matrix to them as , and the measured Jones vectors of the sample can be represented as
| (7) |
The measured Jones vectors at the sample surface can be represented as
| (8) |
To extract the sample phase retardation, we multiplyby the inverse of to cancel the unknown [42]:
| (9) |
Here, and are combined into a new term. It is easy to see that is similar to regardless of the value of. By eigendecomposition, the double-pass sample phase retardation (DPPR) can be correctly recovered from the two eigenvalues and of [42, 57]:
| (10) |
Therefore, lemma 1 is proved. In practice, we can mechanically immobilize the short fiber segments and and leave PC3 and PC4 fixed once the system is calibrated. No further alignment is required.
2.1.3 Jones averaging without phase stabilization
Type II PS-OCT unitizes complex data for birefringence calculation, and therefore phase stability is important. For SSOCT, there can be laser sweep jitter or sampling fluctuations which can make the phase unstable over successive A-scans. Several methods have been proposed to stabilize the phase in SSOCT systems. Methods requiring acquisition of calibration Mach–Zehnder Interferometer (MZI) traces [58] are often not possible because many high speed data acquisition (DAQ) cards only have two input channels which are already dedicated to polarization sensitive detection. Methods using a fiber Bragg grating (FBG) in one of the balanced detection arms require exact matching of fiber length in the other arm [59], which is complicated for PS-OCT because four detection paths have to be matched. Adding an FBG in the detection channel also reduces SNR, which is already compromised in Type II PS-OCT due to polarization multiplexing. Methods using an extra reference reflection [60, 61] for calibration are a feasible solution. But the added reflections will further reduce the imaging range and require post-processing. As a result, phase stabilization usually results in significant PS-OCT system complexity. Furthermore, the requirement of phase stability limits the ability to average results from multiple acquisitions and to use motion correction registration algorithms.
Therefore, rather than phase-stabilize the system, we seek methods that can relax the demand for phase stabilization. First, passive polarization multiplexing provides intrinsic phase stability between the two illumination states. This is because the two depth-encoded images are only separated by picoseconds, and no external synchronization is needed, as in active polarization multiplexing [44, 46], therefore potential phase fluctuations from the active components can be avoided. Second, we use the optical clock generated by the swept laser or from a separate MZI to directly sample the OCT signals with equally spaced wavenumber intervals [62]. Sampling with an external, variable optical clock generates a more stable phase than sampling using the fixed internal clock from the DAQ. Third, we propose the following method to average PS-OCT signals for speckle noise reduction with relaxed requirements for phase stability over successive A-scans.
Assuming there are random phase shifts caused by laser sweep jitter ∆k and unpredictable phase shift θz that is associated with the axial depth position of the sample. For each A-scan, we assume the same axial depth of the sample from the two depth-encoded copies has the same θz. If we denote the axial positions of the sample surface and measurement within the sample to be Zsurf and Zmeas respectively, and the depth separation between the two multiplexed images to be ∆z, we can represent the measured signals with the random phase shifts as
| (11) |
Equation (9) is rewritten as:
| (12) |
Where. Consider the analytical equations for calculating the eigenvalues:
| (13) |
Where and are the trace and determinant of respectively. The eigenvalues of with the random phases become:
| (14) |
It should be emphasized that the order of the two eigenvalues in Eq. (14) can be one of the two indicated above depending on the value of δ. Taking the ratio of the eigenvalues will cancel the unknown random phases:
| (15) |
In contrast to previous averaging methods which are performed either on the surface Jones matrices over adjacent A-lines [41, 44], directly on the stokes vectors [63], or the complex Jones matrices of each pixel [12], where phase instability will generate errors, we can average directly, because any unstable phase has already been canceled. Averaging can be either performed within a small window (e.g. 3-by-3) in the same frame, or between frames if repeated B-scans are acquired. To avoid surface speckle noise from the result of the surface segmentation (Section 2.2.2), the brightest pixel within a small axial window (e.g. 3-by-1) is used to determine. Because the order of the two eigenvalues can be unspecified, it is important to ensure that the two eigenvalues are in sorted orders before averaging. This can be achieved by sorting the two eigenvalues by their magnitudes prior to taking their ratio. Since the magnitudes of the two eigenvalues determine the relative attenuation of polarizations by the sample [57], sorting by eigenvalue magnitude is equivalent to assuming that adjacent pixels have consistent relative attenuation in biological samples. Therefore, this averaging method relaxes the requirement for phase stability by utilizing the spatial uniformity of the sample.
2.2 Ophthalmic PS-OCT
Figure 2 shows the schematic of the ophthalmic PS-OCT system. A commercially available short cavity 1050nm wavelength swept laser (Axsun Technologies Inc.) with a sweep repetition rate of 100kHz was used as the light source. The laser sweep range was 108nm and the average output power was 30mW. The laser output was attenuated by 1.5dB and split with an 80/20 coupler, with 80% directed to the sample path, and 20% to the reference path. A 5m PM fiber (PM980-XP, Thorlabs Inc.) was used for polarization multiplexing, generating a 0.97mm depth separation in air between the two orthogonal polarization states. After the PM fiber, light was further split by an 80/20 coupler, with 20% directed to the patient interface (PIU). The light from the sample and reference arms was recombined by a 50/50 coupler. The horizontally and vertically polarized signals were further split by two FPBS (FiberLogix International Limited.) and detected by two balanced receivers (PDB130C, Thorlabs Inc.) that were modified with fiber coupled diodes and higher trans-impedance gain to achieve ~250 MHz bandwidth. A high speed 12-bit A/D digitizer (ATS9360, Alazar Technologies Inc.) was externally clocked by the laser sweep for data acquisition. To extend the imaging range, we used a clock frequency doubling method described below.
Fig. 2.
Schematic of the ophthalmic PS-OCT system.
2.2.1 Optical clock frequency doubling
The Axsun laser provides a clock frequency of 209-328MHz, corresponding to 3.7mm imaging range (in air). This is insufficient for imaging structures in the eye using depth-encoded PS-OCT. To extend the imaging range, we electronically doubled the k-clock provided by the laser [64]. The advantage of this method over using an external MZI is that the clock quality is not limited by the coherence length of the swept laser.
The clock signal from the laser was first amplified (ZFL-750 + , Mini-circuits), filtered by a high-pass (SHP-200 + , 185-3000MHz, Mini-circuits) and a low-pass filter (ZX75LP-340-S + , DC-340MHz, Mini-circuits), and input to a frequency doubler (MK-2, 5-500MHz, Mini-circuits). After further high-pass filtering (SHP-400 + , 395-3200MHz, Mini-circuits) and amplifying (ZFL-1000 + , Mini-circuits), the doubled clock was connected to an electric switch (ZYSWA-2-50DR, Mini-circuits) and mixed with a fixed frequency dummy clock generated by a Voltage Controlled Oscillator (ZX95-2500W-S + , Mini-circuits). The dummy clock was required by the DAQ in order to continuously acquire the data [65]. The combined RF output from the switch was further high-pass filtered (SHP 100 + , 90-2000MHz, Mini-circuits) and used as the final clock input to the DAQ.
With the frequency-doubled clock, the imaging range was effectively doubled to be 7.4mm in air. The sensitivity of the system for one depth-encoded copy (the two polarization inputs were balanced) was measured to be 96dB with an incident power of 1.8mW, which is a significant improvement over previous passive PS-OCT systems using free-space implementations [47, 48, 61]. The sensitivity rolls off by 6dB at 6mm. The theoretical shot-noise limited SNR was 102dB, taking into account the split ratio from the 80/20 coupler. Note that there was an intrinsic 3dB loss due to polarization multiplexing. The remaining loss was from fiber connectors and the PIU. The axial resolution was 10μm in tissue.
2.2.2 Image processing
Images from the two polarization channels were first processed using standard OCT procedures, including background subtraction, numerical dispersion compensation, spectral shaping and Fast Fourier Transform (FFT). Since each image contains two depth-encoded copies, the image was split to generate two individual images corresponding to the two input polarization states. This was achieved by searching for two fixed size axial windows for the two images with the maximum cross-correlation. For Type II PS-OCT, the tissue boundary must be segmented for DPPR calculation. We employed a robust graph-cut algorithm based on Li et al. [66] for this task. Two coupled surfaces were simultaneously searched in 3D with a global optimum guarantee. In retinal OCT images, individual cost functions were designed for each boundary according to Garvin et al. [67] such that the first surface corresponds to the internal limiting membrane (ILM), and the second surface corresponds to the retinal pigmented epithelium (RPE). Multi-resolution techniques were used to speed up the processing [68]. After the segmentation, the DPPR of each pixel can be calculated using Eq. (9)-(10). Jones averaging (Section 2.1.3) was typically performed with a 3-by-5 kernel. The en face DPPR map can be generated by projecting the DPPR values on the segmented RPE boundary to the en face plane. Median filtering (kernel size: 3-by-7) was performed to smooth the en face DPPR image.
2.3 Catheter-based PS-OCT
Figure 3 shows the schematic of the catheter-based PS-OCT system. A 1310nm MEMS-tunable VCSEL laser operating at a sweep rate of 200kHz and a sweep range 110nm was used as the light source. The VCSEL generates a single longitudinal mode instead of multiple modes and therefore has extremely long coherence lengths [50, 52]. The minimum sensitivity roll-off and superb clock quality provided by VCSEL is especially suitable for depth-encoded PS-OCT. The VCSEL generated an average output power of 75mW, with 5% of the light coupled to a MZI to generate an optical clock signal with a maximum frequency of 1.1GHz for data acquisition (corresponding to a 5.8mm imaging range in air), and the remaining 95% light was delivered to the OCT system. The OCT system used an 80/20 coupler to split the light into the sample and reference arms. In the sample arm, an 11m PM fiber (PM1300-XP, Nufern) was used to generate a 1.78mm depth separation in air between two orthogonal polarization states. A corresponding 11m SM fiber was used to match the reference arm. Two 50/50 couplers were used in the sample and reference arms to deliver and recombine light, respectively. Similar to the ophthalmic PS-OCT, two FPBS (Advanced Fiber Resources Ltd.) and two 1.6GHz bandwidth receivers (PDB480C-AC, Thorlabs, Inc.) were used for polarization sensitive detection. Low pass filters (SLP-550 + , 0-550MHz, Mini-circuits) after the detectors were used to remove high-frequency noise and suppress aliasing. A high speed 12-bit A/D card (ATS9360, Alazar Technologies Inc.) was used for data acquisition. Polarization controllers were employed to balance the power between the input polarization states and detection channels and to calibrate the FPBS as described in Section 2.1.2.
Fig. 3.
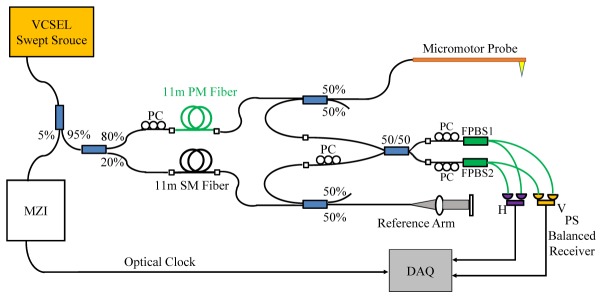
Schematic of the catheter-based PS-OCT system using a VCSEL light source with a micromotor probe.
The details of the micromotor imaging catheter were described previously [53]. Briefly, the OCT beam was focused by a fiber-GRIN lens assembly, reflected by a rotating micro-prism mounted on a 2mm diameter, 6mm long micromotor (Namiki Precision of California, Inc.). The motor and GRIN lens were mounted inside a precision machined brass tube with an outer diameter (OD) of 2.6mm. The assembly was enclosed by a fluorinated ethylene propylene (FEP) plastic sheath (3.2mm OD, ZEUS). Customized software written in C + + was developed to precisely control and synchronize the micromotor with the laser trigger and data acquisition. In this study, the micromotor was driven at 200frames/s. The output power from the probe was 10mW. The system sensitivity was measured to be 96dB for one depth-encoded image. The signal roll-off rate was 0.66dB/mm. Axial resolution was 10μm in tissue.
Only the forward sweep of the VCSEL was used for processing. Catheter-based PS-OCT processing was performed using methods similar to those described in Section 2.2.2. However, instead of detecting the tissue boundaries, the two boundaries of the plastic sheath were segmented simultaneously using the graph-cut algorithm. The inner boundary of the sheath was used as the surface Jones matrix reference (Eq. (8)-(9)).
3 Results
3.1 Validation of PS-OCT by measuring a wave plate
We verified the accuracy of the PS-OCT systems by imaging a zero-order, quarter-wave plate designed for 1053nm wavelength (WPQ05M-1053, Thorlabs Inc.). For the ophthalmic system, we set the wave plate at different axis orientations and performed 500 measurements at each orientation. The measured DPPR was consistent for different axis orientations (Fig. 4(A)), and the mean value was 174.3°, which agreed with the specified manufactured value of 180°. The small measurement offset was due to the broad bandwidth of light source. For the catheter-based PS-OCT system, we imaged the same wave plate. To confirm that the measurement did not depend on fiber birefringence, we twisted the sample arm fiber during measurement to simulate motion that would occur in catheter or endoscopic imaging and performed 500 measurements each time. The measured DPPR was consistent despite the birefringence changes in the sample arm fiber (Fig. 4(B)) and the measured mean value was 140.6° matching the theoretical value ~142° (provided by Thorlabs Inc.). The measured DPPR with and without Jones averaging was 174.3° ± 1.3° and 174.3° ± 3.5° for the ophthalmic PS-OCT system, and 140.6° ± 1.3° and 140.6° ± 3.6° for the catheter-based system (averaging kernel: 1 × 7). This demonstrates that the Jones averaging method significantly reduced the noise in the DPPR measurement without introducing bias. An example is shown in Fig. 4(C) and 4(D).
Fig. 4.
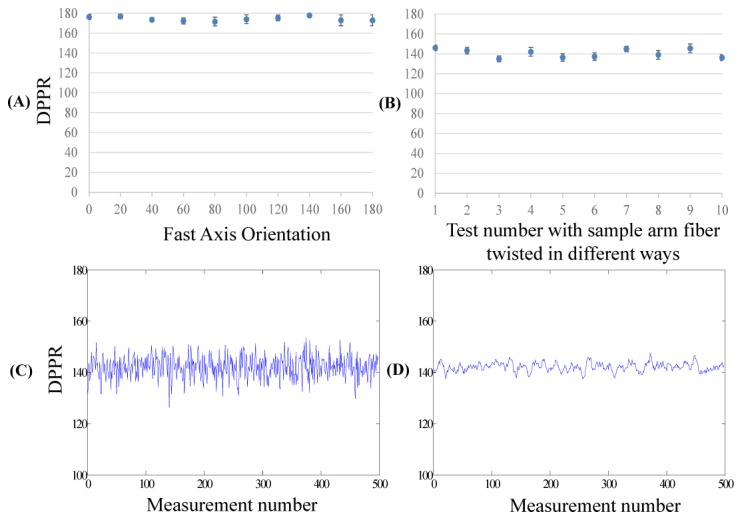
Wave plate measurement. (A) Measured double-pass phase retardation (DPPR) of the quarter-wave plate at different orientations using the ophthalmic PS-OCT system at 1050nm. At each orientation, 500 measurements were performed. (B) Measured DPPR of the same wave plate using the catheter-based PS-OCT system at 1310nm. For each 500 measurements, the sample arm fibers were twisted to induce birefringence. The theoretical DPPR of the wave plate was ~142° at 1310nm. (C-D) Measured DPPR using the catheter-based PS-OCT system without (C) and with (D) the Jones averaging method.
3.2 Human retinal imaging using ophthalmic PS-OCT
Retinal imaging was performed in healthy volunteers with a 1.8mW incident power at the cornea, consistent with American National Standards Institute (ANSI) safe exposure limits. The study protocol was approved by the Committee on Use of Humans as Experimental Subjects (COUHES) at M.I.T. Written informed consent was obtained prior to the study.
Figure 5(A)-5(D) shows volumetric retinal imaging centered at the optic nerve head (ONH). The scanned area is 6mm × 6mm, with 1000 × 200 A-lines/volume acquired in 2.0s. A single B-scan frame (Fig. 5(A)) shows high sensitivity for the two depth-encoded copies. The corresponding DPPR image (Fig. 5(B)) shows high DPPR at the RNFL and sclera, and low DPPR in other layers of the retina, consistent with previous reports [13, 33, 47, 48]. The fundus intensity image was generated by projecting all pixels of each A-line onto the en face view (Fig. 5(C)). The fundus DPPR map shows high retardance around the optic disc region (Fig. 5(D)). Figure 5(E) shows a polarization-insensitive intensity image of the fovea region from a healthy subject. Low DPPR is observed in the macular region (Fig. 5(F)). Figure 6 shows 3mm × 3mm volumetric imaging centered at the ONH region (300 × 300 × 5 A-lines/volume) with 5 repeated B-scans at each location. The enhanced DPPR map with 5 frames averaging (Fig. 6(D)) shows reduced speckle noise. By calculating the speckle de-correlation of the repeated B-scans [69], retinal angiograms can also be generated, enabling multifunctional assessment of retinal pathology with a single system.
Fig. 5.

PS-OCT retinal imaging in healthy subjects. (A-D) Optic nerve head imaging. The scan area is 6mm × 6mm, with 1000 × 200 A-lines/volume acquired in 2.0s. (A) A cross-sectional intensity image with two depth-encoded copies. (B) Corresponding DPPR image shows high retardance in the RNFL and sclera. (C) OCT fundus image. (D) Corresponding fundus DPPR map shows high retardance around the optic disc region. (E-F) Macular imaging. (E) A single frame intensity image at the fovea region. (F) Corresponding DPPR image shows low retardance in the retinal layers. Scale bar: 500µm.
Fig. 6.
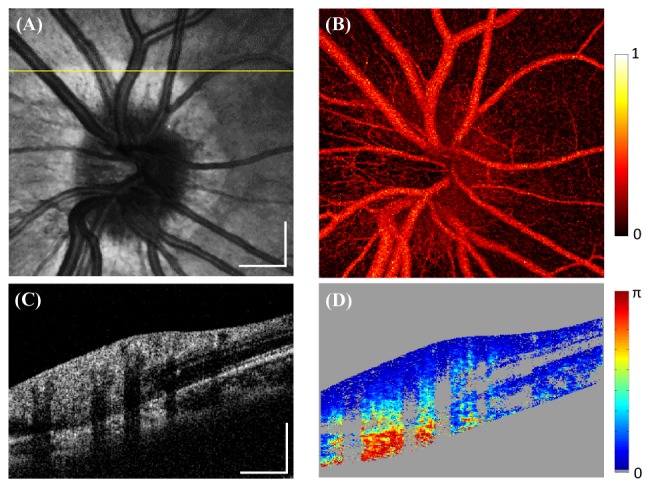
Multifunctional human retinal imaging. The scan area is 3mm × 3mm with 300 × 300 × 5 A-lines/volume (5 repeated B-scans per location). (A) OCT fundus image. (B) OCT angiography using speckle de-correlation of repeated B-scans. The signals from two channels were first compounded and speckle-decorrelation was computed for the two depth-encoded copies separately, then the two copies were averaged. Color scale represents speckle-decorrelation of range 0-1. (C) Single frame cross-sectional intensity image. (D) Corresponding DPPR image with 5 frames averaged. Scale bar: 500µm.
3.3 Catheter based PS-OCT imaging
3.3.1 In vivo human finger and lip imaging
Figures 7(A) and 7(B) show single frame intensity and DPPR images of thick skin from a human index finger tip. High DPPR can be observed in the dermal papillae that lie between the inter-papillary pegs. The DPPR of epidermis is not visualized due to its low reflectivity. Figures 7(C) and 7(D) show examples of human lip images. The thick squamous epithelium exhibits low DPPR while underlining lamina propria has strong DPPR.
Fig. 7.
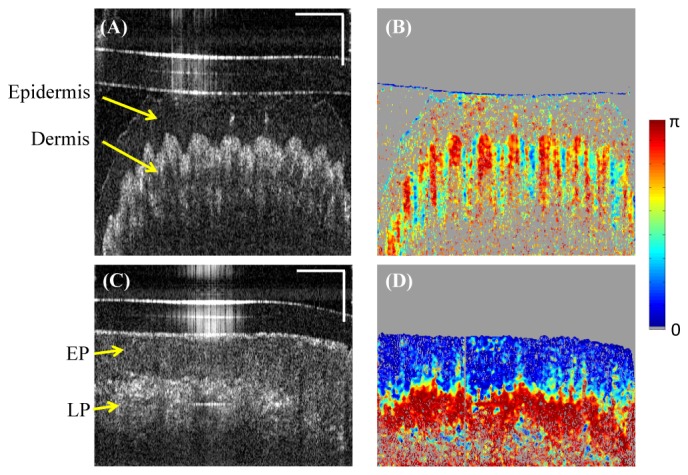
Human skin and oral mucosa imaging in vivo by the catheter-based PS-OCT. (A) A single frame intensity image of the thick skin from a human index finger tip. (B) Corresponding DPPR image shows high retardance at the dermal papillae. (C) A single frame intensity image of human lip. (D) Corresponding DPPR image shows low retardance at the epithelium (EP) and high retardance at the lamia propria (LP). Horizontal scale bar: 30 degree; vertical scale bar: 500µm.
3.3.2 Ex vivo swine esophagus imaging
Sections of porcine esophagus ex vivo were obtained from a supplier and stored in Dulbecco's Modified Eagle's Media (DMEM) (Cellgro, Corning Inc.) at 4 degrees prior to the experiment. The swine esophagus was dissected, flattened and imaged by the catheter-based PS-OCT system from the luminal side. Figure 8 shows a single frame cross-section of the esophagus. The low retardance epithelium and high retardance lamina propria/muscularis mucosa layers can be clearly differentiated from the DPPR image.
Fig. 8.
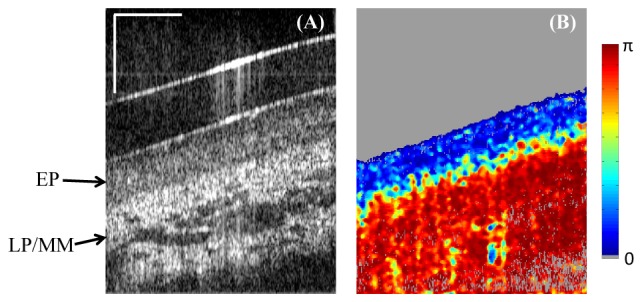
Ex vivo swine esophagus imaging by the catheter-based PS-OCT. (A) Single frame intensity shows the epithelium (EP) and lamia propria (LP) / muscularis mucosa (MM) layers. (B) Corresponding DPPR image shows low retardance at EP but high retardance at LP/MM. Horizontal scale bar: 30 degree; vertical scale bar: 500µm.
3.3.3 Ex vivo swine cardiovascular imaging
An ex vivo swine heart was stored in DMEM at 4 degrees prior to the experiment. The right coronary artery was dissected from the heart. The micromotor imaging catheter was inserted into the artery and intravascular imaging was performed. In the coronary artery image (Fig. 9), the intima layer shows low DPPR and delineates a clear boundary from the underlying media and adventitia which are highly birefringent.
Fig. 9.
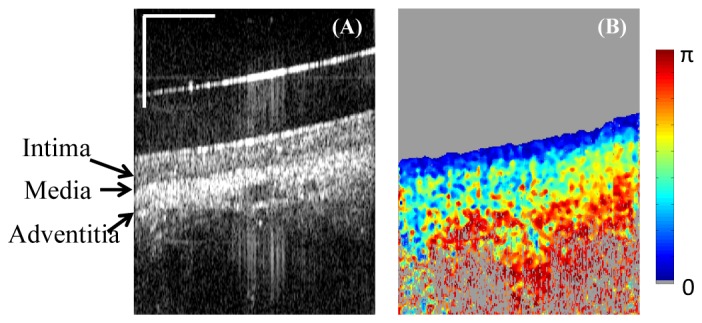
Ex vivo swine cardiovascular imaging using catheter-based PS-OCT. (A) Single frame intensity image of the right coronary artery. (B) Corresponding DPPR image shows low retardance in the intima layer, and high retardance in the media and adventitia. Horizontal scale bar: 30 degree; vertical scale bar: 500µm.
4. Discussion
A simplified and robust all-fiber PS-OCT was demonstrated for both ophthalmic and catheter-based OCT. Compared to previous PS-OCT systems, the depth-encoded all-fiber design simplifies system implementation and improves sensitivity. Compared to Type I ophthalmic PS-OCT [32, 33], the system requires minimal alignment, and is robust against system birefringence changes during the imaging procedure. Compared to previous Type II PS-OCT [43, 44, 46, 48, 61], the system is simpler and relaxes the requirement for sophisticated synchronization control and additional phase stabilization protocols.
In the depth-encoded all-fiber PS-OCT system, polarization multiplexing is achieved with a single PM fiber. Distinction should be made between this approach and other Type I PS-OCT systems where PM fibers are used for polarization maintaining purposes [34–37]. In the current system, careful splicing to orient the slow axis of the PM fiber is not required, because the fiber was only used to generate and delay orthogonal polarization states. Importantly, SM fiber couplers were used in place of circulators to separate and recombine the sample and reference light. Circulators can generate significant PMD and cause tissue birefringence measurement errors [54, 55]. For the same reason, PM couplers were not used. Although fiber couplers are less efficient than circulators, the all-fiber design mitigated potential losses in other coupling locations and made PS-OCT imaging feasible.
We also investigated the effect of potential PMD from SM fibers in the system. For ophthalmic all-fiber PS-OCT, the SM fibers in the system are typically short, and PMD would be negligible. For the catheter-based PS-OCT, light traveled through ~25m SM fibers (double pass) in the reference arm, generating 0.016ps PMD (PMD for SMF-28 fibers: 0.1ps/). This corresponds to 1.76μm mismatch in tissue between light traveling through the fast and slow axis, which is ~1/6 of the axial resolution of the system. A simple way to remove the reference arm PMD is to add a fiber in-line polarizer and a polarization controller right before the 50/50 coupler prior to interference. We compared the DPPR image with and without adding a fiber polarizer in the reference arm, and found no noticeable differences in the resulting DPPR measurements. In fact, adding the fiber polarizer assists power balancing between the two detection channels and the FPBS calibration. However, the fiber polarizers we tested generated additional reflections in the image and therefore were not adopted.
We also reported a new Jones averaging algorithm for speckle noise reduction with relaxed demand for phase stability. Despite its simplicity, the method has good performance when applied to the depth-encoded all-fiber PS-OCT. Regarding the specific averaging algorithm, we only tested simple intra- and inter-frame arithmetic averaging within a small kernel. It is likely that more advanced methods using the statistical properties of polarimetry noise with respect to speckle may further improve performance. We will investigate this in future studies.
One requirement for the Jones averaging method is that the two eigenvalues need to be sorted before averaging. Without sorting, the phase retardation images may exhibit salt-and-pepper noise. Our experimental data demonstrates that sorting by eigenvalue magnitude is valid in practice, because the relative polarization attenuation of biological samples can be considered consistent within the small averaging kernel. However, we cannot exclude the possibility that the two eigenvalues may have the same magnitude which results in ambiguous ordering. In such situations, one empirical solution is to compare the sign of the phase retardation of neighboring pixels and change the order if necessary. Fundamentally, the eigenvalue order ambiguity is from the unstable phase δ in Eq. (12). If there are no unstable phases in the measured signals, the analytical equations Eq. (13) yield eigenvalues that are in sorted orders. The threshold of unstable phase δ to flip the eigenvalue order is π. According to Eq. (12), if we assume that there are 1024 pixels acquired for each A-scan covering a 100nm spectrum range, this translates to ~3 pixel spectrum jitter for the 1050nm swept laser and ~5 pixel shift for the 1310nm swept laser for an imaging depth of 1.5mm. Therefore, using a quasi-phase-stable light source may further relax the need for eigenvalue sorting. Overall, the proposed Jones averaging method provides an economical solution to simplify the system design and enables averaging data from multiple acquisitions, which was difficult using previous averaging methods.
For fiber-based PS-OCT, only relative, rather than absolute optic axis information can be determined due to the unknown birefringence imposed by SM fibers [70]. To determine the absolute optic axis, additional calibration by measuring samples with different illumination angles [71, 72], or by placing two quarter-wave plates before the samples have been reported [72]. We will explore alternative methods for catheter-based PS-OCT in future studies without significantly complicating the current system design. The current design of the catheter provides only a partial view of the scanned field. Future improvement in the catheter design will expand the useable field of view.
We demonstrated PS-OCT imaging in several different, but representative applications, including ophthalmic, skin, esophageal and cardiovascular imaging, covering areas of current OCT applications. The robust and simple all-fiber PS-OCT design makes it easily translatable for a variety of clinical applications. To our knowledge, this is the first demonstration of polarization sensitive imaging in esophagus using a catheter-based PS-OCT system. PS-OCT may play an important role in diagnosis of gastrointestinal pathology and guidance of ablative treatments. For example, previous OCT studies have shown that the epithelial thickness prior to, as well as the presence of residual pathology after radio frequency ablation (RFA) is a predictor for therapy response in dysplastic Barrett’s esophagus (BE) [73]. Therefore, improving the contrast for accurately identifying the lamina propria/muscularis propria layer might have major implications in the treatment of dysplastic BE. For cardiovascular imaging, PS-OCT promises to enhance atherosclerotic plaque characterization [3, 27–29].
5. Conclusions
In conclusion, we demonstrated a depth-encoded all-fiber swept source PS-OCT method that is simple and robust to implement in both ophthalmic and catheter-based OCT systems. We also presented a Jones matrix averaging method for noise reduction in PS-OCT data which relaxes the demand for phase stability. We demonstrated the performance of the system in representative applications including in vivo human retinal imaging, finger and lip imaging, as well as ex vivo swine esophagus and cardiovascular imaging.
Acknowledgments
The authors thank the reviewer of this manuscript for the careful and detailed review as well as valuable suggestions on improvements and clarification of the Jones matrix theory in Section 2.1.2 and Section 2.1.3. We acknowledge the early work of Dr. Al-Hafeez Dhalla and Kathrin Mohler on PS-OCT. We thank Dr. Haibo Jia from Massachusetts General Hospital (Boston MA) and The Second Affiliated Hospital of Harbin Medical University (Harbin, China) for help with animal tissue preparation. We are grateful to Chen Lu from MIT and Dr. Xiaoyong Fu from Case Western Reserve University (Cleveland OH) for helpful discussions. This research is sponsored in part by the National Institutes of Health R01-EY011289-26, R44-EY022864-02, R01-CA075289-16, R44-CA101067-05, R01-CA178636-02 and Air Force Office of Scientific Research AFOSR contracts FA9550-10-1-0063 and FA9550-12-1-0499, Deutsche Forschungsgemeinschaft DFG-GSC80-SAOT, DFG-HO-1791/11-1, and DFG Training Group 1773 “Heterogeneous Image Systems”.
References and links
- 1.Huang D., Swanson E. A., Lin C. P., Schuman J. S., Stinson W. G., Chang W., Hee M. R., Flotte T., Gregory K., Puliafito C. A., Fujimoto J. G., “Optical coherence tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Tearney G. J., Brezinski M. E., Bouma B. E., Boppart S. A., Pitris C., Southern J. F., Fujimoto J. G., “In Vivo Endoscopic Optical Biopsy with Optical Coherence Tomography,” Science 276(5321), 2037–2039 (1997). 10.1126/science.276.5321.2037 [DOI] [PubMed] [Google Scholar]
- 3.Jang I. K., Tearney G. J., MacNeill B., Takano M., Moselewski F., Iftima N., Shishkov M., Houser S., Aretz H. T., Halpern E. F., Bouma B. E., “In vivo characterization of coronary atherosclerotic plaque by use of optical coherence tomography,” Circulation 111(12), 1551–1555 (2005). 10.1161/01.CIR.0000159354.43778.69 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bezerra H. G., Costa M. A., Guagliumi G., Rollins A. M., Simon D. I., “Intracoronary optical coherence tomography: a comprehensive review clinical and research applications,” JACC Cardiovasc. Interv. 2(11), 1035–1046 (2009). 10.1016/j.jcin.2009.06.019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Adler D. C., Chen Y., Huber R., Schmitt J., Connolly J., Fujimoto J. G., “Three-dimensional endomicroscopy using optical coherence tomography,” Nat. Photonics 1(12), 709–716 (2007). 10.1038/nphoton.2007.228 [DOI] [Google Scholar]
- 6.Vakoc B. J., Shishko M., Yun S. H., Oh W.-Y., Suter M. J., Desjardins A. E., Evans J. A., Nishioka N. S., Tearney G. J., Bouma B. E., “Comprehensive esophageal microscopy by using optical frequency-domain imaging (with video),” Gastrointest. Endosc. 65(6), 898–905 (2007). 10.1016/j.gie.2006.08.009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.de Boer J. F., Milner T. E., “Review of polarization sensitive optical coherence tomography and Stokes vector determination,” J. Biomed. Opt. 7(3), 359–371 (2002). 10.1117/1.1483879 [DOI] [PubMed] [Google Scholar]
- 8.Weinreb R. N., Shakiba S., Zangwill L., “Scanning laser polarimetry to measure the nerve fiber layer of normal and glaucomatous eyes,” Am. J. Ophthalmol. 119(5), 627–636 (1995). [DOI] [PubMed] [Google Scholar]
- 9.Bagga H., Greenfield D. S., Feuer W., Knighton R. W., “Scanning laser polarimetry with variable corneal compensation and optical coherence tomography in normal and glaucomatous eyes,” Am. J. Ophthalmol. 135(4), 521–529 (2003). 10.1016/S0002-9394(02)02077-9 [DOI] [PubMed] [Google Scholar]
- 10.Götzinger E., Pircher M., Sticker M., Fercher A. F., Hitzenberger C. K., “Measurement and imaging of birefringent properties of the human cornea with phase-resolved, polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 9(1), 94–102 (2004). 10.1117/1.1629308 [DOI] [PubMed] [Google Scholar]
- 11.Pircher M., Goetzinger E., Leitgeb R., Hitzenberger C. K., “Transversal phase resolved polarization sensitive optical coherence tomography,” Phys. Med. Biol. 49(7), 1257–1263 (2004). 10.1088/0031-9155/49/7/013 [DOI] [PubMed] [Google Scholar]
- 12.Lim Y., Yamanari M., Fukuda S., Kaji Y., Kiuchi T., Miura M., Oshika T., Yasuno Y., “Birefringence measurement of cornea and anterior segment by office-based polarization-sensitive optical coherence tomography,” Biomed. Opt. Express 2(8), 2392–2402 (2011). 10.1364/BOE.2.002392 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pircher M., Hitzenberger C. K., Schmidt-Erfurth U., “Polarization sensitive optical coherence tomography in the human eye,” Prog. Retin. Eye Res. 30(6), 431–451 (2011). 10.1016/j.preteyeres.2011.06.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Cense B., Chen T. C., Park B. H., Pierce M. C., de Boer J. F., “In vivo depth-resolved birefringence measurements of the human retinal nerve fiber layer by polarization-sensitive optical coherence tomography,” Opt. Lett. 27(18), 1610–1612 (2002). 10.1364/OL.27.001610 [DOI] [PubMed] [Google Scholar]
- 15.Pircher M., Götzinger E., Leitgeb R., Sattmann H., Findl O., Hitzenberger C. K., “Imaging of polarization properties of human retina in vivo with phase resolved transversal PS-OCT,” Opt. Express 12(24), 5940–5951 (2004). 10.1364/OPEX.12.005940 [DOI] [PubMed] [Google Scholar]
- 16.Pircher M., Götzinger E., Findl O., Michels S., Geitzenauer W., Leydolt C., Schmidt-Erfurth U., Hitzenberger C. K., “Human macula investigated in vivo with polarization-sensitive optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 47(12), 5487–5494 (2006). 10.1167/iovs.05-1589 [DOI] [PubMed] [Google Scholar]
- 17.Yasuno Y., Makita S., Sutoh Y., Itoh M., Yatagai T., “Birefringence imaging of human skin by polarization-sensitive spectral interferometric optical coherence tomography,” Opt. Lett. 27(20), 1803–1805 (2002). 10.1364/OL.27.001803 [DOI] [PubMed] [Google Scholar]
- 18.Pierce M. C., Strasswimmer J., Hyle Park B., Cense B., de Boer J. F., “Birefringence measurements in human skin using polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 9(2), 287–291 (2004). 10.1117/1.1645797 [DOI] [PubMed] [Google Scholar]
- 19.Pircher M., Goetzinger E., Leitgeb R., Hitzenberger C. K., “Three dimensional polarization sensitive OCT of human skin in vivo,” Opt. Express 12(14), 3236–3244 (2004). 10.1364/OPEX.12.003236 [DOI] [PubMed] [Google Scholar]
- 20.Strasswimmer J., Pierce M. C., Park B. H., Neel V., de Boer J. F., “Polarization-sensitive optical coherence tomography of invasive basal cell carcinoma,” J. Biomed. Opt. 9(2), 292–298 (2004). 10.1117/1.1644118 [DOI] [PubMed] [Google Scholar]
- 21.de Boer J. F., Srinivas S. M., Malekafzali A., Chen Z., Nelson J. S., “Imaging thermally damaged tissue by Polarization Sensitive Optical Coherence Tomography,” Opt. Express 3(6), 212–218 (1998). 10.1364/OE.3.000212 [DOI] [PubMed] [Google Scholar]
- 22.Pierce M. C., Sheridan R. L., Hyle Park B., Cense B., de Boer J. F., “Collagen denaturation can be quantified in burned human skin using polarization-sensitive optical coherence tomography,” Burns 30(6), 511–517 (2004). 10.1016/j.burns.2004.02.004 [DOI] [PubMed] [Google Scholar]
- 23.Srinivas S. M., de Boer J. F., Park H., Keikhanzadeh K., Huang H. E., Zhang J., Jung W. Q., Chen Z., Nelson J. S., “Determination of burn depth by polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 9(1), 207–212 (2004). 10.1117/1.1629680 [DOI] [PubMed] [Google Scholar]
- 24.Kim K. H., Pierce M. C., Maguluri G., Park B. H., Yoon S. J., Lydon M., Sheridan R., de Boer J. F., “In vivo imaging of human burn injuries with polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 17(6), 066012 (2012). 10.1117/1.JBO.17.6.066012 [DOI] [PubMed] [Google Scholar]
- 25.Baumgartner A., Dichtl S., Hitzenberger C. K., Sattmann H., Robl B., Moritz A., Fercher A. F., Sperr W., “Polarization-sensitive optical coherence tomography of dental structures,” Caries Res. 34(1), 59–69 (2000). 10.1159/000016571 [DOI] [PubMed] [Google Scholar]
- 26.Wang X.-J., Milner T. E., de Boer J. F., Zhang Y., Pashley D. H., Nelson J. S., “Characterization of dentin and enamel by use of optical coherence tomography,” Appl. Opt. 38(10), 2092–2096 (1999). 10.1364/AO.38.002092 [DOI] [PubMed] [Google Scholar]
- 27.Giattina S. D., Courtney B. K., Herz P. R., Harman M., Shortkroff S., Stamper D. L., Liu B., Fujimoto J. G., Brezinski M. E., “Assessment of coronary plaque collagen with polarization sensitive optical coherence tomography (PS-OCT),” Int. J. Cardiol. 107(3), 400–409 (2006). 10.1016/j.ijcard.2005.11.036 [DOI] [PubMed] [Google Scholar]
- 28.Kuo W.-C., Chou N.-K., Chou C., Lai C.-M., Huang H.-J., Wang S.-S., Shyu J.-J., “Polarization-sensitive optical coherence tomography for imaging human atherosclerosis,” Appl. Opt. 46(13), 2520–2527 (2007). 10.1364/AO.46.002520 [DOI] [PubMed] [Google Scholar]
- 29.Nadkarni S. K., Pierce M. C., Park B. H., de Boer J. F., Whittaker P., Bouma B. E., Bressner J. E., Halpern E., Houser S. L., Tearney G. J., “Measurement of collagen and smooth muscle cell content in atherosclerotic plaques using polarization-sensitive optical coherence tomography,” J. Am. Coll. Cardiol. 49(13), 1474–1481 (2007). 10.1016/j.jacc.2006.11.040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Hee M. R., Huang D., Swanson E. A., Fujimoto J. G., “Polarization-sensitive low-coherence reflectometer for birefringence characterization and ranging,” J. Opt. Soc. Am. B 9(6), 903–908 (1992). 10.1364/JOSAB.9.000903 [DOI] [Google Scholar]
- 31.de Boer J. F., Milner T. E., van Gemert M. J. C., Nelson J. S., “Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography,” Opt. Lett. 22(12), 934–936 (1997). 10.1364/OL.22.000934 [DOI] [PubMed] [Google Scholar]
- 32.Hitzenberger C. K., Goetzinger E., Sticker M., Pircher M., Fercher A. F., “Measurement and imaging of birefringence and optic axis orientation by phase resolved polarization sensitive optical coherence tomography,” Opt. Express 9(13), 780–790 (2001). 10.1364/OE.9.000780 [DOI] [PubMed] [Google Scholar]
- 33.Götzinger E., Pircher M., Hitzenberger C. K., “High speed spectral domain polarization sensitive optical coherence tomography of the human retina,” Opt. Express 13(25), 10217–10229 (2005). 10.1364/OPEX.13.010217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Davé D. P., Akkin T., Milner T. E., “Polarization-maintaining fiber-based optical low-coherence reflectometer for characterization and ranging of birefringence,” Opt. Lett. 28(19), 1775–1777 (2003). 10.1364/OL.28.001775 [DOI] [PubMed] [Google Scholar]
- 35.Al-Qaisi M. K., Akkin T., “Polarization-sensitive optical coherence tomography based on polarization-maintaining fibers and frequency multiplexing,” Opt. Express 16(17), 13032–13041 (2008). 10.1364/OE.16.013032 [DOI] [PubMed] [Google Scholar]
- 36.Götzinger E., Baumann B., Pircher M., Hitzenberger C. K., “Polarization maintaining fiber based ultra-high resolution spectral domain polarization sensitive optical coherence tomography,” Opt. Express 17(25), 22704–22717 (2009). 10.1364/OE.17.022704 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Al-Qaisi M. K., Akkin T., “Swept-source polarization-sensitive optical coherence tomography based on polarization-maintaining fiber,” Opt. Express 18(4), 3392–3403 (2010). 10.1364/OE.18.003392 [DOI] [PubMed] [Google Scholar]
- 38.Bonesi M., Sattmann H., Torzicky T., Zotter S., Baumann B., Pircher M., Götzinger E., Eigenwillig C., Wieser W., Huber R., Hitzenberger C. K., “High-speed polarization sensitive optical coherence tomography scan engine based on Fourier domain mode locked laser,” Biomed. Opt. Express 3(11), 2987–3000 (2012). 10.1364/BOE.3.002987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Roth J. E., Kozak J. A., Yazdanfar S., Rollins A. M., Izatt J. A., “Simplified method for polarization-sensitive optical coherence tomography,” Opt. Lett. 26(14), 1069–1071 (2001). 10.1364/OL.26.001069 [DOI] [PubMed] [Google Scholar]
- 40.Pierce M. C., Shishkov M., Park B. H., Nassif N. A., Bouma B. E., Tearney G. J., de Boer J. F., “Effects of sample arm motion in endoscopic polarization-sensitive optical coherence tomography,” Opt. Express 13(15), 5739–5749 (2005). 10.1364/OPEX.13.005739 [DOI] [PubMed] [Google Scholar]
- 41.Saxer C. E., de Boer J. F., Park B. H., Zhao Y., Chen Z., Nelson J. S., “High-speed fiber based polarization-sensitive optical coherence tomography of in vivo human skin,” Opt. Lett. 25(18), 1355–1357 (2000). 10.1364/OL.25.001355 [DOI] [PubMed] [Google Scholar]
- 42.Park B. H., Pierce M. C., Cense B., de Boer J. F., “Jones matrix analysis for a polarization-sensitive optical coherence tomography system using fiber-optic components,” Opt. Lett. 29(21), 2512–2514 (2004). 10.1364/OL.29.002512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Oh W. Y., Vakoc B. J., Yun S. H., Tearney G. J., Bouma B. E., “Single-detector polarization-sensitive optical frequency domain imaging using high-speed intra A-line polarization modulation,” Opt. Lett. 33(12), 1330–1332 (2008). 10.1364/OL.33.001330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Yamanari M., Makita S., Yasuno Y., “Polarization-sensitive swept-source optical coherence tomography with continuous source polarization modulation,” Opt. Express 16(8), 5892–5906 (2008). 10.1364/OE.16.005892 [DOI] [PubMed] [Google Scholar]
- 45.Yamanari M., Lim Y., Makita S., Yasuno Y., “Visualization of phase retardation of deep posterior eye by polarization-sensitive swept-source optical coherence tomography with 1- µm probe,” Opt. Express 17(15), 12385–12396 (2009). 10.1364/OE.17.012385 [DOI] [PubMed] [Google Scholar]
- 46.Oh W. Y., Yun S. H., Vakoc B. J., Shishkov M., Desjardins A. E., Park B. H., de Boer J. F., Tearney G. J., Bouma B. E., “High-speed polarization sensitive optical frequency domain imaging with frequency multiplexing,” Opt. Express 16(2), 1096–1103 (2008). 10.1364/OE.16.001096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Baumann B., Choi W., Potsaid B., Huang D., Duker J. S., Fujimoto J. G., “Swept source/Fourier domain polarization sensitive optical coherence tomography with a passive polarization delay unit,” Opt. Express 20(9), 10229–10241 (2012). 10.1364/OE.20.010229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Lim Y., Hong Y.-J., Duan L., Yamanari M., Yasuno Y., “Passive component based multifunctional Jones matrix swept source optical coherence tomography for Doppler and polarization imaging,” Opt. Lett. 37(11), 1958–1960 (2012). 10.1364/OL.37.001958 [DOI] [PubMed] [Google Scholar]
- 49.Fan C., Wang Y., Wang R. K., “Spectral domain polarization sensitive optical coherence tomography achieved by single camera detection,” Opt. Express 15(13), 7950–7961 (2007). 10.1364/OE.15.007950 [DOI] [PubMed] [Google Scholar]
- 50.V. Jayaraman, J. Jiang, H. Li, P. Heim, G. Cole, B. Potsaid, J. G. Fujimoto, and A. E. Cable, “OCT imaging up to 760kHz axial scan rate using single-mode 1310nm MEMs-tunable VCSELs with> 100nm tuning range,” in CLEO: Science and Innovations, (Optical Society of America, 2011), PDPB2. [Google Scholar]
- 51.Jayaraman V., Cole G. D., Robertson M., Uddin A., Cable A. E., “High-sweep-rate 1310 nm MEMS-VCSEL with 150 nm continuous tuning range,” Electron. Lett. 48(14), 867–869 (2012). 10.1049/el.2012.1552 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Potsaid B., Jayaraman V., Fujimoto, Jiang J., Heim P. J., Cable A. E., “MEMS tunable VCSEL light source for ultrahigh speed 60kHz-1MHz axial scan rate and long range centimeter class OCT imaging,” In SPIE BiOS, (International Society for Optics and Photonics, 2012), 82130M–82130M. [Google Scholar]
- 53.Tsai T.-H., Potsaid B., Tao Y. K., Jayaraman V., Jiang J., Heim P. J. S., Kraus M. F., Zhou C., Hornegger J., Mashimo H., Cable A. E., Fujimoto J. G., “Ultrahigh speed endoscopic optical coherence tomography using micromotor imaging catheter and VCSEL technology,” Biomed. Opt. Express 4(7), 1119–1132 (2013). 10.1364/BOE.4.001119 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Zhang E. Z., Vakoc B. J., “Polarimetry noise in fiber-based optical coherence tomography instrumentation,” Opt. Express 19(18), 16830–16842 (2011). 10.1364/OE.19.016830 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zhang E. Z., Oh W.-Y., Villiger M. L., Chen L., Bouma B. E., Vakoc B. J., “Numerical compensation of system polarization mode dispersion in polarization-sensitive optical coherence tomography,” Opt. Express 21(1), 1163–1180 (2013). 10.1364/OE.21.001163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.VanWiggeren G. D., Roy R., “Transmission of linearly polarized light through a single-mode fiber with random fluctuations of birefringence,” Appl. Opt. 38(18), 3888–3892 (1999). 10.1364/AO.38.003888 [DOI] [PubMed] [Google Scholar]
- 57.Makita S., Yamanari M., Yasuno Y., “Generalized Jones matrix optical coherence tomography: performance and local birefringence imaging,” Opt. Express 18(2), 854–876 (2010). 10.1364/OE.18.000854 [DOI] [PubMed] [Google Scholar]
- 58.Braaf B., Vermeer K. A., Sicam V. A. D. P., van Zeeburg E., van Meurs J. C., de Boer J. F., “Phase-stabilized optical frequency domain imaging at 1-µm for the measurement of blood flow in the human choroid,” Opt. Express 19(21), 20886–20903 (2011). 10.1364/OE.19.020886 [DOI] [PubMed] [Google Scholar]
- 59.Choi W., Potsaid B., Jayaraman V., Baumann B., Grulkowski I., Liu J. J., Lu C. D., Cable A. E., Huang D., Duker J. S., Fujimoto J. G., “Phase-sensitive swept-source optical coherence tomography imaging of the human retina with a vertical cavity surface-emitting laser light source,” Opt. Lett. 38(3), 338–340 (2013). 10.1364/OL.38.000338 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Vakoc B. J., Yun S. H., de Boer J. F., Tearney G. J., Bouma B. E., “Phase-resolved optical frequency domain imaging,” Opt. Express 13(14), 5483–5493 (2005). 10.1364/OPEX.13.005483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ju M. J., Hong Y.-J., Makita S., Lim Y., Kurokawa K., Duan L., Miura M., Tang S., Yasuno Y., “Advanced multi-contrast Jones matrix optical coherence tomography for Doppler and polarization sensitive imaging,” Opt. Express 21(16), 19412–19436 (2013). 10.1364/OE.21.019412 [DOI] [PubMed] [Google Scholar]
- 62.Potsaid B., Baumann B., Huang D., Barry S., Cable A. E., Schuman J. S., Duker J. S., Fujimoto J. G., “Ultrahigh speed 1050nm swept source/Fourier domain OCT retinal and anterior segment imaging at 100,000 to 400,000 axial scans per second,” Opt. Express 18(19), 20029–20048 (2010). 10.1364/OE.18.020029 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Park B. H., Pierce M. C., Cense B., Yun S.-H., Mujat M., Tearney G. J., Bouma B. E., de Boer J. F., “Real-time fiber-based multi-functional spectral-domain optical coherence tomography at 1.3 um,” Opt. Express 13(11), 3931–3944 (2005). 10.1364/OPEX.13.003931 [DOI] [PubMed] [Google Scholar]
- 64.J. M. Schmitt, “Methods and apparatus for swept-source optical coherence tomography,” Lightlab Imaging, Inc., US Patent 7,916,387 (2011).
- 65.Xi J., Huo L., Li J., Li X., “Generic real-time uniform K-space sampling method for high-speed swept-source optical coherence tomography,” Opt. Express 18(9), 9511–9517 (2010). 10.1364/OE.18.009511 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Li K., Wu X., Chen D. Z., Sonka M., “Optimal surface segmentation in volumetric images--a graph-theoretic approach,” IEEE Trans. Pattern Anal. Mach. Intell. 28(1), 119–134 (2006). 10.1109/TPAMI.2006.19 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Garvin M. K., Abramoff M. D., Kardon R., Russell S. R., Wu X., Sonka M., “Intraretinal layer segmentation of macular optical coherence tomography images using optimal 3-D graph search,” IEEE Trans. Med. Imaging 27(10), 1495–1505 (2008). 10.1109/TMI.2008.923966 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.H. Lombaert, Y. Sun, L. Grady, and C. Xu, “A multilevel banded graph cuts method for fast image segmentation,” in Tenth IEEE International Conference on Computer Vision, (IEEE 2005), 259–265. 10.1109/ICCV.2005.13 [DOI] [Google Scholar]
- 69.Jia Y., Tan O., Tokayer J., Potsaid B., Wang Y., Liu J. J., Kraus M. F., Subhash H., Fujimoto J. G., Hornegger J., Huang D., “Split-spectrum amplitude-decorrelation angiography with optical coherence tomography,” Opt. Express 20(4), 4710–4725 (2012). 10.1364/OE.20.004710 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Park B. H., Pierce M. C., Cense B., de Boer J. F., “Optic axis determination accuracy for fiber-based polarization-sensitive optical coherence tomography,” Opt. Lett. 30(19), 2587–2589 (2005). 10.1364/OL.30.002587 [DOI] [PubMed] [Google Scholar]
- 71.Ugryumova N., Gangnus S. V., Matcher S. J., “Three-dimensional optic axis determination using variable-incidence-angle polarization-optical coherence tomography,” Opt. Lett. 31(15), 2305–2307 (2006). 10.1364/OL.31.002305 [DOI] [PubMed] [Google Scholar]
- 72.Lu Z., Matcher S. J., “Absolute fast axis determination using non-polarization-maintaining fiber-based polarization-sensitive optical coherence tomography,” Opt. Lett. 37(11), 1931–1933 (2012). 10.1364/OL.37.001931 [DOI] [PubMed] [Google Scholar]
- 73.Tsai T.-H., Zhou C., Tao Y. K., Lee H.-C., Ahsen O. O., Figueiredo M., Kirtane T., Adler D. C., Schmitt J. M., Huang Q., Fujimoto J. G., Mashimo H., “Structural markers observed with endoscopic 3-dimensional optical coherence tomography correlating with Barrett’s esophagus radiofrequency ablation treatment response (with videos),” Gastrointest. Endosc. 76(6), 1104–1112 (2012). 10.1016/j.gie.2012.05.024 [DOI] [PMC free article] [PubMed] [Google Scholar]