Abstract
Ecology, with a traditional focus on plants and animals, seeks to understand the mechanisms underlying structure and dynamics of communities. In microbial ecology, the focus is changing from planktonic communities to attached biofilms that dominate microbial life in numerous systems. Therefore, interest in the structure and function of biofilms is on the rise. Biofilms can form reproducible physical structures (i.e. architecture) at the millimetre-scale, which are central to their functioning. However, the spatial dynamics of the clusters conferring physical structure to biofilms remains often elusive. By experimenting with complex microbial communities forming biofilms in contrasting hydrodynamic microenvironments in stream mesocosms, we show that morphogenesis results in ‘ripple-like’ and ‘star-like’ architectures – as they have also been reported from monospecies bacterial biofilms, for instance. To explore the potential contribution of demographic processes to these architectures, we propose a size-structured population model to simulate the dynamics of biofilm growth and cluster size distribution. Our findings establish that basic physical and demographic processes are key forces that shape apparently universal biofilm architectures as they occur in diverse microbial but also in single-species bacterial biofilms.
Introduction
The realization of the extent to which microorganisms develop on surfaces, as matrix-enclosed communities has increasingly moved the interest of microbial ecology from planktonic to biofilm communities over the last decades (Costerton and Lewandowski, 1995; Hall-Stoodley et al., 2004). Biofilms dominate microbial life in numerous aquatic ecosystems where they orchestrate key biogeochemical processes (Battin et al., 2003; 2008). Biofilms are also important agents of biofouling and biocorrosion in technical systems (Bixler and Bushan, 2012) and account for numerous persistent and chronic infections (Costerton et al., 1999; Hall-Stoodley et al., 2004; Percival et al., 2012). It is notably the recognition of the role biofilms play in medical and technical systems, which has boosted biofilm research over the last decades with a clear focus on monospecies bacterial cultures grown in vitro (Costerton and Lewandowski, 1995; Costerton et al., 1999; Hall-Stoodley et al., 2004; Percival et al., 2012). This approach is now shifting towards multispecies bacterial biofilms if possible grown under more realistic in vivo conditions (Hibbing et al., 2010; Elias and Banin, 2012; Rendueles and Ghigo, 2012).
The ability of biofilms to form highly differentiated architectural structures is thought to be an ancient and integral characteristic of microorganisms, which over evolutionary time has lead to strategies of microorganisms to optimize growth even in adverse environments (Costerton and Lewandowski, 1995; Stoodley et al., 2002; Hall-Stoodley et al., 2004). Biofilms, whether monospecies or multispecies bacterial communities or even more complex communities, also including algae, protozoa and non-living particles as occurring in streams or tidal flats, can form reproducible architectures across scales. Mushroom-like caps, microcolonies with pores and channels (Parsek and Tolker-Nielsen, 2008), filamentous streamers (Stoodley et al., 1999), and even quasipolygonal or reticulated geometries (Stoodley et al., 1999; 2002; Battin et al., 2003; Cogan and Wolgemuth, 2005; Parsek and Tolker-Nielsen, 2008; Baum et al., 2009; Xavier et al., 2009; Shepard and Sumner, 2010; Elias and Banin, 2012) figure among the most commonly observed architectures of microbial biofilms. An enduring question remains, what are the key forces driving biofilm structural differentiation (i.e. morphogenesis) and resulting architectures? Addressing this question is fundamental as morphogenesis can determine functional properties of biological systems (Bourgine and Lesne, 2011). Notably the spatial organization of biofilm architecture at the mesoscale (millimetre range) is recognized to affect biofilm functions and, well beyond, even ecosystem and engineering processes (Battin et al., 2003; Morgenroth and Milferstedt, 2009; Wagner et al., 2010). Understanding biofilm morphogenesis may also be helpful to unveil the success of the biofilm mode of life as biofilm function is tightly connected to architecture.
Over the last decades, various conceptual and theoretical models were put forward to explain biofilm formation and structural differentiation (Wimpenny and Colasanti, 1997; Picioreanu et al., 1998; 2007; Kreft et al., 2001; Stoodley et al., 2002; Parsek and Tolker-Nielsen, 2008; Monds and O'Toole, 2009). For instance, the developmental model (Monds and O'Toole, 2009) proposes genetic networks to guide phase transition in biofilm formation and emphasizes selection for the evolution of cooperation between microorganisms. Alternative models propose that stochastic interactions of microorganisms with the environment shape biofilm structure and function; here, biofilm morphogenesis is supposedly driven by selection in dynamic environments (Monds and O'Toole, 2009; Xavier et al., 2009). Mathematical studies have related biofilm architecture to the availability of nutrients, carbon and oxygen, which ultimately results from the interplay between replenishment and uptake, processes that are linked to hydrodynamics (Wimpenny and Colasanti, 1997; Picioreanu et al., 1998; 2007; Kreft et al., 2001; Cogan and Keener, 2004; Klapper and Dockery, 2010). The hydrodynamics of the bulk liquid above the biofilms affects solute replenishment (Picioreanu et al., 1998; Battin et al., 2003) and, at the same time, imposes a physical control on architectural differentiation (Battin et al., 2003; 2007,; Hall-Stoodley et al., 2004). For instance, turbulent flow induces the formation of filamentous streamers oscillating in the water, whereas laminar flow seems to favour the formation of largely isotropic microcolonies (Stoodley et al., 1999; 2002,; Hall-Stoodley et al., 2004). Furthermore, as purported by the emerging field of sociomicrobiology, the balance between microbial growth and competition for nutrients, including cell motility, may also contribute to the emergence of higher order biofilm structures from individual clusters (Picioreanu et al., 2007; Xavier et al., 2009; Mabrouk et al., 2010).
By experimenting with complex biofilms under quasinatural flow and by applying a mathematical model, we study physical and demographic mechanisms that possibly underlie biofilm morphogenesis and mesoscale architectures in contrasting hydrodynamic microenvironments. Experiments were conducted in 40 m long streamside flumes where biofilm communities could assemble from the natural microbial communities suspended in the stream water (Besemer et al., 2012). In these flumes, graded bedforms (n = 40) induced reproducible flow landscapes typical of low-submergence headwater streams. Within these landscapes, we compared biofilm morphogenesis at the bedform crest and in the trough between consecutive bedforms as two contrasting and well-defined hydrodynamic microenvironments. We deliberately included into our study other biofilm components beside prokaryotes (i.e. bacteria and archaea), such as algae and non-living particles, as these are common in stream biofilms. Furthermore, we purposely focused on the dynamics of individual clusters such as microcolonies, but also single cells and non-living particles, as they are the fundamental building blocks of biofilms. Biomass clusters have traditionally received attention to study mass transfer phenomena and both chemical and microbial heterogeneity in biofilms (Stoodley et al., 1998; Stewart, 2003; Stewart and Franklin, 2008).
Results
Hydrodynamic microenvironment
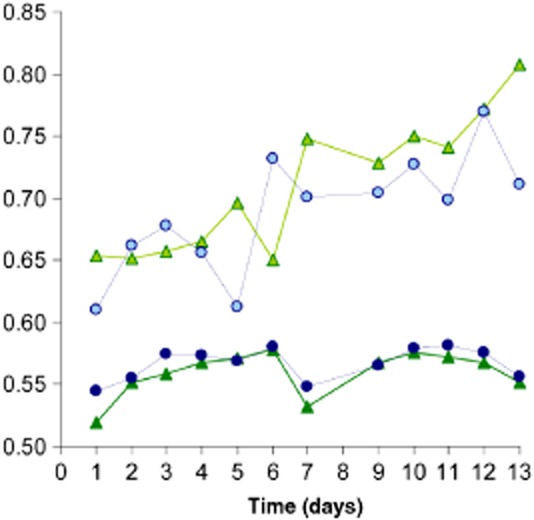
The hydrodynamic microenvironments in our flumes were characterized by high-resolution mapping of the three-dimensional flow velocity using Acoustic Doppler Velocimetry (ADV). At the bedform crests, flow was unidirectional with velocities averaging 0.13 ± 0.01 m s−1 (Fig. 1A). In the trough between consecutive bedforms, an eddy imposed multidirectionality on the flow, including a pronounced vertical dimension, and with overall reduced average flow velocity (0.04 ± 0.01 m s−1). These velocities are typical for headwater streams where microbial biofilm impact is significant (Battin et al., 2003) but remarkably higher than flow velocities applied in laboratory-based flow chambers used to grow model bacterial biofilms (Bakker et al., 2003; Zhang et al., 2011). Turbulent shear stress, calculated for the downstream flow direction, was higher in the trough (0.82 ± 0.19 N m2) than in the crest (0.63 ± 0.06 N m2). Similarly, turbulence intensity as a measure of the temporal variation (fluctuation) of turbulent shear stress was also five times higher in the trough than at the crest (see Hödl et al., 2011) for further details on fine-scale hydraulics. Overall, the flow environment at the crest is characterized by higher flow velocities but by more constant conditions than in the trough. In these contrasting hydrodynamic microenvironments, we monitored the morphogenesis of nascent biofilms over 13 days (Fig. 1B,C). Microbial biomass on days 4 and 12 did not significantly differ between both flow environments (Table S1).
Figure 1.
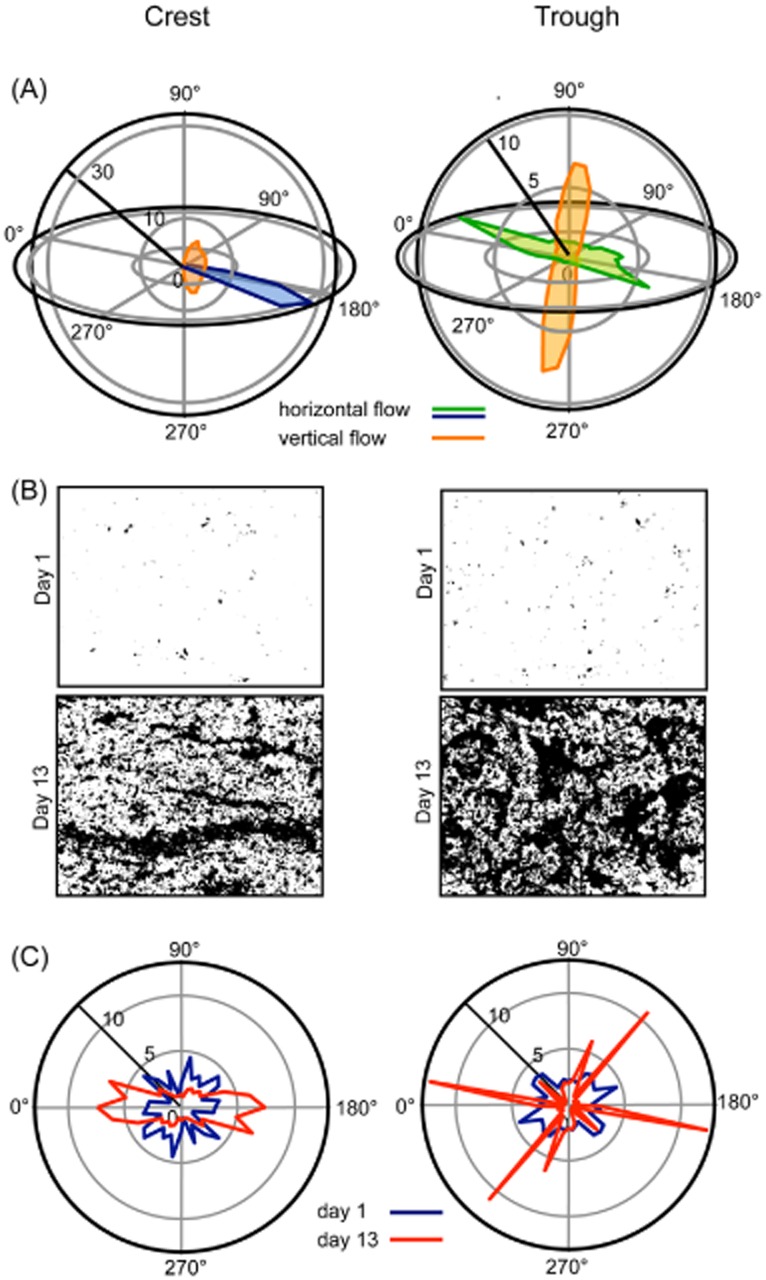
Characterization of flow velocity and biofilm clusters in two contrasting hydrodynamic microenvironments.A. Frequency distributions of three-dimensional flow velocity (x, y and z axes) as determined by Acoustic Doppler Velocimetry at the crest and in the trough of graded bedforms.B. Microphotographs of biofilm clusters at day 1 and at day 13 at the crest and in the trough.C. Growth patterns of biofilm clusters at the crest and in the trough of graded bedforms.
Cluster dynamics and biofilm morphogenesis
Initially, small isotropic clusters (average surface area: crest, 7.62 ± 0.29 μm2; trough, 14.61 ± 6.37 μm2) characterized biofilms both at the crest and in the trough. These initial clusters, consisting to a large extent of individual prokaryotic and algal cells, but also of non-living particles, constitute the seeding material from the water column that continuously deposits onto the benthic surfaces. As these initial clusters proliferate, their shape increasingly becomes anisotropic. At the crest, clusters developed ‘ripple-like’ pattern parallel to the prevailing direction (x-axis) of the water flow. In the trough, however, ‘star-like’ clusters characterized biofilm architecture, obviously reflecting the multidirectional water flow in this microenvironment.
To further explore the transition from isotropic to anisotropic clusters, we quantified the shape of clusters and their temporal dynamics (Fig. 2). This was achieved by analysing how the cluster perimeter scales with the cluster surface area for both seeding (< 130 μm2) and proliferating (> 130 μm2) clusters. The expected exponents for idealized isotropic and anisotropic growth were derived from basic geometries, an exponent of 0.5 describes isotropic growth, whereas exponents larger than 0.5 indicate increasing anisotropic growth (Supporting Information). Deviation from isotropy of seeding clusters did not change during colonization. However, scaling exponents were significantly (paired t-test: tdf:11 = 3.69, P < 0.01) higher in the trough (average ± standard deviation 0.57 ± 0.01) than at the crest (0.56 ± 0.02). Scaling exponents of proliferating clusters were consistently higher than those of the seeding clusters but did not differ significantly (paired t-test: tdf:6 = 0.86, P = 0.88) between crest and trough. This indicates anisotropic growth already during initial colonization but without any clear effect of hydrodynamics at this stage. After a transition phase around day 6, anisotropy became more pronounced for the growing clusters with slightly but significantly (paired t-test: tdf:6 = 3.64, P < 0.05) higher scaling exponents at the crest (0.74 ± 0.05) than in the trough (0.72 ± 0.02). This pattern reflects the elongated growth at the crest and the star-like growth in the trough.
Figure 2.
Transition from isotropic to anisotropic biofilm clusters in contrasting flow environments. Green symbols refer to the clusters at the crest, and blue symbols refer to clusters in the trough; dark colours refer to cluster smaller than 130 μm2 considered as seeding material, and light colours refer to clusters larger than 131 μm2 subject to growth. The scaling exponent describes the relationship between cluster surface area and perimeter, and describes departure from isotropy (Supporting Information).
To further explore biofilm morphogenesis, we analysed the temporal dynamics of biofilm spatial coverage, cluster abundance and cluster size distribution. Biofilm spatial coverage, indicative of space availability and exploitation, was consistently higher in the trough than at the crest (Fig. 3A,C). Concomitantly, higher spatial coverage at quasi-equilibrium in the trough (52.5 ± 6.95% coverage) than at the crest (37.2 ± 3.92% coverage) indicates different levels of optimal filling of space in the two microenvironments. Cluster abundance was higher in the trough than at the crest until day 6 when a decline in cluster abundance inversed this pattern (Fig. 3B,D), indicating the coalescence of adjacent clusters into larger but fewer clusters. Cluster coalescence at day 6 may also hasten anisotropic growth as shown in Fig. 2.
Figure 3.
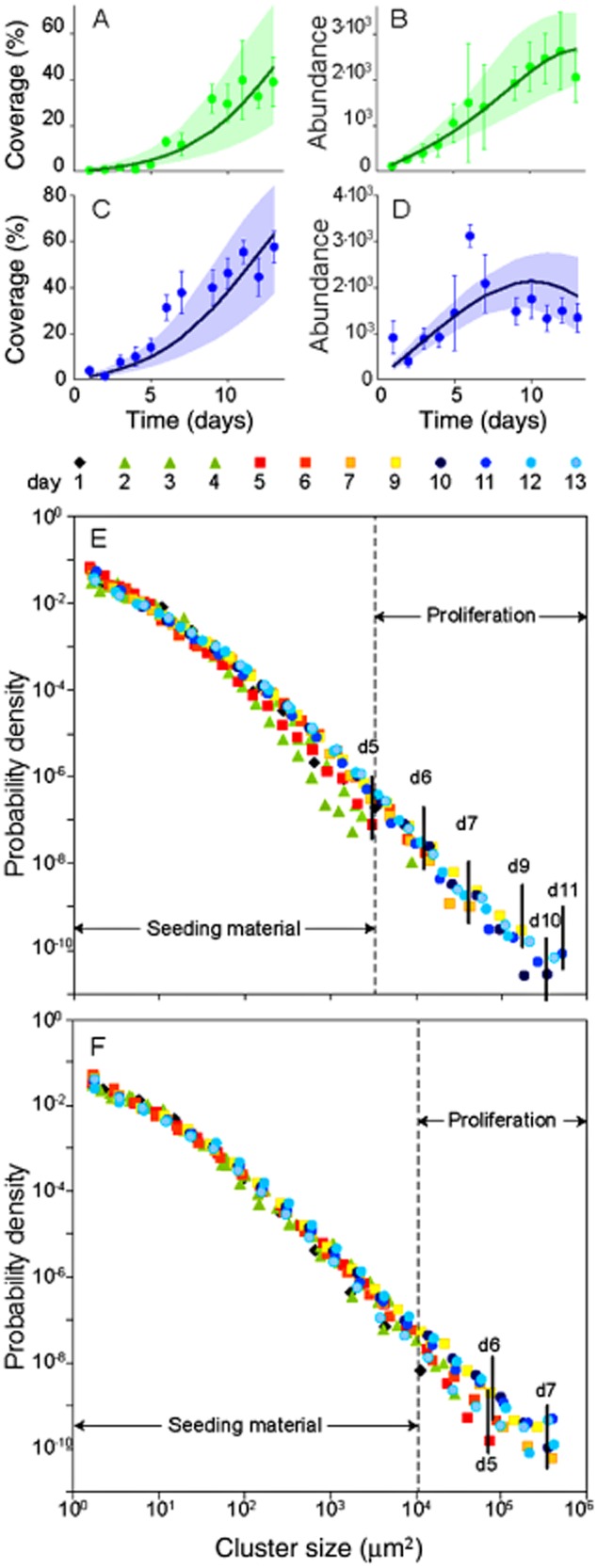
Morphogenesis of biofilms in contrasting flow environments. Temporal dynamics of cluster abundance and coverage at the crest (A,B) and in the trough (C,D). Green and blue symbols refer to observed data, the solid line refers to the best-fit simulation of the model, and the shaded envelope refers to the confidence interval of the simulations. Cluster size distributions as probability density functions at the crest (E) and in the trough (F) for daily sampling points. Highlighted are days with clear shifts in cluster size distributions during proliferation. The size distribution of the seeding material remained largely constant during the growth period.
Cluster size distributions (described by probability density functions) and their temporal dynamics provided further information on biofilm morphogenesis. Cluster size distributions at day 1 were characterized by prokaryotic cells (averaging 2.3 μm2), algae (e.g. single cells of Diatoma vulgare, up to 130 μm2), the smallest non-living particles in the size range of prokaryotic cells and various aggregates, even including entire biofilm sloughs from upstream. This size spectrum is comparable with that of particles suspended in aquatic ecosystems (Wotton, 1994). The cluster size spectra grew during the experiment because of cell reproduction, deposition of suspended particles and coalescence of adjacent clusters. At the crest, maximal cluster size steadily increased, in accordance with the steady increase of cluster abundance and total coverage (up to days 11–12, Fig. 3E). In the trough, maximum cluster size did not increase further after day 7, following a sizeable decrease of cluster abundance (Fig. 3F).
Size-structured model
To explore, besides the apparent physical controls on biofilm morphogenesis, also the potential contributions of demographic processes to cluster dynamics, we developed a size-structured model (Von Foerster, 1959; Sinko and Streifer, 1967). Our modelling approach is not spatially explicit nor does it contain terms that explicitly describe the hydraulics; however, similar models have been successfully applied to study the dynamics of benthic (Pascual and Levin, 1999) and forest (Strigul et al., 2008) communities, for instance. Our model accounts for deposition of suspended particles, cell reproduction, the fraction of migrating (i.e. migration as a neutral behaviour) cells among adjacent clusters and cluster coalescence (Supporting Information). Model simulations captured the dynamics of observed spatial coverage and cluster abundance (Fig. 3A–D) and of cluster size distributions well (Fig. 4 and Supporting Information). The model revealed higher deposition rate in the trough than at the crest (Table 1), which most likely reflects the pronounced vertical flow component in the trough. Cell reproduction rates did not differ in the two microenvironments, which is intuitive given that the model averages over the physiologies of the diverse prokaryotes in the biofilms. These estimates of cell reproduction rates agree well with measured rates across various aquatic ecosystems also including streams (Bott, 1975; White et al., 1991) and hence support the robustness of our model. Cluster coalescence and the fraction of cells migrating over a short range differed in the two microenvironments (Table 1), which underscores the potential relevance of these processes for the diverging biofilm morphogenesis.
Figure 4.
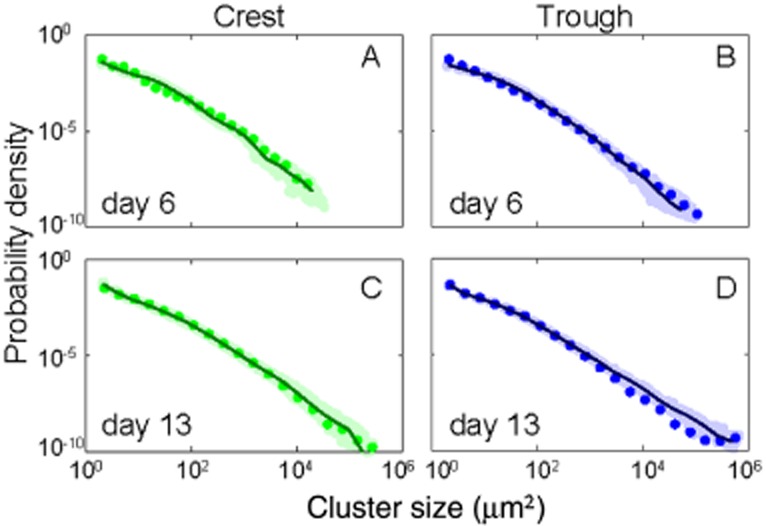
Model simulation of cluster size distribution of biofilms. (A,B) at day 6 and (C,D) at day 13 at the crest and in the trough, respectively. See Supporting Information for the remaining dates.
Table 1.
Estimates of model parameter estimates for biofilm morphogenesis at the crest and in the trough
| Parameter | Microenvironment |
|
|---|---|---|
| Crest | Trough | |
| Deposition rate, d (day−1) | 2.1 × 102 | 4.0 × 102 |
| Reproduction rate, f0 (day−1) | 1.8 × 10−1 | 1.7 × 10−1 |
| Fractions of migrating cells, m (%) | 5.2 × 10−3 | 2.9 × 10−3 |
| Coalescence rate, b0 (day−1) | 3.6 × 10−8 | 8.9 × 10−8 |
See Supporting Information for further explanation.
To disentangle the impact of parameter variation on the dynamics of biofilm coverage and cluster abundance, we run a sensitivity analysis varying the model parameters and evaluating the resulting effects at the transition from isotropic to anisotropic clusters at day 6 and for a later stage at day 13 (Fig. 5 and Supporting Information). Variations of parameters generally support our experimental observations and notion of biofilm morphogenesis. For instance, during the transition phase, deposition rate and, to some extent, also reproduction rate were most influential on coverage and cluster abundance both at the crest and in the trough. As expected, coalescence and the fraction of migration cells were rather negligible for coverage in both microenvironments.
Figure 5.
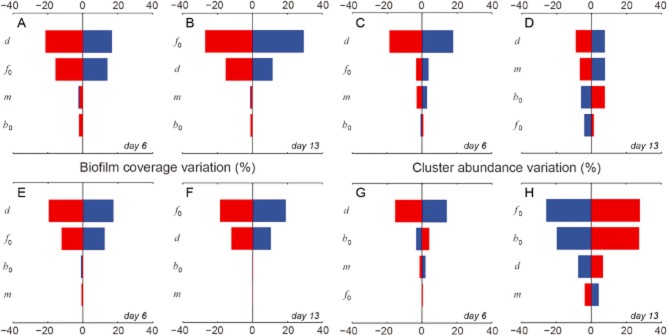
Results of model parameter variation. The analysis was performed for biofilms at the transition from isotropic to anisotropic growth (day 6) and for matured biofilms (day 13). Variations of biofilm coverage at day 6 (A) and at day 13 (B), and for cluster abundance at day 6 (C) and at day 13 (D) at the crest. (E to H) same as (A to D) but in the trough. In each plot the effects of positive variations (+20%) from the reference parameter sets (Table 1 in the main text) are reported in blue, while negative variations (-20%) are reported in red. Note that the parameters are sorted in descending order of their overall impact. d is the deposition rate, f0 is the reproduction rate, m is the fraction of cells migrating over a short range, and b0 is the coalescence rate.
At low cluster density (on an areal basis) proliferation is initially driven by external input and growth of particles and cells rather than by their coalescence. At day 13, deposition was no longer the most sensitive parameter, suggesting that other processes drive morphogenesis at this stage. Reproduction rate was most sensitive for biofilm coverage at crest and in the trough, whereas deposition and reproduction were most sensitive for cluster abundance at the crest and in the trough, respectively. The response to parameter variation was relatively consistent for cluster coverage between crest and trough but differed remarkably between both microenvironments for cluster abundance. Here, deposition and the fraction of migrating cells were most sensitive at the crest while reproduction and coalescence dominated in the trough.
We note that parameter variations may lead to non-trivial outcomes of biofilm morphogenesis. For instance, higher reproduction rates may result in lower cluster abundance as biofilms mature. A similar pattern was found with respect to the deposition rate but only for clusters in the trough. These results can be explained by the fact that higher reproduction and deposition rates induce the formation of larger clusters, which in turn increases the rate of coalescence ultimately resulting in a lower number of clusters. It is remarkable that these model outcomes support our empirical observations on the coverage, abundance and size distribution of clusters as fundamental entities of biofilm architecture.
Discussion
The study of the effects of hydrodynamics on biofilm formation and structural differentiation has been at the core of biofilm research (de Beer et al., 1994; Lewandowski et al., 1994; Stoodley et al., 1998; Eberl et al., 2000; Purevdorj et al., 2002; Horn et al., 2003). Our combined experimental and modelling findings expand on those suggesting that hydrodynamics imposes a major physical template on cluster dynamics and resulting biofilm morphogenesis. Biofilms were exposed to the same seeding material from untreated streamwater and had comparable biomass and even comparable bacterial community composition (Besemer et al., 2009). Remarkably, however, biofilm morphogenesis resulted in diverging architectures in both hydrodynamic microenvironments. Despite quantitative differences of cluster size distributions in the two microenvironments, cluster size distributions were very similar from a qualitative perspective. This observation indicates that few basic processes linked to the different hydrodynamics at the crest and in the trough suffice to impose a major physical template on biofilm morphogenesis. Non-living particles, which contribute significantly to stream biofilms, but also cells with low motility are likely most susceptible to the physical constraints. More motile microorganisms may escape these constraints and contribute to biofilm morphogenesis and resulting structures via migration and coalescence, for instance.
Mesoscale biofilm structures largely shaped by physical processes seem comparable with sand dune formation and other landform patterns (Werner, 1999; Bourgine and Lesne, 2011; Zhang et al., 2012). Here, longitudinal dunes may elongate parallel to the prevailing wind, whereas star dunes may result from the combination of individual longitudinal dunes depending on the frequency of wind reorientation (Zhang et al., 2012). These observations are in line with the concept of biofilms as microbial landscapes, where the interplay between hydrodynamics and substratum topography was postulated to shape biofilm architecture (Battin et al., 2007).
Multidirectional flow, as prevalent in the trough, allows higher degrees of freedom to the directionality of growing cluster to spread through cell migration and coalescence. This enhances the chance to interconnect with adjacent clusters and may ultimately result in the star-like architecture of larger clusters, which in turn causes the observed decline of cluster abundance in the trough. However, we are presently not able to provide a suitable mechanistic explanation for the onset of this process. In fact, the complexity of stream biofilms entails innumerable biotic interactions, internal elemental fluxes and even feedback loops between microbial heterotrophs and photoautotrophs (Lyon and Ziegler, 2009), which altogether would require highly sophisticated modelling approaches. Work on more simple systems such as on Pseudomonas aeruginosa biofilms has shown that the coalescence of adjacent cluster with similar pattern formation as observed in our biofilms involves the interplay between cell proliferation, surface-associated motility and the production of extracellular polymeric substances that form the biofilm matrix (Parsek and Tolker-Nielsen, 2008; Mabrouk et al., 2010). Mabrouk and colleagues (2010) suggest that interconnected microcolonies in these P. aeruginosa biofilms appear when extracellular polymers are expressed at low rate and persist on the path generated by motile cells.
We suggest that star-like structures as observed in the trough between bedforms optimize the exploitation of space, especially in an environment where turbulent wakes may impede solute replenishment. In fact, given that microbial biomass did not differ between crest and trough, it is reasonable to assume that diverging morphogenesis and concurrently different spatial coverage optimize space in contrasting flow environments. The connection of star-like clusters may ultimately result in quasipolygons as reported from laboratory-based bacterial (Xavier et al., 2009; Mabrouk et al., 2010) and stream biofilms (Battin et al., 2003), and from cyanobacterial mats (Shepard and Sumner, 2010). General ecology relates such polygonal shapes to foraging optimality (Covich, 1976), which would support that such biofilm structures may be dynamically accessible optimal states frustrated by the physical constraints like the local turbulence structure.
The unidirectional flow at the crest reduces the degrees of freedom to migrating cells and cluster coalescence to spread in space. This constrains cluster anisotropy with elongated shapes characterizing biofilm architecture. Shear stress is higher at the crest because of elevated flow velocity and may induce the higher fraction of cells migrating over short ranges (Table 1). Guided by the unidirectional flow, cells may preferentially settle downstream in the wake of the parental cluster. The reduced capacity of areal growth (as coverage) in this microenvironment is consistent with general ecological theory predicting physical disturbance to reduce growth efficiency (White and Pickett, 1985).
Our study suggests that basic physical and demographic processes are sufficient to explain the morphogenesis and resulting higher order structures of biofilms containing high microbial diversity and even non-living particles. This may run counter the view of sociomicrobiology stating that multispecies bacterial biofilms with high cell density result from the balance between cooperation and competition, and that the understanding of this balance is essential to model biofilm formation (Kreft et al., 2001; West et al., 2006; Nadell et al., 2009). The fact that hydrodynamics is a major control on cluster dynamics and resulting biofilm morphogenesis in our study may be attributable to the complex flow environment and flow velocities that reflect natural conditions in streams yet not the environment typically mimicked in flow chambers. However, our experimental results, emphasizing hydrodynamics as a physical forcing, are essentially consistent with mathematical models that predict biofilm architecture from hydrodynamics and related mass transfer phenomena (Cogan and Wolgemuth, 2005; Klapper and Dockery, 2010). We acknowledge that we have not attempted to study mass transfer in our biofilms and future studies will therefore focus on this aspect, also including metabolic capabilities of biofilms that diverge in architecture. Still, our study, combining physical forces and ecological processes, offers a fresh view on biofilm architectures, which appears universal independent of scale and community complexity.
Experimental procedures
Hydrodynamic environment
A flow landscape typical for streams with low submergence was mimicked in a streamside flume (L: 40 m, W: 0.40 m). Graded and periodically installed bedforms (bottom length: 1 m; width: 0.40 m; ascending slope: 0.75 m; descending slope: 0.25 m; maximum elevation: 0.08 m) sealed with a polyvinylchloride-foil induced variable flow over the whole flume length. The flume was continuously fed in a once-through mode with streamwater (Oberer Seebach) containing the natural microbial inoculum (not characterized). The flow rate was adjusted to 2.25 l s−1 with an average flume-scale flow velocity of 0.08 m s−1; average residence time of water was 8 min in the flume. The crest and the trough were selected as hydrodynamic extremes. High-resolution ADV (Nortek Vectrino, Norway; side-looking probe) was used to capture the three-dimensional flow velocity over the bedforms. Hydraulic parameters were computed as described in Hödl and colleagues (2011).
Biofilm growth
We grew biofilms on initially sterile glass slides that were ignited (450°C, 4 h) to remove organic compounds (Hödl et al., 2011). Replicate glass slides were exposed at the crest and in the trough of repeated bedform. Growth of complex biofilms including bacteria, algae and non-living particles in streamside flumes typically occurs within 2 weeks and reflects the communities in the streamwater (Besemer et al., 2009; Singer et al., 2010; Hödl et al., 2011).
We determined chlorophyll a as a proxy for algal biomass and quantified prokaryotic cell abundance of the biofilms on two occasions. Briefly, chlorophyll a was extracted with acetone (12 h, 4°C) and assayed fluorometrically (EX435/EM675). Prokaryotic cells were detached (0.025 mmol l−1 tetrasodium pyrophosphate, sonication at 40 W), stained with SYTOX (Invitrogen, USA) and counted on a flow cytometer (Cell-Lab-Quanta; Beckman Coulter, USA).
Imaging and image analysis
At each sampling date, triplicate glass slides from the trough and the crest were sampled after the first 24 h of exposure and then daily for the following 13 days of colonization and growth (with exception of day 8). In the laboratory, microphotographs were taken with a compound microscope (60×) with a 3.9 megapixel camera. Twelve individual microphotographs were taken randomly in the central zone of each slide. Dark field microscopy served to visualize clusters and cells. Colour images (2272 × 1704 pixel; 1 pixel = 0.31 μm) were split into the red, green and blue channel. The resulting greyscale images were thresholded and converted to binary images. The binary images where used to compute coverage, cluster abundance, surface area, perimeter and orientation using the ImageJ plugin ‘shape descriptors’. The fluorescent nucleic acid stain SytoGreen (Invitrogen) served to differentiate prokaryotic cells from mineral particles. Combining epifluorescence and dark field illumination, we were able to estimate the contribution of organic and inorganic material to individual clusters. Autofluorescence of algal cells was used to determine the size of individual algae.
Size-structured population model
The theoretical framework for our model describing biofilm cluster dynamics is provided by the Sinko–Streifer model (Sinko and Streifer, 1967), which offers a generalization of the widely used Lotka–Von Foerster age-structured model (Von Foerster, 1959). Specifically, we formalize a density-dependent age- and size-structured model accounting for a few basic mechanisms that are deemed important for biofilm morphogenesis, namely: (i) deposition of suspended particles (organic/inorganic) from the water column, which can contribute to either the formation of new clusters on bare portions of the streambed or to the growth of existing clusters by inclusion of the deposited material; (ii) cell reproduction, which allows clusters to grow in size; (iii) fraction of cells migrating over short ranges, which allows the exchange of cells among existing clusters, as well as the formation of new clusters; (iv) cluster coalescence as the merging of two existing clusters into a unique larger cluster; and (v) cluster erosion because of the shear effects of the water flow. We assume that each cluster is composed not only of organic cells but also by inorganic matter; the inorganic fraction is not involved in reproduction and migration. Model derivation is detailed in the Supporting Information. To run model simulations, we have implemented an exact stochastic simulation algorithm, which also allows us to account for a closed-form solution for the model outlined earlier.
Therefore, we relied on numerical simulations to study its behaviour. Specifically, we implement an exact stochastic simulation algorithm, which also allows the accounting of the inherent fluctuations and correlations that are necessarily ignored in a deterministic formulation (Gillespie, 1977). In order to initialize model simulations, we consider the size spectrum of clusters found at day 1, which is typical of suspended particles in streams (Wotton, 1994), as the size distribution of the seeding material from which biofilms can develop. Preliminary simulations of the model have shown that in the range of hydrodynamic conditions observed during the experiment, cluster erosion has no significant effects on biofilm dynamics. Parameter estimation is performed by simultaneously fitting biofilm coverage and cluster abundance (details in the Supporting Information), and is repeated independently for biofilms at the crest and in the trough (Table 1).
Acknowledgments
We are grateful to Herman Hofreiter and Engelbert Sollböck for the operation of the experimental flumes and to Gabriel Singer for support and advice. Financial support came from the Austrian Science Fund (START Y420-B17) to TJB and from the PhD School ‘Symbiosis and Biotic Interactions’, University of Vienna, to IH. LM, EB, SS and AR acknowledge the financial support from the ERC grant RINEC-227612 and by the SNSF projects 124930 and 140661.
Supporting Information
Additional Supporting Information may be found in the online version of this article at the publisher's web-site
Supporting Information A. Isotropic and anisotropic growth.
Supporting Information B. The model.
Supporting Information C. Model implementation: an exact stochastic simulator.
Supporting Information D. Model calibration.
Fig. S1. Relationship between cluster surface area and perimeter for clusters in the trough at day 13. For all scaling relationships, the coefficient of determination (R2) was greater than 0.93 and significance (P) better than 0.0001. (a) The relationship of area versus perimeter results in an exponent between 0 and 1. Isotropic growth yields an exponent of 0.5. Increasing deviation of an exponent of 0.5 indicates an isotropic growth. Independent of the geometric shape (here circle and square) isotropic growth results in an exponent of 0.5. The example for anisotropic growth in one axis is given by ‘square’, where the doubling of one axis results in an exponent 0.83. The ‘ellipse’ is an example of anisotropic growth in both axis with the ratio of 4:1 (a:b), resulting in an exponent of 0.63.
Fig. S2. Schematic representation of one iteration of the multi-objective procedure used to calibrate model parameters. (a) Several simulations are run with different parameter sets (blue dots) chosen from broad parameter ranges (grey shading) through Latin hypercube sampling (steps 1–3 of the calibration procedure). (b) The candidate simulations are evaluated according to different objectives (blue dots); then Pareto-efficient candidates are identified (red dots); finally, top-ranked simulations (green dots) are selected (steps 4–6). After these steps, the search space is narrowed down (step 7), and the procedure is repeated until convergence (step 8). Note that the fitting procedure is portrayed here for a generic problem with two tuning parameters and two calibration objectives (e.g. minimization of the RSS's for two observed/simulated quantities).
Fig. S3. Probability density functions of daily size distributions for clusters located at the crest. Red dots: experimental data; blue circles: reference model simulation; grey dots: results from 500 model simulations with parameter values randomly selected from uniform distributions centred around the reference parameter set (±20% variations).
Fig. S4. Q-Q plot of modelled versus observed size distributions for clusters located at the crest. The closer the blue crosses to the green line (where model results are exactly equal to experimental observations), the higher the explanatory power of the model. The values of R2 have been computed as R2 = 1 − RSS/TSS, where TSS is the total sum of squares of the observations (quantiles of cluster log-sizes).
Fig. S5. Probability density functions of daily size distributions for clusters located in the trough (details as in Fig. S3).
Fig. S6. Q–Q plot of modelled versus observed size distributions for clusters located in the trough (details as in Fig. S4).
Table S1. Chlorophyll-a concentration and bacterial abundance at the crest and in the trough at day 4 and day 12 of the experiment. Given are mean values (n = 3) ± SD. Both chlorophyll-a concentration (paired t-test: tdf:5 = 2.06, P = 0.1) and bacterial abundance (paired t-test: tdf:5 = 1.13, P = 0.31) did not differ significantly between crest and trough.
References
- Bakker DP, van der Plaats A, Verkerke GJ, Busscher HJ. van der Mei HC. Comparisons of velocity profiles for different flow chamber designs used in studies of microbial adhesion to surfaces. Appl Environ Microbiol. 2003;69:6280–6287. doi: 10.1128/AEM.69.10.6280-6287.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battin TJ, Kaplan LA, Newbold JD, Cheng XH. Hansen C. Effects of current velocity on the nascent architecture of stream microbial biofilms. Appl Environ Microbiol. 2003;69:5443–5452. doi: 10.1128/AEM.69.9.5443-5452.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Battin TJ, Sloan WT, Kjelleberg S, Daims H, Head IM, Curtis TP. Eberl L. Microbial landscapes: new paths to biofilm research. Nat Rev Microbiol. 2007;5:76–81. doi: 10.1038/nrmicro1556. [DOI] [PubMed] [Google Scholar]
- Battin TJ, Kaplan LA, Findlay S, Hopkinson CS, Marti E, Packman AI, et al. Biophysical controls on organic carbon fluxes in fluvial networks. Nat Geosci. 2008;1:95–100. [Google Scholar]
- Baum M, Kainović A, O'Keeffe T, Pandita R, McDonald K, Wu S. Webster P. Characterization of structures in biofilms formed by a Pseudomonas fluorescens isolated from soil. BMC Microbiol. 2009;9:103. doi: 10.1186/1471-2180-9-103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Beer D, Stoodley P. Lewandowski Z. Liquid flow in heterogeneous biofilms. Biotechnol Bioeng. 1994;44:636–641. doi: 10.1002/bit.260440510. [DOI] [PubMed] [Google Scholar]
- Besemer K, Hödl I, Singer G. Battin TJ. Architectural differentiation reflects bacterial community structure in stream biofilms. ISME J. 2009;3:1318–1324. doi: 10.1038/ismej.2009.73. [DOI] [PubMed] [Google Scholar]
- Besemer K, Peter H, Logue JB, Langenheder S, Lindström ES, Tranvik LJ. Battin TJ. Unravelling assembly of stream biofilm communities. ISME J. 2012;6:1459–1468. doi: 10.1038/ismej.2011.205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bixler GD. Bushan B. Biofouling: lessons from nature. Philos Transact Ser A Math Phys Eng Sci. 2012;370:2381–2417. doi: 10.1098/rsta.2011.0502. [DOI] [PubMed] [Google Scholar]
- Bott TL. Bacterial growth rates and temperature optima in a stream with a fluctuating thermal regime. Limnol Oceanogr. 1975;20:191–197. [Google Scholar]
- Bourgine P. Lesne A. Morphogenesis: Origins of Pattern and Shapes. Berlin, Heidelberg, Germany: Springer; 2011. [Google Scholar]
- Cogan NG. Wolgemuth CW. Pattern formation by bacteria-driven flow. Biophys J. 2005;88:2525–2529. doi: 10.1529/biophysj.104.053348. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cogan NJ. Keener JP. The role of the biofilm matrix in structural development. Math Med Biol. 2004;21:147–166. doi: 10.1093/imammb/21.2.147. [DOI] [PubMed] [Google Scholar]
- Costerton JW. Lewandowski Z. Microbial biofilms. Annu Rev Microbiol. 1995;49:711–745. doi: 10.1146/annurev.mi.49.100195.003431. [DOI] [PubMed] [Google Scholar]
- Costerton JW, Steward PS. Greenberg EP. Bacterial biofilms: a common cause of persistent infections. Science. 1999;284:1318–1322. doi: 10.1126/science.284.5418.1318. [DOI] [PubMed] [Google Scholar]
- Covich AP. Analyzing shapes of foraging areas: some ecological and economic theories. Ann Rev Ecol Syst. 1976;7:235–257. [Google Scholar]
- Eberl HJ, Picioreanu C, Heijnen JJ. Van Loosdrecht MCM. A three-dimensional numerical study on the correlation of spatial structure, hydrodynamic conditions, and mass transfer and conversion in biofilms. Chem Eng Sci. 2000;55:6209–6222. [Google Scholar]
- Elias S. Banin E. Multi-species biofilms: living with friendly neighbors. FEMS Microbiol Rev. 2012;36:990–1004. doi: 10.1111/j.1574-6976.2012.00325.x. [DOI] [PubMed] [Google Scholar]
- Gillespie DT. Exact stochastic simulation of coupled chemical reactions. J Phys Chem. 1977;81:2340–2361. [Google Scholar]
- Hall-Stoodley L, Costerton JW. Stoodley P. Bacterial biofilms: from the natural environment to infectious diseases. Nat Rev Microbiol. 2004;2:95–108. doi: 10.1038/nrmicro821. [DOI] [PubMed] [Google Scholar]
- Hibbing ME, Fuqua C, Parsek MR. Peterson SB. Bacterial competition: surviving in the microbial jungle. Nat Rev Microbiol. 2010;8:15–25. doi: 10.1038/nrmicro2259. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hödl I, Hödl J, Wörman A, Singer GA, Besemer K. Battin TJ. Voronoi tessellation captures very early clustering of single primary cells as induced by interactions in nascent biofilms. PLoS ONE. 2011;6:e26368. doi: 10.1371/journal.pone.0026368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horn H, Reiff H. Morgenroth E. Simulation of growth and detachment in biofilm systems under defined hydrodynamic conditions. Biotechnol Bioeng. 2003;81:607–617. doi: 10.1002/bit.10503. [DOI] [PubMed] [Google Scholar]
- Klapper I. Dockery J. Mathematical description of microbial biofilms. SIAM Rev. 2010;52:221–265. [Google Scholar]
- Kreft J-U, Picioreanu C, Wimpenny JWT. van Loosdrecht MCM. Individual-based modelling of biofilms. Microbiology. 2001;147:2897–2912. doi: 10.1099/00221287-147-11-2897. [DOI] [PubMed] [Google Scholar]
- Lewandowski Z, Stoodley P, Altobelli S. Fukushima E. Hydrodynamics and kinetics in biofilm systems-recent advances and new problems. Water Sci Technol. 1994;29:223–229. [Google Scholar]
- Lyon DR. Ziegler SE. Carbon cycling within epilithic biofilm communities across a nutrient gradient of headwater streams. Limnol Oceanogr. 2009;54:439–449. [Google Scholar]
- Mabrouk N, Deffuant G, Tolker-Nielsen T. Lobry C. Bacteria can form interconnected microcolonies when a self-excreted product reduces their surface motility: evidence from individual-based model simulations. Theory Biosci. 2010;129:1–13. doi: 10.1007/s12064-009-0078-8. [DOI] [PubMed] [Google Scholar]
- Monds RD. O'Toole GA. The developmental model of microbial biofilms: ten years of a paradigm up for review. Trends Microbiol. 2009;17:73–87. doi: 10.1016/j.tim.2008.11.001. [DOI] [PubMed] [Google Scholar]
- Morgenroth E. Milferstedt K. Biofilm engineering: linking biofilm development at different length and time scales. Rev Environ Sci Biotechnol. 2009;8:203–208. [Google Scholar]
- Nadell CD, Xavier JB. Foster KR. The sociobiology of biofilms. FEMS Microbiol Rev. 2009;33:206–224. doi: 10.1111/j.1574-6976.2008.00150.x. [DOI] [PubMed] [Google Scholar]
- Parsek MR. Tolker-Nielsen T. Pattern formation in Pseudomonas aeruginosa biofilms. Curr Opin Microbiol. 2008;11:560–566. doi: 10.1016/j.mib.2008.09.015. [DOI] [PubMed] [Google Scholar]
- Pascual M. Levin SA. Spatial scaling in a benthic population model with density-dependent disturbance. Theor Popul Biol. 1999;56:106–122. doi: 10.1006/tpbi.1999.1417. [DOI] [PubMed] [Google Scholar]
- Percival SL, Hill KE, Williams DW, Hooper SJ, Thomas DW. Costerton JW. A review of the scientific evidence for biofilm in wounds. Wound Repair Regen. 2012;20:647–657. doi: 10.1111/j.1524-475X.2012.00836.x. [DOI] [PubMed] [Google Scholar]
- Picioreanu C, van Loosdrecht MCM. Heijnen JJ. Mathematical modeling of biofilm structure with a hybrid differential-discrete cellular automaton approach. Biotechnol Bioeng. 1998;58:101–116. doi: 10.1002/(sici)1097-0290(19980405)58:1<101::aid-bit11>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- Picioreanu C, Kreft JU, Klausen M, Haagensen JAJ, Tolker-Nielsen T. Molin S. Microbial motility involvement in biofilm structure formation: a 3D modelling study. Water Sci Technol. 2007;55:337–343. doi: 10.2166/wst.2007.275. [DOI] [PubMed] [Google Scholar]
- Purevdorj B, Costerton JW. Stoodley P. Influence of hydrodynamics and cell signaling on the structure and behavior of Pseudomonas aeruginosa biofilms. Appl Environ Microbiol. 2002;68:4457–4464. doi: 10.1128/AEM.68.9.4457-4464.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rendueles O. Ghigo J-M. Multi-species biofilms: how to avoid unfriendly neighbors. FEMS Microbiol Rev. 2012;36:972–989. doi: 10.1111/j.1574-6976.2012.00328.x. [DOI] [PubMed] [Google Scholar]
- Shepard RN. Sumner DY. Undirected motility of filamentous cyanobacteria produces reticulate mats. Geobiology. 2010;8:179–190. doi: 10.1111/j.1472-4669.2010.00235.x. [DOI] [PubMed] [Google Scholar]
- Singer G, Besemer K, Schmitt-Kopplin P, Hödl I. Battin TJ. Physical heterogeneity increases biofilm resource use and its molecular diversity in stream mesocosms. PLoS ONE. 2010;5:e9988. doi: 10.1371/journal.pone.0009988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sinko JW. Streifer W. A new model for age-size structure of a population. Ecology. 1967;48:910–918. [Google Scholar]
- Stewart PS. Diffusion in biofilms. J Bacteriol. 2003;185:1485–1491. doi: 10.1128/JB.185.5.1485-1491.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart PS. Franklin MJ. Physiological heterogeneity in biofilms. Nat Rev Microbiol. 2008;6:199–210. doi: 10.1038/nrmicro1838. [DOI] [PubMed] [Google Scholar]
- Stoodley P, Dodds I, Boyle JD. Lappin-Scott HM. Influence of hyrodynamics and nutrients on biofilm structure. J Appl Microbiol. 1998;85:19S–28S. doi: 10.1111/j.1365-2672.1998.tb05279.x. [DOI] [PubMed] [Google Scholar]
- Stoodley P, Lewandowski Z, Boyle JD. Lappin-Scott HM. Structural deformation of bacterial biofilms caused by short-term fluctuations in fluid shear: an in situ investigation of biofilm rheology. Biotechnol Bioeng. 1999;65:83–92. [PubMed] [Google Scholar]
- Stoodley P, Sauer K, Davies DG. Costerton JW. Biofilms as complex differentiated communities. Annu Rev Microbiol. 2002;56:187–209. doi: 10.1146/annurev.micro.56.012302.160705. [DOI] [PubMed] [Google Scholar]
- Strigul N, Pristinski D, Purves D, Dushoff J. Pacala S. Scaling from trees to forests: tractable macroscopic equations for forest dynamics. Ecol Monogr. 2008;78:523–545. [Google Scholar]
- Von Foerster H. Some remarks on changing populations. In: Stohlman J, editor. The Kinetics of Cellular Proliferation. New York, NY, USA: Grune and Stratton; 1959. pp. 382–407. [Google Scholar]
- Wagner M, Taherzadeh D, Haisch C. Horn H. Investigation of the mesoscale structure and volumetric features of biofilms using optical coherence tomography. Biotechnol Bioeng. 2010;107:844–853. doi: 10.1002/bit.22864. [DOI] [PubMed] [Google Scholar]
- Werner BT. Complexity in natural landform patterns. Science. 1999;284:102–104. doi: 10.1126/science.284.5411.102. [DOI] [PubMed] [Google Scholar]
- West SA, Griffin AS, Gardner A. Diggle SP. Social evolution theory for microorganisms. Nat Rev Microbiol. 2006;4:597–607. doi: 10.1038/nrmicro1461. [DOI] [PubMed] [Google Scholar]
- White P, Kalff J, Rasmussen J. Gasol J. The effect of temperature and algal biomass on bacterial production and specific growth rate in freshwater and marine habitats. Microb Ecol. 1991;21:99–118. doi: 10.1007/BF02539147. [DOI] [PubMed] [Google Scholar]
- White PS. Pickett STA. Natural disturbance and patch dynamics: an introduction. In: White PS, editor; Pickett STA, editor. The Ecology of Natural Disturbance and Patch Dynamics. New York, NY, USA: Academic Press; 1985. pp. 3–13. [Google Scholar]
- Wimpenny JWT. Colasanti R. A unifying hypothesis for the structure of microbial biofilms based on cellular automaton models. FEMS Microbiol Ecol. 1997;22:1–16. [Google Scholar]
- Wotton RS. The Biology of Particles in Aquatic Systems. Boca Raton, FL, USA: Lewis Publishers; 1994. [Google Scholar]
- Xavier JB, Martinez GE. Foster KR. Social evolution of spatial patterns in bacterial biofilms: when conflict drives disorder. Am Nat. 2009;174:1–12. doi: 10.1086/599297. [DOI] [PubMed] [Google Scholar]
- Zhang D, Narteau C, Rozier O. Courrech du Pont S. Morphology and dynamics of star dunes from numerical modelling. Nat Geosci. 2012;5:463–467. [Google Scholar]
- Zhang W, Sileika TS, Chen C, Liu Y, Lee J. Packman AI. A novel planar flow cell for studies of biofilm heterogeneity and flow – biofilm interactions. Biotechnol Bioeng. 2011;108:2571–2582. doi: 10.1002/bit.23234. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information A. Isotropic and anisotropic growth.
Supporting Information B. The model.
Supporting Information C. Model implementation: an exact stochastic simulator.
Supporting Information D. Model calibration.
Fig. S1. Relationship between cluster surface area and perimeter for clusters in the trough at day 13. For all scaling relationships, the coefficient of determination (R2) was greater than 0.93 and significance (P) better than 0.0001. (a) The relationship of area versus perimeter results in an exponent between 0 and 1. Isotropic growth yields an exponent of 0.5. Increasing deviation of an exponent of 0.5 indicates an isotropic growth. Independent of the geometric shape (here circle and square) isotropic growth results in an exponent of 0.5. The example for anisotropic growth in one axis is given by ‘square’, where the doubling of one axis results in an exponent 0.83. The ‘ellipse’ is an example of anisotropic growth in both axis with the ratio of 4:1 (a:b), resulting in an exponent of 0.63.
Fig. S2. Schematic representation of one iteration of the multi-objective procedure used to calibrate model parameters. (a) Several simulations are run with different parameter sets (blue dots) chosen from broad parameter ranges (grey shading) through Latin hypercube sampling (steps 1–3 of the calibration procedure). (b) The candidate simulations are evaluated according to different objectives (blue dots); then Pareto-efficient candidates are identified (red dots); finally, top-ranked simulations (green dots) are selected (steps 4–6). After these steps, the search space is narrowed down (step 7), and the procedure is repeated until convergence (step 8). Note that the fitting procedure is portrayed here for a generic problem with two tuning parameters and two calibration objectives (e.g. minimization of the RSS's for two observed/simulated quantities).
Fig. S3. Probability density functions of daily size distributions for clusters located at the crest. Red dots: experimental data; blue circles: reference model simulation; grey dots: results from 500 model simulations with parameter values randomly selected from uniform distributions centred around the reference parameter set (±20% variations).
Fig. S4. Q-Q plot of modelled versus observed size distributions for clusters located at the crest. The closer the blue crosses to the green line (where model results are exactly equal to experimental observations), the higher the explanatory power of the model. The values of R2 have been computed as R2 = 1 − RSS/TSS, where TSS is the total sum of squares of the observations (quantiles of cluster log-sizes).
Fig. S5. Probability density functions of daily size distributions for clusters located in the trough (details as in Fig. S3).
Fig. S6. Q–Q plot of modelled versus observed size distributions for clusters located in the trough (details as in Fig. S4).
Table S1. Chlorophyll-a concentration and bacterial abundance at the crest and in the trough at day 4 and day 12 of the experiment. Given are mean values (n = 3) ± SD. Both chlorophyll-a concentration (paired t-test: tdf:5 = 2.06, P = 0.1) and bacterial abundance (paired t-test: tdf:5 = 1.13, P = 0.31) did not differ significantly between crest and trough.


