Can Marginal Rates of Substitution Be Inferred From Happiness Data? Evidence from Residency Choices

Abstract

We survey 561 students from U.S. medical schools shortly after they submit choice rankings over residencies to the National Resident Matching Program. We elicit (a) these choice rankings, (b) anticipated subjective well-being (SWB) rankings, and (c) expected features of the residencies (such as prestige). We find substantial differences between choice and anticipated-SWB rankings in the implied tradeoffs between residency features. In our data, evaluative SWB measures (life satisfaction and Cantril's ladder) imply tradeoffs closer to choice than does affective happiness (even time-integrated), and as close as do multi-measure SWB indices. We discuss implications for using SWB data in applied work.

The marginal rate of substitution (MRS) is the magnitude that characterizes preferences: as (minus) the slope of an individual's indifference curve, it quantifies the tradeoffs that individuals are willing to make. Traditionally, MRSs are estimated from choice data. Economists must resort to alternatives, however, in settings where the relevant choices are not observed (as is often the case when externalities, non-market goods, and certain government policies are involved) or where individuals' choices are likely to reflect mistakes. An increasingly-used alternative source of data is survey responses to subjective well-being (SWB) questions—most commonly, questions about respondents' happiness, life satisfaction, or life's ranking on a ladder. In a typical application, a measure of SWB is regressed on respondents' quantities of a bundle of non-market goods, and the ratio of the coefficients on two goods yields an estimate of the goods' rate of tradeoff that would leave SWB unchanged. SWB data have been used in this way, for example, to estimate the tradeoffs between inflation and unemployment (Di Tella, MacCulloch, and Oswald, 2001); between own and others' income (for a recent review, see Clark, Frijters, and Shields, 2008); and between money and a relative's life (by comparing the coefficient on losing a family member with the coefficient on income; Oswald and Powdthavee, 2008, and Deaton, Fortson, and Tortora, 2010).¹

The purpose of this paper is to explore empirically the extent to which such SWB-based tradeoffs reflect preference-based MRSs, where by “preferences” we mean what would be inferred from well-informed, deliberated choice data were the relevant choices observed. To that end, we elicit: (a) choice rankings over a set of options, in a setting where choice is arguably deliberated and well-informed; (b) the anticipated SWB consequences of the different choice options; and (c) the expected quantities of the (non-market) goods that comprise the relevant consumption bundle under each choice option. We estimate the tradeoffs between the goods implied by choice and those implied by different SWB measures, and we investigate the differences between them. We do not take a stand on which, if any, of such tradeoff estimates should be normatively privileged; we merely study measures that are already widely used in applied work.

While the literature estimates the tradeoffs implied by experienced SWB, it is crucial for our purposes to compare choice tradeoffs with anticipated-SWB tradeoffs in order to hold constant the conditions (including information and beliefs) under which the choice is made. Divergences between choice and experienced-SWB tradeoffs have been well documented and are often assumed to be fully explained by mispredictions of SWB at the time of choice (e.g., Loewenstein, O'Donoghue, and Rabin, 2003; Gilbert, 2006). In contrast, comparing choice and anticipated-SWB tradeoffs permits assessing the individual's intentions at the time of choice: divergences can then be attributed to SWB not fully capturing the relative importance of the individual's goals. The presence of such divergences would imply that (the much discussed) SWB misprediction is not the whole story for explaining divergences between choice and experienced-SWB tradeoffs (for an alternative view, see e.g., Kahneman and Snell, 1992; Hsee, Hastie, and Chen, 2008). In the conclusion of this paper, we discuss how our results on choice tradeoffs vs. anticipated-SWB tradeoffs may carry over to comparisons of choice tradeoffs vs. experienced-SWB tradeoffs, when our results are combined with findings from the existing literature on anticipated-SWB tradeoffs vs. experienced-SWB tradeoffs.

In section I we describe the setting we study: graduating U.S. medical students' preference rankings over residency programs. These preference rankings submitted by students to the National Resident Matching Program (NRMP), combined with the preference rankings over students submitted by the residency programs, determine which students are matched to which programs. This setting has a number of attractive features for our purposes: the matching mechanism is designed to be incentive-compatible; the choice is a deliberated, well-informed, and important career decision; the choice set is well-defined and straightforward to elicit; and due to a submission deadline, there is an identifiable moment in time when the decision is irreversibly made. We conduct a survey among a sample of 561 students from 23 U.S. medical schools shortly after they submit their residency preferences to the NRMP, so that our survey is conducted under information and beliefs as close as possible to those held during the actual choice.

Section II describes our sample and survey design. We ask about each student's four most-preferred residency programs. In addition to eliciting each student's preference ranking over the four residencies as submitted to the NRMP, we also elicit her anticipated SWB rankings over the residencies, both during the residency and for the rest of her life. We focus on three commonly-used SWB measures: happiness, life satisfaction, and a Cantril-ladder measure.² We also ask each student to rate each of the four residencies on each of nine features that we expected to be the most important determinants of program choice (based on our past research in settings other than residency choice as well as on conversations with medical school officials and with past and present students).³ These include the desirability of residency location, residency prestige-and-status, expected stress level, and future career prospects.

Section III reports our analyses and results. We model residencies as bundles of attributes, and we use the choice- and SWB-rankings as alternative dependent variables in regressions where the independent variables are students' beliefs about these attributes. In our main analysis we compare the coefficients and coefficient ratios across regressions. Because our survey elicits anticipated SWB soon after it elicits choice, coefficient similarities across the regressions may be overstated in our data and may hence be thought of as upper bounds, while coefficient differences may be understated and may hence be interpreted as lower bounds.

While the coefficients of the attributes do not reverse sign and are reasonably highly correlated across the choice and SWB regressions, we find large and significant differences in the implied tradeoffs. For example, relative to the choice-based estimates, all anticipated-SWB estimates underweight residency prestige-and-status and residency desirability for the respondent's significant other, while overweighting social life and life seeming worthwhile during the residency. We also find that our evaluative SWB measures—life satisfaction and Cantril's ladder—generally yield results closer to the choice-based estimates than our more affective happiness measure. The choice-SWB differences we find are robust to plausible forms of measurement error and biases in survey response and hold across empirical specifications and across subsets of our respondents.

We also explore whether multi-question SWB indices more accurately reflect revealed-preference tradeoffs. We consider three such indices: the first, a “3-SWB-measure” index, is a weighted sum of our three SWB questions; the second, a “4-period-happiness” index, consists of happiness predictions for four time intervals that together cover the rest of a respondent's life; the third index combines the other two. While such indices have not been commonly used to estimate tradeoffs, we are motivated by the ideas, respectively, that well-being is multidimensional (e.g., Stiglitz, Sen, and Fitoussi, 2009) and that well-being consists of instantaneous affect integrated over time (Kahneman, Wakker, and Sarin, 1997), as well as by the empirical observation that different SWB measures could imply dramatically different tradeoffs (e.g., Kahneman and Deaton, 2010; Deaton, Fortson, and Tortora, 2010). We estimate the optimal weights of the indices as best linear predictors of choice in our data; our indices are hence constructed to perform better than those likely to be used in realistic applications, where choice data are not available (an additional reason for a lower-bound interpretation of any choice-SWB differences found in our data). We find that while some tradeoffs based on these multi-question indices are closer to our choice-based MRSs than the tradeoffs based on the indices' underlying questions, overall the indices do not reflect the MRSs more reliably than the single evaluative-SWB questions.

In section IV, we explore an alternative use of SWB data: assessing which of two concrete choice options is preferred. We find that despite the differences in implied tradeoffs between choice and SWB in our data, the two often coincide in pairwise comparisons. We present a simple model that illustrates the relationship between pairwise predictions and tradeoffs, and we discuss the conditions under which SWB data may correctly predict choice even when the implied tradeoffs differ.

We conclude in section V.

Our work builds upon and differs from past attempts to study the relationship between choice and SWB measures in several important ways. First, while almost all existing work (Tversky and Griffin, 1991; Hsee, 1999; Hsee, Zhang, Yu, and Xi, 2003; Benjamin, Heffetz, Kimball, and Rees-Jones, 2012) compares anticipated-SWB rankings with choices that are either hypothetical or involve very small stakes, we present evidence on real, deliberated choices in a high-stakes field environment—the sort of choices one would like to observe for reliably estimating MRSs. Second, while the earlier studies document cases where choices between pairs of options do not maximize anticipated SWB, we focus on the implications for estimating MRSs. Third, our evidence is from a setting where ordinal preferences over a well-defined and observable choice set are directly elicited. While preferences can sometimes be inferred indirectly—for example, as in Dolan and Metcalfe (2008), who, for pricing the welfare effects of an urban regeneration project, compare estimates based on contingent-valuation and hedonic-pricing methods with those based on SWB—such indirect approaches necessarily hinge on many maintained assumptions. Moreover, unlike existing work, our paper studies a field setting that allows the direct elicitation not only of preference orderings but also of anticipated-SWB rankings of the options in the choice set—an ideal setting for studying choice-SWB alignment. Fourth, while prior work considers only single SWB questions, we also consider indices that include multiple SWB measures and multi-period affective happiness. Finally, drawing on theoretical considerations as well as on empirical results from this and previous papers, we offer guidance regarding the interpretation and use of SWB data, vis-à-vis choice data, in applied research. For example, while our findings suggest that SWB data are inadequate for precise inference regarding (preference-based) MRSs, in binary welfare comparisons they may in some settings yield conclusions that line up with preferences—although their use is still subject to assumptions and caveats not studied in this paper (see, e.g., Adler, 2013).

I. Choice Setting: The National Resident Matching Program (NRMP)

I.A. Background

After graduating from a U.S. medical school, most students enroll in a residency program. The residency is a three- to seven-year period of training in a specialty such as anesthesiology, emergency medicine, family medicine, general surgery, internal medicine, pediatrics, or psychiatry. Students apply to programs at the beginning of their fourth (and final) year. In late fall programs invite selected students to visit and be interviewed. Students subsequently submit to the NRMP their preferences over the programs where they interviewed, while programs submit their preferences over students. The NRMP determines the final allocation of students to residencies. In 2012, students were allowed to submit their preference ordering through the NRMP website between January 15 and February 22, and the resulting match was announced on March 16; among students graduating from non-homeopathic U.S. medical schools, 16,875 submitted their preferences, and 15,712 (93 percent) ended up getting matched (NRMP, 2012).

The matching algorithm, described in detail in Roth and Peranson (1999), was designed to incentivize truthful preference reporting from students and to generate stable matches (in which no student and program prefer to be matched to one another over their current matches). It is based on the student-proposing deferred acceptance algorithm of Gale and Shapley (1962), which is guaranteed to produce a stable match, and where truthful reporting is a weakly dominant strategy for students. The original, simple algorithm, however, could not accommodate certain requirements of the medical matching market (such as the requirement for couples to match to residencies in the same city). The modifications to the algorithm complicate the strategic incentives and allow the possibility that no stable match exists, but simulations in Roth and Peranson (1999) suggest that effectively all students remain incentivized to truthfully reveal their preferences.

I.B. Key Features for Our Study

For our purposes, medical residency choices are an especially useful context for the following reasons:

Choice versus preferences

While choice in our setting is observed, preferences—defined as would-be choices under certain idealized conditions—are never directly observable. The NRMP setup, however, may be as close as one can get to a setting where choice reveals preferences.⁴ Residency choice is arguably one of the most important career-related decisions a medical student makes, with short- and long-term consequences for career path, geographic location, friendships, and family. Like many of the most important life decisions, it is only made once, but because of its importance, students deliberate over their decision for months and have a great deal of information and advising available to assist them in becoming well informed. Their submitted ranking is not visible to peers or residency programs, and hence, relative to many other decisions, the scope for strategic or signaling concerns is reduced. Finally and crucially, students are incentivized by the matching mechanism to report their true preference ranking.

Identifiable moment of choice

Unlike many other important life decisions, the NRMP submission has an identifiable moment when the decision is irreversibly committed. By surveying students shortly after they submit their preference ranking to the NRMP (and before they learn the match outcome), we elicit their SWB predictions under essentially the same information set and beliefs as at the moment of making the choice.

Identifiable choice set and ranking

In most economic settings, observable choice data consist of only the one chosen option, often leaving the econometrician uncertain as to the exact choice set from which that option was chosen. In our setting, choice data consist of a ranking over a set of residencies, making the choice set effectively observable, and enabling us to elicit anticipated SWB and residency features over that same set of options. Also, observing a choice ranking over multiple options confers more statistical power than observing only which option was chosen from a set.

Intertemporal tradeoff

A residency is expected to be a period of hard work, long hours, and intensive training, the benefits of which will be realized once the student becomes a practicing doctor. The investment aspect of the decision allows us to distinguish instantaneous utility from lifetime utility (the expected present discounted value of instantaneous utility), where lifetime utility is a representation of (choice-revealed) preferences. Hence we can explore the extent to which our affective SWB question—anticipated happiness during the residency—is related both to expected instantaneous utility and to expected lifetime utility. That distinction, which we consider and discuss in section III.C, is crucial for exploring the intertemporal aspects of the relationship between SWB tradeoffs and choice MRSs.

Heterogeneity in attribute evaluations

Residency choice offers rich variation in individuals' evaluations of programs' attributes: students' assessments of fit, locational preferences, and social considerations are all reasonably idiosyncratic. This heterogeneity, together with differences in choice sets (i.e., the sets of programs where different students had interviewed), is the source of variation identifying our regression coefficients.

One limitation of residency choice for our purposes is that it is not well suited for studying tradeoffs with money—the typical numeraire used in the literature. Our original intention was to use expected income for each residency to price the other residency attributes. However, in the process of designing the survey we learned—by being explicitly told by representatives of medical schools and by medical students we consulted—that expected income is largely unrelated to this decision. The primary determinant of expected income for medical students is their choice of specialty, a decision typically made years before choosing a residency. Indeed, most NRMP participants apply to residencies for a single specialty and hence should not expect their future income to vary meaningfully across their top choices. While pricing residency attributes in dollars would have been convenient, it is by no means crucial for our purposes; we instead focus on comparing MRSs and tradeoffs between the attributes directly. We elicited expected income in our survey anyway but do not use it in this paper.⁵

II. Sample and Survey Design

II.A. Sample

From September 2011 to January 2012, we contacted virtually all 122 U.S. medical schools with full accreditation from the Liaison Committee on Medical Education by sending an email to a school representative (typically an Associate Dean of Student Affairs) and asking for permission to survey graduating medical students. We followed up with phone calls, further emails, and/or face-to-face meetings at the Association of American Medical Colleges Annual Meeting. As a result, 23 schools (19 percent of our initial list) agreed to participate in our study. These 23 represent a wide range of class sizes (from 60 to 299 students in 2011) and locations, and they graduated a total of 3,224 students in 2011. Our survey appendix reproduces the initial email sent to schools, lists the participating schools, their class sizes, and the numbers of their students starting vs. completing our survey. It also shows the geographic distribution of participating and non-participating schools, and, using US News data, compares participating and non-participating schools on six school characteristics (relating to size, quality, grades, and gender composition). We find essentially no evidence of selection on these characteristics. (A common reason schools gave us for not participating was that their students are already asked to participate in “too many” surveys.)

Between February 22 at 9pm EST (the deadline for submitting residency preferences) and March 3, students in participating schools received an email from their school's dean, student council representative, or registrar, inviting them to respond to our web survey by clicking on a link. The email is reproduced in the survey appendix. It explained, among other things, that “…The results of this study will provide better information on how medical students select residency programs, and can assist in the advising and preparation of future generations of students”; that the survey is estimated to take 15 minutes to complete; and that we offer participants at least a 1/50 chance to win an iPod.⁶ Reminder emails were sent near the March 3 deadline. When the survey closed, at 11:59pm EST that day, we had received 579 complete responses (approximately 18 percent of the roughly 3,224 students contacted).⁷ Our analysis is based on the 561 who entered name and specialty information for at least two programs (540 of whom entered information for all four programs). While we find little evidence of selection on observables (see survey appendix), our sample is unlikely to be representative of U.S. medical students due to potential selection on unobservables. Nonetheless, if MRSs could in general be inferred from SWB data, then we would expect the same to hold in our sample.

428 of our respondents agreed, when asked at the end of the survey, to be re-contacted. They received, on a randomly-drawn date between March 7 and 9, another email inviting them to participate in a repeat survey, with a March 11 deadline. The repeat survey consisted of the same questions as the original survey, with a few new questions added at the end. Comparing responses across these two waves allows us to assess the reliability of our measures, as we do below. 133 respondents completed the repeat survey, and 131 of them (23 percent of our main sample) provided information for at least two programs. The median time between completion of the original and the repeat surveys was 13 days. As reported in the survey appendix, female respondents were slightly less likely to respond to the repeat survey (for summary statistics by survey, see Web Appendix Table A1).

II.B. Survey Design

Our survey appendix provides screenshots of our survey. Here we briefly summarize important survey details. Following an introductory screen, respondents are asked: “Please enter the top four programs from the preference ordering you submitted to the NRMP.” Respondents separately enter program (e.g., “Massachusetts General Hospital”) and specialty (e.g., “Anesthesiology”). While “the top four” is not the entire preference ordering, it is likely to be the relevant portion of the list for our respondents: in 2012, 83.6 percent of NRMP participants graduating from U.S. medical schools were matched to one of their top four choices (first choice: 54.1 percent; second: 14.9 percent; third: 9.1 percent; fourth: 5.5 percent; NRMP, 2012).

Respondents are then asked: “On what date did you submit your rank order list to the NRMP?” Figure 1 reports the distributions of submission dates (lighter bars) and survey response dates (gray bars) among our 561 main-sample respondents. The median number of days between choice submission and response to our survey is 11. The figure also shows the subsequent distribution of response dates for the 131 main-sample respondents who participated in our repeat survey (darker bars).

Figure 1. Survey Response Timeline.

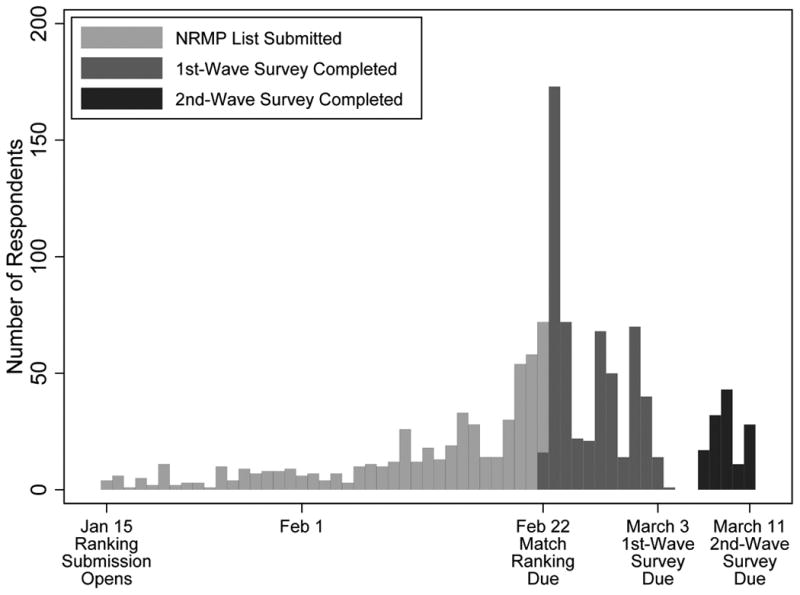
Notes: Frequency distribution of survey responses by date. Each bar corresponds to one day. NRMP submission and 1^st-wave data are for the 561 respondents in our main sample (with the exception that five respondents did not report their date of NRMP submission, and two reported invalid dates). 2^nd-wave data are for the 131 respondents in the main sample who completed the repeat survey. The 1^st-wave responses entered on February 22^nd occurred after 9pm EST, the deadline for NRMP submission. On that date, where bars overlap, they are not stacked, and the longer bar continues behind the shorter bar.

On the next screen, respondents are asked about their relationship status and whether they are registered with the NRMP for a “dual match.”⁸ Their answer to the relationship question determines whether the question “On a scale from 1 to 100, how desirable is this residency for your spouse or significant other?” will be included as a residency attribute on a later screen.

Next, the following instructions appear on the screen:

For the following section, you will be asked to individually consider the top four programs you ranked. For each of these possibilities, you will be asked to report your predictions on how attending that residency program will affect a variety of aspects of your life. Please answer as carefully and truthfully as possible.

For some questions you will be asked to rate aspects on a 1-100 scale. Let 100 represent the absolute best possible outcome, 1 represent the absolute worst possible outcome, and 50 represent the midpoint.

The ranked residencies are then looped through in random order, and two screens appear for each residency. The first screen elicits respondents' rating of the residency, using the 1–100 scale, on the main three anticipated-SWB questions and on the nine residency attributes. The second screen includes questions about expected income that we do not use in this paper.

Table 1 reproduces the three anticipated-SWB questions and the nine attribute questions as they appear on the first screen below the instruction: “Thinking about how your life would be if you matriculate into the residency program in [specialty] at [program], please answer the questions below.” The SWB and attribute questions are purposefully designed to resemble each other as much as possible in terms of language and structure, and they appear on the screen mixed together as twelve questions in random order. As a practical matter of survey design, this symmetric treatment allows us (in section IV below) to compare the twelve questions on how useful each one is as a single predictor of choice, without confounds due to question language or order. Moreover, on a conceptual level it could be argued that the classification of questions as “SWB” versus “attribute” is in some cases arbitrary and has little basis in theory (a point that we return to in section V). Nonetheless, when planning our empirical strategy and prior to data collection, we set apart the three SWB questions to be compared with choice as dependent variables in regressions on the attributes (see section III below), because in the happiness literature these are the questions that are routinely used as alternatives to choice data.

Table 1. Main SWB and Residency Attribute Survey Questions.

Variable label	Question prompt (beginning “On a scale from 1 to 100, …”)
Happiness during residency	…how happy do you think you would feel on a typical day during this residency?
Life satisfaction during residency	…how satisfied do you think you would be with your life as a whole while attending this residency?
Ladder	…where 1 is “worst possible life for you” and 100 is “best possible life for you” where do you think the residency would put you?
Residency prestige and status	…how would you rate the prestige and status associated with this residency?
Social life during residency	…what would you expect the quality of your social life to be during this residency?
Desirability of location	…taking into account city quality and access to family and friends, how desirable do you find the location of this residency?
Anxiety during residency	…how anxious do you think you would feel on a typical day during this residency?
Worthwhile life during residency	…to what extent do you think your life would seem worthwhile during this residency?
Stress during residency	…how stressed do you think you would feel on a typical day during this residency?
Future career prospects	…how would you rate your future career prospects and future employment opportunities if you get matched with this residency?
Control over life	…how do you expect this residency to affect your control over your life?
Desirable for significant other	…how desirable is this residency for your spouse or significant other?

Mixed together and arranged here roughly by the time interval they refer to, the twelve SWB and attribute questions include: three affective measures that refer to a typical day during the residency (in Table 1 these are labeled happiness, anxiety, and stress during residency); three evaluative/eudaimonic measures that refer more generally to the time during the residency (life satisfaction, social life, and worthwhile life during residency); one measure that refers implicitly to the time during the residency (desirability of location); one measure that refers implicitly to the time after the residency (future career prospects); one measure that simply refers to one's “life” (ladder); and three measures that come with no specification of period (residency prestige and status, control over life, and—for respondents in a relationship—desirable for significant other).

Next, the top three residencies (rather than four, to keep the survey from becoming too long and repetitive) are cycled through again, in a new random order. For each residency we elicit anticipated happiness at different future time intervals (we provide more details when analyzing the resulting data, in section III.C below).

The survey concludes with a sequence of screens that include four questions regarding the relationship between a respondent's submitted NRMP ranking and her or his “true” preferences; a question regarding experiences with residency-program representatives' attempts at manipulating the match; and questions about gender, age, college GPA, MCAT score, and Medical Licensing Examination scores (for summary statistics, see Web Appendix Table A1). We explore these data in section III.B below. On the last screen, respondents are thanked for their participation and asked for permission to be contacted for the follow-up survey.

As a brief overview of our data, Figure 2 presents kernel density estimates of the distribution of our primary variables by residency rank (for means and standard deviations, see Web Appendix Table A2; for a version of Figure 2 demeaned at the respondent level, see Web Appendix Figure A1). As is visually clear, all have substantial variation across respondents, and many have clear differences in distribution across program ranks. For example, looking at the three primary SWB measures (top row), it is clear that higher-ranked programs have higher mean anticipated SWB. Web Appendix Table A3 presents the test-retest correlations of these variables, as calculated with the repeat survey. We view the relatively high correlations of responses across waves as evidence that our survey measures elicit meaningful information.

Figure 2. Distributions of Variables by Program Rank.

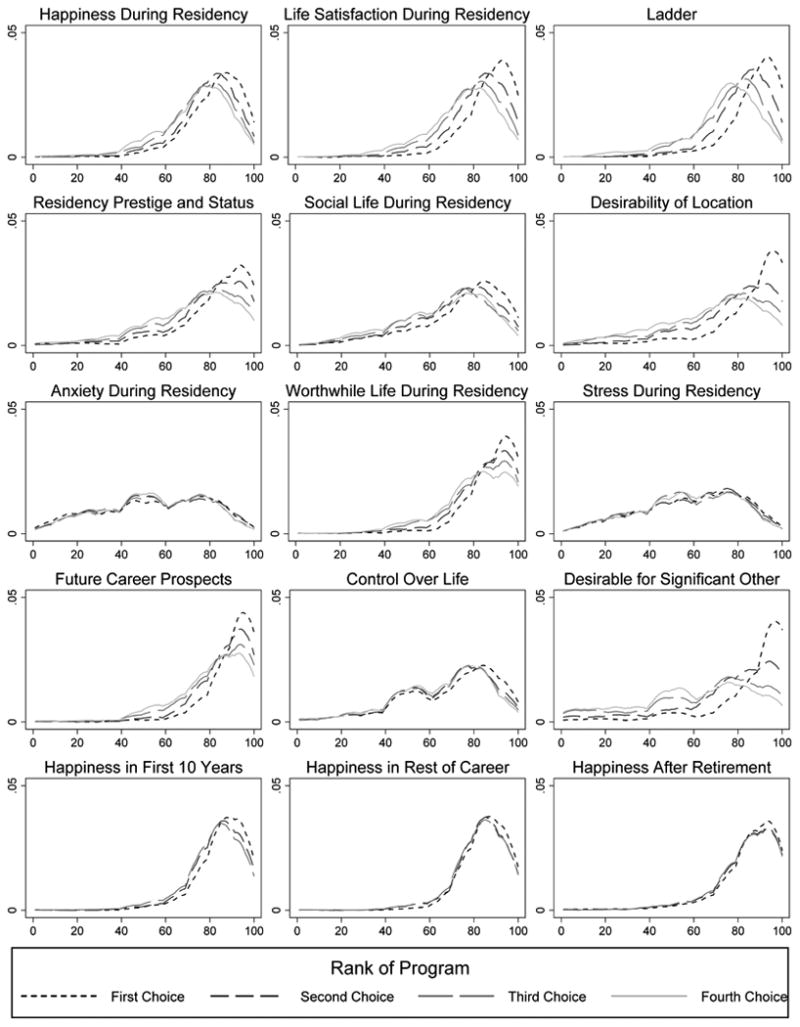
Notes: Kernel density plots of residency attributes by preference order. (Epanechnikov; Bandwidth 5.) Based on the 561 respondents in the main sample.

III. Main Analysis and Results

III.A. Single SWB Measures

As a first step in constructing choice-based and SWB-based tradeoff estimates, we estimate the associations of residency attributes with the choice-based and SWB-based residency rankings. The first four columns of Table 2 report four separate regressions of, respectively, choice, anticipated happiness, anticipated life satisfaction, and anticipated ladder questions on the nine residency attributes. Each column estimates a rank-ordered logit model (Beggs, Cardell, and Hausman, 1981), which generalizes the standard binary-choice logit model to more than two ranked options. To avoid confusion, we emphasize that rank-ordered logit is different from ordered logit, an econometric technique commonly used in the happiness literature. When using rank-ordered logit, we assume that each individual i's ordinal ranking of residencies, denoted by their rank r ∈ {1, 2, 3, 4}, is rationalized by a random latent index, U_ir = β_XX_ir + ε_ir . The parameters of the latent index, β_X, are estimated by maximizing the sum of the individual-level log-likelihoods that U_i1 > U_i2 > U_i3 > U_i4, the condition necessary for generating the observed ordering of residencies. The unobserved error term is assumed to follow a type I extreme-value distribution, yielding a closed-form solution to the maximum-likelihood problem. We construct the regressors by dividing the attribute variables by 100 (so the regressors range from 0.01 to 1). The coefficients can be interpreted analogously to standard logit coefficients: for any pair of residencies A and B, all else equal, a one-unit increase in the difference in regressor j, X_i,A,j − X_i,B,j, is associated with a β_j increase in the log odds ratio of choosing A over B. We report a within-subject modification of McKelvey and Zavoina's R², a statistic that measures the fraction of within-subject variation of the latent index explained by the fitted model.⁹

Table 2. Rank-Ordered Logit Estimates: Choice vs. Anticipated SWB.

	(1) Choice	(2) Happiness during residency	(3) Life satisfaction during residency	(4) Ladder	(5) 4-period-happiness index	(6) 3-SWB-measure index	(7) 6-SWB-question index
Residency prestige and status	2.5*** (0.3)	0.0 (0.3)	0.7* (0.3)	0.9** (0.4)	0.3 (0.4)	0.8** (0.3)	1.1** (0.4)
Social life during residency	1.6*** (0.3)	3.3*** (0.4)	2.7*** (0.4)	3.2*** (0.4)	2.6*** (0.4)	3.6*** (0.3)	3.5*** (0.5)
Desirability of location	1.7*** (0.2)	0.4* (0.2)	1.7*** (0.3)	1.9*** (0.3)	0.5* (0.3)	1.9*** (0.2)	1.6*** (0.3)
Anxiety during residency	-0.3 (0.3)	-1.3*** (0.3)	-0.5 (0.4)	-0.8** (0.3)	-1.8*** (0.4)	-0.9*** (0.3)	-1.4*** (0.4)
Worthwhile life during residency	4.4*** (0.5)	6.3*** (0.6)	7.0*** (0.6)	6.4*** (0.6)	5.9*** (0.7)	6.5*** (0.6)	6.9*** (0.8)
Stress during residency	-0.1 (0.3)	-1.0*** (0.4)	-0.7** (0.4)	-0.6* (0.3)	0.5 (0.4)	-0.7** (0.3)	0.0 (0.4)
Future career prospects	3.2*** (0.5)	0.9* (0.5)	1.8*** (0.5)	3.0*** (0.5)	1.2** (0.6)	2.6*** (0.5)	2.8*** (0.7)
Control over life	0.4 (0.3)	0.9** (0.3)	0.4 (0.3)	0.4 (0.3)	1.0** (0.4)	0.4 (0.3)	1.5*** (0.4)
Desirable for significant other	2.6*** (0.3)	0.5* (0.3)	0.7*** (0.3)	1.0*** (0.3)	0.3 (0.3)	1.2*** (0.2)	0.9*** (0.3)
# Observations	2169	2167	2169	2168	1591	2166	1590
# Students	557	557	557	557	540	557	540
McKelvey & Zavoina R2, within variance only	0.46	0.34	0.42	0.46	0.25	0.48	0.42
Joint significance of differences with choice coefficients		0.000	0.000	0.000	0.000	0.000	0.000

Notes: Standard errors in parentheses. Rank-ordered logit regressions of either choice (column 1) or a SWB measure (columns 2–7) on residency attributes. Only ordinal information on the dependent variables is used. Columns 2–4 use the ordinal rankings implied by the main three SWB measures. Columns 5–7 use the ordinal rankings implied by an optimal linear utility index, created by a first-stage rank-ordered logit regression of choice on the index components (reported in Table 4). All attribute ratings are divided by 100 before being included in the regression. For the 35 percent of students who report being single, “Desirable for significant other” is set to a constant (since identification is within-subject, its value is irrelevant). Joint significance of the differences with choice coefficients (bottom row): p-value from a Wald test of the joint equality of all coefficients in the column with all coefficients in the choice column.

^*p < .1,

^**p < .05,

^***p < .01

Consider Table 2's two leftmost columns (“Choice” and “Happiness during residency”). The first row indicates that the coefficient on residency prestige and status is 2.5 in the choice regression and 0.0 in the happiness regression. This difference is highly statistically significant (Wald test p-value = 0.000). To interpret these coefficients, consider their implication for the ranking of two residency programs that are identical in all measured dimensions except for a 20-point difference in their prestige and status on the survey's 100-point scale. The choice coefficient implies that the probability of choosing the more prestigious program would be (e^2.5*^20/100)/(e^2.5*^20/100 + 1) = 62 percent The happiness coefficient implies that the probability of ranking the more prestigious program higher on anticipated happiness would be 50 percent. Of course, our coefficient estimates (and hence our tradeoff estimates below) may be subject to omitted-variable bias. However, if choice-based MRSs were identical to SWB tradeoffs, any resulting bias would equally affect the choice-based and SWB-based estimates. The same is true more generally regarding any concern that is related to only the independent variables—a point we return to in our robustness analysis in the next subsection. Our discussion below is therefore focused less on the point estimates themselves and more on whether they differ across choice and SWB.

Our estimate of the relationship between a residency's ranking and the residency's perceived prestige and status hence strongly depends on whether we use the choice ranking or an anticipated-happiness ranking. Examining the rest of the coefficient pairs across the choice and happiness columns reveals that, within a pair, while there are no sign reversals, there are many significant differences in coefficient magnitudes. With the exception of control over life, they are all statistically significant at the 10 percent level. Five of the differences are significant at the 1 percent level: like residency prestige and status, also desirability of location, future career prospects, and desirability for significant other are associated significantly more with choice than with anticipated-happiness, while the reverse is true for social life during the residency. As reported in the table's bottom row, joint equality of coefficients between the two columns is strongly rejected.

Examining the next two columns (“Life satisfaction during residency” and “Ladder”) reveals that with few exceptions, these two measures' coefficients lie between those of choice and those of happiness. These two evaluative measures seem on some attributes closer to happiness, an affective measure, and on other attributes closer to choice. For example, while on social life during the residency, the two are virtually indistinguishable from happiness, all with coefficients larger than that on choice, on desirability of location the two are indistinguishable from choice, with coefficients much larger than that on happiness. Across the rows, most of the ladder estimates appear closer to the choice estimates than the life satisfaction estimates; statistically, however, we cannot distinguish the two evaluative measures from each other. Indeed, Wald tests of the joint equality of coefficients between any pair among the four columns strongly reject the null of equality (p = 0.000) for all pairs except the life satisfaction and ladder pair (p = 0.52).

To what extent do these differences in coefficient estimates translate to differences in estimated tradeoffs? To answer this question regarding a given tradeoff—for example, between prestige and social life—one can compare, across Table 2's columns, the within-column ratio of the two relevant coefficients. To answer this question regarding a given attribute—for example, “How large are the cross-column differences in estimated tradeoffs between prestige-and-status and the other eight attributes?”—we could use that attribute as a numeraire and report nine tables (one per numeraire), each with relatively noisy ratio estimates. Instead, we report Table 3, a single table that summarizes each attribute's eight relevant within-column ratios using a single, less noisy measure that can be compared across columns. Table 3 reports the ratio of each coefficient from Table 2 to the average absolute value of coefficients in its Table 2 column. With this normalization, each of Table 3's entries can be interpreted as an average weight in tradeoffs. For example, a higher normalized coefficient on an attribute in the choice column relative to the happiness column would mean that on average, the MRS between another attribute and this one is lower in the choice column than the corresponding tradeoff estimate in the happiness column. Standard errors are calculated using the delta method.

Table 3. Tradeoff Estimates: Choice vs. Anticipated SWB.

	(1) Choice	(2) Happiness during residency	(3) Life satisfaction during residency	(4) Ladder	(5) 4-period-happiness index	(6) 3-SWB-measure index	(7) 6-SWB-question index
Residency prestige and status	1.4*** (0.2)	0.0 (0.2)	0.4* (0.2)	0.4** (0.2)	0.2 (0.3)	0.4** (0.2)	0.5** (0.2)
Social life during residency	0.8*** (0.2)	2.0*** (0.2)	1.5*** (0.2)	1.6*** (0.2)	1.7*** (0.3)	1.7*** (0.2)	1.6*** (0.2)
Desirability of location	0.9*** (0.1)	0.3* (0.2)	1.0*** (0.1)	0.9*** (0.1)	0.3* (0.2)	0.9*** (0.1)	0.7*** (0.1)
Anxiety during residency	-0.1 (0.2)	-0.8*** (0.2)	-0.3 (0.2)	-0.4** (0.2)	-1.1*** (0.2)	-0.4*** (0.2)	-0.6*** (0.2)
Worthwhile life during residency	2.4*** (0.2)	3.9*** (0.3)	3.9*** (0.3)	3.2*** (0.3)	3.7*** (0.4)	3.1*** (0.2)	3.2*** (0.3)
Stress during residency	-0.1 (0.2)	-0.6*** (0.2)	-0.4** (0.2)	-0.3* (0.2)	0.3 (0.3)	-0.3** (0.2)	0.0 (0.2)
Future career prospects	1.7*** (0.3)	0.5* (0.3)	1.0*** (0.3)	1.5*** (0.3)	0.8** (0.4)	1.3*** (0.2)	1.3*** (0.3)
Control over life	0.2 (0.2)	0.5*** (0.2)	0.2 (0.2)	0.2 (0.2)	0.6** (0.3)	0.2 (0.1)	0.7*** (0.2)
Desirable for significant other	1.4*** (0.1)	0.3* (0.2)	0.4*** (0.1)	0.5*** (0.1)	0.2 (0.2)	0.6*** (0.1)	0.4*** (0.1)
# Observations	2169	2167	2169	2168	1591	2166	1590
# Students	557	557	557	557	540	557	540
Joint significance of differences with choice coefficients		0.000	0.000	0.000	0.000	0.000	0.000

Notes: Delta-method standard errors in parentheses. Entries are coefficients from Table 2, normalized by taking their ratio to the average absolute value of the nine coefficients in their Table 2 column. Joint significance of the differences with choice entries (bottom row): p-value from a Wald test of the joint equality of all entries in the column with all entries in the choice column.

^*p < .1,

^**p < .05,

^***p < .01

Examining Table 3's first row and comparing column 1 with columns 2–4 reveals that residency prestige and status's regression coefficient in the choice column is 1.4 times the average of the nine attributes' regression coefficients; with any of the three anticipated-SWB measures, however, prestige and status's regression coefficients are below average, ranging from 0.0 to 0.4 times the average. This difference in implied tradeoffs is rather dramatic: the estimate in the choice column is more than three times larger than the largest SWB estimate.

To examine the statistical significance of this and other differences, Web Appendix Table A4 replaces each estimate in columns 2–7 of Table 3 with its difference from the corresponding estimate in Table 3's column 1 (the choice column). Table A4 also reports the p-value of each difference. Relative to the choice-based estimates, all three SWB measures underweight residency prestige-and-status and desirability for significant other, and overweight the importance of social life and life seeming worthwhile during the residency. Other attributes also show significant differences, but they appear to be less systematic. As reported in Table 3's bottom row, we again easily reject joint equality—in this table, of normalized coefficients— between any of the three SWB measures and choice.

Comparing across Table 3's SWB columns, the life satisfaction and ladder columns appear similar to each other (as in Table 2), with virtually all estimates in between the choice estimates and the (always equally signed) happiness estimates. Considered jointly, the coefficients in both the life satisfaction and ladder columns are again statistically different from the happiness column (p = 0.000) but are not distinguishable from each other (p = 0.63).

Since comparing the choice and SWB columns of Table 3 is one of the central aims of our paper, Figure 3 provides a visual rendering of the table. Each of the figure's six graphs is based on Table 3's column 1 and one other column (from among columns 2–7). Within each graph, each of the nine points represents an attribute. Each attribute's x- and y-coordinates correspond, respectively, with its choice and SWB estimates from Table 3, with their 95 percent confidence intervals represented by the horizontal and vertical capped bars. Points in the northeast or southwest quadrants hence represent cases where choice and SWB estimates have the same sign; on the solid 45-degree line, the estimates are equal. To assist in visually assessing how far a point is from the 45-degree line, the dashed lines demarcate the boundaries outside of which estimates differ by more than a factor of two.

Figure 3. Tradeoff Estimates: Choice vs. Anticipated SWB.

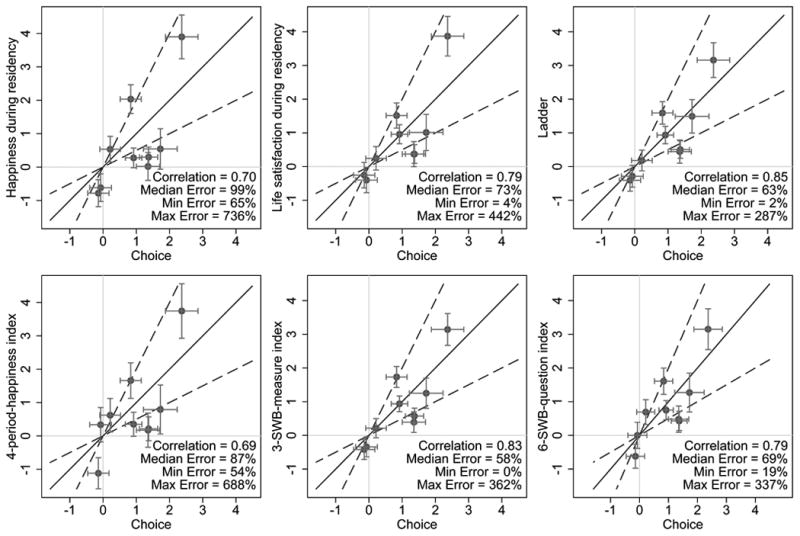
Notes: Based on Table 3 estimates. Each graph presents a comparison of one SWB measure (columns 2– 7 of Table 3) to choice (column 1 of Table 3). Each point represents one of the nine attributes included in the regressions, and its x- and y-coordinates correspond to the normalized choice and SWB coefficients, respectively. 95 percent confidence intervals are represented by the horizontal and vertical capped bars. The dashed lines demarcate the boundaries outside of which the normalized choice and SWB coefficients differ by more than a factor of two. See section III.A for discussion of the prediction-error metrics.

Focusing on the top three graphs, it is visually apparent that almost all points fall in the same-sign quadrants and that, additionally, there is substantial positive correlation between the choice and SWB estimates (correlations are reported in each graph). However, there are also substantial differences between the estimates, often by a factor of two or more. To quantify these differences, we define a prediction-error measure of SWB-based estimates relative to the choice-based benchmarks: |(β^SWB − β^Choice) / β^Choice |, where the βs represent an attribute's estimates in Table 3, and the superscript SWB represents one of the SWB columns. An error of 60 percent, for example, corresponds to cases where the SWB estimate is either 40 percent or 160 percent of the choice estimate. Each graph reports the minimum, median, and maximum error among the nine attributes. The median ranges from 63 percent for the ladder measure to 99 percent for the happiness-during-residency measure. While such margins of error may be tolerable for some applications that use SWB as a proxy for choice utility—for example, applications that focus only on the sign of an effect—they are a serious limitation to the interpretation of these measures as precise MRS estimates.

III.B. Robustness

In this subsection, we probe the robustness of our main results to several possible sources of bias.

Biases in survey response

Due to a halo effect, respondents' overall assessments of residencies might leak into their subjective assessments of either anticipated SWB or residency attributes (or both). Similarly, cognitive dissonance might lead respondents to modify their subjective assessments to rationalize the choice order they reported earlier in the survey. To the extent that the ratings of the residency attributes are affected, the coefficients in our regressions are biased upward. Such a bias, however, could not by itself explain the differences in coefficients across columns. Moreover, to the extent that the ratings of anticipated SWB measures are affected, the concordance between the SWB-based rankings and the choice ranking would increase, biasing downward any choice-SWB differences across the columns. Therefore, the differences we do observe should be viewed as a lower bound on the actual divergence—and the similarities we observe, as an upper bound on the actual concordance—between anticipated-SWB and choice rankings.

Econometric specification

The estimates in Tables 2 and 3 are based on a rank-ordered logit model, which is designed for analyses where the dependent variable is—like our choice data—a rank ordering. Using this same specification for our SWB data makes our estimates comparable across columns and allows us to avoid making assumptions regarding similar use of the SWB rating scales across respondents. In contrast, typical happiness regressions in the literature use OLS or ordered logit/probit, where dependent-variable scale use is assumed to be identical across respondents (or identical up to differences in means, in fixed-effects regressions). To examine the sensitivity of our findings to specification, we conduct side-by-side comparisons of the SWB columns from Table 3 with analogous estimates using OLS with respondent fixed effects (Web Appendix Table A5) and ordered logit (Table A6). These alternative specifications yield estimates similar to the rank-ordered logit regressions and do not change our conclusions from the previous subsection.

Measurement error

Our respondents' attribute and SWB assessments are likely subject to measurement error. To the extent that the attribute ratings are affected, the coefficients in our regressions are biased. As with the survey-response biases above, however, this bias could not explain the differences in coefficients across columns. Of greater potential concern is the possibility that anticipated SWB is affected: while classical measurement error in the dependent variable would not bias coefficient estimates in OLS, it would bias our rank-ordered logit estimates. Consequently, if anticipated SWB is a noisy measure of choice utility, then measurement error could generate differences in coefficients across the choice and SWB columns. That the coefficients from the fixed-effects OLS specification mentioned above (Web Appendix Table A5) do not meaningfully differ from those in Table 2 suggests, however, that such measurement error cannot drive our results.

Heterogeneity in response-scale use

Our analysis above assumes that respondents are identical in their use of the attributes' 1–100 response scales. While heterogeneity in attribute scale use could not explain the choice-SWB differences we find, we verify that our conclusions are unchanged when we re-estimate Table 3 after first normalizing the response scales at the respondent level (Web Appendix Table A7; each attribute is demeaned at the respondent level, and then divided by the respondent-specific standard deviation, prior to entering the regressions).

Heterogeneity in tradeoffs

Our analysis above imposes identical coefficients across respondents. Heterogeneity in coefficients could not by itself explain the choice-SWB differences we find. However, it is possible that our results are driven by a particular subpopulation, and that for many or most in the sample, the tradeoffs represented by their anticipated SWB are more similar to those implied by their choices. To assess this possibility, we cut the sample along various respondent characteristics. For each sample cut, we re-estimate Table 3 (web appendix, pp. 19–34). Our main findings continue to hold across these sample cuts, suggesting that they are pervasive across subgroups within our sample. For example, comparing the choice column with each of the SWB columns, we reject at the 1 percent level the null hypothesis of jointly identical tradeoffs in each of these cross-column comparisons when cutting the sample by: gender, above and below median MCAT scores, above and below median age, above and below median survey-completion time (as a proxy for respondent effort), whether or not the respondent agreed to be re-contacted for the follow-up survey (76 percent of our respondents agreed), and whether or not the respondent completed the follow-up survey (23 percent); and when excluding dual-match participants (7 percent). When cutting the sample three ways by relationship status (single, in a long-term relationship, and married), we reject the null of jointly identical tradeoffs at the 5 percent level in all nine cross-column comparisons and at the 1 percent level in eight.

Choice versus preferences

As discussed in section I.B, an important advantage of the NRMP setting is that the mechanism incentivizes students to truthfully submit their preference ranking. However, some students may deviate from truthful reporting—for example, due to misunderstanding the mechanism. To assess this possibility, we re-estimate Table 3 three more times: excluding respondents who report manipulation attempts by schools (3 percent of our sample); excluding respondents who report that their NRMP submission did not represent their “true preference order” (17 percent);¹⁰ and including only these 17 percent of respondents, but as dependent variable in the choice column replacing their submitted NRMP ranking with what they report as their “true preference order” (web appendix, pp. 35–37). As above, our conclusions do not change, and we continue to reject joint equality across the choice and SWB columns at the 1 percent level.

III.C. Multi-Question SWB Indices

Our results thus far suggest that none of our single-question anticipated-SWB measures generates tradeoff estimates that reliably reflect choice tradeoffs. However, two distinct hypotheses separately imply that combinations of questions may better capture choice utility and hence may yield more similar tradeoffs. We now explore these two hypotheses.

Happiness as instantaneous utility

When a survey respondent reports feeling happy, to what extent is her report related either to her instantaneous utility or to her lifetime utility? (Recall that by “lifetime utility,” we mean a representation of (choice-revealed) preferences as the expected present discounted value of instantaneous utility.) Our evidence above suggests that happiness-during-residency tradeoffs do not reflect expected-lifetime-utility MRSs. Do they reflect expected-instantaneous-utility MRSs?

To explore this possibility—the SWB-as-instantaneous-utility hypothesis—we examine whether anticipated happiness would better reflect choice if it integrated happiness predictions over the full expected horizon of life, rather than over only the residency years. For that purpose, we elicit additional happiness predictions in our survey. As mentioned in section II.B above, after responding to questions about each of the top four residencies, the respondents cycle again through the top three, in a new random order. They are instructed as follows:

For the following section, you will again be asked to individually consider the top three programs you ranked. For each of these possibilities, you will be asked to report your predictions on how attending that residency program will affect your happiness during different periods of your life. Please answer as carefully and truthfully as possible.

For each residency, respondents see a screen with questions. The three primary questions read: “On a scale from 1 to 100, how happy do you think you would be on average [during the first ten years of your career]/[for the remainder of your career before retirement]/[after retirement]?” Each is followed by questions assessing the uncertainty of the forecast.

Aggregating such questions into a present-discounted-value-of-happiness index requires weighting them by appropriate discount factors (taking into account the different lengths of their respective intervals). In a field setting where choice data are not available, the researcher would have to choose weights based on her beliefs regarding the discount factor. Since we have choice data, we instead conduct a rank-ordered logit regression predicting choice with our four anticipated happiness questions and use the estimated latent-index coefficients as our weights. Under the logit model assumptions, this is the best linear index that could be constructed for predicting choice in our data and hence represents a best-case scenario (by this choice-prediction criterion) for a present-discounted-value-of-happiness measure that might be used in a realistic application.

The regression for constructing the index is reported in column 1 of Table 4. The coefficients on the happiness variables are roughly declining over time, in spite of the increase in time-interval length, consistent with steep discounting.¹¹ However, the McKelvey and Zavoina R² of 0.17 indicates relatively low goodness-of-fit, suggesting that the index still omits significant amounts of choice-relevant information.

Table 4. Weight Estimates for Multi-Question Indices.

	(1) Choice	(2) Choice	(3) Choice
Happiness during residency	4.5*** (0.5)	0.6 (0.4)	0.9 (0.6)
Happiness in first 10 years	4.6*** (0.8)		3.5*** (0.9)
Happiness in rest of career	2.1** (0.9)		2.4*** (0.9)
Happiness after retirement	1.2 (0.8)		2.0** (0.9)
Life satisfaction during residency		4.4*** (0.5)	3.9*** (0.7)
Ladder		5.5*** (0.4)	5.4*** (0.6)
# Observations	1609	2192	1607
# Students	544	561	544
McKelvey & Zavoina R2, within variance only	0.17	0.37	0.37

Notes: Standard errors in parentheses. Rank-ordered logit regressions of choice on SWB measures. All aspect ratings are divided by 100 prior to inclusion in the regressions. Since future happiness measures are only elicited for three of the four ranked residencies, less data are available for conducting these regressions relative to those with only the primary SWB questions. However, restricting all three regressions to the same sample of 1607 observations has only minor impact on the coefficient estimates (although column 2's R² decreases to 0.32); see Web Appendix Table A10.

^*p < .1,

^**p < .05,

^***p < .01

Returning to Tables 2 and 3, in column 5 we use the ordering implied by this multi-period anticipated-happiness index as the dependent variable (“4-period-happiness index”).¹² In Table 3, on most of the attributes column 5 is slightly closer to column 1 (choice) than column 2 (happiness during residency) is, but on some of the attributes column 5 is slightly farther. Overall, the 4-period-happiness tradeoff estimates still exhibit substantial differences from the estimates in column 1 (joint significance of differences p = 0.000 between columns 1 and 5; p = 0.08 between columns 2 and 5). Moreover, columns 3 and 4—life satisfaction and ladder—seem in general closer to column 1 than column 5 is (both columns 3 and 4 are statistically different from column 5, with p = 0.01 or less). Indeed, while Figure 3 reports that the median error for the 4-period-happiness index is smaller than for happiness during residency, it is larger than for life satisfaction and ladder.

In summary, we find limited support for the SWB-as-instantaneous-utility hypothesis; our four-time-period anticipated-happiness index is far from matching the choice-based MRS estimates.

Multidimensional SWB

Although much of the economics literature treats different SWB questions as interchangeable, several recent papers mentioned in the introduction find that different questions have different correlates and argue that they capture distinct components of well-being. To the extent that well-being is multidimensional, a multi-question SWB index might yield tradeoff estimates that are closer to our choice-based MRS estimates than those yielded by any single measure.

To explore this possibility, we construct a “3-SWB-measure” index from our main three SWB questions, and a “6-SWB-question” index by also including the three beyond-residency happiness questions (from the 4-period-happiness index above). To maximize the predictive power of the indices for choice, we again use as weights the coefficients estimated in first-stage rank-ordered logit regressions of choice on the components of each index.

Columns 2 and 3 of Table 4 report our first-stage regressions. In both regressions the coefficient on happiness during the residency is indistinguishable from zero, and is substantially smaller than the corresponding coefficient in column 1 as well as smaller than the coefficients on the two evaluative measures in columns 2 and 3 (life satisfaction during the residency and ladder). In other words, once the two evaluative measures are controlled for, happiness during the residency contributes significantly less to predicting choice. The fit of the indices in columns 2 and 3, as measured by the McKelvey and Zavoina R², is substantially better than in column 1.

Returning to Tables 2 and 3, their columns 6 and 7 use, respectively, the orderings implied by each of the two SWB indices as the dependent variable in the regression. We easily reject, in both tables, joint equality of coefficients between each of the two multi-SWB regressions and: choice (p = 0.000; see each table's bottom row), happiness (p = 0.000), and, less strongly, the 4-period-happiness index (p = 0.06 or less). Nonetheless, we cannot distinguish the two from each other or from either life satisfaction or ladder (p-values range from 0.15 to 0.97); indeed, in Figure 3 the four relevant graphs appear rather similar.

To summarize, we find no support for the multidimensional-SWB-as-(choice)-utility hypothesis; our indices that incorporate multiple SWB measures not only fail to match the choice-based MRS estimates, but also fail to do significantly better than our single-question evaluative SWB measures. Of course, the SWB measures we include in these indices are far from exhausting every conceivable measurable dimension (and time period) of the inputs into preferences, and hence we cannot rule out the possibility that an index based on a sufficiently rich set of questions might yield reliable MRS estimates—indeed, an index that captured all the aspects that our respondents consider when making decisions should, in principle, match choice quite closely. Nonetheless, since the SWB measures we use in this paper are modeled after those most common in existing social surveys and applied research, our results suggest that a straightforward extension of current practices—using a linear combination of a few commonly-used SWB measures—would not be a substantial improvement for estimating MRSs.

IV. From Slopes to Orderings: Predicting Choice Ranking from Anticipated-SWB Ranking

While our finding of substantial differences between the tradeoffs implied by widely-used SWB measures and those revealed by choices warns against using SWB data for estimating MRSs, it leaves open the possibility of using SWB data for assessing which among a set of options is most preferred. We begin this section by exploring the usefulness of our anticipated-SWB data in predicting pairwise choices.

Table 5 examines all possible within-respondent pairwise comparisons of residency programs. Each row corresponds to a single SWB or attribute question (top two panels) or a multi-question index (bottom panel). Columns 1, 2, and 3, respectively, report the percent of cases where the program that is ranked higher in choice is ranked higher, the same, or lower than the other program by the row's measure. We assess each measure's usefulness in predicting choice with two yardsticks: the “correct-prediction rate” (another way to think of column 1) and the “conditional correct-prediction rate” (column 4). The latter equals column 1 divided by the difference between 100 percent and column 2; it is the share of cases where choice and a row's measure yield the same ranking, conditional on the measure ranking one option above the other.

Table 5. Predicting Binary Choice from Anticipated-SWB and Attribute Questions.

	(1) Preferred program rates higher (Correct-prediction rate)	(2) The two programs have same rating	(3) Preferred program rates lower	(4) Conditional correct-prediction rate $\left(\frac{\text{column}(1)}{100\%-\text{column}(2)}\right)$	(5) # Pairwise program comparisons
Happiness during residency	52%	27%	21%	71%	3240
Life satisfaction during residency	59%	23%	18%	77%	3244
Ladder	65%	18%	17%	80%	3245
Residency prestige and status	56%	16%	28%	67%	3244
Social life during residency	52%	20%	28%	65%	3247
Desirability of location	61%	14%	25%	71%	3241
Anxiety during residency	38%	29%	33%	53%	3236
Worthwhile life during residency	44%	40%	16%	73%	3235
Stress during residency	40%	26%	34%	54%	3236
Future career prospects	49%	30%	21%	70%	3247
Control over life	40%	30%	30%	57%	3235
Desirable for significant other	65%	16%	19%	77%	2087
Average happiness in first 10 years	34%	53%	13%	72%	1603
Average happiness in rest of career	28%	56%	16%	64%	1603
Average happiness after retirement	22%	64%	14%	62%	1605
4-period-happiness index	62%	10%	28%	69%	1592
3-SWB-measure index	75%	3%	22%	77%	3233
6-SWB-question index	76%	2%	22%	78%	1588
12-question index (3 SWB + 9 attribute)	81%	0%	19%	81%	3179
15-question index (6 SWB + 9 attribute)	82%	0%	18%	82%	1566

Notes: Based on only the ordinal ranking of the variable in each row. All six binary comparisons among the top four programs are considered. Columns 1–3 sum to 100 percent in each row. Column 4 reports the correct prediction rate in cases where a prediction is made; that is, excluding cases of indifference (column 2). Column 5 reports sample size.

As can be seen in the top panel of the table, the ladder question has the highest correct-prediction rate (65 percent) among our three SWB and nine residency attribute questions. It also has the highest conditional correct-prediction rate [80 percent]. Among the 64 percent of respondents in a relationship, the next-best predictor is desirability to one's partner (correct-prediction rate 65 percent)[conditional correct-prediction rate 77 percent]. In decreasing order of correct-prediction rate, the other questions are: desirability of location (61 percent)[71 percent]; life satisfaction during residency (59 percent)[77 percent]; residency prestige and status (56 percent)[67 percent]; happiness during residency (52 percent)[71 percent]; social life during residency (52 percent)[65 percent]; future career prospects (49 percent)[70 percent]; worthwhile life during residency (44 percent)[73 percent]; stress during residency (40 percent)[54 percent]; control over life (40 percent)[57 percent]; and anxiety during residency (38 percent)[53 percent]. Due to potential biases in survey response such as the halo effect and cognitive dissonance discussed above (in section III.B), we interpret these rates as upper bounds and caution against focusing on their absolute magnitudes. However, under the assumption that such biases affect each of the twelve SWB and attribute questions roughly equally, comparing the rates across questions is informative. While our survey design—the similar framing and random ordering of the twelve questions (see section II.B)—is meant to increase comparability, this assumption should be borne in mind when interpreting such comparisons.

Regardless of whether we assess usefulness by the conditional or unconditional correct-prediction rate, we find in Table 5's top panel that the evaluative SWB questions—ladder and life satisfaction—as well as desirability to one's significant other, are among the single-question measures that match choice most closely. Comparing the three SWB measures with each other, in both columns 1 and 4 the ladder does statistically significantly better than life satisfaction, which in turn does better than happiness (treating each pairwise program comparison as an observation, Fisher's exact p < 0.02 in all tests; treating each respondent's prediction rate as an observation, paired-t-test p < 0.06 in all tests). At the other extreme, anticipated negative feelings—anxiety and stress during the residency—do not predict choice well (with a conditional correct-prediction rate only slightly better than a 50-50 guess).

The middle panel of Table 5 analyzes the three beyond-residency happiness questions. While for happiness in the first ten years of one's career, the conditional correct-prediction rate is nearly the same as for happiness during the residency [72 percent vs. 71 percent], the unconditional rate is much lower (34 percent vs. 52 percent), reflecting many ties (column 2). For happiness measures further in the future, both rates are lower. Therefore, these measures are of relatively limited usefulness in our data as single-question predictors of pairwise choices.

Finally, for comparison with these single-question measures, the bottom panel of the table examines our three multi-question indices (discussed in III.C) and two additional indices that incorporate the nine attribute questions into the multidimensional SWB indices. The weights in these two additional indices are estimated from regressions analogous to those in Table 4 (Web Appendix Table A8). The 4-period-happiness index's conditional correct-prediction rate is slightly below that of the happiness-during-the-residency question [69 percent vs. 71 percent], but, with far fewer ties (column 2), the index's unconditional rate is much higher (62 percent vs. 52 percent). The rest of the indices, which are based on increasing numbers of questions (3, 6, 12, and 15), have relatively high (and increasing) conditional correct-prediction rates [77 percent, 78 percent, 81 percent, and 82 percent, respectively]. As including more questions in an index yields fewer ties, the indices' unconditional rates are similar to their conditional rates and are much higher than that of any single question (75 percent, 76 percent, 81 percent, and 82 percent, respectively).

It may seem puzzling that the evaluative SWB questions and, to an even larger extent, the 3- and 6-question indices correctly predict choice at relatively high rates, in light of our finding that the tradeoffs they imply are so different from the MRSs implied by choice. Figure 4 presents a simple model with two attributes that illustrates the relationship between pairwise predictions and tradeoffs. We orient the attributes so that both are “goods”: preferences are monotonically increasing in each. We assume that anticipated-SWB is also monotonically increasing in each good. (This assumption is consistent with our no-sign-reversals finding in the previous section— however, recall our caveat that that finding may be overstated.) The solid line represents an individual's (choice-revealed) iso-utility curve, while the dashed line represents her anticipated iso-SWB curve; we assume these curves satisfy standard regularity conditions. The respective slopes at choice option A differ: the SWB tradeoff does not coincide with the MRS. Indeed, while option A is preferred to option C, SWB is higher at C than at A. In contrast, despite the difference in slopes, option B ranks higher than option A in both choice and SWB. More generally, SWB-based comparison of option A with any option in the unshaded areas—the “discordance region”—would conflict with choice-based comparison; while SWB-based comparison of A with an option in any of the shaded areas—the “concordance region”—would agree with choice-based comparison. Locally, the discordance region is larger the greater is the difference in slopes. Globally, it is always strictly limited to the northwest and southeast quadrants—the quadrants where an alternative to A involves sacrificing one good for the other, i.e., where neither option vector-dominates the other.

Figure 4. Implications of Iso-Utility and Iso-SWB Curves for Ordinal Prediction.

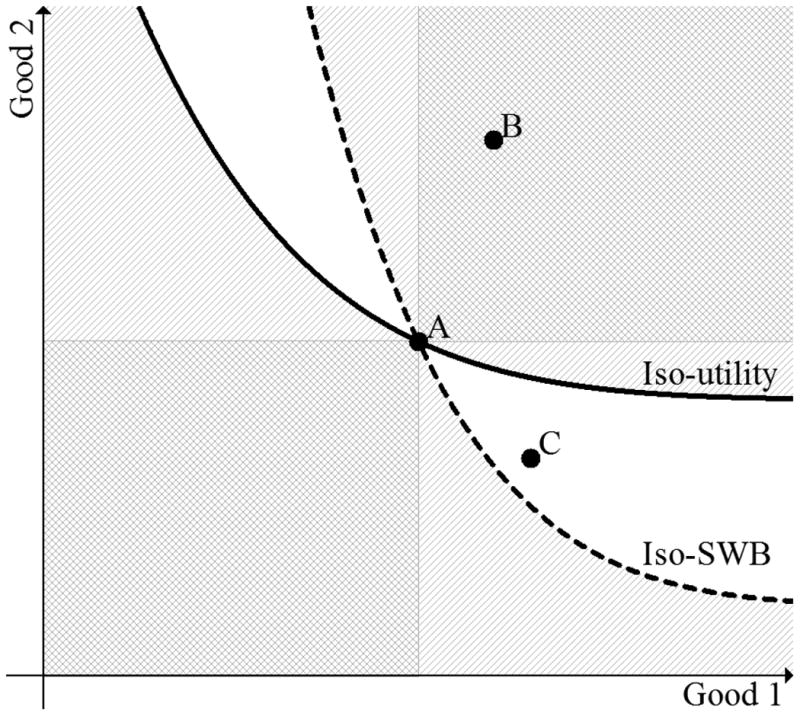
Notes: This figure illustrates the implications of different tradeoffs in choice-utility and anticipated SWB for binary comparisons. The solid line represents an individual's iso-utility curve, while the dashed line represents her iso-SWB curve. Comparing option A to options in any of the shaded areas (for example, option B), the iso-utility and iso-SWB curves imply the same binary ordering. Comparing option A to options in the unshaded areas, the curves imply different orderings (option C, for example, has higher SWB but is less preferred).

More generally, with any number of goods, the “closer” one choice option is to vector-dominating the other, the more likely it is that the alternative to A lies in the concordance region. In our data, weak vector dominance (i.e., weak inequality component by component) occurs in 16 percent of binary comparisons—a high percentage relative to what might be expected with nine independently and symmetrically distributed attributes (2 ×1/2⁹), assuming no ties). Indeed, with the exception of stress and anxiety during residency, within-respondent attribute ratings are generally moderately positively correlated across residencies (Web Appendix Table A9). These positive correlations may help explain why we find reasonably high rates of concordance in spite of large differences in tradeoffs (i.e., in slopes).¹³

The empirical settings where SWB comparisons would be most useful for drawing inferences about the preference ranking of options, however, are settings that involve sacrificing some goods for others. For example, Gruber and Mullainathan (2005) conduct SWB comparisons among smokers who face higher versus lower cigarette taxes—a setting that involves an inherent tradeoff between health and wealth, and where SWB data could be particularly attractive because, in the presence of self-control problems, choices may not reveal preferences. In such no-vector-dominance settings, the model above does not make a clear prediction on whether preference and SWB would yield the same ranking. To answer this question, setting-specific empirical evidence of the sort we collect in this paper would be needed.

Due to the inherent difficulty of observing choice and anticipated SWB in many of the situations where SWB data might be useful, Benjamin, Heffetz, Kimball, and Rees-Jones (2012) study hypothetical choices and anticipated SWB in thirteen settings designed to have no vector dominance. They find an overall correct-prediction rate of 83 percent, with wide variation across choice settings, and they identify features of the settings that are associated with higher rates. Evidence from more settings is needed before we would be confident in drawing generalizations regarding the concordance rate between anticipated-SWB rankings and choice rankings.

V. Discussion and Concluding Remarks

Scholars and lay people alike have long been fascinated by happiness and its correlates. By regressing subjective well-being (SWB) measures on bundles of non-market goods and examining coefficient ratios, researchers have been able to compare in common units the associations between SWB measures and a wide variety of goods. Such comparisons have generated a large and growing number of interesting findings. To what extent do these coefficient ratios line up with economists' notion of revealed-preference marginal rates of substitution?

Our main finding is that, among the medical students in our sample, the MRSs of residency program attributes implied by their preference rankings are far from equal to the tradeoffs implied by their anticipated-SWB responses—regardless of whether we use (1) a happiness measure, (2) a life satisfaction measure, (3) a ladder measure, (4) a simple combination of such measures, or (5) a simple combination of anticipated happiness over the near and distant future. At the same time (and perhaps, at least partially, due to our survey design), we find no sign reversals between choice and our SWB measures in their association with any of the nine attributes; we find relatively high correlations across the nine attributes between their choice-regression and SWB-regression coefficients; and we find relatively high choice-SWB concordance rates in binary residency comparisons.

Our evidence relates choice to anticipated SWB, not to the realized SWB that individuals will end up experiencing. Anticipated SWB is directly relevant for assessing to what extent SWB measures accurately summarize the goals people aim to achieve when making choices. Yet for assessing how well MRSs are aligned with coefficient ratios from happiness regressions, it is experienced-SWB tradeoffs that are relevant. It is logically possible that the differences between experienced-SWB and choice tradeoffs are smaller than the differences we find between anticipated-SWB and choice tradeoffs. However, this possibility would require that while individuals deliberately deviate, at the moment of making the choice, from choosing what they believe would maximize their SWB, their experienced SWB systematically differs from their anticipated SWB in a way that happens to partially (or fully) cancel out those deviations. We have assumed away this possibility because we find it hard to think of a plausible theory that would generate such behavior. Moreover, available evidence on systematic anticipated-vs.-experienced-SWB differences suggests that far from canceling out the choice-vs.-anticipated-SWB deviations we find, they may in fact exacerbate the deviations: for example, while we find that anticipated quality of social life is more strongly associated with anticipated happiness than with choice, Dunn, Wilson, and Gilbert (2003) find that quality of social life is more strongly associated with experienced happiness than with anticipated happiness.

While we focus on the question of how SWB tradeoffs relate to choice tradeoffs, our findings could also be viewed as informative regarding another question of broad interest to users of SWB data, namely, how survey respondents interpret SWB questions. This latter question can be viewed as a “dual” to the former if one imagines an idealized (or a yet-unfound) anticipated-SWB-type measure eliciting responses that coincided with a utility function representing preferences. The differences we find between anticipated-SWB and choice could then be viewed as revealing differences between widely used SWB measures and such an idealized SWB measure. From this perspective, relative to the idealized benchmark, the widely used SWB measures we study seem to be interpreted by our respondents as placing more weight on the importance of social life and life seeming worthwhile during the residency, and less weight on residency prestige-and-status and desirability for significant other.

Of course, our sample of medical students is a convenience sample, our evidence is limited to the specific context of residency choice, and the nine residency attributes that constitute our bundle of goods are far from exhaustive. Nonetheless, we view our real-choice field evidence as an important advance over and complement to existing evidence from prior work. When we consider them together, some common themes emerge across the findings in this paper and those in previous work that studies hypothetical choices in a range of realistic scenarios (Benjamin, Heffetz, Kimball, and Rees-Jones, 2012; henceforth BHKR) and abstract scenarios (Benjamin, Heffetz, Kimball, and Szembrot, forthcoming; henceforth BHKS). We highlight four such themes, emphasizing evidence that bears on the question of their generalizability.

First, our main conclusion that anticipated-SWB tradeoffs differ from choice MRSs is consistent with results from the earlier papers: attributes of the options help to predict hypothetical choices, controlling for anticipated SWB. In BHKR, this result is especially strong in scenarios designed to be representative of typical important decisions facing a sample of undergraduate students—scenarios that may have parallels with the important-life-decision setting in the present paper—and is weak in a scenario about consuming an apple vs. an orange—the type of minor decision that possibly comprises most decisions in life.

Second, as mentioned above, our finding of high concordance rates between choice and anticipated-SWB in binary comparisons is similar to BHKR's finding. Moreover, in BHKR the high concordance rates are not easily explained by the survey having elicited both choice and anticipated SWB: BHKR explore this issue with a between-subjects version of the survey, where half the sample is asked only about choice and the other half is asked only about anticipated SWB.

Third, all three papers conclude that evaluative SWB measures are on average closer to choice than affective happiness measures. In BHKR, this result holds in some scenarios more than in others, but further evidence is needed before we feel comfortable drawing general conclusions by type of setting. (Also notice that anticipated affective measures may feel more evaluative than their experienced counterparts due to the cognitive process involved in prediction; while this may make all of our anticipated SWB measures more alike, we still find differences between anticipated affective and anticipated evaluative measures.) Comparing across evaluative measures, in the present paper we cannot statistically distinguish the tradeoffs implied by the ladder from those implied by life satisfaction during residency (Table 3), but the ladder does better in the pairwise predictions of choice (Table 5).¹⁴

Finally, all three papers find that measures of family well-being—family happiness (in the previous work) and residency desirability to one's spouse or significant other (in the present paper)—are among the strongest predictors of choice. However, in BHKR this result varies substantially across scenarios: it is strong in human-capital-investment scenarios with parallels to the present paper's setting (for example, choosing between attending a more fun and social college vs. a highly selective one, and between an interesting summer internship vs. a boring but career-advancing one), and it disappears in personal consumption decisions (for example, choosing between attending a birthday vs. a concert, and between consuming an apple vs. an orange).

To the extent that it generalizes to a particular setting of interest, each of these findings has practical implications for empirical researchers. We list four such implications, in respective order paralleling the four themes above. First, SWB tradeoffs should not be interpreted as MRSs, and vice versa. Second, binary SWB rankings may in some settings be highly predictive of choice rankings—even when SWB tradeoffs are far from MRSs. This of course also means that high choice-SWB concordance in pairwise comparisons should not be interpreted as implying that SWB data and choice data would yield the same tradeoffs. Third, evaluative SWB measures may more reliably align with choice than affective happiness measures—even when happiness is integrated over several time periods. Finally, measures of family SWB may in some settings align with choice at least as reliably as evaluative measures of own SWB. Such family-SWB measures are not commonly used in empirical applications but warrant exploration. Indeed, in their exploration of novel question wordings, BHKS find that measures of “the happiness of your family” and “the overall well-being of you and your family” may align with hypothetical choice more closely than widely-used evaluative measures.

While we hope that researchers find these practical implications useful, we also caution that using SWB data in empirical work typically requires additional assumptions, often strong ones—for example, about interpersonal comparability of SWB survey responses (see, e.g., Adler, 2013)—that we do not evaluate in this paper.

From a theoretical perspective, if different choice consequences are all viewed as inputs into (choice-revealed) preferences, then it could be argued that the specific consequences captured by traditional SWB measures should not be treated differently a priori from other choice consequences. From this point of view, rather than regressing SWB on other goods, estimating preferences requires regressing choice on a bundle that includes SWB measures together with those other goods. As mentioned above, we run such regressions in Web Appendix Table A8; BHKR and BHKS run them with hypothetical choice. From this theoretical perspective, the findings from this and those papers would suggest that while the well-being aspects captured by traditional SWB measures are among the most important inputs into preferences, they are not the only important inputs.

If tradeoffs estimated from SWB data differ from MRSs, how should they be interpreted from a preference point of view? In one possible interpretation, SWB tradeoffs may be viewed as technical rates of substitution (TRSs) that characterize the production function for SWB (as in Kimball and Willis, 2006, and Becker and Rayo, 2008). Just as it is valuable for economists and policymakers to estimate TRSs for other important preference inputs such as health, estimates of TRSs for subjective well-being have generated and will likely continue to generate valuable insights into the production of subjective well-being.