Early Changes in Myocardial Microcirculation in Asymptomatic Hypercholesterolemic Subjects: As Detected by Perfusion CT

Abstract

Intramyocardial microvessels show functional changes in early stages of atherosclerosis prior to epicardial coronary artery stenosis. However, clinical CT does not have adequate spatial resolution to resolve the microvessels. To clinically detect changes in the function of the intramyocardial microcirculation, the spatial heterogeneity of the distribution of myocardial perfusion (F) and intramyocardial microcirculatory blood volume (Bv) was determined by perfusion CT. Two human subject groups were studied: (i) a “Control” group (24) with no risk factors nor evidence of coronary artery disease (CAD), and (ii) an “At-Risk” group (24) with hypercholesterolemia, but no evidence of CAD. In the perfusion CT image, a region of interest (ROI) covering the left ventricular myocardium was subdivided into multiple nested ROI (nROI) of equal size and used to compute F and Bv for each nROI. No significant differences between the groups were demonstrable in overall myocardial F, or Bv. The nROI data showed significantly increased spatial heterogeneity in the “At Risk” group when compared to “Control” subjects. This study demonstrates that subresolution distribution at the microcirculatory level can be quantified with myocardial perfusion CT and significant changes in these parameters occur in hypercholesterolemic subjects before they have developed significant changes in conventional perfusion parameters.

INTRODUCTION

Microcirculatory disturbances within the myocardium have been shown to precede angiographically visible narrowing of epicardial coronary arteries, i.e., before significant structural changes in the arterial wall.³⁵ Dong and Ritman¹² have previously demonstrated early changes in microcirculatory function in an acute, hypercholesterolemic animal model, while more global parameters of myocardial blood volume (Bv) and myocardial blood flow (F) remained normal. This current study was, therefore, designed to detect and quantify the early stages of atherosclerosis in human subjects prior to appearance of symptoms or other signs of coronary artery disease (CAD).

The maximum spatial resolution of current clinical CT scanners cannot resolve vessels less than 200 μm in diameter. To overcome this, a method based on the characterization of spatial heterogeneity of Bv and F was applied^3,11,18 which provides estimates of the size of hypoperfused territories without direct visualization of the micro-vascular bed anatomy. Our approach to dealing with the subresolution pathophysiology of the myocardial arterioles is based on four biological observations which suggest that use of perfusion status of arteriolar perfusion territories is a surrogate for subresolution arterioles, and a fifth, mathematical, technique of “fractal” analysis of spatially distributed features as follows:

1. The perfusion territories of arterioles are about 10× the diameter of the arterioles,²¹ the volume of the perfusion territory of a 30 μm diameter arteriole being approximately (270 μm)³.

2. At rest, only a fraction of myocardial capillaries convey blood flow at any one time with capillary recruitment during exercise or situations of increased flow demand.³⁶

3. Arterioles “open” and “close” over a period of up to minutes (“twinkling”) so that, when averaged over time, the entire myocardium is uniformly perfused.³⁷ The sub-second CT scan images therefore provide a snapshot of the perfused and non-perfused arteriolar perfusion territories within the myocardium.

4. Progressive elimination of arterioles (by reduced flow due to increased arteriolar tone or occlusion) has the seemingly paradoxical effect of increasing myocardial perfusion^16,20 up to a certain point. Once more than 40% of capillaries receive no flow, progressive reduction of myocardial perfusion results.

5. Random distribution of small particles (arteriolar perfusion territories in this case) has a power-law relationship to the variation of the number of particles measured within individual multiscale regions of interest used to estimate the number of particles.² In addition, the frequency of occurrence of the size of particle clusters is predictably related to the sizes of the clusters.⁷ Hence, the measurement of the cluster size/frequency histogram of large (i.e., resolvable) clusters can be used to extrapolate to the frequency of the subresolution particles.³³

In summary, the overall goal of this study was to quantify the spatial heterogeneity of myocardial perfusion using a nested sampling methodology to quantify the increase in F and Bv values with decreasing size of the nested regions-of-interest (nROI) within the master region of interest (ROI), i.e., the LV wall in the CT image. The hypothesis to be tested was that early atherosclerosis manifests as increased spatial heterogeneity due to intramyocardial microvascular dysfunction.

In this study we used a gamma variate curve fit to the TAC data. The Gamma variate function is a much-used model of washin–washout indicator dilution kinetics from concatenated sequential or parallel well-stirred compartments in which indicators are progressively diluted. The simplest example involves a steady input of indicator into a single stirred compartment and simultaneous washout from that compartment. The washin, in isolation, would result in a steady increase in indicator content of the chamber (i.e., C(t) = m*t, where m is a constant depending on rate of indicator infusion and t is time). If the compartment has no further indicator input (i.e., zero concentration in delivery fluid) but has a starting concentration of indicator, then the indicator content in the washout of a stirred chamber falls off exponentially—i.e., C(t) = n · exp(−p · t) where n and p are constants depending on the starting concentration of the indicator and the rate of washout relative to the chamber volume respectively. Thus, if both occur simultaneously the C(t) = m · t · n · exp(−p · t). If multiple compartments are concatenated then the washin component is well presented by t^q where q is a constant related to the number of compartments. If two compartments are parallel then the two processes add rather than multiply.

METHODS

Patient Selection

This study was reviewed and approved by Mayo Clinic Institutional Review Board. Subjects recruited included 12 men and 12 women for both the study group as well as the control group. All subjects were between 45 and 55 years of age and all of the study participants did not have any symptoms nor a clinical history of CAD. Plasma lipids were within normal range according to NCEP III Guidelines²⁴ for the “Control” group and elevated for the “At Risk” group. The “At Risk” group had a family history and/ or evidence of early CAD. All subjects had minimal or no coronary calcification (<100 Agatston units)¹ and no history or ECG evidence of myocardial infarction. Potential study participants were excluded if they were in atrial fibrillation, had a history or evidence of symptomatic CAD, or had additional risk factors, e.g., smoking, hypertension or diabetes. Participants were also excluded if the screening coronary calcium scan, performed prior to the perfusion CT scan, exceeded an Agatston score of 100, 58 subjects were screened, ten subjects were excluded, forty-eight participants were included in the analysis. All subjects were consented prior to the CT scan. Additional exclusion criterion were serum creatinine >1.5 mg dL⁻¹, allergy to IV contrast, renal disease (proteinuria >1 g per 24 h. hematuria, pyrexia, history of glomerulonephritis pregnancy or lactating exposure to IV contrast in previous 48 h.

A SOMATOM Definition Flash dual-source CT scanner (Siemens Medical Solutions, Forchheim, Germany) was used for scanning the subjects. At a rotation rate of 280 ms/rotation a temporal resolution of 70 ms was achieved. This is achieved by virtue of the fact that just over one half a rotation’s worth of scan data are needed for tomographic reconstruction. As the scanner has two X-ray sources at 90° separation, this means that those scan data are acquired in (280 ms/2) × ½ = 70 ms. A tube current of 90 mA at 120 kV was used during the ECG gated end-diastolic period. The tube current was reduced to 10% during the rest of the cardiac cycle to provide the 360° scan data needed to minimize the partial rotation artifact. ^27,28 The CT scanner is calibrated prior to the day’s scanning. This involves a number of tasks but the most directly relevant aspect is the scanning of a special test phantom which provides the measurements of the CT image gray-scale values of air and water. If these values and image variation (noise) are not within the required values then adjustments are made in the scanner’s operational characteristics to achieve the required values. As a consequence the CT image grayscale values within any one patient, and between patients, are reproducible within the limits of the CT image noise. Consequently no significant differences in the CT image gray-scale calibration, intra and inter subject, should be introduced.

Table 1 summarizes the scanning parameters. Subjects were scanned without drugs to slow the heart rate. No table translation occurred during the scan sequence, which ensured that the same mid ventricular heart sections were scanned during each sequential diastole. At heart rates less than or equal to 60 bpm the heart was scanned every sequential heart cycle, but at rates exceeding 60 bpm the heart was scanned every other heart beat. Each CT image consists of small voxels, each with a gray scale proportional to the X-ray attenuation coefficient (μ). The scanner’s accuracy and sensitivity is frequently calibrated to ensure that this value is reproducible in different subjects. In clinical CT scanner images, the gray scale is expressed as Hounsfield units (HU) = 1000 [μ(tissue) − μ(water)]/[(μwater)].

TABLE 1.

CT scan and reconstruction parameters for cardiac perfusion.

Parameter	Details
Scan type	Sequential
Collimator	32 × 1.2 mm
kVp	120
mAs per rotation	90
Phase Start (% of QRS to QRS Interval)	60%
Total scan sequence duration	30 s
Start of Scan after start of IV Injection	6 s
Temporal resolution	75 ms
Contrast medium concentration	350 mg Iodine mL−1
Contrast injection rate	5 cc s−1
Amount of contrast injected	0.25 mL kg−1
Site of injection	Antecubital vein
Reconstruction kernel	B25
Reconstructed image thickness	4.8 mm
Reconstructed image interval	2.4 mm
Voxel size	0.39 × 0.39 × 4.8 mm3

Patients were coached in the use of an interactive breath control device system (bellows)⁶ in order to keep their diaphragm in the same position and hence to ensure that the subjects’ heart position did not change throughout the 30 s scan sequence.²³ A peripherally injected bolus of contrast medium was used to generate time attenuation curves (TAC) to estimate cardiac output (CO), Bv and F.⁸ The ECG-triggered scans were obtained during diastole in order to limit heart movement during each scan, as well as to image the heart at a state of maximum F^4,32 and Bv.¹⁹

The nonionic contrast agent used contained 350 mg mL⁻¹ of iodine and injected at a volume of 0.25 mL kg⁻¹ into the antecubital vein at 5 mL s⁻¹. Six seconds after start of the injection the X-ray of the CT scanner was turned on for the 30 s scan sequence. Subjects were asked to hold their breath for at least 30 s during which they were asked to keep the diaphragm at the same level by watching the LED indicator of thoracic circumference. Subsequent to the scan, the amount of beat to beat motion of the LV free wall epicardial/lung interface motion was measured in the CT images to confirm the subjects’ adherence to the breath-holding regime.

Computing Bv and F

Figure 1a shows a typical LV chamber and myocardial TAC. The CT-derived myocardial TAC tends to have a peak value that is only 30 HU above the noncontrast- enhanced myocardium. As illustrated in Fig. 1b, the effect of CT image noise on the smoothness of the TAC can be greatly reduced by fitting the CT-based data with a gamma variate curve.³¹ Gamma-variate curves describe the change in contrast concentration in the LV chamber³⁴ as

FIGURE 1.

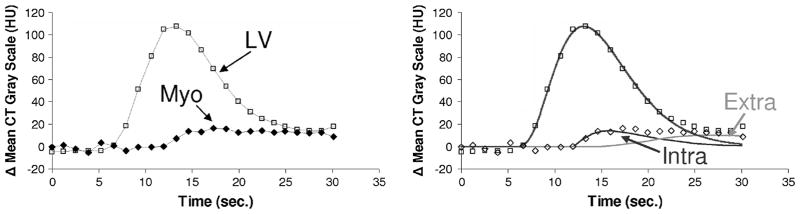
Left panel: example of TAC generated from CT images during passage of a bolus of non-ionic contrast agent injected into a cubital vein (0.25 mL kg⁻¹ of a 350 mg Iodine mL⁻¹ solution). A series of CT images (each reconstructed from scan data collected for 75 ms), of the same transaxial slices, are recorded for every cardiac cycle during a breath-hold period of 30 s. The TAC curves are generated from a region-of-interest (ROI) within this series of images, and computing the average gray scale within the ROI at each time point. Right panel shows the same TAC data plus the least squares fit of gamma variant curves, a single curve for the LV and the intravascular and extravascular curves for the myocardium as computed using Eqs. (1) and (2) respectively. The discordence between the gamma variate curves at the tail of the curves is largely due to recirculation of the contrast agent. The gamma variate curves serve, in part, to eliminate the influence of recirculation.³⁴

$$C(t)={ct}^a·exp(-t/b),$$ (1)

where C(t) is contrast medium concentration as a function of time, which is represented by the CT numbers in HU above the background CT value, t is the time (in seconds) beginning at the appearance of the curve, and a, b, and c are the curve-fitting parameters (derived by the fitting procedure). It has been shown that a single gamma variate curve well describes the LV and aortic curves, but the myocardial curve is best represented by the superposition of an intravascular component and an extravascular component (caused by contrast in the extravascular space resulting from the permeability of the capillary endothelium).²⁹ In this case, a double gamma variate of the form

$$C(t)=c{t}^a·[exp(-t/b)+d·exp(-t/h)],$$ (2)

was used. The intravascular component is described by the ct^a exp(−t/b) component and was used in our analysis of the myocardial perfusion and intramyocardial Bv. As the extravascular contrast agent sometimes does not washout completely by the time the CT scan sequence is completed, the fitting of the gamma variate is not significantly affected provided the peak myocardial opacification is included in the scan sequence.

We assume that regional intra-microvascular volume within the myocardium behaves like two, parallel (and therefore have added rather than multiplicative impact) well stirred, chambers so that the washin/ washout behavior of that region of microvasculature can be well represented by two superimposed Gamma Variate functions, one for the intravascular and one for the extra-vascular compartments. The parameters used in this Gamma Variate analysis of myocardial perfusion and micro-vascular Bv relate to the example used in the Introduction section such that “a” is the equivalent of “n,” “b” is the equivalent of “p” and “c” is the equivalent of “m.” The “d” and “h” constants of the extravascular compartment are equivalent to the “c” and “b” of the parallel intravascular compartment. We do not use these constants to derive any particular meaning because the area under the TAC (i.e., zeroth moment) and the mean transit time (i.e., first moment) of the TAC can be calculated directly from the fitted Gamma Variate curves. Nonetheless, those constant do relate to the first (area), second (variance) and third (i.e., the asymmetry of the TAC) moments of the Gamma Variate curve.

Using the derived gamma-variate curves, the Bv was calculated as the ratio of the area under the myocardial TAC divided by the area under the LV chamber TAC. F was also derived from the gamma variate fitting curves as described elsewhere.²³

Briefly, myocardial F was calculated as the Bv divided by the bolus transit time through the myocardium. The transit time is computed from the “first moment” of the intravascular myocardial TAC curve.

Analysis of CO

We used the well established indicator dilution– based formula¹⁴ to estimate CO

$$\text{CO}=M/(\text{area}\text{under}\text{arterial}\text{dye}\text{dilution}\text{curve}),$$ (3)

where M is the amount of indicator (i.e., Iodine in the contrast medium bolus) injected, i.e. CO = 0.25 (mL kg⁻¹) × 350 (mg Iodine mL⁻¹) × body weight (kg)/area of LV chamber TAC (mg Iodine mL⁻¹). The CT gray scale (HU) value relationship to blood concentration of iodine was established in a prior calibration CT scan which showed that the concentration of Iodine (mg mL⁻¹) = ((CT − 7.7)19.9), where CT is the TAC gray scale value in HU.

Analysis of Transient Myocardial Opacification during Passage of Contrast Bolus

The LV myocardium (free wall and septum) was outlined manually, guided by the opacified RV and LV chambers and lung interfaces displayed at a fixed CT image gray scale “window” for all analyses. This is called the “master ROI.” Figure 2 shows a typical CT image of the heart region and an outline of that master ROI. To calculate the index of spatial heterogeneity, the master ROI over the LV wall was subdivided into a number of nested transmural ROIs (nROIs) of equal area (or volume if multiplied by thickness of myocardium within a single CT slice image). As different subjects had different heart sizes, the master ROI would differ for each subject. We developed computer software to accomplish this goal to avoid subjective error and reduce processing time. Each one of the nROIs is then used to generate its own myocardial TAC. The minimum allowable size of the nROI was established by examining the role of CT image noise in this analysis. Increasingly smaller nROI regions were analyzed within the left ventricular chamber (where no microscopic perfusion defects exist). Hence, any variation in CT image gray scale of the LV chamber is primarily due to CT image noise. The analysis was performed on a CT image at peak contrast enhancement for the left ventricular chamber. The point at which this “random noise” log(SD/M) vs. log(area of nROI) regression intercepts with the regression generated from the myocardial nROI data was used to determine the lower limit for nROI size—below which the CT noise dominates over the TAC signal.

FIGURE 2.

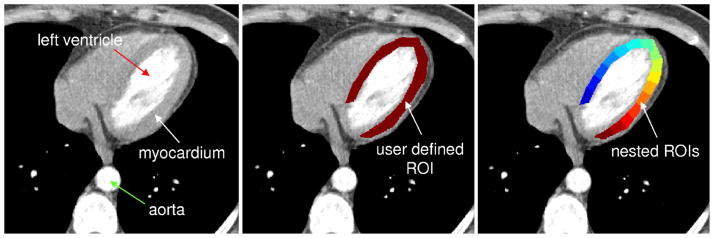
Example of nROIs generated within an annular shaped ROI. Top-left panel: CT gray scale image of left and right ventricular chambers and their myocardium. Middle panel: user-defined ROI of the left ventricular wall. The volume of this ROI is 6500 mm³. Right panel: result of the automatic region-of-interest sub-division algorithm. Here the ROI has been divided into 16 equal area regions which follow the curvature of the original object. Note that the nonuniform opacification (i.e., gray scale) of the LV chamber: this is due to both incomplete contrast mixing in the LV chamber at this time point in the scan sequence and due to possible partial volume effect from papillary muscle only partially imaged within the thickness of this imaged slice.

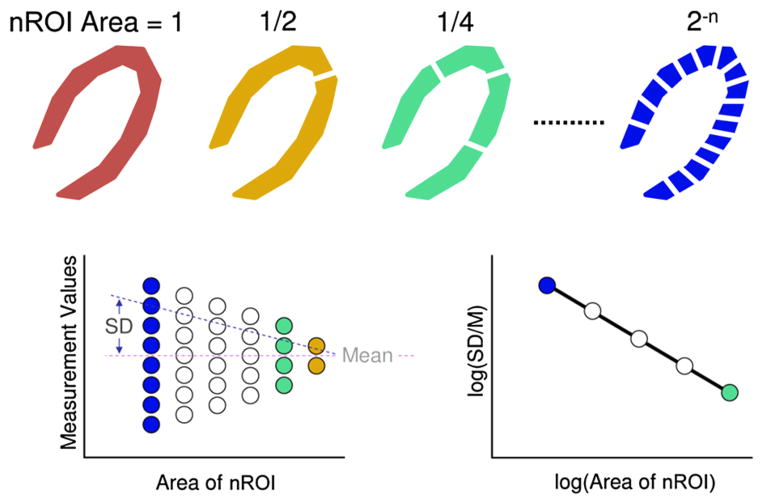
As illustrated schematically in Fig. 3, the master ROI was divided into 2, 4, 8 and 16 (the minimum size as “allowed” by the noise analysis) nROI. When the myocardial TACs were computed for each nROI, then the F and Bv were calculated for each nROI. The mean and standard deviation were then calculated for the values obtained for each set of nROI of the same size. These data were then used to calculate the slope and offset (bias) of the linear regression of the scatter plot Log(SD/M) vs. Log(size of one nROI). The slope of this regression would be −0.5 if the distribution of hypoperfused territories is random² and would be 0.0 if the distribution is homogeneous. Slope values between these extremes are consistent with the local correlation between perfusion territories.² The above analysis was performed in the up to 14 4.8 mm thick CT slices in each subject.

FIGURE 3.

Upper panel: schematic of myocardial cross-sections. The gray scale distribution in the wall varies randomly. The defined ROI of the left ventricular wall is increasingly subdivided into smaller nROIs of equal area. Lower left panel: the myocardial perfusion or Bv values estimated for each set of nROIs show an increasingly greater range of values [relative dispersion (RD) = standard deviation/mean] with decreasing size of the nROI. Lower right panel: the log(RD at selected size nROI) plotted against the log(area of one nROI) results in a linear relationship if the heterogeneity follows a fractal pattern. There are no data points for the red and yellow divisions as the standard deviation has little meaning. This figure is based on concepts presented in King et al.¹⁸).

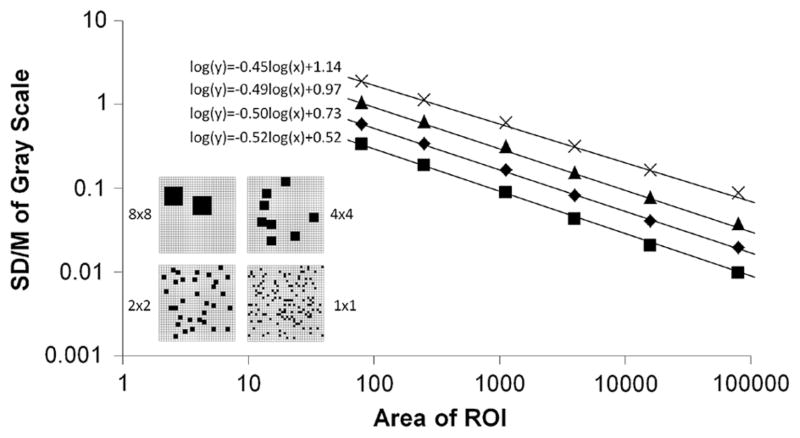
Figure 4 is a schematic representation of the impact of the simulated microperfusion territory size on the nROI analysis. Note, the decrease in bias of the regression with decreasing microperfusion territory size. There is no change in regression slope because the distribution is random in all cases.

FIGURE 4.

Simulation of a ROI within the myocardium with different sized microperfusion territories, the total myocardium perfused remains unchanged. Each ROI was analyzed with multiple nROI over an range of nROI sizes to generate the regressions. Note, the decrease in bias with decreasing size of microperfusion territory.

Statistical Analysis

The statistical characteristics of overall group parameters, overall LV myocardium values, and regional myocardial Bv and F data were analyzed with the software package Matlab (R2011b, The Math-Works, Natick, MA). A t test was performed to compare both the control to at-risk groups, as well as compare male to female within the same group. In the case of the regional myocardial Bv and F data, for each subject a regression line was computed. The slope and intercept were considered as individual measurements for each group. The t test was used to analyze the slope and bias difference between the control and at-risk groups, as well as compare male to female within the same group. The results were deemed significant when p<0.05.

RESULTS

Subject Characteristics

Table 2 lists the clinical characteristics and demo-graphics collected for each individual prior to scanning. The statistically significant differences (p<0.05) were, by design, between the LDL values and between the triglyceride values of the control and “at risk” groups of females and males.

TABLE 2.

Summary of group parameter values.

Parameter	Female Control	Female At risk	Male Control	Male At risk
Number of subjects—total	12	12	12	12
Mass (kg)	69.7 ± 13.7a	82.0 ± 17.6	86.6 ± 9.1a	85.0 ± 12.5
Number—(70–90 kg)	4(78.3 ± 6.0)	4(79.5 ± 7.0)	7(80.2 ± 5.4)	7(80.5 + 6.6)
Heart rate for group (bpm)	60.7 ± 7.6	65.2 ± 6.9	61.0 ± 11.3	59.2 ± 6.6
Number—(≤60 bpm)	6(54.2 ± 4.4)	2(57.5 ± 0.7)	6(54.7 ± 3.1)	5(53.8 ± 2.9)
Age (years)	45.4 ± 4.0	45.5 ± 4.7	45.8 ± 5.5	45.3 ± 3.6
LDL (mg dL−1)	86.3 ± 24.6a,b	125.2 ± 22.6a,b	93.8 ± 17.7a,b	132.5 ± 26.9a,b
HDL (mg dL−1)	62.3 ± 12.3a	55.5 ± 11.3	47.1 + 11.7a	48.8 ± 13.1
Triglycerides (mg dL−1)	89.8 ± 41.3b	144.5 ± 48.6b	100.0 ± 26.5	142.3 ± 110.9
C-React Protein (mg dL−1)	0.31 ± 0.28	0.37 ± 0.40	0.12 ± 0.11	0.13 ± 0.09
Interleukin-6 (pg dL−1)	2.2 ± 1.8	1.4 ± 0.3	1.2 ± 0.9	1.1 ± 0.7
Calcium score (Agatston)	0.0 ± 0.0	1.1 ± 3.6	4.1 ± 7.9	2.0 ± 5.2

^aStatistical difference across sex.

^bStatistical difference between control and at-risk.

Subject X-Ray Dose

These scans were all performed at 321 mA and 120 kV with exposure over a 4 cm cephalo-caudal extent. This resulted in a total patient X-ray dose (assuming the conversion factor described in Ref. 13) of 9.12–11.59 mSv between 50 and 60 bpm when the heart was scanned at every sequential heart cycle or 6.77–8.71 mSv between 70 and 90 bpm when the heart was scanned every other heart cycle.

Confirmation of Beat to Beat Stability of LV Heart Wall Position

The spatial location of the LV free wall epicardial to lung interface surface changed slightly in a beat-to-beat basis throughout the breath-hold period over a range of distances with a standard deviation of 0.274 mm, i.e., 70% of one in-plane pixel (0.390 mm side dimension).

Determination of Minimum nROI Size

The linear regression analysis outlined above using the LV chamber noise analysis to determine the lower limit for a useful nROI volume gave a lower bound of 15 mm³ (i.e., 1.77 × 1.77 mm² in-plane area) for the smallest nROI size that could be used in the analysis in order to prevent significant corruption by CT image noise.

CT Image Analysis Values of Overall LV Myocardium

Table 3 lists the CT image analysis-based CO and average myocardial perfusion (F) and Bv values for each group. No statistically significant differences were identified between the groups, or between males or between females in the two groups for F and Bv. Male CO was significantly higher than females in both control and at-risk groups.

TABLE 3.

CT image analysis-based parameters.

Parameter	Female control	Female at risk	Male control	Male at risk
CO/BMI (L m2 min−1 kg−1)	0.25 ± 0.09a	0.20 ± 0.09a	0.35 ± 0.10a	0.33 ± 0.14a
Myocardial Bv (myocardium volume fraction)	0.11 ± 0.04	0.10 ± 0.03	0.10 ± 0.02	0.12 ± 0.03
Myocardial Perfusion (mL min−1 cm−3)	0.92 ± 0.54	1.07 ± 0.72	0.82 ± 0.18	1.08 ± 0.35

^aStatistical difference across sex.

Regional CT Image Analysis Values of LV Myocardium

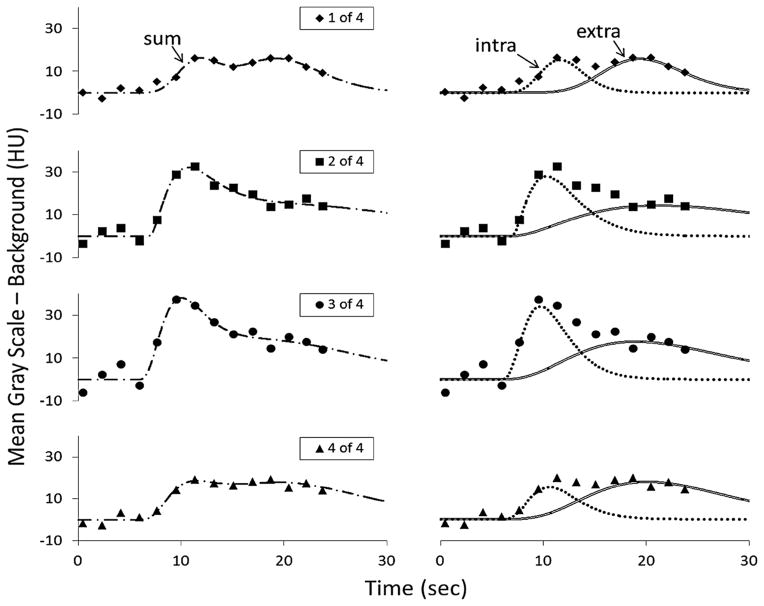
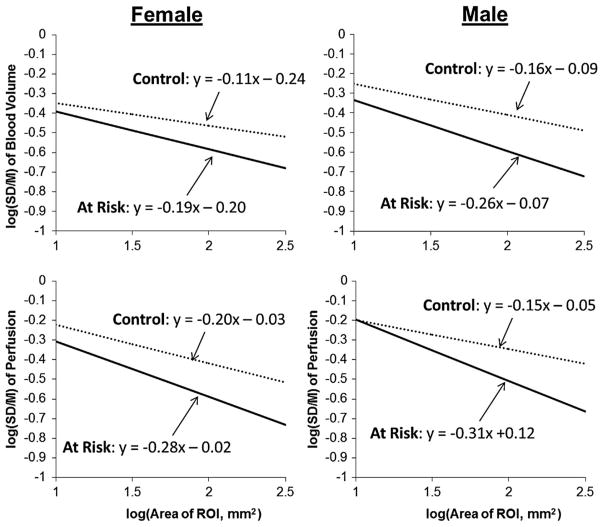
Figure 5 shows the fidelity of a typical set of individual nROI-derived TAC curves and their gamma variate-fitted versions. The fitted TAC of the transient passage of myocardial intravascular contrast show both the different peak deflections of the TAC in the different nROIs (of the same size) and of the baseline value. Figure 6 shows the regression analysis findings for both the spatial heterogeneity of Bv and of F of all groups. The feature of note is that the slope of the “At Risk” group is significantly (p<0.05) more negative than the “Control” group, consistent with the “At Risk” group having reduced local correlation between perfusion territories. The slope and bias values of the nROI analysis for the individual subjects showed no correlation to BMI (the R² value for females were −0.005 for the slope and 0.011 for the bias and for males those were 0.039 for the slope and 0.019 for bias). For the heart rate, the respective R² values were 0.051, 0.029 and 0.001 and 0.0037.

FIGURE 5.

Individual TAC and intravascular gamma variate fit from each of four nROI, in one individual subject for each of the nROI sampling the myocardium over the entire breathhold CT scan sequence. Note the slightly different arrival times of the curves. The left panels show the TAC data points for sequential heart cycles and the dual component gamma variate curve fit to those TAC data. The right panels show the two individual gamma variate curve components of the composite gamma variate curve shown in the left panels. One of those curves is for the intravascular component of the TAC and the other is for the extravascular component of the TAC. The upper to lower panels show the same data format for each of four nROI. In this example all four nROI it is the intravascular component of the TAC that is used in our analysis.

FIGURE 6.

Results of nROI analysis where the TAC were analyzed by a gamma variate-based analysis. The input to the myocardium was determined from an analysis of the aortic curve. Left upper panel: analysis of Bv within myocardium for both a control, and an at-risk subject for the females. The two regressions’ slopes are statistically different at the p<0.05 level (p = 0.001). Right upper panel: Bv for the same control and an at risk subject for the males. The two regressions’ slopes are also statistically different at the p<0.05 level (p = 0.006). The at-risk subjects have more negative slopes (p <0.05) than control, consistent with a greater degree of spatial heterogeneity of the Bv and F spatial distributions. The Lower panels are the same as the upper panels for the myocardial perfusion. The slopes differed in the same manner at the p <0.05 level (p = 0.017 for females, p = 0.019 for males). The intercept of the regressions is at log(area of ROI) = 0, i.e., ROI area = 1 mm². We showed that the smallest area of the ROI that was not significantly affected by CT image noise if the ROI area was 3.13 mm² (i.e., ROI volume = 15 mm³ if CT slice thickness is included) or log(3.13 mm²) = 0.496, well below the smallest nested ROI area = 15 mm². Consequently, we elect to use the SD/M bias at that nROI area. The differences in slopes of the regressions is taken to be an index of local correlation between perfusion areas (i.e., reduce the chance that a contiguous perfusion territory is “open” at the same time as the “open” perfusion territory of interest). The inherent noise in the CT image gray-scale values impacts on the SD/M vs. ROI area data regression, mostly in terms of slightly increasing the regression vertical bias (at the ROI area value of interest in our analysis), but this increase in bias is much smaller than the change in bias observed between the two subject groups.

Because some of the subjects had coronary calcium scores (albeit all were selected to have scores of <100 Agatston Units) the comparison of the “At Risk” to the “Control” group was repeated without those subjects with evidence of coronary calcification. The analysis showed that there was no statistically significant difference to the prior analysis of differences in the slopes or biases of the log/log regressions between “Control,” and “At Risk,” subjects for both male-to-male and female-to-female comparisons.

Because there were significant differences in body weight and heart rate (those with HR ≤ 60 bpm had a scan every heart cycle whereas those with HR>60 bpm were scanned every second heart cycle) within each group we re-analyzed the data for just those with body weight between 70 and 90 kg and those with heart rates ≤ 60 bpm. Table 2 shows that within those limits there was no statistically significant difference (t test) of body weight or heart rate between the groups. Also, the analysis within those limits did not show any significant differences between the regression slopes (p>0.05) for F and Bv spatial heterogeneity in the females and in the male subsets within the “Control” and “At Risk” groups relative to the analysis involving all subjects in each group.

DISCUSSION

This is a study to demonstrate analysis of the microcirculation at the level of the arterioles which have, up to now, involved invasive techniques.⁵ It has been observed that cardiovascular risk factors that affect the epicardial coronary arteries also affect coronary microcirculatory function, but this study addresses the first two classes of microvascular dysfunction (microvascular dysfunction in the absence of obstructive CAD and myocardial diseases, and coronary microvascular dysfunction in the presence of myocardial diseases). Indeed, the microcirculatory changes generally precede changes seen in the epicardial arteries. There are also diseases which may exclusively involve the microvasculature (e.g., “Syndrome X”),²² and would allow analysis of possible patchy distribution of ischemia. The factor common to all these entities is possibly a defect in endothelial-mediated vasomotor regulation, and subsequent dysregulation of micro-arteriolar blood flow, which can be assessed clinically by measuring vasomotor reactivity of the microcirculation and/or vasodilator reserve under various stimuli during a selective coronary catheterization. As of yet, non-invasive direct assessment of the coronary microcirculation has not been clinically possible, thus there has not been a universally accepted therapy for these patients.²⁵

Rubinshtein et al.³⁰ examined over 1000 patients assessed with the endothelium-independent flow dilator adenosine and demonstrating a significantly higher Framingham Risk Score in this cohort. Whereas the number of participants in our prospective study was much smaller, it included a control group demonstrating significantly different microcirculatory flow even with only hypercholesterolemia as a risk factor. Panza et al.²⁶ states “intensive risk factor modification should be pursued in all appropriate patients.” Our proposed method would allow to identify patients in whom exposure to risk factors has led to pathological changes in microcirculatory function and thus allow targeting the appropriate treatment population.

Several cardiac risk factors are associated with both coronary and peripheral coronary disease particularly endothelial dysfunction, e.g., cigarette smoking,¹⁷ hyperlipidemia and elevation in lipid subfractions,⁹ have been shown to result in endothelial dysfunction, sometimes reversible. Our model would allow assessment of reversibility and could help in demonstrating the transition to irreversible and possible structural heart disease. Diabetes has been classified as a CAD equivalent and appears to be preceded, at least in young individuals, with uncomplicated endotheliumin dependent flow aberrations¹⁰ in the early stages of disease, which could also be studied with our technique.

The results of this study show that there was no significant difference between the two groups in the conventional parameters of global LV myocardial perfusion and intramyocardial Bv. This observation is consistent with the well-established finding that hemodynamically significant coronary artery stenosis is a late feature in the progression of atherosclerosis.¹⁵ Similarly, there were no obvious differences of average F and Bv between the different groups. However, the nested Region-of-Interest analysis method does indicate the subresolution differences in perfusion distribution. As indicated in Fig. 6, the difference in the regression slope of the “At Risk” group is consistent with a tendency for the spatial distribution in the “At Risk” group to be more random than in the “Control” group. In the “Control” group the local correlation could be due to any one active perfusion territory providing adequate perfusion to its neighboring perfusion territories. This effect would likely result in “discouragement,” i.e., less perfusion of contiguous territories as adjacent territories supply sufficient nutrients, which would be at odds with the chances of some of the contiguous perfusion territories being active if the spatial distribution was purely random.

In an effort to miminize invasiveness only 0.25 mL contrast per kg (i.e., on average, 20 mL) was injected intravenously over 5 s. It is doubtful that the contrast volume can be further reduced, but it is likely that the X-ray exposure can be further reduced by additional application of post-scan image analysis noise-reduction approaches.

Because differences of body weight could influence CT image noise due to differences in X-ray attenuation and beam hardening, and because differences in TAC curve sampling intervals (due to scans occurring every heart cycle at ≤60 bpm vs. every second heart cycle at >60 bpm) could affect the fidelity of the curve analysis, we also performed analysis in a subset of subjects so as to minimize these plausible impacts. As we could show no differences (p>0.05) from the analysis of entire group, we conclude that even the smallest nested ROI was still large enough to render the “photon noise” component of CT image noise insignificant for our analysis. Moreover, the lack of impact of the TAC sampling intervals is consistent with the relatively long duration of the TAC (≥ than the 4 s injection duration) rendered these sampling differences insignificant.

This methodology needs to be confirmed and further evaluated in future studies. Nonetheless, if these promising results are confirmed, this may be a method for triaging asymptomatic individuals with elevated risk of coronary artery atherosclerosis before any structural changes have occurred. Those subject who show the microvascular changes might be candidates for more aggressive management beyond with life-style changes which is currently recommended in this group, and might benefit from pharmaceutical therapy.

CONCLUSION

This study demonstrates in human subjects that subresolution spatial distribution at the microcirculatory level can be quantified with perfusion CT and shows significant changes in spatial heterogeneity of Bv and F in hypercholesterolemic subjects before they have developed significant changes in conventional perfusion parameters.

Nearly half of all life-threatening cardiovascular disease events occur in previously asymptomatic people, who may have undetected subclinical disease. Hence, development of a technique to detect presymptomatic disease in subjects deemed to be at risk for CAD could reduce expense by restricting treatment to those who really need it and this increased certainty would likely encourage compliance with the treatment.

Waiting for the occurrence of symptom is often too late for reversal of the damage resulting from the disease process. The proposed CT-based imaging method has potential for detecting the presence of the disease process prior to symptomatology and hence leading to more effective treatment. Hence, our proposed methodology, possibly as part of a CT-based coronary angiogram, may be able to detect these changes in microvascular function who would benefit from risk-reducing therapy.

ABBREVIATIONS

BPM

Beats per minute

Bv

Blood volume (mL cm⁻³)

CAD

Coronary artery disease

CO

Cardiac output (L min⁻¹)

CT

Computed tomography

F

Myocardial perfusion (mL g⁻¹ min⁻¹)

HU

Hounsfield units of CT image gray scale

HR

Heart rate (beats per minute)

LED

Light emitting diode

nROI

Nested region of interest

RD

Relative dispersion (standard deviation/mean)

ROI

Region of interest within LV wall in CT image

TAC

Time attenuation curves