Do Fertility Transitions Influence Infant Mortality Declines? Evidence from Early Modern Germany

Abstract

The timing and sequencing of fertility transitions and early-life mortality declines in historical Western societies indicates that reductions in sibship (number of siblings) may have contributed to improvements in infant health. Surprisingly however, this demographic relationship has received little attention in empirical research. We outline the difficulties associated with establishing the causal effect of sibship on infant mortality, and discuss the inherent bias associated with conventional empirical approaches. We offer a solution that permits an empirical test of this relationship whilst accounting for reverse causality. Our approach is illustrated by evaluating the causal impact of family size on infant mortality using genealogical data from 13 German parishes spanning the 16th, 17th, 18th and 19th centuries. Overall, our findings do not support the hypothesis that declining fertility led to increased infant survival probabilities in historical populations.

1 Introduction

The turn of the 20th century was marked by a dramatic change in Western Europe’s demographic landscape. This change encompassed unprecedented reductions in both fertility and mortality. A striking feature of the mortality change was the decline in the infant death rate. That the fall in infant mortality appeared to occur in tandem with fertility reductions suggests that these events may have been related. Our aim is to shed light on this relationship, investigating whether reductions in fertility led to improvements in infant survival. To do this, we use micro-level data collected from 13 German villages covering the 16th, 17th, 18th, and 19th centuries.

Econometric modeling of this relationship is problematic for a number of reasons. Firstly, the measure of fertility at an individual level, sibship, must be adjusted so that it does not induce a spurious correlation with infant mortality. For example, the total number of children born in each household cannot be used as a measure of sibship because this does not account for the ‘replacement effect’—where parents have more births in order to compensate for previous child deaths. The number of surviving children (completed net fertility) is also an inadequate measure because, by definition, this value will be lower for families who experience a higher number of infant deaths. A further complication is that it is not possible to observe all the confounding variation which affects infant mortality, and therefore the estimated conditional effect of fertility may suffer from omitted variable bias.

We propose an alternative indicator of family size: sibship at birth. This measure takes the child as the observation unit and thus allows sibship to vary within each family. The death of older siblings are not counted in this total, so this measure is not confounded by child replacement effects. In addition, each child’s sibship at birth is unaffected by their fate in infancy. Because we observe the temporal ordering of these events, this sequencing removes the potential for a structural reverse-correlation connecting infant mortality with sibship. We acknowledge that the results of a single equation analysis may suffer from endogeneity bias, and address this issue using an instrumental variables (IV) estimator. Our approach instruments fertility using a measure of marital fecundity (Agüero and Marks, 2011; Klemp and Weisdorf, 2012).

Our use of historic micro-level data permits us to assess the causal importance of fertility change. Therefore, we can evaluate whether a counterfactual fertility transition would have caused infant mortality to fall prior to the actual fertility transition and infant mortality decline. In summary, our analysis does not support the hypothesis that an earlier fertility transition would have caused a subsequent infant mortality decline. Interestingly, our results may indicate the opposite, as sibship at birth is negatively correlated to infant mortality. A one child increase in sibship at birth is associated with a moderate reduction in infant mortality of about 1.5%. However, once we use an IV estimator to capture potential endogeneity, we cannot reject that there is no relationship.

The remainder of this paper is structured as follows. Section 2 elaborates both our motivation and the context for his study. In Section 3 we introduce our data, formalize our empirical strategy, and present our results. Finally, Section 4 concludes.

2 Context and Literature

Knodel (1974) provided a comprehensive overview of the German demographic transition.¹ In 1875, the average married couple had 5.4 surviving children, while life expectancy was roughly 37 years. By 1933, the average number of surviving children had fallen to 2.6, and mortality change contributed to an increased life expectancy of 61.3 years—a 66% increase. The contribution of reductions in the number of deaths in infancy and childhood to the mortality decline was immense. The probability of death before the age of 15 fell from 39% to 12% and 36% to 10% for German males and females, respectively, during the period 1871–1934. Births outside marriage averaged around 10% throughout this time period, and displayed a similar decline to births within marriage. Marriage patterns also did not contribute much to changes in overall fertility.²

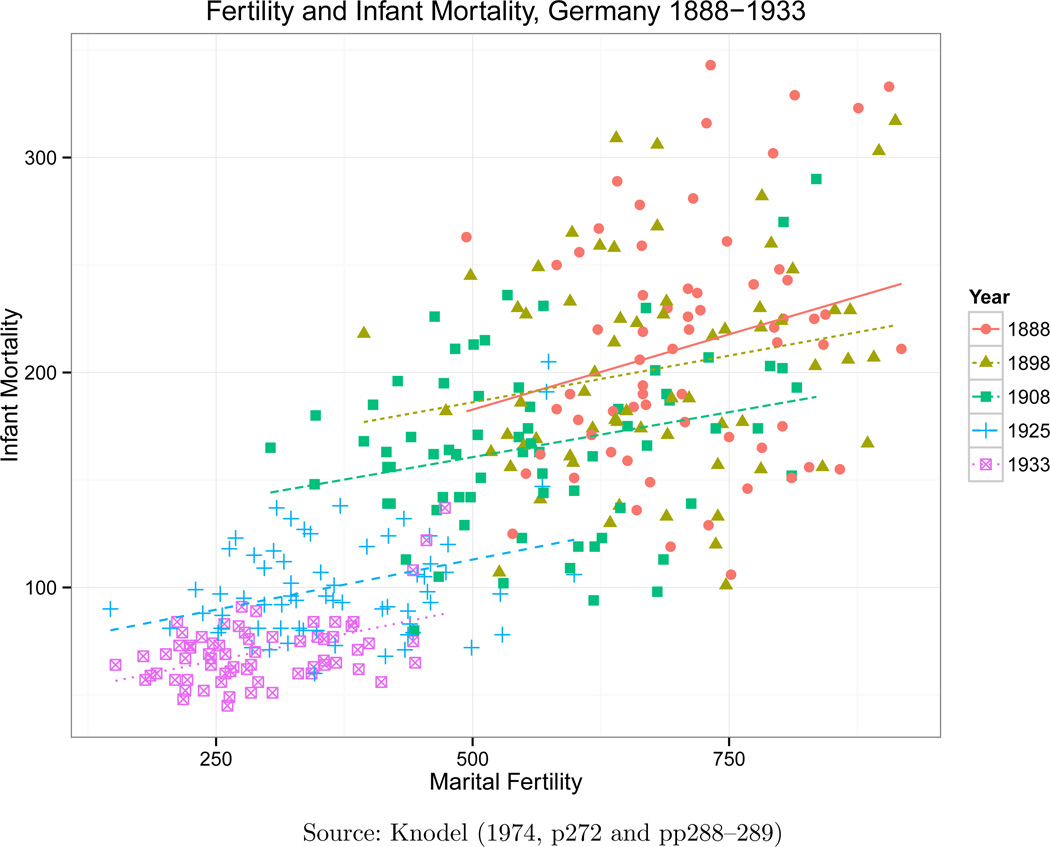
At the macro level, the extent to which these events were causally related (in either direction) is not obvious. Figure 1 illustrates the relationship between fertility and mortality over time. In Section 3, we discuss the importance of choosing the correct indicator of sibship when attempting to address the issue of causality, but here we present the index of marital fertility used by the European Fertility Project to document the overall association between fertility and mortality.³ There is a clear positive correlation; regions with higher levels of infant mortality tended to have higher levels of fertility. This also holds within a particular time period. It is also clear from this graph that both infant mortality and fertility experienced significant falls over the period.

Figure 1.

The Relationship Between Marital Fertility and Infant Mortality During the German Demographic Transition

The literature has identified a number of potential routes through which sibship size could potentially have influenced infant mortality in historical populations. For example, parents with fewer children could have devoted more care and attention to their newborn. Theoretically, if family-level resources determined infant mortality, reductions in sibship size would have improved infant survival probabilities. In other words, we assume that finite family-level resources are positively related to infant mortality through some (unknown) function. This is one mechanism through which we propose that fertility affects infant survival, as a larger sibship results in a greater division of family-level inputs into the infant-survival function. However, this is not the only way in which fertility could impact the probability of infant survival. For example, extra siblings may increase the probability of infectious disease spreading in a household. The relationship between fertility and mortality is therefore open to evidence from empirical investigation, the issue which we address in this paper.

The child resource dilution and contagion models sketched above are distinct from various forms of the child Quantity-Quality (QQ) model originally proposed by Becker and Lewis (1973). In the child QQ model, parents choose their optimal levels of child investment and fertility based on a given set of prices and income. Given the dynamic nature of our question, one in which children are born after siblings have died, we do not attempt to view our results in a child QQ framework because QQ models involve completed fertility. In effect, our analysis measures the direct effect of fertility on infant mortality.

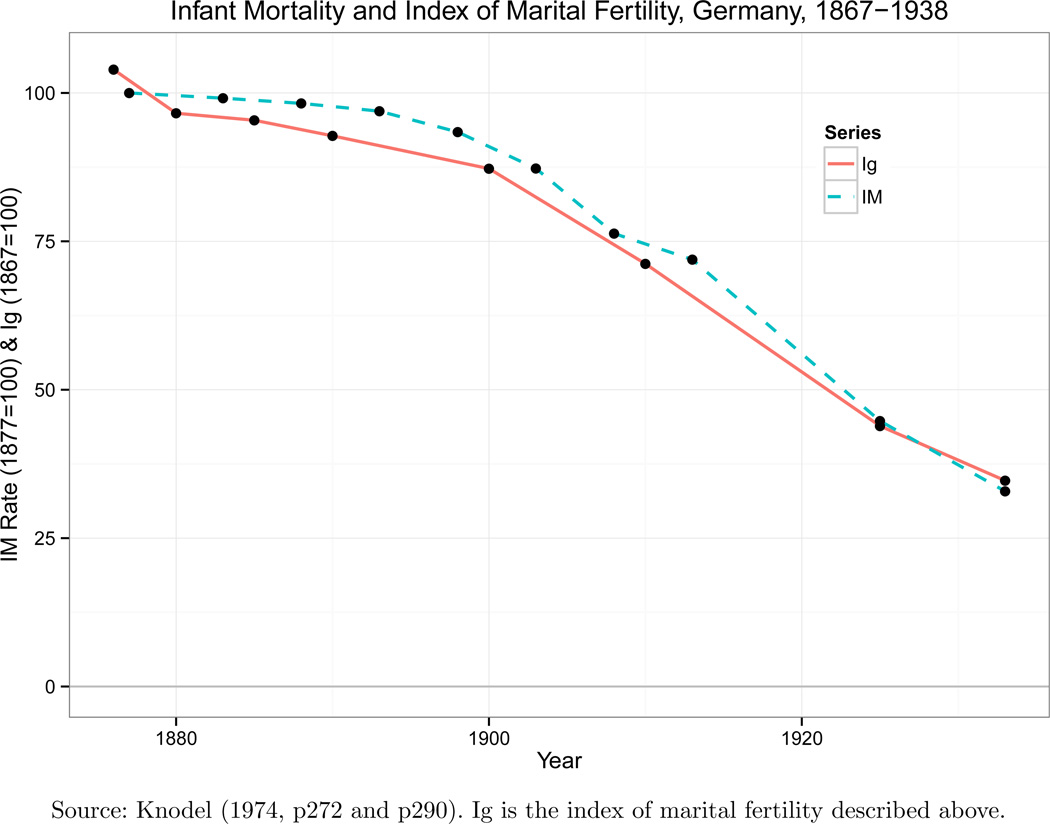
Figure 2 depicts a time-series of both the fertility and infant mortality transitions in historical Germany. Two elements are worth drawing attention to. Firstly, both transitions occurred at the same time. Knodel (1974) studied regional patterns and found that declines in fertility almost always preceded the declines in infant mortality. This finding is important because it is inconsistent with the notion that the infant mortality decline was an initiating factor determining the fertility decline, and also suggests that the fertility decline may have been a component of the infant mortality transition.

Figure 2.

Marital Fertility and Infant Mortality During the German Demographic Transition

Previous research suggests that economic growth played an important role in longevity improvements (Floud et al., 2011). However, a body of literature suggests that the infant mortality decline had alternative proximate causes than per capita income growth. For example, Bengtsson (1999) showed that the risk of infant death was unrelated to economic changes in 18th and 19th century Sweden. Public health initiatives are recognized as a vital source in the improvement of infant survival probabilities in the late 19th and early 20th centuries (Delaney et al., 2011). Cutler and Miller (2005) estimated the effect of water filtration in a number of cities in the United States during this period. Their results showed how a large portion of this decline was caused by the implementation of policies which provided clean water for household use. Similarly, this period was also marked by a revolution in household knowledge surrounding germs, microbes and general cleanliness (Mokyr, 2000).

The relationship between fertility control and infant mortality has been proposed by a number of scholars. For example, Woods (2000) discussed the link between the decline in infant mortality and fertility in England and Wales, but also highlighted the problematic nature of establishing this as a causal relationship with regional/macro level data, as well as the potentially confounding variation induced by prolonged breastfeeding. We discuss this issue further in the next section. The relationship between sibship size and infant mortality has also been explored by Knodel and Hermalin (1984). Their findings indicated that sibship size was positively correlated with the probability of infant mortality in rural Germany. Our study improves upon the Knodel and Hermalin (1984) analysis in a number of ways. Firstly, by taking advantage of the dynamic nature of these data, our methodology highlights the importance of removing reverse causality caused by child replacement effects and the structural relationship between fertility and infant mortality at the household level. Secondly, as discussed in the above, our methodology is robust to potential endogeneity biases. Finally, we deliberately ignore the distinction between birth order and sibship size. Both variables are structurally correlated (Booth and Kee, 2009), and we argue that distinguishing between the two does not constitute a sensible strategy because the fertility transition would have resulted in changes to birth order composition through its effect on fertility.

3 Empirical Analysis

3.1 Data

This study uses historical genealogies from 13 German villages which span the onset of the demographic transition. We argue that this type of life history data allow us to answer questions of causality in a manner which is not possible with aggregate statistics. These data are obtained from parish records which contain details of the major events for all families in that particular locality. Demographic information pertaining to parents and children (such as dates of birth and marriage) are included, as well as measures of socioeconomic status (parental occupation) and health (age at death), all over the course of multiple generations.

The written parish records began to be collated in the early part of the 20th century, as part of a project to document genealogy in each locality throughout Germany. This project was interrupted with the outbreak of the Second World War, and consequently these data are only available for a limited number of parishes. These villages were therefore not intended to be a representative sample of the German population, however subsequent verification exercises have suggested that the quality of these genealogies is high, as they also match up well with the available registration data (Knodel, 2002).

A limited number of papers (for example Klemp and Weisdorf, 2012) have examined the effects of sibship using Anglican records collected from 26 parishes in England. Cohort studies have also been used in researching this topic, including Boyd-Orr (Frijters et al., 2010) and the Swedish Uppsala Birth Cohort Study (Modin, 2002). In our case these data have a number of advantages. Specifically, the quality of the reconstruction, the comprehensive multi-generational nature of the database, and the fact that the genealogies span the beginning of the demographic transition in Germany. Our empirical data contain information on the factors that we expect may confound the fertility-infant mortality relationship. These variables include parents’ age at birth and child's place of birth. Additionally, we are able to control for a number of typically unobserved variables, including measures of parental health and socioeconomic status. These control variables reduce the risk of an unobserved confounder inducing selection into both large families and high mortality.

However, while we can control for these factors, we cannot definitively rule out the possibility that variation from some omitted source may simultaneously affect infant mortality and fertility. Examples of these include measures of parenting “quality”, or breastfeeding (Brown and Guinanne, 2001). Breastfeeding is an important determinant of both fertility and infant mortality (Knodel, 2002). Extended breastfeeding acts as a form of contraception, and thus lengthens birth intervals with the consequence of reducing gross fertility. In historical populations, a premature cessation of breastfeeding could increase the hazard of infant death substantially, since it exposed vulnerable infants to potentially contaminated, and therefore unhygienic, food sources. Thus, breastfeeding is an example of a variable which would bias the relationship between sibship and mortality upwards. Alternatively, net sibship itself could also represent a measure of maternal or paternal ability. Thus, a bigger net sibship at birth may capture the fact that some parents are better able to carry babies to term and help them survive, and that this reproductive success is transmitted intergenerationally though a combination of environmental or genetic endowments. This is an example of an omitted variable which would bias the effects of sibsize downwards. It is difficult to determine a priori which effect would dominate. We return to this issue when discussing our results.

Fortunately, it is easier to identify plausibly exogenous sources of fertility differences at the individual level than it is at the macro level. If we observe variation in sibship which is unrelated to potential confounders, this can be used to obtain a consistent estimate of the effects of sibship size on mortality. We adopt the approach proposed in Agüero and Marks (2011), and also used in Klemp and Weisdorf (2012). We take advantage of the fact that there is a random component to natural fertility, in the sense that some couples are more ‘biologically compatible’, and find it easier to conceive than others. Agüero and Marks (2011) highlight the fact that the epidemiology literature on the subject has found surprisingly few robust predictors of this natural fecundity. For example, biological fertility has been found to be unrelated to family background characteristics (Joffe and Barnes, 2000), as well as lifestyle factors and behavior (Buck et al., 1997). This is important, as the identifying assumption is that the instrument (in this case natural fertility) should affect the outcome (infant mortality) only through its effect on sibship. As in Klemp and Weisdorf (2012), we take the length of time between marriage and first birth (standardized for the mother’s age at marriage) as our indicator of natural fecundity. This variable is standardized using the residuals from a regression estimating the predicted number of days from marriage to the first birth date, controlling for age at marriage. We use a quadratic in age at marriage, however using a higher order polynomial or a semi-parametric model does not affect the results. We find that fecundity is strongly predictive of sibship, so couples who conceived soon after getting married appear to have been more compatible biologically, and went on to have larger families.

The main disadvantage of using these data relates to the extent to which it is possible to generalize from these particular 13 German villages. However, the trajectories for both infant mortality and fertility were similar across regions and type of location (urban and rural localities). Furthermore, as is shown in Figure 3, the villages are relatively geographically dispersed, and incorporate important variation such as religion, and economic and social structures. Therefore, while these data tell a rural story, it is reasonable to assume that our results have wider implications.

Figure 3.

Approximate Village Locations

3.2 Summary Statistics

A number of papers have used these German parish register data, particularly in the historical demography literature. This research stems from a series of contributions by Knodel who was among the first to popularize the analysis of this data source. Much of this research is collected in Knodel (2002). Summary statistics for the analysis sample are presented in Table 1.

Table 1.

Summary Statistics

Variable	Obs	Mean	Std. Dev.	Min	Max
Infant Death	47,665	0.203	0.402	0.000	1.000
Stillbirth	47,665	0.023	0.151	0.000	1.000
Sibship at Birth	47,665	1.889	1.699	0.000	8.000
Completed Sibship (Gross)	47,665	5.963	3.087	0.000	18.000
Male	47,665	0.514	0.500	0.000	1.000
Year/100	47,665	18.169	0.560	15.910	18.990
(Year/100)2/100	47,665	0.330	0.020	0.253	0.361
Mother’s Age at Birth/100	42,539	0.315	0.061	0.148	0.542
Father’s Age at Birth/100	40,525	0.356	0.076	0.150	0.770
Mother’s Age at Death/100	40,404	0.609	0.152	0.184	0.986
Father’s Age at Death/100	38,789	0.641	0.136	0.207	0.979
Mother Survived until the Age of 40	42,796	1.000	0.000	1.000	1.000
Parent with Missing Vital Record Dates	34,171	1.000	0.000	1.000	1.000
Time Till First Birth (Days)	30,080	480.899	352.876	270.000	6855.000
Time Till First Birth-	26,644	−0.186	0.938	−1.224	17.134
Orthogonal to Mother’s Age at Marriage
Occupation	Obs	%	Village	Obs	%
Artisan	9,755	20.466	Anhausen	1,350	2.832
Businessman	3,331	6.988	Braunsen	1,150	2.413
Cottager	3,238	6.793	Gabelbach	1,331	2.792
Civil Servant	369	0.774	Grafenhausen	5,684	11.925
Farmer	14,263	29.923	Herbolzheim	9,879	20.726
Home Industry	759	1.592	Hoeringhausen	2,703	5.671
Kneckt	563	1.181	Kreuth	765	1.605
Labourer	1,264	2.652	Massenhausen	1,968	4.129
Professional	860	1.804	Middels	2,918	6.122
Unknown	2,069	4.341	Oeshelbronn	4,996	10.481
Rural Labourer	3,129	6.565	Rust	7,390	15.504
Soldier	232	0.487	Vasbeck	2,469	5.180
Tenant Farmer	228	0.478	Werdum	5,062	10.620
Unskilled	396	0.831
Weaver	2,411	5.058
None	3,649	7.656
Legal Status	714	1.498
Honorary Title or Position	435	0.913

The summary statistics displayed in Table 1 provide an overview of both the variables used in our empirical exercise, and potentially missing data. On average, infant mortality afflicted about 20% of all observations. Around 2% of the sample were stillborn, and we have also included these in the Infant Death variable. Our sibship at birth variable was constructed by taking account of all births, deaths, and the timing of these events in each relevant family. To capture maturity, as we might expect older children to exit the household or start to contribute towards the household’s income, we assume that children no longer matter for sibship at birth upon reaching the age of 15. The completed sibship variable measures how many births have occurred in each household. We divide a number of our variables by 100. This aids an interpretation of the regression coefficients presented later. The maximum year is 1899, as we do not consider the small number (2,264) of observations born in the 20th century because there are no marriages after this date in these data.

Each of the parental age variables indicate the potential for missing data. To highlight these numbers we have created an indicator showing if at least one of these variables is missing for an observation: Parent with Missing Vital Record Dates. 34,171 observations contain the complete set of parental vital date measures. Table 1 also displays the potential for missing data in our marital fecundity measure: Time Till First Birth. This variable cannot be constructed for pre-marital conceptions. Thus, we do not consider observations where a birth occurs in under 270 days of the marriage date. A similar restriction is advised in Klemp and Weisdorf (2012). Since mother’s age at marriage is highly correlated with the time till first birth measure, we construct a orthogonalized measure, as described in the Data subsection. However, since this measure requires the mother’s age at marriage, there are slightly fewer observations where this variable is available. Another restriction, recommended by Knodel (2002), is to focus on families where the mother has survived until at least reaching the menopause, and hence not curtailing any opportunity to have a larger family. We set a low bound of 40 for the age at menopause, although setting a higher bound does not alter our results. Table 1 indicates that this restriction only applies to a minority of our data sample. We evaluate the sensitivity of our results to sample selection in the following analysis.

3.3 Measuring Fertility

The simultaneous decline of both fertility and infant mortality, as demonstrated in the previous section, strongly suggests the existence of a relationship, or relationships, connecting the two phenomena. However, there are a number of important methodological issues that must be addressed in order to establish whether there is a causal relationship between fertility and infant mortality. Firstly, there exists a number structural relationship between fertility and mortality which must be accounted for in empirical modeling. Secondly, the economics literature on the effects of family size has focused on identification in the presence of enogeneity (Black et al., 2005), for example both fertility and child mortality may be determined by unobservables, such as some measure of parenting ability.

Therefore, in what follows we adopt a strategy to deal with both of these problems. In this section we focus on describing the first issue of reverse causality. We argue that it is first necessary to use micro-level data, and secondly that the correct measure of sibship size must be used. Because mortality and fertility are observed simultaneously in aggregate data, it is difficult to establish whether reductions in fertility are reducing mortality, or whether reductions in mortality are reducing fertility.

Doepke (2005) analyzed a number of theoretical fertility choice models and found that decreases in infant mortality would have led to increases in the number of surviving children. This finding contradicts the historical record and leaves Doepke to conclude that the fertility transition was not caused by the changes in infant mortality. Theoretically, the positive relationship between infant mortality and net fertility strengthens our motivation for examining whether fertility determined infant mortality because the causality might run the other way—from fertility to infant mortality. Therefore, we examine what occurs when infant mortality conditions are endogenous with respect to fertility. However, completed measures of fertility are ambiguously related to infant mortality, and as such we argue that the inclusion of endogenously determined infant mortality requires the modeling of the sequential discrete-time process jointly associated with both family formation and infant mortality.

The mechanics and distinction between discrete-time and time-invariant completed measure of fertility and how they interact with infant mortality can be described as follows. Let d_ij = 1 denote whether an individual child i from family j dies in infancy, so d_ij = 0 indicates survival. To simplify matters, imagine d_ij is determined by an as of yet undefined function f_ij (•) with d_ij =1{f_ij (•) > 0}. If we allow B_j and N_j to denote the number of births and number of surviving infants from family j respectively, the completed infant survival coefficient θ_j for the jth family is derived from the following discrete-time process:

$${\theta }_j=1-\frac{{\sum }_{i=1}^{B_j}{d}_{ij}}{B_j}$$ (1)

Eq. (1) underlines the problematic nature of using completed fertility measures, as both the replacement effect, driven by B_j , and the structurally induced net correlation, driven by N_j , can cause changes in in θ_j independently of the term determining infant mortality, d_ij. Therefore, it is apparent that modeling the effect of fertility on infant mortality involves modeling d_ij =1{f_ij(•) > 0}, such that the function f_ij(•) incorporates an individual or time specific measure of fertility.

We propose sibship size at birth for the ith child in family $j(n_{ij}=[B_j-i]-{\sum }_{k=1}^{i-1}{d}_k)$ as the measure through which fertility influences infant mortality. To the best of our knowledge this is the first use of this measure of sibship as the economics literature has focused exclusively on completed sibships (for example Black et al., 2005). The sibship at birth measure is consistent with the sequential discrete-time ordering associated with family level demographic patterns. We can summarize our argument as follows. If infant mortality is the outcome of interest, then we argue that the only appropriate measure of sibship to use is sibship at birth. It is hard to see why a completed sibship measure should be related to infant survival. For example, suppose that an individual has 2 siblings at birth, but has 10 siblings at age 15. It is not clear how any event which occurs after the age of 1 (in this case the birth of additional siblings) could affect whether the individual survived their first year or not, especially in a model of resource dilution. Finally, because we observe these events sequentially in our data, at the individual level a person’s fate in infancy cannot affect their sibship at birth, thereby removing the structural reverse correlation which generally connects infant mortality with an alternative measure of sibship. When we observe a birth in these data, we are able to establish the number of living siblings, which we then hold constant. Following this, we observe whether the individual suffered an infant death. So we measure our outcome (mortality), after our ‘treatment’ (sibship) is fixed. A previous version of this paper outlines this argument more formally, and provides simulation based evidence on the bias of alternative measures (Fernihough and McGovern, 2013).

3.4 Empirical Results

We begin our formal analysis by implementing regression models that control for observable characteristics. As outlined above, our data allow us to control for parental health and socioeconomic status, which are likely to be the most important confounding variables. We control for both the age of the mother and father at birth in order to account for changes in fertility over time within families. We estimate the following linear probability model for infant mortality:⁴

$${\mathbf{\text{IM}}}_i={\mathbf{X}}_i\beta +{\mathbf{\text{SSAB}}}_i\gamma +{\epsilon }_i$$ (2)

where the event of infant death (IM_i—with individuals denoted i), is a function of sibship size at birth (SSAB_i), and a number of other control variables (X_i). Our main parameter of interest is γ, the effect of sibship size at birth on the probability of infant mortality. Results from this model are presented in Table 2.

Table 2.

Infant Mortality and the Effect of Sibship at Birth: OLS Regressions

	OLS	OLS	OLS	OLS	OLS
	(1)	(2)	(3)	(4)	(5)
Sibship at Birth	−0.003***	−0.013***	−0.014***	−0.014***	−0.017***
	(0.001)	(0.002)	(0.002)	(0.002)	(0.002)
Male	0.031***	0.033***	0.033***	0.034***	0.033***
	(0.004)	(0.004)	(0.004)	(0.005)	(0.006)
Year/100	0.179	0.146	0.704***	0.605**	0.808**
	(0.195)	(0.266)	(0.271)	(0.280)	(0.345)
(Year/100)2/100	−3.275	−2.239	−17.576**	−15.016*	−20.832**
	(5.434)	(7.361)	(7.492)	(7.751)	(9.555)
Mother’s Age at Birth/100		0.560***	0.483***	0.471***	0.549***
		(0.061)	(0.061)	(0.064)	(0.078)
Father’s Age at Birth/100		0.067	0.147***	0.143***	0.165***
		(0.048)	(0.047)	(0.051)	(0.064)
Mother’s Age at Death/100		−0.198***	−0.183***	−0.097***	−0.089***
		(0.018)	(0.018)	(0.023)	(0.029)
Father’s Age at Death/100		−0.013	−0.030	−0.020	−0.046*
		(0.020)	(0.019)	(0.021)	(0.026)
Father’s Occupation	N	Y	Y	Y	Y
Village Fixed Effects	N	N	Y	Y	Y
Mother Survived until the Age of 40	N	N	N	Y	Y
Time Till First Birth >269 Days	N	N	N	N	Y
Observations	47,665	34,171	34,171	30,442	18,878

^***p<0.01,

^**p<0.05,

^*p<0.1.

Clustered, at the family level, standard errors in parentheses.

The coefficients in Table 2 display how sibship at birth affects infant mortality across a variety of specifications. We examine how robust this effect is by introducing additional control variables, and placing additional restrictions on our sample. Overall, these results run counter to our prior expectation as sibship at birth appears to have a negative on infant mortality. In each of the five specifications, we find that sibship at birth reduces the likelihood of infant death. This effect strengthens once controls are introduced in our preferred specifications. However, we do not find that the magnitude of this correlation reduces with the inclusion of additional controls or further sample restrictions, shown in columns (3) to (5). These results indicate that an additional sibling at birth will reduce the probability of death by around 1.5%. One possible mechanism through which this effect operates is experience—as both bringing a child to term and ensuring that it survives the first year of life represents a skill. In other words, we can think of this as a learning-by-doing process whereby sibship at birth represents the parent’s ability to keep their offspring alive. Therefore, a larger sibship at birth, a net measure of fertility, will be indicative of the parent’s success in this regard. This effect is conditional on parent’s age at birth, so this explanation is robust to the alternative hypothesis that this is a pure age effect for parents. Regardless, our finding of a negative correlation is not consistent with the theory that fertility reductions played a role in the decline of infant mortality.

In contrast to the results in Table 2, all of the fertility—Completed Sibship (Gross)—coefficients in Table 3 are positive. Clearly, this is the result we would expect to obtain considering the replacement effect. In other words, reverse causality is at play here and the number of births for a family will be higher for families that experience infant mortality as they ‘replace’ these children. Like in Table 2, the coefficients, although likely biased, are remarkably stable across each of the five specifications. Table 3 underlines our motivation for using sibship at birth as our measure of fertility, and is consistent with our simulation results (Fernihough and McGovern, 2013).

Table 3.

Infant Mortality and the Effect of Completed Sibship (Gross): OLS Regressions

	OLS	OLS	OLS	OLS	OLS
	(1)	(2)	(3)	(4)	(5)
Completed Sibship (Gross)	0.009***	0.012***	0.010***	0.011***	0.011***
	(0.001)	(0.001)	(0.001)	(0.001)	(0.001)
Male	0.031***	0.033***	0.033***	0.034***	0.034***
	(0.004)	(0.004)	(0.004)	(0.005)	(0.006)
Year/100	0.142	0.167	0.640**	0.535*	0.622*
	(0.191)	(0.260)	(0.267)	(0.274)	(0.340)
(Year/100)2/100	−2.306	−2.725	−15.711**	−12.985*	−15.425
	(5.311)	(7.183)	(7.390)	(7.586)	(9.407)
Mother’s Age at Birth/100		0.406***	0.327***	0.330***	0.385***
		(0.055)	(0.055)	(0.058)	(0.071)
Father’s Age at Birth/100		−0.015	0.061	0.056	0.059
		(0.047)	(0.047)	(0.050)	(0.063)
Mother’s Age at Death/100		−0.228***	−0.211***	−0.094***	−0.085***
		(0.018)	(0.018)	(0.023)	(0.029)
Father’s Age at Death/100		−0.050**	−0.060***	−0.059***	−0.085***
		(0.020)	(0.019)	(0.021)	(0.027)
Father’s Occupation	N	Y	Y	Y	Y
Village Fixed Effects	N	N	Y	Y	Y
Mother Survived until the Age of 40	N	N	N	Y	Y
Time Till First Birth >269 Days	N	N	N	N	Y
Observations	47,665	34,171	34,171	30,442	18,878

^***p<0.01,

^**p<0.05,

^*p<0.1.

Clustered, at the family level, standard errors in parentheses.

We have outlined the structural problem associated with measuring the effects of fertility on mortality. However, a focus of the economics literature has been on accounting for both omitted variable and simultaneity bias in this relationship (e.g. Black et al., 2005). Therefore, we extend the analysis to deal with the potential endogeneity of sibsize. These data allow us to control for a number of observable characteristics. Nevertheless, we are still concerned that some unobservable factor, like breastfeeding, could be simultaneously correlated with both infant mortality and sibship at birth. Table 4 demonstrates the results of an analysis that captures potential omitted variables bias. Here we use an instrumental variables (IV) estimator with our marital fecundity variable. A further discussion on the validity of this variable as an instrument for fertility is provided in the text below. We perform two two-stage least-squares (TSLS) regressions, reporting both the first-stage, columns (1) and (3), and second-stage, columns (2) and (4), results.⁵ Here we are stratifying our analysis based on whether the mother of the individual survived until 40, although our results appear to be consistent regardless of the specification.

Table 4.

Infant Mortality and the Effect of Sibship at Birth: IV Regressions

	Sibship at Birth	Infant Mortality	Sibship at Birth	Infant Mortality
	First Stage		First Stage
	OLS	TSLS	OLS	TSLS
	(1)	(2)	(3)	(4)
Sibship at Birth		−0.007		−0.014
		(0.011)		(0.012)
Time Till First Birth—Orthogonalized	−0.293***		−0.297***
	(0.021)		(0.023)
Male	0.003	0.033***	0.005	0.033***
	(0.018)	(0.006)	(0.019)	(0.006)
Year/100	−2.541	0.884***	−2.530	0.815**
	(1.822)	(0.338)	(1.931)	(0.347)
(Year/100)2/100	65.238	−22.638**	65.242	−21.016**
	(50.548)	(9.333)	(53.579)	(9.602)
Mother’s Age at Birth/100	12.256***	0.444***	12.163***	0.514***
	(0.363)	(0.151)	(0.387)	(0.157)
Father’s Age at Birth/100	4.532***	0.109	4.452***	0.152*
	(0.333)	(0.076)	(0.361)	(0.080)
Mother’s Age at Death/100	0.031	−0.189***	−0.071	−0.089***
	(0.121)	(0.022)	(0.173)	(0.029)
Father’s Age at Death/100	0.115	−0.058**	0.035	−0.046*
	(0.141)	(0.025)	(0.155)	(0.027)
Father’s Occupation	Y	Y	Y	Y
Village Fixed Effects	Y	Y	Y	Y
Mother Survived until the Age of 40	N	N	Y	Y
Time Till First Birth >269 Days	Y	Y	Y	Y
First-Stage Partial F-Statistic	191.75	165.65
Observations	21,264	21,264	18,878	18,878

^***p<0.01,

^**p<0.05,

^*p<0.1.

Clustered, at the family level, standard errors in parentheses.

Both first-stage regressions indicate that our martial fecundity variable—time till first birth—is highly correlated with fertility. The first-stage partial F-statistics, 191.75 and 165.65, are well in excess of the conventional weak instrument threshold level. Thus, this instrument satisfies one of the key assumptions regarding IV methodology, that the IV is sufficiently correlated with the endogenous regressor. Our findings in Table 4 are somewhat mixed. On one hand, the sibship at birth coefficients tally well with the equivalent effects displayed in Table 2. The coefficients are both negative and of a similar magnitude. On the other hand, these IV estimates are a lot less precise compared to the OLS equivalents in Table 2. Consequently, the standard errors on the sibship at birth variable are lot larger, and the t-test statistics are much below any conventional level regarded to claim statistical significance.

Overall, the IV results in Table 4 present ambiguous evidence on the hypothesis that sibship at birth and infant mortality were negatively related. Irregardless, these results, like those in Table 2, do not support the hypothesis that historic falls in infant mortality were caused by the fertility decline. If anything, these results may indicate that a counterfactual fertility transition would have caused infant mortality to rise. One mechanism that may lie behind this claim is that increased net fertility provides parents with more opportunities to learn about infant care, and therefore the infant mortality probability falls with the number of ‘successes’ that parent’s have in raising their children. However, given the size of the standard errors in Table 4, we must refrain from placing too much emphasis on this finding as we cannot reject the hypothesis that fertility and infant mortality are unrelated.

The validity of the results in Table 4 are conditional on the instrument meeting the exclusion restriction. Namely, our measure of marital fecundity must only affect infant mortality through its impact on sibship at birth. If families with lower net fertility also differ in terms of some other factor influencing infant mortality, then the exclusion restriction is not satisfied and our IV results could be biased. For example, maternal health could affect both fertility and child health. Our argument is that marriage generally signaled the desire to start a family and conceive during this time period, and therefore the time between the marriage date and the date of the first birth represents a measure of natural fertility which has been found to be mainly exogenous in the literature (Joffe and Barns, 2000; Buck et al., 1997). However, it is important to provide some test of whether this is a reasonable assumption in this context. Table 5 demonstrates that the instrument has no predictive power for either maternal longevity, or infant mortality of the first born. If time till first birth was affected by maternal health, we would expect it to predict life expectancy of the mother, however this is not the case. Secondly, suppose some parents had lower desired fertility (which also affected infant mortality), and therefore had greater time to first birth, then we would expect time to first birth to affect the mortality of the first born. This is an important test as clearly all firstborns have the same sibship.⁶ As with maternal mortality, there is no evidence that the instrument affects this outcome. We therefore conclude that the exclusion restriction is plausible in our application.⁷ However, as with all instrumental variable models, it is not possible to prove that the exclusion restriction holds, given that, by definition, we do not observe the omitted factors which may be biasing the estimates. Our test of the relationship between time to first birth and maternal mortality and mortality of the first born support the interpretation that biological fertility is exogenous. Nevertheless, due to the nature of this approach it is important that future research should focus on validating these results using alternative data and alternative sources of exogenous variation in fertility.

Table 5.

Test of Instrument Validity, Time Till First Birth—Orthogonalized

	Mother’s Age at	Mother’s Age at
	Death/100	Death/100	Infant Mortality	Infant Mortality
	OLS	OLS	OLS	OLS
	(1)	(2)	(3)	(4)
Time Till First Birth—Orthogonalized	0.001	0.001	0.001	0.005
	(0.002)	(0.001)	(0.005)	(0.006)
Year/100	−0.670***	−0.735***	2.148***	2.276***
	(0.228)	(0.179)	(0.564)	(0.575)
(Year/100)2/100	19.554***	21.581***	−58.523***	−62.365***
	(6.331)	(4.954)	(15.642)	(15.948)
Mother’s Age at Birth/100	0.294***	0.011	0.488***	0.471***
	(0.050)	(0.041)	(0.142)	(0.152)
Father’s Age at Birth/100	−0.030	−0.034	0.136	0.136
	(0.037)	(0.031)	(0.102)	(0.108)
Father’s Age at Death/100	0.105***	0.074***	−0.048	−0.036
	(0.018)	(0.014)	(0.043)	(0.047)
Male			0.044***	0.043***
			(0.012)	(0.013)
Mother’s Age at Death/100			−0.193***	−0.067
			(0.039)	(0.055)
Father’s Occupation	Y	Y	Y	Y
Village Fixed Effects	Y	Y	Y	Y
Mother Survived until the Age of 40	N	Y	N	Y
Time Till First Birth >269 Days	Y	Y	Y	Y
Observations	4,296	3,602	4,296	3,602

^***p<0.01,

^**p<0.05,

^*p<0.1.

Robust standard errors in parentheses.

4 Conclusions

All developed nations have undergone dramatic changes in fertility, which tended to be accompanied by equally dramatic reductions in mortality. The sequencing of these two events within countries is almost always suggestive of interdependency; however there has been surprisingly little research examining the causal relationship between these two demographic phenomena. A potential explanation for this absence is that the types of aggregate data which tend to be most readily available for analysis are plagued by the problem of reverse causality. In this paper, we present our case that individual level data, which allow for the temporal ordering of mortality and fertility, are required to address this issue.

We discuss the biases that are inherent in conventional measures of fertility, and propose sibship at birth as a fertility measure that is free from these biases. Since sibship at birth does not include previous deaths, we account for the so-called replacement effect. In addition, this measure is unaffected by the individual’s fate in infancy, removing the structural reverse-correlation connecting infant mortality to sibship. Essentially, as we observe the person’s sibship at birth first, and then whether they died in infancy or not, we can use this sequential timing to address reverse causality.

We also address potential omitted variable bias by instrumenting for sibship with a measure of natural fertility that has been used previously as a source of exogenous variation in sibship (Agüero and Marks, 2011; Klemp and Weisdorf, 2012). This approach accounts for the possibility that parents may select to have higher fertility on the basis of some unobserved characteristic which is correlated with risk of mortality (such as some form of parental quality).

To empirically evaluate the impact of a counterfactual fertility transition in a historical population, we use micro-level data from German parish records that span the 16th, 17th, 18th and 19th centuries. The results from our empirical models do not support the hypothesis that fertility transitions influence infant mortality declines. In fact, our results appear to indicate the opposite—that infant mortality would have increased in response to a reduction in net fertility. However, our IV effect estimates are quite imprecise, and we would caution any definitive interpretation regarding this negative effect. Thus, we conclude that declining fertility had little effect on infant mortality, despite the suggestive timing of these two events in Germany, and elsewhere.

Our results have a number of consequences. Our conclusion that infant mortality was not affected by the fertility transition stands in contrast to previous research which has relied on macro data (e.g. Galloway et al., 1998). We highlight the importance of choosing the correct measure of sibship. Many developing nations are currently in the midst of undergoing a similar reduction in fertility, and an interesting extension of this research would be to address whether the results obtained in this paper can be extended to this contemporary context.