Grouping of large populations into few CTL immune ‘response-types' from influenza H1N1 genome analysis

Abstract

Despite extensive work on influenza, a number of questions still remain open about why individuals are differently susceptible to the disease and why only some strains lead to epidemics. Here we study the effect of human leukocyte antigen (HLA) genotype heterogeneity on possible cytotoxic T-lymphocyte (CTL) response to 186 influenza H1N1 genomes. To enable such analysis, we reconstruct HLA genotypes in different populations using a probabilistic method. We find that epidemic strains in general correlate with poor CTL response in populations. Our analysis shows that large populations can be classified into a small number of groups called response-types, specific to a given viral strain. Individuals of a response-type are expected to exhibit similar CTL responses. Extent of CTL responses varies significantly across different populations and increases with increase in genetic heterogeneity. Overall, our analysis presents a conceptual advance towards understanding how genetic heterogeneity influences disease susceptibility in individuals and in populations. We also obtain lists of top-ranking epitopes and proteins, ranked on the basis of conservation, antigenic cross-reactivity and population coverage, which provide ready short-lists for rational vaccine design. Our method is fairly generic and has the potential to be applied for studying other viruses.

Influenza virus (IFV) is engaged in an arms-race with its host, evolving rapidly often under negative selection.^{1, 2} Consequently, there exists a large pool of closely related viral strains yet diverse enough to be differently virulent,² affecting different human populations differently.³ Some strains turn out to be so highly virulent that they have caused epidemic outbreaks in some regions, causing many deaths, such as the 1918⁴ and 2009^{5, 6} outbreaks. It is well understood that influenza is controlled either by antibodies or CD8⁺ T-cells.^{1, 7, 8, 9} In fact, one of the vaccine strategies currently being tested involves inactivated IFVs capable of inducing cytotoxic T-lymphocyte (CTL) responses.^{1, 10} Individuals differ significantly in their ability to respond to an infection. Among the factors that govern the outcome of an infection, human leukocyte antigen (HLA) polymorphism in the host is one of the most important.¹¹ A few associations between HLA allele types and susceptibilities to different diseases have been discovered through a variety of approaches, including linkage analysis and genome-wide association studies.^{12, 13} No such clear associations are well known for influenza. There is, however, a recent report that links A*24 allele to H1N1 infection.¹⁴ Although pathogen diversity remains a main cause for heterogeneity in disease outcome, host genetic heterogeneity is another important cause, making host responses highly complex in nature, yet inadequately studied.

Typically in humans, each individual carries two sets each of HLA A, B and C alleles, co-dominantly.¹⁵ Based on the precise combination of HLA alleles, individuals differ from each other in their immune potential and hence in the susceptibility to a given infection. HLA alllele frequencies in different ethnic groups have been determined by extensive sequencing of alleles and has been documented in public databases.^{16, 17} A large amount of data has been accumulated about the viruses too, including genome sequences of hundreds of strains.¹⁸ Major advances have also occurred on the epitope mapping front, with several well-validated methods for prediction of strong epitopes from genome sequences.^{19, 20} Clinical data about the severity of the disease in different locations and strains that have led to outbreaks are also available from different resources.⁵

Despite these advances, much needs to be understood about how host HLA diversity affects disease susceptibilities. Particularly, there are no clear answers for why different individuals show varied susceptibility, why does the presence of a high-risk allele not always lead to the same extent of disease susceptibility, why some individuals with different HLA alleles show similar CTL responses to a given pathogen, why do some variations in the pathogen genome trigger major differences in response while some others do not and why do some strains cause outbreaks but not all? Clearly these are complex questions. The complexity due to the number of HLA polymorphs and also the complex pattern of interactions with epitopes makes it necessary to employ computational approaches to obtain global perspectives. In this study, we seek to address some of these questions through a molecular systems approach starting with mining ‘big data'from literature and then using the insights obtained from that to investigate the effect of heterogeneity in a population in terms of the impact it makes on recognizing a pathogen.

Data we use are (a) the set of CTL epitopes from different strains of IFV along with their cognate HLA alleles, (b) genome sequences of hundreds of IFV strains presenting strain variation and (c) host heterogeneity in terms of allele frequencies in different populations. Making use of the vast data on these from IMGT¹⁶ and IEDB²¹ resources, through computational analyses, we show that despite high extents of diversity or polymorphism in HLA genotypes, different individuals can be grouped into a small number of response-types, typing being pathogen and strain-specific. Individuals in a response-type theoretically ‘see' the IFV in a similar way. Strains that have caused epidemics are predicted to elicit very poor response in the corresponding population, due to the low number of epitopes to the HLA alleles in that population. Some populations show high response to all the studied strains, indicating very low incidences of H1N1 infections. Rank lists of strains, epitopes, alleles, and populations based on the expected CTL response are obtained, which can serve as useful pointers for vaccine design. Finally, we show the effect of heterogeneity in hypothetical populations in terms of CTL response to IFV and that heterogeneity in populations could help in restricting the spread of H1N1 influenza.

Results

Genome-wide epitope detection and viral strain diversity

The CD8⁺ immunome of IFV was identified using three well-established methods from IEDB,^{22, 23, 24} from which consensus predictions were obtained. Example consensus epitopes for strain A/mallard/Alberta/965/1979 are listed in Supplementary Table 1, and data for all strains are made available on a web resource FluTope (http://proline.biochem.iisc.ernet.in/flutope). Forty-one of the predicted epitopes are seen to match exactly with those identified experimentally from various biochemical binding and T-cell stimulation studies in literature^{21, 25} (Supplementary Table 2). The epitope positions and their conservation patterns in each protein are shown in Figure 1, along with a scatter plot of epitope-based distances versus whole-genome sequence-based distances. It is seen that, on the whole, epitope regions as compared with whole polypeptide chains show higher variation across strains, indicating the significance of these regions and the selection pressure leading to mutations. We note that variation cannot be uniform for all epitopes in a protein as it will be determined by both selection pressure due to antigenicity and extent of mutability of the particular residues in order to retain protein structure and function. Indeed, we observe a small set of highly conserved epitopes in some proteins, particularly PB2 and PB1 (Supplementary Tables 3 and 10). For some viral proteins such as PB1 and PA, it is interesting to observe that some strains form separate clusters (Figure 1; Supplementary Figure 5), indicating higher variation and higher host-immune selection pressure in such strains. This is similar to antigenic shifts for B-cell antigens reported for other IFV subtypes.²⁶

Figure 1.

Epitope conservation in 186 strains of Influenza A virus. Positions of consensus epitopes in 186 strains of IFV for proteins PB1 and NP are shown (Supplementary Figure 6 shows similar figures for other 6 proteins as well). Protein names are labelled. Rows represent different strains in the order in which they are listed in the database (Supplementary Table 1a) while columns represent amino-acid residues along the length of the polypeptide chain of the corresponding protein. Each protein from different strains is aligned by multiple sequence alignment using Muscle. Consensus epitopes, each of 9 aa length are indicated in red. Marked below the alignment for each protein, in green, is a measure of Shannon entropy indicating the extent of sequence variability. Scatter plots of whole protein-sequence based distances of all-pairs of strains (x axis) against epitope-based distances for the same pairs of strains (y axis) is given for all eight proteins. The scatter is predominant in the upper part of the diagonal, as is evident in all cases, indicating higher variation in epitope regions.

Epitope pools vary in size in different strains (distribution in Supplementary Figure 1a), despite retaining similar overall length of each protein. Figure 2a illustrates the relative number of epitopes from each protein along with the major alleles that they recognize for one example strain. Similar figures for all 186 strains are in FluTope. It is seen that the major alleles that recognize IFV epitopes vary in the range of 10–12 for different strains. Biclustering performed to capture cross-reactivity between epitopes and the alleles is shown in Figure 2b for one example strain, indicating a relative ranking of the theoretical potential of different alleles and pool of epitopes from different proteins in generating a CTL response. A dendrogram of 186 IFV strains, based on the extent of similarities in their epitope sets for each protein (Supplementary Table 4a) is seen to be different from those constructed based on sequence similarities in whole proteins (Supplementary Table 4b). These branching patterns, with higher number of branches in epitope trees, indicate that even subtle variations in the genome can give rise to significant differences in the CD8⁺ immunomes.

Figure 2.

(a) Representation of the set of CD8⁺ epitopes on the IFV genome from consensus predictions. The innermost pie chart reflects the relative ratios of the different HLA alleles that are theoretically capable of recognizing the given strain of the IFV. The outer doughnut represents the number of epitopes for a pool of HLA alleles for each of the eight protein in the genome (size of the segments proportional to the number of epitopes). The histograms shown outside the doughnut reflects the corresponding HLA cognate alleles for epitopes of that protein. Proteins are labelled while the HLA alleles are as indicated in the colour key. (b) A biclustering diagram with columns representing different proteins in the viral genome and rows representing different HLA alleles that recognize the set of epitopes in each protein. The colour in each cell indicates the predicted recognition strength, as a factor of the number of epitopes in that protein for a given allele. Clustering patterns indicate similarity in responses both from an allele's perspective as well as from a protein's. The total antigenicity in terms of the number of epitopes is indicated for each protein. Also indicated is the recognition strength of each HLA in terms of the number of epitopes it can bind.

Modelling host diversity

Next, we model host diversity by reconstructing all possible HLA genotypes in a population. About 1884, 2490 and 1384 HLA genes are listed for A, B and C loci, respectively, leading to an astronomical ∼4.6 quintillion genotypes. Although, such a large number of genotypes are theoretically possible, available data suggest that only about a hundred alleles are known to occur predominantly, leading to a much reduced but still daunting number of combinations of about 1.2 million genotypes. The number becomes even smaller when allele frequencies in individual ethnic groups are considered. Variations in allele frequencies in 59 ethnic groups are collated from public repositories¹⁷ (shown in FluTope). The distribution provides a basis to understand allele frequencies in a population and point to the expected propensity of each allele in an individual's HLA genotype. A further filtering in the list of alleles that can be considered comes from the extent of information available on the epitopes an allele can bind. Based on such data and application of well-tested and benchmarked algorithms for epitope prediction from the IEDB resource, it is currently possible to study 79 HLA Class-1 alleles (29, 28 and 13 A, B and C, respectively). Hence further analysis in this study is restricted to these 79 alleles and the genotypes that can be constructed from them. These 79 are among the most predominant alleles listed in IMGT. The number of genotypes thus constructed (see Supplementary Algorithm 1) differ for different populations and range from 313 for ‘Brazil Mixed' to 4858 for ‘USA North American Natives' (see Supplementary Figure 2).

A dendrogram is constructed from all-pair distances of populations of 59 ethnic groups by considering extent of dissimilarity in the HLA alleles in the genotypes of each population (see Supplementary Figure S3). Each node represents an ethnic group, and distances between nodes indicates extent of difference in their HLA distribution profiles. Their arrangement into clades tells us which leaves are most similar to each other. We observe, for example, clustering of ‘Brazil Mixed' and ‘Italy Population 2' in the same clade while ‘USA Arizona Gila River American' and ‘Australia Yuendumu Aborigin' cluster together in another clade. Observation of such clades would imply that, in general, populations in the respective leaf nodes are likely to respond to any given pathogen in a similar manner. However, it must be pointed out that differences in genotypes is a first-level description of the host diversity for CD8⁺ immune responses, but their specific responses will depend upon not only the host HLA genotypes but also on the epitope set counterpart from the specific pathogenic strain. Although similar genotypes are expected to respond similarly, it is possible that different HLA genotypes can also recognize a given pathogen in a similar fashion.

Grouping populations into ‘response-types'

As the next step therefore, we map epitopes from each strain of IFV for each individual HLA genotype in a population and compare similarities between different ethnic groups by considering the corresponding pools of epitopes of their component alleles. Our predictions show that, on an average, an individual recognizes about 14 epitopes (Supplementary Figure 1b), the number varies from 0 to 109 for different individuals in all populations (all data in FluTope). We perform clustering of different HLA genotypes in a population on the basis of commonality in the epitope pools that they recognize. We observe for all 59 ethnic groups studied here thousands of HLA genotypes in each group indeed cluster into only a few types. We refer to these clusters as ‘response-types' (Figure 3a). The number of clusters in individual ethnic groups vary from as few as 2 to about 20 (see Supplementary Figure 4). Figure 3b illustrates a hierarchical diagram, reflecting relative ranking of proteins, epitopes and the alleles they recognize in a given population. As an example, for 1034 HLA genotypes in Mexican population, there are only 15 different response-types. This grouping varies for different strains in a given population and for different populations in response to a given strain (Supplementary Figure 4). Higher the number of response-types signifies the strong effect of genetic heterogeneity in the pathogen recognition.

Figure 3.

Response-type analysis performed on Kentucky/96/2009 H1N1 strains for Japan Central population. (a) A network representation of HLA genotypes (different individuals) in a population. Nodes (circles) represent response-type, which are clusters of HLA genotypes. Each genotype is denoted by the human symbol, and they are clustered based on similarity in terms of epitopes they recognize. Despite clustering, a small amount of cross-presentation of epitopes are seen between clusters (response-types) indicated as edges in the network (curved arcs). The overlap between clusters are very small compared with the epitope pool recognized by a response-type. The size of nodes are proportional to the number of HLA genotypes that group into a cluster. Each cluster is shown in a different colour. The workflow for deriving the response-type is also indicated. (b) An illustration of a hierarchical network involving different interconnected levels. Level 1 represents the viral genome. Level 2 depicts viral proteins, each containing different number of Class-1 HLA epitopes shown in level 3. The size of each node in level 2 is representative of the epitope set size. Connections between levels 2 and 3 are shown from the epitope to the protein(s) that contains it. The size of the nodes in level 3 represents the number of HLA alleles that particular epitope can bind to. The top node is labelled. This level is in turn connected to level 4 that represents different HLA alleles that recognize the entire pool of epitopes on all proteins in the influenza genome. HLA nodes are sized according to the number of epitopes they recognize. Different individuals contain different HLA genotypes. Individuals are clustered together based on the extent of commonality in the pool of epitopes they recognize, which is shown in the top most level (in purple). Each cluster represents a ‘response-type'. The size of the nodes representing a response-type indicates their relative importance in recognizing the epitope pool from the pathogen. The histogram above reflects likelihood of the occurrence of each cluster in a given population based on known allele frequencies. The red circles indicate extent of response of each response-type. Corresponding figures for all combinations of ethnic groups and IFV strains can be obtained from the web resource FluTope.

Effect of viral strain diversity and host heterogeneity on overall CTL response

Next, we evaluated the effect of strain diversity on the stability of the clusters or response-types by analysing different strains of the virus. Through this analysis, we study whether a given response-type, derived from the study of one viral strain, holds good generally for other strains as well. Stable clusters can result from one of the following: (a) minimal changes in the epitope regions of the viral strains, and (b) similar overall recognition by a given population despite changes in epitope regions, accounted for by cross-reactivities. Figure 4 illustrates an example of stability diagram for Japanese population for five viral strains. Different strains show different epitope set sizes for a given population. Major epidemic outbreaks (Supplementary Table 9) are reported for A/Japan/921/2009 and A/Mexico/4486/2009 strains, which correlate well with the least size of the epitope set (all data in FluTope) indicating that these strains exhibit least number of epitopes for these alleles seen in the given population and hence show poor CTL responses. The number of clusters representing response-types are seen to reduce dramatically for epidemic strains, while they are reasonably robust for all other strains (all data in FluTope).

Figure 4.

Influence diagram depicting cluster stability upon strain variation. The leftmost panel indicates strain diversity with the size of the circle rendered proportional to the number of epitopes it has. They are clustered based on the extent of commonality in their epitope sets. Distribution of HLA alleles that can recognize the epitope pool is indicated in the histogram where the number of epitopes a given allele can recognize is shown as the frequency. Individuals in a given ethnic group are grouped into non-overlapping clusters (see Methods) on the basis of the number of epitopes they recognize by their HLA genotypes. The number of clusters vary for each strain as the number of epitopes vary, which is shown in the right panel. Thus, in a given row, information about CD8⁺ antigenicity from a given strain (left) and their inter-relatedness, the distribution of HLA alleles that can recognize them (middle) and the number of response-types (people clusters) in a given ethnic group, the relative sizes of each response group (number of people in that group) (right panel). Lines connecting the response groups between strains indicate the stability of the cluster based on the number of common individuals in the group (which is based on the extent of commonality in the epitope pool for that group). Light grey lines indicate shared epitopes between different response groups as strains diverge. Strains are ordered on the basis of their similarity to each other in terms of the epitope pools and variation.

Figure 5 illustrates a 3D ranked plot of variation of total CTL response for 59 different populations for 45 selected strains. Total response is seen to vary from high to low across strains and populations, which is clearly poor for some ethnic groups and some strains, suggesting that some populations are strong CTL responders, whereas others are not, at least for the set of strains studied here. African nations are examples of the former while Chinese and Vietnamese are examples of the latter. Likewise, variations in total response across strains is also clearly evident. Two observations emerge for epidemic strains: (a) in general the total response in the population is seen to be poor, and (b) such populations contain very few response-types for that strain, as a result of which there is more homogeneous but overall very poor total response (see Supplementary Figure 5).

Figure 5.

A three-dimensional plot indicating 59 different ethnic groups on one axis, 45 selected viral strains on the other axis and the total CTL response on the z axis (height of each bar). Each ethnic group response is plotted in a distinct colour. Only 45 out of the 186 strains are shown for clarity in the figure. These are obtained by uniform sampling from a ranked plot of all 186 strains' list. The plot is sorted on the total average response of a given strain across different populations. The first row corresponding to 45 strains is seen to have the least response by any population. Ethnic group ‘China Yunnan Province Bulang' in this set shows the poorest response to the strains studied while ‘Uganda Kampala' shows the highest response. The height of each bar indicating overall CTL response is based on the pool of epitopes in the strain that can be recognized by the set of HLA genotypes in that population grouped into response-types.

Based on overall response, we compute ranked lists of (a) major epitopes that can be recognized by one allele or another in a given population, (b) major alleles that contribute to the recognition in each ethnic group and (c) proteins or individual subunits that contain the largest number of epitopes that can be recognized by the largest number of alleles in a given population (Supplementary Tables 5–8). From this, we see that viral proteins PB1 and NP, alleles B*15:01, B*58:01, A*30:01, A*02:01 and A*32:01 are examples of major responders. Interestingly, PB1 and NP have been reported earlier to be the most antigenic proteins in ferrets.^{27, 28, 29}

As pure populations of an ethnic group does not reflect the real world accurately, we hypothetically reconstruct heterogeneous populations and studied the effect of heterogeneity on the total CTL response. Figure 6 illustrates the predicted response for randomly chosen combination of six ethnic groups to the same strain (results for different combinations provided in FluTope). An increase in response-types and non-linearity in extent of response is clearly evident with increasing heterogeneity. Some combinations are also seen to confer more response than others. Overall, situations of very poor response as in the case of epidemics can be avoided in heterogeneous populations, hypothetically amounting to inducing herd immunity naturally.

Figure 6.

Barycentric plots illustrating the effect of heterogeneity on total recognition response to IFV. Seven ethnic groups have been considered. In each plot, vertices represent recognition response (red: strong , blue: weak) of a pure ethnic group. Each cell represents response of a particular HLA distribution obtained by linear combination of different pure ethnic groups to varying extents such that the centre of the plot is a well-mixed population with equal contributions from all ethnic groups in terms of the HLA distributions while the outermost grid at each vertex indicates response from the pure ethnic groups.

Discussion

HLA genetic heterogeneity has been well addressed in literature, which has resulted in many insights about the complex evolution, including effect of balancing selection, influence of demographic factors and past human migrations.³⁰ For several diseases, specific HLA alleles have been associated with increased or decreased susceptibilities.^{12, 14} However, little is known about the effect of HLA heterogeneity in a population as a whole on susceptibility to infectious diseases, such as influenza.

Many studies in literature consider one HLA allele at a time, somewhat independent of the combinations they exist in. As the entire HLA genotype in an individual will make an impact in recognizing a given pathogen, here we consider each genotype as an integrated unit and estimate its response to a given pathogen. Cross-reactivity between HLA alleles and epitopes make one-to-many and many-to-one associations between individuals or HLA genotypes and proteins in the IFV, making it difficult to correlate susceptibility with individual alleles. This problem is overcome by our approach, which, based on molecular systems data of hundreds of viral strains together with exhaustive reconstruction of HLA genotypes for different populations, provides global perspectives of how individuals ‘see' the pathogen. Our analysis shows that whole populations can be grouped into only a few response-types, presenting a significant conceptual advance as compared with considering single alleles individually. Several insights are obtained from this study: (a) total response to the epidemic strains is generally poor, due to both few epitopes and low responder phenotypes, (b) grouping into response-types is strain-specific, (c) only a few alleles possibly contribute to CD8⁺ responses for IFV, (d) some ethnic groups are more vulnerable than others for most strains of the virus as indicated in the ranked lists, (e) ethnic groups that have a high extent of allele polymorphism in their HLA genotypes consisting of the contributing alleles on the whole show higher response than ethnic groups that show high skewness in allele distributions, (f) on an average variation in total response from a population across different strains is 10-fold higher than response variation of a given strain across ethnicities, and (g) finally, as populations get heterogeneous, such as due to combinations of ethnic groups, total response to the virus increases in general, thus proportionately decreasing chances of susceptibility. Increasing heterogeneity in populations is clearly seen to increase robustness in the pathogen recognition profile by substantially increasing overall recognition levels in a mixed population of different ethnicities. It seems plausible to understand how lack of heterogeneity in a population can lead to epidemics if their HLA genotypes do not contain the right alleles to recognize the pathogen, consistent with the general notion of the importance of heterogeneity.

It is possible that our results, to some extent, are influenced by some of the simplifying assumptions that have been necessary to carry out this work. These are: (a) only A, B and C HLA alleles are considered but not the non-classical alleles, (b) in an individual different alleles are considered to be equally important for recognizing a pathogen, provided suitable epitopes are available, and (c) influences of either CD4⁺ or B-cell responses or interaction with killer cells are not explicitly considered. Further, generating combinations of HLA genotypes is an approximation and has not considered selection pressures or any environmental triggers. The epitope set has been derived from predictions and hence depends on prediction accuracies. Although prediction accuracies are seen to be quite high, it is possible that there are a small number of false positives and also false negatives, especially for epitopes containing poorly characterized patterns.³¹ Selection of only the consensus predictions of epitopes, although greatly increases precision, comes at a cost of losing some epitopes that are predicted by one or two but not all three methods. Nevertheless, the omissions would form only a small fraction of the data used and are unlikely to affect the conclusions in any significant manner. In any case, the framework provided here, however, facilitates easy incorporation of such data, when it becomes available, which should be helpful in refining the analysis.

The analysis presented here provides a conceptual advance in understanding population-wide T-cell responses to IFV and hence disease susceptibilities. Pointers obtained from an analysis of this type have the potential to be useful in a clinical setting in several ways. If HLA genotype data of different populations and also the genome data of different viral strains become commonly available, it will be possible to explain differences between strains and between populations in terms of disease potential. For a given strain and a given population, lists of majorly contributing alleles in responder genotypes can be obtained and simultaneously also a ranked list of conserved epitopes, both useful for rational vaccine design. Assessment of responsiveness of a genotype naturally leads to prediction of disease susceptibility of an individual or a population to a given viral strain. Future possibilities using this approach include study of co-infections with multiple strains or even multiple viruses. Large-scale data analytics is indeed leading to a powerful paradigm shift in medicine, a shift from studying single molecules with a reductionist philosophy to the study of systems and populations as a whole, to get holistic perspectives of the systems' behaviour. Insights obtained from such models can ultimately translate into more rational strategies in clinical practice.

Methods

Nomenclature

HLA: refers to the human leukocyte antigen molecules that represent the major histocompatibility complex in humans. Different HLA alleles in this study represent different polymorphic forms of this molecule across A, B and C loci.

HLA genotype: refers to the set of six Class-1 HLA alleles, two each from A, B and C loci, contained in an individual.

Epitope: refers to a typical Class-1 T-lymphocyte antigen of nine amino acids length from one of the proteins of the IFV proteome.

HLA-pool: refers to the pool of all different HLA alleles considered in a given population.

Epitope set: refers to the pool of all epitopes present in the given viral strain that can be recognized by a HLA-pool.

Population: refers to a notional population of a given ethnic group of about one million individuals. Heterogeneous populations are hypothetical constructs consisting of combinations of HLA pools in the indicated proportions from different ethnic groups.

Response: refers to CTL response in an individual that would be expected by the binding and downstream action of the given epitope set to the HLA genotype. In populations, it refers to the expected effect from the binding of the epitope set to the HLA pool of a given population.

Epidemic: refers to widespread occurrence of disease in a population at a given time, as collated from cited literature.^{5, 32}

Mathematical notations

Let P represent the IFV proteome, consisting of various proteins, P={p₁, p₂,..., p_m} where m is the number of proteins in the H1N1 genome. Each protein contains multiple CD8⁺ epitopes, represented by E_i={e_i1, e_i2,...e_φ(i)}, where E_i is the epitope set for i^th protein. H represents the HLA pool, H={h₁, h₂, …h₃}, h_x represents the individual alleles. The HLA mediated antigen response is represented as a φ-function. .

We have used set symmetric distance (⊖), to measure distance between any two given set A and B given as . This distance measure is normalized between 0 and 1.

Genome analysis of the IFV and immunome definition

Genome sequence of IFV (H1N1) was obtained from UniprotKB.^{33, 34} CD8⁺ T-cell epitopes in the genome were identified by a consensus prediction method based on three independent methods available through the IEDB portal.³⁵ The methods compute a consensus rank for the three individual predictions based on (a) artificial neural network,²² (b) stabilizing matrix method²³ and (c) combinatorial peptide library-based method.²⁴ Those peptide segments that are identified as strong binders for any HLA Class-1 allele are considered as the set of epitopes. A peptide that binds to a HLA molecule with a predicted IC₅₀ of <50 nM is regarded as a strong binder. The same exercise is repeated for 186 different strains of IFV, and the set of epitopes from each of these are collected and further analysed. List of epidemic strains were obtained from Expasy¹⁸ and FluDB³⁶ (Supplementary Table 1).

Computing epitope-based distances and phylogenetic distances of pairs of IFV strains

Let represent set of viral proteins, where the number of distinct protein count is m. Protein sequence obtained from different strains are aligned using MUSCLE,³⁷ a k-mer based progressive alignment algorithm. Let l_j be the length of the j^th protein. represents the amino acids at l^th location, on the aligned sequence length, obtained from j^th protein from strain i. 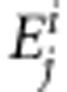represents the epitope sites in the j^th proteins from strain i. Therefore unigram set presenting the sequence j from strain i is and unigram presenting the epitopes' sequence in protein i is .

We measure the sequence distance in protein j from any two strains i₁ and i₂ and are given as κ(i₁, j)⊖κ(i₂, j). Similarly, the distance only in the epitope segments are given as κ_E(i₁, j)⊖κ_E(i₂, j).

As mutation rates at different sites are distinct, we used positional Shannon Entropy³⁸ to measure the extent of variation at any particular site. The measure of entropy for j^th protein at site l is given by , where AA represents the set of all possible amino acids and represents frequency of i^th amino acid at position l in protein j.

Reconstruction of HLA genotypes in a population

Distribution of HLA pool in a given population is given as ℰ. ℰ assigns a probability measure for every h_i. An individual will have three pairs of HLA genes (A, B and C loci, respectively).The probability of occurrence of HLA h_i, in a population is given as ℰ(h_i). Therefore Σ_iℰ(h_i)=1, over each group of HLA genes.

We assume the occurrence of HLA genes in an individual is an independent event, S_(i)={h_1(i),h_2(i),h_3(i),h_4(i),h_5(i),h_6(i)} represents six HLA genes present in i^th individual, which we refer to as HLA genotype. By independence assumption, the likelihood of an individual present in the population with HLA set S_(i) can be estimated as . As we consider a finite-sized population, we reject HLA genotypes with likelihood <1e⁻⁶. This approach is similar to the method used in IEDB population coverage analysis.³⁹

Distance between ethnic groups

Let ℰ_i and ℰ_j represent HLA genotype distributions of two ethnic groups, obtained by considering allele frequencies in the individual ethnic groups. The distance between two ethnic HLA distributions is given as

Comparison of total epitope pools between individuals within and across populations

Epitopes recognized by an individual in a given population is called epitope set, (S_(i))={e_ij ∀ φ(h_k,e_ij)=1, where h_k ∈S_(i)}. Thus individuals can be represented by the set of recognized epitopes in the pathogen recognition space. Let ={e_ij} be the epitope set for a given ethnic group ℰ and pathogen P. m is the number of pathogen proteins in the strain P. We represent an individual l in pathogen recognition space as X_l ∈ ^m ,where X_l={x_i}_i=1…m, x_i= #{e_ik ∀e_ik ∈ and {φ(h_u, e_ik)=1 ∀ h_u ∈ S_(l)}}.Therefore, in this vector representation, X_l each dimension represents recognition strength or the total number of epitopes of a given viral protein.

Response group and stability analysis

Individuals are further clustered into response-types ℛ={r₁, r₂…r_t}. Individuals of a given response-type are expected to recognize the pathogen in a similar fashion. ℛ partition the population space into non-overlapping classes, r_i∩r_j=Φ ∀ i≠j. The grouping into non-overlapping clusters were performed by Lloyd's K-mean clustering. The estimation for appropriate value t value is obtained using the Elbow method.⁴⁰

Given an ethnic HLA distribution ℰ, the population space remains the same. Response groups' partitioning of population space are determined by the epitope sets. Epitope sets vary with the viral strains. If P₁ and P₂ are two viral strains, giving rise to E₁ and E₂ epitope pool, restrained by the selected HLA alleles, present in ℰ. ℛ₁ and ℛ₂ are the response-type partitions. Γ is the map function, between two response-type partitions. Let, η₁ and η₂ represents the partitions sizes of ℛ₁ and ℛ₂, respectively. . Γ maps the response-type correspondences, by maximum overlap between the two partitions. Γ need not generate one to one map, as in many cases the response-types merges or splits into subtypes on changing the pathogenic strains. Under such situations, it generates one to many or many to one maps.

We define a distance between two partitions as .

Similarly, the distance between the viral strains are given by their epitope pools as d(E_1,E₂)=E₁⊖E₂. The stability of the cluster is defined as .

Generating hypothetical mixed population model

ℰ₁ and ℰ₂ are two given HLA distributions, pertaining to two pure ethnic groups. A drift in population HLA distribution from one pure profile to another pure profile can be modelled by a simple affine combination, ℰ_1→2(λ)=λℰ₁+(1−λ)ℰ₂ , where λ∈(0, 1) is a parameter capturing the extent of genetic drift. Drift between multiple HLA profile can similarly be modelled as Σ_jλ_jℰ_j, such that Σ_jλ_j=1. For each value of λ, resulting in HLA distribution ℰ(λ), it generates a specific population genotype distribution.

The authors declare no conflict of interest.