A generalization of the Π-theorem and dimensional analysis

Abstract

This article introduces a generalization of dimensional analysis and its corollary, the Π-theorem, to the class of problems in which some of the quantities that define the problem have fixed values in all the cases that are of interest. The procedure can reduce the number of dimensionless similarity variables beyond the prediction of Buckingham's theorem. The generalized Π-theorem tells when and how large a reduction is attainable.

Dimensional analysis is a method for reducing complex physical problems to their simplest (most economical) forms prior to quantitative analysis or experimental investigation (1). Its use in science and engineering is ubiquitous. Applications are many, including astrophysics, electromagnetic theory, radiation, aerodynamics, ship design, heat and mass transfer, mechanics of elastic and plastic structures, explosions, chemical reactions and processing (2–7), simulation of nuclear reactor accidents (8–10), biology (11, 12), and even economics (13). Dimensional analysis reduces a problem's degrees of freedom to the minimum and thus suggests the most economical scaling laws. It can be particularly useful in exploratory investigations of novel phenomena for which the equations and boundary conditions have not yet been fully articulated.

Buckingham's Π-theorem (14) states that if a quantity Q₀ (a dependent variable) is completely determined by the values of a set of n independent quantities, of which a number k form a complete, dimensionally independent subset, then a suitable dimensionless Q₀ will be completely determined by n – k dimensionless similarity parameters. In other words, the number of independent variables (the problem's inherent “degrees of freedom”) may be reduced by the number k. The value of k and the forms of the similarity parameters emerge from dimensional analysis.

There exist, however, numerous instances in which some of the independent variables that define Q₀ have essentially invariant values in all of the cases that are under consideration. The question then arises: does this lead to a further simplification, that is, to an additional reduction in the problem's inherent degrees of freedom? If so, how is the process of dimensional analysis, and with it the Π-theorem, altered?

Simply omitting the quantities that have fixed values and performing dimensional analysis on the rest will not answer this question. Dimensional analysis must be based on a complete set of independent quantities that define the quantity of interest (1), that is, all quantities with values that may affect the quantity of interest must be included regardless of whether some have invariant values in the cases that are under consideration. Omitting even one relevant independent variable can fatally damage the analysis.

In what follows, we show that the Π-theorem takes the following form.

Generalized Π-Theorem. If a quantity Q₀ is completely determined by a set of n independent quantities, of which k are dimensionally independent, and if n_F of the independent quantities have fixed values in all the cases being considered, a number k_F of which are dimensionally independent, then a suitable dimensionless Q₀ will be completely determined by (n – k) – (n_F – k_F) dimensionless similarity parameters, where k_F ≤ n_F.

In other words, the fact that a number n_F of the independent quantities have fixed values further reduces the number of independent similarity parameters by (n_F – k_F) ≥ 0. This theorem is a generalization of Buckingham's Π-theorem and reduces to it when n_F = 0.

The generalized Π-theorem emerges from the following procedure. Suppose we are interested in a quantity Q₀ (a dependent variable) that is completely determined by the values of n independent quantities Q_i, of which n_F are held at fixed values in all the cases that concern us. Let the independent quantities that define the problem be the first (n – n_F)of Q_i, and designate by F_i the n_F quantities that have fixed values. Thus

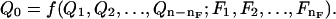[1]

Step 1: Choose a complete, dimensionally independent subset of the set F_i with invariant values. Let these be the first k_F of the fixed set k_F ≤ n_F. Using the variables in this subset, nondimensionalize the remaining (n_F – k_F) fixed quantities and write the relationship (Eq. 1) in the alternative form

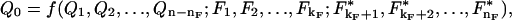[2]

where the asterisks indicate dimensionless quantities that are invariant in the cases that concern us. For cases in which the asterisked quantities have invariant values, we may write Eq. 2 as

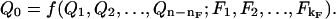[3]

The value of Q₀ is thus completely determined by a reduced set of (n – n_F + k_F) independent quantities, comprising those that are not fixed plus the dimensionally independent subset of the invariant quantities.

Step 2: Now perform dimensional analysis on the relationship 3. Select from the set of (n – n_F + k_F) independent quantities in Eq. 3 a complete, dimensionally independent subset of k quantities. Let this subset be the first k of the quantities. Because Eq. 3 contains all the variable independent quantities, plus the dimensionally independent subset of the invariant independent variables, the subset we thus obtain is also a complete, dimensionally independent subset for the whole original set of n quantities.

According to Eq. 3, Q₀ depends on (n – n_F + k_F) independent variables, of which k are dimensionally independent. Dimensional analysis thus yields the result

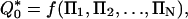[4]

where 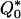is a dimensionless Q₀,

[5]

and n_F – k_F ≥ 0. This proves the generalized Π-theorem. The proof follows not so much from mathematics as from constraints that result from the fundamental properties of physical quantities and physical equations (1).

The theorem states the following: The fact that a number n_F of the independent quantities always have the same fixed values in a particular phenomenon reduces the number of independent similarity parameters in that problem by (n_F – k_F), where n_F ≥ k_F. This theorem is a generalization of Buckingham's Π-theorem and reduces to it when n_F = 0.

Example 1: As a very simple example, consider the similarity law for the hydrodynamic drag force D on a fully submerged, very long, neutrally buoyant cable being dragged behind a boat. Basic fluid mechanics tells us that, barring surface roughness on the cable, the drag force should be completely determined by the cable's length L and diameter d, the boat's speed V, and the water's density ρ and viscosity μ. Three of these five quantities are dimensionally independent, and Buckingham's Π-theorem tells us that an appropriately defined dimensionless drag is a function of n – k = 2 dimensionless similarity parameters. Dimensional analysis shows that this relation can be written

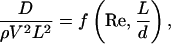[6]

where Re = ρVL/μ is a Reynolds number and L/d defines the cable's aspect ratio. Eq. 6 is a general similarity relationship for the cable-towing problem as stated.

If, however, ρ and μ have essentially the same values in all the applications that are of interest (as may be expected in this problem), the number of independent quantities that actually vary from case to case is really not five but three. Does this lead to a further reduction of similarity parameters? Simply omitting the invariant quantities and performing dimensional analysis on the rest will not answer this question. Were we to omit the density and viscosity, the relationship D = f(L, d, V, ρ, μ) would reduce to D = f(L, d, V), which is clearly incorrect because the relationship is not dimensionally homogeneous: the dimension of D on the left (a force) cannot be written in terms of just length and velocity.

The generalized Π-theorem gives the answer: the invariance of ρ and μ brings about an additional reduction of (n_F – k_F) = 2 – 2 = 0 dimensionless parameters; that is, no further reduction in degrees of freedom (dimensionless parameters) is obtained in this case. This result is by no means self-evident.

A further reduction in independent variables (beyond the prediction of Buckingham's Π-theorem) can be achieved only when n_F > k_F, that is, when not all independent quantities are dimensionally independent.

Example 2: As an example for which invariant variables do lead to a reduction of the problem's degrees of freedom, consider the steady-state heat transfer rate Q from a hot sphere in an infinite ambient fluid at uniform pressure and temperature in a gravitational field. The heat flux Q is completely determined by eight quantities,

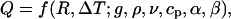[7]

where R is the sphere's radius, ΔT is its surface temperature relative to the ambient atmosphere, g is the acceleration of gravity, and the remaining five quantities are fluid properties: density ρ, kinematic viscosity ν, specific heat c_p, thermal diffusivity α, and coefficient of thermal expansion β. Buckingham's Π-theorem tells us that a dimensionless Q is a function of n – k = 8 – 4 = 4 dimensionless independent quantities. One way of writing this relationship is

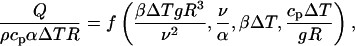[8]

where the quantity on the left is a (modified) Nusselt number and the first two on the right are the Grashof and Prandtl numbers, respectively.

If, however, we are interested only in spheres in a particular fluid, R and ΔT may take on arbitrary values whereas the values of g and the five fluid properties in Eq. 7 remain invariant. For this case, the generalized Π-theorem yields the result that a suitably chosen dimensionless Q will depend on (n – k) – (n_F – k_F) = (8 – 4) – (6 – 4) = 2 dimensionless parameters. The forms of the two parameters emerge from the procedure outlined in Eqs. 1–5 and the accompanying text. For the present case, with ρ, ν, β, and g selected as the dimensionally independent subset of the fixed quantities, Eq. 3 reads

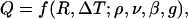[9]

and dimensional analysis of Eq. 9 gives

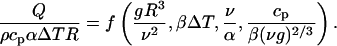[10]

The last two parameters in Eq. 10, composed now entirely of invariant quantities, have fixed values. This leads to the simplification that, for all spheres in the same fluid,

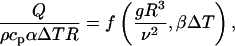[11]

which is in accord with the generalized Π-theorem. The number of Π-groups has been reduced from Buckingham's four to the generalized theorem's two.

We note that in the Boussinesq limit (βΔT → 0), where β and g appear not separately but only as the product βg, Eq. 11 simplifies further to

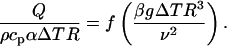[12]

In summary, we have introduced a Π-theorem and a formal dimensional analysis procedure for problems in which some of the independent quantities that specify the problem have fixed values in all the cases that are of interest. We show when and how some such problems can be simplified further, that is, when their Π-groups can be reduced below the number predicted by Buckingham's theorem.