Abstract
Many of the large structures of the cell, such as the cytoskeleton, are assembled and maintained far from equilibrium. We study the stabilities of various structures for a simple model of such a far-from-equilibrium organized assembly in which spherical particles move under the influence of attached motors. From the variational solutions of the many-body master equation for Brownian motion with motorized kicking we obtain a closed equation for the order parameter of localization. Thus, we obtain the transition criterion for localization and stability limits for the crystalline phase and frozen amorphous structures of motorized particles. The theory also allows an estimate of nonequilibrium effective temperatures characterizing the response and fluctuations of motorized asemblies.
Assemblies of molecular-size particles are seldom far from equilibrium owing to the relative strength of the thermal buffeting inherent at this scale. As we consider assemblies of larger and larger particles, the thermal forces become less capable of moving and reorganizing such assemblies. At the size scale of biological cells, objects are not rearranged just by equilibrium thermal forces but are moved about by motors or by polymerization processes that use and dissipate chemical energy (1). What are the rules that govern the formation of periodically ordered or permanently organized assemblies at this scale? Does the far-from-equilibrium character of the fluctuating forces due to motors and polymer assembly change the relative stability of different colloidal phases? These problems are not unique for intracellular dynamics but belong to an emerging family of nonequilibrium assembly problems ranging from driven particles (2), swarms (3), and jamming (4, 5) to microscopic pattern formation and mesoscopic self-organization (6, 7).
Motivated by these considerations, which may be relevant for the dynamics of the cytoskeleton (1, 8) and other far-from-equilibrium aggregation systems, we study a simple motorized version of the standard hard-sphere fluid often used to model colloids (9). Both motors and nonequilibrium polymer assemblies can convert the chemical energy of high-energy phosphate hydrolysis to mechanical motions, which one would ordinarily think would “stir” and hence destabilize ordered structures. We will show these systems, in some circumstances, may have an enlarged range of stability relative to those with purely thermal motions.
We adopt a stochastic description of the motions of a collection of motorized particles. The overdamped Langevin dynamics is 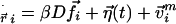 . Here,
. Here, 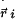 is the position of the ith particle,
is the position of the ith particle, 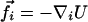 is the mechanical force that comes from the usual potential
is the mechanical force that comes from the usual potential 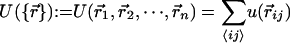 among particles. The random variable
among particles. The random variable 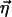 vanishes on average and is Gaussian with
vanishes on average and is Gaussian with 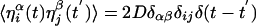 . The motor term
. The motor term 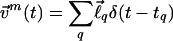 is a time series of shot-noise-like kicks. Its properties depend on the underlying biochemical mechanism of the motors. The stochastic nature of the motors also leads to a master equation description (10, 11) for the dynamics of the probability distribution function Ψ of the particle configurations,
is a time series of shot-noise-like kicks. Its properties depend on the underlying biochemical mechanism of the motors. The stochastic nature of the motors also leads to a master equation description (10, 11) for the dynamics of the probability distribution function Ψ of the particle configurations,
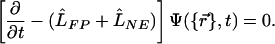 |
[1] |
Here 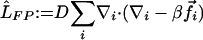 is the Fokker–Planck operator. An integral operator
is the Fokker–Planck operator. An integral operator 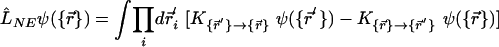 summarizes the nonequilibrium kicking effect of the motors.
summarizes the nonequilibrium kicking effect of the motors.
The motors are firmly built in the particles. They work by consuming chemical energy sources, like ATP. In a single chemical reaction event, the motor makes a power stroke (which induces a discrete conformation change) that moves the particle by a distance of 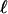 in the direction n̂. Motor kicking can be modeled as a two-step stochastic process: step 1, the energy source binds to the motor; and step 2, the reaction ensues and the resulting conformational change makes a power stroke. The rate of the first step, k1, depends on the energy source concentration, whereas the rate of the second step, k2, depends on the coupling between the structural rearrangement and the external forces,
in the direction n̂. Motor kicking can be modeled as a two-step stochastic process: step 1, the energy source binds to the motor; and step 2, the reaction ensues and the resulting conformational change makes a power stroke. The rate of the first step, k1, depends on the energy source concentration, whereas the rate of the second step, k2, depends on the coupling between the structural rearrangement and the external forces, 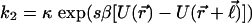 , i.e., motors slow down when they work against mechanical obstacles. Such slowing has been demonstrated in microtubules (12, 13). s, the coupling strength, measures the relative location of the transition state for the power-stroke step and ranges from 0 to 1. At the limit s → 1 we have a susceptible motor, whereas s → 0 corresponds to an adamant motor. We use these names in the sense that an adamant motor is not sensitive to its thermal-mechanical environment, so each power stroke uses and wastes a lot of energy; in contrast, a susceptible motor saves energy running faster downhill (free energy) and slower uphill.
, i.e., motors slow down when they work against mechanical obstacles. Such slowing has been demonstrated in microtubules (12, 13). s, the coupling strength, measures the relative location of the transition state for the power-stroke step and ranges from 0 to 1. At the limit s → 1 we have a susceptible motor, whereas s → 0 corresponds to an adamant motor. We use these names in the sense that an adamant motor is not sensitive to its thermal-mechanical environment, so each power stroke uses and wastes a lot of energy; in contrast, a susceptible motor saves energy running faster downhill (free energy) and slower uphill.
We assumed that step 2 is the bottleneck of kinetics, i.e., the overall rate k ≈ k2 ≪ k1. To make our model suitable for a variety of situations, we specify different variables, s and s′, for the degree of susceptibility for going uphill and downhill, respectively. Thus, 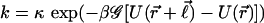 with a switch function
with a switch function 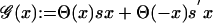 . Here Θ is the Heaviside function. Thus, the overall temporal statistics of the kicks is position-dependent Poisson distribution.
. Here Θ is the Heaviside function. Thus, the overall temporal statistics of the kicks is position-dependent Poisson distribution.
The kicking direction n̂(t) fluctuates on the timescale τ of the particle tumbling. We will study explicitly two extremes: the isotropic kicking case when τ is very small and the persistent kicking case when τ is very large compared with κ–1, i.e., each motor always kicks in a predefined direction. The direction of persistence will be assumed to vary randomly from particle to particle.
To solve the dynamics of probability distributions, researchers often pose the problem as the solution of a variational problem. Due to the L̂NE part of Eq. 1, we cannot perform the usual transformations of the left and right state vector to make L̂ hermitian (10). For this type of problem, nevertheless, we can obtain the solution of the many-particle master equation by using nonhermitian variational methods as described by Eyink (14) and Eyink and Alexander (15) or by using the squared (therefore hermitianized) operator L̂†L̂ (e.g., ref. 10, p. 159).
Eyink's nonhermitian variational formulation is similar to the Rayleigh–Ritz method in ordinary quantum mechanics but uses independent left and right state vectors. For isotropic kicking, we start with a Jastrow-like trial function
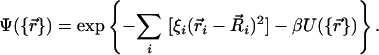 |
[2] |
Similar to the quantum hard spheres (16), such a trial function avoids any singularities of L̂FP arising from the hard-sphere potentials uij(rij) between particles i and j used in this study. For simplicity, we set 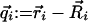 and a uniform ξi := ξ. The nonhermitian variational method implies for steady states that the second moment of
and a uniform ξi := ξ. The nonhermitian variational method implies for steady states that the second moment of 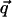 satisfies the moment closure (17) equation:
satisfies the moment closure (17) equation:
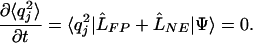 |
[3] |
To effectively evaluate Eq. 3, we need to simplify the many-body integration 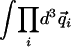 involving exp
involving exp 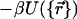 . Here, we use cluster expansion (18, 19) to render the many-body Boltzmann factor a product of effective single-body terms by averaging over the neighbors' fluctuations. We thus have e–βU = Πie–βui ≈ Πie–βûi. Here, the original
. Here, we use cluster expansion (18, 19) to render the many-body Boltzmann factor a product of effective single-body terms by averaging over the neighbors' fluctuations. We thus have e–βU = Πie–βui ≈ Πie–βûi. Here, the original 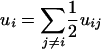 depends on the many-body configuration, whereas ûi depends on
depends on the many-body configuration, whereas ûi depends on 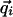 (and constant {
(and constant {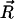 }) only. In fact, we keep it to the harmonic order for consistency, i.e.,
}) only. In fact, we keep it to the harmonic order for consistency, i.e., 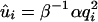 . Here, α is the effective spring constant from the mechanical feedback from neighbors. α depends on its neighbors' overall fluctuations controlled by
. Here, α is the effective spring constant from the mechanical feedback from neighbors. α depends on its neighbors' overall fluctuations controlled by 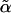 and their mean position {
and their mean position {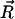 }. In turn, the positions of the neighbors are controlled by the lattice spacing for crystals or radial distribution functions for glasses and ultimately by the nature of the structure and the particle density n. That is, for fcc lattice, we have
}. In turn, the positions of the neighbors are controlled by the lattice spacing for crystals or radial distribution functions for glasses and ultimately by the nature of the structure and the particle density n. That is, for fcc lattice, we have 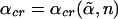 as the eigenvalues of the Hessian matrix constructed from the effective potential
as the eigenvalues of the Hessian matrix constructed from the effective potential 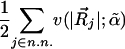 . Here,
. Here, 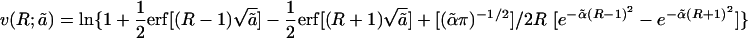 and the sum of
and the sum of 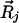 is over the 12 nearest-neighbor positions of the origin of a fcc lattice
is over the 12 nearest-neighbor positions of the origin of a fcc lattice
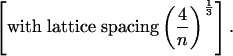 |
For glasses (20, 21), we replace the summation over discrete crystalline neighbor location with a mean-field average over the first shell of the pair-distribution function of the hard-sphere liquids, 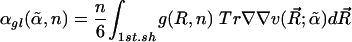 . For numerical work, we take g(R, n) as the Verlet and Weis's corrected radial-distribution function (22).
. For numerical work, we take g(R, n) as the Verlet and Weis's corrected radial-distribution function (22).
After some calculations, we obtain the steady-state many-body probability-distribution function as a product of localized Gaussians of the form 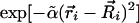 with
with 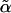 , the final localization strength, satisfying two equations:
, the final localization strength, satisfying two equations:
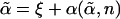 |
[4] |
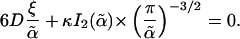 |
[5] |
The first and second terms of Eq. 5 come from 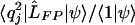 and
and 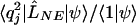 , respectively. The integral
, respectively. The integral 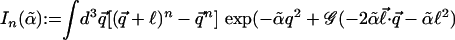 can be further expressed as explicit but complicated analytical formulas with incomplete Gamma functions. Thus, using Eq. 4 in Eq. 5, we finally derive the order parameter for localization,
can be further expressed as explicit but complicated analytical formulas with incomplete Gamma functions. Thus, using Eq. 4 in Eq. 5, we finally derive the order parameter for localization, 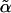 , in a closed form with parameters
, in a closed form with parameters 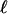 , D, κ, s, s′, and n. When
, D, κ, s, s′, and n. When 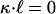 , we have ξ = 0 and the equilibrium equation
, we have ξ = 0 and the equilibrium equation 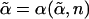 , which returns to the self-consistent phonon solution (18–21, 23). A nonzero solution
, which returns to the self-consistent phonon solution (18–21, 23). A nonzero solution 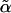 of Eq. 5 is only obtained at sufficiently high density, i.e., for n > nc. For low density, the system cannot support stable localized vibrations and is in the fluid phase with
of Eq. 5 is only obtained at sufficiently high density, i.e., for n > nc. For low density, the system cannot support stable localized vibrations and is in the fluid phase with 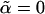 . An instability density nc separates these two phases. This phase transition is first-order-like, characterized by a discontinuous jump of
. An instability density nc separates these two phases. This phase transition is first-order-like, characterized by a discontinuous jump of 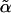 .
.
We calculated nc as a function of two independent parameters, s and s′, nc(s, s′) for various κ, D, and 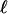 . An important dimensionless ratio
. An important dimensionless ratio 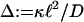 measures the strength of chemical versus thermal noise. For an actin polymer solution (1), we can relate the effective kicking rate to the speed of nonequilibrium polymerization. Here,
measures the strength of chemical versus thermal noise. For an actin polymer solution (1), we can relate the effective kicking rate to the speed of nonequilibrium polymerization. Here, 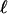 is the monomer size 0.01 μm (μ = 10–6). The treadmill concentration is ctr = 0.17 μM. The chemical reaction rates of the barbed and pointed ends of actin are k+ = 11.6 μM–1·s–1 and k– = 1.3 μM–1·s–1, respectively. The diffusion constants of rod are given by the Kirkwood equation (24). This equation relates the diffusion to solvent viscosity, ηs, and gives the translational diffusion constants: D∥ = kBT ln(L/d)/(2πηsL) and D⊥ = D∥/2. With the typical length of the actin filaments, L ≈ 20 μm, and typical width, d of ≈0.015 μm, an estimate of the hydrodynamic diffusion along the rod gives D∥ ≈ 0.1 μm2·s–1. Thus, for a dilute solution of typical actin filaments, Δ ≈ 10–3–10–2. However, in vivo, the actin monomer concentration is kept much higher than ctr (with the help of capping proteins that prevent actin filaments from growing longer). Also, the viscosity of the cell medium is higher than ηs of pure water because of the presence of other macromolecular components. These components lower the effective diffusion constant and raise the value of κ; therefore, they could push Δ above 1. The limit Δ≫ 1 corresponds to entirely motorized motion.
is the monomer size 0.01 μm (μ = 10–6). The treadmill concentration is ctr = 0.17 μM. The chemical reaction rates of the barbed and pointed ends of actin are k+ = 11.6 μM–1·s–1 and k– = 1.3 μM–1·s–1, respectively. The diffusion constants of rod are given by the Kirkwood equation (24). This equation relates the diffusion to solvent viscosity, ηs, and gives the translational diffusion constants: D∥ = kBT ln(L/d)/(2πηsL) and D⊥ = D∥/2. With the typical length of the actin filaments, L ≈ 20 μm, and typical width, d of ≈0.015 μm, an estimate of the hydrodynamic diffusion along the rod gives D∥ ≈ 0.1 μm2·s–1. Thus, for a dilute solution of typical actin filaments, Δ ≈ 10–3–10–2. However, in vivo, the actin monomer concentration is kept much higher than ctr (with the help of capping proteins that prevent actin filaments from growing longer). Also, the viscosity of the cell medium is higher than ηs of pure water because of the presence of other macromolecular components. These components lower the effective diffusion constant and raise the value of κ; therefore, they could push Δ above 1. The limit Δ≫ 1 corresponds to entirely motorized motion.
The resulting densities nc(s, s′) are shown in Figs. 1 and 2. Fig. 1 shows some 1D plots that come from vertical slices of nc for several special cases. Fig. 2 shows the 2D view of the critical surfaces nc for variety of parameters. For the case shown with Δ ≫ 1, α(n) (which is the only n-dependent part of 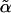 ) drops to zero, but we still have a nonzero solution
) drops to zero, but we still have a nonzero solution 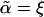 for a corner of (s, s′) space. In the opposite corner we stopped searching for solutions when nc approached the maximum packing density
for a corner of (s, s′) space. In the opposite corner we stopped searching for solutions when nc approached the maximum packing density 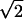 . Thus we have three distinct regions.
. Thus we have three distinct regions.
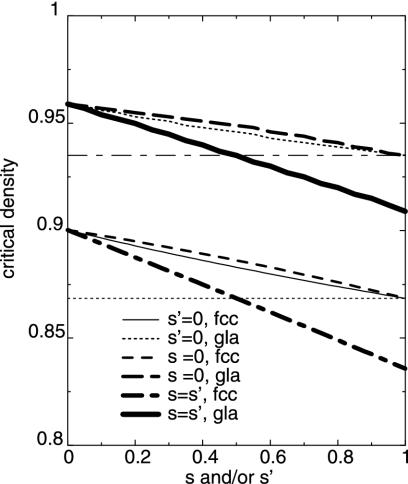
Fig. 1.
The instability density of the motorized fcc lattice and the glass as functions of the coupling parameters for these cases: (i) s = 0; (ii) s′ = 0; and (iii) s = s′. In these plots 3D isotropic kicking occurs with D = 0.1, κ = 10, and 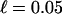 . Therefore
. Therefore 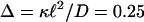 . The two horizontal lines are the corresponding equilibrium (
. The two horizontal lines are the corresponding equilibrium (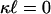 ) cases.
) cases.
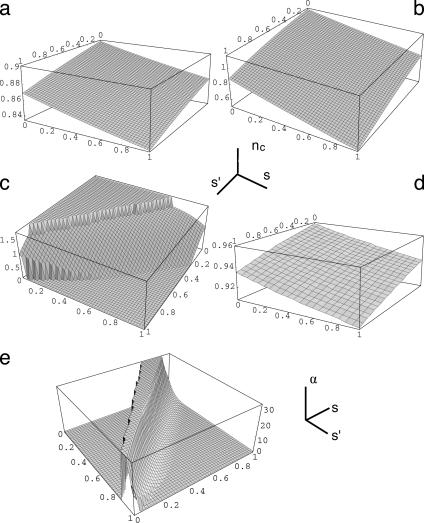
Fig. 2.
The instability densities nc(s, s′) surface are shown for motorized fcc lattice cases, Δ = 0.25 (a), Δ = 2.5 (b), Δ = 25 (c), and a glass case Δ = 0.25 (d) for the 3D isotropic kicking with κ = 10 and 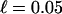 . The corresponding surface for the Lindemann parameter αc(s, s′) of c is shown in e.
. The corresponding surface for the Lindemann parameter αc(s, s′) of c is shown in e.
As seen from these figures, kicking noise does not always destabilize the structures. Instead, the localized phases have an enlarged stability range when s + s′ > 1. When s′ = 1 – s, the same stability limits are obtained as in the equilibrium thermodynamic theory. Both the frozen disordered glass and the ordered fcc lattice can be stabilized by kicking motors. The motor effects on the fcc lattice are more pronounced. The fcc phase has a larger stable region than the glass.
Besides the Eyink variational method, we also calculated 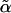 , α, and therefore nc by another method. From the mechanical feedback procedure, we first obtain the mapping from a hardsphere environment to an effective harmonic potential
, α, and therefore nc by another method. From the mechanical feedback procedure, we first obtain the mapping from a hardsphere environment to an effective harmonic potential 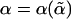 . Here, α depends on the steady-state probability distribution of its neighbors. Conversely,
. Here, α depends on the steady-state probability distribution of its neighbors. Conversely, 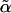 can be viewed as the final effective spring constant of a kicking particle in an harmonic potential of α. Next, we numerically solve
can be viewed as the final effective spring constant of a kicking particle in an harmonic potential of α. Next, we numerically solve 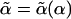 from single-particle master equations by using a variational method based on the square hermitianized operator l̂†l̂ with single-particle trial functions. The two sets of operations are iterated to obtain a pair of self-consistent results (
from single-particle master equations by using a variational method based on the square hermitianized operator l̂†l̂ with single-particle trial functions. The two sets of operations are iterated to obtain a pair of self-consistent results (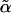 , α). The critical density predicted by this self-consistent squared hermitian variational method agrees very well with results from the nonhermitian variational method. The difference of instability density is <0.1% when Δ < 1. The corresponding critical
, α). The critical density predicted by this self-consistent squared hermitian variational method agrees very well with results from the nonhermitian variational method. The difference of instability density is <0.1% when Δ < 1. The corresponding critical 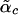 is also similar. The two methods do give different results when Δ ≫ 1.
is also similar. The two methods do give different results when Δ ≫ 1.
For persistent kicking, the trial functions have to be modified. Each localized particle now has a distribution of locations of the form 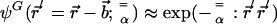 . Here,
. Here, 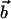 is an off-center shift vector parallel to n̂. We must consider the effects of the variational parameter b on α along with the direct changes of
is an off-center shift vector parallel to n̂. We must consider the effects of the variational parameter b on α along with the direct changes of 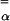 . The additional decrease of α arises from the distortion of the structures caused by always kicking in the same directions. We model the distortion effect of persistent kicking on the pair distributions by replacing each initial position with a dispersed distribution. For the crystal, this means the initial neighboring position of
. The additional decrease of α arises from the distortion of the structures caused by always kicking in the same directions. We model the distortion effect of persistent kicking on the pair distributions by replacing each initial position with a dispersed distribution. For the crystal, this means the initial neighboring position of 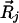 is replaced by an average over positions
is replaced by an average over positions 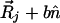 with n̂ is an arbitrary unit direction. Likewise, the radial distribution function of the glass case is broadened from the initial
with n̂ is an arbitrary unit direction. Likewise, the radial distribution function of the glass case is broadened from the initial 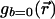 to
to
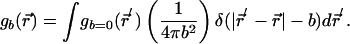 |
In this case, an additional normalization of the first peak enforces the condition g = 0 for r < 1.
For persistent kicking, s has similar effects on 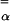 , as were found for the isotropic case. The shift b agrees quite well (within several percentages for the practical range of parameters) with the estimate
, as were found for the isotropic case. The shift b agrees quite well (within several percentages for the practical range of parameters) with the estimate 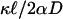 based on a small
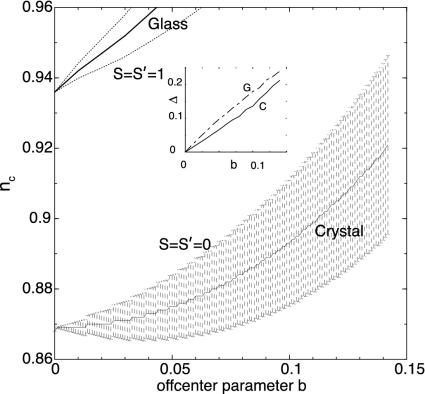
based on a small 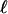 expansion of the master equation. The resulting displacement amplitude b is large enough to distort the stable structure so that any increased stability that may arise from kicking (if any) is now very modest, as shown in Fig. 3.
expansion of the master equation. The resulting displacement amplitude b is large enough to distort the stable structure so that any increased stability that may arise from kicking (if any) is now very modest, as shown in Fig. 3.
Fig. 3.
The instability density of the persistent motorized fcc lattice and the glass as parametric functions of b, which depends on Δ. Here, 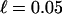 . Both are bounded with middle line s + s′ = 1, with upper- and lower-bound s = s′ = 0 and 1, respectively.
. Both are bounded with middle line s + s′ = 1, with upper- and lower-bound s = s′ = 0 and 1, respectively.
Since the kicking noise enlarges the stability region in the isotropic case with s + s′ > 1, we wondered whether susceptible kicking may sometimes actually decrease the effective temperature of this nonequilibrium system. An effective temperature can be defined by the fluctuation–dissipation relation even for far-from-equilibrium situations like the motorized crystal (25). The ratio of the thermal temperature to the effective temperature is also called the fluctuation-dissipation theorem violation factor. The effective temperature can be computed by comparing the fluctuations of a motorized particle with its response to an external force. Teff depends on the frequency or time duration, the absolute time (in the case of an aging system), and even possibly on the choice of the observable itself. To compute the needed time-dependent quantities, we solve the time-dependent master equations for nonhermitian operators, again using a Gaussian ansatz characterized now with dynamic first and second moments.
For illustration, we carry out the analysis of the dynamics for the 1D symmetric case in a harmonic potential αx2 with s = s′. Thus, 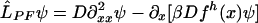 and
and
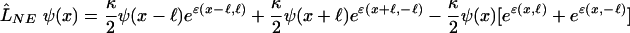 |
with 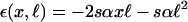 . The parameters in the Gaussian ansatz
. The parameters in the Gaussian ansatz
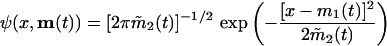 |
with 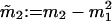 and mi = 〈xi〉ψ satisfy the time-dependent dynamics described by a set of differential equations with
and mi = 〈xi〉ψ satisfy the time-dependent dynamics described by a set of differential equations with 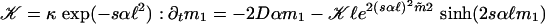 and
and 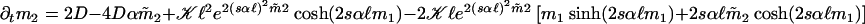 .
.
To obtain the Green's function, G(x, x′; t, 0), m1(t), and m2(t) must satisfy the equations above with the initial conditions m1(0) = x′ and m2(0) = x′2. We denote m(t; x′) for this pair solution of the differential equation. Green's function yields the correlations and responses. The correlation functions are given by C(t) = ∫ dx′x′m1(t; x′)ψ(x′, m*). Here, * donates the steady-state value, and the response to a pulse is 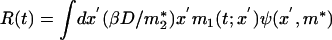 . Combining these yields the effective temperature:
. Combining these yields the effective temperature:
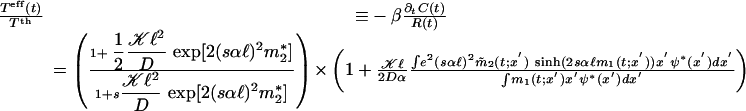 |
[6] |
Thus, we see that fluctuation-dissipation theorem violation is a product of two ratios. One ratio is the steady-state variance compared with the corresponding thermal equilibrium value. The other ratio depends on the rate at which the system reaches the steady state, i.e., the larger the variance and the faster the dynamics, the hotter the system and vice versa. Compared with the cases without kicking, susceptible motors yield a smaller variance, whereas, on the other hand, they relax faster. In the short time limit, m1(t;x′) → x′ and m̃2(t;x′) → 0, and the second ratio becomes
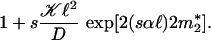 |
For long times, m1 → 0, 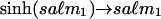 , and
, and 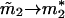 . At this limit, we find the value of the ratio exactly same as the short time limit. Therefore,
. At this limit, we find the value of the ratio exactly same as the short time limit. Therefore,
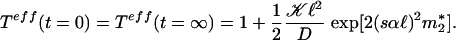 |
Yet for intermediate times, the ratio is not constant and differs from either limiting value. In general, Teff > Tth, i.e., the system is “hotter” although chemical noise apparently enlarges the stability range of the localized phase.
We have studied the stability and dynamics of localized nonequilibrium structures of motorized particles. The nonequilibrium noise from kicking motors sometimes increases the effective spring constant and enlarges the mechanical stability range of both crystal and frozen glass structures. We see that for systems like the cytoskeleton, nonequilibrium noise may speed up the dynamics without sacrificing structural stability. This model can be further developed to include anisotropy of the particles or under other types of nonequilibrium noise or driven forces. Besides taking this solid-state viewpoint, one can also study the transition from the liquid side by mode-coupling theory, a problem for future studies.
Acknowledgments
We thank Prof. R.W. Hall for reading the manuscript and suggestions. T.S. thanks Prof. J. A. McCammon for his kind help and support, especially in the early stage of the work. This work was supported by the National Science Foundation and the Center for Theoretical Biological Physics.
References
- 1.Pollard, T. D. & Earnshaw, W. C. (2002) Cell Biology (Saunders, New York).
- 2.Vicsek, T., Czirok, A., Ben-Jacob, E., Cohen, I. & Shochet, O. (1995) Phys. Rev. Lett. 75, 1226–1229. [DOI] [PubMed] [Google Scholar]
- 3.Ebeling, W. & Erdmann, U. (2003) Complexity 8, 23–30. [Google Scholar]
- 4.Liu., A. J. & Nagel, S. R., eds. (2001) Jamming and Rheology: Constrained Dynamics on Microscopic and Macroscopic Scales (Taylor & Francis, New York).
- 5.Trappe, V., Prasad, V., Cipelletti, L., Segre, P. N. & Weitz, D. A. (2001) Nature 411, 772–775. [DOI] [PubMed] [Google Scholar]
- 6.Grzybowski, B. A., Stone, H. A. & Whitesides, G. M. (2002) Proc. Natl. Acad. Sci. USA 99, 4147–4151. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Whitesides, G. M. & Boncheva, M. (2002) Proc. Natl. Acad. Sci. USA 99, 4769–4774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Amos, L. A. & Amos, W. B. (1991) Molecules of the Cytoskeleton (Guilford Press, New York).
- 9.Dhont, J. K. G. (1996) An Introduction to Dynamics of Colloids (Elsevier, New York).
- 10.Risken, H. (1996) The Fokker-Planck Equation (Springer, New York), 2nd Ed.
- 11.van Kampen, N. G. (1992) Stochastic Process in Physics and Chemistry (North-Holland, New York), 2nd Ed.
- 12.Dogterom, M. & Yurke, B. (1997) Science 278, 856–860. [DOI] [PubMed] [Google Scholar]
- 13.Howard, J. (2001) Mechanics of Motor Proteins and the Cytoskeleton (Sinauer, Sunderland, MA).
- 14.Eyink, G. L. (1996) Phys. Rev. E 54, 3419–3435. [DOI] [PubMed] [Google Scholar]
- 15.Eyink, G. L. & Alexander, F. J. (1997) Phys. Rev. Lett. 78, 2563–2566. [Google Scholar]
- 16.Jastrow, R. (1955) Phys. Rev. 98, 1479–1484. [Google Scholar]
- 17.Chen, H., Chen, S. & Kraichnan, R. H. (1989) Phys. Rev. Lett. 63, 2657–2660. [DOI] [PubMed] [Google Scholar]
- 18.Fixman, M. (1969) J. Chem. Phys. 51, 3270–3279. [Google Scholar]
- 19.Stoessel, J. P. & Wolynes, P. G. (1984) J. Chem. Phys. 80, 4502–4512. [Google Scholar]
- 20.Hall, R. W. & Wolynes, P. G. (2003) Phys. Rev. Lett. 90, 085505. [DOI] [PubMed] [Google Scholar]
- 21.Singh, Y., Stoessel, J. P. & Wolynes, P. G. (1985) Phys. Rev. Lett. 54, 1059–1062. [DOI] [PubMed] [Google Scholar]
- 22.Verlet, L. & Weis, J.-J. (1972) Phys. Rev. A 5, 939–952. [Google Scholar]
- 23.Mezard, M. & Parisi, G. (1999) Phys. Rev. Lett. 82, 747–750. [Google Scholar]
- 24.Doi, M. & Edwards, S. F. (1986) The Theory of Polymer Dynamics (Oxford Univ. Press, Oxford), 2nd Ed.
- 25.Cugliandolo, L. F., Kurchan, J. & Peliti, L. (1997) Phys. Rev. E 55, 3898–3914. [Google Scholar]