Dimensionality and Reliability of the Self-Care of Heart Failure Index Scales: Further Evidence from Confirmatory Factor Analysis

Abstract

The Self-Care of Heart Failure Index (SCHFI) is used widely, but issues with reliability have been evident. Cronbach alpha coefficient is usually used to assess reliability, but this approach assumes a unidimensional scale. The purpose of this article is to address the dimensionality and internal consistency reliability of the SCHFI. This was a secondary analysis of data from 629 adults with heart failure enrolled in three separate studies conducted in the northeastern and northwestern United States. Following testing for scale dimensionality using confirmatory factor analysis, reliability was tested using coefficient alpha and alternative options. Confirmatory factor analysis demonstrated that: a) the self-care maintenance scale has a multidimensional 4-factor structure; b) the self-care management scale has a 2-factor structure, but the primary factors loaded on a common higher-order factor; and c) the self-care confidence scale is unidimensional. Reliability estimates for the three scales, obtained with methods compatible with each scale’s dimensionality, were adequate or high. The results of the analysis demonstrate that issues of dimensionality and reliability cannot be separated. Appropriate estimates of reliability that are consistent with the dimensionality of the scale must be used. In the case of the SCHFI, coefficient alpha should not be used to assess reliability of the self-care maintenance and the self-care management scales, due to their multidimensionality. We recommend testing dimensionality before assessing reliability, as well using multiple indices of reliability, such as model-based internal consistency, composite reliability, and omega and maximal reliability coefficients.

Heart failure (HF) is one of the most common chronic illnesses among adults worldwide (Bui, Horwich, & Fonarow, 2011; Huffman & Prabhakaran, 2010; McDonagh, 2013). Population longevity, better survival rates after acute myocardial infarction (Ford et al., 2007), and the increasing prevalence of hypertension (Ong, Cheung, Man, Lau, & Lam, 2007) have ballooned the incidence of HF in recent years. In the United States, among those older than 80 years of age, almost 12% of men and women have HF (Go et al., 2014) and the prevalence is projected to increase by 25% between 2013 and 2030 (Heidenreich et al., 2013). HF is associated with a high symptom burden, poor quality of life (Banerjee et al., 2013), high mortality, and frequent hospital admissions that contribute enormously to health care costs (Heidenreich et al., 2013). Self-care has been shown to improve symptoms, quality of life, hospitalization rates, cost, and mortality (Jones et al., 2012; Lee, Moser, Lennie, & Riegel, 2011; Lee, Moser, et al., 2011a; Rathman, Lee, Sarkar, & Small, 2011).

Much of our understanding of the contributions of self-care to HF outcomes followed publication of the Self-Care of HF Index (SCHFI; Riegel et al., 2004), a self-report, disease-specific measure of HF self-care based on the situation-specific theory of HF self-care (Riegel & Dickson, 2008). The SCHFI, last updated in 2009 (Riegel, Lee, Dickson, & Carlson, 2009), is freely available in the public domain (http://www.self-careofheartfailureindex.com/) and is used worldwide (Jaarsma et al., 2013). However, a consistent finding among investigators using the SCHFI has been marginal or poor reliability of the self-care maintenance and self-care management scales.

Reliability is a reflection of measurement error, defined as “chance effects that are momentary and have nothing to do with the construct being measured” (Raykov & Marcoulides, 2011, p. 116). Internal consistency reliability of the SCHFI has been tested mainly with Cronbach alpha coefficient, which may not be the best approach for an instrument with multiple dimensions. Raykov (1997) demonstrated that alpha is a lower-bound estimate for reliability (or even fairly close to reliability) only when 1) the indicators composing the scale are congeneric (i.e., there is a single factor explaining their correlations), 2) their unique variances are not correlated, and 3) their loadings on the single factor are “uniformly high” (≥ |0.6|), that is when items are at least tau equivalent (Novick & Lewis, 1967). When these three conditions are not met, alpha can give a biased (upward or downward) estimate of reliability (Maxwell, 1968; Raykov, 1997, 1998, 2001a, 2001b). However, because population reliability of the Index is unknown, there is no way of knowing whether these conditions are met, so alpha can be unpredictable, and reliance on it can be seriously misleading.

Thus, the purpose of this study was to assess dimensionality of the SCHFI and then assess reliability of each scale using the best alternative approaches. In doing so, we produced evidence of the critical importance of considering alpha as a measure of test homogeneity, rather than measurement error or reliability, in the absence of a thorough assessment of dimensionality.

Measurement of Self-Care

The situation-specific theory of HF self-care defines self-care as a naturalistic decision making process composed of two dimensions: self-care maintenance and self-care management (Riegel & Dickson, 2008). Self-care maintenance reflects behaviors in which patients engage to maintain physiological stability, including monitoring of signs and symptoms (e.g., checking ankle edema) and adhering to prescribed treatments (e.g., being physically active). Self-care management is a process of recognizing symptoms (e.g., shortness of breath), implementing treatments aimed at addressing the symptoms (e.g., limiting salt intake) and evaluating the effectiveness of the treatment implemented. This process was recently confirmed in an Italian sample (Vellone, Riegel, D’Agostino, et al., 2013c). Self-care confidence (i.e., self-efficacy related to the specific tasks of self-care) is thought to be an important influence on the effectiveness of HF self-care, and there is evidence to support this proposition (Cene et al., 2013; Lee, Moser, et al., 2011b; Lee, Suwanno, & Riegel, 2009).

The SCHFI version 6.2 directly reflects this naturalistic decision-making process and thus is useful to investigators seeking to describe self-care and test the effectiveness of interventions. However, reliability is a continuing issue with the SCHFI. In the earlier version (SCHFI V.4), when all three scales were added to yield a single self-care score, Cronbach alpha was .76 for the full scale, and .56, .70 and .82 for the self-care maintenance, management and confidence scales respectively (Riegel et al., 2004). Similar results have been reported by others. Yu and colleagues found that Cronbach alpha of the aggregated scales was .73; separate scale coefficients were not reported (Yu et al., 2011). Kato and colleagues tested SCHFI v.6.1 and reported Cronbach alpha coefficients of .68, .58, and .87 for the self-care maintenance, management, and confidence scales respectively (Kato et al., 2013). When the SCHFI v.6.2 update was published, Cronbach alpha was reported to be .55 for self-care maintenance, .60 for self-care management, and .83 for self-care confidence (Riegel et al., 2009).

One reason why Cronbach alpha coefficient is low may be that the SCHFI is not unidimensional. The alpha coefficient is an index of the degree to which an instrument’s items are correlated on average (Sijtsma, 2009). The SCHFI, however, has three scales. For example, items in the SCHFI self-care maintenance scale reflect the many behaviors noted in clinical guidelines to be important to maintaining physiologic stability (e.g., following a low-salt diet, exercising), but the items reflect more than one dimension of self-care maintenance. Accordingly, items are homogeneous within the specific facets constituting self-care maintenance, but they may not be homogenous when considering the construct as a whole.

Use and Misuse of Cronbach Alpha Coefficients

Internal consistency has been improperly used as a synonym of homogeneity, that is, of unidimensionality of the scale, and a high alpha coefficient has been used as proof that a single factor explains correlations among scale items (Raykov, 2012; Raykov & Marcoulides, 2011). However, while homogeneity refers to the fact that only one latent dimension explains the correlations among a set of items composing a scale, internal consistency refers to the fact that items are simply related, but sheds no light on their latent structure (Schmitt, 1996).

Alpha as a measure of internal consistency is basically an index of how much the items are correlated on average, assuming that all item covariances are positive. Moreover, the alpha value is strictly dependent on the sum of the inter-item covariances (Sijtsma, 2009), as well as on the number of items composing the test (Nunnally & Bernstein, 1994). Alpha does not tell anything about how many latent dimensions are responsible for item covariances. Evidence of unidimensionality comes from exploratory and confirmatory factor analysis (EFA and CFA), with goodness of fit indices that explicitly test the null hypothesis that all covariances among items are explained by a single latent dimension and/or with goodness of fit indices that measure the magnitude of residual covariance once a single latent dimension is partialled out (see also Hattie [1985] and McDonald [1981] on this topic). Thus, only a careful examination of the items’ latent structure (e.g., dimensionality) can guide the definition of a pertinent summed score. The risk of not doing so is ending up with summed scores that reflect mixed sources of variance. This eventually jeopardizes the validity of the scale or the extent to which the scale measures the construct it is intended to measure.

In summary, scale dimensionality must be assessed before choosing a method for estimating reliability. If a scale, such as the SCHFI, is multidimensional, especially if the different dimensions composing the scale are measured with a relatively small number of items, other approaches than alpha to assessing reliability are more appropriate. These options are discussed below.

Linking Reliability Estimates to Factor Analysis Results

In this section we will consider indices of scale reliability that are alternatives to Cronbach alpha. These indices use results from previous confirmatory or exploratory factor analysis in their computations.

Model-based internal consistency coefficients: Congeneric scales

Fornell and Larcker (1981) introduced two different indices to assess scale reliability. When items are congeneric (i.e., a model with one homogenous factor that fits the data) and measurement errors are not correlated, the reliability of a single item can be estimated from factor analysis results, as shown in equation 1:

$${\rho }_y=\frac{{\lambda }_y^2}{{\lambda }_y^2+\mathit{Var}({\epsilon }_y)}$$ (1)

In equation 1, λ is the factor loading of the indicator, and Var(ε_y) is its residual variance, assuming that ϕ, the variance of the factor is fixed at 1 for identification purposes and that the factor and the measurement error are independent. Under the same assumptions, the composite reliability index can be computed for a set of p congeneric indicators of a construct η, as shown in Equation 2 (see Raykov & Marcoulides [2011] for a generalization when measurement errors are correlated):

$${\rho }_{\eta }=\frac{{({\displaystyle \sum _{i=1}^p}{\lambda }_i)}^2}{{({\displaystyle \sum _{i=1}^p}{\lambda }_i)}^2+{\displaystyle \sum _{i=1}^p}\mathit{Var}({\epsilon }_i)}$$ (2)

These coefficients are consistent estimators of scale reliability (Raykov, 2012) and can be easily computed using standard output for exploratory or confirmatory factor analysis from commercial or freeware software. This coefficient has a close resemblance to the so-called omega coefficient (McDonald, 1999; Revelle & Zinbarg, 2009). Omega can be used as a measure of reliability only when one latent variable accounts for item correlations (McDonald, 1999).

Multidimensional scales

Composite reliability coefficient can be extended to consider the more general case of a multidimensional scale, that is, a scale where more the one latent variable explains correlations among observed variables in a data set (Camilli, Wang, & Fesq, 1995) such as the SCHFI. The formula for the global reliability index for multidimensional scales proposed by Raykov and Marcoulides (2011) is shown in equation 3:

$${\rho }_U=\frac{{\mathbf{1}}^{\prime }\mathbf{A}\mathbf{\Phi }{\mathbf{A}}^{\prime }\mathbf{1}}{({\mathbf{1}}^{\prime }\mathbf{A}\mathbf{\Phi }{\mathbf{A}}^{\prime }\mathbf{1}+{\mathbf{1}}^{\prime }\mathbf{\Theta }\mathbf{1})}$$ (3)

Here, A is the matrix of factor loadings onto common factors and A′ its transpose, Φ is the covariance matrix of the common factors, Θ is the covariance matrix of measurement errors, 1 is a unity vector and 1′ its transpose. This formula assumes that it is rarely possible to distinguish among specific factor and measurement errors (Bollen, 1989; McDonald, 1985; McDonald, 1999), and that these two components sum into the uniqueness term (Bollen, 1989).

Another model-based internal consistency index that can be used when a scale has more than one factor was proposed by Bentler (2009) and shown in equation 4:

$${\widehat{\rho }}_{xx}=1-\frac{{\mathbf{1}}^{\prime }\widehat{\mathbf{\Psi }}\mathbf{1}}{{\mathbf{1}}^{\prime }\widehat{\mathbf{\sum }}\mathbf{1}},$$ (4)

Here Σ̂ is the fitted covariance matrix obtained from model parameter estimates, and Ψ̂ is the error covariance matrix.

Maximal reliability (MR)

Items in a scale can be appropriately weighted so that the weighted combination of the items has a higher reliability in comparison to that obtained when the items are summed using a uniform weight of 1. This situation seems to be particularly relevant when the items show remarkable differences in their factor loading (i.e., when they are simply congeneric measures of the construct, with a different “true” component as well as different precision). Optimal weights w_j are then obtainable for each item from the ratio of the loading and the unique variance, so that w_j = b_j/θ_j. The maximal reliability index can be obtained as shown in equation 5 (Raykov, 2012):

$${\rho }_{U,m}=\frac{{\displaystyle \sum _{j=1}^r}({\lambda }_j^2/{\theta }_j)}{1+{\displaystyle \sum _{j=1}^r}({\lambda }_j^2/{\theta }_j)}$$ (5)

Factor score determinacy coefficient

The similarities between classical test theory and common factor analysis are well-known (e.g., Kline, 2005). In this domain, the factor score determinacy coefficient is used to evaluate the internal consistency of the factor solution (Tabachnick & Fidell, 2013). As noted by Brown (2003), this coefficient represents an important result of factor analysis. In particular, a high degree of determinacy indicates that “the factor score estimates could serve as suitable substitutes for the factor itself” (Brown, 2003, p. 1418).

Factor score determinacy represents the correlation between the estimated and true factor scores. It ranges from 0 to 1 and describes how well the factor is measured, with 1 being the best value (Muthén & Muthén, 1998–2012; see also Grice, 2001). The factor score determinacy coefficient (ρ²) is given by f′R⁻¹′f (McDonald & Mulaik, 1979, equation 6, p. 299) where f are common factor loadings and R is the correlation matrix among indicators (items) of the factor. The larger the coefficient (e.g., ≥ .70, Tabachnick & Fidell, 2013), the more stable the factors, in the sense that the observed variables account for substantial variance in the factor scores, while low values mean the factors are poorly defined by the observed variables.

Alternative Approaches to Reliability of the SCHFI

As noted above, it is critical that dimensionality testing precede reliability testing. Evidence of dimensionality comes from exploratory and confirmatory factor analysis. As the SCHFI is based on theory, confirmatory factor analysis (CFA) is typically preferred.

In the first psychometric testing of the SCHFI v.6.2 (Riegel et al., 2009) self-care maintenance, self-care management and self-care confidence scales were tested in a single CFA. Results showed poor fit: χ² = 356.92, comparative fit index (CFI) = .73 and root mean square error of approximation (RMSEA) = .07. In a recent study from Italy (Vellone et al., 2013a), a combination of EFA and CFA was used to test the dimensionality of each scale of the SCHFI v.6.2. This analysis revealed a new factorial structure within each scale that fits the data with better, more supportive fit indices (CFI = .92, RMSEA = .05 for the self-care maintenance scale; CFI = .95, RMSEA = .07 for the self-care management scale; CFI = .99, RMSEA = .02 for the self-care confidence scale). In the Italian study, reliability was tested with factor score determinacy coefficients that were adequate (Tabachnick & Fidell, 2013), ranging from .74 to .90. In these analyses, when the data were normally distributed we used maximum likelihood estimation, and when not normally distributed we used the Satorra-Bentler correction.

Based on this evidence of multidimensionality and promising evidence of reliability using approaches other than Cronbach alpha, in the current study we explored the factorial structure of the SCHFI v.6.2 in US samples and used those results to identify the best method for users of the SCHFI to assess reliability.

Methods

Instrument

This was a secondary analysis of data from 629 adults with heart failure enrolled in three separate studies conducted in the northeastern and northwestern United States. In each study, self-care was measured using the Self-Care of HF Index (SCHFI) v.6.2, a 22-item instrument with three scales that measure the two components of HF self-care: maintenance and management, and confidence - a major influence on self-care (Riegel et al., 2004; Riegel et al., 2009).

The self-care maintenance scale has 10 items that measure symptom monitoring and adherence to behaviors that are advocated in clinical guidelines (Yancy et al., 2013) to maintain patients in a stable state (e.g., monitoring weight, eating a low salt diet, exercising). The 6 items of the self-care management scale measure patients’ abilities to recognize symptoms when they occur, treatment implementation in response to symptoms (e.g., reduce fluid intake, take an extra water pill), and treatment evaluation. A self-care management scale score is calculated only in patients who have been recently symptomatic. The self-care confidence scale uses 6 items to evaluate patients’ perceived abilities to engage in each phase of the self-care process (e.g., preventing symptom onset, recognizing symptom changes).

Each scale uses a 4-point self-report response format (never or rarely, sometimes, frequently, always or daily). The Institutional Review Boards of each site approved the studies before data collection began, and all participants gave informed consent.

Participants

Sample 1

The first sample consisted of 280 adults with chronic HF enrolled from three outpatient settings in Philadelphia, Pennsylvania, and Newark, Delaware. The purpose of this longitudinal descriptive study was to test the relationship between excessive daytime sleepiness and HF self-care. Only baseline data were used in the current analysis. Participants had a diagnosis of HF, confirmed by echocardiography and clinical evidence, were 18 years of age or older, and were medically stable, without an acute coronary event in the past three months. Patients were excluded if they had evidence of dementia, major depression, or drug or alcohol abuse within the past year. Because this was a study of daytime sleepiness, patients who worked the night shift also were excluded. Data collection took place during home visits by trained research associates, as described in detail elsewhere (Riegel, Moelter, et al., 2011). These patients were predominately older adults, male, and Caucasian. Their demographic and clinical characteristics are shown in Table 1.

Table 1.

Demographic and Clinical Characteristics of the Three Samples

Variable	Sample #1 (n=280)		Sample #2 (n=202)		Sample #3 (n=146)
	M	SD	M	SD	M	SD
Age (years)	62.0	12.5	56.9	13.3	57.4	12.8
Body mass index (BMI)	31.0	8.0	30.7	7.4	32.0	7.1
Systolic blood pressure	116.1	18.4	109.3	16.8	109.3	13.9
Diastolic blood pressure	69.0	11.2	67.2	10.2	68.7	9.5
Months with HF	73.4	71.1	67.8	71.0	72.4	62.4
Ejection fraction	35.4	17.0	28.6	12.4	28.4	11.6
Number of comorbid illnesses	3.1	2.1	2.3	1.5	2.2	1.1
	n	%	n	%	n	%
Male	180	64.3	101	50.0	102	69.9
Race/Ethnicity
White	175	62.5	173	85.6	126	86.3
Black	96	34.3	2	1.0	5	3.4
Other	9	3.2	27	13.4	11	10.3
Education
Less than high school	27	9.7	14	6.9	12	8.2
High school	101	36.2	51	25.3	33	22.6
At least some college	78	28.0	137	67.8	101	69.2
Household income insufficient to make ends meet	45	16.1	76	37.8	61	41.8
Perceived overall health
Excellent/very good	34	12.1	7	3.5	8	5.5
Good	94	33.6	49	24.2	40	27.4
Fair/poor	152	54.3	146	72.3	98	67.1
Atrial fibrillation	94	33.6	78	38.6	63	42.2
Diabetic	108	38.6	48	23.8	37	25.3
Cerebrovascular disease	42	15.0	25	12.4	13	8.9
Renal disease	74	26.4	53	26.2	40	27.9
Heart failure type
Systolic/mixed	226	80.7	187	92.6	142	97.3
Diastolic	53	18.9	15	7.4	4	2.7
NYHA functional class
Class I & II	66	23.6	81	40.1	60	41.1
Class III	164	58.6	113	55.9	83	56.8
Class IV	50	17.9	8	4.0	3	2.1
Angiotensin-Converting	162	57.9	107	53.0	81	55.5
Enzyme (ACE) inhibitor
Angiotensin II Receptor	83	29.6	56	27.7	45	30.8
Blocker (ARB)
Diuretic	226	80.7	173	85.6	127	87.0
Beta-Blocker	259	92.5	183	90.6	134	91.8

Sample 2

The second sample consisted of 202 adults with moderate to advanced chronic HF enrolled through a single outpatient HF clinic in Portland, Oregon. The purpose of this prospective cohort study was to describe gender differences in HF symptoms, self-care behaviors, and event-free survival (Lee, Gelow, Denfeld, et al., 2013). All participants had a confirmed diagnosis of HF by echocardiographic and physical examination evidence, were 21 years of age or older and responsible for making their own decisions about their care, and had New York Heart Association (NYHA) class II-IV HF (current symptoms). Patients were excluded if they had a diagnosis of moderate or greater cognitive impairment (i.e., dementia), major and uncorrected visual or hearing deficits, or had received a heart transplant or mechanical circulatory support to manage their HF. Questionnaires including the SCHFI were completed in the clinic or at home and returned by mail; only baseline data were used for this analysis. In general, the sample was mainly middle-aged adults, predominantly Caucasian, and with an equal proportion of males and females (Table 1).

Sample 3

The third sample consisted of 146 adults with moderate to advanced chronic HF enrolled through the same single outpatient HF clinic in Portland, Oregon as sample 2. The purpose of this prospective cohort study was to characterize naturally-occurring patterns of change in HF self-care management and their association with quality of life (Lee, Gelow, Mudd, et al., 2013). All participants had a confirmed diagnosis of HF by echocardiographic evidence and history and physical examination, were 21 years of age or older, and had NYHA class II–IV HF. Patients were excluded if they had a diagnosis of dementia, major and uncorrected visual or hearing deficits, or had received a heart transplant or mechanical circulatory support to manage their HF. Questionnaire data were completed in the clinic or at home and submitted by mail; only baseline data were used for this analysis. Many patients participated in both studies in Portland; thus, the total number of unique participants from Studies 2 and 3 for this analysis was 273. The characteristics of these patients are detailed in Table 1, and they were predominantly male, Caucasian, and in middle adulthood.

Data Analysis

As the inclusion criteria were essentially the same, data from the three samples were combined for analysis. Analyses using the combined sample were then conducted separately on each of the three scales comprising the SCHFI. Consistent with our arguments in the previous section, the following reliability coefficients were considered: a) standardized Cronbach alpha; b) composite reliability (Fornell & Larcker, 1981) or omega (McDonald, 1999); c) maximal reliability (Raykov, 2012); and d) factor score determinacy (McDonald & Mulaik, 1979).

Reliability coefficient α (which does not use any parameter from the factor model) was obtained from the freeware software FACTOR (Lorenzo-Seva & Ferrando, 2006). All other coefficients were computed from the Mplus output (see below).

As dimensionality testing must precede reliability testing, we began the analysis with CFA and then assessed reliability. Confirmatory factor analyses were conducted using Mplus 7.1 (Muthén & Muthén, 1998–2012). Because the SCHFI item response format presents only four ordered categories, and due to non-normality in the data, the following methods were used for parameter estimation in CFA: a) robust maximum likelihood (ML) estimator, the Satorra-Bentler correction, implemented in Mplus via the estimator MLM); and b) WLS-MV estimator (Muthén & Muthén, 1998–2012).

While ML-based estimators are suitable for continuous (or almost continuous) indicators, they may introduce bias in parameter estimation when used with categorical data. Thus, we expected that internal coherence estimates derived from ML would be underestimated, although this bias may be moderated if data do not present floor or ceiling effects (B. O. Muthén, personal communication, March 24, 2014).

WLS-MV is a weighted least square method highly recommended to applied researchers for the analysis of ordinal or dichotomous variables (Flora & Curran, 2004) and appears to be the ideal choice for data such as those of the SCHFI. However, Raykov and Marcoulides (2011) warned to use internal coherence coefficients such as those introduced above when items have fewer than 5 possible ordinal responses. In fact, WLS-MV method, like other methods for factor-analyzing categorical ordinal variables, considers dichotomous and observed categorical variables as discretization of an underlying continuous variable. In this approach the focus is not on X, the scale obtained by summing the observed categorical variables, but on Z, the sum of the underlying normal variables.

As noted by Bentler (2009), internal consistency reliability of Z can be derived once correlations among underlying normal variables are estimated using polychoric or tetrachoric correlations, and these correlations are used as an input for factor analysis. It must be noted, however, that when internal coherence estimates are based on parameters derived from polychoric correlations, these estimates correspond to the Z continuous variable that underlies the X observed discrete responses, not to the latter. In practice, these hypothetical latent variables are never available, so the internal consistency obtained from polychoric coefficients does not reflect the sum of observed items. Finally, in the same way that the polychoric-based factor loadings are generally higher than the product-moment-based factor loadings (due to attenuation to coarse grouping in categorical variables), we expected that these internal coherence estimates would be higher than those corresponding to the observed discrete scores. Therefore, we believed that to have a complete picture of internal coherence of the SCHFI scales, estimates deriving from both robust ML and WLS-MV should be presented.

Based on Hoyle’s (1995) recommendations, and according to a multifaceted approach to the assessment of model fit (Tanaka, 1993), we considered a number of goodness of fit indices. Table 2 presents a summary of appropriate fit cut-points (Bentler, 1990; Jöreskog & Sörbom, 1984; Hu and Bentler, 1999; Yu, 2002). Additionally, traditional chi-square statistics are reported. However, due to the sample size and the sensitivity of the chi-square likelihood ratio test to sample size, chi-square test results were not used in interpreting model fit.

Table 2.

Summary of Appropriate Fit Statistics and Acceptable Cut-Points

Statistic	Indicator of Acceptable Fit	Source
Comparative Fit Index (CFI) or Tucker and Lewis Index (TLI)	.90–.95 indicates acceptable fit > .95 indicates good fit	Hu & Bentler,1999
Root Mean Square Error of Approximation (RMSEA) estimates lack of model fit and compensates for model complexity	≤ .05 indicates a well- fitting model, .05–.08 indicates a moderate fit, ≥ .10 indicates poor fit	Browne & Cudeck, 1993
RMSEA is given along with 90% confidence interval limits	≤ .05 to ≤.08 indicates good fit
RMSEA is given along with the test of close fit examining the probability that the approximation error is low	p-values > .05 indicate good fit
Standardized Root Mean Square Residual (SRMR); Jöreskog & Sörbom, 1984) is based on residual covariance matrix, assesses discrepancy between observed and predicted covariances	≤ .08 indicates good fit	Hu & Bentler,1999
The Weighted Root Mean Square Residual (WRMR) is used with WLS-MV estimators Traditional chi-square statistics should be are reported as well	≤ 1.0 indicates a good fit	Yu, 2002

One may question whether the results regarding the dimensionality of SCHFI scales are generalizable across the different datasets in this study. Accordingly a series of multiple-group (MG) confirmatory factor analyses was devised. First, data from samples 2 and 3 (from the two studies conducted in the Pacific Northwest) were merged to a single sample because the number of unique and complete responses from each group was too small for separate analysis. Many of these subjects participated in both studies, and the Self-Care Management scale is completed only by symptomatic patients, leaving insufficient cases in each group. M-Box tests of homogeneity of covariances (Tabachnick & Fidell, 2013) between samples 2 and 3 were non-significant, so covariances in samples 2 and 3 were considered as homogenous. Then, MG-CFAs were performed for the two resulting groups: Sample 1 vs. Samples 2 and 3 combined. In these analyses, we constrained factor loadings to be equal, in order to test for so-called metric invariance (see Meredith, 1993). Because we did not address differences in latent or in observed means, we believed this was an appropriate level of invariance for this analysis.

Results

Correlations and Normality of Distribution within Scales

Average correlation (Table 3) for the self-care maintenance items was r=.15. While there were some higher correlations, in the order of .62 and .49, many other correlations were much lower, illustrating a complex pattern unlikely to be consistent with a single-dimension factor structure. Notably, item 8 (the one reversed item) was poorly correlated with the other items.

Table 3.

Self-Care Maintenance Scale: Correlations and Descriptors of Distribution and Normality (N = 549)

	Item 1	Item 2	Item 3	Item 4	Item 5	Item 6	Item 7	Item 8	Item 9	M	SD	S	K
Item 1	--									3.05	1.22	−0.65	−0.94
Item 2	.40	--								3.02	1.39	−0.69	−0.91
Item 3	.18	.32	--							3.36	0.70	−1.33	0.76
Item 4	.19	.01	.03	--						2.70	0.97	−0.11	−1.10
Item 5	.18	.17	.24	−.06	--					3.43	0.39	−1.23	0.67
Item 6	.26	.20	.16	.14	.13	--				3.20	0.77	−0.87	−0.34
Item 7	.18	.06	.07	.62	−.01	.13	--			2.10	1.17	0.48	−0.99
Item 8	.02	.04	.05	.15	.00	.06	.13	--		3.63	0.17	−2.05	4.89
Item 9	.27	.30	.15	.06	.14	.49	.14	.02	--	2.34	1.90	0.20	−1.45
Item 10	.15	.12	.22	.05	.19	.13	.11	.05	.09	3.30	2.01	−1.25	−0.27

Note. S = skewness; K = kurtosis. All correlations are statistically significant (p<.05) except those in italics.

Average correlation for the self-care management items (Table 4) was .21. Again, some correlations were fairly adequate, but others were much lower, providing evidence of a complex pattern. Item 14 (extra diuretic) was poorly correlated with all other items.

Table 4.

Self-Care Management Scale: Correlations and Descriptors of Distribution and Normality (n = 322)

	Item 11	Item 12	Item 13	Item 14	Item 15	M	SD	S	K
Item 11	--					2.67	3.23	−0.75	−0.53
Item 12	.15	--				3.39	0.81	−1.43	0.89
Item 13	.20	.50	--			2.88	1.57	−0.49	−1.17
Item 14	.19	.08	.25	--		2.78	3.36	0.26	0.94
Item 15	.05	.35	.31	.13	--	2.72	1.94	−0.23	−1.47
Item 16	.34	.16	.06	.20	.11	2.45	3.13	−0.49	−0.85

Note. S = skewness; K = kurtosis. All correlations are statistically significant (p<.05) except those in italics.

Average correlation for the self-care confidence items (Table 5) was .47. All correlations in the matrix were higher than .30, reaching high values such as .60, a pattern that is often compatible with a one-factor structure.

Table 5.

Self-Care Confidence Scale: Correlations and Descriptors of Distribution and Normality (n = 554)

	Item 17	Item 18	Item 19	Item 20	Item 21	M	SD	S	K
Item 17	--					2.32	0.65	0.22	−0.70
Item 18	.30	--				3.22	0.34	−0.58	−0.47
Item 19	.36	.46	--			3.16	0.37	−0.63	−0.13
Item 20	.35	.51	.52	--		3.11	0.42	−0.53	−0.41
Item 21	.45	.44	.53	.53	--	3.08	0.43	−0.55	−0.30
Item 22	.39	.46	.49	.60	.60	2.94	0.49	−0.36	−0.57

Note. S = skewness; K = kurtosis. All correlations are statistically significant (p<.05).

Regarding normality of distribution (Tables 3, 4, and 5), the self-care maintenance scale items presented low to moderate non-normality, with the sole exception of item 8, which had high negative skewness and kurtosis. Self-care management scale and self-care confidence scale items had low to moderate non-normality.

Self-care Maintenance Scale

Dimensionality

Riegel and colleagues (2009) posited a single factor underlying the 10 items composing the self-care maintenance scale. Thus, we first specified a one-factor model. This model proved to be largely unsatisfactory, with poor fit indices shown in Tables 6 and 7, row 1. Two different multidimensional alternative models were then specified.

Table 6.

Fit Indices from CFA Models (Analysis of Covariance Matrix Using MLM Robust Estimator)

Model	χ2	DF	p(χ2)	TLI	CFI	SRMR	RMSEA	p(RMSEA<.05)	RMSEA 90% CI
Self-care maintenance (n = 549)
1. One-Factor Model	380.00	35	.001	.41	.54	.090	.130	(.001)	[.12, .15]
2. Two-Factor Model	354.00	34	.001	.43	.57	.090	.130	(.001)	[.12, .14]
3. Four-Factor Model	65.34	29	.001	.93	.95	.040	.048	(.570)	[.032, .063]
4. Four-Factor Model without item #8	49.19	21	.001	.93	.96	.035	.049	(.490)	[.032, .068]
Self-care management (n = 322)
5. One-Factor Model	55.13	9	.001	.62	.77	.074	.130	(.001)	[.095, .16]
6. Two-Factor Model	57.89	8	.001	.54	.75	.074	.140	(.001)	[.11, .17]
7. One-Factor Model without item #14	39.00	5	.001	.63	.81	.070	.140	(.001)	[.10, .19]
8. Two-Factor Model without item #14	8.32	4	.080	.94	.98	.023	.058	(.340)	[.00, .11]
Self-care confidence (n = 554)
9. One-Factor Model	23.35	9	.010	.99	.99	.023	.050	(.370)	[.03, .08]

Note. DF = degree of freedom; TLI = Tucker Lewis Index; CFI = comparative fit index; SRMR = Standardized Root Mean Square Residual; RMSEA = Root Mean Square Error of Approximation; CI = confidence interval.

Table 7.

Fit Indices from CFA Models (Analysis of Polychoric Correlations Using WLS-MV Estimator)

Model	χ2	DF	p(χ2)	TLI	CFI	WRMR	RMSEA	p(RMSEA<.05)	RMSEA 90% CI
Self-care maintenance (n = 549)
1. One-Factor Model	589.00	35	.001	.55	.65	2.770	.170	(.001)	[.16, .18]
2. Two-Factor Model	555.00	34	.001	.57	.68	2.680	.170	(.001)	[.15, .18]
3. Four-Factor Model	83.58	29	.001	.95	.97	.917	.059	(.160)	[.044, .073]
4. Four Factor Model without item #8	59.13	21	.001	.98	.96	.795	.058	(.220)	[.040, .075]
Self-care management (n = 322)
5. One-Factor Model	96.96	9	.001	.67	.80	1.392	.170	(.001)	[.14, .21]
6. Two-Factor Model	97.27	8	.001	.62	.80	1.389	.190	(.001)	[.15, .22]
7. One-Factor Model without item #14	79.00	5	.001	.60	.80	1.410	.210	(.001)	[.17, .26]
8. Two-Factor Model without item #14	7.04	4	.130	.99	.98	.391	.049	(.440)	[.00, .106]
Self-care confidence (n = 554)
9. One-Factor Model	36.18	9	.001	.99	.99	.715	.070	(.052)	[.05, .10]

Note. DF = degree of freedom; TLI = Tucker Lewis Index; CFI = comparative fit index; WRMR = Weighted Root Mean Square Residual; RMSEA = Root Mean Square Error of Approximation; CI = confidence interval.

First a two-factor model derived from the Italian analysis of the SCHFI described above (Vellone et al., 2013a) was tested. Here, items 1, 2, 4, 5, 6 and 9 were tested as indicators of an Autonomous Maintenance factor and items 3, 5, 8 and 10 were tested as indicators of a Provider-Directed Maintenance factor. We also tested a four-factor model derived from Vellone, Riegel and colleagues (2013b), where items 1, 2 were measures of a Symptom Monitoring factor, items 4, 7 were measures of a Physical Activity factor, items 6, 9 were measures of a Sodium Intake factor, and items, 3, 5, 8, 10 were measures of a Medical Treatment Adherence factor. The two-factor model resulted in poor fit, while the four-factor model resulted in an excellent fit (see Tables 6 and 7, rows 2 and 3).

However, item 8 (“Forget to take one of your medicines”) was extremely problematic, showing low and non-significant loading on the posited factor. As previously noted, this item also had very low zero-order correlations (see Table 3) with all other items. Notably, this item is the only negatively worded item in the scale (its scores were reversed before the analysis in order to avoid negative signs in loadings). We believed that item 8 could be considered an outlying variable (Comrey & Lee, 1992), so it was excluded from the next analyses.

The four-factor model was then re-specified without item 8, and this model resulted in an excellent fit (see Tables 6 and 7, row 4). Figure 1 gives a graphic representation of this four-factor model, including estimates from the Mplus output’s completely standardized solutions. Factor loadings were generally medium to high, attesting to a substantial proportion of common variance among the items. All factor correlations but one were positive and significant, attesting to a significant and coherent association among the different facets of self-care maintenance.

Figure 1.

Confirmatory factor analysis model for the Self-Care Maintenance Scale (N=549). All factor correlations are significant (p<.05 or lower) except those with asterisks. The standardized coefficients derived from MLM estimators are followed by coefficients (in parentheses) derived from WLS-MV estimators.

Internal coherence

The self-care maintenance scale was intended to yield a single score and not four different scores related to the different aspects of the construct. It is possible, however, to achieve this aim despite the substantial multidimensionality seen in the scale. When the alpha coefficient was computed with the nine remaining items in the scale, a poor coefficient of .65 was obtained. However, alpha assumes that the items are satisfying a unidimensional structure. Knowing that there are four dimensions represented in this scale, more appropriate reliability coefficients that takes into account the multidimensionality of the scale are the global reliability index for multidimensional scales (Raykov, 2012) and the model-based internal consistency coefficient (Bentler, 2009). These coefficients were.75 and .76, respectively, when derived from MLM results, and .82 and .83 when derived from WLS-MV results. Although the dimensionality of this scale is complex, Bentler (2006) noted, “every multidimensional coefficient implies a particular composite with maximal unidimensional reliability” (p. 343). Thus, the final reliability estimates derived with appropriate methods “can be interpreted to represent a unidimensional composite” (Bentler, 2006, p. 341).

Self-care Management Scale

Dimensionality

Riegel and colleagues (2009) posited a single factor underlying the 6 items composing the self-care management scale. Accordingly we first specified a one-factor model. This model proved to be largely unsatisfactory, with poor fit indices (see Tables 6 and 7, row 5).

An alternative model was then specified, derived from the Italian study discussed above (Vellone et al., 2013b), in which items 11, 12, 13, and 16 were measures of an Autonomous Management factor, and items 14 and 15 were measures of a Provider-Directed Management factor. This model also proved to be largely unsatisfactory (see Tables 6 and 7, row 6). A close scrutiny of the correlation matrix revealed that item 14 (“Take an extra water pill”) was not adequately correlated with any of the other items in the scale (average correlation = .16). The poor correlation was not entirely unexpected, as patients having trouble recognizing shortness of breath or ankle swelling would be unlikely to take an extra water pill as a remedy (Cocchieri et al., 2014; Prasun, Kocheril, Klass, Dunlap, & Piano, 2005). Further, self-administration of diuretics is not uniformly advocated by providers, and not all patients are willing or able to self-medicate. Thus, the response to this item is dependent on the instructions patients receive from their providers, as well as individual motivation. Following this reasoning, we eliminated item 14 from subsequent analyses and tested the original one-factor model with the remaining 5 items. However, this solution did not improve sufficiently (see Tables 6 and 7, row 7).

In the one-factor solution, items 12 (reduce the salt in your diet), 13 (reduce your fluid intake), and 15 (call your doctor or nurse for guidance) had high loadings on the specified factor (treatment implementation), while items 11 (symptom recognition) and 16 (treatment evaluation) were poorly associated with it. Thus, while items 12, 13 and 15 reflect treatment implementation as in the original theory (Riegel & Dickson, 2008), items 11 and 16 seem to reflect uncertainty in the evaluation of symptoms and the management thereof. Accordingly, we specified a correlated two-factor model. When the model was tested with two factors (Evaluation, items 11 and 16, and Implementation, items 12, 13, and 15), this model now showed an excellent fit to the data (see Tables 6 and 7, row 8).

This final model was statistically equivalent with a second-order model in which the two primary factors of Evaluation and Implementation loaded on a second-order factor of Self-Care Management, which has always been conceptualized as entailing elements of both evaluation and implementation. Figure 2 gives a graphic representation of the hierarchical model including estimates from the Mplus output’s completely standardized solution. In the 2-correlated-factors model shown in Figure 2, the five items are shown as loading on two primary factors, while the second-order factor is replaced by a correlation (r = .33 on MLM and .34 on WLS-MV) between the two factors. As can be seen in Figure 2, factor loadings were generally medium to high, attesting to a substantial proportion of common variance among the items.

Figure 2.

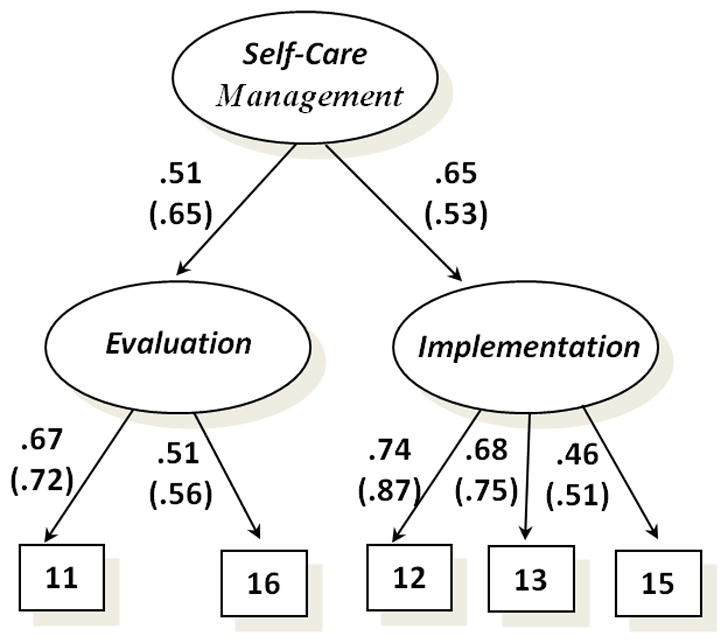
Confirmatory factor analysis model for Self-Care Management Scale (N=322). The standardized coefficients derived from MLM estimators are followed by coefficients (in parentheses) derived from WLS-MV estimators.

Internal coherence

As in the case of the self-care maintenance scale, the self-care management scale was intended to yield a single score and not different scores related to the different aspects of the construct. When the alpha coefficient was computed for the five remaining items in the scale, a poor coefficient of .59 was obtained. As alpha assumes that the items are satisfying a unidimensional structure, and this scale is not unidimensional, we again computed the global reliability index for multidimensional scales (Raykov, 2012) and the model-based internal consistency coefficient (Bentler, 2009). These coefficients were.68 and .66, respectively, when derived from MLM results, and .77 and .76 when derived from WLS-MV results. Although these coefficients are all better than the alpha coefficient, they reached the .70 level of an adequate reliability only when based on WLS-MV estimates (Nunnally & Bernstein, 1994). As noted above, while internal coherence coefficients based on MLM may tend to be downward-biased (due to the low number of ordered categories of item responses), coefficients derived from WLS-MV estimates measure the internal coherence of the latent variables underlying the coarse categorical responses, and may tend to be upward-biased. Therefore, the reliability of the composite obtained by summing the 5 observed scores of self-care management scale must be interpreted with caution.

Self-care Confidence Scale

Dimensionality

Riegel and colleagues (2009) posited a single factor underlying the 6 items composing this scale. Accordingly, we first specified a one-factor model. This model showed an excellent fit (see Tables 6 and 7, row 9). Figure 3 presents the final fitted model: all factor loadings were high, significant and positive.

Figure 3.

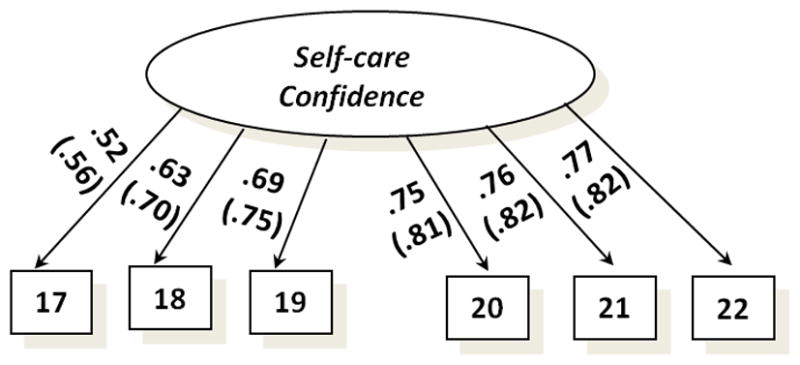
Confirmatory factor analysis model for the Self-Care Confidence Scale (N=554). The standardized coefficients derived from MLM estimators are followed by coefficients (in parentheses) derived from WLS-MV estimators.

Internal coherence

Table 8 presents reliability estimates for this final model. All the coefficients, regardless of the estimator used, confirm the high reliability of the scale obtained by summing the 6 items related to self-care confidence.

Table 8.

Self-Care Confidence Scale: Reliability Estimates for Single Factor in Confirmatory Factor Analyses

Index	Coefficients Derived from MLM Estimators	Coefficients Derived from WLS-MV Estimators
Standardized Cronbach alpha (α)	.84	.88
Composite Reliability (CR)	.84	.88
McDonald’s Omega (ωt)	.84	.88
Maximal Reliability (MR)	.86	.90
Factor Score Determinacy (FSD)	.86	a

Note. The FSD coefficient has been derived from results of the CFA solution using the coefficient described in McDonald & Mulaik (1979).

^aFSD is not presented in the solution derived from WLS-MV because this index does not make sense for categorical factor indicators.

Generalizability of the Results

The model parameters are substantially consistent between the two samples included in this analysis, with good or very good fit indices, both in the MLM and WLS-MV models (see Table 9). In all these solutions, none of the modification indices associated with constrained parameters resulted in significance at the p =.05 level or below, with the sole exception of item 8 in MLM analysis of the Self-Care Maintenance scale; when the constraint was relaxed, item 8 showed a factor loading of .87 in Sample 1 and.54 in Samples 2+3.

Table 9.

Fit Indices from Multiple-Groups Confirmatory Factor Analysis Models

	χ2	DF	p(χ2)	TLI	CFI	SRMR or WRMR	RMSEA	p(RMSEA<.05)
Self-care Maintenance Scale (n = 549)
ML	100.62	51	.001	.91	.94	.055	.059	(.17)
WLS	91.59	51	.001	.97	.98	1.03	.054	(.35)
Self-care Management Scale (n = 322)
ML	15.24	11	.170	.97	.99	.038	.042	(.55)
WLS	15.96	11	.140	.98	.99	.652	.046	(.51)
Self-care Confidence Scale (n = 554)
ML	35.00	20	.020	.98	.99	.055	.052	(.42)
WLS	48.87	21	.001	.99	.99	.971	.07	(.10)

Note. DF = degree of freedom; TLI = Tucker Lewis Index; CFI = comparative fit index; WRMR = Weighted Root Mean Square Residual; RMSEA = Root Mean Square Error of Approximation.

Discussion

The purpose of this study was to assess the psychometric properties of the SCHFI. To do so, we first tested the dimensionality of each scale using CFA and then chose measures of internal consistency based on scale dimensionality. This analysis revealed that only the self-care confidence scale is unidimensional, while both self-care maintenance and self-care management scales are multidimensional. After eliminating one item from each of these scales, excellent model fit was obtained for each scale. Internal consistency coefficients ranged from .75 to .83 for the self-care maintenance scale and from .66 to .77 for the self-care management scale, using indices that consider the multidimensionality of the scales. Internal consistency of the self-care confidence scale ranged from .84 to .90 when tested using a variety of indices.

The finding that the self-care maintenance and management scales are not unidimensional illustrates that reliability of the SCHFI should not be assessed using coefficient alpha. When the reliability of the self-care maintenance scale was measured with a coefficient that reflects its multidimensional nature, the results were adequate, attesting to the possibility of using a fairly reliable total summed score as a measure of the general construct. Reliability would be higher with subscale scores, but two items are insufficient to produce a robust subscale.

The self-care management scale also is not unidimensional. When reliability was measured with a coefficient that reflects its multidimensional nature, the results were better but not completely adequate, especially when the internal consistency index was computed using MLM-based estimates. Given these results, we recommend that a total summed score be used with caution. Again, reliability would certainly be higher with subscale scores, but new items would be needed.

At this point we advocate that scoring of the self-care management scale take into account whether patients have been instructed to self-administer a diuretic dose for a weight gain. In the most recent update, we noted that item 14 (“Take an extra water pill”) can be skipped and the scoring adjusted using the same general formula (raw score sum minus lowest possible raw score, then divided by the possible range of scores, and finally multiplied by 100). In this update, we go a step further to specify that patients who report that they are “not likely” to take an extra water pill should be asked what they were told to do by their provider. If the provider has not advocated taking an extra water pill, this item should be skipped in the scoring. The scoring formula would need to be adjusted as noted above. Efforts are underway to update the SCHFI in a more thorough fashion in the near future. As we gain insight into differentiating self-care from provider-guided care (Lee, Gelow, Mudd, et al., 2013), and get better at identifying experts in self-care (Riegel, Lee, et al., 2011) who may be well-positioned to self-titrate diuretics in response to symptoms, this item on taking an extra water pill may gain increasing importance.

In practical applications, we often rely on the illusion that factor analysis (exploratory or confirmatory) would remove from the observed variable any sources of variability extraneous to that due to common factors. However, although the factor model accounts for the common variance among the indicators of a construct, it does not remove other sources of variability from the indicators. Therefore, if item scores are simply added together to obtain the total score on a scale, this scale score will reflect both what is due to the common factor and what is due to the residual components (DeShon, 2004).

To limit the impact of such unwanted components, using factor scores to compute total scores may be a possible solution (see Tabachnick & Fidell, 2013). In computing such scores, observed variables would be weighted by a coefficient that is proportional to the factor loading obtained in the factor solution. While factor score coefficients can be easily derived from software output for CFA or for EFA, the computation of weighted scores is more complex and not currently easily implemented. Moreover, factor scores are dependent on the data set in which they were developed, making them difficult to generalize unless they are calibrated on large samples. Thus, at this point, our recommendation is that total scores continue to be used; we hope to devise and make public a more refined scoring method in the near future.

We acknowledge several limitations to the approach used in this study. We adopted a top-down approach in the definition of the factor models based on prior testing through CFA. In doing so, we considered as a starting point the many studies of the dimensionality of the SCHFI in prior years. Although the present results generally supported the previously-tested models, we still eliminated two items with poor correlations. Doing so introduced a post-hoc modification in our top-down model-testing strategy. One may question whether a fully exploratory approach based on EFA could have provided useful information about the number of dimensions. One approach might have been to split the sample and perform an EFA on one half and CFA on the other, using a cross-validation approach. However, this approach would have resulted in a dramatic reduction in sample size, especially in the analysis of the self-care management scale, for which we had only a sample of 322 subjects. Investigators with more subjects could test such an approach in future studies.

Future investigators also should clarify whether using global scores for constructs that are multidimensional is preferable to using specific scores for the facets or components of these multidimensional constructs. While we demonstrated the reliability of these global scores in our sample, reliability must be demonstrated in other samples to extend the generalizability of the results. Moreover, the current SCHFI intentionally includes only a limited number of items, which constrains its ability to produce robust subscale scores. The trade-off between simplicity and the potential for enlargement with subscale scores is an issue requiring serious consideration. In conclusion, we reaffirm the wisdom of Bentler (2009) that coefficients of internal coherence are only ancillary measures, and the more important objective of the analysis of psychometric characteristics of a scale is to understand its underlying structure.