Abstract
In type 1 diabetes, an autoimmune disease mediated by autoreactive T-cells that attack insulin-secreting pancreatic beta-cells, it has been suggested that disease progression may additionally require protective mechanisms in the target tissue to impede such auto-destructive mechanisms. We hypothesize that the autoimmune attack against beta-cells causes endoplasmic reticulum stress by forcing the remaining beta-cells to synthesize and secrete defective insulin. To rescue beta-cell from the endoplasmic reticulum stress, beta-cells activate the unfolded protein response to restore protein homeostasis and normal insulin synthesis. Here we investigate the compensatory role of unfolded protein response by developing a multi-state model of type 1 diabetes that takes into account beta-cell destruction caused by pathogenic autoreactive T-cells and apoptosis triggered by endoplasmic reticulum stress. We discuss the mechanism of unfolded protein response activation and how it counters beta-cell extinction caused by an autoimmune attack and/or irreversible damage by endoplasmic reticulum stress. Our results reveal important insights about the balance between beta-cell destruction by autoimmune attack (beta-cell homicide) and beta-cell apoptosis by endoplasmic reticulum stress (beta-cell suicide). It also provides an explanation as to why the unfolded protein response may not be a successful therapeutic target to treat type 1 diabetes.
Keywords: ER-stress in T1D, Unfolded protein response, Mathematical model, Beta-cell homicide and suicide, Uncertainty and sensitivity analysis
1. Introduction
Patients with autoimmune type 1 diabetes (T1D) are insulin dependent for life. The autoimmune disease is characterized by the destruction of pancreatic beta-cells, which causes the absolute deficiency of insulin. It is estimated that 90% of insulin-secreting beta-cells are lost due to autoimmune destructive mechanisms commanded by (CD8+ and CD4+) cytotoxic T lymphocytes and proinflammatory cytokines. The loss of insulin causes abnormal regulation of glucose homeostasis in T1D patients (Atkinson et al., 2011; Jacob and Baltimore, 1999; Morran et al., 2010, 2008; Valitutti et al., 1995; Veiga-Fernandes et al., 2000).
During the progress of T1D, the processing of proteins from apoptotic beta-cells phagocytized by antigen presenting cells (APCs), such as macrophages, then drives peptide-major histo-compatibility complex (pMHC) formation and expression on APCs for further T-cell activation and amplification of the autoimmune response. Cytokine secretion (such as IL-1 and TNF) during these immunological processes by APCs and CD4+ T-cells is also implicated in the activation of these (and other) immune cells and in beta-cell destruction (Cardozo et al., 2005; Homann and Eisenbarth, 2006; Kopito and Ron, 2000; Nepom, 2008; Viola and Lanzavecchia, 1996; Wells et al., 1997). The latter is done by either the induction of free radicals in beta-cells, and/or the upregulation of Fas expression on beta-cell surface, leading to an increase in the interaction with Fas ligand on infiltrating lymphocytes (Atkinson and Eisenbarth, 2001; Moriwaki et al., 1999; Petrovsky et al., 2002).
However, clinical and experimental evidence indicates that massive beta-cell death also results from a combination of factors, such as beta-cell stress, inflammation and insulin resistance (O'Sullivan-Murphy and Urano, 2012). As a matter of fact, Bottazzo (1986) questioned whether beta-cell death was mainly driven by beta-cell death triggered by immune response (i.e., beta-cell homicide) or beta-cell apoptosis triggered by cellular stress and inflammation (i.e., beta-cell suicide).
The degree of beta-cell destruction by autoreactive CD8+ and CD4+ T-cells (homicide) depends on both the affinity/avidity of T-cell receptor (TCR) binding with pMHC class I and class II molecules, and the population sizes of the different clones of islet-specific autoreactive T-cells, possessing various levels of avidities and autoantigenic specificities, that is governed by the level of (inter- and intra-clonal) competition between them (Bluestone et al., 2010; Jaberi-Douraki et al., 2014; Khadra et al., 2011; Morran et al., 2010). As T1D progresses, the avidity of autoreactive T-cells increases during the course of the immune response in a process that is called avidity maturation, which is regulated by tolerance and competition (Standifer et al., 2009). Persistent changes in beta-cell physiology, e.g., hyperexpression of MHC class I molecules once autoimmunity has been initiated, likely enhance their sensitivity to such autoimmune destruction. Understanding the mechanisms defining the interactions between these clones may provide important insights about the dynamics of this disease and how to systematically block autoreactivity without compromising the immune system as a whole.
On the other hand, the degree of beta-cell destruction by inflammation and cellular stress (suicide) is triggered by endo-plasmic reticulum (ER) stress during the progression of T1D. Beta-cells are professional secretory cells, which make extensive use of the ER machinery to synthesize insulin and other proteins (Alberts et al., 2002; Ghaemmaghami et al., 2003; Rutkowski and Kaufman, 2004; Schnell, 2009). Insulin is synthesized in the ER at a rate of 1 million molecules per minute (Anelli and Sitia, 2008; Liu et al., 2007; Schuit et al., 1988). It has been suggested that mild persistent hyperglycemia and inflammatory signaling, e.g., through IL-1, can trigger ER-stress (as well as oxidative stress and mitochondrial stress, respectively) and beta-cell apoptosis (Atkinson et al., 2011; Marchetti et al., 2007). When the ER protein-folding need exceeds beta-cell functional capacity and ER-stress is ensued, another intracellular process, called the adaptive unfolded protein response (UPR), is triggered to meet the challenge of processing larger insulin loads. By augmenting the ER's complement of molecular chaperones and other folding activities, the UPR elevates protein folding capacity to match need. In T1D, the attrition of beta-cell population can cause severe elevations in ER-stress in the remaining beta-cells, which are forced to synthesize and secrete larger amounts of insulin. To restore protein homeostasis in the beta-cells under autoimmune attack, the UPR is activated, reversing ER-stress in beta-cells (i.e., acting as an important secondary modifier of the overall disease process). If the UPR is unable to restore protein homeostasis, beta-cells eventually succumb to damage and apoptosis (Atkinson et al., 2011; Bottazzo, 1986).
Interestingly, it was shown that the decline in beta-cell number/function, due to autoimmune responses, can be reduced in early T1D patients that received intensive insulin treatment (The Diabetes Control and Complications Trial Research Group, 1998). Hyperglycemia alone is not sufficient to induce beta-cell death, but can lead to dysfunction (Fontés et al., 2010). Modest hyperglycemia, together with cytokine-mediated (oxidative) and ER-stress, on the other hand, may exacerbate beta-cell death and dysfunction (Atkinson et al., 2011). The contribution from hyperglycemia in accelerating this destructive process could be important when considering the recovery of beta-cell function that occurs in the honeymoon period for many new-onset T1D patients, once the hyperglycemia is treated (Atkinson et al., 2011; Fontés et al., 2010).
Because of the experimental difficulty in accessing the pancreatic tissue and lymph nodes from subjects at risk of developing T1D, it is imperative to develop predictive mathematical models of pancreatic beta-cell destruction to understand the role of the autoimmune response (leading to beta-cell homicide) and ER-stress (leading to beta-cell suicide). There has been several modeling studies of ER-stress and UPR (Aldridge et al., 2006; Kholodenko, 2006; Kitano, 2002; Schnell, 2009; Schnell et al., 2007; Erguler et al., 2013) that have focused on understanding the molecular mechanisms regulating both of these processes. We aim in this study to model ER-stress and UPR macroscopically as two independent processes affecting beta-cell population dynamics, and combine them with other autoimmune processes involving T-cell mediated destruction. Our goal is to address the following three fundamental questions: What levels of pancreatic beta-cells during the progression of T1D trigger ER-stress? How does ER-stress contribute to the beta-cell extinction rate during the progression of T1D? And, what level of ER-stress triggers UPR signaling?
2. Formulation of the mathematical model
2.1. Non-scaled model
Applying similar approaches to those used in modeling T-cell dynamics in autoimmune T1D (Jaberi-Douraki et al., 2014; Khadra et al., 2011, 2009, 2010b; Marée et al., 2006), we develop a model that consists of three subclones of T-cells with an ascending order of avidities. For simplicity, the three subclones are assumed to have the same autoantigenic specificity, representing the whole pool of beta-cell specific autoantigens. As illustrated in Fig. 1, the positive selection of islet-specific autoreactive T-cells in the thymus (Pietropaolo et al., 2012) leads to T-cell escape and autoimmune destruction of beta-cells (homicide) in the pancreas. The diminishing number of beta-cells in turn triggers ER-stress in surviving beta-cells because they are forced to overwork to compensate for the insulin deficit. In these individual pancreatic beta-cells that are unable to balance the insulin protein load display a rough ER distended with protein aggregates, and undergo accelerated cell apoptosis (suicide), hastening the decline of functional beta-cell mass. We assume that during this process, UPR is activated to reverse both ER-stress and, to a certain degree, beta-cell extinction. The uptake of dead beta-cells by APCs and the expression of pMHCs on their surface lead to further priming of autoreactive T-cells and the intensification of the autoimmune response. Cytokines secreted by T-cells are assumed to be at quasi-steady state (QSS), making their total concentration proportional to the population sizes of the three subclones of T-cells.
Fig. 1.
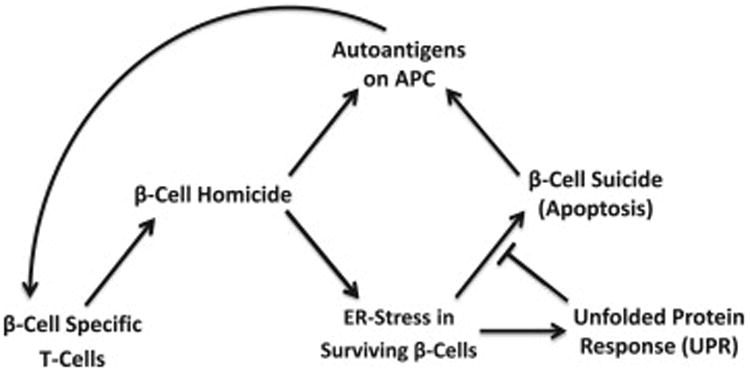
A scheme displaying the different factors involved in beta-cell suicide and homicide in autoimmune T1D. T-cell induced destruction of beta-cells triggers both ER-stress that causes beta-cell suicide, and the unfolded protein response (UPR) in surviving beta-cells. Autoantigens from dead beta-cells are expressed as peptide-major histocompatibility complexes (pMHCs) on antigen presenting cells (APCs) for further T-cell activation and recruitment in an autocatalytic way.
By labeling the population sizes of the three subclones of T-cells by Ti, i = 1, 2, 3, beta-cells by β and pMHC expression level on APCs by P, the scheme of Fig. 1 implies that their dynamics are given by
| (1) |
| (2) |
| (3) |
where σiP/(P+ki) and αiTiP/(P+ki) are the Michaelis-Menten terms describing the pMHC-dependent thymus input and replication of T-cells within each subclone with maximum rates σi and αi, respectively, and half-maximum activation ki that is inversely correlated with the avidity of the three T-cell subclones (Skowera et al., 2008; Standifer et al., 2009) (i.e., k1 ≥ k2 ≥ k3), δTiTi is the T-cell turnover, is the T-cell homeostasis due to nonuniform but symmetric inter-clonal competition arising from limited space and limited number of pMHC binding sites (symmetry here means that the unitless parameters εij satisfy εij = εji),
is the beta-cell renewal (or growth) due to neogenesis and replication (Khadra et al., 2009), κℋ(T1, T2, T3)β is the autoimmune destruction (homicide) of beta-cells by T-cells occurring at a constant rate κ (also called killing efficacy) Er(β, Upr)β is the ER-stress-induced beta-cell loss (suicide) that depends on both beta-cell number and the strength of UPR signal, R(κℋ(T1, T2, T3)+ρEr(β, Upr))β is the mass-action term describing the production of pMHCs from dead beta-cells (Atkinson et al., 2011), and δPP is the pMHC turnover. The parameter ρ here represents the relative efficiency of APCs in processing beta-cell specific peptides from the two destructive processes.
The two important features of this model are (i) the inclusion of beta-cell homicide described by the function
| (4) |
where 0 < r1 ≤ r2 ≤ r3 = 3 represent the relative killing efficacies of the three subclones, which are compatible with their increasing level of avidities, and (ii) the inclusion of beta-cell suicide occurring at a rate Er(β, Upr) due to ER-stress. To make the model more accurate physiologically, we impose the following three conditions on the rate Er: limβ→0Er(β, Upr) is finite, which means that ER-stress plateaus by reaching its maximum level; limβ→0Er(β, Upr)β = 0 (i.e., ER-stress-induced beta-cell death is biphasic); and limβ→∞Er(β, Upr) = 0, which means that ER-stress is negligible when the beta-cell loss is insignificant. To meet these criteria, we choose the Er(β, Upr) to be
| (5) |
where ae is the maximum ER-stress, n = 2 is the Hill coefficient, ke is the half-maximum ER-stress, and Upr is the negative feedback from UPR signaling cascade. To model the inhibitory effect of UPR and to meet the second criteria of ER-stress, we assume that Upr is of Holling type IV formalism (Jost et al., 1973), given by
| (6) |
where āu is the maximum UPR and k̄u is the half-maximum activation of UPR. Due to the recursive nature of Eqs. (5) and (6), we simplify Eq. (6) by assuming that Upr depends on Er(β, 0). In other words,
| (7) |
where and . Notice that the expression of Upr in Eq. (7) is biphasic with Upr(0) = limβ→∞ Upr = 0, which is considered physiological in view of the fact that UPR is negligible at both high and low beta-cell numbers.
2.2. Model rescaling
We simplify the model (1)–(3) by making the following substitutions:
| (8) |
where and β0 is the maximal number of beta-cells. The model then becomes
| (9) |
| (10) |
| (11) |
where the new non-italicized parametric quantities introduced into Eqs. (9)-(11) are given by
| (12) |
and
| (13) |
with
is the scaled form of Upr (see Eq. (7)) and
To maintain the ascending order of avidity, we maintain our previous assumption that k3 ≤ k2 ≤ k1. For the rest of the paper, we will use the scaled model Eqs. (9)–(11) to perform our analysis and simulations.
2.3. Parameter estimation
Some of the parameters of the model have been previously estimated in Khadra et al. (2009) and Sugarman et al. (2013). Data from non-obese diabetic (NOD) mice, prone to developing insulin-dependent diabetes similar to human T1D, was used to determine the ballpark values of these parameters. This was done by applying steady state and stability analysis on similar T-cells models. However, the parameters associated with the role of ER-stress in beta-cell suicide, including those that appear in Eq. (13), remain unknown. To find estimates and ranges for these parameters, we apply similar nonlinear stability analysis approaches to the scaled model described by Eqs. (9)–(11).
We begin first by noting that in the absence of an autoimmune assault, it is expected that only one stable steady state for β is attained; namely, the healthy state βss = 1. In view of Eq. (10), this steady state must also satisfy the equation
| (14) |
where ℋ(
 1,
1,
 2,
2,
 3) = 0 (see Eq. (4)). It then follows from Eq. (14) that
3) = 0 (see Eq. (4)). It then follows from Eq. (14) that
which means that
| (15) |
Since
then by Eq. (15), we have
| (16) |
Furthermore, because the steady state βss = 0 is unstable in the absence of an autoimmune attack, we may conclude from Eq. (10) that in the neighborhood of βss, we have
| (17) |
The two latter inequalities (16) and (17) imply that ae must be bounded by the following range:
| (18) |
whereas ke, according to inequalities (16) and (18), is bounded below by
Using the ranges for s and kβ obtained in Khadra et al. (2009) and listed in Table 1, we can conclude from (17) that ae ∈ [9.1 × 10−4, 0.16] day−1. Moreover, it is estimated that the rate of beta-cell loss during T1D progression in NOD mice is about 4300 cells/ day (Kurrer et al., 1997), a rate that includes the cumulative T-cell-dependent and ER-stress-dependent destruction described by the negative terms in Eq. (10). In other words, we can estimate the range of ER-stress rate at the start of the autoimmune attack (when beta-cell number is still intact) by setting
Table 1.
Values of the parameters appearing in the scaled model described by Eqs. (9)–(11). Parameters without units are dimensionless. For symmetry, we assume that εij = εji, i, j= 1, 2, 3.
| Parameter | Description | Value | Range | Ref. |
|---|---|---|---|---|
| σ1 ≈ σ2 ≈ σ3 | Influx rate of naïve-cells from thymus | ≈ 5.8787 × 10−5 day−1 | [3.8341, 19.596] × 10−5 | Khadra et al. (2009), Sugarman et al. (2013) |
| α1, α2, α3 | Expansion rate of T-cells | 10, 6, 2 day-1 | [2, 20] | Jaberi-Douraki et al. (2014), Khadra et al. (2011, 2009, 2010a, 2010b), Kim et al. (2007) |
| δT1, δT2, δT3, | T-cell turnover rate | 0.1, 0.15, 0.2 day−1 | [0.01, 0.3] | Jaberi-Douraki et al. (2014), Khadra et al. (2011, 2009, 2010a, 2010b), Kim et al. (2007) |
| k1, k2, k3 | Saturation threshold for T-cell activation | 2, 1, 0.1 | [1, 3], [0.5, 2], [10−5, 0.5] | Jaberi-Douraki et al. (2014), Khadra et al. (2011), Standifer et al. (2009), Skowera et al. (2008) |
| ε | T-cell competition | 5 × 10−6 (cell day)−1 | – | Jaberi-Douraki et al. (2014), Khadra et al. (2011, 2009, 2010a) |
| εij (i, j = 1, 2, 3) | Scaling factor for the competition between the ith and jth T-cell subclones | 1 | [0.5, 1.5] | |
| s | Maximal rate of beta-cell renewal per day | 0.0011 day−1 | [9.3, 20] × 10−4 | Dor et al. (2004), Khadra et al. (2009) |
| kβ | Saturation threshold for beta-cell renewal | 0.0159 | [0.0125, 0.022] | Dor et al. (2004), Khadra et al. (2009) |
| κ | Killing rate of beta-cells | 7 × 10−10(cell day)−1 | [10−11, 10−7] | Jaberi-Douraki et al. (2014), Khadra et al. (2011), Khadra et al. (2009), Skowera et al. (2008) |
| ρ | Relative efficiency of peptide processing in APCs | 2.5 | – | Fitted |
| ae | Maximal rate of beta-cell loss induced by ER-stress | 0.1 day−1 | [9.1 × 10−4, 0.16] | Estimated |
| ke | Saturation threshold for ER-stress | 0.2 | [0.11, 0.35] | Estimated |
| ku | Saturation threshold for UPR | 1.5 | [0.3, 2.5] | Estimated |
| au | Maximal rate of UPR signal transduction cascade | 5.3124 | [2.8, 19.8] | Estimated |
| R̂ | Ratio of T-cell net growth rate to competition factor | 8.51 × 105 cells | – | Jaberi-Douraki et al. (2014), Khadra et al. (2011, 2009), Skowera et al. (2008) |
| R | Peptide accumulation rate | 0.4 | – | Jaberi-Douraki et al. (2014), Khadra et al. (2011, 2009), Skowera et al. (2008) |
| δP | Peptide degradation rate | 0.1 day−1 | – | Jaberi-Douraki et al. (2014), Khadra et al. (2011, 2009, 2010a, 2010b), Mahaffy and Edelstein-Keshet (2007) |
| r1, r2, r3 | Relative killing efficacies of the three subclones | 0.7, 0.875, 3 | – | Jaberi-Douraki et al. (2014), Khadra et al. (2011) |
| (19) |
where β0 is the total number of beta-cells in the healthy state, estimated to be between [5,6] × 105 cells (Jo et al., 2007; Khadra et al., 2009). By substituting the known parameter values listed in Table 1 into Eq. (19) and setting β = 1, we find that Er ∈ [0, 0.0914] day−1 (negative values are ignored). Taking inequality (17) into consideration and recognizing that UPR is negligible at the start of the autoimmune attack (i.e., Upr ≈ 0), we can solve for ke in Eq. (13), and obtain the range [0.11, 0.35] for ke.
Finally, according to Eq. (15),
| (20) |
where
which has to be positive to guarantee the positivity of au (as is the case for the default values of the parameters listed in Table 1). The dependence of au on ku in Eq. (20) leaves only one free parameter, ku, to be determined. Knowing that only 10–20% of beta-cells survive destruction during T1D, the range of ku that corresponds to a steady state level for β within the range [0.1, 0.2] can be estimated by plotting the bifurcation diagram of β with respect to ku while keeping other parameters fixed at their default values listed in Table 1. Using this methodology, we observe (not shown here) a steady decline in β while decreasing ku. Thus for β ∈ [0.1, 0.2], we must have ku ∈ [0.3, 2.5] and au ∈ [2.8,19.8] (in view of Eq. (20)).
2.4. Numerical simulations
Model simulations and bifurcation diagrams were produced using either MATLAB (Mathworks), or the public domain software package AUTO.
3. Results
3.1. LHS and PRCC
One important aspect of modeling studies of physiological systems, such as T1D, is the ability to determine how sensitive (or uncertain) different components of the model are to perturbations and thus identify potential targets for therapeutic purposes. Various methodologies for assessing both the sensitivity of any model to small variations in parameter values and its inherent uncertainty are available in the literature. Here, we apply the Latin Hypercube Sampling (LHS) method in combination with Partial Rank Correlation Coefficient (PRCC) to study the global sensitivity of the scaled model, Eqs. (9)–(11), in a multi-dimensional parameter space (Marino et al., 2008).
In the LHS method, random sampling of the parameters is done independent of each other. It is performed by dividing the ranges of K parameters into N bins, where N is the total number of samples or iterates (simulations), and randomly selecting values within these ranges according to probability density functions (pdf). Once a value is selected for a given parameter in a K-tupled parameter combination, the bin containing this value is then discarded in all subsequent K-tuples (i.e., each bin is sampled exactly once without replacement). In our simulations, we apply N=20,000 iterations and use the normal distribution for randomly selecting values. The modes (= means) of these distributions are the default values of the parameters in Table 1 and standard deviations are assumed to be 0.2 of the mean. A matrix is then generated (also called the LHS-matrix), consisting of N rows, representing the sample size, and K columns corresponding to the number of parameters being varied. The resulting N parameter combinations appearing as rows in the LHS-matrix are then used to produce N simulations, yn = (
 1n,
1n,
 2n,
2n,
 3n, βn,
3n, βn,
 n)T, n = 1.2, …, N, from the model described by Eqs. (9)–(11).
n)T, n = 1.2, …, N, from the model described by Eqs. (9)–(11).
By assigning rank 1 to the smallest value obtained for each parameter, rank 2 for the next largest value, an average rank for equal values (which occurs when N is large enough to make two parameter values numerically indistinguishable from each other), and rank N (the sample size) for the largest value, we can generate the input rank-transformation matrix XR by substituting each entry of the LHS-matrix by its rank. Similarly, we can also apply the same ranking process on Y = (y1, y2, …, yN) at every time point and generate the output-rank transformation matrix YR. In other words, a new output-rank transformation matrix is generated at every discrete time point of the numerical method (which is the Nonstandard Finite Difference Schemes in our case, Mickens, 1994, 2005). The correlations between inputs (parameters) and outputs (simulations) of the model are then measured based on the rank transforms XR, YR using partial rank correlation coefficient (PRCC). This is done by evaluating the correlation coefficient
where Cov(U, V) is the covariance between U and V, (Var(U), Var(V)) and (Ū, V̄) are the variances and means of (U, V), respectively, (U, V) are the residuals (XRj − X̂Rj, YR − ŶRj), j = 1, 2, …, K, and (X̂Rj, ŶRj) are the linear regression models (see Marino et al., 2008 for more details).
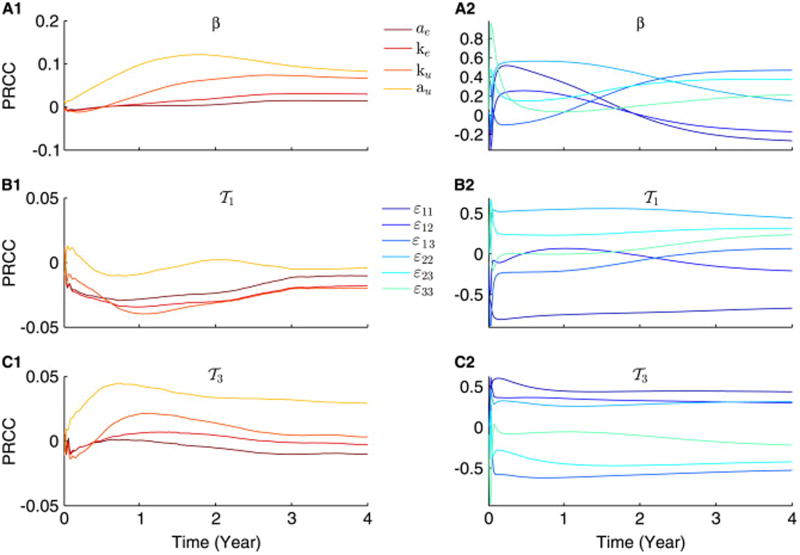
In Fig. 2, we use LHS-based PRCC to study the sensitivity of the scaled model described by Eqs. (9)–(11), to two sets of parameters: {ae, ke, au, ku}, representing the effect of ER-stress, and {ε11, ε12, ε13, ε22, ε23, ε33}, corresponding to non-uniform inter-clonal competition, while keeping all other parameters fixed at their default values listed in Table 1. The results obtained at every given parameter are considered statistically significant when the mean p-value, averaged over 4 years, is below 0.05 (results not shown). According to this latter criterion, we find that
 1 (A2) and
1 (A2) and
 3 (A3) are not significantly affected by ER-stress-related parameters (with p > 0.05), but the UPR associated parameters, au and ku, have significant impact on the dynamics of β (A1). In fact, we observe a general trend in which PRCCs in panel (A1) to be more pronounced than in panels (A2) and (A3) (with p-values that are also significantly lower). These results suggest that ER-stress-induced beta-cell suicide plays negligible role in intensifying the autoimmune response, but UPR is a more sensitive pathway and could have some impact on beta-cell survival.
3 (A3) are not significantly affected by ER-stress-related parameters (with p > 0.05), but the UPR associated parameters, au and ku, have significant impact on the dynamics of β (A1). In fact, we observe a general trend in which PRCCs in panel (A1) to be more pronounced than in panels (A2) and (A3) (with p-values that are also significantly lower). These results suggest that ER-stress-induced beta-cell suicide plays negligible role in intensifying the autoimmune response, but UPR is a more sensitive pathway and could have some impact on beta-cell survival.
Fig. 2.
Progression of PRCCs of the scaled model, described by Eqs. (9)–(11), over time, illustrating how sensitive the model is towards both ER-stress-dependent processes and nonuniform competition. PRCCs of β (A1 and A2),
 1 (B1 and B2) and
1 (B1 and B2) and
 3 (C1 and C2) are performed for the following two sets of parameters {ae, ke, au, ku} (A1–C1) and {ε11, ε12, ε13, ε22, ε23, ε33} (A2–C2). Each color corresponds to one parameter as illustrated by the two legends. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this paper.)
3 (C1 and C2) are performed for the following two sets of parameters {ae, ke, au, ku} (A1–C1) and {ε11, ε12, ε13, ε22, ε23, ε33} (A2–C2). Each color corresponds to one parameter as illustrated by the two legends. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this paper.)
In the presence of nonuniform competition, however, the model becomes very sensitive to variations in {ε11, ε12, ε13, ε22, ε23, ε33}, with mean p-values that are below 0.03 for every single parameter. Such behavior is maintained during both the transient and steady state responses of the scaled model. As expected, the positive effects exerted on
 1, the low avidity subclone, by certain parameters in (B2) become negative when considering
1, the low avidity subclone, by certain parameters in (B2) become negative when considering
 3 in (C2), the high avidity subclone, and vice versa. These results suggest that (nonuniform) competition plays a major role in shaping up the autoimmune response and could be used as a target for manipulating this response by perhaps expanding certain T-cell subclones at the expense of others.
3 in (C2), the high avidity subclone, and vice versa. These results suggest that (nonuniform) competition plays a major role in shaping up the autoimmune response and could be used as a target for manipulating this response by perhaps expanding certain T-cell subclones at the expense of others.
3.2. Effects of ER-stress and UPR on the scaled model
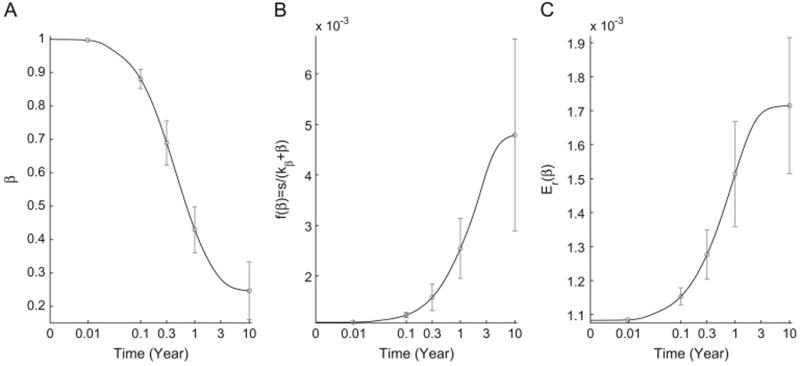
To further analyze the effects of ER-stress and UPR on the dynamics of the scaled model, described by Eqs. (9)–(11), we simulate the response of the model over a heterogeneous population of individuals, generated by randomly selecting values for the parameter set {ae, ke, au, ku}, using the LHS method. The goal is to determine, using the heterogeneous population, how the average beta-cell loss affects the different components of the model. As shown in Fig. 3, the average response of the scaled model over time shows what we would expect in the presence of autoimmunity; namely, a gradual decline in β (A) and a steady but small rise in both beta-cell renewal f(β), described by Eq. (12), and ER-stress Er(β), described by Eq. (13). Both of these outcomes arise from the fact that the decline in β leads to an increase in the pressure exerted on both of these two components. Although the rise in f(β) is still observed, it is not effective in blocking the increase in ER-stress, due to an overall decline in β.
Fig. 3.
Simulations of the scaled model, described by Eqs. (9)–(11), averaged over a heterogeneous population of individuals generated by sampling ER-stress-related parameters, {ae, ke, au, ku}, from the values and ranges listed in Table 1 using LHS method. The 10-year time evolution (black lines) of β (A), f(β) (B) and Er(β) (C) is displayed. Error bars (gray lines) in each panel represent the standard deviation at various time points. As expected, the decline in beta-cell number induces a gradual increase in both beta-cell renewal (neogenesis/proliferation) and ER-stress.
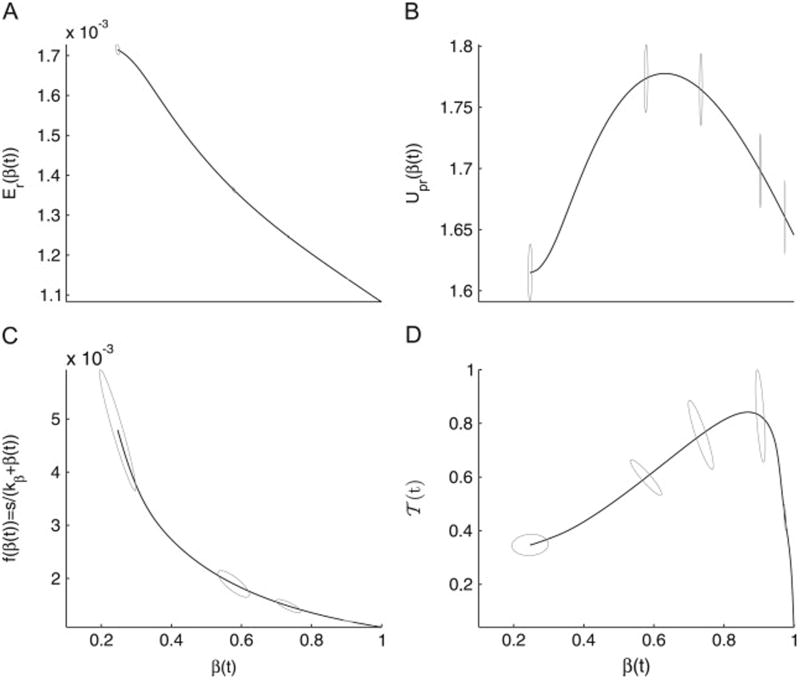
Another way of examining these outcomes can be done by plotting the average response of this heterogeneous population with respect to the time-dependent β(t), described by Eq. (10). The goal here is to determine how the decline in β is correlated with four major components of the model: ER-stress, UPR, beta-cell renewal and the total population-size of T-cells. As demonstrated in Fig. 4, the decline in β, observed in Fig. 3(A), induces a linear increase in Er (panel (A)), but hyperbolic increase in f(β) (panel (C)). It also induces a biphasic response in both UPR (panel (D)) and
 =
=
 1 +
1 +
 2 +
2 +
 3 (panel (D)). Although the UPR-biphasic response produces a maximum, its effect in blocking the steady increase in ER-stress is minimal, implying that the intracellular processes triggered in the beta-cells to meet metabolic demand are insufficient to protect surviving beta-cells from being overwhelmed from synthesizing insulin. In view of the results shown in Fig. 2(A), the sensitivity of the model to au and ku suggests that it is possible to perturb this maximum to increase the impact of UPR on ER-stress, but such an impact will not be substantial enough to block the autoimmune depletion of beta-cells, as suggested by Fig. 2(A1–C1).
3 (panel (D)). Although the UPR-biphasic response produces a maximum, its effect in blocking the steady increase in ER-stress is minimal, implying that the intracellular processes triggered in the beta-cells to meet metabolic demand are insufficient to protect surviving beta-cells from being overwhelmed from synthesizing insulin. In view of the results shown in Fig. 2(A), the sensitivity of the model to au and ku suggests that it is possible to perturb this maximum to increase the impact of UPR on ER-stress, but such an impact will not be substantial enough to block the autoimmune depletion of beta-cells, as suggested by Fig. 2(A1–C1).
Fig. 4.
The graphs (solid lines) of the functions Er (A), Upr (B), f(β) (C) and
 =
=
 1 +
1 +
 2 +
2 +
 3 (C) with respect to the time-varying β during disease progression, averaged over a heterogeneous population of individuals, as described in Fig. 3. The gray circles around the curves represent the two dimensional elliptical Gaussian distribution with a given mean and covariance matrix.
3 (C) with respect to the time-varying β during disease progression, averaged over a heterogeneous population of individuals, as described in Fig. 3. The gray circles around the curves represent the two dimensional elliptical Gaussian distribution with a given mean and covariance matrix.
3.3. T-cell and beta-cell time evolution
In previous modeling studies of T1D, the role of T-cell avidity and the killing efficacy in beta-cell destruction or homicide were investigated without the inclusion of ER-stress and UPR in the dynamics of beta-cells (Khadra et al., 2009, 2011; Jaberi-Douraki et al., 2014). In these studies, it was shown how increasing T-cell avidity and killing efficacy affected beta-cell survival and the timing of disease onset. Here we extend these studies in order to understand the synergy between T-cell-induced beta-cell homicide and ER-stress-induced beta-cell suicide. This is done by applying similar approaches in which the LHS method is utilized to randomly select parameter values from their perspective ranges.
In Fig. 5, we plot the 10-year time evolution of the scaled model, Eqs. (9)–(11), as heat-maps color-coded according to the color-bars on top of each column, by setting κ = 5 × 10−9(day cell)−1, while varying the parameters k1 (A1–D1), k2 (A2–D2) and k3 (A3–D3), one at a time within the ranges listed in Table 1. In all these simulations, the inequality k1 ≥ k2 ≥ k3 is maintained. For each value of ki used to produce one simulation within each heat-map, the LHS method is repetitively applied to select random values for the remaining parameters, taking into consideration the fact that (ki, αi) are positively correlated, (ki, δTi) are negatively correlated and (ki, ri) are negatively correlated. In other words, the values of the parameters used to generate each simulation within a heat-map in Fig. 5 for a given value of ki, i=1, 2, 3, are not the same, causing the heat maps to exhibit a certain degree of noise that is reflective of the stochastic nature of the autoimmune response in T1D.
Fig. 5.
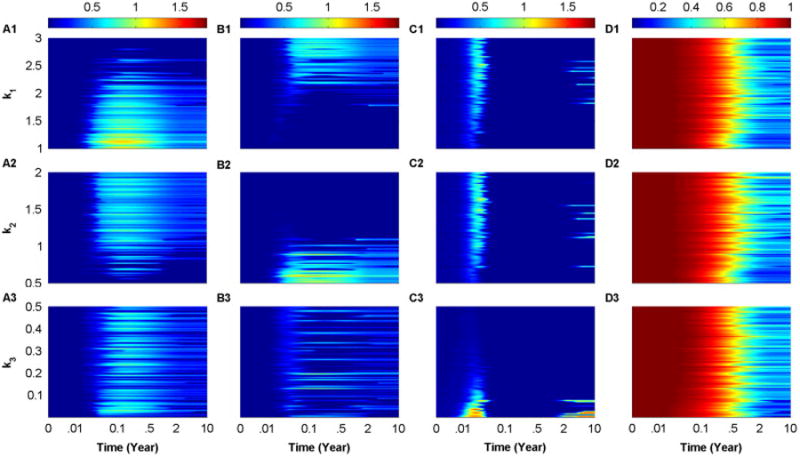
Heat-map simulations of the scaled model, described by Eqs. (9)–(11), at κ = 5 × 10−9(day cell)−1. The 10-year time evolution of
 1 (A1–A3),
1 (A1–A3),
 2 (B1–B3),
2 (B1–B3),
 3 (C1–C3) and β (D1–D3) are displayed. The color-coding in each panel is quantified by the color-bars on the top of each column. The simulations are performed by applying LHS over the following ranges: k1 ∈ [1, 3] (A1–D1), k2 ∈ [0.5, 2] (A2–D2) and k3 ∈ [0.01, 0.5] (A3–D3), given that the inequality k1 ≥ k2 ≥ k3 is always maintained. Notice that the random sampling performed by LHS makes small perturbations in the values of ki, i = 1, 2, 3, have significant implications on the number of surviving beta-cells. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this paper.)
3 (C1–C3) and β (D1–D3) are displayed. The color-coding in each panel is quantified by the color-bars on the top of each column. The simulations are performed by applying LHS over the following ranges: k1 ∈ [1, 3] (A1–D1), k2 ∈ [0.5, 2] (A2–D2) and k3 ∈ [0.01, 0.5] (A3–D3), given that the inequality k1 ≥ k2 ≥ k3 is always maintained. Notice that the random sampling performed by LHS makes small perturbations in the values of ki, i = 1, 2, 3, have significant implications on the number of surviving beta-cells. (For interpretation of the references to color in this figure caption, the reader is referred to the web version of this paper.)
Fig. 5 shows that the scaled level of T-cells
 1 (A1–A3),
1 (A1–A3),
 2 (B1–B3) and
2 (B1–B3) and
 3 (C1–C3) can coexist as well as exhibit a pattern of cyclic waves for certain values of ki, i=1, 2, 3. These waves are reminiscent to those observed in Jaberi-Douraki et al. (2014), and hypothesized to be responsible for making T1D a relapsing-remitting disease. The underlying reason for observing such waves is the presence of quasi-stable (transiently stable) steady states that lose stability when β crosses thresholds determined by the stable manifolds of the saddle points of the model (see next section for more details). The intriguing outcome of these noisy heat-map simulations is the sensitivity of β, shown in panels (D1–D3) to very small perturbations in ki, i=1, 2, 3, during the autoimmune response. In other words, small changes in ki, i=1, 2, 3, can cause a shift in the level of β from diabetic outcomes, in which β < 0.3, to nondiabetic outcomes in which β ≥ 0.3, where the 0.3-threshold represents the 30% of surviving beta-cells required for keeping affected individuals asymptomatic (typically lying between 0.1 and 0.5). These results provide a rationale as to why related high risk subjects (first degree relatives of T1D patients) can exhibit two very different outcomes in terms of disease manifestation; namely, their intrinsic variations in disease parameters. Such outcomes are regularly observed in clinical settings of T1D subjects.
3 (C1–C3) can coexist as well as exhibit a pattern of cyclic waves for certain values of ki, i=1, 2, 3. These waves are reminiscent to those observed in Jaberi-Douraki et al. (2014), and hypothesized to be responsible for making T1D a relapsing-remitting disease. The underlying reason for observing such waves is the presence of quasi-stable (transiently stable) steady states that lose stability when β crosses thresholds determined by the stable manifolds of the saddle points of the model (see next section for more details). The intriguing outcome of these noisy heat-map simulations is the sensitivity of β, shown in panels (D1–D3) to very small perturbations in ki, i=1, 2, 3, during the autoimmune response. In other words, small changes in ki, i=1, 2, 3, can cause a shift in the level of β from diabetic outcomes, in which β < 0.3, to nondiabetic outcomes in which β ≥ 0.3, where the 0.3-threshold represents the 30% of surviving beta-cells required for keeping affected individuals asymptomatic (typically lying between 0.1 and 0.5). These results provide a rationale as to why related high risk subjects (first degree relatives of T1D patients) can exhibit two very different outcomes in terms of disease manifestation; namely, their intrinsic variations in disease parameters. Such outcomes are regularly observed in clinical settings of T1D subjects.
3.4. Model analysis
The two important aspects of T1D progression are the slow decline of beta-cells (in the time scale of months), due to homeostatic mechanisms, and the fast peptide accumulation and processing in APCs (with a time scale of days). Using these two features, one can reduce the size of the scaled model, Eqs. (9)–(11), into a three-variable model by setting β equal to a constant (β = 1) and applying quasi-steady state approximation (QSS) on (11) to obtain
| (21) |
The resulting model, given by Eqs. (9) and (21), becomes a purely T-cell population model that resembles the three dimensional Lotka-Volterra system, given by
| (22) |
which was thoroughly studied by Zeeman (1993) and others (Hofbauer and Sigmund, 1988; Hofbauer and SO, 1994; Zeeman and van den Driessche, 1998). Notice here that one can obtain Eqs. (22) from Eqs. (9) and (21) by setting
| (23) |
where h is a constant. Therefore, many of the well-known results associated with the Lotka–Volterra system can be extended to the T-cell model provided that conditions (23) are satisfied, as illustrated below.
By letting
it was found by Zeeman (1993) that whenever, det(A) = 0, then the Lotka–Volterra system will not have steady states lying entirely in the interior (which excludes the boundaries) of the first quadrant of the N1, N2, N3-space (i.e., every steady state of the system has at least one zero-component). However, when det(A) ≠ 0, then the system can have one interior steady state. [The stability of these steady states and the existence of Hopf bifurcations were also investigated under various conditions.] For the reduced T-cell model satisfying conditions (23), similar results can be deduced, based on the determinant of the competition matrix A.
However, when the function h, defined in Eq. (21), is not a constant, other possibilities may occur, including the existence of an interior equilibrium point (in the first octant) despite having det(A) = 0. In fact, by taking σi = 0, i ∈ {1, 2, 3}, we find, according to Eq. (9), that
| (24) |
for
 i ≠ 0, which shows that
i ≠ 0, which shows that
| (25) |
Since these three functions are strictly increasing, it is plausible for their graphs to intersect at exactly one point for a given set of values attained by the parameters αi, ki and δTi, i=1, 2, 3. Such an intersection may occur at most once. Although this seems to be very unlikely and that the set of parameter values generating such an outcome may not be even physiological, the resulting equilibrium would have nonzero T-cell levels in all three subclones simultaneously.
When the determinant of the matrix A of the T-cell model, given by Eqs. (9)–(11), is nonzero, more interesting dynamics are observed. This is expected in view of the fact that the T-cell model generalizes the notion of competition introduced in the three dimensional Lotka–Volterra system. In this case, not only interior equilibria may exist, but oscillatory solutions that underlie relapse-remission in T1D may also exist, as discussed in von Herrath et al. (2007) and analyzed in Jaberi-Douraki et al. (2014). By making β, the slowly changing variable, a bifurcation parameter, we can plot the effect of declining beta-cell level on the steady states of
 3, the level of the highest avidity T-cell subclone. As shown in Fig. 6(A), when β is below 0.4, we observe a rise in the steady state level of
3, the level of the highest avidity T-cell subclone. As shown in Fig. 6(A), when β is below 0.4, we observe a rise in the steady state level of
 3 along two stable branches, one of which (labeled 1) terminates to the left at an unstable steady state, while the other (labeled 2) terminates at a transcritical bifurcation point. The presence of these two stable branches indicates that bistability and cyclic waves are two important features of the T-cell model. The latter is generated during β decline when the rise in
3 along two stable branches, one of which (labeled 1) terminates to the left at an unstable steady state, while the other (labeled 2) terminates at a transcritical bifurcation point. The presence of these two stable branches indicates that bistability and cyclic waves are two important features of the T-cell model. The latter is generated during β decline when the rise in
 3 along branch 1 eventually drops to branch 2 upon reaching the left-end point of the bistable regime, followed by another rise along branch 2, causing these waves in
3 along branch 1 eventually drops to branch 2 upon reaching the left-end point of the bistable regime, followed by another rise along branch 2, causing these waves in
 3 to occur as observed in Fig. 5. Initial conditions and parameter values of the model will determine if such outcomes can be produced. ER-stress-induced suicide, for example, could act as a perturbing factor that determines which stable branch of the bifurcation diagram is followed.
3 to occur as observed in Fig. 5. Initial conditions and parameter values of the model will determine if such outcomes can be produced. ER-stress-induced suicide, for example, could act as a perturbing factor that determines which stable branch of the bifurcation diagram is followed.
Fig. 6.
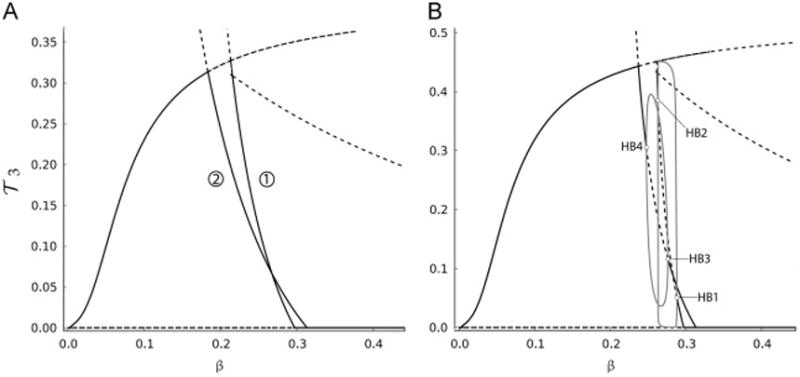
Bifurcation diagrams of
 3, described by Eq. (11), with respect to β, the slowly varying variable in the presence of uniform (A) and nonuniform (B) inter-clonal competitions. To generate nonuniform competition in (B), the following values for the competition scaling factors are used: ε12 = 3, ε13 = 1.1 and ε33 = 0.782. Solid-(dashed-) black lines in panels (A) and (B) represent stable (unstable) steady states and gray-solid lines in panel (B) represent the branches of stable periodic orbits emerging from supercritical Hopf bifurcation points (HB1, HB2, HB3 and HB4). The two panels are truncated at β = 0.45 to magnify the bifurcation diagrams for small β, and because higher values of β do not alter the stable steady state
3, described by Eq. (11), with respect to β, the slowly varying variable in the presence of uniform (A) and nonuniform (B) inter-clonal competitions. To generate nonuniform competition in (B), the following values for the competition scaling factors are used: ε12 = 3, ε13 = 1.1 and ε33 = 0.782. Solid-(dashed-) black lines in panels (A) and (B) represent stable (unstable) steady states and gray-solid lines in panel (B) represent the branches of stable periodic orbits emerging from supercritical Hopf bifurcation points (HB1, HB2, HB3 and HB4). The two panels are truncated at β = 0.45 to magnify the bifurcation diagrams for small β, and because higher values of β do not alter the stable steady state
 3 = 0. As indicated, nonuniform competition induces oscillations in
3 = 0. As indicated, nonuniform competition induces oscillations in
 3.
3.
Another important aspect of the model that should be analyzed is the effect of nonuniform competition on its dynamics. According to previous studies (De Boer and Perelson, 1994), it was found that having such nonuniformity leads to the dominance of one subclone with the highest competition over all others. In view of Fig. 6(B), we find that by setting ε12= 3, ε13 = 1.1 and ε33 = 0.782, coexistence between the three T-cell subclones can transiently occur within certain ranges of β (between 0.2 and 0.3). This coexistence occurs as transient oscillatory solutions that are determined by the stable periodic branches emanating from the supercritical Hopfs. These oscillations are similar to those observed in Jaberi-Douraki et al. (2014) and thought to be another mechanism underlying relapse-remission in T1D.
4. Discussion
During the progression of the clinical onset of T1D, high risk subjects exhibit multiple islet autoantibodies and wide blood glucose excursions associated with beta-cell destruction. The difficulty in collecting in vivo data from pancreatic tissue and pancreatic lymph nodes from these subjects makes developing predictive mathematical models of pancreatic beta-cell destruction a promising and an alternative tool to understand the role of pathogenic T-cell responses and ER-stress in the natural history of the disease. In this study, an ordinary differential equation model, consisting of three competing subclones of T-cells with the same autoantigen specificity but with varying avidities, beta-cells and the expression level of pMHCs on APCs, was developed. The unique aspect of this model is the inclusion of beta-cell ER-stress and UPR signaling that were described as functions of the number of surviving beta-cells. According to this formalism, intracellular pathways responsible for triggering both of these signals were ignored and a more macroscopic formalism is considered instead.
The model provided a quantitative framework to investigate the effects of ER-stress on beta-cell extinction during the progression of T1D, as well as the role of nonuniform competition exerted by the three subclones of T-cells on their dynamics. Using a combination of steady state analysis and statistical approaches, the study provided important insights about the presumed synergy between T-cell induced homicide and ER-stress-induced suicide in the demise of beta-cells in T1D. To determine the sensitivity of the model to these two factors, the Latin hypercube sampling (LHS) method in combination with partial rank correlation coefficient was applied. Our results revealed that the dynamics of T-cells (but not beta-cells) were not significantly affected by the processes involved in ER-stress (which is counter intuitive), while beta-cells and T-cells were both very sensitive to perturbations in the competition scaling factors that were used to generate nonuniform competition. In the former, beta-cell loss exhibited marked dependence on the maximum level and half-maximum activation of UPR. These results indicate that although UPR signaling in beta-cells is an available therapeutic target for improving disease outcomes, it is not sufficient to block the disease because beta-cell autoimmune destruction is too powerful and will continue unabated until disease onset. In other words, our results suggest that it is more effective to target the autoimmune mechanisms (such as the competition between the T-cell (sub)clones) responsible for beta-cell destruction rather than targeting beta-cell activities.
By considering a heterogeneous population of individuals whose parameters were randomly selected using LHS, we analyzed the average response of the model by quantifying ER-stress, UPR and beta-cell renewal over time. Our simulations showed that the presence of compensatory mechanisms to support beta-cell function is insufficient to impede the steady decline in beta-cell number. Furthermore, this steady decline was accompanied by monophasic linear and hyperbolic rise in ER-stress and beta-cell renewal, respectively, but a biphasic response is observed in both UPR and total autoreactive T-cell accumulation. The model showed that the lack of sensitivity of T-cells to ER-stress-related processes makes any elevation in the maximum level of UPR potentially helpful in the short run to meet metabolic demand (as is the case for example in the honeymoon period observed in T1D-patients, Chase et al., 2004; Muhammad et al., 1999; Bober et al., 2001; Robles et al., 2002; von Herrath et al., 2007), but in the long run, this elevation is doomed to fail in maintaining healthy number of beta-cells that can secrete enough insulin to keep normal level of glucose in circulation.
The heterogeneity observed in the time evolution of T1D between different high risk subjects, including first degree relatives, is well known experimentally. The impact of this heterogeneity on the dynamics of the model was analyzed to determine disease outcomes, and to demonstrate its sensitivity to T-cell kinetics. Using the LHS method to randomly select parameters of the model, we showed that small perturbations in the values of the parameters may alter the outcomes completely by shifting the beta-cell survival level above or below the critical threshold for clinical T1D. Fluctuations in T-cells were also exhibited under various conditions of T-cell avidity. These fluctuations were due to the presence of transient bistability responsible for producing recurrent surges in the high avidity T-cell subclone throughout disease progression.
Using bifurcation analysis that assumes beta-cell loss to be a slowly occurring process, we showed in Fig. 6 how bistability (produced by the two branches 1 and 2) for certain values of T-cell avidities was manifested. Altering the values of avidity, however, is expected to modify the configuration of the bifurcation diagram and make the bistability-induced T-cell fluctuations disappear, as illustrated in Fig. 5. Furthermore, based on the bifurcation diagram in Fig. 6(B), we found that in the presence of nonuniform competition, the model could possess up to four Hopf bifurcation points (HB1–HB4) when beta-cell number is within 20–30% of its original population size. By setting the peptide equation (21) to a constant, the model becomes a three dimensional model that is similar to the Lotka–Volterra system analyzed in Gyllenberg et al. (2006), Hofbauer and SO (1994), Lu and Luo (2002), Lu and Luo (2003), May and Leonard (1975), and Wang et al. (2011). It was shown in May and Leonard (1975) that it is plausible for this system to possess four Hopf bifurcation points. Based on our simulations of the full model presented here (i.e., with the peptide assumed to be a dynamic variable), a total of six Hopf bifurcation points may be generated.
As stated earlier, the effect of ER-stress and UPR on beta-cells was described macroscopically as a function of surviving beta-cells. To account for the intracellular biochemical pathways that regulate ER-stress and UPR, a more detailed model, that couples this subcellular world with the supracellular regime defining beta-cell interaction with immune cells, must be also developed. Such study will provide better understanding of how UPR signaling could act as a secondary modifier for T1D.
Footnotes
This work was supported by the National Institute of Diabetes and Digestive and Kidney Diseases (Grants R01 DK53456, R01 DK56200, DP3 DK101083 and R21 DK073724) to MP, the Natural Sciences and Engineering Council of Canada (Discovery Grant Program) to AK, the University of Michigan Protein Folding Diseases Initiative to SS, and Centre for Mathematical Medicine, Fields Institute, Toronto, Canada.
Contributor Information
Majid Jaberi-Douraki, Email: majid.jaberi-douraki@mail.mcgill.ca.
Santiago Schnell, Email: schnells@umich.edu.
Massimo Pietropaolo, Email: maxtp@med.umich.edu.
Anmar Khadra, Email: anmar.khadra@mcgill.ca.
References
- Alberts B, Johnson A, Lewis J, Raff M, Roberts K, Walter P. Molecular Biology of the Cell. 4th. New York: Garland Science; 2002. [Google Scholar]
- Aldridge BB, Burke JM, Lauffenburger DA, Sorger PK. Physicochemical modelling of cell signalling pathways. Nat Cell Biol. 2006;8:1195–1203. doi: 10.1038/ncb1497. [DOI] [PubMed] [Google Scholar]
- Anelli T, Sitia R. Protein quality control in the early secretory pathway. EMBO J. 2008;27:315–327. doi: 10.1038/sj.emboj.7601974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson MA, Bluestone JA, Eisenbarth GS, Hebrok M, Herold KC, Accili D, Pietropaolo M, Arvan PR, Von Herrath M, Markel DS, Rhodes CJ. How does type 1 diabetes develop?: the notion of homicide or β-cell suicide revisited. Diabetes. 2011;60(5):1370–1379. doi: 10.2337/db10-1797. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson MA, Eisenbarth GS. Type 1 diabetes: new perspectives on disease pathogenesis and treatment. Lancet. 2001;358(9277):221–229. doi: 10.1016/S0140-6736(01)05415-0. [DOI] [PubMed] [Google Scholar]
- Bluestone JA, Herold K, Eisenbarth G. Genetics, pathogenesis and clinical interventions in type 1 diabetes. Nature. 2010;464:1293–1300. doi: 10.1038/nature08933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bober E, Dündar B, Büyükgebiz A. Partial remission phase and metabolic control in type 1 diabetes mellitus in children and adolescents. J Pediatr Endocrinol Metab. 2001;14(4):435–442. doi: 10.1515/jpem.2001.14.4.435. [DOI] [PubMed] [Google Scholar]
- Bottazzo GF. Lawrence lecture. Death of a beta cell: homicide or suicide? Diabet Med. 1986;3:119–130. doi: 10.1111/j.1464-5491.1986.tb00722.x. [DOI] [PubMed] [Google Scholar]
- Cardozo AK, Ortis F, Storling J, Feng YM, Rasschaert J, et al. Cytokines downregulate the sarcoendoplasmic reticulum pump Ca2+ ATPase 2b and deplete endoplasmic reticulum Ca2+, leading to induction of endoplasmic reticulum stress in pancreatic b-cells. Diabetes. 2005;54:452–461. doi: 10.2337/diabetes.54.2.452. [DOI] [PubMed] [Google Scholar]
- Chase HP, MacKenzie TA, Burdick J, Fiallo-Scharer R, Walravens P, Klingen-smith G, Rewers M. Redefining the clinical remission period in children with type 1 diabetes. Pediatr diabetes. 2004;5(1):16–19. doi: 10.1111/j.1399-543X.2004.00034.x. [DOI] [PubMed] [Google Scholar]
- De Boer RJ, Perelson AS. T cell repertoires and competitive exclusion. J Theor Biol. 1994;169(4):375–390. doi: 10.1006/jtbi.1994.1160. [DOI] [PubMed] [Google Scholar]
- Dor Y, Brown J, Martinez OI, Melton DA. Adult pancreatic beta-cells are formed by self-duplication rather than stem cell differentiation. Nature. 2004;429:41–46. doi: 10.1038/nature02520. [DOI] [PubMed] [Google Scholar]
- Erguler K, Pieri M, Deltas C. A mathematical model of the unfolded protein stress response reveals the decision mechanism for recovery, adaptation and apoptosis. BMC Syst Biol. 2013;7(16):1–18. doi: 10.1186/1752-0509-7-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fontés G, Zarrouki B, Hagman DK, et al. Glucolipotoxicity age-dependently impairs beta cell function in rats despite a marked increase in beta cell mass. Diabetologia. 2010;53:2369–2379. doi: 10.1007/s00125-010-1850-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghaemmaghami S, Huh W, Bower K, Howson RW, Belle A, et al. Global analysis of protein expression in yeast. Nature. 2003;425:737–741. doi: 10.1038/nature02046. [DOI] [PubMed] [Google Scholar]
- Gyllenberg M, Yan P, Wang Y. A 3D competitive Lotka–Volterra system with three limit cycles: a falsification of a conjecture by Hofbauer and So. Appl Math Lett. 2006;19(1):1–7. [Google Scholar]
- Hofbauer J, Sigmund K. The Theory and Evolution of Dynamical Systems. Cambridge University Press; Cambridge, UK: 1988. [Google Scholar]
- Hofbauer J, So JWH. Multiple limit cycles for three dimensional competitive Lotka–Volterra equations. Appl Math Lett. 1994;7:65–70. [Google Scholar]
- Homann D, Eisenbarth GS. An immunologic homunculus for type 1 diabetes. J Clin Investig. 2006;116:1212–1215. doi: 10.1172/JCI28506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacob J, Baltimore D. Modelling T-cell memory by genetic marking of memory T cells in vivo. Nature. 1999;399:593–597. doi: 10.1038/21208. [DOI] [PubMed] [Google Scholar]
- Jo J, Choi MY, Koh DS. Size distribution of mouse Langerhans islets. Biophys J. 2007;93:2655–2666. doi: 10.1529/biophysj.107.104125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jost JL, Drake JF, Fredrickson AG, Tsuchiya HM. Inter-actions of Tetrahymena pyrisformis, Escherichia cole, Azotobacter vinelandii, and glucose in a minimal medium. J Bacteriol. 1973;113:834–840. doi: 10.1128/jb.113.2.834-840.1973. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jaberi-Douraki M, Pietropaolo M, Khadra A. Predictive models of type 1 diabetes progression: understanding T-cell cycles and their implications on autoantibody release. PLoS ONE. 2014;9(4):e93326. doi: 10.1371/journal.pone.0093326. http://dx.doi.org/10.1371/journal.pone.0093326. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kholodenko BN. Cell-signalling dynamics in time and space. Nat Rev Mol Cell Biol. 2006;7:165–176. doi: 10.1038/nrm1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitano H. Systems biology: a brief overview. Science. 2002;295:1662–1664. doi: 10.1126/science.1069492. [DOI] [PubMed] [Google Scholar]
- Khadra A, Pietropaolo M, Nepom GT, Sherman A. Investigating the role of T-cell avidity and killing efficacy in relation to type 1 Diabetes prediction. PLOS One. 2011;6(5):e14796. doi: 10.1371/journal.pone.0014796. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khadra A, Santamaria P, Edelstein-Keshet L. The role of low avidity T cells in the protection against type 1 diabetes: a modeling investigation. J Theor Biol. 2009;256:126–141. doi: 10.1016/j.jtbi.2008.09.019. [DOI] [PubMed] [Google Scholar]
- Khadra A, Santamaria P, Edelstein-Keshet L. The pathogenicity of self-antigen decreases at high levels of autoantigenicity: a computational approach. Int Immunol. 2010a;22:571–582. doi: 10.1093/intimm/dxq041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khadra A, Tsai S, Santamaria P, Edelstein-Keshet L. On how monospecific memory-like autoregulatory CD8+ T cells can blunt diabetogenic autoimmunity: a computational approach. J Immunol. 2010b;185:5962–5972. doi: 10.4049/jimmunol.1001306. [DOI] [PubMed] [Google Scholar]
- Kim P, Lee P, Levy D. Modeling regulation mechanisms in the immune system. J Theor Biol. 2007;246:33–69. doi: 10.1016/j.jtbi.2006.12.012. [DOI] [PubMed] [Google Scholar]
- Kopito RR, Ron D. Conformational disease. Nat Cell Biol. 2000;2:E207–E209. doi: 10.1038/35041139. [DOI] [PubMed] [Google Scholar]
- Kurrer MO, Pakala SV, Hanson HL, Katz JD. β cell apoptosis in T cell-mediated autoimmune diabetes. Proc Natl Acad Sci. 1997;94(1):213–218. doi: 10.1073/pnas.94.1.213. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu M, Hodish I, Rhodes CJ, Arvan P. Proinsulin maturation, misfolding, and proteotoxicity. Proc Natl Acad Sci. 2007;104:15841–15846. doi: 10.1073/pnas.0702697104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lu Z, Luo Y. Two limit cycles in three-dimensional Lotka–Volterra systems. Comput Math Appl. 2002;44(1):51–66. [Google Scholar]
- Lu Z, Luo Y. Three limit cycles for a three-dimensional Lotka–Volterra competitive system with a heteroclinic cycle. Comput Math Appl. 2003;46(2):231–238. [Google Scholar]
- Mahaffy JM, Edelstein-Keshet L. Modeling cyclic waves of circulating Tcells in autoimmune diabetes. SIAM J Appl Math. 2007;67:915–1937. [Google Scholar]
- Marchetti P, Bugliani M, Lupi R, et al. The endoplasmic reticulum in pancreatic beta cells of type 2 diabetes patients. Diabetologia. 2007;50:2486–2494. doi: 10.1007/s00125-007-0816-8. [DOI] [PubMed] [Google Scholar]
- Marée AFM, Santamaria P, Edelstein-Keshet L. Modeling competition among autoreactive CD8+ T-cells in autoimmune diabetes: implications for antigen-specific therapy. Int Immunol. 2006;18:1067–1077. doi: 10.1093/intimm/dxl040. [DOI] [PubMed] [Google Scholar]
- Marino S, Hogue IB, Ray CJ, Kirschner DE. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J Theor Biol. 2008;254(1):178–196. doi: 10.1016/j.jtbi.2008.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- May RM, Leonard WJ. Nonlinear aspects of competition between three species. SIAM J Appl Math. 1975;29(2):243–253. [Google Scholar]
- Mickens RE. Nonstandard Finite Difference Models of Differential Equations. World Scientific; Singapore: 1994. pp. 311–313. [Google Scholar]
- Mickens RE. Advances in the Applications of Nonstandard Finite Difference Schemes. World Scientific, Clark Atlanta University; USA: 2005. [Google Scholar]
- Moriwaki M, Itoh N, Miyagawa J, Yamamoto K, Imagawa A, Yamagata K, et al. Fas and Fas ligand expression in inflamed islets in pancreas sections of patients with recent-onset Type I diabetes mellitus. Diabetologia. 1999;42(11):1332–1340. doi: 10.1007/s001250051446. [DOI] [PubMed] [Google Scholar]
- Morran MP, Casu A, Arena VC, Pietropaolo S, Zhang YJ, et al. Humoral autoimmunity against the extracellular domain of the neuroendocrine autoantigen IA-2 heightens the risk of type 1 diabetes. Endocrinology. 2010;151:2528–2537. doi: 10.1210/en.2009-1257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morran MP, Omenn GS, Pietropaolo M. Immunology and genetics of type 1 diabetes. Mt Sinai J Med. 2008;75:314–327. doi: 10.1002/msj.20052. [DOI] [PubMed] [Google Scholar]
- Muhammad BJ, Swift PG, Raymond NT, Botha JL. Partial remission phase of diabetes in children younger than age 10 years. Arch Dis Child. 1999;80(4):367–369. doi: 10.1136/adc.80.4.367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nepom GT. Approaching the Heisenberg principle of immunology. Clin Immunol. 2008;129:1–2. doi: 10.1016/j.clim.2008.06.013. [DOI] [PubMed] [Google Scholar]
- O'Sullivan-Murphy B, Urano F. ER Stress as a trigger for β-cell dysfunction and autoimmunity in type 1 diabetes. Diabetes. 2012;61(4):780–781. doi: 10.2337/db12-0091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Petrovsky N, Silva D, Socha L, Slattery R, Charlton B. The role of Fas ligand in beta cell destruction in autoimmune diabetes of NOD mice. Ann N Y Acad Sci. 2002;958(1):204–208. doi: 10.1111/j.1749-6632.2002.tb02970.x. [DOI] [PubMed] [Google Scholar]
- Pietropaolo M, Towns R, Eisenbarth GS. Humoral autoimmunity in type 1 diabetes: prediction, significance, and detection of distinct disease subtypes. Cold Spring Harb Perspect Med. 2012:a012831. doi: 10.1101/cshperspect.a012831. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Robles DT, Eisenbarth GS, Wang T, Erlich HA, Bugawan TL, et al. Identification of children with early onset and high incidence of anti-islet autoantibodies. Clin Immunol. 2002;102(3):217–224. doi: 10.1006/clim.2001.5171. [DOI] [PubMed] [Google Scholar]
- Rutkowski DT, Kaufman RJ. A trip to the ER: coping with stress. Trends Cell Biol. 2004;14:20–28. doi: 10.1016/j.tcb.2003.11.001. [DOI] [PubMed] [Google Scholar]
- Schuit FC, Tveld PAI, Pipeleers DG. Glucose stimulates proinsulin biosynthesis by a dose-dependent recruitment of pacreatic beta-cells. Proc Natl Acad Sci USA. 1988;85:3865–3869. doi: 10.1073/pnas.85.11.3865. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnell S. A model of the unfolded protein response: pancreatic β-cell as a case study. Cell Physiol Biochem. 2009;23(4–6):233–244. doi: 10.1159/000218170. [DOI] [PubMed] [Google Scholar]
- Schnell S, Grima R, Maini PK. Multiscale modeling in biology. Am Sci. 2007;95:134–142. [Google Scholar]
- Skowera A, Ellis RJ, Varela-Calviño R, Arif S, Huang GC, et al. CTLs are targeted to kill β cells in patients with type 1 diabetes through recognition of a glucose-regulated preproinsulin epitope. J Clin Investig. 2008;118:3390–3402. doi: 10.1172/JCI35449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Standifer NE, Burwell EA, Gersuk VH, Greenbaum CJ, Nepom GT. Changes in autoreactive T cell avidity during type 1 diabetes development. Clin Immunol. 2009;132:312–320. doi: 10.1016/j.clim.2009.04.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugarman J, Tsai S, Santamaria P, Khadra A. Quantifying the importance of pMHC valency, total pMHC dose and frequency on nanoparticle therapeutic efficacy. Immunol Cell Biol. 2013;91:350–359. doi: 10.1038/icb.2013.9. [DOI] [PubMed] [Google Scholar]
- The Diabetes Control and Complications Trial Research Group. Effect of intensive therapy on residual beta-cell function in patients with type 1 diabetes in the diabetes control and complications trial. A randomized, controlled trial. Ann Intern Med. 1998;128:517–523. doi: 10.7326/0003-4819-128-7-199804010-00001. [DOI] [PubMed] [Google Scholar]
- Valitutti S, Müller S, Cella M, Padovan E, Lanzavecchia A. Serial triggering of many T-cell receptors by a few peptide-MHC complexes. Nature. 1995;375:148–151. doi: 10.1038/375148a0. [DOI] [PubMed] [Google Scholar]
- Veiga-Fernandes H, Walter U, Bourgeois C, McLean A, Rocha B. Response of naïve and memory CD8+ T cells to antigen stimulation in vivo. Nat Immunol. 2000;1:47–53. doi: 10.1038/76907. [DOI] [PubMed] [Google Scholar]
- Viola A, Lanzavecchia A. T cell activation determined by T cell receptor number and tunable thresholds. Science. 1996;273:104–106. doi: 10.1126/science.273.5271.104. [DOI] [PubMed] [Google Scholar]
- von Herrath M, Sanda S, Herold K. Type 1 diabetes as a relapsing-remitting disease? Nat Rev Immunol. 2007;7:988–994. doi: 10.1038/nri2192. [DOI] [PubMed] [Google Scholar]
- Wang Q, Huang W, Li BL. Limit cycles and singular point quantities for a 3D Lotka–Volterra system. Appl Math Comput. 2011;217(21):8856–8859. [Google Scholar]
- Wells AD, Gudmundsdottir H, Turka LA. Following the fate of individual T cells throughout activation and clonal expansion: signals from T cell receptor and CD28 differentially regulate the induction and duration of a proliferative response. J Clin Investig. 1997;100:3173–3183. doi: 10.1172/JCI119873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zeeman ML. Hopf bifurcations in competitive three dimensional Lotka-Volterra systems. Dyn Stab Syst. 1993;8:189–217. [Google Scholar]
- Zeeman ML, van den Driessche P. Three-Dimensional Competitive Lotka–Volterra Systems with no Periodic Orbits. SIAM J Appl Math. 1998;58(1):227–234. [Google Scholar]