Learning Heterogeneous Hidden Markov Random Fields

Abstract

Hidden Markov random fields (HMRFs) are conventionally assumed to be homogeneous in the sense that the potential functions are invariant across different sites. However in some biological applications, it is desirable to make HMRFs heterogeneous, especially when there exists some background knowledge about how the potential functions vary. We formally define heterogeneous HMRFs and propose an EM algorithm whose M-step combines a contrastive divergence learner with a kernel smoothing step to incorporate the background knowledge. Simulations show that our algorithm is effective for learning heterogeneous HMRFs and outperforms alternative binning methods. We learn a heterogeneous HMRF in a real-world study.

1 Introduction

Hidden Markov models (HMMs) and hidden Markov random fields (HMRFs) are useful approaches for modelling structured data such as speech, text, vision and biological data. HMMs and HMRFs have been extended in many ways, such as the infinite models [Beal et al., 2002, Gael et al., 2008, Chatzis and Tsechpenakis, 2009], the factorial models [Ghahramani and Jordan, 1997, Kim and Zabih, 2002], the high-order models [Lan et al., 2006] and the nonparametric models [Hsu et al., 2009, Song et al., 2010]. HMMs are homogeneous in the sense that the transition matrix stays the same across different sites. HMRFs, intensively used in image segmentation tasks [Zhang et al., 2001, Celeux et al., 2003, Chatzis and Varvarigou, 2008], are also homogeneous. The homogeneity assumption for HMRFs in image segmentation tasks is legitimate, because people usually assume that the neighborhood system on an image is invariant across different regions. However, it is necessary to bring heterogeneity to HMMs and HMRFs in some biological applications where the correlation structure can change over different sites. For example, a heterogeneous HMM is used for segmenting array CGH data [Marioni et al., 2006], and the transition matrix depends on some background knowledge, i.e. some distance measurement which changes over the sites. A heterogeneous HMRF is used to filter SNPs in genome-wide association studies [Liu et al., 2012a], and the pairwise potential functions depend on some background knowledge, i.e. some correlation measure between the SNPs which can be different between different pairs. In both of these applications, the transition matrix and the pairwise potential functions are heterogeneous and are parameterized as monotone parametric functions of the background knowledge. Although the algorithms tune the parameters in the monotone functions, there is no justification that the parameterization of the monotone functions is correct. Can we adopt the background knowledge about these heterogeneous parameters adaptively during HMRF learning, and recover the relation between the parameters and the background knowledge nonparametrically?

Our paper is the first to learn HMRFs with heterogeneous parameters by adaptively incorporating the background knowledge. It is an EM algorithm whose M-step combines a contrastive divergence style learner with a kernel smoothing step to incorporate the background knowledge. Details about our EM-kernel-PCD algorithm are given in Section 3 after we formally define heterogeneous HMRFs in Section 2. Simulations in Section 4 show that our EM-kernel-PCD algorithm is effective for learning heterogeneous HMRFs and outperforms alternative methods. In Section 5, we learn a heterogeneous HMRF in a real-world genome-wide association study. We conclude in Section 6.

2 Models

2.1 HMRFs And Homogeneity Assumption

Suppose that 𝕏 = {0, 1, …, m − 1} is a discrete space, and we have a Markov random field (MRF) defined on a random vector X ∈ 𝕏^d. The conditional independence is described by an undirected graph 𝔾(𝕍, 𝔼). The node set 𝕍 consists of d nodes. The edge set 𝔼 consists of r edges. The probability of x from the MRF with parameters θ is

$$P(\mathbf{x},\mathit{\theta })=\frac{Q(\mathbf{x};\mathit{\theta })}{Z(\mathit{\theta })}=\frac{1}{Z(\mathit{\theta })}\prod _{c\in ℂ(𝔾)}{\varphi }_c(\mathbf{x};{\mathit{\theta }}_c),$$ (1)

where Z(θ) is the normalizing constant. Q(x; θ) is some unnormalized measure with ℂ(𝔾) being some subset of the cliques in 𝔾. The potential function ϕ_c is defined on the clique c and is parameterized by θ_c. For simplicity in this paper, we consider pairwise MRFs, whose potential functions are defined on the edges, namely |ℂ(𝔾)| = r. We further assume that each pairwise potential function is parameterized by a single parameter, i.e. θ_c = {θ_c}.

A hidden Markov random field [Zhang et al., 2001, Celeux et al., 2003, Chatzis and Varvarigou, 2008] consists of a hidden random field X ∈ 𝕏^d and an observable random field Y ∈ 𝕐^d where 𝕐 is another space (either continuous or discrete). The random field X is a Markov random field with density P(x; θ), as defined in Formula (1), and its instantiation x cannot be measured directly. Instead, we can observe the emitted random field Y with its individual dimension Y_i depending on X_i for i = 1, …, d, namely $P(\mathbf{y}|\mathbf{x};\phi )={\prod }_{i=1}^{d}P(y_i|x_i;\phi )$ where φ = {φ₀, …, φ_m−1} and φ_xi parameterizes the emitting distribution of Y_i under the state x_i. Therefore, the joint probablity of x and y is

$$P(\mathbf{x},\mathbf{y};\mathit{\theta },\phi )=P(\mathbf{x};\mathit{\theta })P(\mathbf{y}|\mathbf{x};\phi )=\frac{1}{Z(\mathit{\theta })}\prod _{c\in ℂ(𝔾)}{\varphi }_c(\mathbf{x};{\mathit{\theta }}_c)\prod _{i=1}^{d}P(y_i|x_i;\phi ).$$ (2)

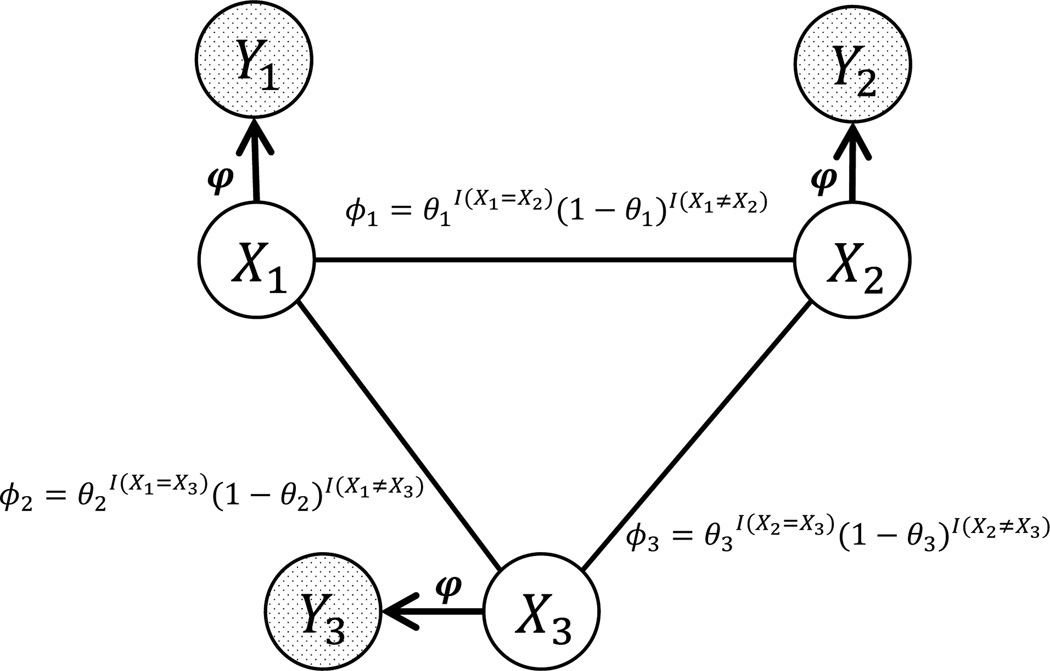
Example 1: One pairwise HMRF model with three latent variables (X₁, X₂, X₃) and three observable variables (Y₁, Y₂, Y₃) is given in Figure 1. Let 𝕏 = {0, 1}. X₁, X₂ and X₃ are connected by three edges. The pairwise potential function ϕ_i on edge i (connecting X_u and X_v) parameterized by θ_i (0<θ_i<1) is ${\varphi }_i(\mathbf{X};{\theta }_i)={\theta }_i^{I(X_u=X_v)}{(1-{\theta }_i)}^{I(X_u\ne X_v)}$ for i = 1, 2, 3, where I is an indicator variable. Let 𝕐 = R. For i = 1, 2, 3, $Y_i|X_i=0~N({\mu }_0,{\sigma }_0^2)$ and $Y_i|X_i=1~N({\mu }_1,{\sigma }_1^2)$, namely φ₀ = {μ₀, σ₀} and φ₁ = {μ₁, σ₁}.

Figure 1.

The pairwise HMRF model with three latent nodes (X₁, X₂, X₃) and observable nodes (Y₁, Y₂, Y₃) with parameters θ = {θ₁, θ₂, θ₃} and φ = {φ₀, φ₁}.

In common applications of HMRFs, we observe only one instantiation y which is emitted according to the hidden state vector x, and the task is to infer the most probable state configuration of X, or to compute the marginal probabilities of X. In both tasks, we need to estimate the parameters θ = {θ₁, …, θ_r} and φ = {φ₀, …, φ_m−1}. Usually, we seek maximum likelihood estimates of θ and φ which maximize the log likelihood

$$ℒ(\mathit{\theta },\phi )=\text{log}P(\mathbf{y};\mathit{\theta },\phi )=\text{log}\sum _{\mathbf{x}\in {𝕏}^{\mathbf{d}}}P(\mathbf{x},\mathbf{y};\mathit{\theta },\phi ).$$ (3)

Since we only have one instantiation (x, y), we usually have to assume that θ_i’s are the same for i = 1, …, r for effective parameter learning. This homogeneity assumption is widely used in computer vision problems because people usually assume that the neighborhood system on an image is invariant across its different regions. Therefore, conventional HMRFs refer to homogeneous HMRFs, similar to conventional HMMs whose transition matrix is invariant across different sites.

2.2 Heterogeneous HMRFs

In a heterogeneous HMRF, the potential functions on different cliques can be different. Taking the model in Figure 1 as an example, θ₁, θ₂ and θ₃ can be different if the HMRF is heterogeneous. As with conventional HMRFs, we want to be able to address applications that have one instantiation (x, y) where y is observable and x is hidden. Therefore, learning an HMRF from one instantiation y is infeasible if we free all θ’s. To partially free the parameters, we assume that there is some background knowledge k = {k₁, …, k_r} about the parameters θ = {θ₁, …, θ_r} in the form of some unknown smooth mapping function which maps θ_i to k_i for i = 1, …, r. The background knowledge describes how these potential functions are different across different cliques. Taking pairwise HMRFs for example, the potentials on the edges with similar background knowledge should have similar parameters. We can regard the homogeneity assumption in conventional HMRFs as an extreme type of background knowledge that k₁ = k₂ = … = k_r. The problem we solve in this paper is to estimate θ and φ which maximize the log likelihood ℒ(θ, φ) in Formula (3), subject to the condition that the estimate of θ is smooth with respect to k.

3 Parameter Learning Methods

Learning heterogeneous HMRFs in above manner involves three difficulties, (i) the intractable Z(θ), (ii) the latent x, and (iii) the heterogeneous θ. The way we handle the intractable Z(θ) is similar to using contrastive divergence [Hinton, 2002] to learn MRFs. We review contrastive divergence and its variations in Section 3.1. To handle the latent x in HMRF learning, we introduce an EM algorithm in Section 3.2, which is applicable to conventional HMRFs. In Section 3.3, we further address the heterogeneity of θ in the M-step of the EM algorithm.

3.1 Contrastive Divergence for MRFs

Assume that we observe s independent samples 𝒳 = {x¹, x², …, x^s} from (1), and we want to estimate θ. The log likelihood ℒ(θ|𝒳) is concave w.r.t. θ, and we can use gradient ascent to find the MLE of θ. The partial derivative of ℒ(θ|𝒳) with respect to θ_i is

$$\frac{\partial ℒ(\mathit{\theta }|𝒳)}{\partial {\theta }_i}=\frac{1}{s}\sum _{j=1}^s{\psi }_i({\mathbf{x}}^j)-E_{\mathit{\theta }}{\psi }_i=E_{𝒳}{\psi }_i-E_{\mathit{\theta }}{\psi }_i,$$ (4)

where ψ_i is the sufficient statistic corresponding to θ_i, and E_θψ_i is the expectation of ψ_i with respect to the distribution specified by θ. In the i-th iteration of gradient ascent, the parameter update is

$${\mathit{\theta }}_{(i+1)}={\mathit{\theta }}_{(i)}+\eta \nabla ℒ({\mathit{\theta }}_{(i)}|𝒳)={\mathit{\theta }}_{(i)}+\eta (E_{𝒳}\psi -E_{{\mathit{\theta }}_{(i)}}\psi ),$$

where η is the learning rate. However the exact computation of E_θψ_i takes time exponential in the treewidth of 𝔾. A few sampling-based methods have been proposed to solve this problem. The key differences among these methods are how to draw particles and how to compute E_θψ from the particles. MCMC-MLE [Geyer, 1991, Zhu and Liu, 2002] uses importance sampling, but might suffer from degeneracy when θ_(i) is far away from θ₍₁₎. Contrastive divergence [Hinton, 2002] generates new particles in each iteration according to the current θ_(i) and does not require the particles to reach equilibrium, so as to save computation. Variations of contrastive divergence include particle-filtered MCMC-MLE [Asuncion et al., 2010], persistent contrastive divergence (PCD) [Tieleman, 2008] and fast PCD [Tieleman and Hinton, 2009]. Because PCD is efficient and easy to implement, we employ it in this paper. Its pseudocode is provided in Algorithm 1. Other than contrastive divergence, MRF can be learned via ratio matching [Hyvärinen, 2007], non-local contrastive objectives [Vickrey et al., 2010], noise-contrastive estimation [Gutmann and Hyvärinen, 2010] and minimum KL contraction [Lyu, 2011].

Algorithm 1.

PCD-n Algorithm [Tieleman, 2008]

1:	Input: independent samples 𝒳 = {x1, x2, …, xs} from P(x; θ), maximum iteration number T
2:	Output: θ̂ from the last iteration
3:	Procedure:
4:	Initialize θ(1) and initialize particles
5:	Calculate E𝒳ψ from 𝒳
6:	for i = 1 to T do
7:	Advance particles n steps under θ(i)
8:	Calculate Eθ(i) ψ from the particles
9:	θ(i+1) = θ(i) + η (E𝒳 ψ − Eθ(i) ψ)
10:	Adjust η
11:	end for

3.2 Expectation-Maximization for Learning Conventional HMRFs

We begin with a lower bound of the log likelihood function, and then introduce the EM algorithm which handles the latent variables in HMRFs. Let q_x(x) be any distribution on x∈𝕏^d. It is well known that there exists a lower bound of the log likelihood ℒ(θ, φ) in (3), which is provided by an auxiliary function ℱ(q_x(x), {θ, φ}) defined as follows,

$$ℱ(q_{\mathbf{x}}(\mathbf{x}),\{\mathit{\theta },\phi \})=\sum _{\mathbf{x}\in {𝕏}^{\mathbf{d}}}{q}_{\mathbf{x}}(\mathbf{x})\text{log}\frac{P(\mathbf{x},\mathbf{y};\mathit{\theta },\phi )}{q_{\mathbf{x}}(\mathbf{x})}=ℒ(\mathit{\theta },\phi )-\text{KL}[q_{\mathbf{x}}(\mathbf{x})|P(\mathbf{x}|\mathbf{y},\mathit{\theta },\phi )],$$ (5)

where KL[q_x(x)|P(x|y, θ, φ)] is the Kullback-Leibler divergence between q_x(x) and P(x|y, θ, φ), the posterior distribution of the hidden variables. This Kullback-Leibler divergence is the distance between ℒ(θ, φ) and ℱ(q_x(x), {θ, φ}).

Expectation-Maximization: We maximize ℒ(θ, φ) with an expectation-maximization (EM) algorithm which iteratively maximizes its lower bound ℱ(q_x(x), {θ, φ}). We first initialize θ⁽⁰⁾ and φ⁽⁰⁾. In the t-th iteration, the updates in the expectation (E) step and the maximization (M) step are

$$q_{\mathbf{x}}^t=\underset{q_{\mathbf{x}}}{\text{arg max}}ℱ(q_{\mathbf{x}}(\mathbf{x}),\{{\mathit{\theta }}^{(t-1)},{\phi }^{(t-1)}\}),$$ (E)

$${\mathit{\theta }}^{(t)},{\phi }^{(t)}=\underset{\{\mathit{\theta },\phi \}}{\text{arg max}}ℱ(q_{\mathbf{x}}^{(t)},\{\mathit{\theta },\phi \}).$$ (M)

In the E-step, we maximize ℱ(q_x(x), {θ^(t−1), φ^(t−1)}) with respect to q_x(x). Because the difference between ℱ(q_x(x), {θ, φ}) and ℒ(θ, φ) is KL[q_x(x)|P(x|y, θ, φ)], the maximizer in the E-step $q_{\mathbf{x}}^{(t)}$ is P(x|y, θ^(t−1), φ^(t−1), namely the posterior distribution of x|y under the current estimated parameters θ^(t−1) and φ^(t−1). This posterior distribution can be calculated by Markov chain Monte Carlo for general graphs.

In the M-step, we maximize $ℱ(q_{\mathbf{x}}^{(t)}(\mathbf{x}),\{\mathit{\theta },\phi \})$ with respect to {θ, φ}, which can be rewritten as

$$\underset{\{\mathit{\theta },\phi \}}{\text{arg max}}ℱ(q_{\mathbf{x}}^{(t)}(\mathbf{x}),\{\mathit{\theta },\phi \})=\underset{\{\mathit{\theta },\phi \}}{\text{arg max}}\sum _{\mathbf{x}\in {𝕏}^{\mathbf{d}}}{q}_{\mathbf{x}}^{(t)}(\mathbf{x})\text{log}P(\mathbf{x},\mathbf{y};\mathit{\theta },\phi )=\underset{\{\mathit{\theta },\phi \}}{\text{arg max}}\sum _{\mathbf{x}\in {𝕏}^{\mathbf{d}}}{q}_{\mathbf{x}}^{(t)}(\mathbf{x})\{\text{log}P(\mathbf{x};\mathit{\theta })+\text{log}P(\mathbf{y}|\mathbf{x};\phi )\}.$$

It is obvious that this function can be maximized with respect to φ and θ separately as

$${\mathit{\theta }}^{(t)}=\underset{\mathit{\theta }}{\text{arg max}}\sum _{\mathbf{x}\in {𝕏}^{\mathbf{d}}}{q}_{\mathbf{x}}^{(t)}(\mathbf{x})\text{log}P(\mathbf{x};\mathit{\theta }),{\phi }^{(t)}=\underset{\phi }{\text{arg max}}\sum _{\mathbf{x}\in {𝕏}^{\mathbf{d}}}{q}_{\mathbf{x}}^{(t)}(\mathbf{x})\text{log}P(\mathbf{y}|\mathbf{x};\phi ).$$ (6)

Estimating φ: Estimating φ in this maximum likelihood manner is straightforward, because the maximization can be rewritten as follows,

$$\underset{\phi }{\text{arg max}}\sum _{\mathbf{x}\in {𝕏}^{\mathbf{d}}}{q}_{\mathbf{x}}^{(t)}(\mathbf{x})\text{log}P(\mathbf{y}|\mathbf{x};\phi )=\underset{\phi }{\text{arg max}}\sum _{i=1}^d\sum _{x_i\in 𝕏}{q}_{x_i}^{(t)}(x_i)\text{log}P(y_i|x_i;\phi ),$$

where $q_{\mathbf{x}}^{(t)}(\mathbf{x})={\prod }_{i=1}^d{q}_{x_i}^{(t)}(x_i)$.

Estimating θ: Estimating θ in Formula (6) is difficult due to the intractable Z(θ). Some approaches [Zhang et al., 2001, Celeux et al., 2003] use pseudo-likelihood [Besag, 1975] to estimate θ in the M-step. It can be shown that ${\sum }_{\mathbf{x}\in {𝕏}^{\mathbf{d}}}{q}_{\mathbf{x}}^{(t)}(\mathbf{x})\text{log}P(\mathbf{x};\mathit{\theta })$ is convex with respect to θ. Therefore, we can use gradient ascent to find the MLE of θ, which is similar to using contrastive divergence [Hinton, 2002] to learn MRFs in Section 3.1.

Denote ${\sum }_{\mathbf{x}\in {𝕏}^{\mathbf{d}}}{q}_{\mathbf{x}}^{(t)}(\mathbf{x})\text{log}P(\mathbf{x};\mathit{\theta })$ by ${ℒ}_M(\mathit{\theta }|q_{\mathbf{x}}^{(t)})$. The partial derivative of ${ℒ}_M(\mathit{\theta }|q_{\mathbf{x}}^{(t)})$ with respect to θ_i is

$$\frac{\partial {ℒ}_M(\mathit{\theta }|q_{\mathbf{x}}^{(t)})}{\partial {\theta }_i}=\sum _{\mathbf{x}\in {𝕏}^{\mathbf{d}}}{q}_{\mathbf{x}}^{(t)}(\mathbf{x})\{{\psi }_i(\mathbf{x})-E_{\mathit{\theta }}{\psi }_i(\mathbf{x})\}.$$

.

Therefore, the derivative here is similar to the derivative in contrastive divergence in Formula (4) except we have to reweight it to $q_{\mathbf{x}}^{(t)}$. We run the EM algorithm until both θ and φ converge. Note that when learning homogeneous HMRFs with this algorithm, we tie all θ’s all the time, namely θ = {θ}. Therefore, we name this parameter learning algorithm for conventional HMRFs the EM-homo-PCD algorithm.

3.3 Learning Heterogeneous HMRFs

Learning heterogeneous HMRFs is different from learning conventional homogeneous HMRFs in two ways. First, we need to free the θ’s in heterogeneous HMRFs. Second, there is some background knowledge k about how the θ’s are different, as introduced in Section 2. Therefore, we make two modifications to the EM-homo-PCD algorithm in order to learn heterogeneous HMRFs with background knowledge. First, we estimate the θ’s separately, which obviously brings more variance in estimation. Second, within each iteration of the contrastive divergence update, we apply a kernel regression to smooth the estimate of the θ’s with respect to the background knowledge k. Specifically, in the i-th iteration of PCD update, we advance the particles under θ̂_(i) for n steps, and calculate the moments E_θ̂(i) ψ from the particles. Therefore, we can update the estimate as

$${\tilde{\mathit{\theta }}}_{(i+1)}={\widehat{\mathit{\theta }}}_{(i)}+\eta \nabla {ℒ}_M(\mathit{\theta }|q_{\mathbf{x}}^{(t)}).$$

Then we regress θ̃_(i+1) with respect to k via Nadaraya-Watson kernel regression [Nadaraya, 1964, Watson, 1964], and set θ̂_(i+1) to be the fitted values. For ease of notation, we drop the iteration index (i + 1). Suppose that θ̃ = {θ̃₁, …, θ̃_r} is the estimate before kernel smoothing; we set the smoothed estimate θ̂ = {θ̂₁, …, θ̂_r} as

$${\widehat{\theta }}_j={\sum }_{i=1}^r{\gamma }_{\mathit{\text{ij}}}{\tilde{\theta }}_i,\forall j=1,\dots ,r,$$

where

$${\gamma }_{\mathit{\text{ij}}}=\frac{K(\frac{k_i-k_j}{h})}{{\sum }_{m=1}^{r}K(\frac{k_m-k_j}{h})}.$$

For the kernel function K, we use the Epanechnikov kernel, which is usually computationally more efficient than a Gaussian kernel. We tune the bandwidth h through cross-validation, namely we select the bandwidth which minimizes the leave-one-out score

$$\frac{1}{r}{\sum }_{i=1}^r{\left(\frac{{\tilde{\theta }}_i-{\widehat{\theta }}_i}{1-{\gamma }_{\mathit{\text{ii}}}}\right)}^2.$$

Tuning the bandwidth is usually computation-intensive, so we tune it every t₀ iterations to save computation. We name our parameter learning algorithm for heterogeneous HMRFs the EM-kernel-PCD algorithm. Its pseudo-code is given in Algorithm 2.

Another intuitive way of handling background knowledge about these heterogeneous parameters is to create bins according to the background knowledge and tie the θ’s that are in the same bin. Suppose that we have b bins after we carefully select the binwidth,

Algorithm 2.

EM-kernel-PCD Algorithm

1:	Input: sample y, background knowledge k, max iteration number T, initial bandwidth h
2:	Output: θ̂ from the last iteration
3:	Procedure:
4:	Initialize θ̂, φ̂ and particles
5:	while not converge do
6:	E-step: infer x̂ from y
7:	Calculate Ex̂ φ from x̂
8:	for i = 1 to T do
9:	Advance particles for n steps under θ̂(i)
10:	Calculate Eθ̂(i) φ from the particles
11:	${\tilde{\mathit{\theta }}}_{(i+1)}={\widehat{\mathit{\theta }}}_{(i)}+\eta \nabla {ℒ}_M(\mathit{\theta }|q_{\mathbf{x}}^{(t)})$
12:	θ̂(i+1) = kernelRegFit(θ̃(i+1), k, h)
13:	Adjust η and tune bandwidth h
14:	end for
15:	MLE φ̂ from x̂ and y
16:	end while

namely we have θ = {θ₁, …, θ_b}. The rest of the algorithm is the same as the EM-homo-PCD algorithm in Section 3.2. We name this parameter learning algorithm via binning the EM-binning-PCD algorithm. We can also regard our EM-kernel-PCD algorithm as a soft-binning version of EM-binning-PCD.

4 Simulations

We investigate the performance of our EM-kernel-PCD algorithm on heterogeneous HMRFs with different structures, namely a tree-structure HMRF and a grid-structure HMRF. In the simulations, we first set the ground truth of the parameters, and then set the background knowledge. We then generate one example x and then generate one example y|x. With the observable y, we apply EM-kernel-PCD, EM-binning-PCD and EM-homo-PCD to learn the parameters θ. We eventually compare the three algorithms by their average absolute estimate error $1/r{\sum }_{i=1}^r|{\theta }_i-{\widehat{\theta }}_i|$ where θ̂_i is the estimate of θ_i.

For the HMRFs, each dimension of X takes values in {0, 1}. The pairwise potential function ϕ_i on edge i (connecting X_u and X_v) parameterized by ϕ_i (0 < ϕ_i < 1) is ${\varphi }_i(\mathbf{X};{\theta }_i)={\theta }_i^{I(X_u=X_v)}{(1-{\theta }_i)}^{I(X_u\ne X_v)}$ for i = 1, 2, 3, where I is an indicator variable. For the tree structure, we choose a perfect binary tree of height 12, which yields a total number of 8,191 nodes and 8,190 parameters, i.e. d = 8,191 and r = 8,190. For the grid-structure HMRFs, we choose a grid of 100 rows and 100 columns, which yields a total number of 10,000 nodes and 19,800 parameters, i.e. d = 10,000 and r = 19,800. For both of the two models, we generate θ_i ~ U(0.5, 1) independently and then generate the background knowledge k_i. We have two types of background knowledge. In the first type of background knowledge, we set k_i = sin θ_i + ε. In the second type of background knowledge, we set $k_i={\theta }_i^2+\epsilon$, where ε is some random Gaussian noise from $N(0,{\sigma }_{\epsilon }^2)$. We try three values for σ_ε, namely 0.0, 0.01 and 0.02. Then we generate one instantiation x. Finally, we generate one observable y from a d dimensional multivariate normal distribution N(μx, σ²𝕀) where μ = 2 is the strength of signal, and σ² = 1.0 is the variance of the manifestation, and 𝕀 is the identity matrix of dimension d. For our EM-kernel-PCD algorithm, we use an Epanechnikov kernel with α = β = 5. For tuning bandwidth h, we try 100 values in total, namely 0.005, 0.01, 0.015, …, 0.5. For the EM-binning-PCD algorithm, we set the binwidth to be 0.005. The rest of the parameter settings for the three algorithms are the same, including the n parameter in PCD which is set to be 1 and the number of particles which is set to be 100. We also replicate each experiment 20 times, and the averaged results are reported.

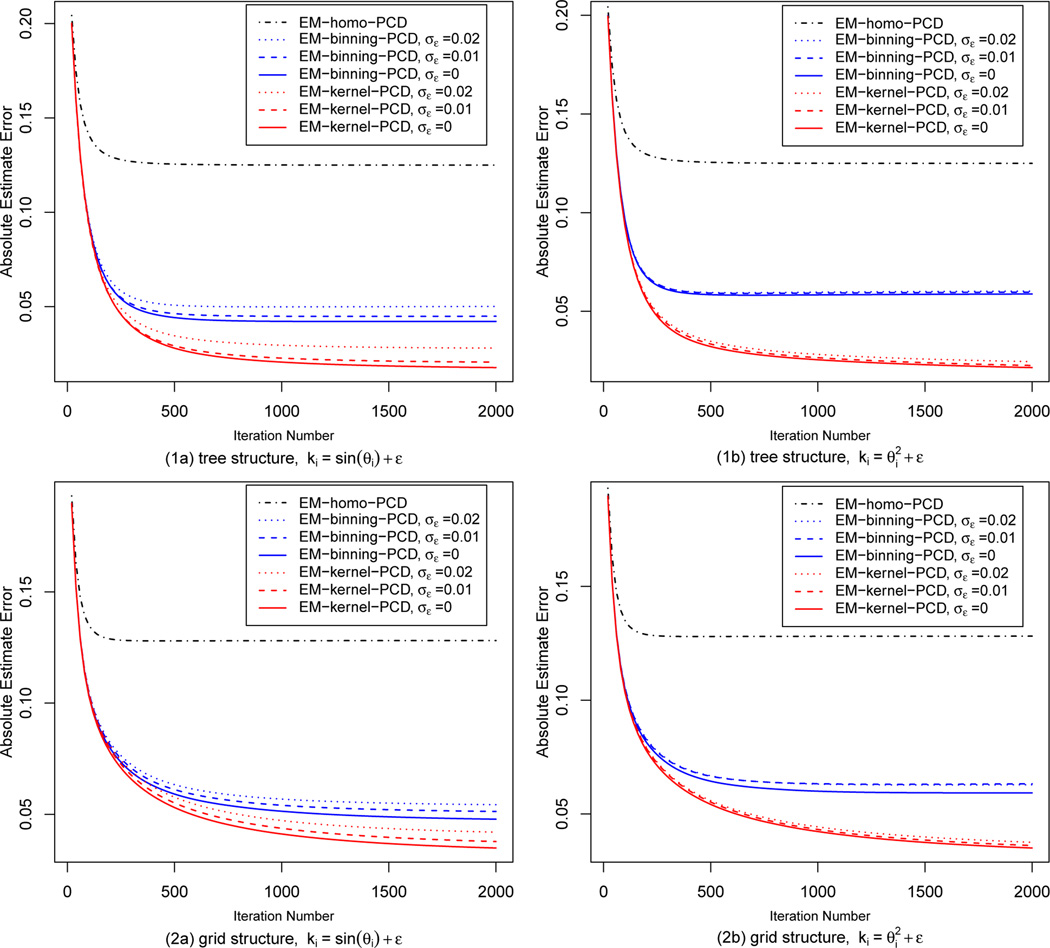
Performance of the algorithms The results from the tree-structure HMRFs and the grid-structure HMRFs are reported in Figure 2. We plot the average absolute error of the estimate of the three algorithms against the number of iterations of PCD update. We have separate plots for background knowledge k_i = sin θ_i + ε, and background knowledge $k_i={\theta }_i^2+\epsilon$. Since there are three noise levels for background knowledge, both the EM-kernel-PCD algorithm and the EM-binning-PCD algorithm have three variations. All the three algorithms converge as they iterate. It is observed that the absolute estimate error of the EM-homo-PCD algorithm reduces to 0.125 as it converges. Since the parameters θ_i’s are drawn independently from the uniform distribution on the interval [0.5, 1], the EM-homo-PCD algorithm ties all the θ_i’s and estimates them to be 0.75. Therefore, the averaged absolute error is ${\int }_{0.5}^{1.0}2|x-0.75|\mathrm{d}x=0.125$. Our EM-kernel-PCD algorithm significantly outperforms the EM-binning-PCD algorithm and the EM-homo-PCD algorithm. It is also observed that as the noise level of background knowledge increases, the performance of the EM-kernel-PCD algorithm and the EM-binning-PCD algorithm deteriorates. However, as long as the noise level is moderate, the performance of our EM-kernel-PCD algorithm is satisfactory. The results from the tree-structure HMRFs and the grid-structure HMRFs are comparable except that it takes more iterations to converge in grid-structure HMRFs than in tree-structure HMRFs.

Figure 2.

Performance of EM-homo-PCD, EM-binning-PCD and EM-kernel-PCD in tree-HMRFs and grid-HMRFs for two types of background knowledge: (a) k_i = sin θ_i + ε, and (b) $k_i={\theta }_i^2+\epsilon$.

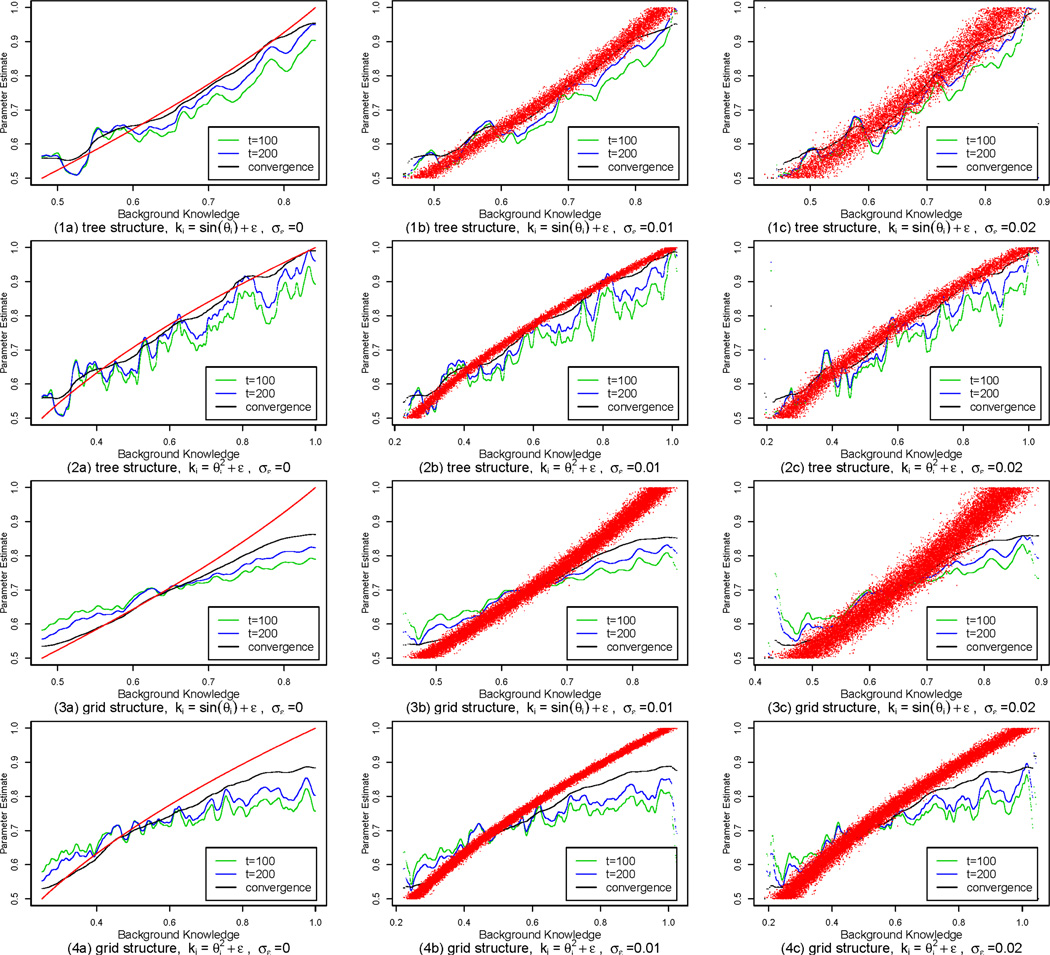
Behavior of the algorithms We then plot the estimated parameters against their background knowledge in the iterations of our EM-kernel-PCD algorithm. We provide plots for after 100 iterations, after 200 iterations and after convergence respectively, to show how the EM-kernel-PCD algorithm behaves during the gradient ascent. Figure 3 shows the plots for the background knowledge k_i = sin θ_i + ε and the background knowledge $k_i={\theta }_i^2+\epsilon$ with three levels of noise (namely σ_ε=0, 0.01 and 0.02) for both the tree-structure HMRFs and the grid-structure HMRFs. It is observed that as the algorithm iterates, it gradually recovers the relationship between the parameters and the background knowledge. There is still a gap between our estimate and the ground truth. This is because we only have one hidden instantiation x and we have to infer x from the observed y in the E-step. Especially at the boundaries, we can observe a certain amount of estimate bias. The boundary bias is very common in kernel regression problems because there are fewer data points at the boundaries [Fan, 1992].

Figure 3.

The behavior of the EM-kernel-PCD algorithm during gradient ascent for different types of background knowledge with different levels of noise in the tree-structure HMRFs and the grid-structure HMRFs. The red dots show the mapping pattern between the ground truth of the parameters and their background knowledge.

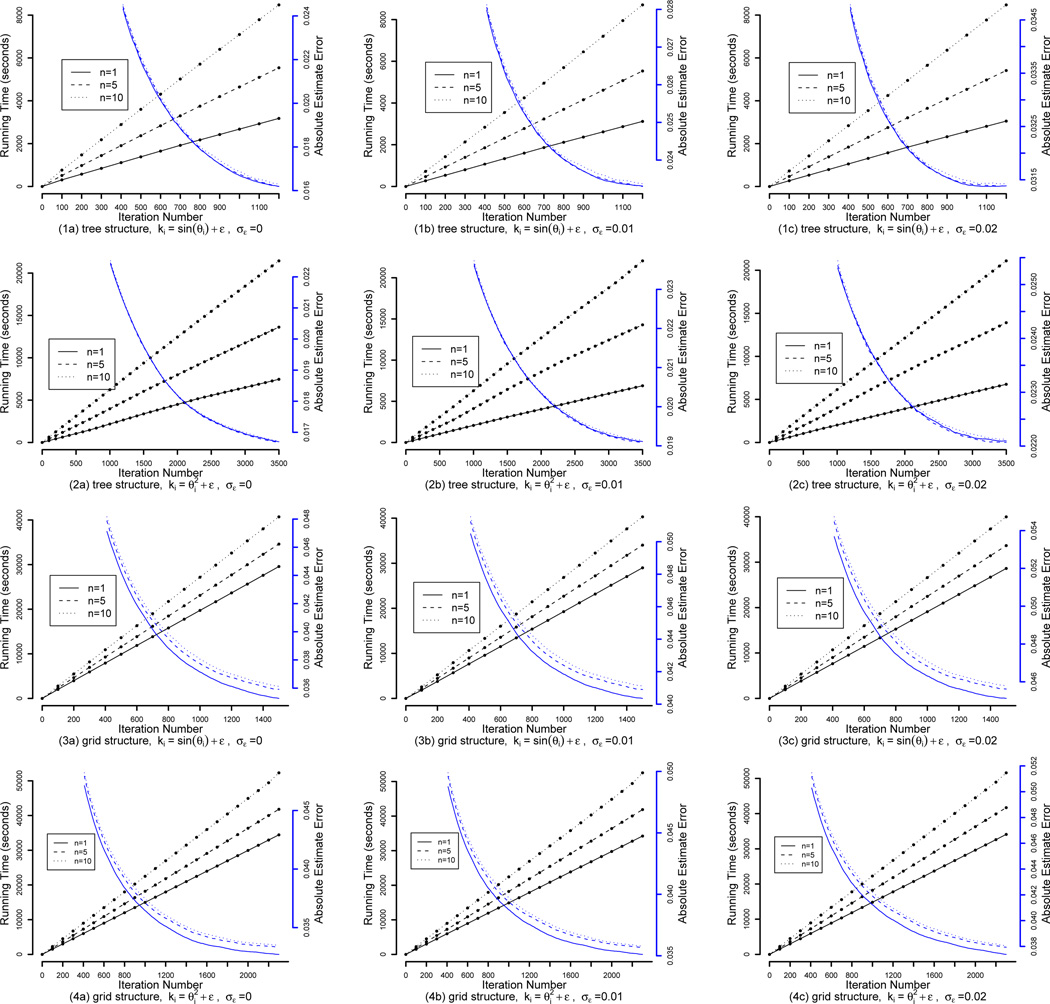
Choosing parameter n One parameter in contrastive divergence algorithms is n, the number of MCMC steps we need to perform under the current parameters in order to generate the particles. The rationale of contrastive divergence is that it is enough to find the direction to update the parameters by a few MCMC steps using the current parameters, and we do not have to reach the equilibrium. Therefore, the parameter n is usually set to be very small to save computation when we are learning general Markov random fields. Here we explore how we should choose the n parameter in our EM-kernel-PCD algorithm for learning HMRFs. We choose three values for n in the simulations, namely 1, 5 and 10. In Figure 4, the running time and absolute estimate error are plotted for the three choices in the tree-structure HMRFs and grid-structure HMRFs under different levels of noise in the background knowledge k_i = sin θ_i + ε and the background knowledge $k_i={\theta }_i^2+\epsilon$. The running time increases as n increases, but the estimation accuracy does not increase. This observation stays the same for different structures and different levels of noise in different types of background knowledge. This suggests that we can simply choose n = 1 in our EM-kernel-PCD algorithm.

Figure 4.

Absolute estimate error (plotted in blue, in the units on the right axes) and running time (plotted in black, in minutes on the left axes) of the EM-kernel-PCD algorithm in the tree-structure HMRFs and the grid-structure HMRFs when we choose different n values; n is the number of MCMC steps for advancing particles in the PCD algorithm. The absolute estimate error in the first 400 iterations is not shown in the plots.

5 Real-world Application

We use our EM-kernel-PCD algorithm to learn a heterogeneous HMRF model in a real-world genome-wide association study on breast cancer. The dataset is from NCI’s Cancer Genetics Markers of Susceptibility (CGEMS) study [Hunter et al., 2007]. In total, 528,173 genetic markers (single-nucleotide polymorphisms or SNPs) for 1,145 breast cancer cases and 1,142 controls are genotyped on the Illumina HumanHap500 array, and the task is to identify the SNPs which are associated with breast cancer. This dataset has been used in the study of Liu et al. [2012b]. We build a heterogeneous HMRF model to identify the associated SNPs. In the HMRF model, the hidden vector X ∈ {0, 1}^d denotes whether the SNPs are associated with breast cancer, i.e. X_i = 1 means that the SNP_i is associated with breast cancer. For each SNP, we can perform a two-proportion z-test from the minor allele count in cases and the minor allele count in controls. Denote Y_i to be the test statistic from the two-proportion z-test for SNP_i. It can be derived that Y_i|X_i=0 ~ N(0, 1) and Y_i|X_i=1 ~ N(μ₁, 1) for some unknown μ₁ (μ₁ ≠ 0). We assume that X forms a pairwise Markov random field with respect to the graph 𝔾. The graph 𝔾 is built as follows. We query the squared correlation coefficients (r² values) among the SNPs from HapMap [The International HapMap Consortium, 2003]. Each SNP becomes a node in the graph. For each SNP, we connect it with the SNP having the highest r² value with it. We also remove the edges whose r² values are below 0.25. There are in total 340,601 edges in the graph. The pairwise potential function ϕ_i on edge i (connecting X_u and X_v) parameterized by θ_i (0 < θ_i < 1) is ${\varphi }_i(\mathbf{X};{\theta }_i)={\theta }_i^{I(X_u=X_v)}{(1-{\theta }_i)}^{I(X_u\ne X_v)}$ for i = 1, …, 340,601, where I is an indicator variable. It is believed that two SNPs with a higher level of correlation are more likely to agree in their association with breast cancer. Therefore, we set the background knowledge k about the parameters to be the r² values between the SNPs on the edge. We first perform the two-proportion z-test and set y to be the calculated test statistics. Then we estimate θ|y, k in the heterogeneous HMRF with respect to 𝔾 using our EM-kernel-PCD algorithm. After we estimate θ and μ₁, we calculate the marginal probabilities of the hidden X. Eventually, we rank the SNPs by the marginal probabilities P(X_i = 1|y; θ̂, μ̂₁), and select the SNPs with the largest marginal probabilities.

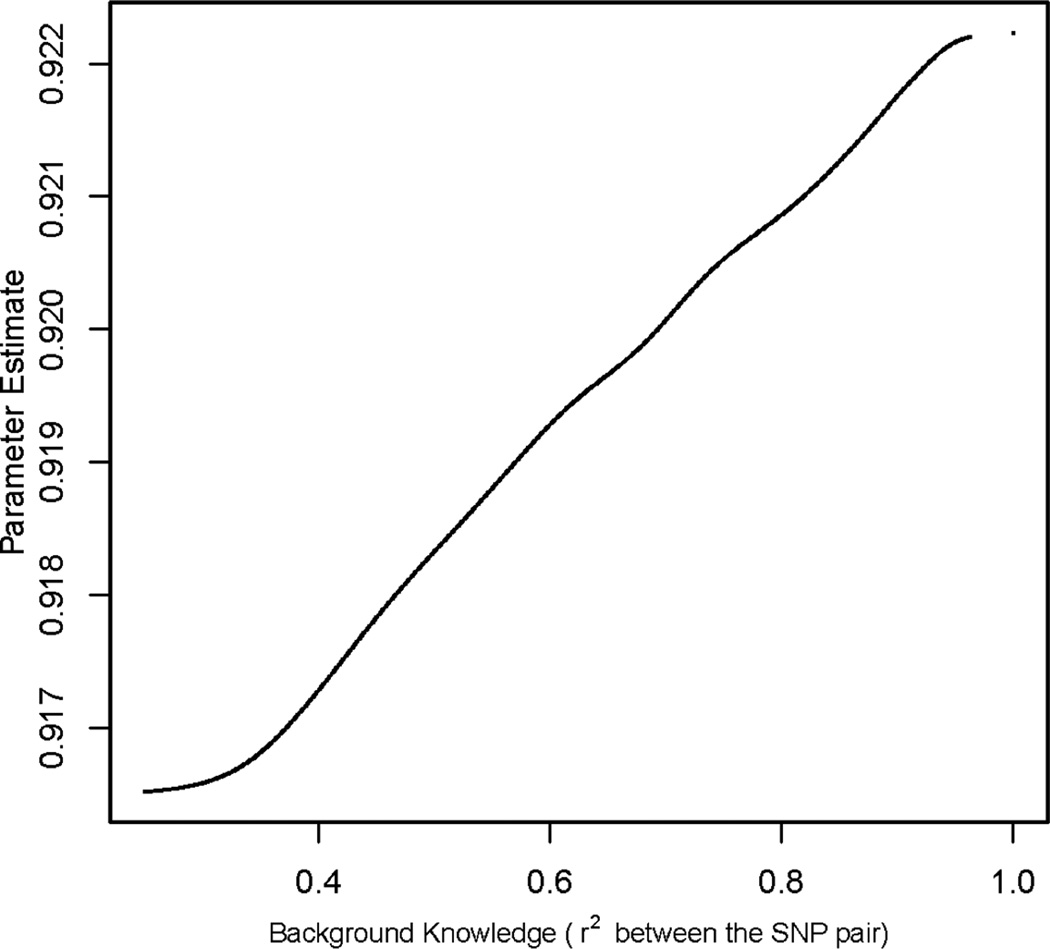
The algorithm ran for 46 days on a single processor (AMD Opteron Processor, 3300 MHz) before it converged. We plotted the estimated parameters against their background knowledge, namely the r² values between the pairs of SNPs on the edges. The plot is provided in Figure 5. It is observed that the mapping between the estimated parameters and the background knowledge is monotone increasing, as we expect. Finally we calculated the marginal probabilities of the hidden X, and ranked the SNPs by the marginal probabilities P(X_i = 1|y; θ̂, μ̂₁). There are in total five SNPs with P(X_i = 1|y; θ̂, μ̂₁) greater than 0.99, which means they are associated with breast cancer with a probability greater than 0.99 given the observed test statistics y under the estimated parameters θ̂ and μ̂₁. There is strong evidence in the literature that supports the association with breast cancer for three of them. The two SNPs rs2420946 and rs1219648 on chromosome 10 are reported by Hunter et al (2007), and have been further validated by 1,776 cases and 2,072 controls from three additional studies. Their associated gene FGFR2 is very well known to be associated with breast cancer in the literature. There is also strong evidence supporting the association of the SNP rs7712949 on chromosome 5. The SNP rs7712949 is highly correlated (r²=0.948) with SNP rs4415084 which has been identified to be associated with breast cancer by another six large-scale studies. ¹

Figure 5.

The estimated parameters against their background knowledge, namely the r² values between the pairs of SNPs.

6 Conclusion

Capturing parameter heterogeneity is an important issue in machine learning and statistics, and it is particular challenging in HMRFs due to both the intractable Z(θ) and the latent x. In this paper, we propose the EM-kernel-PCD algorithm for learning the heterogeneous parameters with background knowledge. Our algorithm is built upon the PCD algorithm which handles the intractable Z(θ). The EM part we add is for dealing with the hidden x. The kernel smoothing part we add is to adaptively incorporate the background knowledge about the heterogeneity in parameters in the gradient ascent learning. Eventually, the relation between the parameters and the background knowledge is recovered in a nonparametric way, which is also adaptive to the data. Simulations show that our algorithm is effective for learning heterogeneous HMRFs and outperforms alternative binning methods.

Similar to other EM algorithms, our algorithm only converges to a local maximum of the likelihood ℒ(θ, φ), although the lower bound ℱ(q_x(x), {θ, φ}) nondecreases over the EM iterations (except for some MCMC error introduced in the E-step). Our algorithm also suffers from long run time due to computationally expensive PCD algorithm within each M-step. These two issues are important directions for future work.