TAILOR THE LONGITUDINAL ANAYSIS FOR NIH LONGITUDINAL NORMAL BRAIN DEVELOPMENTAL STUDY

Abstract

There are imminent needs for longitudinal analysis to make physiological inferences on NIH MRI study of normal brain development. But up to date, two critical aspects for longitudinal analysis, namely the selections of mean and covariance structures have not been addressed by the neuroimaging community. For the mean structure, we employed a linear free-knot B-spline regression in combination with quasi-least square estimating equations to approximate a nonlinear growth trajectory with piecewise linear segments for a friendly physiological interpretation. For covariance structure selection, we have proposed a novel time varying correlation structure considering not only the time separation between the repeated measures but also when these acquisitions occurred. We have demonstrated that the proposed covariance structure has a lower Akaike information criterion value than the commonly used Markov correlation structure.

1. INTRODUCTION

Neuroimaging with a longitudinal design has gained increasing interests in neuroscience community especially with the release of multicenter imaging data such as NIH MRI study of normal brain development. Compared to cross-sectional studies, longitudinal analysis is less subjected to sporadic across subject variation and enables an improved robustness in quantifying temporal changes of brain either due to disease progression or normal maturation [1–3]. The increased statistical power of longitudinal analysis in detecting temporal changes is due to the inclusion of repeated measurements from the same individual. Thus, longitudinal analysis is ideal for both population and individual level based growth studies.

Currently, there are two widely employed approaches to analyzing longitudinal neuroimaging data, which are based upon generalized estimating equations (GEE) or linear mixed effects models (LME) [4–8]. GEE is used to fit a marginal distribution to estimate population level growth trajectories, while LME takes a conditional approach for the same estimation. LME is advantageous in predicting individual temporal changes due to its inherent fixed and random effects modeling design. Further-more, the information criteria such as Akaike (AIC) or Bayesian information criterion (BIC) can be directly applied to LME for model selection but not with GEE, which is not based upon likelihood estimation [9].

Brain maturation is a highly nonlinear process by nature [10–11]. Most of the studies employed empirical global parametric models such as polynomials [10], logarithm of time [4], or exponential fitting [7]. Even though we have gained invaluable in-sights into brain growth with these models, a word of caution is that these models may not be optimal in approximating complex growth trajectories if their inherent assumptions do not agree with the underlying physiology. For instance, quadratic fitting imposes a velocity/acceleration prior constraint on the growth trajectory and it always renders a U (or reversed U) shaped growth trajectory. Logarithm or exponential fittings always assume a flat trajectory at the end with increased time. More importantly, these global nonlinear parametric models complicate the sequential physiological inferences, and they cannot provide a natural velocity-based inference on brain growth. This problem persists in the current LME based longitudinal analysis in neuroimaging. In this study, we proposed to model the growth trajectory with a linear free-knot B-spline (FKBS) based nonparametric regression analysis [12]. To overcome the over-fittings associated with FKBS, quasi-least squares (QLS) based statistical tests were performed to remove the knots making insignificant contributions to the population growth trajectory [13]. In this way, we introduced a data-driven mean structure for LME to be utilized with the NIH pediatric study.

Different from cross-sectional analysis, longitudinal study models correlation between the repeated measurements from the same individual at different time points with a suitable covariance structure to boost the statistical power. Similar to the mean structure selection discussed previously, the covariance structure also depends upon the given data. Up to now, this issue has not been addressed in neuroimaging studies even though statistical methods concerning covariance structure selection is well established with LME for longitudinal analysis. In previous GEE based early brain developmental studies, Markov correlation structure which assumes a weaker correlation between the repeated measurements from the same subject with a wider time separation has been used [4–5]. But this correlation structure did not consider when the acquisitions occurred. Given the fact that the more dynamic of brain growth happened in earlier than later stages, it is expected that for the same individual, the measurements acquired at birth and 1 year old correlate weakly compared to the measurements acquired at 15 and 16 years old, even though the measurements are all one year apart. To overcome this limitation, we have developed a novel time varying Markov (tvMarkov) correlation structure which is able to model not only the weaker correlation with a longer time separation (like Markov correlation structure), but also a weaker correlation if one acquisition happened closer to birth. With LME, we have demonstrated that tvMarkov has a significantly lower AIC compared to both working independence and Markov correlation structures.

2. METHODS

2.1. Free-knot B-spline regression

B-spline regression is data-driven without a prior temporal constraint imposed by a parametric model. Conventional spline regression employs a fixed number of knots and fitting is performed through seeking the coefficients minimizing the sum of squared residuals. In contrast, FKBS allows the inside knots to move freely, thus a greater flexibility to approximate the data is expected [12]. Usually, the fitting is started with a large number of uniformly placed knots and the knots causing a small increase in residual error are removed gradually [14]. After removing one or a few knots, the remaining knots will be replaced to new locations through a constrained nonlinear optimization to keep knots from coalescing.

The growth data are given as pairs of {x_i, y_i} with observation times 0≤x₁≤x₂,…≤x_n. The measurements is modeled as y_i = f(x_i) + e_i (e_i is the noise associated with the i^th measurement). The function f is inferred using a spline model with a knot sequence, t₁=t₂=…t_k<t_k+1<t_k+2<..<t_n=t_n+1=..t_n+k (order k). Fitting was performed through minimizing the residual sum as:

$$\begin{array}{l}min\{\psi (\stackrel{\sim }{\mathit{t}},\mathit{\alpha })=1/2\ast {\Vert \mathit{y}-B(\stackrel{\sim }{\mathit{t}})\mathit{\alpha }\Vert }^2:\mathit{C}\stackrel{\sim }{\mathit{t}}\ge \mathit{h}\},\text{with}\\ \mathit{\alpha }=B{(\stackrel{\sim }{\mathit{t}})}^{+}\mathit{y}.\end{array}$$ (1)

Where, B(t̃) is the B-spline basis function, α is the B-spline coefficient and Ct̃ ≥ h is the constraint keeping knots from coalescing, and it is imposed on the neighboring knots as in the format of t_j ≥ t_j−1 + ε( t_j+1 − t_j−1) and t_j ≥ t_j+1 − ε( t_j+1 − t_j−1) with ε = 0.0625 [15]. B(t̃)⁺ denotes the Moore-Penrose inverse of B(t̃). As in [12], Eq. (1) can be further written as:

$$\begin{array}{l}min\{\mathrm{\Phi }(\stackrel{\sim }{t})=1/2\ast {\Vert \mathit{I}-B(\stackrel{\sim }{\mathit{t}})B{(\stackrel{\sim }{\mathit{t}})}^{+}\mathit{y}\Vert }^2=1/2\ast \\ {\Vert G(\stackrel{\sim }{\mathit{t}})\Vert }^2:\mathit{C}\stackrel{\sim }{\mathit{t}}\ge \mathit{h}\},\end{array}$$ (2)

which can be solved iteratively with Kaufman approximation of the derivative, K = G′(t̃) = −I[I − B(t̃)B(t̃)⁺]B′(t̃)B(t̃)⁺ y[16]. The derivatives of B-splines w.r.t. knots were computed with finite differences [12]. Line search is limited within the space satisfying the non-coalescing constraint. Please also be noted that if the problem is ill conditioned, a regularization term may need to be included jointly with the least square fitting (Eq. (1) and (2)).

2.1. Quasi-least squares (QLS) testing for mean structure selection

QLS was developed based upon GEE under the generalized least square principle [13], while GEE estimates covariance structures using moment-based estimating equations [3]. Compared to GEE, QLS is able to produce a better estimation of correlation parameter between the repeated measurements from the same subject and more likely to guarantee the positive-definite nature of the covariance matrix [13].

For a given series of measurement ${\mathit{y}}_i^{\prime }=(y_{i,1},y_{i,2},\dots y_{i,n_i})$ taken on subject i at time points ${\mathit{t}}_i^{\prime }=(t_{i,1},t_{i,2},\dots t_{i,n_i})$. With the assumption that the measurements from the same subject are correlated, the covariance matrix assumes the form:

$$\mathit{V}=\mathit{diag}({\mathit{V}}_1,{\mathit{V}}_2,\dots {\mathit{V}}_s);{\mathit{V}}_i={({\mathit{\gamma }}_i{\mathit{A}}_i)}^{1/2}{\mathit{R}}_i(\rho ){({\mathit{\gamma }}_i{\mathit{A}}_i)}^{1/2},$$

where A is a diagonal covariance matrix, R is the correlation matrix and a function of ρ (the correlation coefficient between the repeated measurements) and s is the total number of subjects. γ is a diagonal matrix for dispersion coefficients. The quadratic form as in Eq. (3) is minimized through gradient descents to find the optimal values for β and ρ.

$${\sum }_{i=1}^n{Z}_i^{\prime }(\mathit{\beta })R_i^{-1}(\rho )Z_i^{\prime }(\mathit{\beta });Z_i(\mathit{\beta })={{\mathit{A}}_i}^{-1/2}({\mathit{y}}_i-u_i(\mathit{\beta })).$$ (3)

u_i(β) is the linear model approximated (with coefficient β) expectation of y_i.

Given a knot sequence identified with the linear FKBS, the initial regression equation assumes the form:

$$\begin{array}{l}y={\beta }_0+{\beta }_{1}t+{\beta }_2{(t-k_1)}^{+}+{\beta }_3{(t-k_2)}^{+}+\cdots +\\ {\beta }_{n+1}{(t-k_n)}^{+},\text{with}\\ {(t-k_i)}^{+}=\{t-k_i,ift>k_i;0,\mathit{otherwise}\}\end{array}$$ (4)

To overcome over-fitting, the identified knots were combined first as the average of neighboring knots if their incremental (or relative) difference is less than a certain threshold (e.g. k_i+1 − k_i ≤ 0.1 or (k_i+1 − k_i)/k_i ≤ 5%)). Or more ideally, a spike removal technique may be employed here to enhance performance. For inside knots, we have also removed the ones if either its left or right hand side has less than 2 measurements. Sequentially, all the remaining knots will be tested with the Wald statistics from the robust covariance estimated from QLS, and insignificant knots are removed gradually one after another starting with the one having the highest non-significant p-value. In this way, we are able to decompose a complex nonlinear growth trajectory into linear segments and the physiological interpretation can be made through the transitions in growth velocity occurring around the time of the significant knots.

2.3. Covariance structure selection with linear mixed effects model

In order LME models the growth trajectory with a fixed population level trend in combination with a subject-specific random effect (Eq. (5)).

$${\mathit{Y}}_i={\mathit{X}}_i\mathit{\beta }+{\mathit{Z}}_i\mathit{b}+{\mathit{\epsilon }}_i$$ (5)

where X_i is the design matrix for the fixed effect for subject i depending on age and gender, clinical covariates, and also the identified knot sequence from FKBS/QLS. Z_i is the design matrix for the random effects for subject i. β and b are the regression coefficients for the fixed and random effects, respectively. It is assumed that b for the random effects follows a normal distribution, N(0, G), $\mathit{G}=\mathit{diag}({\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_r^2)$. ε_i is the Gaussian noise of N(0, R), $\mathit{R}=R({\sigma }_{r+1}^2,\rho )$ with ρ representing the correlation between the repeated measurements from the same subject. b and ε_i are commonly assumed independent from each other. It was noteworthy to point out that this correlation structure R has not been explored before in LME based neuroimaging studies [6–7]. The covariance of Y is given as: V = ZGZ′ + R. For growth modeling, it is quite often to assume X_i=Z_i. If given the variance terms ( ${\sigma }_1^2,{\sigma }_2^2,\dots ,{\sigma }_{r+1}^2$) and a correlation structure with ρ, the fixed and random effects are calculated respectively as in Eq. (6):

$$\mathit{\beta }={({\mathit{X}}^{\prime }{\mathit{V}}^{-\mathbf{1}}\mathit{X})}^{-1}{\mathit{X}}^{\prime }{\mathit{V}}^{-\mathbf{1}}\text{and}\mathit{b}={\mathit{GZ}}^{\prime }{\mathit{V}}^{-1}(\mathit{y}-\mathit{X}\beta ).$$ (6)

If G is singular, Henderson proposed an alternative set of model equations based upon Cholesky decomposition of G [17]. When the variance components are unknown, the log-likelihood (Eq. (7)) has to be maximized for a specific given covariance structure of R [18].

$$\mathit{logli}=-0.5\times (n\times \mathit{log}(2\pi )+log(\mid \stackrel{\sim }{\mathit{V}}\mid )+{(\mathit{y}-\mathit{X}\stackrel{\sim }{\beta })}^{\prime }{\stackrel{\sim }{\mathit{V}}}^{-1}(\mathit{y}-\mathit{X}\stackrel{\sim }{\beta }))$$ (7)

Or alternatively, restricted/residual maximum likelihood needs to be maximized to account for the loss of degrees of freedom in estimating the fixed effect.

In previous neuroimaging study, R is either chosen as working independence (using cross sectional analysis for longitudinal data) or Markov [4–5] correlation structures for the unbalanced data. Markov structure assumes a weaker correlation between the measurements with a wider separation, cov(Y_i,p, Y_i,q) = ρ^{|t_i,p − t_i,q|}, with measurement times at t_i,p and t_i,q for subject i. But due to the earlier rapid brain growth, the same time separation at early life may have a weaker correlation than at the later stage. To remedy this time varying effect, we proposed a novel modulated Markov correlation structure with an exponential function considering the time when the earlier scan was acquired (Eq. (8)).

$$\mathit{cov}(Y_{i,p},Y_{i,q})={\rho }^{\mid t_{i,p}-t_{i,q}\mid }{e}^{-\tau /min(t_{i,p},t_{i,q})};\tau \ge 0$$ (8)

where τ is a constant to be determined through maximizing the log-likelihood (Eq. (7)).

In order to compare the proposed covariance structure with the working independence and Markov correlation structures. AIC values were computed with the number of parameters and the respectively optimized log-likelihood functions for all these three covariance structures.

$$\mathit{AIC}=2k+2r-2\times \mathit{logli}$$ (9)

Where, k and r are the number of parameters within the mean and covariance structures, respectively.

3. RESULTS

As We have generated a piece-wise linear trajectories consisting of three segments (y=3−2x+1 (0=x<1);y=2−x+1(1=x<2);y=1 (2=x=3) with added Gaussian noise N(0, 0.3). The simulated trajectory consists of two knots located at x=1 and x=2. The over-fitting was apparent with regression directly from KFBS as the spikes or jumps (Fig. 1(a)) with a knot sequence of [0.189, 0.302, 0.352, 1.085, 1.866, 1.937]. After coalescing the closely located neighboring knots, we obtained a slightly over-fitted regression (Fig. 1(b)) with a knot sequence of [0 0.189, 0.327, 1.085, 1.901]. Finally, after QLS testing, the three piecewise linear segments were recovered (with a knot sequence of [1.085, 1.901]; Fig. 1(c)). (Fig. 2f).

Figure 1.

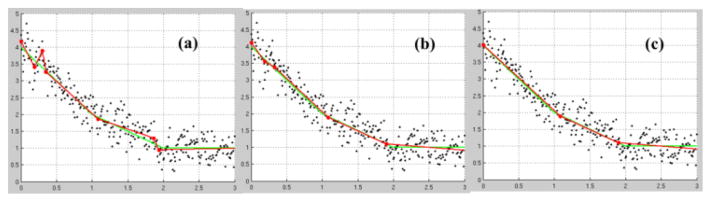
Ground truth (green curves) and the fittings (red curves) from FKBS (a), after coalescing closely located knots (b) and the final results after QLS (c). The knots were marked along the fitted curves.

Figure 2.

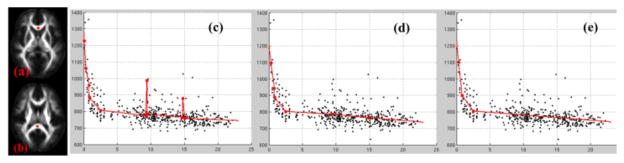
ROIs located in genu (a) and splenium (b) of corpus callosum. The regression results from FKBS (c), after coalescing close knots (d) and the final QLS testing (e). The knots were marked along the curves.

NIH normal brain developmental study consists of 458 longitudinal DTI datasets (release 3). DTI registration was performed through aligning geometrical attributes derived from fractional anisotropy (FA) maps. We evaluated the growth trajectory of mean diffusivities in corpus callosum including genu (Fig. 2(a)) and splenium (Fig. 2(b)). With FKBS, the initial over-fitting was apparent with a knot sequence of [0.069, 0.309, 0.778, 0.809, 2.513, 9.229, 9.403, 9.484, 14.734, 14.795, 15.042] years (Fig. 2(c)). After coalescing the closely located knots, over-fitting was reduced to a knot sequence of [0.309, 0.778, 0.809, 2.513, 9.372, 14.857] (Fig. 2(d)). After QLS, the growth trajectory was decomposed into four linear segments with knots at [0.309, 0.809, 2.513] (Fig. 2(e)).

With the previously identified significant knots, we performed maximization of the log-likelihood from three covariance structures (Independent, Markov and tvMarkov) 10 times each using genetic algorithm with the constraints to ensure the positivity of the variance terms. The averaged population growth trajectories for these three covariance structures were almost identical (Fig. 3(a)) and the AIC values were significantly lower in tvMarkov (tvMarkov vs. Markov: p<10⁻⁸; Markov vs. Independent: p<10⁻¹⁴; Fig. 3(b)). Thus, by considering the time of the repeated measurement, a better longitudinal analysis can be achieved for the large NIH pediatric dataset.

Figure 3.

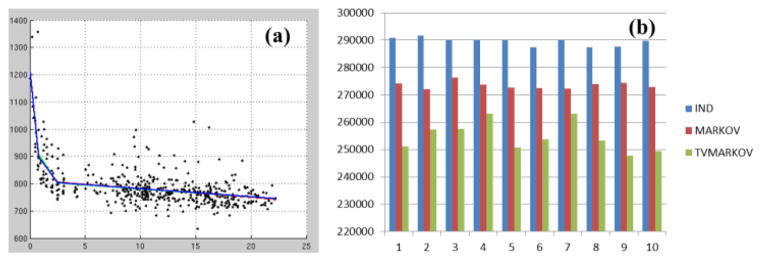
The averaged population growth trajectories from independent (red), Markov (green) and tvMarkov (blue) covariance structures (a). The AIC values from 10 optimizations for the three covariance structures (b).

4. CONCLUSIONS

As In this study, we have introduced a non-parametric fitting scheme for growth trajectory analysis of NIH normal brain developmental study. Compared to the global parametric fitting, the proposed nonparametric approach is more advantageous to discover the transition in growth velocity. Thus, our work allows investigators to seek physiological interpretation on the identified transition time points, which may be related to certain physiological events shaping brain maturation.

Another major contribution of the work is that we have proposed a novel covariance structure tailored for the NIH longitudinal normal brain development study. Especially, we have demonstrated that comparing to other commonly used correlation structures, the proposed one will not bias the population level estimation of the growth trajectory even with a significantly lower AIC. We expect this covariance structure will enable a better statistical power for longitudinal analysis.