A VECTOR MOMENTA FORMULATION OF DIFFEOMORPHISMS FOR IMPROVED GEODESIC REGRESSION AND ATLAS CONSTRUCTION

Abstract

This paper presents a novel approach for diffeomorphic image regression and atlas estimation that results in improved convergence and numerical stability. We use a vector momenta representation of a diffeomorphism's initial conditions instead of the standard scalar momentum that is typically used. The corresponding variational problem results in a closed-form update for template estimation in both the geodesic regression and atlas estimation problems. While we show that the theoretical optimal solution is equivalent to the scalar momenta case, the simplification of the optimization problem leads to more stable and efficient estimation in practice. We demonstrate the effectiveness of our method for atlas estimation and geodesic regression using synthetically generated shapes and 3D MRI brain scans.

1. INTRODUCTION

Within the last 15 years, there has been extensive research in developing methods for representing shapes and their variability across a population [1] and along time [2] as diffeomorphic deformations of a template image. In particular, the optimization methods [2, 3, 4] based on initial deformation momenta, which encode full geodesic paths in the space of diffeomorphisms, have improved the state-of-the-art methods for shape statistics [5].

Previous approaches [2, 3, 4] represent the momenta as a scalar field multiplied by the initial image gradient. In these approaches, the forward evolution of a geodesic and the associated backward adjoint system involve imprecise finite difference gradients of a noisy image. Furthermore, the template and momenta must both be jointly estimated by iterative optimization, leading to poor convergence.

Instead of scalar momenta, we use vector momenta. In our formulation, the evolution of the geodesic and adjoint system is decoupled from the template image. We also derive a closed-form update for the optimal template, which results in more efficient optimization. This novel framework for template estimation applies to both the atlas estimation and the geodesic regression.

2. METHODOLOGY

2.1. Preliminaries

We follow the well-established framework of large deformation diffeomorphic metric mapping (LDDMM) [6, 9], in which anatomical variability is represented by maps of diffeo-morphisms, which are topology-preserving smooth invertible transformations of the underlying coordinate system. We briefly review the mathematical framework of LDDMM.

Let Ω be the coordinate space of the image, I. A diffeo-morphism, ϕ(t), is constructed by the integration of an ordinary differential equations (ODE) on Ω defined via a smooth, time-indexed velocity field, v(t). The deformation of an image I by ϕ is defined as the action of the diffeomorphism, given by ϕ · I = I ○ ϕ⁻¹.

A right-invariant Riemannian metric on the space of diffeomorphisms is obtained by choosing a positive-definite, self-adjoint differential operator L, which acts on velocity fields. This operator induces the structure of a Sobolev space on the collection of velocity fields and determines the norm of a velocity field, ${\Vert v\Vert }^2={\int }_{\Omega }(Lv\left(x\right),v\left(x\right))dx$.

Deformation momenta

The tangent space at identity, V = T_IdDiff(Ω)consists of all vector fields with finite norm. Its dual space, $V^{\ast }=T_{\mathrm{Id}}^{\ast }\mathrm{Diff}\left(\Omega \right)$ consists of vector-valued distributions over Ω. The velocity, v ∈ V , maps to its dual deformation momenta, m ∈ V* , via the operator L such that m = Lv and v = Km. 2 The operator K : V* → V denotes the inverse of L.

In the diffeomorphic image pair registration problem, it has been shown that the optimal initial momentum is orthogonal to the level sets of the deforming image [7]. That is m(x) = α(x)∇I(x) for a scalar function α at all times. Note that constraining ϕ to be a geodesic with initial momentum m₀ = m(0) implies that ϕ, m, I, and α all evolve in a way entirely determined by the metric L, and that the deformation is determined entirely by the initial scalar function α₀ = α(0).

EPDiff for geodesic evolution

Given the initial velocity, v₀ ∈ V , or equivalently, the initial momentum, m(0) = m₀ ∈ V* , the geodesic path ϕ(t) is constructed as per the following EPDiff equation [8, 7]:

$${\partial }_{t}m=-{\mathrm{ad}}_v^{\ast }m=-{\left(Dv\right)}^{T}m-Dmv-\left(\mathrm{div}v\right)m$$ (1)

where D denotes the Jacobian matrix. Operator ad* is dual of the negative Jacobi-Lie bracket of vector fields [7, 8, 9]:

$${\mathrm{ad}}_{v}w=-[v,w]=Dvw-Dwv.$$ (2)

The deformed image I(t) = I₀ ○ ϕ⁻¹(t) evolves via:

$${\partial }_{t}I=-v\cdot \nabla I.$$ (3)

2.2. Geodesic Regression and Atlas Estimation

Geodesic regression in the space of diffeomorphisms is a natural generalization of Euclidean least squares regression. The parameter estimates consist of an “intercept”, i.e., a template image at the initial time point, and a “slope”, i.e., an initial momenta defining a diffeomorphic geodesic evolution of the template image that best describes the time-dependent image data. The atlas estimation problem can be thought of as a special case of the geodesic regression problem, with the initial momenta removed. This is analogous to how linear regression reduces to mean estimation when the slope term is removed. In this section we present a novel formulation of the template estimation problem in geodesic regression and atlas construction using vector momenta, which unlike the scalar momenta formulation has the advantage of stable, closed-form updates to the template.

Geodesic Regression

Given N observed images Jⁱ at time points tⁱ, for i = 1 ... N such that t¹ = 0 and t^N = 1, the geodesic that passes closest, in the least squares sense, to the data minimizes the energy functional

$$\mathcal{E}(I_0,m_0)=\frac{1}{2}{\Vert m_0\Vert }^2+\frac{1}{2{\sigma }^2}\sum _{i=1}^N{\Vert I\left(t^i\right)-J^i\Vert }_{L^2}^2$$ (4)

where I₀ and m₀ are the initial “intercept” and “slope” to be estimated that completely parameterize the geodesic. Here, I(tⁱ) = ϕ^m0(tⁱ) · I₀. As per optimal control theory, we add the Lagrange multipliers to constrain, ϕ^m0(tⁱ) to be along the geodesic path. This is done by introducing time-dependent adjoint variables, m̂, Î and v̂, as per the EPDiff evolution equations (1) to give

$$\tilde{\mathcal{E}}(I_0,m_0)=\mathcal{E}+{\int }_0^1{\langle \widehat{m},\stackrel{.}{m}+{\mathrm{ad}}_v^{\ast }m\rangle }_{L^2}dt+{\int }_0^1{\langle \widehat{I},\stackrel{.}{I}+\nabla I\cdot v\rangle }_{L^2}dt+{\int }_0^1{\langle \widehat{v},m-Lv\rangle }_{L^2}dt.$$

The optimality conditions for m, I, v are given by the following time-dependent system of ODEs, termed the adjoint equations:

$$\phantom{\{}\begin{array}{c}\hfill -\dot{\widehat{m}}+{\mathrm{ad}}_v\widehat{m}+\widehat{v}=0\\ \hfill -\dot{\widehat{I}}-\nabla \cdot \left(\widehat{I}v\right)=0\\ \hfill -{\mathrm{ad}}_{\widehat{m}}^{\ast }m+\widehat{I}\nabla I-L\widehat{v}=0\end{array}\}$$ (5)

subject to boundary conditions

$$\widehat{m}\left(1\right)=0,\widehat{I}\left(1\right)=\frac{1}{{\sigma }^2}(I\left(t^N\right)-J^N)$$ (6)

with added jump conditions at observed measurements, tⁱ, such that, $\widehat{I}\left(t^{i+}\right)-\widehat{I}\left(t^{i-}\right)=\frac{1}{{\sigma }^2}(I\left(t^i\right)-J^i)$ where Î(tⁱ⁺) and Î(tⁱ⁻) denote the limits from above and below, respectively, of the integrated Î.

Finally, the variation of $\tilde{\mathcal{E}}$ with respect to the initial momenta is

$${\delta }_{m_0}\tilde{\mathcal{E}}=K\star m_0-{\widehat{m}}_0$$ (7)

and the variation of $\tilde{\mathcal{E}}$ with respect to the initial image, ${\delta }_{I_0}\tilde{\mathcal{E}}$ can be directly computed from the energy functional $\tilde{\mathcal{E}}$. Notice only the second term has a dependence on I₀ i.e., $I\left(t^i\right)={\varphi }^{m_0}\left(t^i\right)\cdot I_0\circ {\varphi }_{t^i,0}^{m_0}$, where $m_{t^i,0}^{m_0}$ denotes the inverse of ϕ^m0(tⁱ). A change of variable for ϕ implies the derivative with respect to I₀ is

$${\delta }_{I_0}\tilde{\mathcal{E}}=\sum _{i=1}^N(I_0-J^i\circ {\varphi }^{m_0}\left(t^i\right))\mid D{\varphi }^{m_0}\left(t^i\right)\mid .$$ (8)

This results in a closed-form solution for I₀ at optimum:

$$I_0=\frac{{\sum }_{i=1}^N{J}^i\circ {\varphi }^{m_0}\mid D{\varphi }^{m_0}\left(t^i\right)\mid }{{\sum }_{i=1}^N\mid D{\varphi }^{m_0}\left(t^i\right)\mid }.$$ (9)

Notice, at optimum, the resulting vector momentum are horizontal, i.e., along gradient of the image. This follows from taking the gradient in Eq.(4) with respect to velocity, v₀ instead of momenta, m₀ and a change of variables for ϕ such that:

$${\delta }_{v_0}\tilde{\mathcal{E}}=v_0-K\star \frac{1}{{\sigma }^2}\sum _{t^i}\mid D{\varphi }^{v_0}\left(t^i\right)\mid [I_0-J^i\circ {\varphi }^{v_0}\left(t^i\right)]\nabla I_0.$$

Comparison to optimization with scalar momenta

The above analytical update on image, Eq.(9) results in a robust algorithm that does not require joint parameter tuning during optimization unlike previous methods based on scalar momenta. The numerical schemes only optimize on momenta.

However, previously proposed scalar momentum based optimization involve joint optimization over both the template image and the momenta. Moreover, computation of the gradient for image update involves integration of higher order spatial derivatives along time as per the following equations mentioned in [2]:

$${\delta }_{I_0}\tilde{\mathcal{E}}=-\nabla \cdot ({\alpha }_{0}K\star (\nabla I_0{\alpha }_0))-{\int }_0^1\mid D{\varphi }_{0,s}\mid [\nabla \cdot \left(\alpha \widehat{v}\right)]\circ {\varphi }_{0,s}ds+\sum _i\mid D{\varphi }_{0,t_i}\mid (I\left(t^i\right)-J^i)\circ {\varphi }_{0,t_i}.$$

The numerical instability of the optimization for template update for scalar momentum is also evident from this gradient of the energy functional with respect to the template.

Atlas Construction

The Riemannian metric on the space of diffeomorphisms also establishes the Energy minimization problem for atlas construction based on initial momentum, m₀. The minimum mean squared energy, Fréchet atlas construction problem is that of jointly estimating an imageÎ and N individual geodesics emanating from the atlas towards each individual image. The joint energy functional over atlas image, I and initial momenta, $m_0^i$ for i = 1 ... N is:

$$\mathcal{E}(I,m_0^i)=\frac{1}{2N}\sum _{i=1}^N{\Vert m_0^i\Vert }^2+\frac{1}{2{\sigma }^2}{\Vert I^i\left(1\right)-J^i\Vert }_{L^2}^2,$$ (10)

where $I^i\left(t\right)={\varphi }^{m_0^i}\left(t\right)\cdot I$, is the image along the geodesic parameterized by initial momenta for the i^th individual. Similar to the geodesic regression case, solving the constrained variations with respect to atlas image, I and N initial vector momentum result in the similar time-dependent adjoint equations corresponding to m̂ⁱ andÎⁱ for each geodesic:

The variation of $\tilde{\mathcal{E}}$ with respect to initial momenta for individual geodesics, ${\delta }_{m_0^i}\tilde{\mathcal{E}}$ is:

$${\delta }_{m_0^i}\tilde{\mathcal{E}}=K\star m_0^i-{\widehat{m}}^i\left(0\right).$$ (11)

Similar to the geodesic regression case, this results in a closed-form solution for atlas estimate, I at optimum:

$$I=\frac{{\sum }_{i=1}^N{J}^i\circ {\varphi }^{m_0^i}\mid D{\varphi }^{m_0^i}\mid }{\sum _{i=1}^N\mid D{\varphi }^{m_0^i}\mid }.$$ (12)

3. RESULTS

Our implementation of geodesic regression and atlas building is developed based on MPI and the GPU image processing framework by [10]. We evaluate our proposed shooting method using synthetic and real 3D-structural MRI data both for the geodesic regression and the atlas construction problem. In our experiments, the kernel, K corresponds to the invertible and self-adjoint fluid operator, L = –a ∇² – b∇(∇·) + c, with a = 0.01, b = 0.01 and c = 0.001.

Experiments with synthetic data

For geodesic regression

We generated ground truth geodesic on diffeomorphisms by solving the image matching problem and generated sampled shapes along the geodesic. Fig. 1(top) shows our example of shapes along this geodesic: plus to flower. To validate the robustness of estimation of initial conditions at t = 0, geodesic regression was performed given the sampled shapes only for t > 0.5 as input to the algorithm. We used closed-form image update and a simple constant step-size gradient descent for momentum update. The resulting estimated baseline template for this experiment (Fig. 1, bottom right) closely matches the ground truth image at t = 0 (Fig. 1, bottom left). The estimated initial deformation momenta vectors also closely match the ground truth. Fig. 2 reports our experiment with results for assessing the stability of optimization when compared to scalar momenta geodesic regression. The comparison was done based on constant stepsize gradient descent on exactly the same input to both the algorithms. Identical numerical integration methods (fourth order Runge-Kutta) were used in both the algorithms for integrating the evolution equations. We observe that the scalar momentum has difficulty converging even with very small steps for image update while vector momentum converges early to a stable energy.

Fig. 1.

Top: Shapes sampled uniformly along the ground truth geodesic. Bottom: ground truth, I and m at t = 0.0 (left), and estimated I and m at t = 0.0 (right) using only the shape data for t > 0.5

Fig. 2.

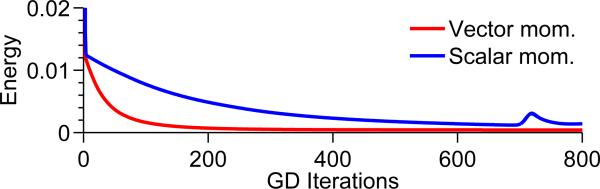
Convergence comparison for same input.

For atlas construction

The atlas was estimated from uniformly rotated ellipses across 180* . Fig. 3 shows the input to the atlas algorithm and the estimated template. The average shape given equally rotated ellipses were expected to be a circle. A perfect circle shape was recovered as the estimated template by our algorithm.

Fig. 3.

Left: evenly rotated ellipses. Right: estimated atlas.

Experiments with brain images from ADNI

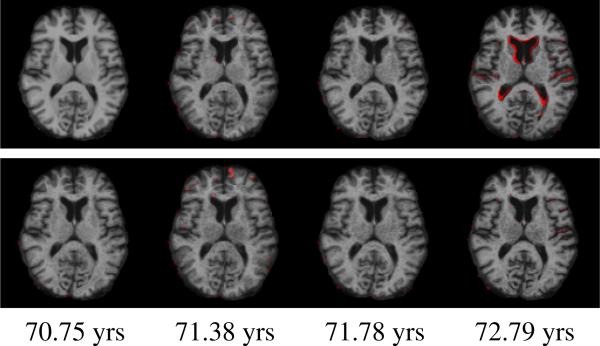
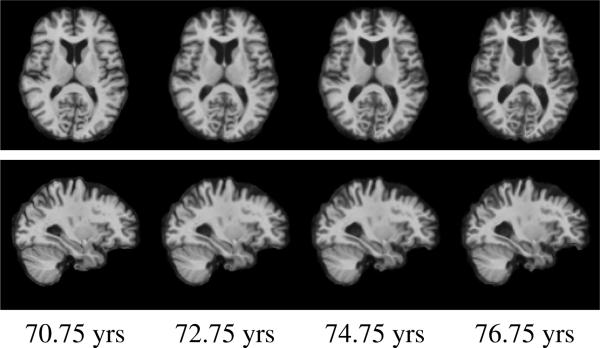
The geodesic regression was performed on longitudinal scans of a subject with Alzheimer's disease (AD) from the ADNI database (adni.loni.ucla.edu). This individual had MRI scans taken at uneven time intervals, i.e., at ages = 70.75, 71.38, 71.78 and 72.79. Fig. 4 (top) shows the original MRI scan data: comparison of the MRI scans with the baseline scan at age=70.75. Expansion of lateral ventricles in this individual is more evident by the end of second year of scan. Our geodesic regression algorithm captures the estimates of the smooth trend of atrophy (Fig. 4 (bottom)). To illustrate reliability of our method, we use the estimated initial conditions to predict the future trend of atrophy for this Alzheimer's subject. The estimated 3D MRI template at t = 70.75 is evolved for 6 years in the future via EPDiff Equations (1). The resulting generated brains exhibit a clear trend in shrinking hippocampus, and expanding ventricles along with cerebro spinal fluid across the whole brain with time. These patterns of atrophy are well known to characterize the disease progression in AD. Fig. 6 shows our atlas estimate of 50 cognitively normal subjects in ADNI database.

Fig. 4.

Top row: Original timepoint scans of an individual overlaid on its baseline scan. Bottom row: Estimated geodesic regression overlaid with original scans at each time-point. Red indicates mismatch.

Fig. 6.

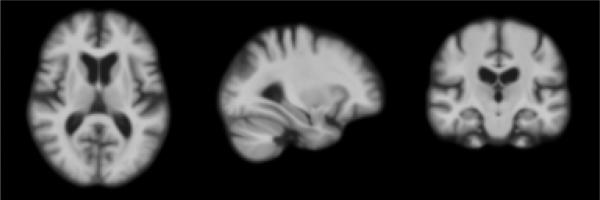
Shooting atlas generated from 50 3D-MRI scans.

Fig. 5.

6 years predicted future brain atrophy.