Detection of molecular binding via charge-induced mechanical response of optical fibers

Abstract

We report a charge sensitive optical detection technique for label-free study of molecular interactions. Traditional label-free optical detection techniques largely rely on the detection of the mass of a molecule, which are insensitive to small molecules. In contrast, the present technique detects the charge of a molecule, where the signal does not diminish with the size of the molecule, thus capable for studying small molecules. In addition, the technique is compatible with the standard microplate platform, making it suitable for high-throughput screening of drug candidates. Using the technique, we have detected 0.2 nM anti-BSA and 15 μM anti-cancer drug (imatinib) with an enzyme modified surface. The achieved effective charge detection limit is ~0.25 electron charge/μm², corresponding to ~0.3 fg/mm² for imatinib, which is orders of magnitude better than traditional label-free optical detection methods.

Introduction

High-throughput detection of molecular interactions is critical for understanding many biological processes, for detecting disease biomarkers, and for screening drug candidates.¹ To date the most widely used detection technique uses labels, such as fluorescence dyes. While popular and useful, the fluorescence-based approach can be problematic, especially when applied to the detection of small molecules, because the dye molecules can significantly alter the activities of small molecules, leading to inaccurate conclusions.² Various label-free techniques, such as surface plasmon resonance (SPR) technique ^3–6 and micro- and nanomechanical biosensors,^7–10 and Quartz Crystal Microbalance¹¹ have been developed, but their sensitivities diminish with the size of the molecule.¹² Electrochemical impedance analysis^13–16 is also label free, but it detects interfacial capacitance or charge transfer taking place on an electrode surface, which is not universally applicable to the detection of different molecules, and its results are often difficult to quantify.^{17, 18} A label-free method to detect small molecules still presents a technical challenge. On the other hand, small molecules are the most popular form of drugs, and play important roles in many biological processes,¹⁹ including post-translational modification of proteins (e.g., phosphorylation), metabolism (e.g., ATP production and consumption), and cellular signalling processes (involving hormones, neurotransmitters and other small molecules). A capability of detecting small molecules will have large impacts on the understanding of these processes, detecting of diseases, and discovery of drugs.

We report here a new optical technique for detecting of both large and small molecules. The technique is based on that most molecules relevant to biomedical research and applications are charged or partially charged. Even if for neutral molecules, they are expected to alter the charge distribution on a sensor surface upon binding. The sensor is an optical fiber, which is dipped into the well of a microplate. It detects the surface charge of the fiber by converting the charge into an optical signal, which does not decrease with the size (mass) of the molecule, making it particularly attractive for studying small molecules, and biochemical interactions that involve small mass changes. In addition, it is compatible with the standard microplate technology for liquid sample handling, which promises high throughput screening and analysis. We describe below the working principle, experimental setup, validation of the working principle, detection of large and small molecules, as well as fundamental detection limit of the technique.

Results and Discussion

Detection principle

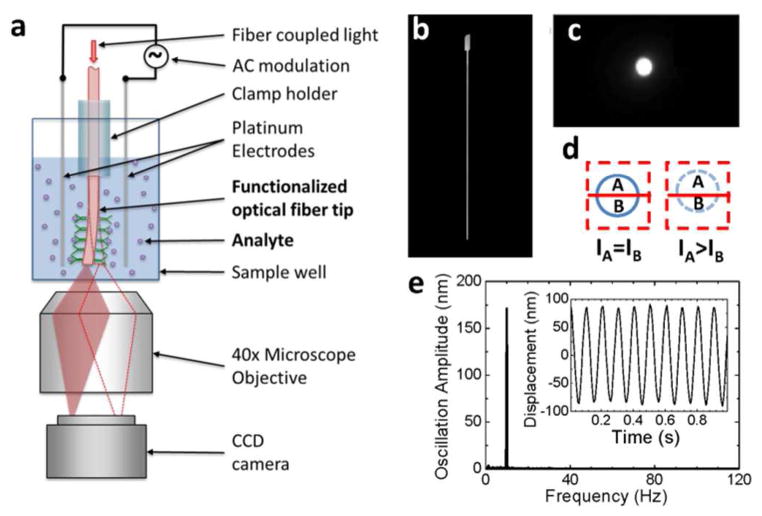
The basic principle of the detection technique is illustrated in Figure 1a, showing a single optical fiber or a bundle of individually detectable optical fibers (Supporting Information) dipped in a well of a standard 96, 384 or 1536-well microplate. An alternating electric field is applied in a direction perpendicular to the fiber. If charge is present on the fiber surface, each fiber will be driven into oscillation by the applied field. The oscillation amplitude is detected optically by tracking the tip position of the fiber using a differential optical detection method detailed later. To study molecular binding, the tip is functionalized with molecular probes. Upon binding of a target molecule onto the molecular probes, the surface charge of the fiber changes, which is detected by monitoring the oscillation amplitude.

Fig. 1.

Overview of the detection technique. (a) Schematic illustration of the setup. (b) A typical optical fiber with etched tip viewed from side. (c) Image of the fiber tip viewed from the bottom of the microplate well. (d) Differential optical detection for accurate determination of the fiber oscillation amplitude. (e) Fast Fourier transform (FFT) of the fiber oscillation. Inset: Oscillation displacement signal in time domain before FFT. The amplitude and frequency of the applied voltage were 2 V and 10 Hz, respectively. The length and diameter of the fiber were 8.5 mm, and 11 μm, respectively. The buffer was 40 times diluted 1X PBS.

The key measurable parameter of the technqiue is the oscillation amplitude of the fiber tip, x_s, at frequency ω, which is proportional to the effective surface charge density, σ, of the fiber, given by

$$x_s=\frac{2\pi \left|\overrightarrow{E(\omega )}\right|\sigma rl}{\sqrt{{(k_{\mathit{eff}}-m_{\mathit{eff}}{\omega }^2)}^2+{(c\omega )}^2}},$$ [1]

where $\mid \overrightarrow{\mathrm{E}(\mathrm{\omega })}\mid$ is the electric field strength, c is the damping coefficient, and k_eff, m_eff, r and l are the effective spring constant, mass, radius and length of the optical fiber (Figures 1b and S1), respectively. $\overrightarrow{E(\omega )}$ is generated by applying a voltage between two electrodes inserted in the solution of the well, which is frequency dependent (Supporting Information). k_eff and m_eff can be calculated from the diameter and length of the fiber, and c can be obtained from the frequency dependent amplitude (See “Validation of the detection principle” section). From the measured oscillation amplitude, x_s, we can determine the surface charge density of the fiber according to Eq. [1], which allows us to monitor the binding of molecules onto the fiber surface.

Differential detection of fiber oscillation amplitude

Accurate measurement of the oscillation amplitude is a key task in the present detection technique, which is achieved by a differential optical detection method that tracks the position of the optical fiber tip via optical imaging. The image of the tip from the bottom of the well, as obtained with an optical microscope, appears as a bright spot (Figure 1c). The differential optical detection method determines the oscillation amplitude of the optical fiber by dividing the bright spot into two regions, A and B, with a line perpendicular to the oscillation direction (Figure 1d). The division line is selected such that the intensities in regions A and B are similar initially, and (I_A−I_B)/(I_A+I_B) is monitored continuously with the camera, where I_A and I_B are the intensities of regions A and B, respectively. We have shown that (I_A−I_B)/( I_A+I_B) is proportional to the oscillation amplitude of the fiber with a calibration factor determined experimentally (Experimental Section, and Figure S3).

This detection method is accurate because it rejects common noises in regions, A and B. It is clear that the sharper the fiber tip, the more sensitive the detection of the oscillation amplitude. For this reason, the fiber tip is etched into a sharp point to create a small bright spot in the image. With the differential optical detection principle we have determined the displacement of a fiber in response to an applied electric field. The inset of Figure 1e shows the oscillation of a fiber driven by a sinusoidal potential with frequency 10 Hz and amplitude 2 V. In addition to the use of the differential optical detection method, Fast Fourier Transform (FFT) filter is used to further remove noises at frequencies different from that of the applied electric field. Figure 1e is the FFT of the time domain data plotted in the inset of Figure 1e, which shows a sharp peak. From the peak height in the FFT spectrum, we determine the oscillation amplitude of the fiber. Using the combined differential detection method and FFT filter, we achieved a detection limit of 0.25 nm for the oscillation amplitude, corresponding to an effective charge detection limit of ~0.25 electron charge/μm². We will return to the discussion of detection limit later. Note that peak quality in the FFT spectrum increases with time duration, and we used a typical time duration of 1 second, which is fast enough for most molecular binding processes.

Validation of detection principle

In order to validate the working principle, it is essential to examine the predictions of Eq. [1]. According to Eq. [1], the oscillation amplitude of the optical fiber is proportional to the applied electric field. To verify this, we measured the oscillation amplitude vs. applied voltage (Note: The voltage is proportional to the electric field.). The result is plotted in Figure 2a, which shows that the oscillation amplitude is indeed proportional to the applied field, as predicted by Eq. [1].

Fig. 2.

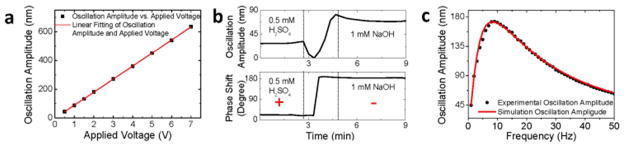
Theory validation of the detection techqniue. (a) Fiber oscillation amplitude vs. applied voltage at 40 Hz, where the square dots are the experiment data, and the red line is the linear fit. Fiber diameter: 8 μm, length: 7.5 mm. Buffer: 40 times diluted 1X PBS buffer. (b) The oscillation amplitude (top panel) and phase (bottom panel) of an amine-modified fiber recorded during the change of the solution from low to high pH values. Fiber diameter: 20 μm, length: 10 mm. (c) Fiber oscillation amplitude vs. frequency, where the black dots are experimental data and the red line is the prediction of Eq. [1]. Fiber diameter: 11 μm, length: 8.5 mm. Buffer: 40 times diluted 1X PBS buffer.

Equation [1] also predicts that the oscillation amplitude is proportional to the surface charge density, and the oscillation phase changes by 180 degrees when the charge changes polarity. To validate these predictions, we coated the fiber surface with amine-terminated silanes. The amine group has a pKa value between 10–11. When pH ≪ 7, the amine group is protonated, resulting in a positive surface charge. In contrast, when pH ≫ 7, the amine group is neutral, but since the background silica is negatively charged, the surface is negatively charged. We measured the oscillation amplitude and phase in 0.5 mM H₂SO₄, then replaced the acidic solution with 1 mM NaOH. In 0.5 mM H₂SO₄, the phase shift is close to 0 degree, indicating that the oscillation is in phase with the applied electric field, which is consistent with the positively charged fiber surface (top panel, Figure 2b). After replacing acidic solution with 1 mM NaOH, the amplitude decreases because of the de-protonation of the amine group, resulting in a decrease in the surface charge. When the amplitude decreases to zero, the phase changes by 180 degrees, indicating the change in the charge polarity (bottom panel, Figure 2b). The amplitude then increases as the surface becomes more and more negatively charged.

Another important prediction of Eq. [1] is the characteristic frequency-dependence of the oscillation amplitude. Figure 2c plots a typical frequency response of the oscillation amplitude, which shows a broad peak near 10 Hz. The frequency response can be fitted with Eq. [1] (red line) with calculated k_eff = 7.6×10⁻⁴ N/m, m_eff = 1.8 ng and fitting parameter c = 7.5×10⁻⁶ N·s/m, and the frequency dependent electric field (Supporting Information). As indicated by the broad peak in Figure 2c and the parameters above, the oscillation is heavily damped, so that the amplitude is insensitive to mass changes associated with molecular binding.

Detection of large molecules

To demonstrate the detection of large molecules, we modified the fiber surface with streptavidin and studied the binding of biotinylated BSA to streptavidin (Figure 3a). Initially, we dipped the fiber into a microplate well filled with 350 μl of PBS buffer, and drove it into oscillation with an applied electric field. We then injected 10 μl of buffer (black arrow) into the well as a control, and observed no detectable changes in the oscillation amplitude, indicating that the injection of solution did not introduce significant mechanical perturbation. We then added 10 μl of 250 μg/ml biotinylated BSA (red arrow) into the microplate well, and found that the amplitude increased and then reached a stable level. The increase in the oscillation amplitude is expected because of the following considerations. The isoelectric point (pI) of streptavidin is 5–6,²⁰ so the streptavidin-coated fiber was negatively charged in PBS buffer, which was confirmed from the phase of the oscillation. BSA was also negatively charged in the buffer because its pI is around 5,²¹ therefore, the binding of biotinylated BSA onto streptavidin added more negative charges onto the fiber surface, causing an increase in the oscillation amplitude.

Fig. 3.

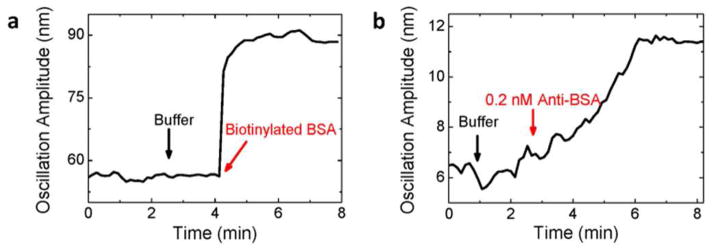
Protein detection. (a) Biotinylated BSA binding onto streptavidin-coated fiber. The black arrow marks the addition of 10 μl buffer and the red arrow marks the addition of 10 μl 250 μg/ml biotinylated BSA (resulting in a final concentration of 100 nM biotinylated BSA). Fiber diameter: 11 μm, length: 7 mm. Buffer: 40 times diluted 1X PBS buffer. (b) Anti-BSA binding onto BSA-modified fiber surface. The black arrow marks the addition of 10 μl buffer, and the red arrow marks the addition of 10 μl 0.5 μg/ml anti- BSA leading to a final concentration of 0.2 nM. Fiber diameter: 18 μm, length: 7.5 mm. Buffer: 40 times diluted 1X PBS buffer.

We further studied the binding of anti-BSA onto the BSA-coated fiber by adding 10 μl of 0.5 μg/ml anti-BSA into the well, which led to a final concentration of 0.2 nM anti-BSA. Figure 3b shows that the amplitude increased initially and then reached a stable value. This observation is consistent with that anti-BSA with a pI between 5.2–6.0²² is also negatively charged in the PBS buffer. Note that before adding anti-BSA into the well, 10 μl of buffer solution was added, and the change of amplitude was within the noise level, which again rules out the possibility that the observed oscillation amplitude change was due to mechanical perturbation by the introduction of the sample solutions.

Detection of small molecules

To demonstrate the small molecule detection capability of the present detection technique, we studied the binding of imatinib to c- Abl (Figure 4a). c-Abl is a nonreceptor tyrosine kinase linked to the growth factor receptor signaling in human,²³ and imatinib is an anticancer drug that inhibits the enzyme activity of c-Abl via binding to the ATP site of the protein.²⁴ The molecular weight of imatinib is 493 Da, which is difficult to detect by traditional label-free detection methods, especially when the surface coverage of c-Abl is low.

Fig. 4.

Small molecule detection. The oscillation amplitude (a) and phase shift (b) of a c-Abl modified fiber during the binding of imatinib onto c-Abl. The black arrow marks the addition of 10 μl buffer, the red arrows mark the additions of 10 μl 500 μM imatinib (final concentration of 15 μM), and the blue arrow indicates the change of the solution back to buffer. Fiber diameter: 11 μm, length: 7 mm. (c) Negative control. Two successive additions of 10 μl 500 μM suberoylanilide hydroxamic acid (red arrows) to the c-Abl modified fiber. Fiber diameter: 12 μm, length: 7.5 mm. (d) Negative control. Response of a fiber modified with myelin basic protein to the addition of 10 μl 500 μM imatinib (marked by a red arrow). Fiber diameter: 10.4 μm, length: 7 mm. (e) Inhibition of c-Abl with AMP-PNP (green arrows), exposure of the inhibited c-Abl to imatinib (red arrow), and replacement of the solution with PBS buffer (blue arrow). Red line is the average of the raw data (black line). Fiber diameter: 10 μm, length: 7.5 mm. (f) Positive control. The fiber was modified with c-kit kinase, which interacts with imatinib. Additions of 10 μl buffer and 10 μl 500 μM imatinib (final concentration: 15 μM), and change of the solution back to buffer are marked with black, red and blue arrows, respectively. Fiber diameter: 16 μm, length: 8 mm. Buffer for above experiments: 2.5 mM Tris-HCl buffer (pH = 7.5) with 1 mM MgCl₂.

The optical fiber coated with c-Abl was first dipped into a microplate well containing 350 μl of 2.5 mM Tris-HCl buffer (pH=7.5) and 1 mM MgCl₂. Then 10 μl of the same buffer was injected into the well, and followed by repeated additions of 10 μl of 510 μM imatinib in 2.5 mM Tris-HCl buffer (pH=7.5) with 1 mM MgCl₂. Each addition corresponded to a 15 μM increase in the imatinib concentration. Similar to the finding described above, the addition of pure buffer resulted in no detectable changes in the amplitude of the optical fiber. In contrast, upon the first addition of imatinib (red arrow), the amplitude decreased sharply, and then reached a stable level. The decrease in the amplitude is expected because imatinib is positively charged. The second addition of imatinib produced a smaller decrease in the amplitude, due to the depletion of the c-Abl binding sites for imatinib. The solution in the well was changed back to the buffer (blue arrow), which led to recovery in the amplitude due to the dissociation of imatinib. The phase shift between oscillation and electric field (Figure 4b) remained constant during the binding process, indicating no change in the charge polarity during the measurement.

To further validate the observation above, we carried out several negative control experiments. The first negative control experiment was to expose a c-Abl coated optical fiber to suberoylanilide hydroxamic acid (SAHA). SAHA is a small molecule, and an inhibitor of pan-histone deacetylase, rather than c-Abl. The second negative control experiment was to coat an optical fiber with myelin basic protein, which does not bind to imatinib. In both cases, as shown in Figures 4 c and d, no changes in the oscillation amplitude were observed, which confirms that the observed changes in the oscillation amplitude in Figure 4a was due to the specific binding of imatinib to c-Abl, and non-specific binding of imatinib onto the areas that were not covered with c-Abl is negligible.

An additional control experiment was performed by first deactivating the binding sites of c-Abl with inhibitor, AMP-PNP, and followed by adding imatinib to the well. As shown in Figure 4e, upon the addition of AMP-PNP, the amplitude increased as AMP-PNP bound onto c-Abl and deactivated c-Abl. Note that the binding of AMP-PNP onto c-Abl caused an increase (green arrow), rather than a decrease in the amplitude as found in the case of imatinib. This is expected because AMP-PNP is negatively charged while imatinib is positively charged. Further addition of imatinib (red arrow) led to a small decrease in the amplitude. This control experiment provided extra evidence that the observed decrease in the amplitude shown in Figure 4a was due to specific binding of imatinib onto c-Abl.

Finally, we carried out a positive control experiment by immobilizing c-kit kinase. Like c-Abl, c-kit kinase can also be inhibited by imatinib.²⁵ Figure 4f shows the response of the oscillation amplitude of a c-kit kinase-coated optical fiber. Upon addition of 10 μl of 500 μM imatinib, the amplitude decreased as imatinib interacted with c-kit kinase, similar to the binding of imatinib onto c-Abl. This observation is consistent with the positive charge polarity of imatinib.

Fundamental detection limit

The noise in the oscillation amplitude of the fiber is about 0.25 nm (averaged over 10 s) as shown in Figure 5a. In terms of charge density, the detection limit is 0.25 electrons/μm². This detection limit is excellent compared to FETs, including conventional silicon-based, nanotube-based^26–28 or nanowire-based FETs,^29–31 which are also sensitive to charge changes. For example, assuming that a 10 nm diameter and 1 μm length silicon nanowire FET reaches detection limit a single electron charge, the corresponding surface charge density detection limit is ~32 electrons/μm², 100 times less sensitive than that achieved with the present detection technique. In other words, FET can reach single electron detection limit in terms of total charge, but this detection limit is achieved at the expense of the effective detection area. The lowest analyte concentration that can be detected by a biosensor is determined by the number of detectable charges per unit area, rather than by the total detectable charges.

Fig. 5.

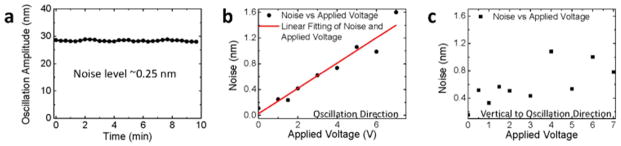
Detection limit and noise analysis. The root-mean-square of the noise level in the amplitude is 0.25 nm (a). Fiber diameter: 20 μm, length: 10 mm. Dependence of noise in the oscillation amplitude on the applied voltage in the parallel (b) and perpendicular (c) directions of the field. Fiber diameter: 10 μm, length: 7 mm. Buffer for above experiments: 40 times diluted 1X PBS buffer.

The detection limit of the present detection technique is determined by many factors, including the light source, optical detector (CCD imager), and mechanical noise of the setup. These noises have been reduced by carefully designing the experimental setup, and by using the differential optical detection and FFT filter techniques, but the ultimate detection limit is determined by the following fundamental factors.

Brownian motion

One of the factors that determine the fundamental detection limit is thermal fluctuations or Brownian motion of the fiber. Based on the damped harmonic oscillator model described by Eq. [1], the thermal fluctuations of the fiber amplitude will lead to thermal noises in the surface charge density and given by³²

$${\sigma }_{\mathit{thremal}}=\frac{\sqrt{2k_{B}Tc\mathrm{\Delta }\omega }}{2\pi \mid \overrightarrow{E}\mid rl},$$ [2]

where k_B is the Boltzmann constant, T is temperature, Δω is the bandwidth of detection. If integrating the signal over ~10 second, Δω is about 0.2π, and the thermal noise limit on the detectable charge density is ~0.03 electron charges/μm² for an optical fiber with r=10 μm and l=1 cm, and electric field |E|=100 V/m at 10 Hz.

Surface charge fluctuations

In aqueous solutions, the surface charge density of the glass fiber is determined by the intrinsic surface properties but also by the balance in the adsorption and desorption of various molecular and ionic species in the solutions. The latter will result in surface charge fluctuations, leading to fluctuations in the oscillation amplitude of the fiber. If the total number of surface charges is N, then the fluctuation in the total surface charge is on the order of $\sqrt{N}$ e, and the corresponding fluctuation in the surface charge density is $\sqrt{N}$ e/2πrl. For a clean silica surface, the surface charge density is ~1 fC/μm^2,33 the total number of surface charge is 2x10⁹ electrons for a fiber of 10 μm in diameter and 10 mm in length, the surface charge density fluctuation according to above formula is ~0.14 electron charges/μm², close to the observed detection limit.

One way to examine the importance of the surface charge density fluctuation on the total noise of the measured oscillation amplitude is to study the noise vs. applied voltage. According to Eq. [1], the noise in the oscillation amplitude in the direction of the electric field caused by surface charge density fluctuations is proportional to the applied voltage. We measured the amplitude noise parallel to the electric field vs. the applied voltage, and found that it indeed increased linearly with the voltage (Figure 5b). We also determined the amplitude noise perpendicular to the electric field, which shows only a weak dependence with the voltage. These observations indicate that the noises in the oscillation amplitude are primarily due to the fluctuations in the surface charge density of the fiber.

Charge screening

The detection limit for x_s in our preliminary experiments is 0.25 nm, corresponding to an effective charge detection limit of ~0.25 electron charge/μm². Ionic screening will reduce the effective charge, and thus affect the actual detection limit. Such screening depends on the ionic concentration as shown in Figure S4. For a 100 mM ionic solution, the ionic screening will reduce the effective charge to ~10% of the actual surface charge, leading to a detection limit of ~2.5 electron charges/μm².

Dynamic range

The dynamic range of a detection technology is determined by the ratio of the maximum to minimum binding signals it can measure. In the present detection technique, the minimum signal is determined by random charge fluctuations, which is about ~0.25 electron charge/μm². The maximum signal is limited only by the size of view of the optical imaging system. Since we can also lower the driving electric field (i.e., lower the gain), the estimated upper limit is ~2.5 x 10⁷ electron charge/μm², leading to an extremely large dynamic range (~10⁸). However, the actual upper limit in the signal is likely to be determined by how many molecules can pack to the surface of the fiber. Assuming a packing density of 10⁶ molecules/μm², the dynamic range would be 10⁶–10⁷. This dynamic range is superior to other detection technologies, including FET and EIM mentioned above.

Towards high throughput detection

One of the most important advantages of the present detection technique is its compatibility with the standard microplate platform, consisting of either 96, 384 or 1536 wells. Unlike most microarray platforms, each of the well is chemically isolated from other wells, preventing cross talking and cross contamination. We have also shown that each optical probe can consist of a bundle of optical fibers (Figure S5), and each fiber in the bundle can be detected simultaneously for parallel analysis of molecular binding processes. The optical bundle probe can be moved from one well to another, controlled with a computer-controlled automation setup to perform high throughput screening tests (Figure S6).

Immunity to interference and temperature drift

Note that FETs mentioned above are sensitive to various processes other than charge, such as binding-induced capacitance changes, and ionic impurity trapping in the electronic materials and interconnections due to the complex biological media. In contrast, only the optical fibers are inserted in the media and the detection is performed optically outside of the solution well. An additional benefit of the present detection technique is its temperature stability. The FETs and SPR are sensitive to temperature because the charged carriers in the FETs and refractive index measured by SPR are strongly temperature dependent. The technique measures the fiber oscillation, which is insensitive to temperature drift (Figure S7), and can provide reproducible measurements of molecular binding processes (Figures S9 and S10).

Conclusions

We have validated the working principle of a detection technique based charge-induced mechanical response with optical fibers, demonstrated its application for the detection of both large and small molecules, and evaluated the detection limit. The method is based on the detection of the charge, so that the output signal does not decrease with the molecular mass. The optical fibers used here are commercially available fibers for optical communications, which are uniform, pure and inexpensive. The setup is based on the conventional microplate platform, making it suitable for high throughout applications, especially when multiple fiber probes are used and automatically switched among different wells. The detection system is based on the conventional optical microscope, which has been shown to be simple and low noise. Using a differential optical detection and FFT filters, the charge detection limit is only limited by the surface charge fluctuations associated with the fundamental molecular and ionic binding processes taking place on a surface. We anticipate that the optical fiber-based technique become a useful tool for high throughput study of molecular interactions, for detection of disease biomarkers and for discovery of drugs.

Experimental section

Materials and methods

Preparation of optical fiber probes

A 125 μm diameter optical fiber from Thorlabs, Inc. was first soaked in acetone for 1 minute, then rinsed with deionized (DI) water, and finally dried out with N₂. The polymer coating of the fiber was stripped off to expose the glass surface of the fiber with an optical fiber stripping tool. The bare optical fiber was dipped in 47% Fluoric Acid (HF) for 30 minute, which etched the fiber down to ~12 μm in diameter. The etched fiber was thoroughly rinsed with DI water and then dried out with N₂. To minimize surface contamination, the fiber was stored in a desiccator filled with N₂ before using it.

The electric field was created with a two-electrode setup. A sinusoidal voltage wave generated by a function generator was applied between the two electrodes via a potentiostat (Pine, model AFCBP1). The applied voltage was controlled with a Matlab program.

Surface functionalization of optical fibers

The etched fiber was first modified with APTES ((3-Aminopropyl)triethoxysilane) to allow crosslinking of APTES to the probe molecules. Before surface functionalization, each etched optical fiber was cleaned with oxygen plasma for 3 minutes. The surface functionalization of the fiber took place in a desiccator, which was first purged with argon for 3 minutes before adding 30 μl of APTES and N,N-Diisopropylethylamine each into two small containers placed inside the desiccator. The desiccator was purged with argon for 3 more minutes and then sealed to allow surface reaction overnight. After the surface functionalization procedure, the optical fiber was placed in an oven heated to 110 °C for 30 minutes before each experiment.

For the detection of BSA, the amine-coated optical fiber was incubated in NHS-Biotin (N-hydroxysuccinimidobiotin) solution for 1 hour. The NHS-Biotin solution was prepared by dissolving 0.2 mg NHS-Biotin in 59 μl DMSO (dimethyl sulfoxide) and then adding it to 1.5 ml of PBS. After incubation, the fiber was rinsed with DI water and dried out with N₂ before experiment. For the detection of imatinib, kinase c-Abl (or c Kit or myelin basic protein) was immobilized on the fiber with 1, 5-Glutaraldehyde by incubating amine-coated fiber in 2.5% 1, 5-Glutaraldehyde for 40 minutes. The fiber was rinsed with DI water and then placed in the 0.8 μg/ml c-Abl solution (or 25 μg/ml c-Kit protein solution or 25 μg/ml myelin basic protein solution) immediately for 1 hour. The c-Abl (or c- Kit or myelin basic protein) modified fiber was rinsed with 1X PBS.

Experimental setup

An inverted optical microscope (Olympus IX70 with 40x objective) was used for the differential optical detection method. A 96-well microplate was placed on the microscope stage. Each optical fiber was placed between two platinum electrodes (1 cm × 0.5 cm) separated with a distance of 3 mm, and the assembly was mounted on a manipulator so that it could be moved in and out of the wells of the microplate easily. A CCD camera controlled by a homemade Matlab program was used to record the image of the optical fiber tip.

Data processing

The oscillation amplitude of the fiber was monitored by the CCD camera at 247 frames per second with the differential optical detection method. The relationship between the oscillation amplitude and the measured differential intensity from the differential optical detection method was determined before each experiment with the following method. The distance for one pixel of the image was known to be 0.74 μm from the optical system and CCD camera. The region of interest (ROI) containing the image of the fiber tip was shifted by different numbers of the pixels manually, and the corresponding changes in the differential intensity were determined from the images. The relationship between the differential intensity and the fiber movement (pixels) was found to be linear, from which the calibration factor of the differential detection method was determined (Supporting Information).