Flocculus Purkinje cell signals in mouse Cacna1a calcium channel mutants of escalating severity: an investigation of the role of firing irregularity in ataxia

Abstract

Mutation of the Cacna1a gene for the P/Q (Ca_V2.1) calcium channel invariably leads to cerebellar dysfunction. The dysfunction has been attributed to disrupted rhythmicity of cerebellar Purkinje cells, but the hypothesis remains unproven. If irregular firing rates cause cerebellar dysfunction, then the irregularity and behavioral deficits should covary in a series of mutant strains of escalating severity. We compared firing irregularity in floccular and anterior vermis Purkinje cells in the mildly affected rocker and moderately affected tottering Cacna1a mutants and normal C57BL/6 mice. We also measured the amplitude and timing of modulations of floccular Purkinje cell firing rate during the horizontal vestibuloocular reflex (VOR, 0.25–1 Hz) and the horizontal and vertical optokinetic reflex (OKR, 0.125–1 Hz). We recorded Purkinje cells selective for rotational stimulation about the vertical axis (VAPCs) and a horizontal axis (HAPCs). Irregularity scaled with behavioral deficit severity in the flocculus but failed to do so in the vermis, challenging the irregularity hypothesis. Mutant VAPCs exhibited unusually strong modulation during VOR and OKR, the response augmentation scaling with phenotypic severity. HAPCs exhibited increased OKR modulation but in tottering only. The data contradict prior claims that modulation amplitude is unaffected in tottering but support the idea that attenuated compensatory eye movements in Cacna1a mutants arise from defective transfer of Purkinje cell signals to downstream circuitry, rather than attenuated synaptic transmission within the cerebellar cortex. Shifts in the relative sizes of the VAPC and HAPC populations raise the possibility that Cacna1a mutations influence the development of floccular zone architecture.

p/q calcium channels play critical roles in the central nervous system, regulating neurotransmitter release from synapses and dendritic excitability. They are strongly expressed in cerebellar Purkinje and granule cells, and thus it is not surprising that the diverse phenotypes resulting from mutations in the genes encoding these channels invariably include an element of cerebellar dysfunction (Llinas et al. 1992; Pietrobon 2005). Common loss-of-function manifestations of mutations in these genes include truncal ataxia, limb ataxia, and abnormalities of both gaze-shifting and gaze-stabilizing eye movements. Studies of P/Q channel mutants offer an opportunity to investigate the linkages between ion currents, single-neuron electrophysiology, neural network function, and behavior. Nowhere in the cerebellum is this goal so feasible as in the flocculus, since our understanding of its connectivity, signals, and computational roles in compensatory eye movements arguably surpasses that of any other cerebellar region (Dean and Porrill 2011; Stahl 2002). In fact, studies of P/Q channel mutant mice such as tottering have contributed substantially to evolving ideas about how endogenous Purkinje cell rhythmicity influences the transfer of signals from the Purkinje cells to their synaptic targets in the deep cerebellar and vestibular nuclei (Alvina and Khodakhah 2010b; Hoebeek et al. 2005; Walter et al. 2006).

tottering carries a recessive mutation in Cacna1a, the gene encoding the pore protein component of the P/Q calcium channel, resulting in a 40% decrease in the channel currents (Wakamori et al. 1998). The mutants exhibit episodic abnormalities including absence seizures and paroxysms of dystonia, as well as continuous loss-of-function abnormalities including truncal ataxia and limb ataxia (Ashcroft 2000; Meier and MacPike 1971; Zwingman et al. 2001). They exhibit multiple abnormalities that would be expected where there is loss of vestibulocerebellar (floccular and nodular) function, including reduced gain of the optokinetic (OKR) and vestibuloocular (VOR) reflexes, hyperactivity of the static maculoocular reflex, deficient time constants of the neural integrator (the network responsible for holding off-center eye positions), and reductions in the ability to plastically adjust the direction and amplitude of the VOR (Hoebeek et al. 2005; Stahl 2004; Stahl et al. 2006, 2012). Hoebeek et al. (2005) recorded flocculus Purkinje cells in awake behaving tottering and compared their signaling properties with those of controls. While an alteration of the signals encoded in Purkinje cell firing rates was expected because of the channels' heavy concentration within the cerebellar cortex, the authors reported that the mutants' Purkinje cells modulated their firing rates normally during compensatory eye movements. The only difference they found was a greater irregularity in the interspike intervals (ISIs) of Purkinje cells. Since the ocular motor deficits in tottering could be approximated in control animals by flocculectomy, the authors concluded that the irregularity of firing nullifies floccular output in tottering. This irregularity hypothesis¹ was subsequently supported by the demonstration of similar reduced Purkinje cell regularity in slices prepared from cerebellar vermis in the Cacna1a mutant leaner and the Cacna2d2 mutant ducky, as well as the ability to improve regularity in vitro and behavioral performance in vivo through application of agents that either augment calcium-activated potassium currents or block voltage-activated potassium currents (Alvina and Khodakhah 2010a, 2010b; Walter et al. 2006). Recordings in tottering deep cerebellar nuclei (Hoebeek et al. 2008) and modeling of cerebellar nuclear cells (Luthman et al. 2011) also supported the idea that irregularity in Purkinje cell firing interferes with the inhibitory influence of Purkinje cells on their synaptic targets.

Unfortunately, no experiments have directly demonstrated that irregularity interferes with transmission of a rate-coded signal from Purkinje cells to their targets, particularly in the flocculus and vestibular nuclei, where such rate-coded signals are particularly well characterized (De Zeeuw et al. 1995; Lisberger et al. 1994; Stahl and Simpson 1995b; Zhang et al. 1995). The seminal study of Hoebeek et al. (2005) cannot exclude the possibility that Purkinje cell irregularity was merely an epiphenomenon and some other property that was not assessed was more directly responsible for the cerebellar dysfunction. The studies performed on cerebellar slices (Alvina and Khodakhah 2010b; Walter et al. 2006) are even more limited in this respect, since the signal content of Purkinje cells cannot be assessed in a slice preparation. Finally, the claim that the irregularity hypothesis is supported by the ability of 4-aminopyridine (4-AP) to increase rhythmicity in vitro and to improve rotarod performance in vivo (Alvina and Khodakhah 2010b) is challenged by the demonstration that 4-AP fails to improve eye movement deficits in tottering that are attributable to dysfunction of the flocculus (Stahl and Thumser 2013). Since the flocculus augments compensatory eye movements in normal animals, improvement in the efficiency of transmission of flocculus outputs to the vestibular nuclei should have augmented the compensatory eye movements. Given the limitations of the experiments underlying the irregularity hypothesis and the challenge leveled by the study of 4-AP's effect on tottering's eye movements, additional investigation of the role of irregularity in cerebellar dysfunction is needed.

If irregularity causes ataxia in Cacna1a mutants, then one might expect that a Cacna1a mutation causing a greater or lesser degree of Purkinje cell irregularity should produce respectively more or less severe behavioral deficits. Conversely, a finding that the degree of irregularity does not covary with the behavioral deficits would argue that an abnormality other than irregularity dictates the behavioral phenotype (Stahl et al. 2006). This prediction can be tested, since multiple Cacna1a mutants covering a spectrum of biophysical and phenotypic severity exist (Miki et al. 2008; Zwingman et al. 2001). Among these allelic mutants, the rocker mutation produces a 23% reduction in P/Q currents (as opposed to 40% in tottering) and similarly less severe truncal and limb ataxia (Kodama et al. 2006; Wakamori et al. 1998; Zwingman et al. 2001) and deficiencies of compensatory eye movements (Stahl 2004; Stahl et al. 2006).

In the present study we conducted extracellular recordings in both the flocculus and vermis of C57BL/6 (C57), rocker, and tottering mice to determine whether the irregularity of rocker Purkinje cells lies intermediate between the normal C57 mouse and tottering. The vermis was the region studied in the in vitro experiments supporting the irregularity hypothesis (Alvina and Khodakhah 2010a, 2010b; Walter et al. 2006), but firing rate regularity of vermis Purkinje cells has not been explored previously in intact, awake Cacna1a mutants. For the flocculus recordings, we also quantified the relationship between Purkinje cell firing rate modulation and compensatory eye movements in all three strains to determine whether rocker exhibits normal modulation, as described previously for tottering (Hoebeek et al. 2005). This study broadens the earlier comparison of tottering and C57 in a number of respects. First, we determined the percentages of floccular Purkinje cells that vary their firing rate in response to optokinetic stimuli, addressing the possibility that the reduced amplitudes of the OKR in Cacna1a mutants derive from reductions in the percentages of optokinetically sensitive Purkinje cells. Second, we studied not only the Purkinje cells responding preferentially to optokinetic stimulation about the vertical axis but also those tuned for rotation about a horizontal axis deviated 135° from the animal's longitudinal axis. Since tottering's eye movement deficit for roll (horizontal axis) stimulation is greater than its deficit for yaw (vertical axis) stimulation (Stahl et al. 2006), it was important to assess whether “horizontal axis Purkinje cells” (HAPCs) exhibited the same normality of modulation that was claimed by Hoebeek et al. (2005) for the “vertical axis Purkinje cells” (VAPCs). Third, we assessed the response of floccular Purkinje cells during rotation in darkness (the VOR) and rotation in the light [the vision-assisted VOR (VVOR)]. Both rocker and tottering exhibit attenuated VOR and VVOR, but the modulation of mouse floccular Purkinje cells during VOR and VVOR has not been studied, and thus the contribution of the flocculus to these behaviors in mice is uncertain.

METHODS

Animals and animal preparation.

Experimental use of mice was approved by the Institutional Animal Care and Use Committees at the Louis Stokes Cleveland Department of Veterans Affairs Medical Center and Case Western Reserve University and conformed to National Institutes of Health guidelines for the use and care of vertebrate animals. tottering and rocker mutants were locally bred. In both tottering and rocker colonies the mutant allele was maintained in repulsion with the oligosyndactylism (Os) mutation, and the homozygous experimental animals were obtained by crossing double heterozygotes (e.g., +Tg/Os+ × +Tg/Os+) (Isaacs and Abbott 1992; Stahl et al. 2006). C57BL/6—the background strain for both the tottering and rocker colonies—served as the control strain; these mice were purchased from The Jackson Laboratory (Bar Harbor, ME). Experimental animals were of either sex. At the time of recording, animals ranged from 3 to 13, 4 to 6, and 3 to 9 mo for C57BL/6 (C57), rocker, and tottering, respectively. Note that we have previously demonstrated that compensatory eye movements in C57 mice are remarkably stable through the first year of life (Stahl 2004). The majority of the data described here were collected from 6 C57, 6 rocker, and 10 tottering animals. Because insufficient C57 VOR data were obtained for a meaningful comparison to the mutants, an additional C57 animal was recorded. Because this last animal was explored specifically for VAPCs and only VOR/VVOR data were systematically collected, this animal's data were not included in the determination of proportions of cell types, nor was it used for the assessments of Purkinje cell spontaneous firing or modulation during OKR.

Animals were prepared for recording by stereotactic surgical implantation of an acrylic head-fixation pedestal as previously described (Oommen and Stahl 2008). Additionally, a craniotomy was drilled over the midline (for vermis recording) or paramedian region (for flocculus recording) and surrounded by a built-up acrylic chamber joined to the fixation pedestal. The chamber incorporated a fiduciary mark to which the position of each electrode track was referenced, thereby facilitating a methodical survey of the flocculus or vermis.

Recording apparatus.

During recordings the mice were fixed by the head pedestal to a rigid armature, which maintained the lambda-bregma plane pitched 20° nose-down. The body was loosely confined in a plastic tube. Vestibular stimuli were generated by a servo-controlled turntable and optokinetic stimuli by a planetarium projector. The animal was surrounded by a cylindrical, lighttight curtain system that allowed testing in darkness and also provided a uniform surface for projection of the planetarium's “star” pattern. Two-dimensional eye movement recording was accomplished with calibrated pupil-tracking video oculography under infrared illumination as previously described (Stahl 2004; Stahl et al. 2000). Video sampling rate was 120 Hz. Animals were pretreated with an ophthalmic solution of 0.5% physostigmine salicylate to limit pupil dilation within the range compatible with accurate pupil tracking. The horizontal and vertical positions of the pupil, horizontal and vertical positions of a reference corneal reflection, and pupil diameter were output from the oculography system as analog signals. These signals, along with turntable position and planetarium velocity, were passed through four-pole Bessel low-pass filters (corner frequency 240 Hz) and then stored to computer via a digital acquisition system (System 3, Tucker-Davis Technologies, Gainesville, FL) at a rate of 500 samples/s.

Extracellular single-unit recordings were performed with glass micropipettes filled with 2 M NaCl and Fast Green, held in a miniature x-y manipulator and hydraulic z-axis (FHC, Bowdoin, ME), mounted behind the head. Neuronal signals were conventionally amplified and stored by the digital acquisition system at a sample rate of 48.8 kHz along with the eye and turntable position and planetarium velocity outputs.

Flocculus and vermis recording procedure and stimuli.

The mouse flocculus consists of a single folium resting on the temporal bone, easily recognized by the dramatic optokinetic sensitivity of the Purkinje cell complex spikes (CS). The simple architecture of the mouse flocculus means that a dorsoventral pass through its center results in an orderly sequence of molecular layer (ML), Purkinje cell layer (PCL), granule cell layer (GCL), PCL, ML, and then departure from the cerebellum. This orderly sequence usually allowed us to recognize and exclude Purkinje cells that resided in the overlying ventral paraflocculus (where CS frequently exhibit some degree of optokinetic sensitivity and cells might be mistaken as floccular if the layer sequence were not taken into consideration).

While searching for the flocculus, we oscillated the planetarium sinusoidally at 0.4 Hz, ±10°/s, with its axis positioned at 135° with respect to the nose and elevated 45° above the horizontal. In this position, the eye is driven in a diagonal trajectory; the CS of VAPCs are stimulated in the hemiphase of rotation that drives the eye nasally and down, while HAPCs are excited in the hemiphase that drives the eye temporally and up. Upon entering the ML of the flocculus, we tentatively identified the preferred axis of the CS from the response to the diagonal stimulus and then realigned the planetarium, to a vertical axis for a presumptive vertical axis (VA) zone or a horizontal axis deviated 135° from the nose for a presumptive horizontal axis (HA) zone. We then drove the electrode further so as to isolate the Purkinje cell simple spikes (SS) within the PCL. If subsequent recording raised questions as to the preferred axis of the isolated Purkinje cell (because the SS modulated poorly or with a phase grossly unexpected for a VAPC or a HAPC), we reoriented the planetarium to test the cell's sensitivity in the other axis. In this fashion it was possible to quickly and qualitatively identify a cell as VAPC or HAPC. Where doubt remained, we attempted to collect data for both VA and HA stimuli, and the data set we ultimately used was determined according to the cell's final classification (see below).

One goal of this study was to reassess the modulation of floccular Purkinje cells with less bias against nonmodulated cells than would exist if the analysis pool was limited to cells selected for overt sensitivity to optokinetic stimulation. Accordingly, we acquired data both from Purkinje cells that were optokinetically responsive and from those that were unresponsive but located on a track in which optokinetically responsive Purkinje cells were encountered. The minimum criterion of optokinetic sensitivity being found within the same electrode track was required to ensure that the cell was within one of the eye movement-related zones of the flocculus (Schonewille et al. 2006).

Once the planetarium orientation was set, we collected eye and neuronal responses of the following types: 1) spontaneous activity with lights on; 2) a sinusoidal OKR “frequency series” of 0.125 Hz ± 8°/s, 0.25 ± 8°/s, 0.4 ± 10°/s, 0.5 ± 8°/s, and 1.0 ± 8°/s amplitude; 3) an OKR “linearity series” at 0.4 Hz and amplitudes ±5°/s, ±10°/s, and ±15°/s; 4) sinusoidal VVOR of 0.8 Hz ± 4.6°; 5) sinusoidal VOR of 0.25 ± 9.9°, 0.5 ± 7.8°, 0.8 ± 4.6°, and 1.0 ± 4.4°. The VOR and VVOR were only collected for cells tentatively identified online as VAPCs, since the turntable apparatus limited us to a head rotation about the VA. Stimulus parameters were chosen to accord with prior behavioral and neuronal studies comparing tottering to C57 (Hoebeek et al. 2005; Stahl et al. 2006; Stahl and Thumser 2013) as well as to minimize occurrence of nystagmus fast phases. Each data record lasted 30–56 s, depending on the stimulus frequency, collecting a number of stimulus cycles ranging from 7 (for the 0.125-Hz stimulus) to 32 (for the 0.8-Hz stimulus). For cells that remained isolated long enough to obtain a full data set, we obtained additional records of the responses to the various stimuli. Only a minority of cells provided a complete data set; the largest body of data was collected for the 0.4 Hz ± 10°/s OKR stimulus, which we considered our preferred stimulus for classifying the response axis and which was accordingly the first stimulus in the series.

The procedure for vermis recording was similar to that for flocculus recording, except that no vestibular or optokinetic stimuli were delivered; a sample of activity was acquired with the planetarium illuminated but stationary and the animal resting quietly, as judged by its eye remaining relatively motionless. Most Purkinje cells were acquired in the deeper portions of lobules 4–6, which were less likely to be injured by exposure within the craniotomy or the electrode passes.

Data processing and statistical analysis.

Eye movement and neuronal data were initially processed as previously detailed (Stahl and Thumser 2012). Briefly, SS were discriminated with Offline Spike Sorter (Plexon, Dallas, TX). The resultant trains of spike times were convolved with a Gaussian kernel (SD = 20 ms, width = ±100 ms) to generate firing frequency as a function of time, which was then resampled at 500 samples/s to match the sample rates of the eye and stimulus feedback signals. The output of the video oculography system was converted to eye position with a trigonometric method (Stahl 2002, 2004; Stahl et al. 2000). This position signal was then numerically smoothed with MATLAB's “filtfilt” function (a zero-phase, forward and reverse digital filter) with cutoff frequency set to 40 Hz, and differentiated with the five-point stencil algorithm to generate eye velocity. A turntable velocity signal (equivalent to head velocity) was similarly generated from the turntable position feedback, while the planetarium position signal was generated by numerical integration from the planetarium's tachometer feedback.

The relationship between SS firing rate and eye movement was quantified as previously described (Stahl and Simpson 1995a; Stahl and Thumser 2012). Briefly, firing rate was regressed on eye position and eye velocity to yield the “apparent” eye position and eye velocity sensitivities (k and r, respectively). The magnitude of the neuronal modulation as a function of eye position magnitude was then calculated as magsensE = √[k² + (2πfr)²], where f is stimulus frequency in Hz, and the phase of the neuronal modulation with respect to eye position was defined as NphaseE = arctan(2πfr/k). MATLAB's “atan2” function was used to eliminate the degeneracy inherent in the mathematical arctangent function. It should be recognized that magsensE and NphaseE reflect the signal processing that occurs as signals flow downstream from the floccular Purkinje cells, to floccular target neurons in the vestibular nucleus, to extraocular motoneurons, and are ultimately transformed into eye movement by the force generation characteristics of the extraocular myofibrils and the passive mechanics of the ocular motor “plant” (Robinson 1981; Stahl and Thumser 2012). The same firing rate data used in calculating magsensE and NphaseE were also regressed against the stimulus position and velocity to measure magsensH and NphaseH. Here the “H” denotes either actual head position during turntable stimuli or the head position with respect to the planetarium projection during planetarium stimuli. In contrast to magensE and NphaseE, magsensH and NphaseH are influenced by the signal processing occurring “upstream” of the flocculus, as signals flow from semicircular canal primary afferents or the direction-sensitive retinal ganglion cells of the accessory optic system (Simpson 1984). The same regression strategy used to determine neural sensitivity and phase was used to measure the gain and phase of the eye movement with respect to stimulus position (Stahl and Thumser 2012). In this case, we regressed eye position (rather than firing rates) on stimulus position and velocity. This approach to obtaining eye (“performance”) gain and phase allows the performance to be measured from the very same data used to quantify the neuronal response.

Prior to the regression analysis we preprocessed the data to exclude portions of the record in which the eye track or neuronal isolation was lost or the neuron was silenced (a relatively unusual occurrence for Purkinje cells). We also eliminated any saccades and their immediate aftermath, as the analysis approach presupposes that the ocular motor system is at steady state, describing a sinusoidal profile at a specific frequency. We also eliminated any periods in which the animal became nonalert, as judged by the eye gain and pupil size declining and then rebounding as the animal was alerted by the experimenter (Stahl and Thumser 2012). After all exclusions had been performed, we averaged the remaining interruption-free cycles and performed the aforementioned regression on the averaged record. Where few or no uninterrupted cycles survived the preprocessing, the regression was performed on the nonaveraged record, with additional “dummy” regression terms added to compensate for slow variations in firing rate or eye position occurring over many seconds (Stahl and Simpson 1995a). Analysis from nonaveraged records was relatively rare and mostly limited to the lowest stimulus frequency, where the larger stimulus position amplitudes rendered saccades more common and the longer cycle period resulted in both a higher chance of a saccade occurring in a cycle and a smaller number of cycles being acquired.

Resting firing records from flocculus and vermis were processed to remove any regions where neuronal isolation was compromised. For flocculus recordings, the eye movement trace was also inspected and regions of the record were discarded during saccades or any portions in which the eye was far removed from its usual central resting position (an approximate position determined during the calibration process). From the selected regions and the spike times we calculated average SS firing rate as the mean of the reciprocals of the ISIs as well as ISI coefficient of variation (CV). We also calculated CV2 in running fashion from each pair of ISIs as 2|ISI_n+1 − ISI_n|/|ISI_n+1 + ISI_n| (Holt et al. 1996) and then averaged across the record. Note that all references to CV2 refer to these averages of CV2 across data records.

Values of k and r (for both the eye-referenced and stimulus-referenced regression analyses), eye gain, and eye phase from each record were averaged across records to yield a single value for the neuron for each stimulus type. The average k and r were then further converted to average magnitude sensitivities and neural phases for the cell/stimulus as described above. Results for each cell were then pooled across cells to yield averages and SDs for each Purkinje cell type in each strain. All neuronal phase data were processed with circular statistics functions available from the MATLAB Central File Exchange Site (http://www.mathworks.com/matlabcentral/fileexchange); mean phase was obtained with “circ_mean” and SD with “circ_std.” Mean eye phase was obtained as a simple arithmetic average (not a circular average) because the values were close to each other and well removed from the phase discontinuity at ±180°. For spontaneous activity data, the rate, ISI CV, and ISI CV2 were averaged across multiple records for each cell and then pooled across cells to yield averages and SDs for each strain. Throughout, averaged values are reported as means ± SD in the text and portrayed in the figures as means ± SE except as noted.

Statistical comparisons of eye gain, eye phase, and magnitude sensitivity vs. frequency curves were performed with ANOVAs with animal strain and stimulus frequency as factors. When the ANOVA was significant for strain, further pairwise comparisons of strains (i.e., tottering vs. C57 or tottering vs. rocker) with multiple-comparison correction (Tukey's “honestly significant difference criterion”) were accomplished with the MATLAB “multcompare” function. The multcompare function returns a binary result (significant or nonsignificant) for a specified statistical α. To extract a P value, we ran multcompare iteratively until we determined the lowest α that returned a significant result; this α was taken as the P of the comparison. Since neuronal phase, in contrast to eye phase, exhibited significant scatter, statistical comparisons were performed with Welsh's unpaired t-test from the circular means and SDs at each stimulus frequency (there being no ANOVA-type test for circular data). Correlation analyses were performed with MATLAB's “corr” function, which computes a Pearson's linear correlation coefficient (r, which we subsequently squared) with a 2-tailed P value representing the probability of obtaining the r value (or better value, up to 1.0) if a relationship between the variables was actually lacking.

Purkinje cell classification.

As noted above, Purkinje cells were tentatively classified as VAPC, HAPC, or “uncertain” online. Final classification was made after analysis had reached the point of our having values of magsensH during OKR. Classification was based principally on the response to the 0.4 Hz, ±10°/s optokinetic stimulus, because this stimulus produced a robust behavioral response in control animals while its short period facilitated gathering enough cycles to form a smooth averaged response within a practical sample length. Where a cell's 0.4 Hz data proved unusable (usually because of issues of neuronal isolation), we substituted another OKR stimulus in the following order of preference: 0.4 Hz, ±15°/s; 0.5 Hz, ±8°/s; 1.0 Hz, ±8°/s; 0.4 Hz, ±5°/s; 0.25 Hz, ±8°/s; and 0.125 ±8°/s. From the responses to the selected stimulus we calculated a sensitivity index as the product of magsensH and r², the multivariate coefficient of determination from the regression analysis. Multiplication by r² corrected for the situation in which neuronal modulation was minimal but noise effects produced spuriously large values of k or r with correspondingly low values of r². In practice, we found that a sensitivity index > 1 corresponded to a clearly apparent modulation in the regression analysis and accordingly made this our threshold for classifying a cell as sensitive or nonsensitive.

In the most frequent classification situation, a cell was observed online to clearly prefer VA or HA stimulation and data were collected only in the apparent preferred axis. If the sensitivity index exceeded 1, the cell was ultimately classified according to the tested axis as VAPC or HAPC. If the sensitivity index was below 1, the cell was classified as nonsensitive. If the preferred axis was ambiguous at the time of recording and data were taken in both vertical and horizontal stimulation axes, the cell was classified as nonsensitive if both sensitivity indexes were below 1, unclassified if both sensitivity indexes exceeded 1, or as a VAPC or HAPC if only the VA or HA stimulus, respectively, yielded a sensitivity index greater than 1. On occasion, a cell appeared nonsensitive online and we collected a response to the diagonal (search) stimulus but lost the cell before we could acquire samples of responses to pure VA or HA stimulation. In this case we derived sensitivity indexes with respect to both the horizontal and vertical components of the diagonal planetarium motion. Usually the sensitivity index from both analyses was <1 and the cell was classified as nonsensitive. If the sensitivity index of one or both axes exceeded 1, the cell was classified as nonclassified. Note that according to this scheme the nonclassified group was a mixed population, including 1) neurons that modulated strongly for both VA and HA stimulation or modulated poorly for monoaxis stimulation and better for diagonal stimulation; 2) cells that were incorrectly believed, online, to be nonsensitive and recorded only with diagonal stimuli but subsequent analysis proved to just exceed the criterion established for sensitivity; and 3) a few cells for which we collected spontaneous activity (and thus included in the statistics for spontaneous activity) but lost before obtaining a usable optokinetic response. Although conditions 1–3 are diverse, the unclassified group was small and there was little that could be achieved by subdividing them. They were used only for determination of resting firing parameters (spontaneous rate, CV, CV2) and subtype percentages.

RESULTS

Eye movement performance.

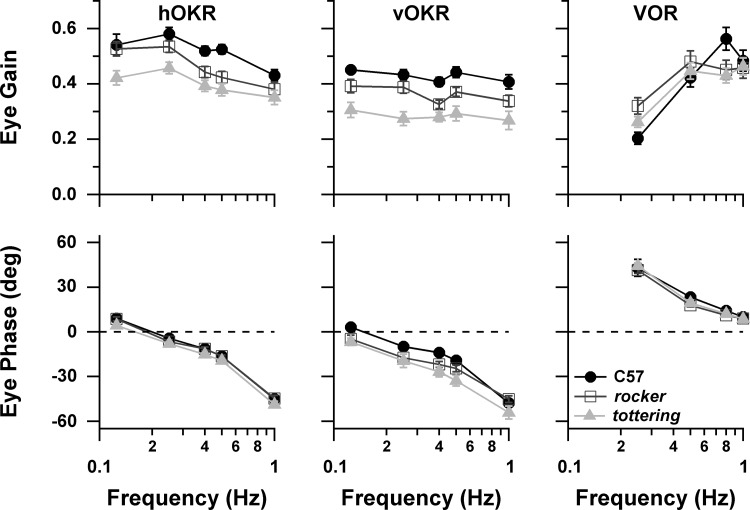
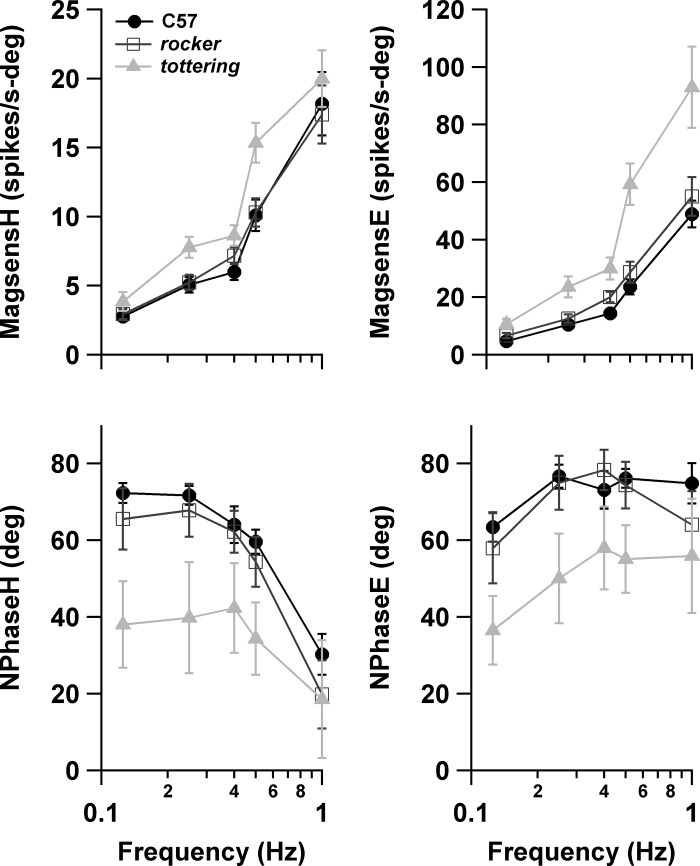
As in the previous purely behavioral study (Stahl et al. 2006), mutants exhibited attenuated compensatory eye movements, with tottering being more attenuated than rocker. Figure 1 summarizes the eye movement performance for the horizontal OKR (hOKR) and VOR collected while recording VAPCs and the vertical OKR (vOKR) collected while recording HAPCs. hOKR gain was depressed in the mutants across the tested frequency range, with gain consistently following the order C57 > rocker > tottering. ANOVA confirmed a significant effect of genotype, with each genotype differing from the other at P < 0.0001. Phase behavior of mutants and C57 was very similar, although tottering eye movements exhibited slightly greater phase lag than C57 with respect to planetarium position at all frequencies (multicomparison ANOVA significant, P < 0.0001). For the vOKR, gain followed the C57 > rocker > tottering pattern at all tested frequencies. Phase lag was also slightly greater for both mutant strains, with rocker and tottering each differing significantly from C57 (P = 0.0029, P < 0.0001) and from each other (P = 0.00066). In the previous behavioral study, mutant VOR gains were depressed at higher stimulus frequencies (0.4–1.6 Hz) for rocker, and at all frequencies for tottering, the disparity between mutants and C57 maximizing around 0.8 Hz. In the present data set tottering gains were slightly below rocker gains throughout, but control gains actually fell below mutants at all but the highest frequencies (ANOVA nonsignificant for strain, P = 0.48). VVOR data are only available at 0.8 Hz. VVOR gain of C57 (0.916 ± 0.113) significantly exceeded that of mutants (C57 vs. rocker, P = 0.0003; C57 vs. tottering, P = 0.0003), while, as in the comparable young age group of the prior behavioral study, rocker and tottering were very similar (0.687 ± 0.147 and 0.682 ± 0.128, respectively). VOR and VVOR phase was very similar in all strains.

Fig. 1.

Performance gain (top) and phase (bottom) for horizontal optokinetic reflex (hOKR), vertical optokinetic reflex (vOKR), and horizontal vestibuloocular reflex (VOR). In this and subsequent plots, values are means ± SE unless otherwise noted. Positive phase values denote lead with respect to stimulus position.

The eye movement performance data indicate that the neuronal data were drawn from individual animals that exhibited the prominent optokinetic deficit, as well as the milder deficit of rocker relative to tottering, documented in the larger behavioral study (Stahl et al. 2006). Although the generally higher VOR gains of C57 were not reproduced, the steeper slope of the C57 gain curve of the prior study was replicated, and that steeper slope still causes C57 to surpass the mutants at 0.8 Hz. The slight difference in gains between rocker and tottering was also reproduced. The difference in C57 VOR gain in the two studies may relate in part to the fact that the methods of the behavioral study allowed gain to be calculated from cycles containing fast phases. In the present study, performance measures were extracted from the same data used for neuronal analyses. Since the neuronal analysis was based on averaged fast phase-free cycles whenever possible, the performance results of the present study would favor periods in which animals were performing at lower gains and thus executing fewer fast phases. This bias against high-gain cycles would tend to impact the control animals more than the mutant animals, since C57 mice have been shown to execute fast phases more readily than the lower-gain mutant mice (Stahl et al. 2006).

Proportions of Purkinje cell types.

In the previous comparison of floccular Purkinje cells in tottering and C57 (Hoebeek et al. 2005) Purkinje cell modulation was reported to be similar in the two strains, but as reviewed in the introduction the approach would not have detected a decrease in floccular output due to a decrease in the percentage of modulating cells. We attempted to circumvent this limitation by scrutinizing the proportions of cell types encountered among all cells isolated within the optokinetically sensitive zones of the flocculus. Cells were classified according to their SS response to optokinetic stimulation as VAPC, HAPC, nonsensitive, and nonclassified. Table 1 shows the numbers and percentages of cells obtained in each strain, indicating that the percentages of nonsensitive Purkinje cells were no greater in the mutant groups. Intriguingly, there was a trend in which VAPCs made up an increasing percentage of the Purkinje cell population, and HAPCs made up a smaller proportion, as one proceeds from C57 to rocker to tottering. The difference in the proportion of VAPCs just reached significance (χ² P = 0.0308) for the C57 vs. tottering comparison, while the difference in proportion of HAPCs for C57 vs. tottering missed significance (P = 0.176). The increase in percentages of VAPCs in mutants bears a resemblance to the increase in VAPC magnitude sensitivity in the mutants (see below) and may represent a form of compensation for attenuated compensatory eye movements (addressed further in discussion). It also raises the possibility that a reduction in the numbers of HAPCs in tottering contributes to tottering's vOKR performance deficit, which is greater, on a percentage basis, than its deficit in hOKR. For example, Fig. 1 shows that at 0.4 Hz tottering's vOKR gain is 66% of control, whereas its hOKR gain is 77% of control. Thus while the data reject the possibility that a reduction in the percentage of modulating Purkinje cells is the principal cause of optokinetic performance deficits, alterations in the distribution of Purkinje cell preferred axes could still play a role in determining the interstrain performance differences.

Table 1.

Numbers and percentages of flocculus Purkinje cell types

	C57	rkr	tg
VAPC	41 (38.0%)	39 (41.5%)	46 (53.5%)
HAPC	36 (33.3%)	28 (29.8%)	21 (24.4%)
Nonsensitive	16 (14.8%)	13 (13.8%)	12 (14.0%)
Nonclassified	15 (13.9%)	14 (14.9%)	7 (8.1%)
Total	108 (100%)	94 (100%)	86 (100%)

C57, C57BL/6; rkr, rocker; tg, tottering; VAPC, vertical axis Purkinje cell; HAPC, horizontal axis Purkinje cell.

Optokinetic responsiveness, VAPCs.

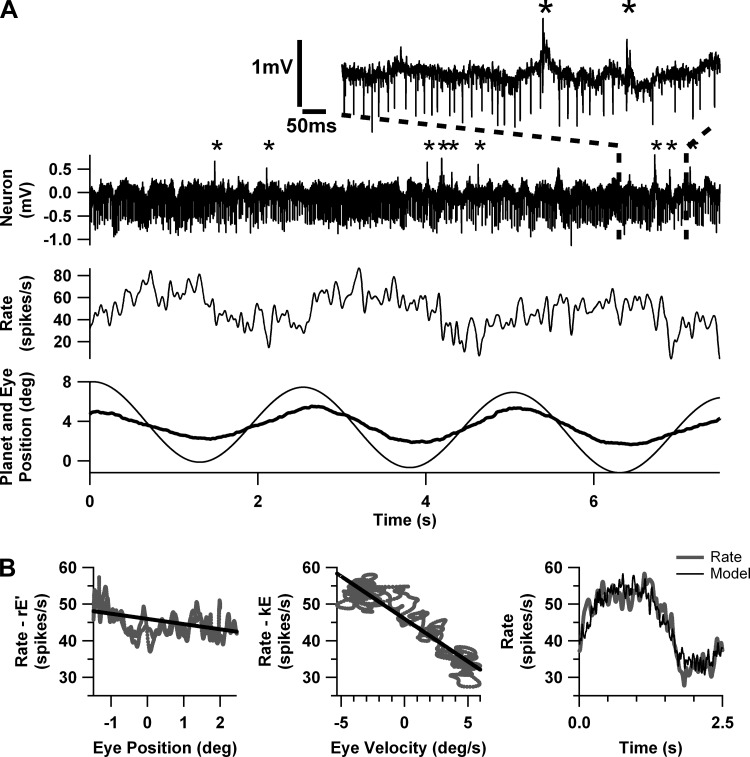
Figure 2 illustrates the response of a typical VAPC during 0.4-Hz hOKR. Figure 2A shows a short sample of the raw spike trace, together with the firing rate (calculated by convolving the spike times with a unit Gaussian, as described in methods), eye position, and planetarium position. Several CS are visible in the spike trace in Fig. 2A, distinguished from the negative-going SS by asterisks; CS-induced SS pauses are visible in the exploded view. SS firing rate increases as the eye rotates temporally, i.e., toward the side of recording, and CS and SS firing rates vary in reciprocal fashion. The peak of SS firing rate aligns more closely with maximal eye velocity than eye position, as is typical for floccular Purkinje cells. Figure 2B illustrates the extraction of eye position and eye velocity sensitivities (k, r, respectively) by multivariate regression from a record averaged over 11 stimulus cycles. Figure 2B, left and center, are partial regression plots to show, respectively, the individual relationships of SS firing rate to eye position and eye velocity; the graphs share the same vertical scale, and the steeper slope of the center plot reflects the close alignment of maximal firing rates with eye velocity. Figure 2B, right, shows the typically excellent fit of the regression model to the averaged firing rate.

Fig. 2.

Response of a typical vertical axis Purkinje cell (VAPC) during 0.4-Hz hOKR. A, top to bottom: raw spike trace, calculated firing rate, eye position (heavy line), and planetarium position (thin line). Asterisks in raw spike trace and the exploded view denote occurrence of complex spikes (CS). B: regression analysis on data averaged from 11 stimulus cycles (including the 3 cycles depicted in A). Left graph emphasizes the dependence on eye position by deducting the eye velocity (r×E′) component. The regression curve is superimposed. Center graph emphasizes the eye velocity dependence by deducting the eye position (k×E) component. Right graph demonstrates excellent fit of the regression model to firing rate.

Since any sine wave can be fit by a linear combination of two linearly independent sine waves (in this case eye position and eye velocity) and both the neuronal modulation and the eye and planetarium motion were grossly sinusoidal, it is not surprising that neuronal modulation was well fit as a function of either planetarium or eye movement. Mean coefficients of determination for the regression with respect to stimulus motion exceeded 0.8 for VAPCs and HAPCs of control animals at 1.0 Hz. Coefficients predictably declined as stimulus frequency fell, as these analyses were based on averages calculated from fewer stimulus cycles (and thus were more noisy) or, where necessary, from analyses of nonaveraged data. For the HAPC, there was an orderly decline of r² as one moves from C57 to rocker to tottering, which stems at least in part from the higher irregularity of firing rates in the mutants. The relationship is more complicated for the VAPC, partly because the stronger modulation of mutant VAPCs (see below) must increase r², counteracting the depressing effects of greater irregularity. Coefficients of determination are predictably slightly lower in analyses with respect to eye movement, since the independent variables (eye position and eye velocity) are inherently noisier than planetarium position and velocity (Levi 1973). This effect predominantly impacts lower stimulus frequencies, where the eye data are noisier because of the lower number of stimulus cycles; at 1.0 Hz, r² of the analysis with respect to eye movement still reached ∼0.8 for both C57 VAPCs and HAPCs.

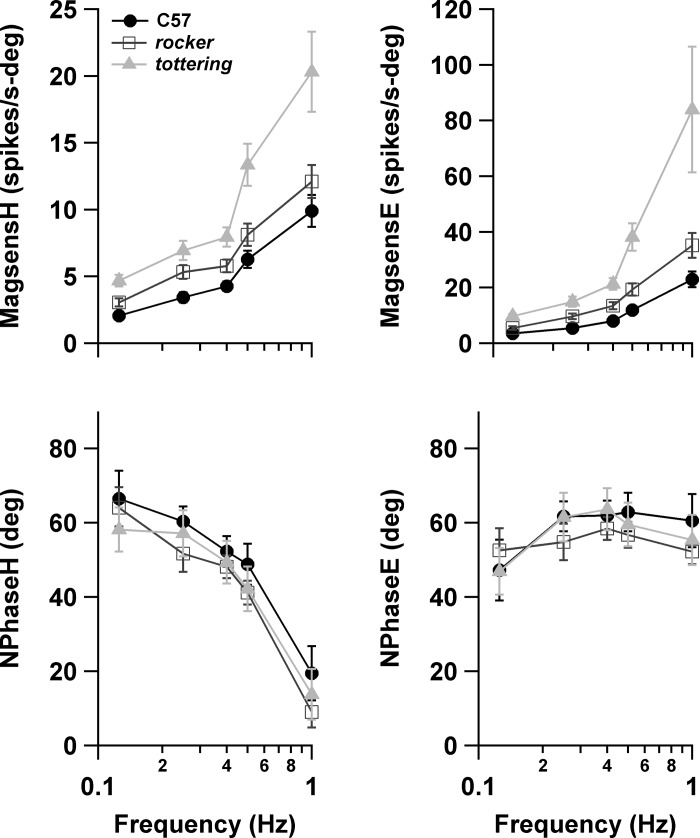
Figure 3 shows the magnitude sensitivity and neuronal phase of VAPCs during hOKR computed with the regression procedure. Separate plots are provided for the analysis with respect to planetarium (virtual head) movement and eye movement. Note that since data were available at all stimulus frequencies for only a fraction of the VAPCs represented in the plot (18/41, 21/39, and 29/46 cells in C57, rocker, and tottering curves, respectively), the numbers and identities of the cells contributing to each frequency point vary. (Table 2 provides the cell numbers contributing to each data point.) However, the curves shown in Fig. 3 superimposed almost perfectly on the curves generated from the subset of cells with complete data (comparison plot not shown). MagsensH increases at all stimulus frequencies as one proceeds from C57 to rocker to tottering, with the disparity maximizing at the highest frequencies. The interstrain difference is significant (ANOVA P < 0.0001). Further analysis of interstrain differences (using MATLAB's “multcompare” function, see methods) demonstrates that the C57 vs. tottering differences are highly significant (P < 0.0001) and the C57 vs. rocker comparisons narrowly miss significance (P = 0.090). magsensE (Fig. 3, top right) demonstrates a similar increase in the mutants, but with a more pronounced and consistent divergence with increasing stimulus frequency. The effect of strain was highly significant (P < 0.0001), as was the interaction of strain and stimulus frequency (P = 0.0043), reflecting the divergence with stimulus frequency. In single interstrain comparisons of magsensE, only the differences between tottering and C57 and tottering and rocker were significant (P < 0.0001, P = 0.00029, respectively, vs. P = 0.40 for rocker vs. C57). However, the consistency of the separation between rocker and C57 suggests that rocker and C57 are not statistically equivalent, and suggests that the rocker vs. control difference would reach significance if the pattern were replicated in a larger sample.

Fig. 3.

Neuronal sensitivity (magsens; top) and phase (Nphase; bottom) of VAPCs during hOKR plotted vs. stimulus frequency. Left plots are measured with respect to planetarium (head) movement (H). Right plots are measured with respect to eye movement (E). Positive phase values denote lead with respect to position.

Table 2.

Numbers of cells contributing to each point in plots of Purkinje cell response characteristics vs. stimulus frequency

	0.125 Hz	0.25 Hz	0.4 Hz	0.5 Hz	1.0 Hz
VAPC hOKR frequency series
C57	17	24	38	23	19
rkr	22	25	37	25	24
tg	31	30	43	32	32
HAPC vOKR frequency series
C57	20	25	35	24	22
rkr	17	18	28	17	14
tg	13	15	21	12	12

hOKR, horizontal optokinetic reflex; vOKR, vertical optokinetic reflex.

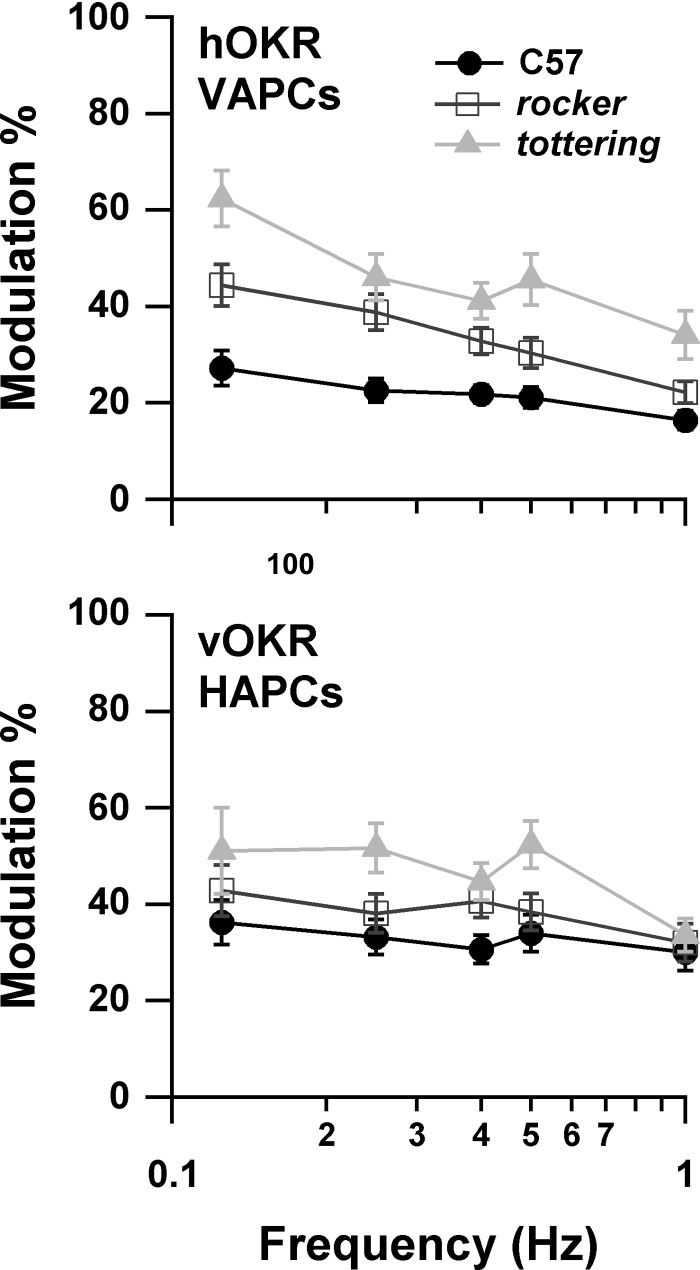
The present results differ qualitatively from the previous study comparing modulation of VAPCs in C57 and tottering (Hoebeek et al. 2005), in which the responses associated with OKR were concluded to be equivalent in the two strains. In that study, neuronal responses were reported in terms of modulation percentage (ratio of amplitude of modulation to mean firing rate) rather than the magnitude sensitivity used here. We converted our measurements to modulation percentage by averaging the magsensH values across cells, then multiplying by the planetarium position amplitude and dividing by the mean spontaneous rate for each genotype. The resulting plot of modulation percentage vs. stimulus frequency is shown in Fig. 4. The plot recapitulates the interstrain differences seen in the magnitude sensitivity plots. The mild decline with increasing stimulus frequency disagrees with the increase found for C57 (but not tottering) by Hoebeek et al. (2005) but is consonant with the properties of the accessory optic system (AOS), which ultimately drives the OKR. The AOS output declines above image slip velocities of 1°/s in rabbits (Soodak and Simpson 1988). Corresponding nicely with the rabbit data, mouse OKR gain during constant-velocity stimuli declines above stimulus velocities of 2.5°/s, where the slip velocity is ∼1.8°/s (Stahl et al. 2006). With a stimulus amplitude of 8°/s (10°/s at 0.4 Hz) in the present study, peak slip velocity for the C57 group was ∼3°/s at 0.25 Hz and increased further with increasing stimulus frequency. Thus a decline in modulation with increasing stimulus frequency is expected. Furthermore, our previous behavioral study demonstrated that hOKR gain rolls off faster in mutants than in C57 as stimulus velocity increases. This faster gain roll-off would create more rapidly increasing slip velocities in the mutants and lower their AOS output, and could thereby account for the somewhat steeper slope of the mutants' modulation curves in Fig. 4.

Fig. 4.

magsensH data from Fig. 3 for VAPCs (top) and horizontal axis Purkinje cells (HAPCs; bottom) reexpressed as modulation amplitude as % of average resting rate. Modulation amplitude is augmented in the mutants.

Figure 3, bottom, show the phase of neuronal modulation with respect to planetarium position (NphaseH) and eye position (NphaseE). As expected for a reflex ultimately driven from retinal image velocity and processed through sluggish visual mechanisms, the neurons lag planetarium velocity and that lag increases with stimulus frequency (or equivalently, the lead with respect to planetarium position decreases). Taken together, the two mutant strains always lag controls slightly, but the difference is on the order of 2–3° and comparisons of the circular mean phase values for C57 vs. rocker, C57 vs. tottering, and rocker vs. tottering with t-tests are far from significance at all tested stimulus frequencies (P values 0.18 or greater). The relative normality of NphaseH for VAPCs parallels the relative normality of eye movement phase for hOKR. When neuronal phase was calculated with respect to eye position, the VAPCs exhibited a fairly constant phase lead across all stimulus frequencies, without any consistent effects of animal strain. From a computational standpoint, the lack of any difference in NPhaseE is not surprising given the normality of NphaseH and performance phase, which together determine NPhaseE. Note that a similar flat relationship of neuronal phase with respect to eye position vs. stimulus frequency was described in the only prior study of mouse flocculus Purkinje cells that reported these data (Goossens et al. 2004).

Optokinetic responsiveness, HAPCs.

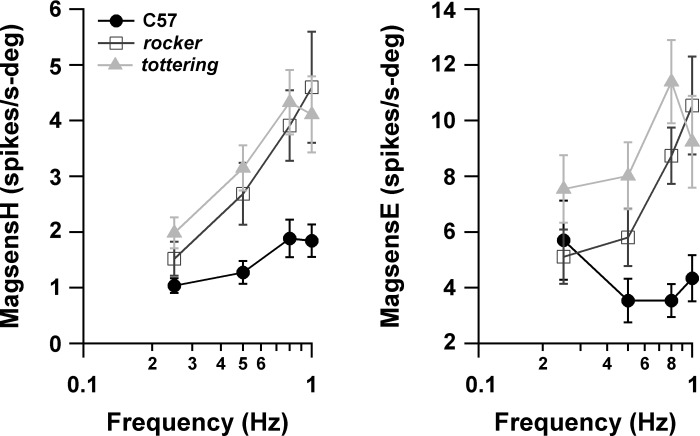
HAPC SS firing rates increased during downward motion of the eye ipsilateral to the recorded flocculus. Figure 5 shows the magnitude sensitivity and neuronal phase of HAPCs during vOKR with respect to planetarium (virtual head) movement or eye movement. As for VAPCs, the magsensH of HAPCs increased steeply as a function of stimulus frequency. Curiously, for C57 (as well as rocker), the HAPCs exhibited greater magsensH than was seen in VAPCs, suggesting that the VA and HA circuits do not have identical properties, a possibility also raised by the fact that the eye movement response during vOKR is always somewhat smaller than hOKR (see Fig. 1; also Stahl et al. 2006). tottering magsensH was consistently greater than that of C57. A two-way ANOVA on genotype and frequency was significant (P = 0.0005) for genotype, with significant differences between both tottering and C57 (P = 0.00058) and tottering and rocker (P = 0.0033) in the multiple-comparison testing. The increased modulation of tottering HAPCs echoes the finding for the VAPCs, although in HAPCs it was less robust and consistent. In contrast, rocker HAPCs did not exhibit the intermediate increase in magsensH exhibited by the rocker VAPCs; the magsensH curve for rocker HAPCs superimposed nearly perfectly on that of controls, despite the fact that vOKR performance gain did exhibit an orderly decrement as one moves from C57 to rocker to tottering. The observation that rocker exhibited a mild degree of enhanced magsensH for VAPCs but not HAPCs is further evidence that VA and HA circuits differ by more than their sensitivity axis. The failure of rocker HAPCs to exhibit enhanced magsensH also suggests that the increase in magsensH of tottering and rocker VAPCs and tottering HAPCs does not follow as a simple or incontrovertible consequence of the alterations in P/Q channel function.

Fig. 5.

Magnitude sensitivity and neuronal phase of HAPCs during vOKR plotted vs. stimulus frequency. Left plots are measured with respect to planetarium (head) movement; right plots are measured with respect to eye movement. Positive phase values denote lead with respect to position.

The plot of magsensE vs. frequency exhibits a greater divergence of tottering from C57, as well as the appearance of a separation between rocker and C57. These differences from the magsensH plot are attributable to the lower performance gains of the mutants, which consequently inflate the magsensE. In fact, a comparison of the correlation between magsensH and eye gain with the correlation between magsensE and eye gain demonstrates that in the HAPCs eye gain influences magsensE, whereas magsensH (and thus flocculus modulation) does not influence eye gain. For instance, for the 0.4 Hz 10°/s data, magsensE negatively correlates with eye gain (r = −0.500, P < 0.0001), while there is no correlation between magsensH and eye gain (r = −0.094, P = 0.39). The general lack of correlation between magsensH and eye gain reinforces the conclusion that reduced vOKR performance in mutants is not due to altered HAPC modulation.

As for VAPCs, the mutant HAPC NphaseH curves in Fig. 5 fall below the C57 curves (lesser lead with respect to planetarium position), but in the case of tottering the divergence from C57 mean values is pronounced. tottering also exhibits a high degree of neuron-to-neuron heterogeneity (phase dispersion). That tottering HAPCs lag control HAPCs may relate to the approximate 10° lag of tottering's eye movement with respect to controls. rocker NphaseH is intermediate between C57 and tottering, as was its performance phase in Fig. 1. However, the relative position of the rocker neural phase between C57 and tottering bears little resemblance to the relative position of rocker's phase between C57 and tottering in the performance phase plot. For instance, the NphaseH of rocker is identical to tottering at high frequencies, but rocker's performance phase is closer to tottering at low frequencies. Error bars are large, and some of the mismatch between relative positions of rocker in NphaseH and performance phase curves could reflect insufficient statistical power to explore such small differences in phase.

The wide error bars for tottering's phase data raise the possibility that greater phase dispersion contributes to the attenuated eye movements of the mutants. If the summation of floccular Purkinje cells on their targets acts as a two-dimensional vectorial sum (with each Purkinje cell acting as a vector of length magsensH and orientation NphaseH), then a greater phase dispersion—even about a normal mean phase—would reduce the magnitude of the averaged vector (equivalent to net floccular output) and, ultimately, eye movement amplitude. To test this possibility, we recomputed the average magnitude sensitivity vs. frequency plots of Figs. 3 and 5 with vectorial averaging (plots not shown). The effect was to collapse the HAPC curves of the three strains on top of each other, but there was no effect on the increased sensitivity of the mutant VAPC curves. Thus the increased phase dispersion of the mutants does not account for the apparent deficiency of floccular function.

Amplitude dependence of Purkinje cell optokinetic response.

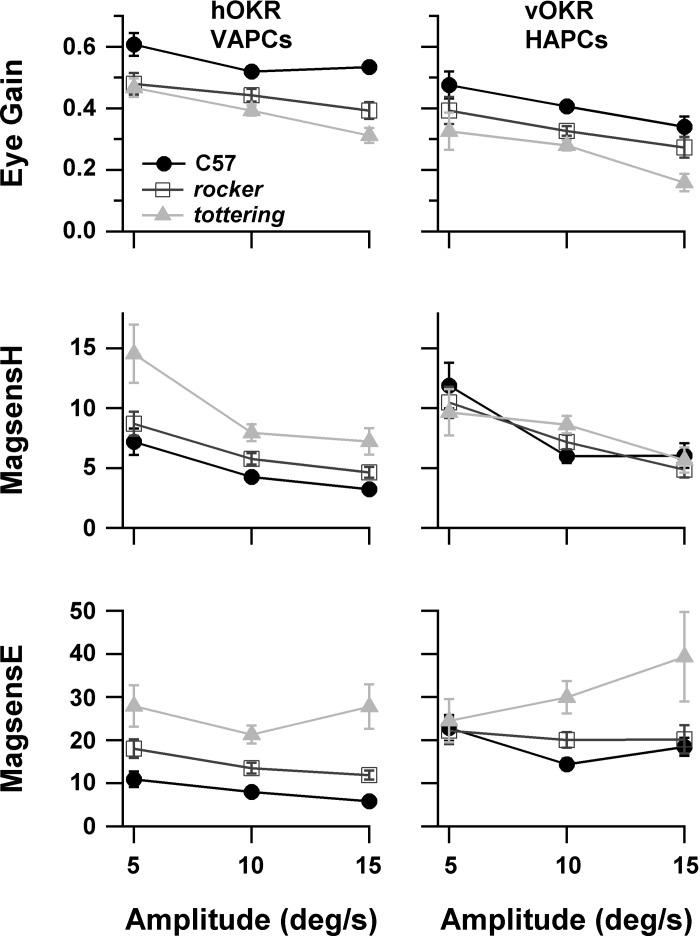
To aid in relating the results of this study to future studies that may employ different stimulus amplitudes, we formally assessed the effects of stimulus amplitude on modulation of VAPCs and HAPCs during 0.4-Hz OKR. It was anticipated that magsensH would decline with increasing amplitude due to the speed tuning properties of the AOS (Soodak and Simpson 1988). It was also likely that magsensE would decline with amplitude because the relationship of floccular modulation to eye position incorporates the transformation from motoneuron firing to eye position, which exhibits a mild dependence of sensitivity on amplitude in both mice and rabbits (Stahl and Simpson 1995a; Stahl and Thumser 2012). The 0.4 Hz frequency was chosen for the same reasons cited in methods that we selected it for determining sensitivity axis, and the upper and lower amplitudes were selected to flank the 8–10°/s range used in the OKR frequency-dependence evaluations described above. Figure 6 shows eye gain, magsensH, and magsensE for VAPCs and HAPCs during 0.4-Hz OKR at stimulus amplitudes ±5, ±10, and ± 15°/s. The numbers of cells available at each stimulus amplitude appear in Table 3. As expected from the AOS properties, performance gain and magsensH declined mildly and similarly for all strains as stimulus amplitude increased. Mutant VAPCs exhibited increased magsensH compared with C57 at all stimulus amplitudes, whereas mutant HAPCs did not exhibit this disparity. This finding reenforces the results presented in Figs. 3 and 5, and indicates that this difference between VAPC and HAPC was not peculiar to the specific stimulus amplitudes selected for our determination of the sensitivity vs. stimulus frequency relationships.

Fig. 6.

Linearity characteristics of VAPCs (left) and HAPCs (right) during OKR. The dependence of the sensitivities on stimulus amplitude is attributable to nonlinearities of the accessory optic system and the ocular motor plant. Animal performance gain (top) during acquisition of the neuronal data is provided for reference.

Table 3.

Numbers of cells contributing to each point in plots of Purkinje cell response characteristics vs. stimulus amplitude

	5°/s	10°/s	15°/s
C57 VAPC	7	38	5
rkr VAPC	19	37	21
tg VAPC	20	43	20
C57 HAPC	10	35	9
rkr HAPC	14	28	13
tg HAPC	5	21	6

Responses of VAPCs during VOR and VVOR.

The magsensH and magsensE of VAPCs during VOR are displayed in Fig. 7, with the numbers of cells at each data point shown in Table 4. In contrast to the plots for OKR, the phase plot is omitted because phase results are spurious when the neuronal modulation is small or absent, as was the case for a large proportion of the neurons, particularly in the C57 strain. Modulation during VOR was much weaker than during OKR; the maximum magsensH reached anywhere in the plot was 4 spikes/s-°, which is on the order of the minimum modulation generated during hOKR (see Fig. 3). Apart from the lower modulation strength, the magsensH graph for VOR bears a strong resemblance to the graph for hOKR, with modulation strength increasing as one proceeds from C57 to rocker to tottering and the divergence of tottering from C57 increasing with stimulus frequency. At 0.8 Hz, where the largest data set is available (C57 n = 20; tottering n = 26), tottering's magsensH is a little over twice control, similar to the ratio of magsensH for hOKR at both 0.5 and 1 Hz (these being the stimulus frequencies closest to the 0.8 Hz of the OKR series). This quantitative match breaks down for rocker, since its 0.8 Hz VOR magsensH is 2.1 times control whereas its hOKR magsensH values at 0.5 and 1.0 Hz are 1.3 and 1.2 times control, respectively. Nevertheless, the qualitative similarities between the comparisons of mutant vs. control magsensH curves for hOKR and VOR suggest the existence of a single phenomenon that is responsible for the unusually strong modulation of mutant Purkinje cells during both reflexes. It also provides further evidence that, contrary to the conclusions of the earlier study, Purkinje cell modulation differs between C57 and tottering (Hoebeek et al. 2005). The magsensE plot is more irregular than magsensH, particularly for controls, and can be explained to some extent by the variations in performance gain shown in Fig. 1. For instance, the depression of C57's magsensE at 0.8 Hz accords with the increased eye movement amplitude at that frequency, and the greater divergence of tottering from rocker reflects the fact that magsensH of tottering was greater than rocker but its eye amplitude was lower.

Fig. 7.

magsensH and magsensE of VAPCs during VOR vs. stimulus frequency.

Table 4.

Numbers of cells contributing to each point in plots of VAPC response characteristics during VOR vs. stimulus frequency

	0.25 Hz	0.5 Hz	0.8 Hz	1.0 Hz
C57	16	15	20	14
rkr	16	14	23	13
tg	22	20	26	16

VOR, vestibuloocular reflex.

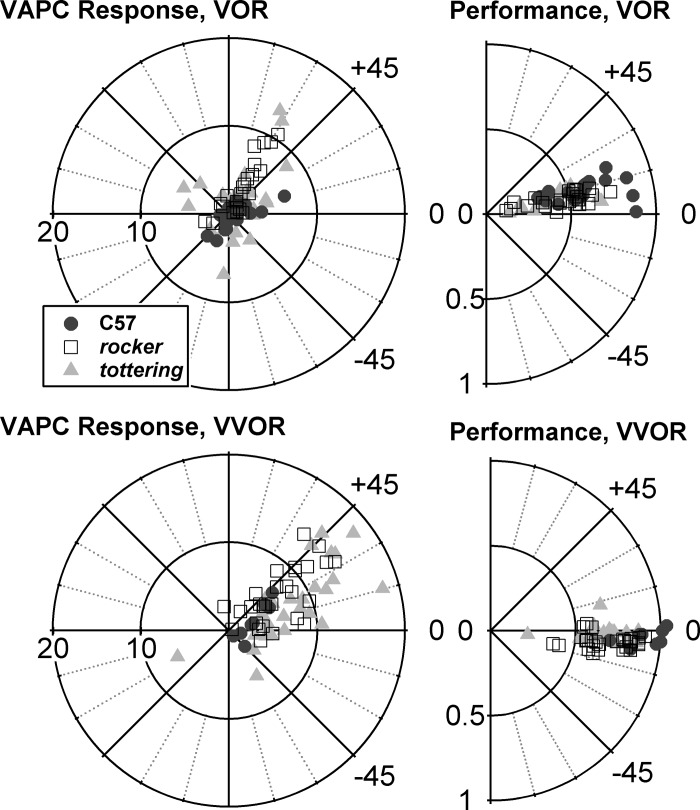
This is the first report of VAPC modulation during VOR in awake, nonparalyzed mice, but the weak modulation of VAPCs during VOR was unexpected. We anticipated that mouse VAPCs would respond similarly to those in the rabbit, another species that, like the mouse, lacks a fovea or equivalent retinal structure and the associated gaze-shifting ocular motor repertoire. In the rabbit, flocculus Purkinje cell modulation during VOR is robust, and only slightly less than that obtained during VVOR or OKR (De Zeeuw et al. 1995; Nagao 1989). In primates, gaze velocity Purkinje cells (GVPs, the dominant subtype of flocculus Purkinje cell and the one that has received most attention in the literature) modulate poorly during VOR, because gaze velocity amplitude falls to zero as VOR gain approaches unity (Miles et al. 1980). The poor modulation of mouse VAPCs during VOR raises the possibility of mouse VAPCs encoding gaze velocity, although obviously the gaze velocity signal would be derived by a mechanism different from that in primates, where the gaze velocity signal is believed to be constructed with inputs from smooth pursuit or other fovea-directing circuits that the mouse lacks (Lisberger and Fuchs 1978). Figure 8 explores the possibility. It shows polar plots comparing VAPC responses for 0.8-Hz VOR and VVOR, along with the corresponding polar plots for eye movement performance. Distance of points from the origin represents modulation amplitude (Fig. 8, left) and eye gain (Fig. 8, right). Figure 8 demonstrates that during VVOR the gain is higher (and consequently gaze velocity is lower) than during VOR, yet modulation amplitude during VVOR is actually greater than during VOR. Thus the VAPCs are not behaving as analogs of the primate GVP. The stronger modulation of the mouse VAPCs when vision is present (i.e., during VVOR and OKR, as opposed to VOR) indicates that Purkinje cells are more strongly driven from signals ultimately derived from the AOS than from signals derived from the vestibular labyrinth. VVOR magsensH averaged 3.40 ± 2.03 for C57 (n = 8), 7.20 ± 3.93 for rocker (n = 28), and 8.96 ± 4.60 for tottering (n = 27), so in VVOR as in VOR and OKR Purkinje cell modulation was enhanced in the mutants.

Fig. 8.

Left: polar plots of magsensH and NphaseH of VAPCs during VOR (top) and vision-assisted VOR (VVOR; bottom). Right: performance gain and phase acquired with the neuronal data. Modulation and performance gain were enhanced together during VVOR, inconsistent with the idea that mouse VAPCs encode gaze velocity.

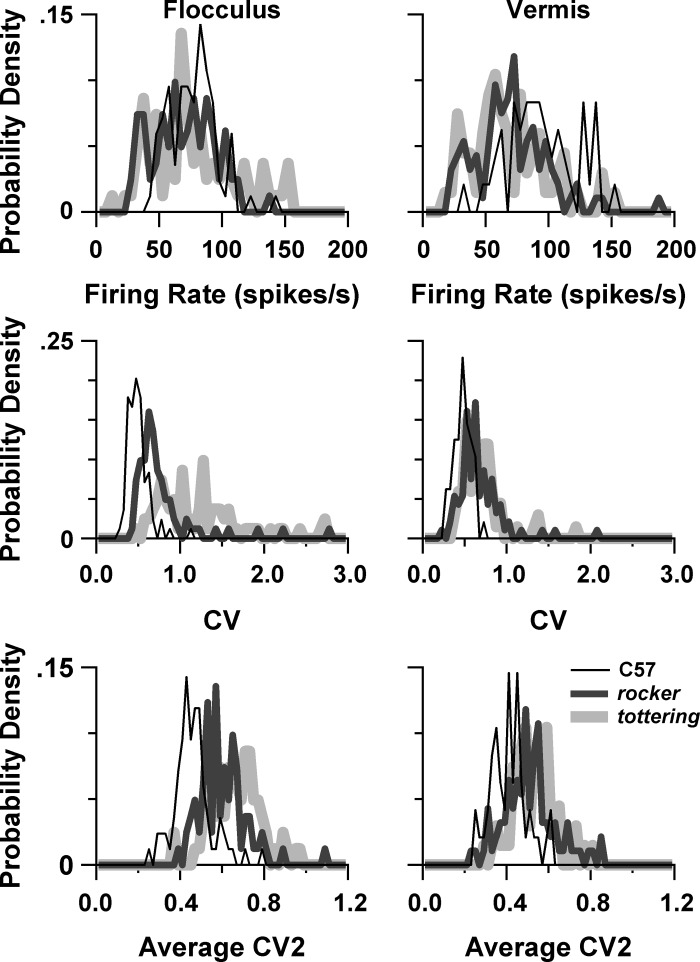
Rhythmicity and spontaneous rate of flocculus and vermis Purkinje cells.

As discussed in the introduction, if Purkinje cell irregularity is the prime cause of cerebellar loss of function in P/Q mutants, then rocker should exhibit irregularity intermediate between tottering and C57. We determined resting rates and ISI regularity of floccular and anterior vermis Purkinje cells. ISI regularity was assessed with CV, which is sensitive to variations of ISI over an entire multisecond sample, and CV2, which measures the variations in ISI between three successive spikes and is thus relatively insensitive to variations evolving over many seconds (Holt et al. 1996). Figure 9, left, shows the distributions of rate, CV, and CV2 for the flocculus Purkinje cells, and the descriptive statistics and P values for comparisons between means are summarized in Table 5. Table 5 also includes P values for selected interstrain and intersubtype comparisons. All Purkinje cell subtypes are pooled in Fig. 9, including VAPC, HAPC, nonsensitive, and nonclassified subtypes. The averages from this pooled group appear as the “all” sections of Table 5, which also includes separate results for VAPCs and HAPCs. There was no consistent relationship between mutation severity and floccular Purkinje cell firing rate. C57 and tottering had virtually identical firing rates, while rocker had a slightly lower mean, with the difference between rocker and C57 just reaching statistical significance. Consistent with the irregularity hypothesis, both CV and CV2 increase as one moves from C57 to rocker to tottering, with all strains differing from each other significantly. We also compared CV2 values of VAPCs and HAPCs during OKR, since it could be argued that the most relevant measures of regularity would be obtained during the actual compensatory eye movements that the irregularity is proposed to render deficient. We restricted our comparison to 0.4 Hz, the largest data set, and we only studied CV2, since CV would be affected by the stimulus-related variations in firing rate. These “dynamic” CV2 values were virtually identical to the “spontaneous” CV2 values shown in Table 5, falling within 0–3.4% of each other, and thus the interstrain comparisons were, as for the spontaneous CV2s, all statistically significant.

Fig. 9.

Resting rate and regularity (CV, CV2) distributions of flocculus Purkinje cells (left) and vermis Purkinje cells (right).

Table 5.

Spontaneous firing descriptive statistics for flocculus Purkinje cells and results of interstrain and inter-cell group statistical comparisons

	N	Group	Rate, spikes/s	CV	CV2
C57	84	All	76.7 ± 18.8	0.49 ± 0.13	0.46 ± 0.09
	33	VAPC	70.5 ± 17.3	0.49 ± 0.16	0.44 ± 0.10
	29	HAPC	79.3 ± 21.1	0.48 ± 0.08	0.46 ± 0.06
rkr	81	All	69.1 ± 24.4	0.77 ± 0.38	0.60 ± 0.11
	36	VAPC	67.2 ± 22.1	0.73 ± 0.43	0.57 ± 0.12
	23	HAPC	68.9 ± 27.3	0.88 ± 0.37	0.63 ± 0.09
tg	81	All	75.6 ± 34.5	1.23 ± 0.51	0.66 ± 0.12
	41	VAPC	71.5 ± 35.2	1.16 ± 0.47	0.64 ± 0.11
	21	HAPC	94.1 ± 33.2	1.39 ± 0.62	0.71 ± 0.10
P value, 2-tailed t-test of means
C57 vs. rkr		All	0.026	<0.0001	<0.0001
C57 vs. tg		All	0.80	<0.0001	<0.0001
rkr vs. tg		All	0.17	<0.0001	0.0006
VAPC vs. HAPC		All strains	0.0073	0.0416	0.0014
P value, 2-tailed F-test of variance
C57 vs. rkr		All	0.021	<0.0001	0.033
C57 vs. tg		All	<0.0001	<0.0001	0.012
rkr vs. tg		All	0.0022	0.0080	0.69

Values are means ± SD for n cells. The “all” group pools VAPCs, HAPCs, nonsensitive PCs, and nonclassified PCs. P values are for comparisons of means and SDs (via a test of variance) between strains and comparisons of means between HAPCs and VAPCs, as indicated. For the comparisons between HAPCs and VAPCs, “all strains” denotes pooling of C57, rkr, and tg strains.

Table 5 also demonstrates a pattern in which mutants exhibited more dispersion than controls in their distributions of rate, CV, and CV2, echoing the tendency toward greater dispersion of magnitude sensitivities and neural phases previously discussed. SDs of rate, CV, and CV2 all differed significantly from each other, with the exception of the comparison of CV2 for rocker and tottering. Compared with VAPC, HAPC exhibited somewhat higher spontaneous rates, CV, and CV2. The significant differences between VAPC and HAPC regularity measures derived entirely from the mutants, since for C57 animals the VAPCs and HAPCs had virtually identical CV and CV2. Note that irregularity being greater in HAPCs than VAPCs, together with the deficits in mutant vOKR being greater than the deficits in hOKR, accords with the irregularity hypothesis.

Whereas the flocculus results are consistent with the irregularity hypothesis, the vermis results contradict it. The distributions of rate, CV, and CV2 for vermis Purkinje cells are shown in Fig. 9, right, with the corresponding statistics tabulated in Table 6. Resting rates were significantly lower in the mutants compared with C57, but virtually identical to each other. Likewise, CV and CV2 were virtually identical in the two mutant strains. Thus the present results demonstrate that the greater irregularity of vermis Purkinje cells of P/Q mutants found in vitro (Alvina and Khodakhah 2010a; Walter et al. 2006) persists in the awake, intact animal, but the degree of irregularity does not parallel the degree of gait ataxia, as would be expected if there existed a simple causal relationship between irregularity and cerebellar dysfunction.

Table 6.

Spontaneous firing descriptive statistics for vermis Purkinje cells and results of interstrain statistical comparisons

	n	Rate, spikes/s	CV	CV2
C57	48	94.0 ± 27.5	0.48 ± 0.10	0.41 ± 0.09
rkr	93	70.0 ± 28.8	0.67 ± 0.26	0.51 ± 0.13
tg	67	68.4 ± 30.4	0.71 ± 0.25	0.53 ± 0.10
P value, 2-tailed t-test of means
C57 vs. rkr		<0.0001	<0.0001	<0.0001
C57 vs. tg		<0.0001	<0.0001	<0.0001
rkr vs. tg		0.73	0.39	0.30

Values are means ± SD for n cells. P values are for comparisons of means between strains.

The higher mean firing rate of vermis as opposed to flocculus Purkinje cells of the control animals may relate to recent reports that Purkinje cells in Zebrin II-positive zones in C57BL/6 mice and Sprague-Dawley rats have lower firing rates than those of Zebrin II-negative zones (Xiao et al. 2014; Zhou et al. 2014). In both mice and rats, the flocculus is Zebrin positive while the anterior vermis is largely Zebrin negative (Sugihara and Shinoda 2004; Zhou et al. 2014). The difference between flocculus and vermis mean firing rates was not observed in the mutants, but it is unknown whether the relationship between spontaneous rates and Zebrin expression holds true for Cacna1a mutants, or whether Cacna1a mutations depress firing rates in the anterior vermis, obscuring the relationship.

DISCUSSION

One of the motivations for studying Cacna1a mutants has been the opportunity to relate alterations in a basic biophysical property—P/Q calcium currents—to alterations in behavior, and thereby to elucidate the mechanisms underlying both normal and abnormal cerebellar function. Numerous physiological alterations in Cacna1a mutants can be demonstrated in vitro, but the ultimate relevance of each to the behavioral abnormalities is generally unproven. The present comparative study of floccular Purkinje cell activity in C57, rocker, and tottering was motivated by the idea that in the simple situation in which a single physiological abnormality leads to a behavioral deficit, there should be a correspondence between the severity of the abnormality and the severity of the behavioral deficit. We used this cross-strain comparison to investigate the idea that cerebellar dysfunction in Cacna1a mutants derives from irregularity, or disrupted endogenous rhythmicity, of cerebellar Purkinje cells (Hoebeek et al. 2005; Walter et al. 2006). We asked whether the irregularity of Purkinje cells in the mildly ataxic rocker mutant is intermediate between that of C57 control animals and the moderately ataxic mutant tottering. In addition, we assessed the modulation patterns of floccular Purkinje cells during compensatory eye movements to see whether strain-related variations in modulation characteristics might provide an alternative to the irregularity hypothesis of motor dysfunction.

With regard to irregularity, we found that, in the flocculus, rocker Purkinje cells exhibited irregularity intermediate between C57 and tottering, consonant with the irregularity hypothesis. However, in the vermis, irregularity for rocker and tottering was similar despite the dramatic differences in the degree of their truncal and limb ataxia, contrary to the irregularity hypothesis. With regard to modulation during OKR, our results confirmed the original conclusion of Hoebeek et al. (2005) that the attenuated hOKR of Cacna1a mutants does not stem from reduced modulation of floccular Purkinje cells. However, contrary to their conclusion that modulation depth was normal in tottering VAPCs, we found modulation was actually increased in the VAPCs of both tottering and rocker. In a normal animal, this increase would lead to an unusually high OKR gain. Thus, like Hoebeek et al. (2005), we conclude that if the gain deficits are a consequence of reduced floccular function, the flow of signals from the flocculus to the ocular motor neurons must be impeded. VOR modulation of VAPCs was weaker than OKR-related modulation but showed a qualitatively similar (and for tottering, quantitatively similar) augmentation of modulation in the Cacna1a mutants. In contrast to the VAPCs, OKR modulation of tottering and control HAPCs was more nearly matched, OKR modulation of rocker and control HAPCs was essentially identical, and HAPC modulation of all strains was essentially identical if the modulation means were calculated from two-dimensional vector averages rather than simple arithmetic averages. With regard to the proportions of cell types determined with our relatively unbiased sampling method, the results showed a trend in the mutants toward VAPCs making up a larger fraction of the floccular Purkinje cells. This trend opens the possibility that shifts in the numbers of different types of Purkinje cells could contribute to the mutant phenotype. A limitation of these population data is that we only collected Purkinje cells encountered on tracks where complex spikes exhibited optokinetic sensitivity. Thus if the optokinetically sensitive zones of the flocculus occupy a smaller volume in mutants compared with controls, there might be a reduction in total numbers of sensitive cells that would not be detected by our approach. Even given this limitation, the data raise the possibility of shifting population sizes contributing to mutant performance characteristics, and suggest the value of an anatomical study geared toward determining whether the zonal architecture of the flocculus (De Zeeuw et al. 1994; Schonewille et al. 2006) is modified in Cacna1a mutants.

Reexamination of the irregularity hypothesis of ataxia in Cacna1a mutants.

As reviewed in the introduction, the irregularity hypothesis was originally advanced based on in vivo and in vitro studies in which irregularity was concluded to be the critical alteration in Purkinje cell function because it was the only assayed property that was found to be abnormal (Hoebeek et al. 2005; Walter et al. 2006). Studies of the effects of 4-AP and the SK channel agonist EBIO on Purkinje cell rhythmicity in vitro and rotarod performance in vivo provided additional support (Alvina and Khodakhah 2010a, 2010b; Walter et al. 2006). The limitations that render these studies nondefinitive were reviewed in the introduction. The irregularity hypothesis also poses conceptual challenges. Rate-encoded signals appear to be employed in the flocculus (Dean and Porrill 2011; Heck et al. 2013); the contributions of the flocculus to eye movements in afoveate animals can be explained nicely by the addition of the stimulus- and eye movement-related variations in Purkinje cell firing rate to similarly rate-encoded signals in vestibular nucleus neurons (De Zeeuw et al. 1995; Stahl and Simpson 1995b). In a linear system, added noise (the irregularity) would be expected to merely sum with, not nullify, such signals. Moreover, if the noise components were noncorrelated across different Purkinje cells, then the downstream impact of the noise would be attenuated by averaging effects as multiple Purkinje cells converge on single target neurons. This averaging effect would be powerful, as the convergence has been estimated at anywhere from thirty- to several hundred-to-one (Palkovits et al. 1977; Person and Raman 2012). If the noise were correlated across Purkinje cells, then the effect in a linear system would be to render the eye movements noisy, not attenuate them. Thus any nullifying effect of noise in the Purkinje cell firing rate implies the existence of nonlinearities in the vestibulocerebellar circuitry, lying downstream of the Purkinje cell spike initiation site. Two candidate nonlinearities are rebound firing of the target neuron and short-term depression (STD) of the Purkinje cell synapse on the target neuron.

Rebound firing following a period of hyperpolarization is well described in Purkinje cell target neurons, in both the deep cerebellar nuclei and the vestibular nuclei (Aizenman and Linden 1999; Jahnsen 1986; Sekirnjak et al. 2003; Shin et al. 2011; Witter et al. 2013). The phenomenon is principally described for in vitro preparations responding to experimental manipulations of membrane potential, and the degree to which it is relevant to intact preparations has been debated (Jaeger 2011). It might be imagined that the attenuating effects of irregularity on eye movements arise because flurries of Purkinje cell spikes—the “noise”—create pauses and bursts in the flocculus target neuron (FTN) that occlude the cell's response to its vestibular inputs, effectively shutting down the FTN as a conduit for eye movement commands, whether originating in the flocculus, vestibular nucleus, or vestibular primary afferents. An objection to this scenario is that it predicts that flocculectomy in tottering would remove the FTN-nullifying Purkinje cell input and might increase eye movement gain. However, flocculectomy in tottering had no effect on its eye movement gain (Hoebeek et al. 2005). Rebound phenomena figure importantly in models that seek to explain how coordinated firing of multiple Purkinje cells impacts the targets in the deep cerebellar nuclei, and coordinated firing of normal Purkinje cells has been demonstrated during brief periods in which the cells fire in a regular pattern (Heck et al. 2013; Person and Raman 2012; Shin et al. 2007; Witter et al. 2013). Thus it may be imagined that irregularity, by disrupting coordination across Purkinje cells during what would otherwise be periods of regular firing, interferes with the normal rebound-associated mechanisms. However, these modeling and experimental studies were all conducted in regions other than the vestibulocerebellum. Regional variation in cerebellar coding and network properties is now recognized (Person and Raman 2012), and the degree to which cross-correlated epochs of regular firing occur in, and are important to, the function of the floccular-vestibular interactions is entirely unknown. No explanations have been offered as to what function a nonlinear mechanism coupling coordinated Purkinje cell firing to rebound activity would serve in the flocculus, or why this hypothetical mechanism should replace an interpretation of flocculus function based on its documented rate-coded signals (Dean and Porrill 2011).

STD acts at the Purkinje cell synapse to reduce synaptic efficacy whenever the ISI of a pair of action potentials falls below ∼10 ms. It also appears in the context of much longer ISIs (as long as 5 s) during periods of sustained firing (Pedroarena and Schwarz 2003). STD could be a mechanism by which irregularity nullifies Purkinje cell signals in Canca1a mutants if flurries of closely spaced spikes engendered by irregularity evoke STD, thereby attenuating transmission of Purkinje cell signals. An advantage of STD as a mechanism to connect irregularity with floccular deficits is that irregularity would disable only the synapses of Purkinje cells on the FTNs, nullifying Purkinje cell output without interfering with other eye movement signals being transmitted through the FTNs. In a model of Purkinje cells and their targets in the deep cerebellar nuclei incorporating STD, irregularity reduced mean inhibition of nuclear cells by Purkinje cells (Luthman et al. 2011). However, the study did not explore whether irregularity could also attenuate transmission of dynamic, rate-coded signals. Thus, while STD provides a mechanism by which irregularity could produce floccular deficits, its ability to do so has yet to be proven experimentally in this system.

In sum, although electrophysiological phenomena have been demonstrated that might allow irregularity to influence signaling in Purkinje cell targets, their ability to produce the ocular motor deficits remains unproven. The present findings that vermis Purkinje cells in rocker do not exhibit an intermediate degree of irregularity to match the intermediate degree of truncal ataxia, together with the previous finding that 4-AP, which increases Purkinje cell regularity in tottering slices (Alvina and Khodakhah 2010b), does not improve eye movements in tottering, indicate that further investigation of the irregularity hypothesis is necessary, particularly as this hypothesis has already been proposed as a principle to drive drug development for human ataxic disorders (Alvina and Khodakhah 2010a, 2010b).

Contrasting properties of VAPC and HAPC modulation.

This is the first study to report the properties of floccular HAPCs in mice and to compare them with VAPCs. As in the rabbit (Graf et al. 1988), the vast majority of Purkinje cells that were sensitive to the optokinetic search stimulus could be classified as either VAPCs or HAPCs. The long phase leads with respect to eye position at low stimulus frequencies also accord with the phase properties of floccular Purkinje cells in the rabbit, and with the suggestion that the phase of the floccular signal is appropriate to emphasize the velocity component of the eye movement command (De Zeeuw et al. 1995; Stahl and Simpson 1995b). VAPCs and HAPCs differed from each other in several respects. In control animals, HAPCs tended to exhibit stronger modulation and longer phase leads with respect to the stimulus than VAPCs (compare Figs. 3 and 5). The consistent increase in hOKR sensitivity in the mutant VAPCs was less prominent (for tottering) or absent (for rocker) in the HAPCs. Additionally, tottering HAPCs exhibited a prominent—although highly variable—phase lag with respect to controls that was not seen in VAPCs. There was also a trend toward VAPCs making up a larger percentage of the Purkinje cells in the mutants, possibly at the expense of the HAPCs. The lack of a robust increase in modulation in HAPCs in the mutants, and the finding that VAPCs appeared to be more populous and HAPCs, if anything, less populous, may underlie the fact that on a percentage basis the attenuation of vOKR in the mutants was more prominent than the attenuation of hOKR. All these distinctions indicate that the consequences of the Cacna1a mutation differ somewhat for the two subtypes of floccular Purkinje cells, emphasizing the hazard of generalizing from one cerebellar circuit to another, even for circuits lying within the same anatomical region of the cerebellum. This hazard is magnified in studies in the slice preparation, where Purkinje cells from different functional circuits are difficult or impossible to distinguish.

The origin of the increased modulation in the mutant VAPCs is uncertain. Since the increase appeared more prominently in VAPCs, it probably represents an indirect rather than direct consequence of reduced P/Q calcium currents. The increased modulation, perhaps along with an increase in the percentage of VAPCs, may be an attempt of the vestibulocerebellar circuitry to compensate for insufficient performance gain. The fact that the modulation increases in tottering VAPCs are similar for hOKR and VOR suggests that the site at which the compensation occurs is beyond the point at which vestibular and optokinetic signals flowing to the Purkinje cell are combined. Since optokinetic and vestibular signals take multiple paths to the flocculus (Blanks et al. 1983; Voogd and Barmack 2006) and in each path the balance of visuomotor and vestibular signals is likely to differ, the simplest way to engender a similar degree of compensation for both OKR and VOR is if the plastic site lies within the Purkinje cell itself.

The increased modulation in mutant VAPCs could also arise without invoking plasticity, if SS firing rates encode a signal proportional to retinal slip velocity. In that case the firing rate modulation would increase in proportion to the deficiency in OKR gain. There are a number of arguments against this idea. First, since the gain is decreased for both vOKR and hOKR, we would expect that the HAPCs would also exhibit the increased modulation. Second, retinal image velocity should be in phase with eye velocity. If a larger image velocity signal were added to an otherwise unchanged Purkinje cell modulation, the resultant signal would be shifted further toward eye velocity. Yet the firing rate phase of the mutants, if anything, lags with respect to control animals. Third, the enhanced modulation in VAPCs was also seen during VOR, during which there is no retinal image velocity. Fourth, the disparity between mutants and controls is maximal at the highest stimulus frequencies, yet the retinal image velocity signal processed through the sluggish optokinetic pathways should decline at higher stimulus frequencies.

VOR response of floccular Purkinje cells.

This study provides the first description of VAPC modulation during VOR in nonparalyzed mice. In normal animals the modulation during VOR was relatively weak. This result was somewhat unexpected given the comparable modulation in VOR and VVOR reported in one study of the rabbit (De Zeeuw et al. 1995). On the other hand, the modulation of our control VAPCs expressed as a percentage of their spontaneous rate for the 0.25 Hz, ±10° VOR stimulus is 14% (∼1 spikes/s-° × 10° ÷ 71 spikes/s), roughly comparable to the value of 9.8% reported by Nagao in the rabbit during a 0.1 Hz, ±5° stimulus (Nagao 1989). The floccular optokinetic signal being stronger than its vestibular signal is also in line with the conclusions of a study of rabbit medial vestibular nucleus FTNs (Stahl and Simpson 1995b). Some lesion studies have also indicated a preferential role of the flocculus in OKR (Barmack and Pettorossi 1985). In control animals, the sensitivity of Purkinje cells to VOR did increase with stimulus frequency, which may indicate that the contribution of the flocculus to VOR is made primarily at higher stimulus frequencies. This possibility accords with the observation that the VOR deficit in Cacna1a mutants increases with stimulus frequency (Stahl 2004; Stahl et al. 2006).

Ambiguous relationship of vermis activity to behavior.

Our investigation of the relationships between Purkinje cell activity and behavior focused exclusively on the flocculus and compensatory eye movements, a relationship that is particularly well understood in normal animals. Much less is known of the anterior vermis, and we limited our assessments there to firing rate and regularity. Even those characteristics should be interpreted with some caution: Whereas in the flocculus it was possible to obtain these measurements in a resting condition (i.e., when the animal's eye and head and the visual surround are stationary), the anterior vermis likely plays a role in regulation of trunk and limb posture, and as an awake animal continually adjusts its posture the vermis Purkinje cells can never be said to be at rest. However, it is reasonable to assume that the process of averaging over many seconds of recording erased any behavior-related signaling that was occurring on short timescales.

Another uncertainty in the vermis data relates to the effects of any dystonic episodes. One of the “positive deficits” of Cacna1a mutants is stress-induced paroxysms of dystonia affecting limbs and trunk (Shirley et al. 2008). These are common in tottering but also occur in a milder form in female rocker. The events may reflect a pathophysiology peculiar to the vermis and paramedian structures, as they can be blocked by injections of aminopyridines into the anterior vermis (Weisz et al. 2005), and optical recordings of neuronal activity also implicate these regions (Chen et al. 2009). No comparable paroxysmal eye movements have been reported, so the pathological phenomena may not occur in regions of the cerebellum, like the flocculus, that control eye movements. We cannot exclude the possibility that some of the data from vermis Purkinje cells were collected at the time of a dystonic attack, as these attacks are often quite subtle and are not readily detectable when the animal is immobilized for eye movement recording except via electromyographic recordings (Chen et al. 2009). However, it is also possible that dystonia occurs infrequently while the animals are restrained for the recordings; at the end of our recording sessions, tottering animals generally emerged from restraint moving normally. To date, studies of restraint-induced dystonia (Fureman et al. 2002; Weisz et al. 2005) have generally documented dystonia developing after the animals are released. Another argument against dystonic events having strongly influenced our vermis data relates to the fact that dystonic events are rare and mild in rocker and never occur in males, from which we derived 66% of our rocker vermis data and 60% of our flocculus data (Shirley et al. 2008; Zwingman et al. 2001). The similarity between the spontaneous firing characteristics of tottering and rocker vermis Purkinje cells despite the differences in their potential to suffer dystonia therefore argues against tottering data being strongly affected by unrecognized dystonic events.

Concluding comments.

This study supports the utility of comparing Purkinje cell properties in allelic mutants whose deficits are qualitatively similar but differ in severity. The interstrain comparisons provided some insight into the role that specific firing rate alterations play in the mutant phenotype, particularly in regard to the proposition that Purkinje cell irregularity is the unifying cause of cerebellar dysfunction in mutations that disrupt Purkinje cell rhythmicity. An additional benefit is that the two mutant strains serve as independent samples, so that even a mild difference between mutants and controls, if found for both mutants, can be recognized as potentially important. The likelihood of an interstrain difference being meaningful (as opposed to a statistical artifact of multiple interstrain comparisons) is further heightened when the alteration covaries with the severity of the phenotype. In the present data, the slightly decreased values of NphaseH in VAPCs, or the slightly increased percentages of VAPCs in the mutants, are worthy of note precisely because they were seen in both tottering and rocker.

One limitation of the present study is that it only assessed flocculus function with regard to driving the VOR and OKR. Numerous other roles for the flocculus in eye movements have been proposed, and some of these behaviors—such as the time constant of the gaze-holding neural integrator or the ability to plastically modify the amplitude and direction of the VOR—have been shown to be abnormal in Cacna1a mutants (Stahl 2004; Stahl et al. 2006). However, the simple role of the flocculus in augmenting compensatory eye movements is particularly well understood, and the relevant data are more easy to collect than, for instance, alterations in Purkinje cell activity during a 30-min session of VOR direction modification. The present results did not reveal any potential consequences of the physiological abnormalities that have been identified in vitro in addition to irregularity, such as the alterations in synaptic transmission and the balance of excitatory and inhibitory inputs (Kaja et al. 2007; Kodama et al. 2006; Matsushita et al. 2002; Zhou et al. 2003). In fact, the finding that magsensH was either normal or increased in the mutants suggests that the deleterious effects of the P/Q channel alterations on synaptic transmission can be overcome, at least at the synapses lying between the retina or vestibular labyrinth and the floccular Purkinje cells. Nor did we detect signaling abnormalities referable to the effects of altering calcium currents on spatial integration in the Purkinje cell dendrite. Such consequences may only manifest during more complex aspects of eye movement control, for instance, the computations involved in combining translation and rotation inputs (Snyder and King 1992), or in other regions of the cerebellum where codes other than rate codes could be important (Dean and Porrill 2011; Heck et al. 2013). Even given the inherent limitations, the present results indicate that our understanding of the cerebellar pathophysiology affecting compensatory eye movements in Cacna1a mutants is incomplete. Furthering this understanding is important because of the insight it affords into normal vestibulocerebellar function, because it will likely be important in developing drugs to ameliorate eye movement abnormalities in cerebellar disorders (Strupp et al. 2011), and because the pathological processes at work in the flocculus could contribute to dysfunction in other regions of the cerebellum.

GRANTS

This work was supported by the Department of Veterans Affairs (Veterans Health Administration, Office of Research and Development, Biomedical Laboratory Research and Development, application number BX000278-01). Animal breeding was supported by National Eye Institute Grant P30 EY-11373.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.S.S. conception and design of research; J.S.S. and Z.C.T. performed experiments; J.S.S. and Z.C.T. analyzed data; J.S.S. and Z.C.T. interpreted results of experiments; J.S.S. drafted manuscript; J.S.S. edited and revised manuscript; J.S.S. approved final version of manuscript; Z.C.T. prepared figures.