Abstract
Neurons with responses selective for the duration of an auditory stimulus are called duration-tuned neurons (DTNs). Temporal specificity in their spiking suggests that one function of DTNs is to encode stimulus duration; however, the efficacy of duration encoding by DTNs has yet to be investigated. Herein, we characterize the information content of individual cells and a population of DTNs from the mammalian inferior colliculus (IC) by measuring the stimulus-specific information (SSI) and estimated Fisher information (FI) of spike count responses. We found that SSI was typically greatest for those stimulus durations that evoked maximum spike counts, defined as best duration (BD) stimuli, and that FI was maximal for stimulus durations off BD where sensitivity to a change in duration was greatest. Using population data, we demonstrate that a maximum likelihood estimator (MLE) can accurately decode stimulus duration from evoked spike counts. We also simulated a two-alternative forced choice task by having MLE models decide whether two durations were the same or different. With this task we measured the just-noticeable difference threshold for stimulus duration and calculated the corresponding Weber fractions across the stimulus domain. Altogether, these results demonstrate that the spiking responses of DTNs from the mammalian IC contain sufficient information for the CNS to encode, decode, and discriminate behaviorally relevant auditory signal durations.
Keywords: big brown bat; Eptesicus fuscus; Fisher information, inferior colliculus; just-noticeable difference; stimulus-specific information, temporal processing; Weber fraction
duration-tuned neurons (DTNs) are ideal candidates for encoding spectral, intensity, and temporal information about an auditory stimulus because they respond selectively to the frequency, amplitude, and duration of acoustic signals. First reported in the torus semicircularis of frogs and subsequently the inferior colliculus (IC) of bats, DTNs have now been recorded from the auditory midbrain, thalamus, and cortex in a variety of vertebrates, and from the mammalian visual cortex (see Sayegh et al. 2011, for review). To date, the electrophysiological properties and underlying synaptic inputs responsible for creating the temporally selective responses of DTNs have been a major research focus, but a quantitative analysis of the information content and encoding efficiency of any neural system is important for linking neurophysiology to behavior and perception because it can suggest limits on the efficacy of information representation. Information theoretic measurements have previously been used to characterize the spiking responses of visual (Strong et al. 1998; Tolhurst et al. 2009), auditory (Hsu et al. 2004; Montgomery and Wehr 2010; Kayser et al. 2010), somatosensory (Arabzadeh 2004; Saal et al. 2009; Panzeri and Diamond 2010), olfactory (Rolls et al. 1996, 2009), and electrosensory neurons (Carlson and Kawasaki 2008; Maler 2009; Vonderschen and Chacron 2014). In this study, we used an information theory-based approach to analyze the information available in the responses of auditory DTNs from the mammalian IC.
Sensory neurons in general, and auditory neurons in particular, are often viewed as feature detectors that have a preferred value in stimulus domains such as frequency or amplitude, and they encode the domain with spike counts (or rates) and latencies that vary as a function of the stimulus. We measured spike counts and latencies from auditory DTNs in the mammalian IC to characterize the information content of duration-selective neural responses. Previous studies, including those by the authors, have characterized the spiking profile of DTNs by the shape of the duration tuning curve (i.e., short-pass, band-pass, or long-pass) and defined the neuronal best duration (BD) to be the stimulus duration that evoked the peak spike count (Casseday et al. 1994, 2000; Ehrlich et al. 1997; Faure et al. 2003; Aubie et al. 2009, 2012; Sayegh et al. 2011). To test this hypothesis, we measured information content of DTN spiking responses by calculating the stimulus-specific information (SSI) and estimated observed Fisher information (FI). Intuitively, SSI can be thought of as a measure of global response uniqueness evoked by a particular stimulus relative to all stimuli, whereas FI is a measure of local response uniqueness to determine how sensitive a response is to small stimulus perturbations. As predicted, the spike counts of DTNs maximally encoded information about stimulus duration for signals presented at BD.
To assess the performance of theoretical neural decoders, we constructed optimal and nonoptimal decoders that used spike count responses from individual cells and a simulated DTN population by pooling single unit responses collected across animals. Both the optimal and nonoptimal decoders were good at decoding all signal durations tested. Finally, we simulated a two-alternative forced choice (2-AFC) decision task using the observed response distributions of DTNs to measure the just-noticeable difference (JND) limens and Weber fractions from the responses. Altogether, the results support the hypothesis that one function of DTNs in normal hearing is to detect and discriminate behaviorally relevant differences in signal duration.
METHODS
Electrophysiological Recordings
The majority of data in this study was taken from a database of single unit extracellular recordings collected at +20 dB (re threshold) from 103 DTNs (short-pass and band-pass only) from the central nucleus of the inferior colliculus (ICc) of the awake big brown bat, Eptesicus fuscus. Of these, 56 cells were recorded at McMaster University and 47 were recorded at the University of Washington. The recordings were collected from 49 adult bats of either sex (29 at McMaster University; 20 at the University of Washington). We also include information about the spontaneous firing rates of DTNs and non-DTNs. Because this information was not restricted to files in our database tested at +20 dB above threshold, it was performed on a larger sample inclusive of the subset tested at +20 dB (n = 228 DTNs and n = 487 non-DTNs).
Detailed procedures for single unit recording from the ICc of the bat and identifying DTN responses are reported elsewhere (Faure et al. 2003; Fremouw et al. 2005; Aubie et al. 2012). Briefly, a stainless steel post was affixed to the dorsal surface of the skull with cyanoacrylate adhesive 24–48 h before the first recording session. One end of a chlorided silver wire glued to the steel post was placed underneath the right temporal muscle and served as the reference electrode. A scalpel was used to make a small opening in the skull and dura mater over the dorsal surface of the IC. Thin-wall borosilicate glass microelectrodes with resistances ranging from 10 to 30 MΩ were advanced into the brain at 1-μm intervals by a hydraulic micropositioner. Action potential times relative to the onset of stimulus presentation were recorded to computer for offline analysis. Recordings lasting 4–6 h were conducted over 1–8 days per bat. All procedures were approved by the University of Washington Laboratory Animal Care and Use Committee and the McMaster University Animal Research Ethics Board and were in accordance with the Guidelines for the Care and Use of Experimental Animals published by the Canadian Council on Animal Care.
Stimulus generation and online data collection were controlled with custom software. Pure tone sound pulses were digitally generated, fed through a digital-to-analog converter, low-pass filtered for anti-aliasing, amplified, and presented either monaurally ∼1 mm in front of the contralateral ear with a Brüel & Kjær 1/4-in. condenser microphone modified for use as a loudspeaker (94 of 103 DTNs) or binaurally with a Tucker Davis Technologies ES1 free-field electrostatic speaker positioned 30 cm from the bat's head at 30° off midline and contralateral to the recording site (9 of 103 DTNs). All stimuli had rise/fall times of 0.4–0.5 ms shaped with a squared cosine wave and were typically presented at a repetition rate of 3 Hz.
Obtaining Single Unit Responses
Single units were isolated by searching with a two-pulse stimulus in which the frequencies, durations, and/or amplitudes of the signals were manually varied until time-locked (stimulus evoked) action potentials were observed. Upon isolation of a unit, its best excitatory (characteristic) frequency, amplitude threshold, and duration tuning curve were measured in that order. Duration tuning profiles were measured with best excitatory frequency pure tones presented at threshold (0 dB) and at +10, +20, and +30 dB above threshold. Stimulus duration was randomly varied from 1 to 25 ms in 1-ms steps, with each stimulus repeated 10–20 times per step.
Duration tuning curves of IC neurons were categorized into one of four response classes (short-pass, band-pass, long-pass, or all-pass) based on the spike count profile (Sayegh et al. 2011). The spiking responses of DTNs are temporally selective and do not reflect the simple integration of stimulus energy. Short-pass DTNs respond maximally to short duration sounds and have spike counts that decrease at durations longer than BD. Band-pass DTNs also respond maximally at BD and have spike counts that decrease at durations both longer and shorter than BD. Long-pass DTNs respond only when the stimulus exceeds some minimum duration. Unlike typical sensory neurons that integrate stimulus energy, the minimum duration for evoking a response in a long-pass DTN does not decrease with increasing stimulus amplitude/energy (Faure et al. 2003; Sayegh et al. 2011; Aubie et al. 2012). Because long-pass DTNs do not have a BD, they were not included in this study.
Spiking responses of short-pass and band-pass DTNs were typically transient and offset-evoked, meaning their first-spike latency (FSL; re stimulus onset) increased with increasing stimulus duration (Faure et al. 2003); however, a minority of DTNs with onset-evoked responses and relatively constant FSLs with increasing stimulus duration were also observed and included in our analyses. Tuning profiles of the DTNs included in this study all showed a clear duration-selective response at +20 dB (re threshold). For comparison, we also include some data from all-pass neurons. By definition, all-pass neurons are not duration tuned, do not have a BD, and responded to all stimulus durations that contained sufficient energy. Spiking responses of non-DTNs were either transient or sustained and were typically onset-evoked with more-or-less constant FSLs (re stimulus onset).
Single Neuron Analysis
To minimize the effects of spontaneous activity, we windowed data to only include spikes evoked after stimulus onset and up to 50 ms after stimulus offset. The majority of data files were collected in +10-dB amplitude steps above threshold; however, when files were collected at a different level, responses were assigned to the nearest 10-dB amplitude bin by rounding down. Separate analyses were performed on responses recorded at 0, +10, +20, and +30 dB (re threshold) and because there was little to no difference in results collected at different levels, except for spontaneous activity, we only present data from cells recorded at +20 dB (re threshold).
Traditionally, BD has been defined as the stimulus duration evoking the maximum spike count (Casseday et al. 1994). In this study, BD was defined as the average of the shortest and longest stimulus durations with evoked spike counts ≥90% of the peak spike count (Fremouw et al. 2005). Application of this definition meant that the calculated BD for a single neuron could fall in-between tested stimulus durations and could be any value (i.e., not just an integer).
Many previous studies, including our own, have used a strict criterion of a 50% decrease in spike count at stimulus durations shorter and/or longer than BD to define DTNs (Faure et al. 2003). In this study, we chose to include all cells that appeared to be duration-tuned based on visual inspection of their duration tuning curve at +20 dB (re threshold) even when the decrease in spiking at durations shorter and/or longer than BD did not quite reach the 50% criterion (e.g., we included cells with spike counts that dropped to only 60% of peak count). Relaxing the inclusion criteria resulted in a more conservative estimate of information metrics, duration encoding, and decoding performance by lowering population-level duration selectivity and decreasing observer bias for highly tuned neural responses. Data from a neuron were included only if the cell responded with at least 0.6 spikes per stimulus at BD; use of this criterion helped to ensure that all included cells were healthy and responsive to acoustic stimulation. All analyses were performed with SpikeDB (http://spikedb.aubie.ca) and the Python programming language (http://www.python.org).
Characterizing spontaneous activity.
To determine whether DTN spiking was correlated with the presence of a stimulus, we measured the rate of spontaneous activity (in Hz) by counting the number of spikes in a time window starting at least 100 ms from stimulus offset (i.e., after all stimulus-evoked spikes) and stopping at the end of the recording buffer for the trial and dividing this value by the duration of the time window (typically 100 ms). Because acoustic stimuli were typically presented to cells at a rate of 3 Hz, this yields a stimulus repetition period of 333 ms; however, owing to limitations in our digital signal processing hardware, spike times were not collected during the final 50 ms of this 333-ms period. Therefore, each trial contained 283 ms for acoustic stimulation and recording neural responses and we calculated a poststimulus rate of spontaneous activity for every neuron during the final 100 ms of the 283-ms time window. Spontaneous activity was only measured from neurons with data files showing no evidence of cell death. Spontaneous activity was compared in DTNs and non-DTNs using the conservative nonparametric Mann-Whitney U-test (Zar 1984). Because our analysis of spontaneous activity was not restricted to cells with data files collected at +20 dB (re threshold), it includes a larger sample size (n = 228 DTNs and n = 487 non-DTNs).
Spike count distributions.
Electrophysiological studies reporting spike counts implicitly assume that the average count for each stimulus accurately represents the distribution of observed spike counts. In the majority of cases, spike count responses for a particular duration and DTN were not normally distributed (Shapiro-Wilk tests; not shown). Therefore, instead of assuming a particular response distribution, our analysis uses the empirically observed distribution of spike probabilities, Pr(s|d), where s denotes the number of spikes evoked by a stimulus of duration d. Although fitting well-defined statistical distributions to DTN responses would be ideal for future theoretical studies of encoding performance by a population of cells, the response heterogeneity we observed in our dataset made such a task beyond the scope of this study. The consequences of using an observed rather than an arbitrarily fitted statistical distribution are discussed in the next section.
Information measures.
Studies characterizing DTNs measure the BD stimulus and the shape (short-pass, band-pass, or long-pass) and bandwidth of the duration tuning curve at an arbitrary fraction of the peak response (e.g., the 50 or 75% temporal response bandwidth; Casseday et al. 1994; Faure et al. 2003; Fremouw et al. 2005; Jen and Wu 2006). In this study we used the midpoint of the 90% temporal bandwidth to define the BD of DTNs (see Single Neuron Analysis). Some reports have also quantified the sharpness of the duration tuning curve (e.g., the critical duration and normalized duration width; Jen and Feng 1999; Jen and Wu 2006). What remains unclear from all of these measures is the quantity of information encoded by the responses of DTNs. For example, when trial-to-trial response variability is low, it is possible that responses with lower evoked spike counts but located along the flanks of a duration tuning curve could encode more information compared with higher spike counts located at the peak of a duration tuning curve (Brand et al. 2002; Butts 2003; Montgomery and Wehr 2010). To determine whether the BD stimulus was actually the duration “best encoded” by the responses of a DTN, we calculated two information measures at each duration, d. First, we calculated the SSI defined as
where d is a stimulus duration, Pr(s|d) is the probability of spike count s given duration d, i(s) is the specific information conveyed by spike count s (DeWeese and Meister 1999), S is the set of all spike counts, and D is the set of all stimulus durations (Butts 2003; Montgomery and Wehr 2010). The SSI can be understood in relation to mutual information, which is a measure of information contained across all responses. Like mutual information, SSI is a measure of the reduction in uncertainty about a random variable (e.g., the stimulus) given knowledge about another random variable (e.g., the response). Specific information is a more focused measure that quantifies the reduction in uncertainty given a specific response; it measures the expected specific information for a particular stimulus over the entire set of responses evoked by a stimulus. Intuitively, SSI is a measure of the expected reduction in uncertainty about a stimulus after observing responses evoked by that stimulus. Alternatively, SSI can be thought of as a measure of encoding uniqueness. A stimulus with high SSI will have relatively unique encoding across the stimulus domain, allowing a theoretical observer to make an informed guess about a stimulus based on the properties of the evoked response. A stimulus with low SSI will have a less unique representation relative to other stimuli, resulting in considerable uncertainty.
Measuring SSI is subject to a sampling bias that can overestimate information content due to an undersampling and thus coarser approximation of the true response distribution (Panzeri et al. 2007; Rolls and Treves 2011). To correct for this, we estimated the SSI sampling bias by calculating the mean SSI of randomly shuffled stimulus-response pairs (Optican et al. 1991; Panzeri et al. 2007; Montgomery and Wehr 2010). Because randomly shuffled stimulus-response combinations were uncorrelated, the expected SSI was zero across the stimulus domain. Therefore, any correlation that exists is a reasonable estimate of the average sampling bias in the original (unshuffled) data. The unbiased SSI was estimated by subtracting the average sampling bias (mean bias = 0.193 bits; SD = 0.082 bits over all DTNs) from the calculated SSI of each DTN as
Second, we calculated an estimate of the observed FI, abbreviated as Iest(d) and defined as
where E denotes the expected value, S is the set of all observed spike counts, d is a given stimulus duration, and ln denotes the natural logarithm base e (Kay 1993). The estimated observed FI of a stimulus duration is a measure of the average slope of the log spike count probability distribution along the stimulus domain. FI is the inverse of the minimum variance of an optimal stimulus estimator and can be used to estimate the lower (Cramér-Rao) bound of a decoder's variance (Kay 1993),
A response with high FI will be decoded with low variance along the stimulus domain. In other words, high FI implies that the response distributions of immediately adjacent stimuli are significantly different from each other. Unlike SSI that measures the uniqueness of encoding a particular stimulus across the entire domain of a stimulus, FI provides the lower (Cramér-Rao) bound on the variability of an optimal decoder and can be thought of as a local measure of the uniqueness of encoding a stimulus having a particular value relative to stimuli with adjacent values. Therefore, FI can also be interpreted as a measure of a system's ability to encode stimulus change.
Because spike counts and stimulus durations are discrete values, we could not compute the analytical first (or second) derivative of the distribution Pr(s|d) as required for calculating the observed FI. Instead, we estimated the slope of the probability distribution for values lying between discrete stimulus durations (dmid = d + 0.5 ms). This enabled us to numerically approximate the derivative of ln[Pr(s|d)] using the difference in spiking probability at adjacent durations. With this formulation, the estimated FI can be written as the expected value of the square of the first derivative of the natural logarithm of the probability density function (Dayan and Abbott 2001). Therefore, FI can be written as a function of the change in the probability distribution across stimulus durations d,
where S is a set of all observed spike counts, s is a particular spike count from S, and d + 1 is the stimulus duration 1 ms longer than d. The calculated FI can take any value between 0 and ∞, where 0 represents no change in response probabilities across the stimulus domain and ∞ represents a change from nonzero to zero probabilities, or vice versa. To avoid calculations with infinite FI values (i.e., calculating the logarithm of 0), we artificially added 1/10100 to all zero spiking probabilities. Note that limiting the absolute FI only makes the absolute difference in FI across stimulus durations finite without changing the relative ordering of FI values. A consequence of this adjustment is that it renders absolute FI values as not particularly meaningful; however, relative FI values can still be used to quantify changes in response sensitivity. Therefore, in this article we present relative FI values normalized to 1.
Although we estimated the observed FI of individual neurons, there is an important caveat: while the Cramér-Rao bound is the best case scenario for the lower bound of the variance in an optimal decoder, there is no guarantee that a decoder's variance will reach this bound. In fact, when the number of neurons is low and the trial-to-trial response variability is high (e.g., when there is high spontaneous activity), an optimal decoder will not perform close to the Cramér-Rao bound (Xie 2002). For example, a response with a signal-to-noise ratio of 1 requires ∼200 neurons before response variability in the population approaches the Cramér-Rao bound. Therefore, FI cannot be interpreted as the absolute encoding efficiency of individual neurons (Yarrow et al. 2012). A decoder that uses a large population of neurons with similar response properties could approach the Cramér-Rao bound, which is why we present the estimated FI for both individual DTNs and the population averages.
RELATING SSI TO FI.
When the trial-to-trial response variability is high, the SSI in a tuning curve peaks at the stimulus evoking the maximum response; however, when the trial-to-trial response variability is low, the SSI peaks at the flanks of a tuning curve. As response variability approaches zero, peaks in SSI approach the same positions as peaks in FI (Butts and Goldman 2006; Yarrow et al. 2012). Intuitively, highly variable responses produce a larger noise floor and are therefore less discriminable at the flanks of a tuning curve, where the FI is maximal, compared with the peak of a tuning curve where the SSI is maximal. In contrast, when the trial-to-trial variability is low, responses located at the flanks of a tuning curve are easier for a decoder to distinguish compared with responses located near the peak. Montgomery and Wehr (2010) demonstrated that the SSI was larger at the flanks of a frequency tuning curve when the coefficient of variation (CV) at the cell's preferred frequency was less than ∼0.06. When the CV was ∼0.2, the SSI at the flanks of the tuning curve was similar to those at the peak, and when the CV was greater than ∼0.2, the SSI was greatest at the peak of the tuning curve. We performed a similar analysis on the duration tuning curves of DTNs. For each cell in the population, we measured the CV at BD (CVBD) by dividing the standard deviation (SD) of the response (i.e., spikes per stimulus) by the mean of the response at BD,
Decoding stimulus duration from spike counts.
For each DTN in the population, we calculated a spike count probability for a given stimulus duration, Pr(s|d), which represents the probability of producing s spikes in response to stimulus duration d ∈ [1, 2, 3,…, 25 ms]. This characterization assumed that a decoder was informed by stimulus presentations evoking zero spikes; however, this also requires the decoder to “know” that a stimulus was presented even though a response was not evoked. To remove the requirement for observing zero spike count responses, we decoded stimulus durations while ignoring responses with zero spikes by setting Pr(s = 0|d) = 0 for all stimulus durations and renormalizing the probabilities of nonzero spiking responses. Our sample population included 10 DTNs that were only tested with stimulus durations ranging from 1 to 15 ms. Because these cells also had zero (or near zero) spiking probabilities at the longest stimulus durations presented, we assumed they would respond with zero spikes for durations ranging between 16 and 25 ms. To decode stimulus duration based on spike count information, we applied Bayes' formula and calculated the posterior probability distribution Pr(d|s), which is the probability that a particular stimulus duration d was presented given an evoked spike count of s:
We used a naive uniform prior, Pr(d) = 1/25, for all stimulus durations, d, to produce a conservative posterior probability estimate. The echolocation calls of E. fuscus are downward FM sweeps that range in duration from <1 to >20 ms, depending on the stage of hunting and the amount of acoustic/vegetative clutter in the foraging habitat (Simmons 1987, 1989; Neuweiler 1990; Moss et al. 2011); however, bats also listen to other types of signals, and the distribution of behaviorally relevant durations for nonecholocation sounds is somewhat open-ended. Stimulus-response probabilities were obtained directly from in vivo spike count functions without modification or distribution fitting.
The posterior probability characterizes responses by observed spike counts and their variability. We used response probabilities and posterior probabilities to compute a decoded probability distribution matrix, DUR, over all stimulus durations, calculated as
where each element in the matrix represents the probability that duration d was the stimulus given that duration dpres was presented. The maximum value in each posterior probability distribution was selected as the decoded stimulus duration.
Population Analysis
Decoding stimulus duration.
We simulated a population of DTNs by combining responses across all cells. Computing the expected optimal duration decoding matrix from a population response requires determining joint response probabilities over all possible responses. Due to the infeasibility of this calculation, it was not reasonable to calculate it directly. For example, if N DTNs each produced x different spike counts with a nonzero probability, calculating the expected optimal population duration decoding matrix would require xN joint probability calculations. In our study of 103 DTNs, ∼7103 ≈ 1.11 × 1087 multiplications would be required for this calculation. To approximate the optimal population duration decoding matrix, we applied a Monte Carlo procedure to take advantage of the fact that posterior probability distributions with naive priors are proportional to the response probability distributions [i.e., Pr(d|S) ∝ Pr(S|d)]. Decoding stimulus duration was then performed by selecting the duration with the highest probability. Because prior probabilities were uniformly distributed [Pr(d) = constant], the duration with the highest posterior probability was equivalent to a maximum likelihood estimator (MLE). For generality, we frame our analysis as a Bayesian decoding procedure to emphasize that known priors could be inserted into the analysis without other modifications. First, we randomly selected observed spike counts from each DTN to calculate Pr(s|dpres). Then, we estimated the posterior probability from the average joint response probability of each Monte Carlo trial (T = 100,000) by
and
where Ssample represents the sampled spike counts over all Monte Carlo trials and si is the ith randomly selected spike count from a jth DTN spike probability distribution, Pr(s|dpres, DTNj).
We also computed an alternative, nonoptimal duration decoding matrix that was more computationally tractable than the average duration decoding matrix over all DTNs by
where Avgi(Xi) calculates the average of each entry across all matrices as indexed by i.
To visualize the relative probabilities of decoded stimulus durations, we normalized individual matrices by
where ScaleMax(X) normalizes each row in the matrix by dividing by the maximum value of the row. Additional optimization of this method could be made by using a weighted average based on the reliability of individual neuron responses; however, in this analysis we assumed that all DTN responses were reliable and thus were weighted equally.
Calculating JNDs.
In psychophysics, the JND is defined as the smallest change in a stimulus that can be detected so that two stimuli are perceived as different (i.e., the difference limen). The JND for stimulus duration is defined as the smallest nonzero increase in duration, Δd, that can be detected. To determine the JND from the spiking responses of our population of DTNs, we simulated a 2-AFC experiment over all unique combinations of presented stimulus durations and repeated this procedure 100 times. For each 2-AFC trial, spike counts were randomly chosen for each stimulus duration from the observed spike count probability distribution for that neuron. The average posterior probability distribution for a simulated stimulus duration presentation (d) can be represented by a summated posterior probability distribution vector (D̄d) calculated over all DTNs by
To determine if two stimulus durations, defined here as the reference (dref) and probe (dprobe = dref + Δd) signals, constitute a “JND” on any given trial, it was necessary to calculate a similarity index between the two posterior probability distribution vectors, S(D̄dref, D̄dprobe). This index was based on the angle between the vectors. First, the inverse cosine of the normalized dot product of the vectors was used to calculate the absolute angle between the vectors. Then, the angle was doubled, divided by π, and subtracted from 1 so that parallel vectors with an angle of 0 had a similarity index of 1 and orthogonal vectors with an angle of had a similarity index of 0.
To decide on an appropriate threshold for classifying 2-AFC stimulus duration pairs as either the “same” or “different,” we plotted the proportional distributions of the similarity indexes for each (dref, dprobe) pair over 250 simulated trials and grouped them into “same duration” and “different duration” trials. Thresholds for our analysis were chosen to be the similarity indexes where the “same” distribution crossed the “different” distribution (Fig. 1, A and B), as is typically chosen in signal detection theory (Wickens 2002). Lower thresholds resulted in more stimulus pairs being incorrectly classified as the “same” when they were actually different (i.e., a miss), and higher thresholds resulted in more stimulus pairs being incorrectly classified as “different” when they were the same (i.e., a false alarm). The calculated threshold for spike count data that included values of zero spikes per stimulus was Sthresh = 0.92 but was lowered to Sthresh = 0.85 when trials with zero spikes per stimulus were ignored.
Fig. 1.
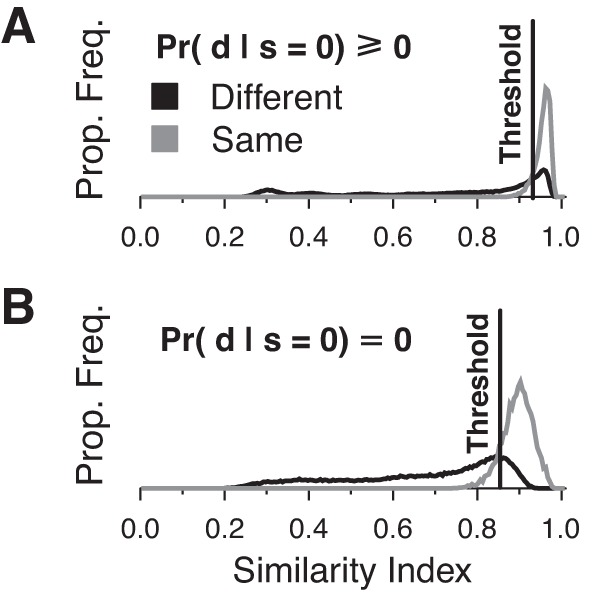
Distribution of similarity index scores from decoding with spike counts including zero spike responses (A) and not including zero spike responses (B). Pairs of stimulus durations were tested 250 times.
When the similarity indexes of the posterior probability distribution vectors for two simulated duration presentations were found to be different and the pair of stimulus durations were actually different, a point was scored. Similarly, a point was scored when the two vectors were found to be above the threshold for similarity and the two stimulus durations were the same. Otherwise, no point was scored for the trial. The JND for a particular reference duration was defined as the smallest Δd > 0 such that ≥75% of trials were scored as “different.” This arbitrary but unbiased threshold is halfway between chance (50%) and perfect performance (100%).
RESULTS
Single Neuron Analysis
Characterizing evoked activity.
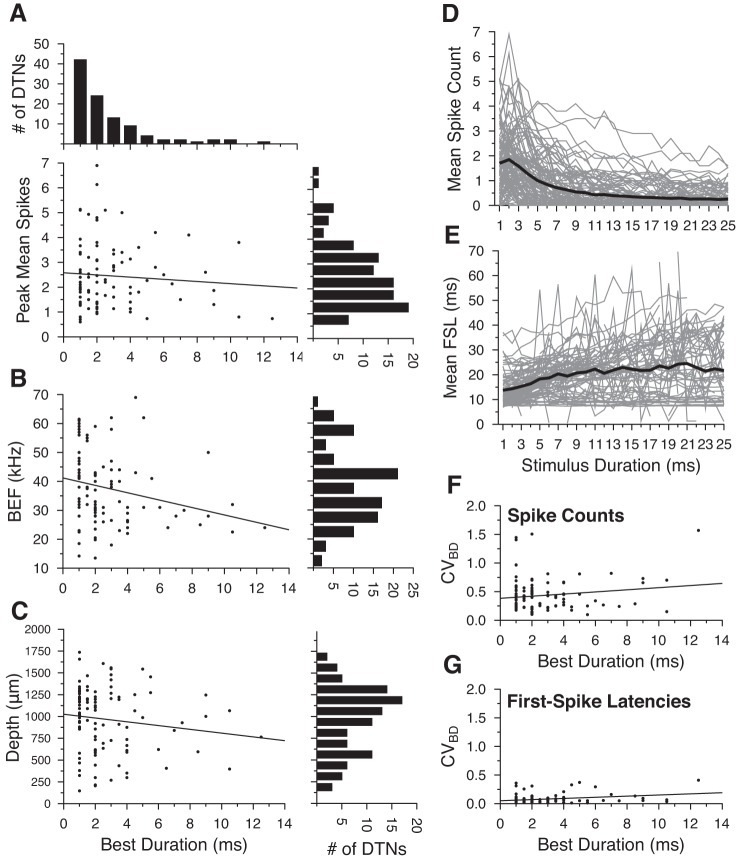
Within the population of DTNs tested at +20 dB above threshold, peak mean spike counts did not correlate with neuronal BDs (Fig. 2A), were weakly negatively correlated with best excitatory frequencies (Fig. 2B), and were not correlated with recording electrode depths (Fig. 2C). The mean spikes per stimulus was highest for 1- and 2-ms stimuli and decreased at longer durations (Fig. 2D). The minimum evoked FSL across the entire population was ≈8 ms (re stimulus onset), and there was a trend for FSLs to increase as stimulus duration lengthened from 1 to 25 ms; however, the mean FSL in the overall population increased by <11 ms (min = 13.74 ms, max = 24.51 ms), very likely due to cells with onset-evoked responses and more-or-less constant FSLs (Fig. 2E).
Fig. 2.
General response properties of duration-tuned neurons (DTNs) from the central nucleus of the inferior colliculus (ICc) of the big brown bat (Eptesicus fuscus), including peak mean spikes per stimulus as a function of neuronal best duration (BD; A), best excitatory frequency (BEF; B) as a function of BD, electrode recording depth as a function of BD for DTNs presented with BEF stimuli randomly varied in duration from 1 to 25 ms (maximum BD = 12.5 ms; C), mean spikes per stimulus (D), and mean first-spike latency (FSL; E) re stimulus onset as a function of stimulus duration, coefficient of variation (CV) at BD (CVBD) for spike counts (F), and CV at BD for FSLs (G). A, top: histogram showing distribution of the number of cells with specific BDs (bin width = 1 ms). A, bottom left: scatter plot of peak mean spike count as a function of BD. Best fit regression line shown as black line with intercept = 2.58 spikes/stimulus and slope = −0.04 spikes/BD (R = 0.084, P = 0.412). A, bottom right: histogram showing distribution of the number of cells with specific peak mean spike counts (bin width = 0.5 spikes/stimulus). B, left: scatter plot of neuronal BEF as a function of BD. Best fit regression line shown as black line with intercept = 41.37 kHz and slope = −1.27 kHz/BD (R = 0.237, P = 0.0157). B, right: histogram showing distribution of the number of cells with particular ranges of BEFs (bin width = 5 kHz). C, left: scatter plot of electrode depth as a function of neuronal BD. Best fit regression line shown as black line with intercept = 1,025 μm and slope = −21.65 μm/BD (R = 0.138, P = 0.1667). C, right: histogram showing distribution of the number of cells located at particular electrode depths in the IC of the bat (bin width = 125 μm). D and E: individual cell responses are shown as gray lines and mean values are shown as bold black lines. F: scatter plot of CVBD for spike counts as a function of BD. Best fit regression line shown as black line with intercept = 0.384 and slope = 0.019 (R = 0.152, P = 0.125). G: scatter plot of the CVBD for FSLs as a function of BD. Best fit regression line shown as black line with intercept = 0.052 and slope = 0.010 (R = 0.283, P = 0.004).
As previously described, stimuli best encoded by a neuron correlated with the trial-to-trial response variability. Therefore, we quantified response variation in our population of DTNs. The CV for the mean spikes per stimulus at BD (CVBD) ranged from 0.099 to 1.570 (mean = 0.435) and did not correlate with BD (Fig. 2F). This large range of variability predicts that SSI will also peak at BD (Montgomery and Wehr 2010). The CV for the mean FSL at BD (CVBD) was significantly lower compared with the CV for spike counts, ranging from 0.011 to 0.410 (mean = 0.079), and showed only a weak positive correlation with BD (Fig. 2G).
Information characterization.
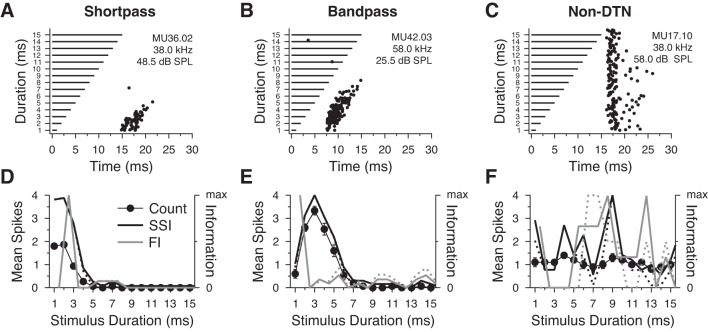
To illustrate variation between neurons and in the corresponding SSI and FI values in the population, Fig. 3 presents two example DTNs with tuning selectivity for short (short-pass DTN; Fig. 3, A and D) and intermediate stimulus durations (band-pass DTN; Fig. 3, B and E) and one example all-pass neuron that was not selective for stimulus duration (non-DTN; Fig. 3, C and F). A–C shows dot raster displays of the spiking responses of each cell to repeated presentations of best excitatory frequency tones randomly varied in duration from 1 to 15 ms (Fig. 3, A–C), while the D–F summarizes the means ± SE spikes per stimulus and the calculated SSI and FI from spike counts across all durations (Fig. 3, D–F). For both example DTNs, the SSI was proportional to the mean spikes per stimulus (Fig. 3, D and E; short-pass DTN spike count CVBD = 0.230, SSI peak = 3.42 bits; band-pass DTN spike count CVBD = 0.217, SSI peak = 2.83 bits), confirming that spike counts are appropriate for characterizing BD stimuli encoded by DTNs. The short-pass DTN (Fig. 3, A and D) had its peak FI value at 2.5 ms where the change in the spike count function was greatest. The maximum FI for the band-pass DTN (Fig. 3, B and E) was at 1.5 ms where the change in spike count was greatest (≈2 spikes/stimulus). The FI and SSI values for the non-DTN (Fig. 3, C and F) were, as expected, low across the stimulus domain (non-DTN SSI peak = 0.41 bits).
Fig. 3.
Examples of spiking responses and information content measures in 3 neurons from the ICc of the big brown bat. A and D: short-pass DTN, CVBD = 0.230, 15 trials/stimulus; B and E: band-pass DTN, CVBD = 0.217, 15 trials per stimulus; C and F: a non-DTN (all-pass neuron) with an onset response, 10 trials/stimulus. A–C: dot raster displays illustrating the timing of spikes (black dots) in response to stimulation with pure tones that were randomly varied in duration (horizontal black bars) and presented at the cell BEF at +20 dB above threshold. D–F: means ± SE spikes per stimulus (filled circles), normalized stimulus-specific information (SSI) where Pr(s = 0|d) ≥ 0 (black line; D: short-pass peak SSI = 3.42 bits; E: band-pass peak SSI = 2.83 bits; F: non-DTN peak SSI = 0.41 bits), normalized SSI where Pr(s = 0|d) = 0 (dashed black line; D: short-pass peak SSI = 3.42; E: band-pass peak SSI = 2.84; F: non-DTN peak SSI = 0.47 bits), normalized estimated Fisher information (FI) where Pr(s = 0|d) ≥ 0 (solid gray line), and normalized estimated FI where Pr(s = 0|d) = 0 (dashed gray line) as a function of stimulus duration. Note that the peak FI, a measure of sensitivity, does not need to align near the peak spike count or peak SSI as in D and E. Information measures were similar in both DTNs regardless of whether we included or excluded responses with zero spikes per stimulus. For the non-DTN, both the SSI and FI fluctuated randomly across the stimulus domain and were essentially a function of the trial-to-trial variance in spiking.
The rate of spontaneous activity sets a neuron's noise floor. Spikes evoked at or below this rate cannot be distinguished from noise and thus convey no information. The mean rate of spontaneous activity for DTNs was 0.611 Hz (n = 228 cells) and for non-DTNs it was 1.976 Hz (n = 487 cells). This difference was highly significant (Mann-Whitney U nonparametric test: U = 44644.0; p2-tailed = 1.56 × 10−5). Because DTNs have little to no spontaneous activity compared with other types of neurons in the IC of the big brown bat (Fig. 4), we calculated SSI and FI while ignoring responses with zero spikes per stimulus and found that the relative ordering of the information values was approximately the same as when responses with zero spikes were included (Fig. 3, D–F, dashed lines).
Fig. 4.
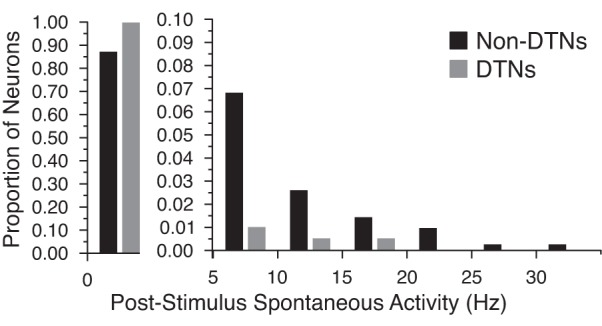
Rates of spontaneous activity in DTNs and non-DTNs in the ICc of the big brown bat. In general, the majority of IC neurons exhibited little to no spontaneous activity (<5 Hz); however, DTNs (n = 228) had significantly lower spontaneous firing rates than non-DTNs (n = 487). Note the change in scale of the ordinate for spontaneous rates between 0 and 5 Hz (left) and for rates ≥5 Hz (right). Bin width = 5 Hz.
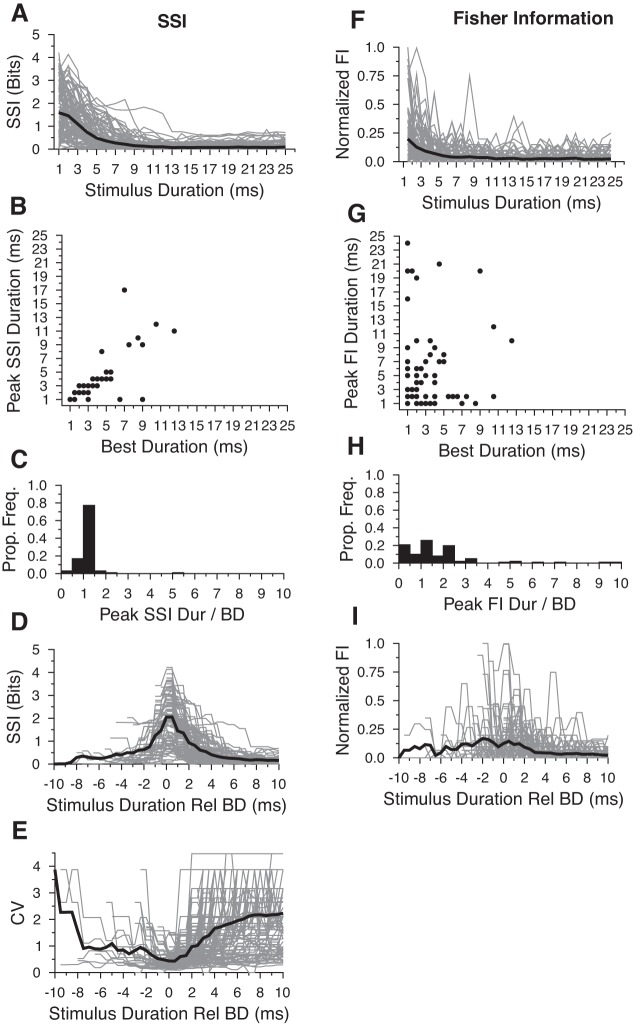
The trends in information content we observed for the three example neurons were mirrored throughout the population of cells studied. For DTNs, the average SSI was highest for 1-ms stimuli and decreased with increasing signal duration (Fig. 5A). Across the population of DTNs, SSI functions peaked at or near a cell's BD when they were calculated with spike counts (Fig. 5, B–D; R = 0.678; P = 3.5 × 10−15). These results demonstrate that information conveyed by spike counts is equally meaningful across many durations and can be independent of BD. Similar trends were observed in the population of DTNs when we calculated SSI and ignored responses with zero spikes per stimulus (data not shown). On average, FI calculated with spike counts was highest for 1-ms stimuli and decreased with increasing stimulus duration (Fig. 5F) and was not correlated with BD (Fig. 5, G–I; R = 0.236; P = 0.016).
Fig. 5.
SSI (A—E) and Fisher Information (FI; F–I) measures calculated from spike counts. A and F: absolute SSI and FI values for individual neurons (gray lines) and the population mean (bold black lines). On average, SSI tended to peak for 1- and 2-ms stimulus durations but monotonically decreased at longer durations. The average FI tended to peak for 1 ms stimuli and monotonically decreased at longer durations. B and G: scatter plot illustrating the stimulus durations that evoked peak SSI values as a function of BD. There was a strong correlation between the peak SSI duration and neuronal BD (R = 0.678; P = 3.5 × 10−15) and a weak correlation between the peak FI and neuronal BD (R = 0.236; P = 0.016). C and H: histograms illustrating the proportion of DTNs with various peak SSI and peak FI values relative to BD. Histogram bin width = 0.5. D and I: same data as A and F only plotted relative to each cell's BD as determined by the peak mean spike count. Note that the mean SSI peaks at the BD and the FI was slightly elevated at stimulus durations adjacent to the neuronal BD. E: trial-to-trial CV plotted as a function of stimulus duration relative to BD.
We also examined trial-to-trial variation in the population of DTN responses by measuring the CV of spike counts at each stimulus duration and found that, on average, the CV for spike counts was lowest at BD (Fig. 5E). This reinforces the assumption that DTNs most efficiently encode the stimulus duration closest to the peak of the duration tuning curve. In the next section, we explore optimal and nonoptimal methods for decoding stimulus duration from spike counts.
Decoding stimulus duration from spike counts.
If the function of DTNs is to encode information about stimulus duration, then there must be a neural mechanism for decoding duration information from their evoked responses. In general, trial-to-trial variation in single neuron responses precludes the existence of a function that directly maps spike counts onto stimulus duration. Instead, a decoder must assign a probability for each duration, taking the stimulus with the highest probability as the most likely presented. To calculate this posterior probability distribution, we used Bayes' formula with naive prior probabilities of Pr(d) = 1/25 = 0.04 for the 25 stimulus durations we presented (see methods). Using spike counts and posterior probability distributions, we estimated the expected posterior probabilities of decoding each stimulus duration, d, given the presentation of a stimulus with duration dpres.
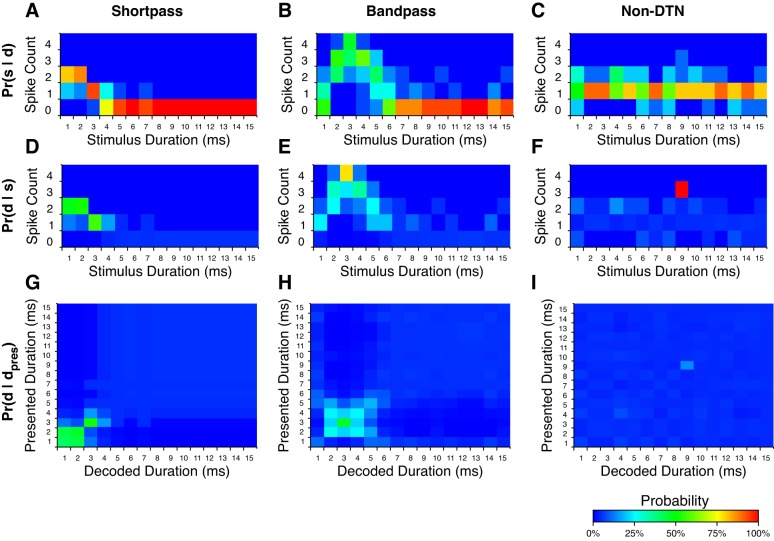
Spike count probability distributions for the three example neurons shown in Fig. 3 are presented in Fig. 6, A–C, along with their corresponding posterior probability distributions (Fig. 6, D–F). Note that stimulus durations with the highest posterior probabilities correlate with the highest SSI values (compare Fig. 6, D–F, with Fig. 3, D–F). Duration decoding matrices for these cells (Fig. 6, G–I) confirm that stimulus durations with the highest SSI values were decoded with the highest probability. Also note that stimulus durations encoded with similar spike count probabilities, and thus low FI values, were ambiguously decoded (e.g., compare 1 and 2 ms for the short-pass DTN in Fig. 6G). As expected, the non-DTN failed to assign substantive decoding probabilities to any stimulus duration (Fig. 6F), regardless of the presented signal duration, due to nonspecific response probabilities across the stimulus domain (Fig. 6C). For a duration to be decoded with high probability, both Pr(d|s) and Pr(s|dpres) must be high for at least one spike count, s. The non-DTN decoder assigned a probability of 100% to Pr(d = 9|s = 3) because this cell produced three spikes on one trial with a 9-ms stimulus but did not produce three spikes for any other duration tested. Therefore, the numerator and denominator in Bayes' formula were equal when s = 3 and thus Pr(d = 9|s = 3) = 1; however, because Pr(s = 3) was low (1/250 trials), the probability of actually decoding a 9-ms duration was low (Fig. 6I).
Fig. 6.
Examples of response, posterior, and decoding probability distributions for 3 neurons from the IC of the big brown bat. See Fig. 3 for the dot raster displays and duration tuning profiles of each cell. A–C: probability of s spikes being evoked given the presentation of stimulus duration d; Pr(s|d) for s ∈ [0, 1, 2, 3, 4] spikes per trial and stimulus durations d ∈ [1, 2, …, 25] ms (values from 16 to 25 ms not shown due to consistent near zero responses). D–F: probability of stimulus duration d having occurred given that s spikes were evoked; Pr(d|s) for the same spike counts and stimulus durations as above calculated using Bayes' formula with naive priors. G–I: stimulus duration decoding matrices for example neurons. These matrices can be interpreted as the probability that stimulus duration d would be decoded given that stimulus duration dpres was presented; Pr(d|dpres), over all stimulus durations d and presented stimulus durations dpres. Note that stimulus durations with the highest decoding probabilities correspond to the stimulus durations with the highest evoked spike counts, with both DTNs outperforming the non-DTN.
Population Analysis
Optimal duration decoding.
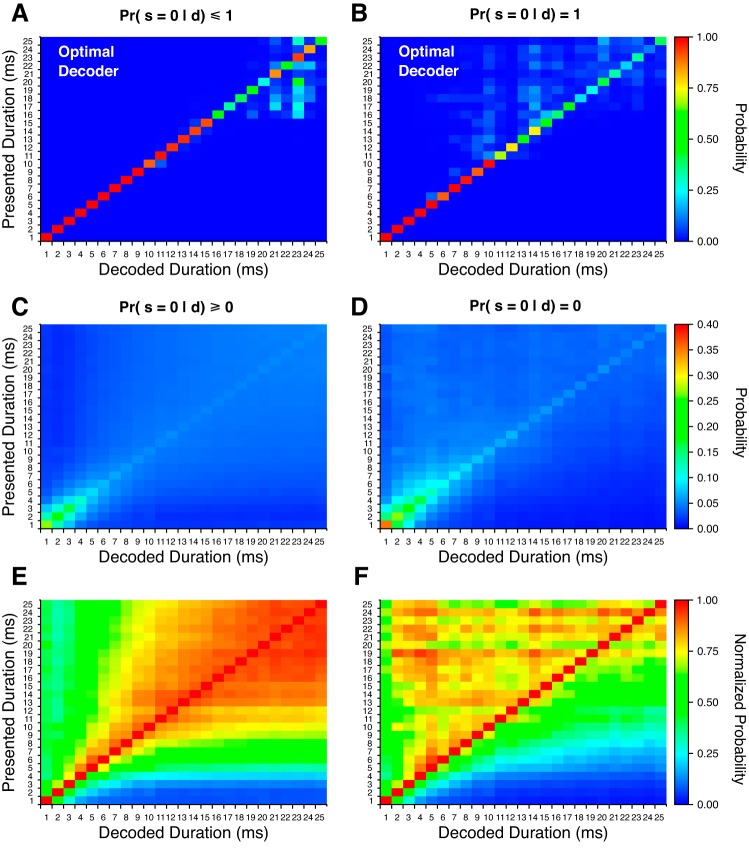
Using a Monte Carlo random sampling procedure (see methods), we estimated optimal posterior probabilities for stimulus duration from the joint response probabilities of 103 DTNs that produced an average maximum response of 7 spikes per stimulus. We did this both while including and ignoring responses from cells with zero spikes per stimulus because it was not obvious if the brain could use the absence of a response or if it required at least one spike from a neuron to gain information. It is possible that a neural decoder receiving information from multiple sources could recognize both the presence of a stimulus from one input and the lack of a DTN response from another. To allow information about stimulus duration when no spikes were produced, we permitted Pr(s = 0|d) ≤ 1 when calculating joint probabilities (Fig. 7A). We then forced Pr(s = 0|d) = 1 for all durations so that responses with zero spikes would not influence the calculated joint probability distributions (Fig. 7B). Both estimates performed well and decoded short stimulus durations perfectly. At longer stimulus durations, posterior probabilities were more spread out over the stimulus domain but both decoders still correctly assigned the presented duration with the highest posterior probability. Note that this decoding strategy assumed response independence, which was likely not true. Unfortunately, we were unable to calculate true joint response probabilities using data from simultaneously recorded DTNs. Future in vivo studies that collect multiunit activity from DTNs are needed to better characterize these joint response probabilities.
Fig. 7.
Posterior response probability matrices from population spike count responses. Estimated optimal decoding probabilities with spike counts across all decoded stimulus durations given the presentation of all stimulus durations [i.e., Pr(d|dpres)] when including responses with zero spikes per stimulus (A) and when ignoring responses with zero spikes per stimulus (B). Nonoptimal decoder with spike counts as the average duration decoding matrix over all DTNs when including responses with zero spikes per stimulus (C) and when ignoring responses with zero spikes per stimulus (D). Note that the probability scale in C and D runs from 0 to 0.4 for improved contrast. E and F: same data as in C and D with each row normalized to the highest probability value across all decoded durations.
Nonoptimal duration decoding.
When we directly calculated nonoptimal population duration decoding matrices, the most reliably decoded stimulus durations with spike counts ranged from 1 to 4 ms (Fig. 7C), a result consistent with the observation that the majority of DTNs had BDs and peak SSI values at similar short durations (Figs. 2C and 5, A–C). One consequence of naively weighting all DTNs equally was that peak decoding probabilities across the entire population were lower than the peak decoding probabilities of individual cells [e.g., the peak probability in Fig. 7B of Pr(d = 1|dpres = 1) was only 0.283]. This occurred because the posterior probability distributions of individual cells were low for the majority of stimuli away from BD, causing the average posterior probabilities to “wash out” and fall toward zero. In particular, because most DTNs showed little to no selectivity for stimulus durations >10 ms, this caused the corresponding posterior probabilities, Pr(d > 10|s), to be uniformly low. Consequently, cells with larger posterior probabilities for longer stimulus durations were obscured in the average of all other responses. To compensate for such low posterior probabilities, a decoder could discard information with low specificity and not including responses from DTNs with zero spikes per stimulus. Additionally, a decoder could care only about relative instead of absolute probabilities and simply decode by selecting the stimulus duration with the highest posterior probability regardless of its value (Beck et al. 2008).
We explored both methods for a decoder to overcome low posterior probabilities. First, we recomputed the population duration decoding matrix under the assumption that no knowledge was gained from a DTN that did not respond to a stimulus (i.e., zero spikes). In other words, we forced Pr(d|s = 0) = 0 for all stimulus durations, which is equivalent to setting Pr(s = 0|d) = 1 in the optimal decoding procedure described above. This change immediately resulted in higher decoding probabilities across the stimulus domain (Fig. 7D), demonstrating that some information can be detrimental to a nonoptimal decoding procedure and should therefore be discarded for improved performance. Second, we calculated a normalized duration decoding matrix by dividing the posterior probabilities at each presented duration by the maximum posterior (decoded) probability in the row. After normalization, stimulus durations with a posterior probability of 1 were always equal to the presented stimulus duration; however, normalized posterior probabilities of nearby stimuli, especially at longer durations, were also very close to 1 (Fig. 7E). For example, when the presented stimulus duration was 24 ms, the normalized decoded duration for a 23-ms signal was PrNorm(d = 23|dpres = 24) = 0.93, a difference of only 7%. The nonnormalized probabilities at these durations differed by only 0.35% (Fig. 7C). Accurate decoding of such responses would require a very selective neural decoder with extremely precise representations of posterior probability distributions.
Combining both methodologies produced the greatest disambiguation for decoding stimulus duration. After the information from trials with zero spikes was discarded and the decoded probabilities were normalized, presented stimulus durations were correctly delineated from all other durations (Fig. 7F). For example, in the combined decoding procedure, PrNorm(d = 23|dpres = 24) = 0.83, creating a probability difference from the correct stimulus duration of 17% more than twice the difference than when information from trials with zero spikes was included. Even though the most probable decoded stimulus durations were always the presented duration, signal durations shorter than the presented duration were also decoded with high probability. This can be seen as a bias for shorter presented durations in the normalized duration decoding matrix and would result in decoding errors that underestimate the true stimulus duration (Fig. 7F).
Interestingly, both nonoptimal decoding methods correctly assigned presented stimulus durations with the highest posterior probabilities even though the range of observed neuronal BDs and peak SSI durations did not cover the same range. Indeed, the maximum neuronal BD in our population was 12.5 ms (Fig. 2). This finding suggests that the range of stimulus durations that can be correctly decoded may not be limited to the range of neuronal BDs in the population of DTNs in the brain. This particular effect was likely exaggerated in our analysis by the limited number of trials collected from DTNs in our electrophysiological recordings, resulting in uncharacteristically distinguishable responses to signals away from BD that, given enough trials, may be indistinguishable from other responses away from the BD. Future studies should measure DTN response distributions with a larger number of stimulus trials to get a more accurate estimation of posterior probabilities from neuron response distributions.
Just-Noticeable Difference
To determine the JND in stimulus duration that could be detected based on the responses of DTNs in our population, we implemented a 2-AFC decision task using posterior probability distributions determined with the nonoptimal duration decoding procedure. We did this because we assumed that in vivo decoders were less than optimal and because the optimal decoding procedure yielded perfect performance (i.e., JND = 1 ms at all durations). The perceived similarity of two durations was calculated with a similarity index that compared the posterior probability distributions of the probe and reference stimuli. The similarity index was a function of the angle between the two posterior probability distributions and was not influenced by the magnitude of the distributions (see methods). Therefore, the normalized probability decoding method yielded equivalent results to the nonnormalized probability method.
We simulated a 2-AFC JND task using spike count data that included trials with zero spikes per stimulus (Fig. 8A) and trials that ignored responses with zero spikes per stimulus (Fig. 8B). When decoding with spike counts that included zero spikes, the calculated neural JND for the probe signal was 1 ms for reference durations between 1 and 6 ms but increased for longer reference durations (Fig. 8A, white line). When responses with zero spikes were ignored, discrimination performance decreased but only slightly (Fig. 8B, white line). This small difference in performance likely resulted from the “zero spikes ignored case” having a larger proportion of “different” trials being scored as the “same” owing to the lower threshold value we employed (Sthresh = 0.85 when ignoring zero spikes per stimulus vs. Sthresh = 0.92 when including zero spikes per stimulus; Fig. 1B).
Fig. 8.
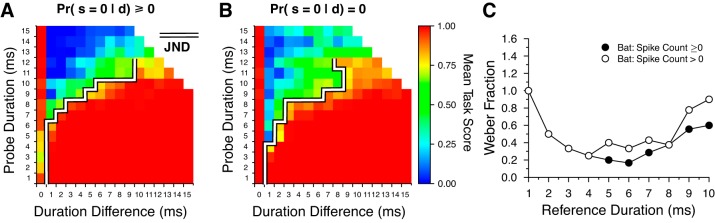
Two-alternative forced choice (2-AFC) duration discrimination performance and calculated Weber fractions. Mean 2-AFC task scores calculated with spike count information a when including responses with zero spikes per stimulus (A) and when ignoring responses with zero spikes per stimulus (B). The just-noticeable difference (JND), determined by the lowest duration difference with a task score of ≥0.75, is outlined with a thick white line. C: computed neural Weber fractions of DTNs from spike count responses.
With these 2-AFC results we calculated Weber fractions at each reference duration, defined as (Fig. 8C). The lowest JNDs measured in our simulation were 1 ms and occurred at the shortest reference durations. Because the minimum duration change between the reference and probe signals was also 1 ms, the smallest possible Weber fraction for a 1-ms reference signal was 1. When responses with zero spikes per stimulus were included, neural Weber fractions for spike count decoding steadily decreased with increasing reference durations between 1 and 6 ms until reaching a minimum of 0.167, after which neural Weber fractions increased for reference durations between 7 and 12 ms (Fig. 8C, filled circles). When responses with zero spikes per stimulus were ignored, a similar V-shaped pattern of change was observed in the neural Weber fraction function only this time the minimum value was 0.25 and it occurred at a reference duration of 4 ms (Fig. 8C, open circles). These data indicate that information contained in the responses of bat DTNs would be well suited for detecting small changes in the duration of an acoustic stimulus for reference durations up to ≈6 ms. Given that the minimum JND we measured with bat DTNs was 1 ms and the smallest difference tested between the reference and probe signals was also 1 ms, this suggests that a neural decoder in the bat using information contained in the responses of DTNs would be able to discriminate submillisecond differences in stimulus duration at short reference durations, and thus the Weber fractions at these durations are likely lower than what we computed here. Unfortunately, behavioral experiments measuring the duration discrimination performance of echolocating bats have not yet been performed.
DISCUSSION
Recent studies on the electrophysiological properties of DTNs from the IC of the big brown bat have begun to shed new light on the possible functions of these neurons in central auditory circuits. Dichotic paired tone stimulation has revealed that monaural pathways contain all of the circuitry necessary for creating the duration-tuned response physiology (Sayegh et al. 2014). This result is also consistent with the finding that some DTNs are sensitive to binaural interaural level difference and interaural time difference cues important for sound localization (Sayegh et al. 2014). Furthermore, a study on the interaction between frequency and duration tuning demonstrated that DTNs exhibited two patterns of spectro-temporal sensitivity and spatial organization within the IC: cells with sharp frequency tuning and broad duration tuning were located in the dorsal IC, and cells with wide spectral tuning and narrow temporal tuning were located in the ventral IC (Morrison et al. 2014). Bats systematically vary the duration of their echolocation calls while foraging, and there are a number of reasons why it would be helpful for the bat to “know” when an external signal of a specific frequency (or bandwidth), amplitude (intensity), and duration was received by each ear. For example, this information would be helpful for localizing sounds from different regions of auditory space based using interaural spectral and intensity differences (Fuzessery and Pollak 1984). This information would also be useful for a bat trying to avoid temporal overlap between the outgoing pulse of its current vocalization and the received echo from a previous vocalization (i.e., pulse-echo overlap; Kalko and Schnitzler 1989). Altogether, the evidence indicates that in both echolocating and nonecholocating animals, including humans, DTNs could function as level-dependent and/or level-tolerant spatio-spectro-temporal auditory filters (i.e., these cells have a minimum and/or maximum acoustic amplitude for evoking spikes, with a more-or-less consistent response strength within this amplitude range, and responses that vary with the frequency and spatial location of the auditory stimulus).
Spiking responses of auditory DTNs have been studied in a variety of vertebrates and most extensively in echolocating bats (for review, see Sayegh et al. 2011); however, until now a rigorous analysis of the efficacy of encoding stimulus duration by DTNs had not been performed. In this study, we measured information contained in the responses of individual cells and from a population of DTNs from the auditory midbrain of the big brown bat to characterize how DTNs encode stimulus duration. We found that responses of individual DTNs with the most spikes were best at encoding information about stimulus duration, supporting the long-held belief that the BD of a DTN encodes information about stimulus duration (Fig. 5, B, C, and D). We also investigated optimal and nonoptimal procedures for decoding stimulus duration from spike count information in a population of DTNs. The optimal decoding procedure had very good decoding accuracy with spike counts and near perfect accuracy with spike latencies (latency data not shown); however, any neural decoder implemented by the vertebrate central nervous system (CNS) is unlikely to perform as well as the optimal decoding procedure due to the intractable requirement of perfectly representing and computing posterior probability distributions with joint response distributions from the population of encoding neurons in the brain. What seems more plausible is that the CNS implements a nonoptimal decoding strategy. Our nonoptimal duration decoder simply averaged the posterior probability distributions of all DTNs, removing the need to calculate joint response probability distributions, thus greatly simplifying the proposed neural computational requirements.
Decoding Stimulus Duration
We implemented two variants of the nonoptimal decoder to explore the effect of including data from stimulus presentations with no response. In the first case, we allowed information to be gained from trials with an absence of spikes. In the second case, we ignored trials that failed to evoke spikes. Because DTNs have low rates of spontaneous activity (Fig. 4), any information gained from responses with zero spikes tended to “wash out” the posterior probabilities, especially at longer stimulus durations where fewer DTNs responded (compare Fig. 7, A, C, and E, to Fig. 7, B, D, and F). Therefore, discarding trials with zero spikes was beneficial for decoding stimulus duration using the nonoptimal strategy.
Analysis of human and nonhuman animal data suggests that perceptual information is processed probabilistically, often in a “Bayes optimal” manner (Geisler and Albrecht 1995; Knill and Pouget 2004; Nelken et al. 2005; Goldreich 2007; Yang and Shadlen 2007). A variety of methods exist for computing posterior probability distributions with neural networks, and often these use the logarithm of posterior probabilities or posterior probability ratios (Rao 2004; Jazayeri and Movshon 2006; Ma et al. 2006; Beck et al. 2008; Deneve 2008). Direct calculation of joint probabilities and posterior probabilities requires a multiplication process; however, the logarithmic equivalent of multiplication is addition, a computation that seems more feasible for neural circuits to perform by simply summing excitatory and inhibitory synaptic inputs (Deneve 2005). Our analysis did not employ logarithmic posterior probabilities, but the monotonicity of logarithms means that the relative ordering of the decoded probabilities would remain unchanged.
The present article uses established techniques in information theory to determine an upper bound of information contained in the responses of DTNs. Our results demonstrate that more information is transmitted when DTNs are stimulated at BD. An alternative decoding scheme not investigated here might reduce a DTN response distribution to a delta function centered at the BD; responses of the cell would then be decoded as this duration whenever the cell spiked. Although quite simple, this decoding scheme discards a large quantity of information available from the flanks of the duration tuning curve where FI (sensitivity to change) can be higher (relative to the peak of the curve) and thus important for interpreting acoustic information.
One question to address for future studies is the effect of population size on decoding performance. In our dataset DTNs varied in their response characteristics from having very narrow (responding to only 1 or 2 durations) to quite broad (responding to a wide range of durations) temporal tuning curves (see also Morrison et al. 2014). Therefore, the performance of a decoder using randomly selected DTNs as inputs would be highly dependent on the particular subset of cells chosen. To best determine the effect of population size on decoding performance, we recommend that future investigations employ multiunit recording to characterize the correlated response properties of DTN populations.
Although not included with the spike count analysis presented here, we applied the same encoding and decoding techniques to the FSL data of our cells and measured very high information content with near perfect decoding performance. There are two major reasons why this analysis was not informative. First, we had to bin FSLs into quantized values before calculating our information measures and applying the algorithms for assessing decoding performance. Unfortunately, bias correction methods could not be used on the FSL data because binned data typically yield bias estimates larger than the true bias owing to the small number of stimulus presentations relative to the number of possible FSL bins (Treves and Panzeri 1995). Therefore, any information measured could simply be a result of bias, making the FSL analysis incomparable to the spike count analysis. Second, an FSL analysis requires at least one spike to be evoked so any cell that did not spike on all trials would have fewer FSL values to inform an empirical response distribution. This would add further potential for bias.
A class of cells not considered in this study were tonically responding neurons with sustained spike trains that increase in spike count with increasing stimulus duration. Long-pass DTNs in the IC require a minimum stimulus duration before spiking, and this minimum duration remains constant or increases with increasing SPL (Faure et al. 2003; Aubie et al. 2009). Theoretically, stimulus duration could be decoded from the responses of a long-pass DTN, or any neuron with tonic responses, by simply integrating spike counts; however, a neural decoder trying to discriminate between two responses with long spike trains would face a similar problem to a decoder trying to discriminate between two responses with long latencies (e.g., the brain may find it difficult to differentiate between a 24-ms stimulus that evoked 20 spikes and a 25-ms stimulus that evoked 21 spikes). This is supported in the mouse where spiking responses of long-pass neurons are far more sensitive to changes in stimulus duration than the behavioral performance of mice in duration discrimination tasks (Klink and Klump 2004).
Just-Noticable Difference
The Weber-Fechner law of psychophysics states that the JND for stimulus magnitude scales proportionally to absolute stimulus magnitude (JND ∝ s ; Fechner 1966). Because the temporal bandwidth of duration tuning measured with spike counts increased in DTNs tuned to longer BDs (Ehrlich et al. 1997), this also predicts that cells with sharp temporal tuning selective for short durations will better discriminate small differences in stimulus duration than DTNs with broad tuning selective for longer stimulus durations. When we measured duration discrimination performance with spike count information using nonoptimal decoding procedures, the JND remained constant at the shortest durations and then increased at longer durations. This result may not be surprising given the decreased performance of the spike count decoder at longer stimulus durations (Fig. 7, C and D). Optimal decoding procedures yielded nearly perfect performance and resulted in a constant JND that was independent of the reference duration (data not shown). These results suggest that if bats obey the Weber-Fechner law for duration discrimination, then they are likely to use a nonoptimal decoding method. In mice it has been demonstrated that the neural sensitivity for duration discrimination is more sensitive than behavioral sensitivity, suggesting that, at least in mice, a suboptimal decoding procedure is employed (Brand et al. 2000; Klink and Klump 2004). Unfortunately, psychophysical studies on the duration discrimination abilities of bats have yet to be conducted, so it is not possible to compare behavioral performance to neural performance as assessed through our simulated 2-AFC experiments.
Conclusions
We have demonstrated, for the first time, that the spike count responses from DTNs contain sufficient information for the CNS to decode information about stimulus duration, especially at short durations. Furthermore, we have shown that the “best duration” acoustic stimulus that evokes the highest spike count is the “best encoded” stimulus duration. Interestingly, the range of neuronal BDs that DTNs are tuned to in the central auditory system may not necessarily define the range of stimulus durations that can be discriminated with spike count responses. Our simulated JND experiments strongly suggest that DTNs of echolocating bats are capable of discriminating submillisecond differences in stimulus duration, and we predict that future behavioral (psychophysical) studies will confirm this remarkable ability.
GRANTS
This research was supported by a Discovery Grant from the Natural Sciences and Engineering Research Council (NSERC) of Canada (to P. A. Faure) and National Institute on Deafness and Other Communication Disorders Operating Grants DC-00287 and DC-00607 (to J. H. Casseday and E. Covey). B. Aubie was supported by a NSERC Canada Graduate Scholarship, and R. Sayegh was supported by an Ontario Graduate Scholarship. The McMaster Bat Laboratory is also supported by infrastructure grants from the Canada Foundation for Innovation and the Ontario Innovation Trust.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the author(s).
AUTHOR CONTRIBUTIONS
Author contributions: B.A., E.C., and P.A.F. conception and design of research; B.A., R.S., T.F., E.C., and P.A.F. performed experiments; B.A. analyzed data; B.A. and P.A.F. interpreted results of experiments; B.A. prepared figures; B.A. and P.A.F. drafted manuscript; B.A., R.S., T.F., E.C., and P.A.F. edited and revised manuscript; B.A., R.S., T.F., E.C., and P.A.F. approved final version of manuscript.
ACKNOWLEDGMENTS
We thank Appalachia Martine and Kimberly Miller for technical assistance and Brandon Warren for expert programming support.
REFERENCES
- Arabzadeh E. Whisker vibration information carried by rat barrel cortex neurons. J Neurosci 24: 6011–6020, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aubie B, Becker S, Faure PA. Computational models of millisecond level duration tuning in neural circuits. J Neurosci 29: 9255–9270, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Aubie B, Sayegh R, Faure PA. Duration tuning across vertebrates. J Neurosci 32: 6373–6390, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beck JM, Ma WJ, Kiani R, Hanks T, Churchland AK, Roitman J, Shadlen MN, Latham PE, Pouget A. Probabilistic population codes for Bayesian decision making. Neuron 60: 1142–1152, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brand A, Behrend O, Marquardt T, McAlpine D, Grothe B. Precise inhibition is essential for microsecond interaural time difference coding. Nature 417: 543–547, 2002. [DOI] [PubMed] [Google Scholar]
- Brand A, Urban A, Grothe B. Duration tuning in the mouse auditory midbrain. J Neurophysiol 84: 1790–1799, 2000. [DOI] [PubMed] [Google Scholar]
- Butts DA. How much information is associated with a particular stimulus? Network 14: 177–187, 2003. [PubMed] [Google Scholar]
- Butts DA, Goldman MS. Tuning curves, neuronal variability, and sensory coding. PLoS Biol 4: e92, 2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carlson BA, Kawasaki M. From stimulus estimation to combination sensitivity: encoding and processing of amplitude and timing information in parallel, convergent sensory pathways. J Comput Neurosci 25: 1–24, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casseday JH, Ehrlich D, Covey E. Neural tuning for sound duration: role of inhibitory mechanisms in the inferior colliculus. Science 264: 847–850, 1994. [DOI] [PubMed] [Google Scholar]
- Casseday JH, Ehrlich D, Covey E. Neural measurement of sound duration: control by excitatory-inhibitory interactions in the inferior colliculus. J Neurophysiol 84: 1475–1487, 2000. [DOI] [PubMed] [Google Scholar]
- Dayan P, Abbott LF. Theoretical Neuroscience: Computational and Mathematical Modeling of Neural Systems. Cambridge, MA: MIT Press, 2001. [Google Scholar]
- Deneve S. Bayesian inference in spiking neurons. In: Advances in Neural Information Processing Systems, 17, edited by Saul LK, Weiss Y, Bottou L. Cambridge, MA: MIT Press, 2005. [Google Scholar]
- Deneve S. Bayesian spiking neurons I: inference. Neural Comput 20: 91–117, 2008. [DOI] [PubMed] [Google Scholar]
- DeWeese MR, Meister M. How to measure the information gained from one symbol. Network 10: 325–340, 1999. [PubMed] [Google Scholar]
- Ehrlich D, Casseday JH, Covey E. Neural tuning to sound duration in the inferior colliculus of the big brown bat, Eptesicus fuscus. J Neurophysiol 77: 2360–2372, 1997. [DOI] [PubMed] [Google Scholar]
- Faure PA, Fremouw T, Casseday JH, Covey E. Temporal masking reveals properties of sound-evoked inhibition in duration-tuned neurons of the inferior colliculus. J Neurosci 23: 3052–3065, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fechner GT. Elements of Psychophysics. New York: Holt, Rinehart and Winston, 1996. [Google Scholar]
- Fremouw T, Faure PA, Casseday JH, Covey E. Duration selectivity of neurons in the inferior colliculus of the big brown bat: tolerance to changes in sound level. J Neurophysiol 94: 1869–1878, 2005. [DOI] [PubMed] [Google Scholar]
- Fuzessery ZM, Pollak GD. Neural mechanisms of sound localization in an echolocating bat. Science 225: 725–728, 1984. [DOI] [PubMed] [Google Scholar]
- Geisler WS, Albrecht DG. Bayesian analysis of identification performance in monkey visual cortex: nonlinear mechanisms and stimulus certainty. Vision Res 35: 2723–2730, 1995. [DOI] [PubMed] [Google Scholar]
- Goldreich D. A Bayesian perceptual model replicates the cutaneous rabbit and other tactile spatiotemporal illusions. PLoS One 2: e333, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hsu A, Woolley SM, Fremouw TE, Theunissen FE. Modulation power and phase spectrum of natural sounds enhance neural encoding performed by single auditory neurons. J Neurosci 24: 9201–9211, 2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jazayeri M, Movshon JA. Optimal representation of sensory information by neural populations. Nat Neurosci 9: 690–696, 2006. [DOI] [PubMed] [Google Scholar]
- Jen PHS, Feng RB. Bicuculline application affects discharge pattern and pulse-duration tuning characteristics of bat inferior collicular neurons. J Comp Physiol A 184: 185–194, 1999. [DOI] [PubMed] [Google Scholar]
- Jen PH, Wu CH. Duration selectivity organization in the inferior colliculus of the big brown bat, Eptesicus fuscus. Brain Res 1108: 76–87, 2006. [DOI] [PubMed] [Google Scholar]
- Kalko EK, Schnitzler HU. The echolocation and hunting behavior of Daubenton's bat, Myotis daubentoni. Behav Ecol Sociobiol 24: 225–238, 1989. [Google Scholar]
- Kay SM. Fundamentals of Statistical Signal Processing: Estimation Theory. Upper Saddle River, NJ: Prentice Hall: vol. 1, 1993. [Google Scholar]
- Kayser C, Logothetis NK, Panzeri S. Millisecond encoding precision of auditory cortex neurons. Proc Natl Acad Sci USA 107: 16976–16981, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klink KB, Klump GM. Duration discrimination in the mouse (Mus musculus). J Comp Physiol A 190: 1039–1046, 2004. [DOI] [PubMed] [Google Scholar]
- Knill DC, Pouget A. The Bayesian brain: the role of uncertainty in neural coding and computation. Trends Neurosci 27: 712–719, 2004. [DOI] [PubMed] [Google Scholar]
- Ma WJ, Beck JM, Latham PE, Pouget A. Bayesian inference with probabilistic population codes. Nat Neurosci 9: 1432–1438, 2006. [DOI] [PubMed] [Google Scholar]
- Maler L. Receptive field organization across multiple electrosensory maps. II. Computational analysis of the effects of receptive field size on prey localization. J Comp Neurol 516: 394–422, 2009. [DOI] [PubMed] [Google Scholar]
- Montgomery N, Wehr M. Auditory cortical neurons convey maximal stimulus-specific information at their best frequency. J Neurosci 30: 13362–13366, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morrison JA, Farzan F, Fremouw T, Sayegh R, Covey E, Faure PA. Organization and trade-off of spectro-temporal tuning properties of duration-tuned neurons in the mammalian inferior colliculus. J Neurophysiol 111: 2047–2060, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moss CF, Chiu C, Surlykke A. Adaptive vocal behavior drives perception by echolocation in bats. Curr Opin Neurobiol 21: 645–652, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nelken I, Chechik G, Mrsic-Flogel TD, King AJ, Schnupp JW. Encoding stimulus information by spike numbers and mean response time in primary auditory cortex. J Comput Neurosci 19: 199–221, 2005. [DOI] [PubMed] [Google Scholar]
- Neuweiler G. Auditory adaptations for prey capture in echolocating bats. Physiol Rev 70: 615–641, 1990. [DOI] [PubMed] [Google Scholar]
- Optican LM, Gawne TJ, Richmond BJ, Joseph PJ. Unbiased measures of transmitted information and channel capacity from multivariate neuronal data. Biol Cybern 65: 305–310, 1991. [DOI] [PubMed] [Google Scholar]
- Panzeri S, Senatore R, Montemurro MA, Petersen RS. Correcting for the sampling bias problem in spike train information measures. J Neurophysiol 98: 1064–1072, 2007. [DOI] [PubMed] [Google Scholar]
- Panzeri S, Diamond ME. Information carried by population spike times in the whisker sensory cortex can be decoded without knowledge of stimulus time. Front Syn Neurosci 2: 17, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao RP. Bayesian computation in recurrent neural circuits. Neural Comput 16: 1–38, 2004. [DOI] [PubMed] [Google Scholar]
- Rolls ET, Critchley HD, Treves A. Representation of olfactory information in the primate orbitofrontal cortex. J Neurophysiol 75: 1982–1996, 1996. [DOI] [PubMed] [Google Scholar]
- Rolls ET, Critchley HD, Verhagen JV, Kadohisa M. The representation of information about taste and odor in the orbitofrontal cortex. Chem Percept 3: 16–33, 2009. [Google Scholar]
- Rolls ET, Treves A. The neuronal encoding of information in the brain. Prog Neurobiol 95: 448–490, 2011. [DOI] [PubMed] [Google Scholar]
- Saal HP, Vijayakumar S, Johansson RS. Information about complex fingertip parameters in individual human tactile afferent neurons. J Neurosci 29: 8022–8031, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sayegh R, Aubie B, Faure PA. Duration tuning in the auditory midbrain of echolocating and nonecholocating vertebrates. J Comp Physiol A 197: 571–583, 2011. [DOI] [PubMed] [Google Scholar]
- Sayegh R, Aubie B, Faure PA. Dichotic sound localization properties of duration-tuned neurons in the inferior colliculus of the big brown bat. Front Physiol 5: 394–422, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sayegh R, Casseday JH, Covey E, Faure PA. Monaural and binaural inhibition underlying duration-tuned neurons in the inferior colliculus. J Neurosci 34: 481–492, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmons JA. Acoustic images of target range in the sonar of bats. Nav Res Rev 39: 11–26, 1987. [Google Scholar]
- Simmons JA. A view of the world through the bat's ear: the formation of acoustic images in echolocation. Cognition 33: 155–199, 1989. [DOI] [PubMed] [Google Scholar]
- Strong SP, Koberle R, de Ruyter van Steveninck RR, Bialek W. Entropy and information in neural spike trains. Phys Rev Lett 80: 197–200, 1998. [Google Scholar]
- Tolhurst DJ, Smyth D, Thompson ID. The sparseness of neuronal responses in ferret primary visual cortex. J Neurosci 29: 2355–2370, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treves A, Panzeri S. The upward bias in measures of information derived from limited data samples. Neural Comput 7: 399–407, 1995. [Google Scholar]
- Vonderschen K, Chacron MJ. Sparse and dense coding of natural stimuli by distinct midbrain neuron subpopulations in weakly electric fish. J Neurophysiol 106: 3102–3118, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wickens TD. Elementary Signal Detection Theory. Oxford, UK: Oxford Univ. Press, 2002. [Google Scholar]
- Xie X. Threshold behaviour of the maximum likelihood method in population decoding. Network 13: 447–456, 2002. [PubMed] [Google Scholar]
- Yang T, Shadlen MN. Probabilistic reasoning by neurons. Nature 447: 1075–1080, 2007. [DOI] [PubMed] [Google Scholar]
- Yarrow S, Challis E, Seriès P. Fisher and Shannon information in finite neural populations. Neural Comput 24: 1740–1780, 2012. [DOI] [PubMed] [Google Scholar]
- Zar JH. Biostatistical Analysis (2nd ed.). Englewood Cliffs, NJ: Prentice-Hall, 1984. [Google Scholar]