Shear-induced force transmission in a multicomponent, multicell model of the endothelium

Abstract

Haemodynamic forces applied at the apical surface of vascular endothelial cells (ECs) provide the mechanical signals at intracellular organelles and through the inter-connected cellular network. The objective of this study is to quantify the intracellular and intercellular stresses in a confluent vascular EC monolayer. A novel three-dimensional, multiscale and multicomponent model of focally adhered ECs is developed to account for the role of potential mechanosensors (glycocalyx layer, actin cortical layer, nucleus, cytoskeleton, focal adhesions (FAs) and adherens junctions (ADJs)) in mechanotransmission and EC deformation. The overriding issue addressed is the stress amplification in these regions, which may play a role in subcellular localization of mechanotransmission. The model predicts that the stresses are amplified 250–600-fold over apical values at ADJs and 175–200-fold at FAs for ECs exposed to a mean shear stress of 10 dyne cm⁻². Estimates of forces per molecule in the cell attachment points to the external cellular matrix and cell–cell adhesion points are of the order of 8 pN at FAs and as high as 3 pN at ADJs, suggesting that direct force-induced mechanotransmission by single molecules is possible in both. The maximum deformation of an EC in the monolayer is calculated as 400 nm in response to a mean shear stress of 1 Pa applied over the EC surface which is in accord with measurements. The model also predicts that the magnitude of the cell–cell junction inclination angle is independent of the cytoskeleton and glycocalyx. The inclination angle of the cell–cell junction is calculated to be 6.6° in an EC monolayer, which is somewhat below the measured value (9.9°) reported previously for ECs subjected to 1.6 Pa shear stress for 30 min. The present model is able, for the first time, to cross the boundaries between different length scales in order to provide a global view of potential locations of mechanotransmission.

1. Introduction

A key mechanotransmission interface between the blood and the vessel wall is the endothelium [1–3]. Responses of endothelial cells (ECs) to haemodynamic forces play a significant role in vascular health and disease [4–9]. It is well known that ECs transduce the fluid shear stress (FSS) resulting from blood flow into intracellular signals that affect gene expression and cellular functions such as proliferation, apoptosis, migration, permeability, cell alignment and mechanical properties [1–20]. The activation of signalling pathways by shear forces arises at discrete locations in ECs by force amplification and force-induced directional biasing of signal propagation [1–4,10–12,16–18,20–23]. Numerous sites have been implicated in transducing mechanical stresses, including the plasma membrane [1,2,5,21,22,24] and its associated glycocalyx [1,5,25–36], focal adhesions (FAs) [4,7,16,17,37–43], the nucleus [44,45], the cytoskeleton [4,7,18,19,24,33,38,39,44–56], the cortical membrane [1,2,5] and the intercellular junctions [57–61].

The glycocalyx layer has been described as a mechanosensor and transducer of FSS on ECs [1,5,25–36]. Theoretical models to describe the transmission of force from fluid flow to the surface of cells covered by glycocalyx have revealed that the surface solid stress at the plasma membrane is one to two orders of magnitude larger than the surface fluid stress which indicates that FSS is sensed by the glycocalyx as solid stress [26–33]. Moreover, several models of the cytoskeleton have been constructed to investigate the hypothesis that this interconnected filamentous structure can act as a mechano-signal transmitter [44–56]. Shafrir & [46] proposed a two-dimensional model of the cytoskeleton as a random network of rigid rods representing the actin filaments and linear Hookean springs representing the actin cross-linkers. However, they assumed that the plasma and nuclear membranes are rigid and immobile, which is unrealistic. Later, more sophisticated models that focused on understanding the rheology of the actin network were presented [45,53,55,56]. The main concern of these studies was to connect these network models to the plasma and nuclear membranes. In addition, it has been found that FSS activates PECAM-1, a protein in cell junctions near the cell surface [23,37]. This activation may lead to production of a diffusible factor which induces activation of integrins in FAs, where stresses may be concentrated. Ferko et al. [23] found that strain and stress were amplified 10–100-fold over apical values in and around the high-modulus nucleus and near FAs. They used a multicomponent, three-dimensional solid elastic continuum model of a single EC. Furthermore, it has been demonstrated that FSS imposes tension on the EC membrane which develops and propagates along an endothelial monolayer. The membrane tension can be propagated to an adjoining upstream cell by transmission of tension at the cell–cell junction. The degree of tension propagation is a function of the angle of inclination of the cell–cell junction relative to the underlying substrate on which the cells are attached [58].

Taken together, these prior studies support the value of mechanical models in predicting stresses experienced at discrete cellular locations where mechanotransduction may occur. Although potential mechanosensors have been identified [1–61], the precise biomechanical mechanisms by which the apical shear stress leads to localized inter-/intracellular signalling at the mechanosensors are not well understood. Thus, there is a need to quantify the force transmission/amplification at inter-/intracellular structures and to quantify the role of intracellular tensions in mechanobiology of confluent cell monolayers. In this study, a confluent vascular EC monolayer is modelled to investigate the redistribution and amplification of haemodynamic forces applied at the glycocalyx surface to inter-/intracellular organelles where forces are transduced to biochemical signals. We will quantify the ‘decentralized’ force transmission model first outlined by Davies [4]. Stress transmission throughout the EC monolayer will be analysed, for the first time, using finite-element methods where all major cellular elements are incorporated in the model (the glycocalyx layer, actin cortical layer, nucleus, FAs, cytoskeleton network and adherens junctions (ADJs)). The mechanical state of the cell and its components upon initial exposure to shear stress are determined in the model. This simulates the early state of the cell in most in vitro studies of FSS-induced mechanotransmission in ECs [12,15,20–23,44,45,47,48,59,60]. Elongated cells that are adapted to shear stress are not considered in this study. The effects of high and low moduli organelles, and constrained and unconstrained regions on displacement, strain and stress distributions at cellular organelles will be quantified. Results may help to identify the role of each individual mechanosensor in early mechanotransmission events.

2. Material and methods

2.1. Geometric model

In this study, the EC monolayer consists of seven ECs. Each EC is modelled as a hexagonal cell at its base. The surface topology of each EC is modelled as a sinusoid based on experimental measurements with atomic force microscopy (AFM) of the surfaces of ECs which have not been exposed to shear stress previously [13,62,63]. It has been observed that cell shape can change detectably within 3 min of shear exposure [64], but such changes that reflect biomolecular responses of the cell are not captured in this model. The surface function is given as [62,63]

2.1

where 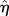is the amplitude of the surface contour. The streamwise and transverse wavenumbers α and β are given by

2.2

where λ_x and λ_z are the surface undulation wavelengths. Note that the amplitude of the sinusoidal boundary modulation is taken small relative to the wavelength, a necessary condition to apply equation (2.1) to the cell surface [62]. The maximum excursion of the surface undulation between peak height (over the nucleus) and minima (at intercellular junctions) is set at 4 µm [13]. The mean height to length ratio, 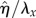, is taken as 0.138 and the aspect ratio, q = λ_x/λ_z (length divided by the width) is assumed as 1.12 [1,13,37,41,62,63,65]. The height of ECs at intercellular junctions is taken as 1 µm [13].

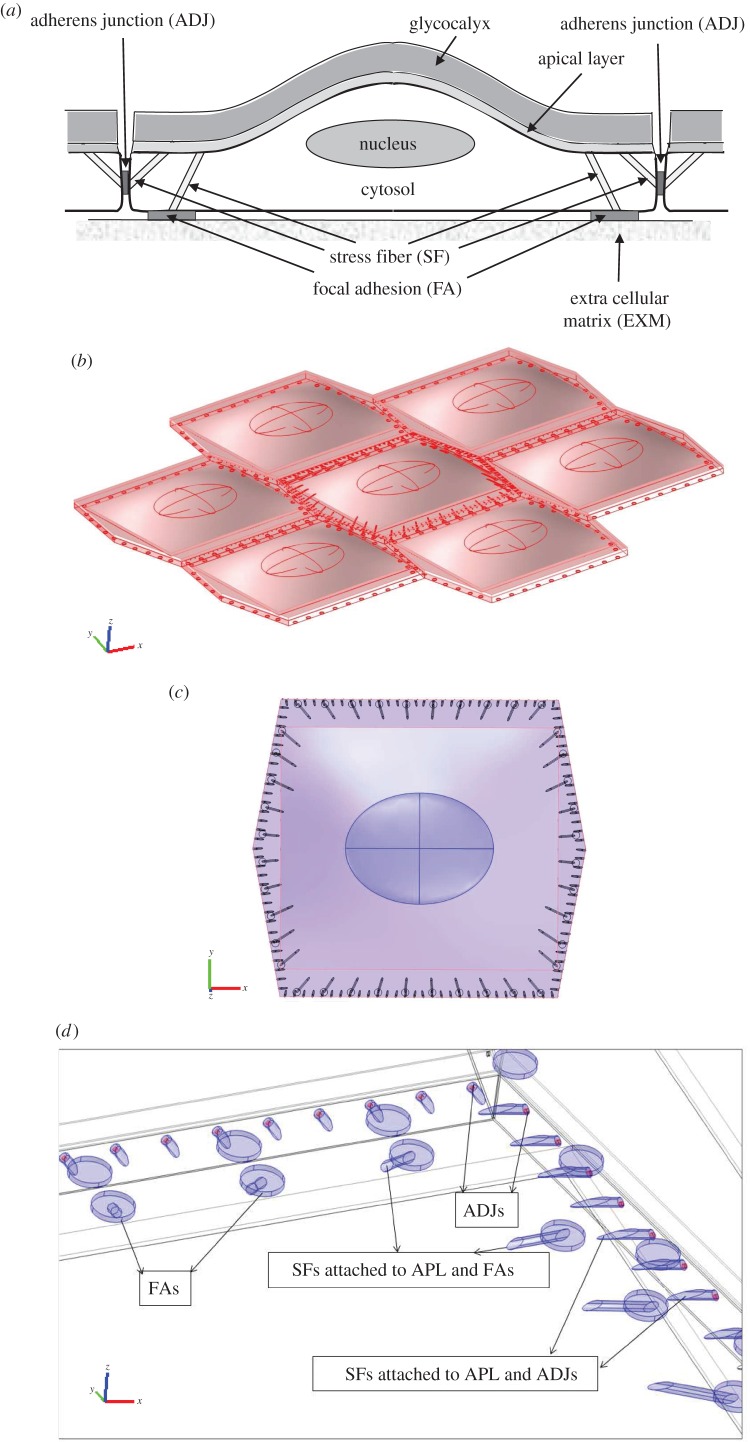
The three-dimensional model of multiple ECs includes the major subcellular load-bearing structures: apical glycocalyx layer that is in direct contact with fluid shear, apical cortical layer, nucleus, cytoskeleton, cytosol, FAs that provide the contact points with the extracellular matrix, and ADJs that bind ECs together at their lateral boundaries. Figure 1a demonstrates a schematic view of an EC, its connection to neighbouring cells and subcellular structures, as present in the current model. Figure 1b shows the EC monolayer from the side. A zoomed view of subcellular structures of the middle EC is displayed in figure 1c,d. Note that the apical plasma membrane/cortical cytoskeleton layer with a thickness of 100 nm [66] and the glycocalyx layer with a thickness of 500 nm [25,27–29] are located over the cytosol. While there is considerable debate about the thickness of the glycocalyx both in vitro and in vivo (reviewed in Ebong et al. [67]), the choice of 500 nm is a reasonable estimate of the thickness of the denser inner layer that is mechanically significant. The thickness of glycocalyx has been shown to be fairly uniform on cultured cells which have not been exposed to shear stress [68,69]. Bai & Wang [25] investigated the spatial distribution and temporal development of the glycocalyx on cultured human umbilical vein ECs (HUVECs). They demonstrated that the endothelial glycocalyx in vitro shows temporal development in the early days in culture. It covers predominantly the edge of cells initially and appears on the apical membrane of cells as time progresses. However, by day 14, the difference in the thickness and Young's modulus at different locations on the cell surface becomes very small. These studies support the use of a uniform thickness for the glycocalyx [25,68,69].

Figure 1.

The EC monolayer applied in the mathematical modelling of the force transmission through inter-/intracellular organelles. (a) Schematic view of EC, its connection to neighbouring cells and subcellular structures. (b) The EC monolayer from the side. (c) The transverse section of middle EC, including the glycocalyx, cortical layer, cytosol, nucleus, SFs, FAs and ADJs. (d) The peripherally distributed SFs are located along the apical plasma membrane of ECs and FAs or apical layer and intercellular junctions.

The length and width of the cytosol are taken as 36 µm and 32.1 µm, respectively [13,65]. The nucleus is modelled as an ellipsoid with the maximum radius of 8 µm (along x-axis in figure 1b), minimum radius of 6 µm (along the y-axis in figure 1b) and the maximum height of 2.5 µm (along the z-axis in figure 1b) [13,23,44]. The nucleus is located at the centre of each EC and 1.25 µm above the cell base [13,14,65].

The cytoskeleton network in this model is characteristic of a cell upon initial exposure to shear stress [5,13,14,38,62,63]. Ultrastructural studies have shown that many stress fibres (SFs) in oriented cells tend to have one attachment at or around the nucleus [5,14,38,70]. However, SFs are not attached to the nucleus upon initial exposure to shear stress [4,5,14,18,24,39,54,57,70]. Nevertheless, mechanical linkage between the apical surface and the nucleus exists through the effective elastic constant used for the cytoplasm. Therefore, it is assumed in the current model that SFs are not attached to the nucleus. The cytoskeleton is modelled as a network of SFs that are peripherally distributed [5,11,14,18,38]. The arrangement of SFs shown in figure 1c,d is based on observations that SFs are primarily located at the periphery of the cell in static situations, or shortly after FSS exposure [5,14,18,24,39,54,57,71]. Figure 1d demonstrates that peripherally distributed SFs emanate from the apical plasma membrane and link to FAs and intercellular junctions. One SF connects each FA on the basal side of the cell to the apical plasma membrane; one SF connects each ADJ to the apical plasma membrane [4,7,23,38,39,41–43,57,59–61]. The time constant characterizing mechanical stimulus transmission through the actin SF network was calculated by Hwang et al. [47] to be of the order of milliseconds to seconds. The current simulations correspond to the equilibrium state of the cell after this rapid transient and before significant biomolecular responses occur that would change the state of the cell [5,7,11,14,20,24,38,39,45,47,48,57,58]. SFs are modelled as bundles with circular cross section of 200 nm diameter [47,48,72]. Note that the surrounding ECs do not contain SFs in order to permit more efficient calculations (see Discussion). However, it is assumed that the cytoplasm of surrounding ECs is composed of cytosol and cytoskeleton. The surrounding cell cytoplasms have a higher Young's modulus than the central cell cytosol (table 1).

Table 1.

Summary of parameters used for the multicomponent, multicell model of the endothelium.

parameter	test range	reference value	reference
α, m−1 (streamwise wavenumber)	1.2–2.3 × 105	1.75 × 105	[5,8,13,26,34,38,70]
β, m−1 (transverse wavenumber)	1.2–3 × 105	1.95 × 105	[5,8,13,26,34,38,70]
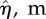(amplitude of surface contour)	4.41 ± 0.7 × 10−6	5 × 10−6	[5,8,13,26,34,38,70]
λx, m (surface undulation wavelengths)	40 ± 13 × 10−6	36 × 10−6	[5,8,13,26,34,38,70]
λz, m (surface undulation wavelengths)	36 ± 15 × 10−6	32.1 × 10−6	[5,8,13,26,34,38,70]
q (aspect ratio)	1.12 ± 0.31	1.12	[5,8,13,26,34,38,70]
μσ, Pa (mean wall shear stress)	—	1.05	[5,8,13,26,34,38,70]
ESFs, Pa (Young's modulus of SFs)	0.3–104 × 106	1.45 × 106	[1,47,48,50,66]
Eg, Pa (Young's modulus of glycocalyx)	390–1000	390	[1,50,57,66,67]
Ecytop, Pa (Young's modulus of cytoplasm)	700–1000	775	[10,15,23,44,64,70]
Ecytos, Pa (Young's modulus of cytosol)	—	500	[10,15,23,44,64]
Enuc, Pa (Young's modulus of nucleus)	5000–6000	6000	[23,44,64,71]
Ecor, Pa (Young's modulus of apical layer)	—	1000	[44]
υFA (Poisson ratio of the FA)	—	0.5	[8,22]
lFA, m (height of the FA)	—	110	[8,22]
AFA, m2 (cross-sectional area of one FA)	0.5–10 × 10−12	0.5003 × 10−12	[8,22]
WFA, nN nm−1 (elastic modulus of FA)	—	0.055	[8,22]
EFA, Pa (Young's modulus of FA)	1650–32 000	32 803	[8,22]
Fcontract, pN (contractile force)	10–150	100	[21,23,26]
AADJ, m2 (area of one ADJ)	—	7.854 × 10−15	[21,23,26]
LADJ, m (finger length as function of Fcontract)	1.75–6 × 10−6	4.5 × 10−6	[21,23,26]
L0ADJ, m (initial finger length)	1.75–3 × 10−6	1.75 × 10−6	[21,23,26]
EADJ, Pa (Young's modulus of ADJ)	5200–89 000	8102	[21,23,26]

It has been shown that the cross-sectional area of FAs varies in the range of 0.5–10 µm², with the magnitude of force applied on them [37,40,42]. The total area of all FAs in a cell covers approximately 2–5% of the complete cellular area [16,17,37,42]. In this study, FAs are modelled as cylinders with a radius of 0.4 µm and length of 110 nm [37,40–42]. Forty FAs are located in the basal aspect of each EC which cover 2.33% of the cell basal area.

ADJs are adhesive motifs joining neighbouring cells. It has been shown that tight junctions are not significant load-bearing structures relative to the ADJ. Therefore, only ADJs are included in the model as direct pathways for intercellular mechanotransmission [7,59–61]. The physical contacts are modelled as finger-like structures which grow perpendicular to the cell–cell interface [59–61]. The fingers are modelled as cylinders with 100 nm diameter [59,60]. Note that the interfinger distance is 1 µm and the density of ADJs is 1 µm⁻² [59–61]. ADJs are located at 25% of the cleft depth or 250 nm from the apical surface [36,73]. The shape, location and distribution of ADJs in the cell–cell interface in this model are shown in figure 1d. Note that one SF is connected to each ADJ.

2.2. Constitutive equations

Our model includes the major subcellular and intracellular structures (FAs, cytoskeleton, nucleus, cytosol, cortical layer, glycocalyx and ADJs). All structures are treated as incompressible neo-Hookean materials [44,45,74], whose strain energy function U is given by the equation

2.3

where C₁₀ is a constant and λ₁, λ₂ and λ₃ are the principal stretches. The constant C₁₀ is related to Young's E modulus by

2.4

All stress components are computed and applied to calculate the von Mises stress (σ_vM), a stress invariant usually referred as the effective stress [23]. The von Mises stress is computed by the equation

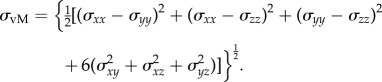2.5

The axial strain (ɛ) along any SF is calculated by the equation [72]

2.6

where L₀ and L₁ are undeformed and deformed lengths of SF, respectively. The undeformed length is obtained from the initial geometry. Viscoelastic effects are not considered.

2.3. Boundary conditions

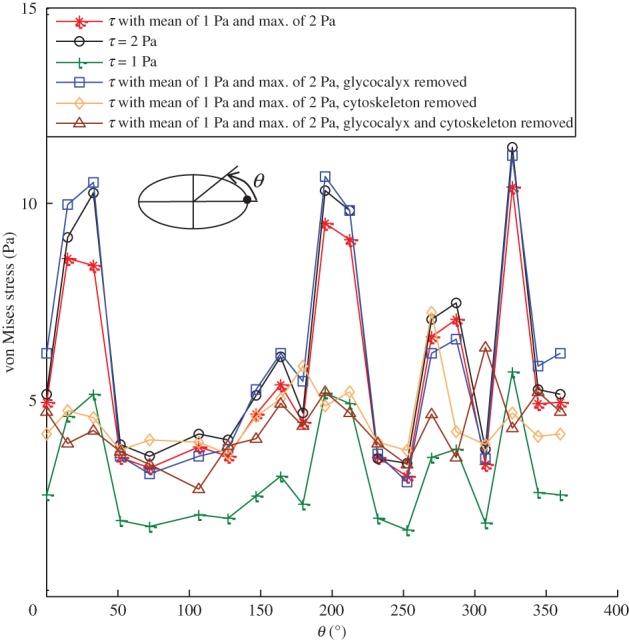
It has been shown that two geometrical parameters, the aspect ratio and the height to length ratio, determine the maximum shear stress and shear stress gradient developed for flow over an idealized sinusoidally undulating surface [62,63]. Our values for 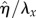and q indicate that the shear stress distribution on the endothelial surface given by refs [62,63] is valid for this model of ECs and is expressed as

2.7

where μ is the dynamic viscosity of blood and σ is the undisturbed shear rate far away from the wall. The term μσ is the mean wall shear stress imposed by the flow far from the EC surface [13,62,63]. Here, μσ = 1.05 Pa is specified for all calculations to produce the maximum FSS of 2 Pa (20 dyne cm⁻²). The shear stress in equation (2.7) is assumed to be applied instantaneously.

The boundaries of basal FAs are constrained in all directions while the apical integrin attachments, the cell base and cell membranes are subject to free displacement. Note that the boundaries of ADJs are interior boundaries which are connected to the two neighbouring ECs.

2.4. Model parameters

The cytosol, nucleus, cytoskeleton, cortical apical layer and glycocalyx are assumed to be homogeneous materials. Young's modulus of the middle cell cytosol, surrounding cell cytoplasm (cytosol + cytoskeleton), nucleus, SFs, cortical layer and glycocalyx are taken as 500 Pa, 775 Pa, 6000 Pa, 1.45 MPa, 1000 Pa and 390 Pa, respectively [12,23,25,27–29,31–33,37,44,70,72,73,75]. The test ranges and the reference values of geometric and mechanical parameters applied in the model are summarized in table 1.

Bai & Wang [25] measured Young's modulus of the glycocalyx on cultured HUVECs as 0.39 kPa (approximately), using AFM nano-indentation. This is consistent with the value of E_g calculated from the theory of Weinbaum et al. [28,29], who developed an indirect approach for estimating the bending rigidity (E_g I) of the glycocalyx, relying on the Brinkman equation, as follows:

2.8

where I is the second moment of inertia, E_g is Young's modulus of the glycocalyx, r_f is the effective radius of core protein fibres, K_p is the Darcy permeability of the glycocalyx, L_g is the thickness of the glycocalyx, β_g is the exponential fit parameter for the experimental recovery curve and c is the fibre volume fraction. E_g is calculated as 0.39 kPa by assigning I = 1.018 m⁴ [28,29], r_f = 6 nm [28,29], K_p = 10⁻¹¹ cm² [13–15], L_g = 0.5 µm [25,27–29,65,66], β_g = 0.38 [28,29] and c = 0.26 [28,29].

Biton & Safran [37] presented a new quantity, W_FA, which is related to Young's modulus of FA, as

2.9

where E_FA is Young's modulus of FA, W_FA is the elastic modulus, A_FA is the cross-sectional area of each FA, υ_FA and l_FA are the Poisson's ratio and the height of the FA. Biton & Safran [37] assumed that, in presence of shear flow, the displacement of the upper end of an FA is of the order of its height, i.e. 110 nm. This yields W_FA ≈ 0.055 nN nm⁻¹. The assumption has been applied to this study. Thus, E_FA is calculated from equation (2.9) as 32.8 kPa.

ADJs are adhesive motifs joining neighbouring cells. Brevier et al. [59–61] showed that the steady-state ADJ length is a function of the contractile force applied by the acceptor cell. The finding has been applied, in this study, to calculate Young's modulus of ADJs as

2.10

where E_ADJ is Young's modulus of ADJs, A_ADJ is the area of a single ADJ, F_contract is the contractile force, assumed to be independent of finger length and time which is equivalent to assuming its equilibrium value achieved in a timescale much shorter than that of its growth. L_0ADJ and L_ADJ are the initial finger length (where F_contract = 0) and finger length as a function of F_contract, respectively. We extracted the values for F_contract and corresponding L_0ADJ and L_ADJ from fig. 4 of Brevier et al. [59] as 100 pN, 1.75 µm and 4.5 µm. Then, A_ADJ is calculated as 7.854 × 10⁻¹⁵ m² (diameter of ADJ finger is assumed constant at approx. 100 nm) and E_ADJ is 8102 Pa.

2.5. Computational method

Figure 1b–d demonstrates the transverse and side views of the EC consisting of the glycocalyx, cortical layer, cytosol, nucleus, SFs, FAs and ADJs. The cytosol, sinusoidal surface of ECs, nucleus, apical cortical layer and glycocalyx were generated by a Matlab code (Matlab R2010b). The subcellular/intracellular components of ECs were imported to/created by means of the computer package, Gambit (v. 2.4.6, Fluent Inc.). The model components generated by Gambit were saved as IGES files. Model geometries were exported to the finite-element solver provided in Comsol Multiphysics, v. 3.5a. All cellular components were assigned by material properties, mesh specifications and boundary conditions. The computational results for the von Mises stress, shear stress and strain were determined to be independent of mesh density. A computational mesh was employed for each EC consisting of 2.15 × 10⁵, 1.2 × 10⁵, 6 × 10⁴, 5000, 300, 200 and 150 tetrahedral elements in cytosol, apical cortical layer, glycocalyx, nucleus, FA, SF and ADJ, respectively. The model was solved using a generalized linear solver, namely the UMFACK solver. Simulations were performed on a Dell PRECISION T3600, 12 processor computer with 64 GB RAM. During the solution process for the entire domain of the seven cell EC monolayer, there were approximately 9.9 × 10⁶ degrees of freedom. Post-processing results for stress, strains and deformations were obtained using post-processing features of Comsol Multiphysics v. 3.5a package.

3. Results

3.1. Deformation of endothelial cells and subcellular organelles due to fluid shear stress exposure

3.1.1. Deformation of endothelial cells due to fluid shear stress exposure

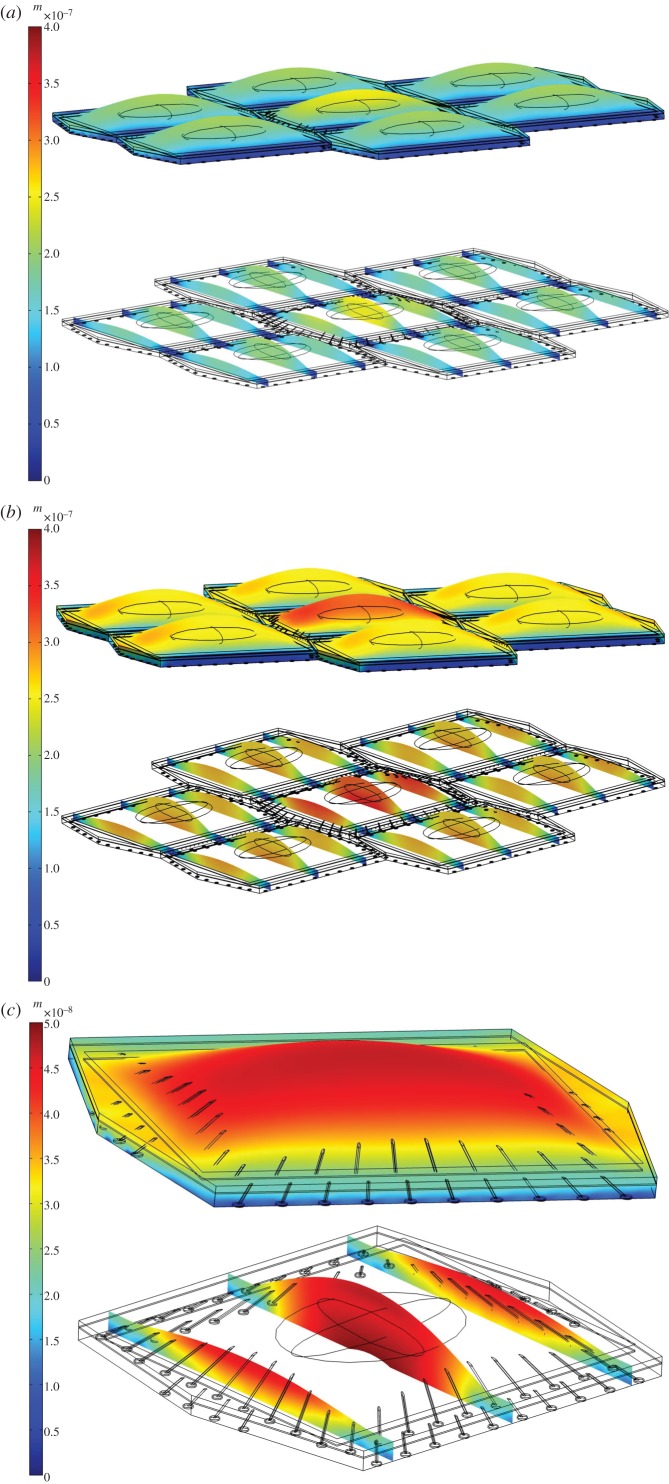
Figure 2a demonstrates the deformation of the EC monolayer in response to simulated fluid flow with imposed surface shear stress given by equation (2.7) having the maximum surface shear stress of 2 Pa (with the mean value of 1 Pa). As shown in figure 2a, large displacements (of up to 300 nm) are observed at the glycocalyx surface. The cross-sectional views demonstrate how the displacement changes from the glycocalyx to the cell surface to the cytosol and from the centre to the boundaries of the cell. These cross-sectional views make it clear that there is no significant displacement of the glycocalyx surface relative to the apical layer and that the glycocalyx follows the deformation of the apical layer and cytoplasm. The shear stress induces a mean deformation of 190 nm in the cytosol of the middle EC. The cytoplasms of neighbouring ECs are displaced with a magnitude of 161 nm. The displacement magnitudes of ECs are in close agreement with the data reported in Ueki et al. [75] that performed direct measurements of displacement in the adherent single EC exposed to FSS, in vitro. They observed maximum displacement of approximately 400 nm at the apical side of the cell, under a uniform shear stress of 2 Pa. We applied a uniform shear stress with magnitude of 2 Pa over the surface of the EC monolayer and observed a maximum displacement of 400 nm over the surface of ECs (figure 2b).

Figure 2.

The displacement of (a) EC monolayer where shear stress given by equation (2.7) is applied over the surface of ECs, with a mean value of 1 Pa and maximum of 2 Pa. (b) EC monolayer where a uniform shear stress of 2 Pa is applied over surface of ECs. (c) Single EC where a uniform shear stress of 1 Pa is applied over the cell surface.

Furthermore, Ferko et al. [23] developed a model of single EC with nucleus, cytosol and FAs, but not including the apical layer and cytoskeleton. They observed a maximum displacement of 30 nm at the apical side of the single EC when a uniform shear stress of 1 Pa was applied on the cell surface. We generated a single cell model with a uniform shear stress of 1 Pa applied on the cell surface, to validate our computational model and compare our results with those reported in Traub & Berk [8]. The one cell model included cytosol, nucleus, SFs, FAs, cortical apical layer and glycocalyx. The model predicts that FSS induces the maximum displacement of 50 nm over the glycocalyx surface (figure 2c—note the change of the colour code scale).

Moreover, our confluent multicell model predicts a maximum deformation of 200 nm over the glycocalyx of ECs when the monolayer is exposed to a uniform shear stress of 1 Pa. This displacement magnitude is in good agreement with the data given by Dangaria & Butler [11] in which the shear-induced deformation of 180 nm was reported in ECs exposed to the uniform shear stress of 1 Pa, in vitro.

3.1.2. Deformation of subcellular organelles due to fluid shear stress exposure

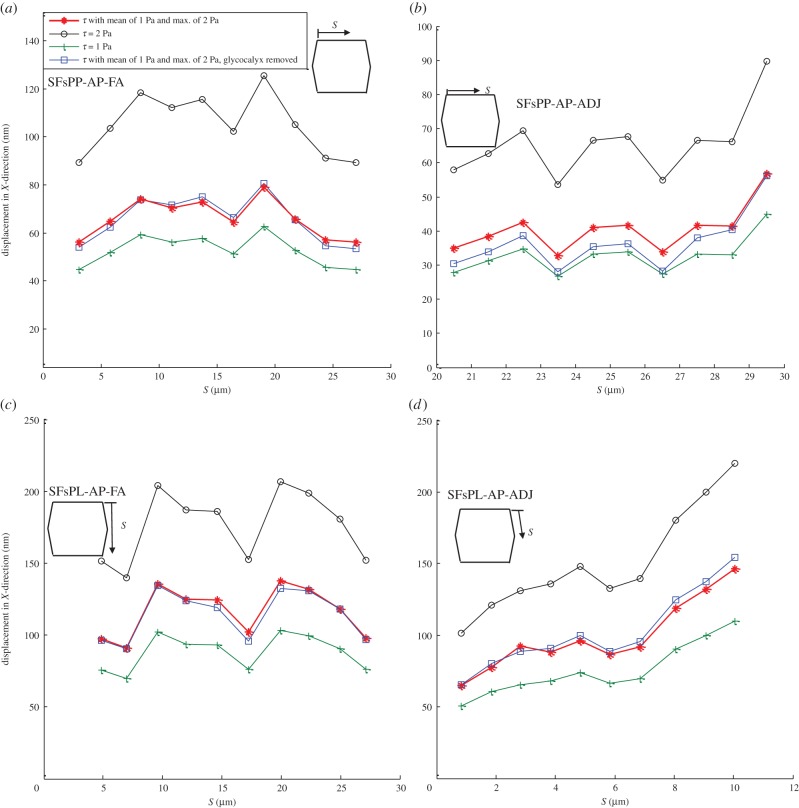
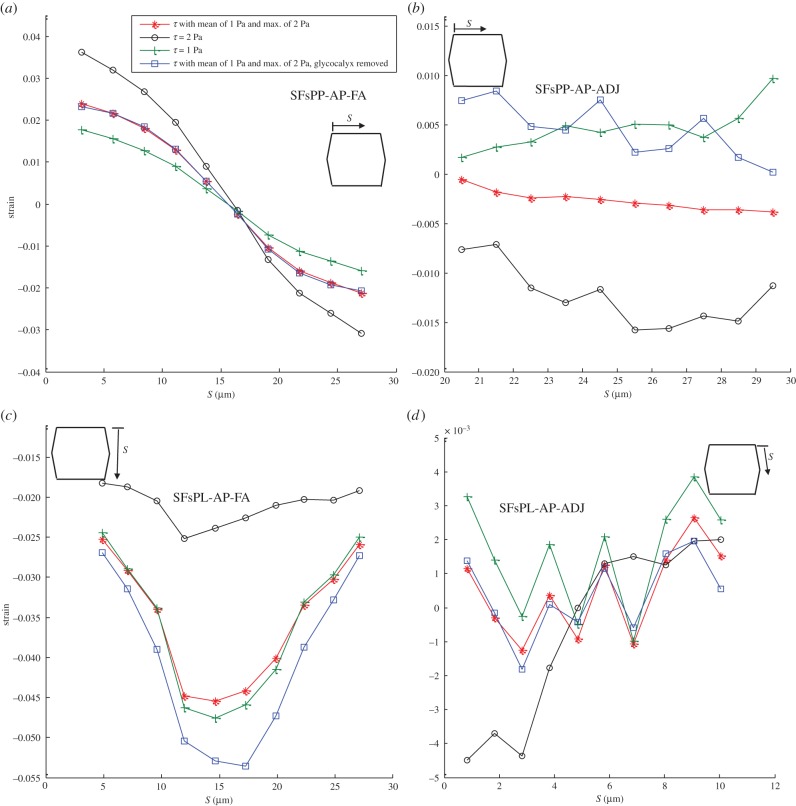
The displacement of SFs due to FSS exposure is shown in figure 3. The displacement of SFs oriented perpendicular to the FSS and attached to the apical layer and FAs (SFsPP-AP-FA) is demonstrated in figure 3a. Figure 3b–d demonstrates the bending of SFs perpendicular to the FSS and attached to the apical layer at one end and ADJs at the other end (SFsPP-AP-ADJ in figure 3b), SFs parallel to FSS and attached to the apical layer and FAs (SFsPL-AP-FA in figure 3c) and SFs parallel to FSS and attached to the apical layer and ADJs (SFsPL-AP-ADJ in figure 3d). The displacement is calculated for the upper edge of SFs which are attached to the apical layer. S represents the distance of the apical attachment point of each SF measured from the starting point of the EC edge that SFs are located along. Figure 3a–d clearly shows that the magnitude and distribution of the applied shear stress affects the bending of SFs. The amplitude of bending motion varies in direct proportion to the applied shear stress. Note that removing the glycocalyx from the EC surface induces only a slight change in SF bending. The displacement magnitudes are in good agreement with the values presented by Ueki et al. [76], who observed, in vitro, a maximum displacement of about 300 nm when a uniform FSS of 10 Pa was applied on the EC surface.

Figure 3.

Displacement of SFs in ECs exposed to shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and maximum of 2 Pa, uniform shear stress of 2 Pa, uniform shear stress of 1 Pa and shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and maximum of 2 Pa while the glycocalyx is removed. The displacement is calculated for the upper edge of SFs which are attached to the apical layer. (a) SFs are located perpendicular to FSS and attached to the apical layer and FAs (SFsPP-AP-FA), (b) SFs are perpendicular to FSS and attached to the apical layer to ADJs (SFsPP-AP-ADJ), (c) SFs are parallel to FSS and attached to the apical layer and FAs (SFsPL-AP-FA) and (d) SFs are parallel to FSS and attached to the apical layer to ADJs (SFsPL-AP-ADJ). S represents the distances of SFs from the starting point of the EC edge that SFs are located along it. (Online version in colour.)

3.1.3. The inclination angle of the endothelial cell–cell junction due to fluid shear stress exposure

The inclination angle of the EC–cell junction relative to an axis perpendicular to the cell substrate is 6.6° in EC monolayers subjected to uniform shear stress of 2 Pa, whereas the cell–cell junction inclines 4.18° for ECs exposed to a mean shear stress of 1 Pa (equation (2.7)) with a maximum FSS of 2 Pa. Note that the inclination angles are calculated for the cell–cell junctions parallel to the FSS. The junction inclination angle in response to a uniform shear stress of 2 Pa was calculated as 6.9°, 6.2° and 7.1° in EC monolayer models when the glycocalyx, cytoskeleton or both were removed, respectively. The EC–cell junctions incline 3.3° in a cell monolayer exposed to a uniform shear stress of 1 Pa.

3.2. Stress and strain distribution in subcellular structures of endothelial cell monolayer due to fluid shear stress exposure

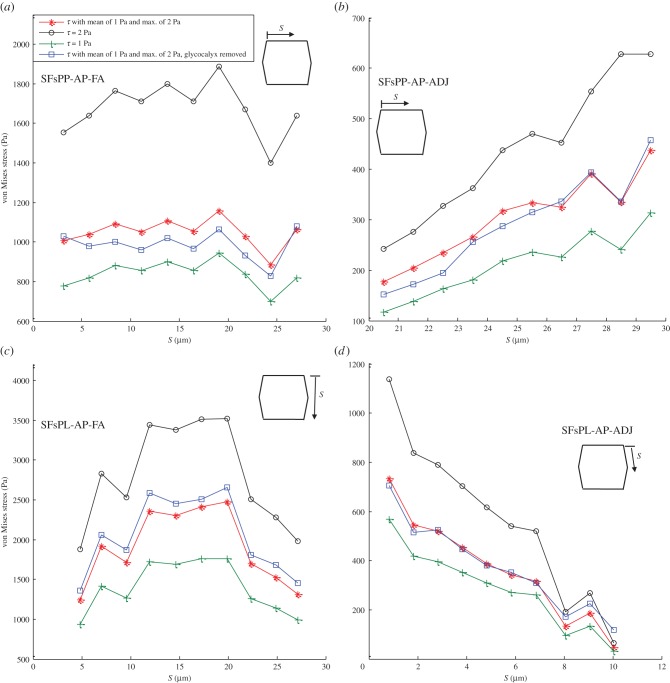
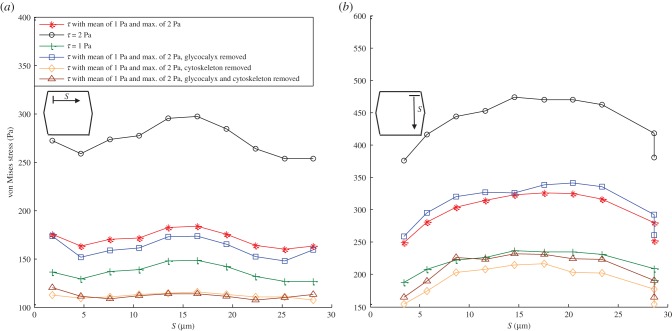
Figure 4 provides the average von Mises stress magnitude over SFs in an EC monolayer exposed to different shear stresses. Panels (a–d) show stresses for SFsPP-AP-FA, SFsPP-AP-ADJ, SFsPL-AP-FA and SFsPL-AP-ADJ, respectively. The maximal stresses of 3500 Pa are observed in SFs that are parallel to the FSS (SFsPL-AP-FA) while SFsPP-AP-ADJ shows the minimum values of stresses. The von Mises stresses are significantly elevated in SFsPP-AP-FA. This reveals the fact that SFs attached to FAs bear higher stresses. Excluding the glycocalyx from the EC monolayer model has opposite effects on SFsPL-AP-FA and SFsPP-AP-FA. The von Mises stress increases after removing the glycocalyx in SFs which are parallel to FSS while it decreases in SFs which are perpendicular to FSS.

Figure 4.

The average von Mises stress magnitude over the SFs in ECs exposed to shear stress given by equation (2.7) with a mean value of 1 Pa and maximum of 2 Pa, uniform shear stress of 2 Pa, uniform shear stress of 1 Pa and shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and the maximum of 2 Pa while the glycocalyx is removed. (a) SFs are located perpendicular to FSS and attached to the apical layer and FAs (SFsPP-AP-FA), (b) SFs are perpendicular to FSS and attached to the apical layer to ADJs (SFsPP-AP-ADJ), (c) SFs are parallel to FSS and attached to the apical layer and FAs (SFsPL-AP-FA) and (d) SFs are parallel to FSS and attached to the apical layer to ADJs (SFsPL-AP-ADJ). (Online version in colour.)

Figure 5 shows the axial strain along the SFs in ECs monolayer exposed to a mean shear stress of 1 Pa (equation (2.7)) with the maximum FSS of 2 Pa, uniform shear stress of 2 Pa, uniform shear stress of 1 Pa and a mean shear stress of 1 Pa (equation (2.7)) with the maximum FSS of 2 Pa while the glycocalyx is removed. The axial strain of any SF is calculated using equation (2.6). The coordinates and displacements of endpoints of SFs are used to calculate the deformed lengths of SFs. The maximal values of strain magnitude in EC monolayers exposed to a mean shear stress of 1 Pa with a maximum FSS of 2 Pa are observed in SFs that are attached to FAs with a maximum of 2.6% in SFsPL-AP-FA and 2.4% in SFsPP-AP-FA. The minimal strains occur in SFsPP-AP-ADJ while they are somewhat larger in SFsPL-AP-ADJ. Large effects of glycocalyx removal are apparent in panels (b,c).

Figure 5.

The axial strain along the SFs in ECs exposed to shear stress given by equation (2.7) with a mean value of 1 Pa and the maximum of 2 Pa, uniform shear stress of 2 Pa, uniform shear stress of 1 Pa, and shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and the maximum of 2 Pa while the glycocalyx is removed. (a) SFs are located perpendicular to FSS and attached to the apical layer and FAs (SFsPP-AP-FA), (b) SFs are perpendicular to FSS and attached to the apical layer to ADJs (SFsPP-AP-ADJ), (c) SFs are parallel to FSS and attached to the apical layer and FAs (SFsPL-AP-FA) and (d) SFs are parallel to FSS and attached to the apical layer to ADJs (SFsPL-AP-ADJ). S represents the distances of SFs from the starting point of the EC edge that SFs are located along it. (Online version in colour.)

Figure 6a,b demonstrates the von Mises stress distributions over the FAs oriented perpendicular and parallel to FSS. The maximum stresses (480 Pa) are observed over FAs which are orientated parallel to the flow direction, whereas FAs perpendicular to FSS experience lower stresses. Removing the glycocalyx layer has small but opposite influences on the von Mises stress magnitude over FAs aligned parallel or perpendicular to FSS. Moreover, excluding the SFs from the model drops the von Mises stress magnitude dramatically over FAs, independent of their orientation relative to FSS. Figure 6a,b shows that FAs induce stress amplification of 75–240-fold over the shear stress at EC surface.

Figure 6.

The von Mises stress distribution over the FAs. (a) FAs located perpendicular to the flow direction. (b) FAs located parallel to the flow direction. The cells are exposed to shear stress given by equation (2.7) with a mean value of 1 Pa and the maximum of 2 Pa, uniform shear stress of 2 Pa, uniform shear stress of 1 Pa, shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and the maximum of 2 Pa while the glycocalyx is removed, shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and the maximum of 2 Pa while the cytoskeleton is removed, and shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and the maximum of 2 Pa while both the glycocalyx and cytoskeleton are removed. (Online version in colour.)

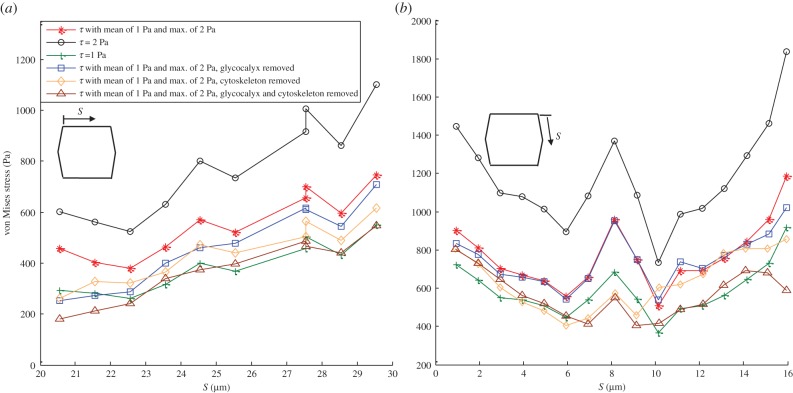
Figure 7a,b demonstrates the von Mises stress magnitude over ADJs located perpendicular to FSS and parallel to FSS for the middle EC where the maximal stresses of 700 and 1200 Pa are observed. ADJs induce stress amplification of 250–600-fold in a monolayer of ECs exposed to a mean shear stress of 1 Pa (equation (2.7)) with a maximum FSS of 2 Pa. The stress magnitude increases significantly when a uniform shear stress of 2 Pa is applied over the ECs (maximum of 1100 and 1850 Pa in figure 7a,b, respectively). Removing the glycocalyx does not affect the stress magnitude significantly in ADJs parallel to FSS while it induces a significant decrease in the stress magnitude of ADJs perpendicular to FSS. However, the exclusion of SFs from the model decreases the stress in cell–cell junctions to a maximal value of 850 and 650 Pa. Removing the glycocalyx and SFs from the model reduces the maximal von Misses stress over ADJs to 600 and 570 Pa.

Figure 7.

The average von Mises stress magnitude over ADJs along (a) the upper edge (perpendicular to FSS) of middle EC and (b) the right-upper edge (parallel to FSS) of the middle EC. The cells are exposed to shear stress given by equation (2.7) with a mean value of 1 Pa and the maximum of 2 Pa, uniform shear stress of 2 Pa, uniform shear stress of 1 Pa, shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and the maximum of 2 Pa while the glycocalyx is removed, shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and the maximum of 2 Pa while the cytoskeleton is removed, and shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and the maximum of 2 Pa while both the glycocalyx and cytoskeleton are removed. S represents the distances of ADJs from the starting point of the EC edge that ADJs are attached to it. (Online version in colour.)

Figure 8 demonstrates the von Mises stress along the perimeter of the cross section of the nucleus of the middle EC. Maximum of 10–12 Pa is observed in the first, third and fourth quadrant around the nucleus. The second quadrant experiences the minimum values (4–6 Pa) of the stress. Overall, the stress imposed on the cell surface has been amplified two- to sixfold at the perimeter of the nucleus. Removing the glycocalyx layer increases the von Mises stress values, moderately. On the other hand, excluding the SFs from the EC model induces a dramatic decrease in stresses around the nucleus. Ferko et al. [23] reported the stress amplification of three- to four-fold around the nucleus in their single cell model where a uniform shear stress of 1 Pa was applied on the surface of the EC. The stresses over the nucleus in our one EC model (results not shown), exposed to a uniform shear stress of 1 Pa, are in the same range of stresses observed by Ferko et al. [23].

Figure 8.

The von Mises stress distribution over the perimeter of the central cross section of the nucleus of the middle EC. The cells are exposed to shear stress given by equation (2.7) with a mean value of 1 Pa and the maximum of 2 Pa, uniform shear stress of 2 Pa, uniform shear stress of 1 Pa, shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and the maximum of 2 Pa while the glycocalyx is removed, shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and the maximum of 2 Pa while the cytoskeleton is removed, and shear stress given by equation (2.7) applied over the surface of ECs with a mean value of 1 Pa and the maximum of 2 Pa while both the glycocalyx and cytoskeleton are removed. (Online version in colour.)

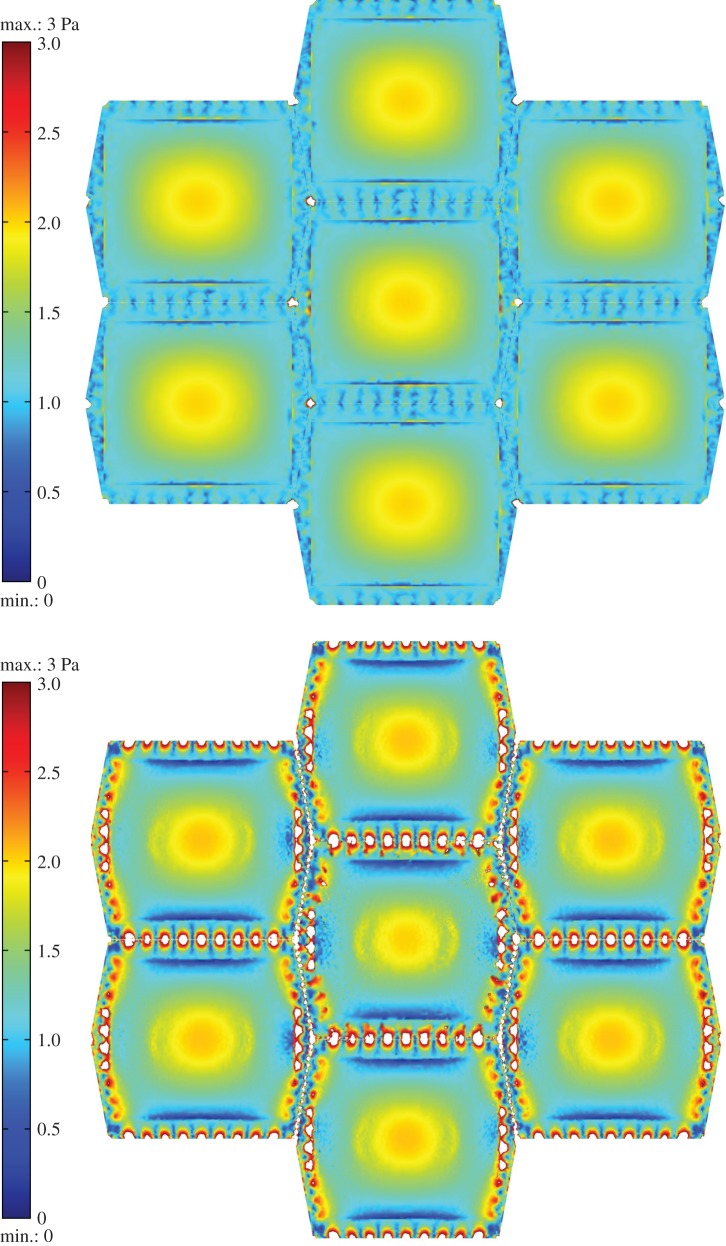
Figure 9a,b displays the von Mises stress distribution at the surface of the glycocalyx and the surface of the cortical apical layer, respectively. The stress distribution pattern on the surface of the glycocalyx reflects the imposed shear stress that has a maximum of 2 Pa over the top of the cell and 1 Pa over the boundaries. A maximum stress of 10 Pa is observed over the apical layer in regions of stress concentration around the SF attachment points.

Figure 9.

The von Mises stress distribution at the surface of (a) glycocalyx. (b) Cortical apical layer. The stresses over 3 Pa appear in white. The EC monolayer is exposed to shear stress given by equation (2.7) with a mean value of 1 Pa and the maximum of 2 Pa.

3.3. The sensitivity of the model to the key mechanical parameters

Table 2 summarizes the influence of variations in key mechanical parameters on the SFs displacement, cell inclination angle and von Mises stresses over SFs, ADJs and FAs. Wide variations in Young's modulus of SFs, ADJs and glycocalyx are taken to examine the sensitivity of the model to these parameters. Large variations in the value of mechanical parameters had small effects on displacements, but larger effects on von Mises stresses, particularly in the SFs.

Table 2.

The sensitivity of the model's predictions to key mechanical parameters. E stands for Young's modulus. All quantities in the table have been normalized by their values when E takes on its reference value given in table 1.

examined quantities	varied parameters
	E of SFs 14 500	E of SFs 145 000 000	E of ADJs 81	E of ADJs 810 000	E of glycocalyx 39	E of glycocalyx 39 000
displacement SFsPP-AP-ADJ	1.27 ± 0.1	0.87 ± 0.1	1.05 ± 0.1	0.99 ± 0.1	1 ± 0.1	1.2 ± 0.1
displacement SFsPP-AP-FA	1.3 ± 0.1	0.81 ± 0.1	1.03 ± 0.1	0.99 ± 0.1	0.96 ± 0.05	1.1 ± 0.1
displacement SFsPL-AP-ADJ	1.23 ± 0.1	0.88 ± 0.1	1.03 ± 0.1	0.99 ± 0.1	1 ± 0.1	1.03 ± 0.1
displacement SFsPL-AP-FA	1.33 ± 0.1	0.86 ± 0.1	1.04 ± 0.1	0.99 ± 0.1	0.99 ± 0.1	0.75 ± 0.1
von Mises stress SFsPP-AP-ADJ	0.2 ± 0.05	6 ± 0.5	0.7 ± 0.05	0.98 ± 0.05	1.04 ± 0.05	0.27 ± 0.05
von Mises stress SFsPP-AP-FA	0.098 ± 0.05	9.8 ± 0.5	1 ± 0.05	1 ± 0.05	1 ± 0.05	1.2 ± 0.05
von Mises stress SFsPL-AP-ADJ	0.11 ± 0.05	3.6 ± 0.1	0.3 ± 0.05	1.04 ± 0.05	0.97 ± 0.05	0.54 ± 0.05
von Mises stress SFsPL-AP-FA	0.08 ± 0.01	6.2 ± 0.1	1 ± 0.01	1 ± 0.01	1.08 ± 0.01	0.77 ± 0.1
von Mises stress ADJ-PP to FSS	1.1 ± 0.01	0.8 ± 0.01	0.33 ± 0.01	1.44 ± 0.01	0.95 ± 0.01	0.33 ± 0.01
von Mises stress ADJ-PL to FSS	0.95 ± 0.02	0.98 ± 0.2	0.23 ± 0.02	1.2 ± 0.02	0.93 ± 0.02	0.8 ± 0.06
von Mises stress FA-PP to FSS	0.8 ± 0.02	1.46 ± 0.2	0.98 ± 0.02	1 ± 0.02	0.98 ± 0.02	1.2 ± 0.02
von Mises stress FA-PL to FSS	0.66 ± 0.05	1.5 ± 0.05	1 ± 0.05	1 ± 0.05	1.03 ± 0.05	0.83 ± 0.09
inclination angle	1.15	0.77	1.1	0.99	1.02	0.6

4. Discussion

The finite-element method was applied to quantify the stress, strain and displacement of inter-/intracellular structures of ECs in a monolayer exposed to apically applied shear stresses. Notably, the multi-celled confluent vascular EC monolayer has not been modelled previously. This study, for the first time, links mechanotransmission models across length scales from nanometres to micrometres in order to provide a more global view of EC cell mechanics. The first quantitative assessment of force transmission via SFs to FAs or ADJs, in ECs exposed to FSS is also presented. Moreover, the multicomponent model of cells allowed us to calculate the bending of EC junctions and SFs. The model predicts that fluid shear-induced stresses are amplified in cellular structures (cortical actin layer, nucleus, SFs, FAs and ADJs). The FAs and ADJs experience the greatest stress amplification mediated to a significant extent by the SFs. There have been several studies previously suggesting that locally applied forces are transmitted through the actin cytoskeleton to distal points [56–59]. However, there has been no previous report computing the force transmission through SFs to FAs or ADJs in cells under physiological mechanical conditions. Furthermore, the influence of the glycocalyx on the force transmission on subcellular organelles has not been investigated previously.

The analysis of a multicomponent, multicell model of ECs demonstrates that SFs attached to FAs have larger bending magnitude than SFs attached to ADJs (figure 3a–d). Results also show that the bending magnitude of SFs parallel to the FSS is almost twofold larger than that of SFs located perpendicular to FSS (figure 3a–d). Moreover, the influence of the glycocalyx on SF bending was investigated. Removing the glycocalyx layer affects the bending of SFs located perpendicular to FSS and attached to ADJs (figure 3a–d).

The analysis reveals novel findings concerning the von Mises stresses along SFs. The stresses are significantly higher on SFs attached to FAs compared with SFs attached to ADJs (figure 4a–d). The SFs parallel to FSS bear double the magnitude of stress compared with SFs perpendicular to FSS. Furthermore, the axial strain is higher along the SFs attached to FAs (figure 5a–d). The findings confirm that the strain in SFs rises due to the bending of SFs which indicates an increase in tensile forces acting on the ends of the SFs. Higher tensile forces are expected over the FAs and ADJs. Results shown in figure 5 reveal that the SFs could be under tensile or compressive strains depending on the location and relative direction of the SFs with respect to the shear flow direction. The axial strain values demonstrated in figure 5a–d are in good agreement with previously reported data by Ueki et al. [76], who measured the strain on single SF in living ECs induced by FSS. They calculated the axial strain only on SFs oriented perpendicular to the flow direction with an accuracy of ±10°. They reported that an FSS of 2 Pa causes axial strain on SFs about 0.1%. However, it was mentioned in their discussion that their FSS-induced strain on SF in ECs is at least 10–100 times smaller than previously reported data [76].

The analyses of force transmission through the cytoskeleton network, in this study, are based on the assumption that the cytoskeleton is a network of SFs. Other components of the cytoskeleton, most notably, microtubules and intermediate filaments, may interact with SFs and affect mechanical force transmission. However, there are serious limitations to the study of mechanical force transmission in realistic SF networks that also take into account the interactions with microtubules and intermediate filaments. First, the nature of these interactions remains poorly understood. Second, microtubules are thought to bear primarily compressive loads and are often highly bent which requires a model with capability to describe large deformations. Third, the mechanical properties of the intermediate filaments have not been well established [47,48]. Thus, instead of including microtubules and intermediate filaments explicitly, we used an effective elasticity for the cytoplasm, which includes these components.

Note that the surrounding ECs did not contain SFs in order to permit more efficient calculations. The presence of cytoskeleton in the neighbouring ECs has been accounted for in the model by assigning a higher value of Young's modulus for the surrounding cell cytoplasm (compare E_cytop to E_cytos in table 1). However, it is recognized that this assumption may affect the predicted results by this model. This possible limitation was examined by adding SFs to two neighbouring ECs (on the lateral sides) and repeating the computations with E_cytos and E_SFs assigned for Young's modulus of the cytosol and SFs of these cells. The results indicate that the von Mises stress magnitude increases 1.7–1.9 times over the ADJs connected to SFs of the two neighbouring ECs. The stresses over SFs (of the middle EC) connected to these ADJs rises with the same trend (1.7–1.9 times). The displacements of the SFs are slightly higher (1.1–1.3 times) than the original model which only included SFs in the middle EC. This limited calculation that incorporated full modelling of only two neighbouring cells (to save on the enormous computational effort) gives an indication of the sensitivity to neighbouring cell modelling based on the assumption that all cells have the same cytoskeletal organization.

The stress magnitude over FAs depends significantly on the presence of the cytoskeleton and glycocalyx layer. FAs located parallel to FSS bear twofold higher stresses than the FAs sited perpendicular to FSS (figure 6a,b). Balaban et al. [16] developed a novel approach for real-time, high-resolution measurement of forces applied by cells at single adhesion sites. They observed that local forces over FAs are correlated with the orientation and area of the FAs. The results of the current model are consistent with the values measured in Balaban et al. [16] and values reported by Orr et al. [2]. Moreover, Ferko et al. [23] reported a maximal von Mises stress of 38 Pa in their one cell model with a uniform shear stress of 1 Pa on the cell surface. We observe the same range of stresses (40 Pa) over FAs in our one cell model with a uniform surface shear stress of 1 Pa (detailed results not shown here). The same trend seen in FAs is observed for the stresses over the ADJs, where cell–cell junctions sited parallel to FSS bear twofold higher stresses (figure 7a,b). The stresses over ADJs located parallel to FSS are independent of the glycocalyx while removing the glycocalyx significantly decreases the stresses over ADJs perpendicular to FSS. Removing the SFs induces a dramatic decrease in the stress magnitudes over ADJs positioned in both directions (figure 7a,b). Note that idealized uniform distributions of FAs and ADJs are employed in this model. We believe that properly modelling the density and nominal spacing of the sensory elements should give good estimates of the stress magnitudes and have not attempted to model non-uniform arrangements.

The angle of inclination at the cell–cell junction in response to flow was calculated for the first time, in the model of confluent ECs. A 6.6° cell–cell junction inclination was computed for an EC monolayer being subjected to uniform shear stress of 2 Pa. Melchior & Frangos [58] reported an inclination of the cell–cell junction of 9.9° in the direction of flow (1.6 Pa) after 30 min of shear exposure in a confluent monolayer of HUVECs. The difference in inclination angle values between the in vitro experiments and our model predictions may be due to biological processes that are not modelled in the present mechanical model that are operative even in the short-term in vitro experiments. On the other hand, Melchior & Frangos [58] demonstrated that the flow-induced junctional inclination was independent of the cytoskeleton or glycocalyx. This independency is confirmed by this model by removing either or both the cytoskeleton and glycocalyx. Note that the current model is most relevant to the in vitro onset of shear experiments after the viscoelastic transients have decayed, but the in vivo situation may be much more complicated with time varying flow and pressure and varying cell morphology.

Table 2 shows that only a few of the model's predictions are sensitive to variations in key mechanical parameters while most model predictions are not greatly affected. One hundred-fold increases and decreases in the Young modulus of SFs, with respect to the reference value, affect the von Mises stresses over SFs significantly while the stresses over FAs and ADJs are not affected very much. One hundred-fold increases and decreases in E of ADJs have modest effects on the stresses over ADJs and SFs attached to ADJs and minimal effects on other model predictions. One hundred-fold increases in E of the glycocalyx have modest effects on cell inclination, the displacement of SFs and inter-/intracellular stresses, whereas 100-fold decreases have virtually no effects.

It is well known that hypertension, diabetes and hypercholesterolemia promote atherosclerosis by disrupting the ability of the endothelium to respond to shear stress [1–9]. Therefore, elucidation of the mechanisms of shear-mediated signal transduction will greatly advance our understanding of atherosclerosis. This study reveals that FSS applied on cell surfaces is directly transmitted through the cytoskeleton to FAs or ADJs where the forces are dramatically amplified. The force transmission to/amplification on all major inter-/intracellular mechanosensors are quantified. The analyses of a multicell, multicomponent model of the endothelium clarifies that physiological shear stress induces sufficient stresses in these regions to directly activate signalling. In order to understand the potential significance of the computed stresses over the SFs, FAs, ADJs and nucleus for gene expression, G protein activation, ion channel activity and protein synthesis, the corresponding traction forces are determined. The reported traction forces are based on the integral of the surface traction force magnitude 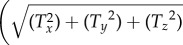, where T_x, T_y and T_z are the Cartesian components of traction force over the contact surface area. The maximum traction forces acting on the SFs, FAs, ADJs and nucleus due to exposure of ECs to FSS are in the ranges of 5–180 pN on the surfaces of SFs attached to the apical layer (the highest values of traction forces are observed on the SFs located parallel to FSS), 600–4100 pN over the surfaces of FAs attached to SFs (the highest values of traction forces occur over the surface of FAs parallel to the flow direction), 4–15 pN over the surfaces of ADJs attached to SFs (the ADJs positioned parallel to FSS experience the highest magnitude of traction forces), and 460 pN over the entire surface of the nucleus. The range of forces required for mechanotransmission mediated by the mechanosensors in FAs or ADJs has been reported to be several to several tens of piconewton [2,3,16,23,33,37,44,55,59,60,72,76]. Therefore, the force values of this study fall in the range of previously reported data.

It has been suggested that the integrin density is 1000 integrins μm⁻² in a single FA [41,43]. This yields a maximum force per integrin molecule of 8 pN (FAs modelled as cylinders of the radius of 0.4 µm and the cross-sectional area of 0.5 µm² per FA). The maximum force per integrin occurs over the FAs that are located close to the upstream joint points of the central EC and two neighbouring cells. Our predictions of forces in FAs are consistent with the experimental observations using the advanced fluorescence techniques based on fluorescence resonance energy transfer (FRET) in which relative forces are quantified [12,75,77]. On the other hand, forces of the order of 2–3 pN across vinculin may be sufficient to induce downstream signalling as reported by ref. [78] using a calibrated FRET-based force sensor. It has been further suggested that the integrin linker protein talin is the likely force sensing protein in the FA complex [79], and molecular dynamics simulations have estimated that the force required to expose cryptic vinculin binding residues is about 4 pN. Other studies reviewed in Hytönen et al. [80] indicate that the force required to unfold the extracellular fibronectin protein that binds integrin is in the order of 100–200 pN. Thus, the 8 pN force on integrin that we estimate is in the range that could activate intracellular signalling by exposing vinculin binding residues without altering the conformation of extracellular fibronectin.

The number of free filaments at the tip of each finger in the ADJ is estimated as 5–100 [59,61]. Thus, a maximum force of 0.15–3 pN per filament is estimated by this model. The filaments over ADJs which are located near to the joint points of three ECs experience the maximum forces. The transmission of FSS to cell–cell junctions has been suggested in previous studies, where PECAM-1 has been identified as a mechanosensor [71,81]. New findings indicate that shear stress triggers the association of PECAM-1 with vimentin, which transmits myosin-generated forces to PECAM-1 [71,81]. The magnitude of the force produced by a single myosin molecule falls in the range of 0.4–4 pN [3,76]. Thus, our estimated junctional forces appear to be in the range that can activate localized signalling proteins. Weinbaum et al. [28] reported forces in the range of 0.1–0.5 pN to deform the boundaries of the microdomains of the cortical actin cytoskeleton. Our computed basal and junctional forces are therefore also in the range that can deform the actin cytoskeleton. Further developments are necessary to link single molecule studies to models of mechanotransmission and intracellular signalling in cells under physiological conditions.

Funding statement

M.D. thanks the Lappeenranta University of Technology (project no: 23B21083TT10) and Academy of Finland (grant no.123938) for financial support. P.J.B. acknowledges financial support from the National Science Foundation (US) (CMMI 1334847), and J.M.T. acknowledges support from US NIH grant no. HL94889.