Fast, high-throughput measurement of collective behaviour in a bacterial population

Abstract

Swimming bacteria explore their environment by performing a random walk, which is biased in response to, for example, chemical stimuli, resulting in a collective drift of bacterial populations towards ‘a better life’. This phenomenon, called chemotaxis, is one of the best known forms of collective behaviour in bacteria, crucial for bacterial survival and virulence. Both single-cell and macroscopic assays have investigated bacterial behaviours. However, theories that relate the two scales have previously been difficult to test directly. We present an image analysis method, inspired by light scattering, which measures the average collective motion of thousands of bacteria simultaneously. Using this method, a time-varying collective drift as small as 50 nm s⁻¹ can be measured. The method, validated using simulations, was applied to chemotactic Escherichia coli bacteria in linear gradients of the attractant α-methylaspartate. This enabled us to test a coarse-grained minimal model of chemotaxis. Our results clearly map the onset of receptor methylation, and the transition from linear to logarithmic sensing in the bacterial response to an external chemoeffector. Our method is broadly applicable to problems involving the measurement of collective drift with high time resolution, such as cell migration and fluid flows measurements, and enables fast screening of tactic behaviours.

1. Introduction

The invention of video tracking methods to examine systems of colloidal particles [1] or bacterial cells [2–4] has enabled a host of advances. A striking diversity in microbial single-cell behaviour has been observed [2,5,6]. Although cell-tracking provides valuable information, it is often slow and sometimes subject to bias—large distributions of cell shapes or speeds might not be sampled properly because of faulty image recognition. Dynamic light scattering (DLS) is a well-established technique in soft matter physics: coherent radiation is used to probe time-varying density fluctuations in a sample [7]. Recently, Cerbino & Trappe [8] presented an intriguing extension to this method—differential dynamic microscopy (DDM)—which calculates the scattering pattern by software fast Fourier transform (FFT) from the video-microscopy images of a sample, and analyses the dynamics in this sample using a framework similar to DLS [9]. The strength of such a technique lies in the idea that local density is being measured, rather than the explicit location of particles. Scattering-based methods rapidly sample all cells, which provides precise, population-averaged measurements, making them well suited to fast screening applications in biology [10,11]. Computational scattering also presents further, unexplored opportunities. Both DLS and DDM measure the amplitude of density fluctuations (from the amplitude of the scattering pattern, which is a complex number), but discard the useful information encoded in their phase (not to be confused with the optical phase of the light used to illuminate the sample in microscopy). The phase of Fourier components has been used to track motion of single objects by the image processing community [12,13], but to the best of our knowledge, has not been applied to a randomly fluctuating population.

The collective behaviour of bacteria is a field of interest both in microbiology [14] and, increasingly, statistical physics [15,16]. The chemotactic behaviour of the model bacterium Escherichia coli is one of the best understood biological systems (see, for example, Refs. [17,18] for recent reviews). These bacteria swim in a series of straight ‘runs’ lasting around a second, separated by roughly 0.1 s ‘tumble’ events. This behaviour is similar to a random walk, which is biased in response to an external chemoeffector. The molecular response machinery is thought to be composed of three blocks: the receptors, an intracellular ‘messenger’ and the flagellar motor. The receptors are called methyl-accepting chemotactic proteins (MCPs). The transmembranar receptors (Tar, Tsr, Trg and Tap) bind to specific target molecules. The binding of a chemoattractant lowers the phosphorylation of the molecule CheA, which is located on the receptor's end. This lowers the phosphorylation level of the intracellular signal transmission molecule CheY. The probability of a tumble is in turn lowered, because the phosphorylated form of CheY (CheY-P) binds to the flagellar motor to induce a motor reversal, hence a tumble. Recent results have shown that the reorientation during a tumble is also reduced when running towards an attractant [19]. Both effects contribute to create a chemotactic drift in the run/tumble random walk in the presence of certain chemical stimuli.

The response of the chemotaxis system is very strong even for small changes in concentration (‘high gain’). This is currently explained through the cooperativity of the receptors, which react in clusters of dimers to the binding of a ligand [20–23], and of the molecules in the ring controlling the flagellar motor rotation [24,25], which can cooperatively rearrange to induce a motor switch in response to a single CheY binding event. The response is also subject to adaptation: the MCPs are desensitized by successive methylations (governed by the proteins CheR and CheB) [17], so that the activity of CheA, and hence the tumbling rate, finally adapts to a new background concentration of the chemoattractant. For methylaspartate, the molecule we used, this adaptation is perfect—the activity always resets to the same value in homogeneous environments. At very low average concentrations of effectors, the response to gradients is thought to depend on the absolute change in chemical concentration, whereas at larger background concentrations, the bacteria respond to the more relevant relative concentration changes, partly thanks to adaptation. This second mode, known as ‘logarithmic sensing’, was observed in early capillary assays [26], as well as more recently in microfluidic devices inferring the response from steady-state cell density distributions [27] and Förster resonance energy transfer assays [28].

Although chemotaxis at the single-cell level is increasingly well understood, there is a whole new layer of complexity in the macroscopic drifts and concentration imbalances at the population level [15,29]. This has been studied both theoretically [18,29–31] and in simulations [32,33], typically taking a mean-field approach to modelling bacterial behaviour. The Keller–Segel model (a diffusion and conservative flux equation) [29,34] is often the starting point for such work, with input parameters such as average cell velocity and binding site occupancy.

We present a new technique, phase differential microscopy (φDM), to measure chemotactic behaviour in a population of bacteria. Our method is insensitive to the shape of the bacteria and fully incorporates three-dimensional motion in the analysis. We demonstrate the utility of this technique by measuring the chemotactic response of wild-type E. coli to methylaspartate under a wide range of anaerobic conditions, finding excellent agreement with a recent parameter-free model for chemotaxis [27]. We also note that our technique is computationally inexpensive compared with video particle tracking at the same scale, while maintaining a similar or better accuracy (see the electronic supplementary material for a full comparison of the methods). Lastly, our method is suitable for real-time implementation, and for measuring fluid flow as well as bacterial chemotaxis.

2. Theory

Under our optical system (phase contrast, 10× magnification, giving 1.41 µm pixel size in the final image), a suspension of E. coli bacteria looks like a collection of moving points, with approximately Gaussian intensity profile. A single cell measures approximately 1 × 2 µm, but this anisotropy is not well resolved at low magnification. The contribution to the image from bacterium j at position r_j = (x_j, y_j) is given by I_j(r, t) = I_s(z_j(t); r − r_j(t)), where I_s(z_j(t); r) is the image of a single particle (dependent on its distance z_j(t) from the focal plane). The illumination and scattering are incoherent, so the separate bacterial images add at the focal plane to give an image

2.1

The spatial Fourier transform of this image is

2.2

The image of a particle changes slowly with z, and therefore with t in most practical situations, so we have dropped the time dependence of 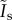. In the presence of a spatially uniform external flow or chemotactic stimulus in the xy-plane, the centre of mass of the particles R(t) will drift over time. In this case, equation (2.2) gains an additional phase applied to all terms in the sum

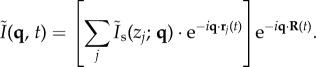2.3

By analysing the phase φ(q, t) of 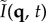as a function of q = (q_x, q_y) and t, we can obtain the displacement of the centre of mass as a function of time, in a process conceptually similar to that used in heterodyne light scattering to measure uniform particle velocities [7]. The phase increment δφ = φ(q, t + δt) − φ(q, t) is computed on a frame-by-frame basis, because, in such a short time, the number of particles in the frame is approximately constant. It is given by

2.4

The first term on the right-hand side of equation (2.4) is the equation of a plane passing through the origin, with a normal vector determined by the average population drift. The second term is a random residual phase, coming from the motion of the particles around the drift, which contributes to measurement uncertainties (see the electronic supplementary material, text). The frame rate of the imaging system must be high enough for the incremental phase shifts to be small, 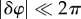. A standard phase unwrapping algorithm then enables the branch cut at φ = 2π to be avoided. For all times t, the cumulative phase shift Δφ(q, t) is fitted by a linear function of q, following equation (2.4) in a square region of the Fourier plane located symmetrically about the origin, of area q_max × q_max, yielding the measured R(t). The choice of q_max has only a small effect on the measurement, which is used to estimate uncertainties (see the electronic supplementary material, figure S1 and its text). The condition |δφ(±q_max/2)| < π sets the absolute maximum drift velocity measurable by the technique. In other words, for a frame rate f_r, we must have δR(t)/δt < 2π f_r/q_max. To measure higher chemotactic velocities, one must increase the frame rate, or decrease q_max. At our frame rates and q_max, we could measure chemotactic velocities up to approximately 250 µm s⁻¹—much higher than that expected from E. coli, and indeed, most bacterial swimming speeds.

3. Results

3.1. Validation of the analysis scheme

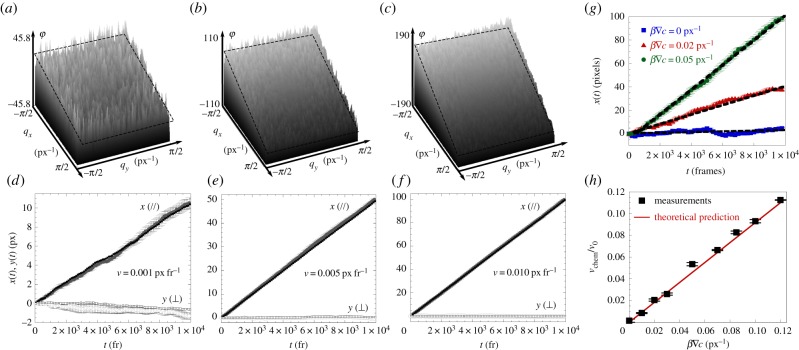
The algorithm was first tested on simulations of two systems: Brownian particles under uniform flow, and particles behaving like run and tumble chemotactic bacteria (see Material and methods). Calculated trajectories were used to make simulated movies, which were analysed using our algorithm. Figure 1a–f shows results for simulations of drifting Brownian particles with various external flow velocities. Figure 1a–c shows Δφ(q, t) of the Fourier components after 10⁴ frames, plotted as a function of q = (q_x, q_y). This phase is the superposition of a random variable and a plane, as predicted by equation (2.4). The plane fit enables the trajectory of the centre of mass R(t) to be computed (along with its uncertainty). This is displayed in figure 1d–f, along with the real drift of the centre of mass, straightforwardly calculated from the simulated particle trajectories. The extracted trajectories are in good agreement with the actual trajectory of the centre of mass, with a good resolution and high accuracy (see the electronic supplementary material, text and figure S1, for more details on uncertainty).

Figure 1.

Simulations demonstrating the ability of φDM to measure drifts. (a–c) The phases φ(q; t) for the last frame (t_rec = 10⁴ fr) in simulations of drifting and diffusing particles (D = 5 × 10 ⁻³ px² fr⁻¹), for input velocities as indicated in (d), (e) and (f), respectively. These phases are the superpositions of tilted planes (emphasized by the dotted planes) resulting from the drift, and a random component coming from Brownian motion. (d–f) The drift in the centre of mass, found from the raw simulation data (black) and from our image analysis method (grey). Its x and y components are shown by closed and open symbols, respectively. The error bars indicate uncertainties as described in the main text; broadly speaking, the accuracy is within a pixel after 10⁴ frames. (g) Measured trajectories of the centre of mass of the simulated bacteria for several chemoattraction strengths. The simulation parameters are chosen to resemble our experiments. A chemotactic velocity is measured from these trajectories (dotted lines). (h) This velocity is a linear function of the normalized gradient β∇c for small gradients and is in excellent agreement with the prediction for the class of models for chemotaxis we used (red line). Chemotactic velocities as low as 50 nm s⁻¹ (0.3% of the bacterial swimming speed) can be measured.

Next, we simulated chemotactic bacteria in a linear gradient of an attractant. The bacteria performed a classic run and tumble random walk [35], with a probability of initiating and terminating a tumble determined by the previously visited concentrations. The chemotactic velocity was predicted [31] in the linear response regime for the class of model we use (see Material and methods). The values of the velocities, diffusion coefficients, film lengths, apparent particle sizes and number density were chosen to match those encountered in our experiments on E. coli. Figure 1g shows the x-component of R(t) for simulated chemotactic bacterial populations in various gradient strengths. R(t) increases linearly with time, allowing us to extract a chemotactic velocity—this is shown in figure 1h. They are found to be in excellent agreement with the theoretical prediction (equation (A 3), Material and methods). We find the lowest measurable chemotactic velocity (our resolution limit) to be 3 × 10⁻³ times the swimming speed, or 0.05 µm s⁻¹ under our conditions.

3.2. Creating a chemical gradient

Experimentally, linear gradients of chemoeffector were created in the type of chemotaxis chamber presented in figure 2a,b, inspired by previous devices used to study chemotaxis [36] (see Material and methods). Two large reservoirs, with initial chemoeffector concentration c = c₀ and c = 0, are in contact through a small channel (length L, between 1.5 and 3 mm, and width w, between 300 and 900 µm). The gradient was quantified using fluorescein solution in water, because the diffusion coefficients of fluorescein and MeAsp are almost equal. The profile of fluorescein concentration is linear with position in the channel and stabilizes in around 3 h, as can be seen in figure 2b,c. The concentration gradient remains stable for several hours after formation, as the time for concentration equilibration across the whole sample cell is on the order of days. Using a series of representative sample chambers, we found that the value of the relative concentration gradient 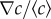in the middle of the channel is a function of its length (and marginally its width) and that the maximal concentration c₀ sets the background concentration (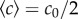—see the electronic supplementary material, figure S2, for details). These calibrations were used to estimate the gradient in each chemotaxis experiment. As fluorescein is slightly acidic, it may interfere with the proton motive force that allows bacteria to swim. Because of this, and because sample cells were not easily reloaded after being used, we could not use fluorescein to find the chemical gradient during each experiment.

Figure 2.

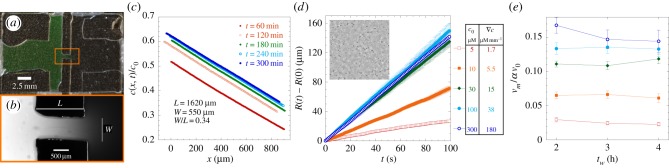
Experimental set-up and measurement of chemotactic fluxes. (a) Top view of the experimental sample chamber made of two reservoirs, containing attractant concentrations c = c₀ and c = 0 (or here, fluorescein, appearing green). The reservoirs are in contact through a narrow channel in the centre (box region). (b) The channel (length L, width w) at higher magnification, observed under fluorescence microscopy (×10), 1 h after making the chamber. The fluorescence intensity is proportional to chemical concentration. (c) The chemical (fluorescein) concentration profile in the middle of the channel is linear and stabilized in t_w = 2–3 h after filling the chamber. The concentration gradient ∇c and background concentration 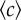were calibrated as a function of c₀, L and w (see the electronic supplementary material, figure S2 and text). (d) R(t) of E. coli bacteria at t_w = 3 h, under different conditions but where the relative gradient 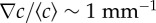is held approximately constant. The measured trajectories are linear functions of time. The inset shows part of a typical image from a movie sequence, with sides of length 180 µm. (e) Measured chemotactic velocity as a function of t_w for the same experiments as (d). The chemotactic velocity is nearly constant as a function of t_w and increases as a function of 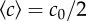. The chemotactic velocities are normalized by the average swimming speed of the bacteria v₀ and the fraction of swimmers α, as described in the main text. The key is common to (d,e).

In the chemotaxis experiments, the first reservoir and channel were loaded with E. coli suspended in motility buffer with glucose. A suspension with the same bacterial density (OD₆₀₀ = 0.4) and glucose concentration (1.1 wt%), but with a concentration c₀ (spanning from 1 µM to 2 mM) of α-methyl-dl-aspartic acid (MeAsp) was then loaded in the second reservoir. After the sample was loaded and sealed, several phenomena occurred. Oxygen was depleted fairly rapidly (in less than an hour), and the bacteria switched to using glucose for anaerobic respiration. A measurable bacterial flux occurred in the channel in response to the chemoattractant gradient. Movies of 100 s duration were recorded at delays (t_w) of between 2 and 5 h after sample loading, in the middle of the channel, halfway through the height of the chamber. These were analysed using both DDM and φDM. A typical frame from a movie can be seen in the inset of figure 2d, where bacteria appear as fairly dilute approximately 1 px dots.

3.3. Measuring bacterial fluxes

Figure 2d shows the displacement of the centre of mass in the direction of the chemical gradient as a function of time, measured from films recorded t_w = 3 h after the beginning of the experiment, for various background concentrations and similar relative gradients. The measured trajectory of the centre of mass is linear with time during the film. A velocity v_m is obtained from a straight-line fit to these data, which is plotted as a function of t_w for several MeAsp gradients in figure 2d. In fact, v_m decreases with t_w by around 20% over the course of a 4-h experiment; the decrease is mostly due to a decrease in the motile fraction of cells α over this period (see the electronic supplementary material, text, and figures S3 and S4), so the vertical axis in figure 2e has been scaled accordingly. Other, more marginal causes for a decrease in v_m over time are explored and modelled in the electronic supplementary material (text, and figures S5 and S6). The chemotactic velocity is also normalized by the average bacterial swimming speed v₀ to account for sample-to-sample variation, to obtain a chemotactic bias v_m/αv₀. The chemotactic bias is a convenient way of describing the bias in a cell's random walk of runs and tumbles. Its value lies in the range 0–1 where a value of zero indicates an unbiased random walk, and v_m/αv₀ = 1 indicates that all cells are swimming directly up the gradient. As v_m/αv₀ is nearly independent of t_w, these data are used for further analysis and comparison to a mean-field model.

3.4. Mapping the mean-field chemotactic response across regimes

Figure 3a displays the chemotactic bias v_m/αv₀ as a function of the MeAsp gradient ∇c. Two sets of data are presented in figure 3a: the red squares correspond to experiments carried out in shorter (approx. 2 mm) channels, hence with larger relative gradients 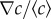; the blue diamonds correspond to those in longer (approx. 3 mm) channels with smaller relative gradients. The background concentrations lay in the range 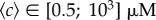, and increase in concert with ∇c. For both longer and shorter channels, the chemotactic bias increases with the chemical gradient up to saturation. Before saturation, when the background concentration is low, both datasets are superposed, indicating that the response is a function of the absolute gradient ∇c. The value of v_m/αv₀ at saturation differs from one set of data to the other (v_m/αv₀ ≈ 0.11 for the longer channels and ≈0.16 for shorter channels), suggesting that the response is now a function of the relative gradient. The transition occurs for a background concentration between 15 and 50 µM. The data from the plateaux (actually corresponding to 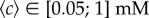, for both datasets) are replotted in figure 3b as a function of the relative gradient. The chemotactic bias is now a linear function of the relative gradient, shown by the dashed line of best fit (constrained to pass through the origin). This behaviour is interpreted as a change from a low background concentration response regime, where the bacteria respond to absolute changes in concentration to a high-concentration response regime, where they respond to relative change in concentration (‘logarithmic sensing’), as previously observed [26].

Figure 3.

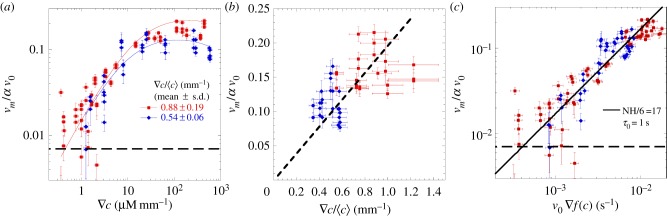
Mapping the chemotactic response. (a) Chemotactic bias as a function of the absolute gradient of MeAsp (∇c), for two channel lengths (and hence two different relative gradients 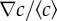). The red squares indicate shorter channels (and higher 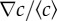) and the blue diamonds represent longer channels (lower 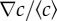). The chemotactic bias first increases as a function of the absolute gradient, the rate of increase being the same for both datasets. For larger gradients, it reaches a plateau, with different plateau values (0.11 ± 0.02 (s.d.) and 0.16 ± 0.03 (s.d.)) for the two relative gradients. This marks the transition to logarithmic sensing. The lines correspond to equation (3.1). (b) The chemotactic bias as a function of the relative gradient in the plateau regime (i.e. for the subset of concentrations 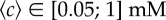). The bias is linear in the relative gradient (dotted line, slope 0.22 ± 0.04 (s.d.) mm). (c) Chemotactic bias as a function of the normalized gradient of MeAsp, as described by equation (3.1), for all our data. The data collapse on to a line, predicted by the parameter-free model (see text for details). In (a,c), the horizontal dashed lines represent the method's sensitivity, agreeing with the amplitude of the drift in control experiments without attractant (see also the electronic supplementary material, figure S7, for details).

Semi-empirical mean-field models have been developed [22,27,37] to explain the large dynamic range of the chemotaxis system. The chemoreceptors cluster in groups of dimers, containing N Tar receptor dimers, which form active or inactive complexes, responding according to an allosteric two-state model to attractant binding [38]. Receptor methylation levels provide a feedback that adapts the chemoresponse. The output of the chemical sensing system is a change in the tumbling rate of the bacterium. The motor response function is a steep sigmoidal curve, described by a Hill response function with Hill coefficient H = 10 [39]. The model assumes perfect adaptation and ignores any motor adaptation mechanism [25]. A prediction for the chemotactic bias can be derived (see [40] and the electronic supplementary material, text) that reduces, in our range of chemoattractant concentration, to

3.1

Equation (3.1) contains several parameters characterizing the chemotactic pathway. The number of Tar receptor dimers in a cluster is known to be dependent on bacterial growth phase. We estimate N = 10 for our growth conditions based on a previous study of this phenomenon [41] (see the electronic supplementary material, text). We take the other parameters in equation (3.1) from [27]: τ₀ is the average run time in the absence of a gradient (approx. 1 s for wt E. coli), and K (K’) is the binding affinity of the attractant to the inactive (active) receptors (K = 18 μM and K’ = 3 mM for MeAsp). We define f(c) = ln[(K + c)/(K’ + c)], the average free energy of binding of MeAsp to a single receptor dimer. We plot the chemotactic bias as a function of v₀∇f(c) in figure 3c. Our data are found to be in excellent quantitative agreement with the model (black line), with no free parameters, providing evidence that the mean-field model contains all the important features of the chemotactic signalling pathway.

4. Discussion

The method presented above (φDM) measures the response of bacteria to a chemical stimulus, averaging over thousands of cells in a single measurement, and with time resolution set by the imaging equipment (10 ms in our case). Unlike previous methods for measuring chemotaxis on a microscopic scale, we measure chemotactic velocity directly, without having to infer dynamic quantities from steady-state distributions of cells. This technique provides an unambiguous method for measuring the collective response of bacteria in a high-throughput fashion and is complementary to standard particle tracking [1] and particle imaging velocimetry (PIV) methods [42]. We have demonstrated the validity of this method through simulations and experiments, showing an effective resolution limit of 3 × 10⁻³ v₀, where v₀ is the average bacterial swimming speed. This is almost an order of magnitude better than particle tracking in optimum conditions (see the electronic supplementary material), and fifty times better than PIV [42]. Moreover, thanks to the simplicity of its implementation, the technique is on the order of ten to a hundred times faster in providing the chemotactic velocity than particle tracking algorithms, which are inefficient when the field of view contains thousands of bacteria. The method is applicable to samples of bacteria at high density (as long as distinguishable features remain), contrary to particle tracking, which does not handle particle collisions well, extending the range of experimental conditions under which chemotactic responses are measurable. The simulated data are designed to replicate experimental data as closely as possible, but contain no explicit description of the image formation physics. This reinforces the idea that φDM is independent of the illumination method (e.g. bright field, phase contrast, differential interference contrast), subject to the restrictions outlined in the theory section.

Experimentally, we tested the response of a bacterial population to a gradient of the non-metabolizable attractant MeAsp and compared the results to a theoretical prediction [27,40], finding excellent agreement with previous work. This coarse-grained chemotaxis model appears to include all of the necessary features to replicate real-world behaviour, at least at our values of the chemical gradient and background concentration. We map the response of the bacterial cells over the transition from linear (absolute) to logarithmic sensing regimes, corresponding to the onset of significant receptor methylation. For larger gradients, second-order effects may become important: the delays due to CheY phosphorylation and diffusion times, bacterial rotational diffusion, directional persistence [43,44] and tuning of reorientation angles [19] or of the motor response [45]. These are limitations of the theoretical model however, and not our technique. Our method could be fruitfully employed to test more refined predictions in the future.

In conclusion, we have developed an image analysis method, φDM, enabling us to measure fluxes and drifts in a sample in a fast and accurate way. This method could be adapted to gain spatial resolution by subdividing video frames into smaller regions. The accuracy within each region would be consequently reduced, in line with the arguments presented in theory section regarding the size of the image, though preliminary tests suggest that we can achieve accuracies similar to PIV, with a smaller computation time. This aspect makes our technique a good complement to PIV and particle tracking in studying population dynamics. Moreover, the relative simplicity of the algorithm means that it could be employed to measure chemotactic drift velocities in real time.

Appendix A. Material and methods

A.1. Cell growth

Escherichia coli bacteria, strain HCB1 (gift of H. C. Berg), from a frozen stock were streaked on a 2% Luria broth (LB) agar plate and grown overnight at 30°C. A single colony was extracted and grown for 18 h to saturation at 30°C in liquid LB medium (10 g l⁻¹ of Difco Bacto Tryptone (Sigma Aldrich), 5 g l⁻¹ of yeast extract and 5 g l⁻¹ of NaCl in DI water). One hundred microlitres of the saturated culture was then mixed into 10 ml of TB medium (10 g l⁻¹ of Difco Bacto Tryptone (Sigma Aldrich) and 5 g l⁻¹ of NaCl in DI water) and grown for 4 h 30 min to an optical density of OD₆₀₀ = 0.45 ± 0.1 (s.d.), and then resuspended in motility buffer (10⁻⁴ M EDTA dipotassium salt, 10⁻² M KPO₄, pH 7, 6.69 × 10⁻² M NaCl). Prior to the experiment, glucose was added to the bacterial suspension to a final concentration of 1.1 wt% (6 × 10⁻² M).

A.2. Chamber fabrication

Our method measures a bacterial flux, meaning that microfluidic devices previously used to generate a steady-state distribution of bacterial density [46] are not appropriate sample holders. The chemotaxis chambers were hand-made using diamond cut glass microscope coverslips, glued on a glass slide using UV-curing glue. They consisted of two reservoirs (0.7 ± 0.1 cm² × 135 ± 5 μm) linked via a small channel. The channel lengths L lay in the range 1.2–2.5 mm, and widths w in the range 300–900 µm. The resulting channel aspect ratios (w/L) ranged from 0.15 to 0.5.

A.3. Sample preparation

Vials were prepared by mixing the bacterial suspension, motility buffer and a 10⁻³ or 10⁻² M solution of MeAsp, so that all vials had the same bacterial concentration (corresponding to OD₆₀₀ = 0.4) and different concentrations of methylaspartate (c). The chambers were loaded by filling a first reservoir and the middle channel with a c = 0 suspension, and then loading the second reservoir with a suspension of concentration c₀. The instant of contact between the two suspensions marked t_w = 0. After filling the chamber, its openings were sealed with petroleum jelly.

A.4. Data acquisition

The sample was kept at room temperature (20 ± 1°C) and the bacteria were observed with a Nikon microscope equipped with a 10× objective, under phase contrast illumination. The movement of the bacteria was recorded in the middle of the channel at regular intervals (usually every hour, for 4–6 h), using a Mikrotron MC-1362 camera running at 100 Hz for 100 s, with a 512 × 512 px² (722 × 722 μm²) field of view. The focal plane was chosen halfway through the 135 ± 5 μm depth of the sample. Background images were computed by time averaging the movie and subtracted from each frame.

A.5. Chamber calibration using fluorescein

As the diffusion coefficients of fluorescein and MeAsp are almost equal (5 × 10 ^{− 10} m² s⁻¹), fluorescein was used to model the diffusive behaviour of MeAsp. One sample chamber reservoir was loaded with DI water, and the other with a 10⁻⁴ M aqueous solution of fluorescein. The chamber was observed with a 10× objective under green fluorescence illumination. Images were recorded using an Andor Clara cooled CCD camera. The fluorescein concentration was chosen to avoid saturation effects, so that the fluorescent emission was proportional to the concentration. Reference images were taken in the 10⁻⁴ M fluorescein reservoir, 4 mm away from the channel. Images of the fluorescent intensity were recorded in the centre channel, every hour for 5 h. The normalized intensity profile was then computed by dividing the image by the reference. The calibration was repeated for 17 channels with various lengths and widths. The gradient was found to depend primarily on the length L of the channel, and also weakly on the channel's aspect ratio w/L (see the electronic supplementary material, text and figure S2, for details).

A.6. Simulation of bacteria

Simulations of non-interacting particles moving in three dimensions in a box of size L with periodic boundary conditions were performed, using Java code written in-house, running under ImageJ (v. 4.6r). The position of the particles was incremented at each time step δt. After calculating the trajectories, a film was generated. The bacteria were modelled as Gaussian dots of half-width 1 px, to match the images of planktonic E. coli observed with a 10× objective. Their height was encoded by modulating the maximum intensity of the dot with height, using a quadratic intensity profile which is maximum at the centre of the simulation box and extinguishes 128 px away from it. We first simulated drifting Brownian particles. The increment in position at each time step was given by 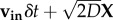, where v_in is the input drift velocity and X is a vector of Gaussian-distributed independent pseudo-random numbers with unit variance. Chemotactic bacteria with run and tumble dynamics were then simulated. A small translational Brownian motion (diffusion coefficient D) was added to the motility. Each bacterium ran at a fixed speed chosen from a Gaussian distribution of mean v₀ and standard deviation σ₀. The direction of the run was chosen randomly from a uniform distribution during the previous tumble (or at the beginning of the simulation). At each time step during a run, the probability of tumbling was given by exp(−δt/τ_RT). The instantaneous run to tumble rate was biased from its default value 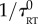when encountering a chemoeffector according to 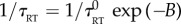(similarly, the tumble to run rate is 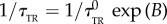). The tumble biasing function B is given by

A1

with β the (constant) strength of the chemoattractant, which has the unit of an inverse concentration, c the chemoattractant concentration at the previous positions of the bacterium and K(u) a memory function, first measured in [47]. We used a simple albeit fairly accurate expression for this function, introduced in [48]

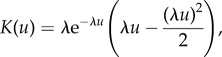A2

where λ is the unique inverse memory time (which encodes both the response and adaptation timescales). In the results we present, the parameters were chosen to be close to expected values for chemotactic bacteria observed with our experimental set-up: v₀ = 0.2 px fr⁻¹, σ₀ = 0.05 px fr⁻¹, 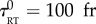, , 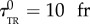λ = 0.067 fr⁻¹, D = 1.25 10⁻³ px² fr⁻¹, N = 10³ bacteria. The linear response theory of this model of bacteria is known for a generic K(u) [31]. In our case, the predicted chemotactic velocity for small gradients is

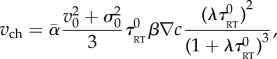A3

where 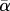is the volume fraction of cells actually swimming at a given time 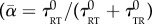, if there are no non-motile cells).

Funding statement

The authors would like to acknowledge financial support from the Rowland Institute at Harvard.