Onset of virus systemic infection in plants is determined by speed of cell-to-cell movement and number of primary infection foci

Abstract

The cornerstone of today's plant virology consists of deciphering the molecular and mechanistic basis of host–pathogen interactions. Among these interactions, the onset of systemic infection is a fundamental variable in studying both within- and between-host infection dynamics, with implications in epidemiology. Here, we developed a mechanistic model using probabilistic and spatio-temporal concepts to explain dynamic signatures of virus systemic infection. The model dealt with the inherent characteristic of plant viruses to use two different and sequential stages for their within-host propagation: cell-to-cell movement from the initial infected cell and systemic spread by reaching the vascular system. We identified the speed of cell-to-cell movement and the number of primary infection foci in the inoculated leaf as the key factors governing this dynamic process. Our results allowed us to quantitatively understand the timing of the onset of systemic infection, describing this global process as a consequence of local spread of viral populations. Finally, we considered the significance of our predictions for the evolution of plant RNA viruses.

1. Introduction

Virus colonization of a multicellular host is a highly complex process that involves interactions within the infecting viral population as well as interactions between the pathogen and the host organism [1]. Unravelling and quantitatively describing these interactions are essential for understanding the infection process in any depth and, moreover, for successfully predicting disease dynamics and to a more efficient design of antiviral interventions. Biochemistry has been harnessed to elucidate mechanisms underlying infection at the cellular and molecular levels, rendering spectacular results and powerful applications [2–4]. Similarly, the application of computational methods to study spread at the population level has led to striking successes in both understanding of infectious diseases and mitigating their impact [5–7]. However, infection dynamics at the within-host level are, in many ways, poorly understood, in particular with respect to providing quantitative descriptions of how infection progresses through time and space. Barriers to scientific progress include the difficulty—using non-destructive methods and in real time of infection—to target tissues where the virus replicates, and the complexity of the host immune system.

Plant RNA viruses are highly suitable model systems for studying within-host infection dynamics, and RNA viruses the main targets of replication—the mesophyll cells—are located in the largely planar leaves. This allows infection to be followed using a wide array of non-destructive approaches, including the expression of marker proteins [8–10]. Moreover, leaves can be easily and cleanly removed, effectively allowing for the removal of host organs at any point during infection and for their further study [11]. Second, plant immune responses to RNA viruses are mainly composed of the hypersensitive response, leading to the formation of visibly discernible local lesions [12,13], RNA interference, where the presence of double-stranded RNA induces the local and systemic destruction of viral RNA [2,14], hormone-mediated (e.g. salicylic acid) defence pathways [15] and, as recently shown, pattern-triggered immunity [16]. This effective set of host immune responses have contributed to a rich tradition of quantitative research on infection dynamics using plant viruses [9,13,17–19]. Moreover, this array of plant immune mechanisms probably contributes to the relatively low between-host variation typically found in experimental settings [20]. Finally, although plants are invaluable model systems, they are also of great agricultural importance, as are the many diseases thwarting crop production.

Here, we consider the dynamics of a critical step during the plant RNA virus infection cycle: the initiation of systemic infection [11]. Plant viruses expand within the host by (i) cell-to-cell movement, the local spread of infection by virions or ribonuclear complexes, and by (ii) systemic movement, whereby the virus accesses the vascular tissue and is transported within and between leaves [8]. Plant viruses are usually phloem transported, meaning that they will spread towards tissues that import photo-assimilates, typically including apical tissues. Therefore, upon the establishment of a primary infection focus—a cell infected following inoculation by a viruliferous vector or mechanical means—a virus can only colonize a small region of the inoculated leaf by cell-to-cell movement [20]. The probability of between-host transmission will be highest if a virus infects the majority of host tissues, including rapidly growing apical tissues. To initiate such a systemic infection of the plant, the virus needs to (i) reach the host vasculature, (ii) be loaded into the phloem to then be transported out of the inoculated leaf and (iii) unload elsewhere in the host [1,21].

Here, we attempt (i) to better understand the timing of the onset of systemic infection, (ii) to identify what are the key factors governing this dynamic process and finally, (iii) to consider its significance for the evolution of plant RNA viruses. We develop a simple theory that is able to explain differences in dynamic signatures of viral systemic infection, based on the speed of cell-to-cell movement and number of primary infection foci in the inoculated leaf (figure 1). Moreover, we confront these models with experimental data in order to test their validity. Our work is of relevance as it contributes to tackle mathematically questions about the relationship between local and global virus movement, the determinants of the variance of infected individual plants in a population and the interaction between virus genetic factors (e.g. speed of cell-to-cell movement) and environmental conditions (e.g. dose of the inoculum) to get systemic infection.

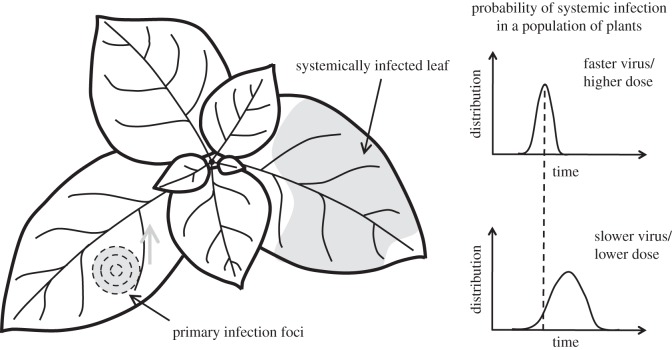
Figure 1.

Scheme of the dynamics of systemic infection. A primary infection focus in the leaf grows, by planar cell-to-cell virus movement, until it reaches the host vascular system for systemic spread. Rapid or slow events of systemic infection in a population of plants can occur depending on the nature of the interaction between the virus and the host organism. We show two different time-dependent distributions of systemic infection. Faster or slower viruses refer to cell-to-cell movement rate, and higher or lower dose to number of virus particles in the inoculum.

2. Results

2.1. Model definition

Primary infection foci tend to be quite circular in form and of approximately the same size [8,9,20]. To model the process of radial expansion of primary infection foci, we introduced the effective diffusion coefficient of the local infection (D). Although viral cell-to-cell movement is complex and there may be stochastic effects, for our model we considered isotropic diffusion. Thus, we could write

2.1

where A(t) is the circular area covered by the virus at a given time t—usually measured in hours post-inoculation (hpi). Typical values of D are 0.01–0.03 mm² h⁻¹ [22,23]. This reaction–diffusion system, where viral particles replicate within cells and then move to neighbour cells to proliferate, constitutes the local infection dynamics—the first step for long-distance infection—before the virus reaches the host vasculature and is loaded into the phloem. We then assumed that the area required to reach the vascular system follows a normal distribution, with mean μ and standard deviation σ. This is justified by the regular spacing observed between veins and the way the particular developmental programmes operate [24], which could reflect a given evolutionary contingency linking leaf shape and vascular patterning. Of note, μ and σ are, at least in theory, host-dependent parameters that vary with the density of the vascular system in the leaf, being independent of the virus.

The time to reach systemic infection needs also to account, among other factors, for latency periods (T₀)—e.g. time for replication in the first infected cell—and vascular movements of the virus (T₁). Following the seminal work by Samuel [25], there is slow cell-to-cell movement of the virus in the infection foci, combined with rapid dissemination throughout the plant via the vascular system. According to recent experimental data, the time required to complete the infection cycle of Tobacco mosaic virus in the primary inoculated cell of Nicotiana tabacum is T₀ = 18–20 hpi [26]. This is in tune with model predictions showing latency periods of about 1 day [17]. In addition, virions move through the veins and midrib at rates of 20–50 mm h⁻¹ [22], which gives 2–5 h to cover a space of 100 mm (typical rough length to reach the stem from the primary infection foci). T₁ also accounts for systemic movements through further vascular tissues to infect the whole plant, a process that may take additional hours, depending on the host molecular infrastructure [1], and that we did not model in this work. For simplicity, we joined together these terms in a single parameter (T = T₀ + T₁), which may depend on the whole plant pathosystem. An upper bound of T can be obtained as the minimal time measured when systemic infection appears—e.g. about 40 hpi for Tobacco etch virus (TEV) infecting N. tabacum [11].

Therefore, by integrating equation (2.1), we had

2.2

where t − T represents the time for which the virus moves locally in the primary infection foci, being t the absolute time. Because, on average, systemic infection is produced when the infected area in the inoculated leaf is μ, we obtained

2.3

where 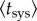is the average time of systemic infection—the time at which 50% of the individuals in the population present systemic infection. Moreover, simply by squaring and averaging equation (2.2), we obtained

2.4

where Δt_sys is the standard deviation of systemic infection time.

To calculate the probability of systemic infection at a given time, P_sys(t), as A(t) is assumed Normally distributed, we followed the corresponding cumulative distribution function (where erf is the error function) to derive

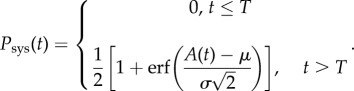2.5

This expression can be rewritten in terms of time, instead of area, by using equations (2.2)–(2.4). In particular, we derived the following equality:

2.6

which shows the equivalence between standardized areas and times.

Importantly, this model can explain differences in dynamic signatures of systemic infection between viruses. Indeed, the speed of cell-to-cell movement (D) appears as a fundamental parameter. For instance, if we denote two viruses infecting a common host organism as A and B, and given that μ and σ are parameters that only depend on the host organism, it turns out

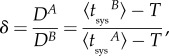2.7

having defined δ as the ratio of speed of cell-to-cell movement between viruses, and

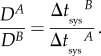2.8

Therefore, we can predict relative changes in the average time of systemic infection and the associated variance—magnitudes that quantify the infection at the global level—according to differences in the speed of cell-to-cell movement, which describes infection dynamics at the local level.

In addition, it has been argued that the number of primary infection foci in the inoculated leaf plays an important role in determining when the plant will become systemically infected [11]. We therefore generalized this theoretical framework by also considering the effect of the number of primary infection foci in the inoculated leaf (N). We derived an analytical expression to calculate the effective probability of systemic infection for N different viral populations spreading at the same time, P_sys(t)_N. Lafforgue et al. [11] showed that systemic infection by multiple viral populations does not depend on their interactions, thus it is justified to assume that P_sys(t)_N = 1 − (1 − P_sys(t))^N, and therefore

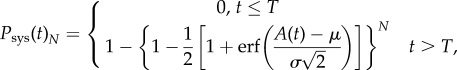2.9

where for N = 1, equations (2.5) and (2.9) are the same. According to equation (2.5), 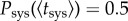, by definition. However, this does not hold for the effective probability, 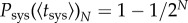. Indeed, the effective average time of systemic infection, 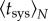, decreases with N, 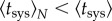, as systemic infection is produced once the vascular system is invaded by the first viral population. By imposing 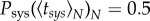, the effective average time of systemic infection was

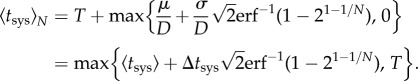2.10

The term erf⁻¹ (1−2^1−(1/N)) is negative, describing the decrease with N. Moreover, by imposing 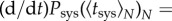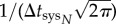, the effective standard deviation of systemic infection time was given by

2.11

where this expression is only valid for 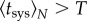. This value also decreases with N.

2.2. Experimental validation

To test this theory, we considered an experimental system with the plant pathogen Turnip mosaic virus (TuMV) and the host plant Nicotiana benthamiana (see [23]). To perform infections, we used a TuMV clone tagged with the enhanced green fluorescent protein (eGFP) [27] and a large population of four-week-old N. benthamiana plants. Five micrograms of infectious TuMV plasmid (GenBank no. AF530055.2) were mixed with 5 μl of inoculation buffer (carborundum 100 mg ml⁻¹, 50 mM potassium phosphate, pH 8) on one leaf per plant and gently rubbed. Inoculated plants were maintained in a growth chamber (16 h light at 25°C, 8 h dark at 22°C). In order to consider two pathogens with biologically relevant differences, we used viruses carrying two alleles of the Pretty Interesting Potyviridae ORF (pipo) cistron of different lengths [23]. PIPO is expressed as a C-terminal fusion to the P3 protein, referred to as P3N-PIPO. One viral strain carries an allele that is 70 amino acids long (pipo⁷⁰), whereas the second strain has a 61 amino acids long allele (pipo⁶¹) [23]. Therefore, as P3N-PIPO is involved in viral movement [28], we expected differences in the speed of cell-to-cell and systemic movements. To obtain empirical estimates of D for each viral strain, we analysed data for the formation of primary infection foci. Plants were mechanically inoculated with virions, and the inoculated leaf was examined at 48, 72 and 96 hpi. In figure 2a, we represent A(t) for these two viral strains. Using equation (2.1), we estimated 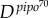= 0.0527 mm² h⁻¹ and 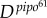= 0.0099 mm² h⁻¹. This gave a ratio 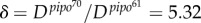, and according to our model we predicte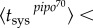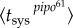d and . We calculated P_sys(t) as the fraction of systemically infected plants at a given time, examining plants at 24, 40, 48, 72 and 96 hpi. In this plant pathosystem, the number of primary infection foci was very limited—perhaps because of a low dose for inoculation—so, for simplicity, we considered N = 1. In fact, this is more a reformulation than a simplification (see equations (2.10) and (2.11)). In figure 2b, we represent P_sys(t) for the two viral strains, showing significantly different dynamic signatures. We considered T ≈ 40 hpi. By nonlinear regression of equation (2.5) to the data (figure 2b), we inferred firstly (with 95% CI [46.96, 47.67]) and 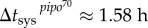(with 95% CI [0.76, 2.40]) (R² = 0.996), and secondly 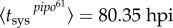(with 95% CI [73.01, 87.70]) and 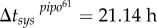(with 95% CI [10.71, 31.57]) (R² = 0.982). The fit of the empirical data to a binary logistic regression model also shows a significant heterogeneity among the two dynamic signatures of systemic infection (Pearson goodness-of-fit test: χ² = 13.606, 7 d.f., p = 0.059), with the average time of systemic infection being significantly larger for pipo⁶¹. This supports the predicted relationship between systemic infection times for these two viruses. We obtained a good approximation of the ratio 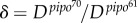with equation (2.7), δ = 5.51, although with equation (2.8) this ratio was higher, δ = 13.38—perhaps because of a fitting with few time points. Finally, using equations (2.3) and (2.4), we calculated μ ≈ 0.4 mm² and σ ≈ 0.2 mm².

Figure 2.

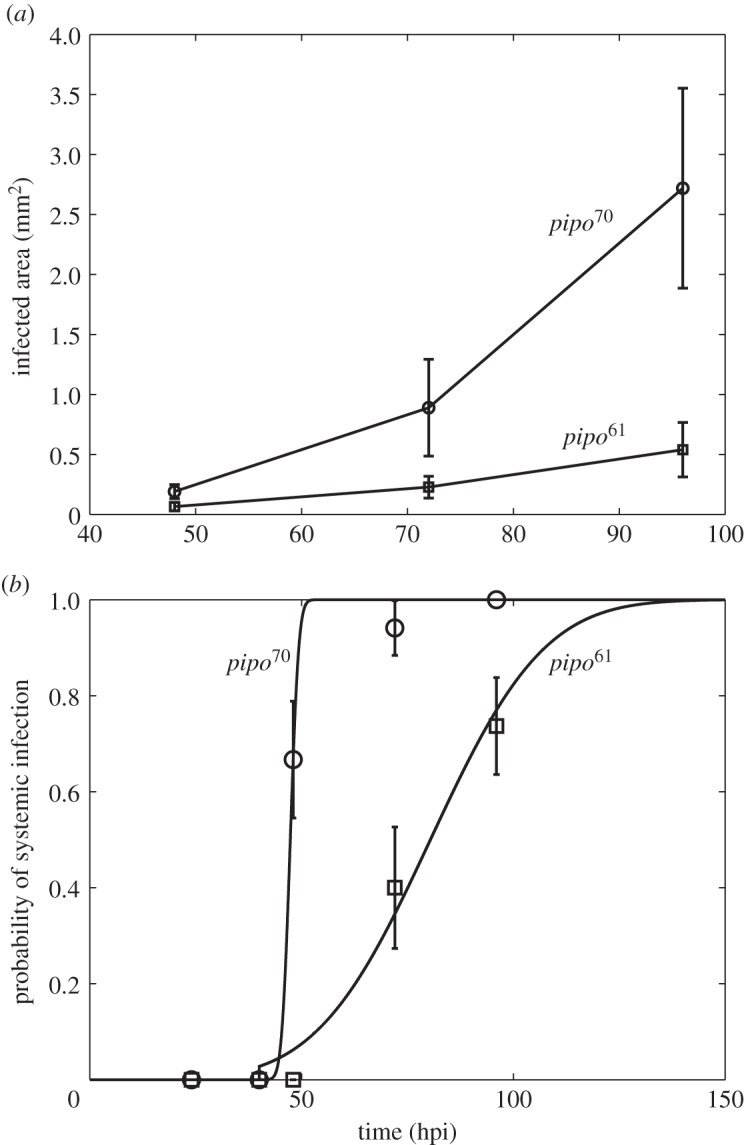
Experimental results of two strains of TuMV with different pipo alleles (pipo⁶¹ and pipo⁷⁰). (a) Dynamics of expansion of infection foci. Error bars correspond to standard deviations. We estimated D = 0.0527 mm² h⁻¹ for pipo⁷⁰ and D = 0.0099 mm² h⁻¹ for pipo⁶¹. (b) Dynamics of systemic infection (circles and squares). Error bars correspond to standard deviations calculated according to a binomial distribution. Solid lines correspond to model predictions (equation (2.5)).

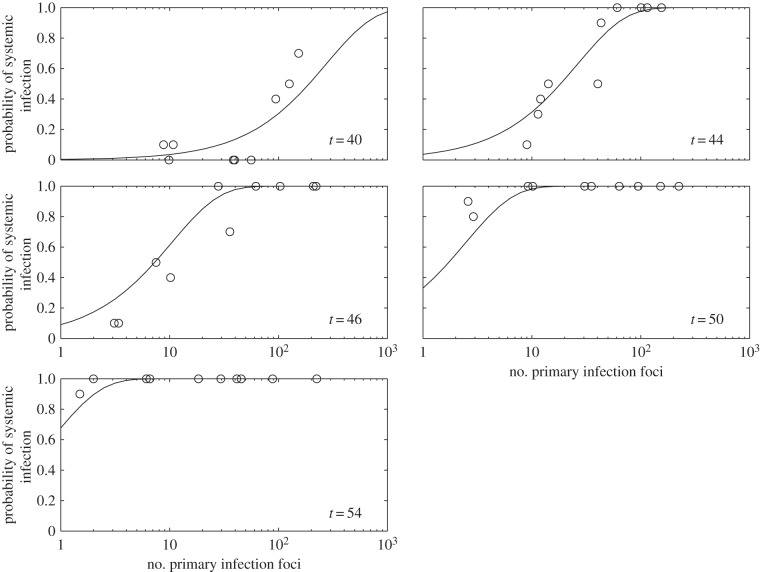
To better study the effect of the number of primary infection foci, we considered further experimental data on systemic infection (reported in [11]). The experimental system consisted of TEV, another potyvirus closely related to TuMV, and N. tabacum as the host plant. To perform infections, a TEV clone tagged with eGFP [27] and a population of 10 four-week-old N. tabacum plants was used for each dose, with variation in dose resulting in different numbers of primary infection foci. Plants were inoculated by abrasion of the third true leaf with 15 μl of the corresponding TEV dose and 5 μl of inoculation buffer. Inoculated plants were maintained in a BSL2 greenhouse at 25°C and 16 h light. In this case, D was fixed (one virus), and the distribution of foci ranged from N = 2–224. Plants were examined at 40, 44, 46, 50 and 54 hpi. By nonlinear regression of equation (2.9) to data shown in figure 3, we obtained 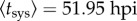(with 95% CI [50.93, 52.96]) and Δt_sys = 4.45 h (with 95% CI [3.95, 4.95]) (R² = 0.917) (figure 3). Once again, these estimates are in good agreement with those obtained by fitting a binary logistic model to the data (Pearson goodness-of-fit test: χ² = 86.084, 44 d.f., p < 0.001). As the model—equation (2.9)—fits the data well, it is safe to assume that there is no evidence for interactions between primary infection foci in terms of the onset of systemic infection. Moreover, using equation (2.10), we predicted for N = 100, as illustrative case, an effective average time of systemic infection of 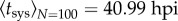, which agrees with the experimental data as P_sys(t = 40)_{N =100} ≈ 0.5 in this plant pathosystem.

Figure 3.

Experimental results of systemic infection at different times (hpi) as a function of the number of primary infection foci (N). Solid lines correspond to model predictions. Equation (2.9), in combination with equation (2.6), was fitted to 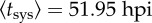and Δt_sys = 4.45 h (nonlinear regression).

3. Discussion

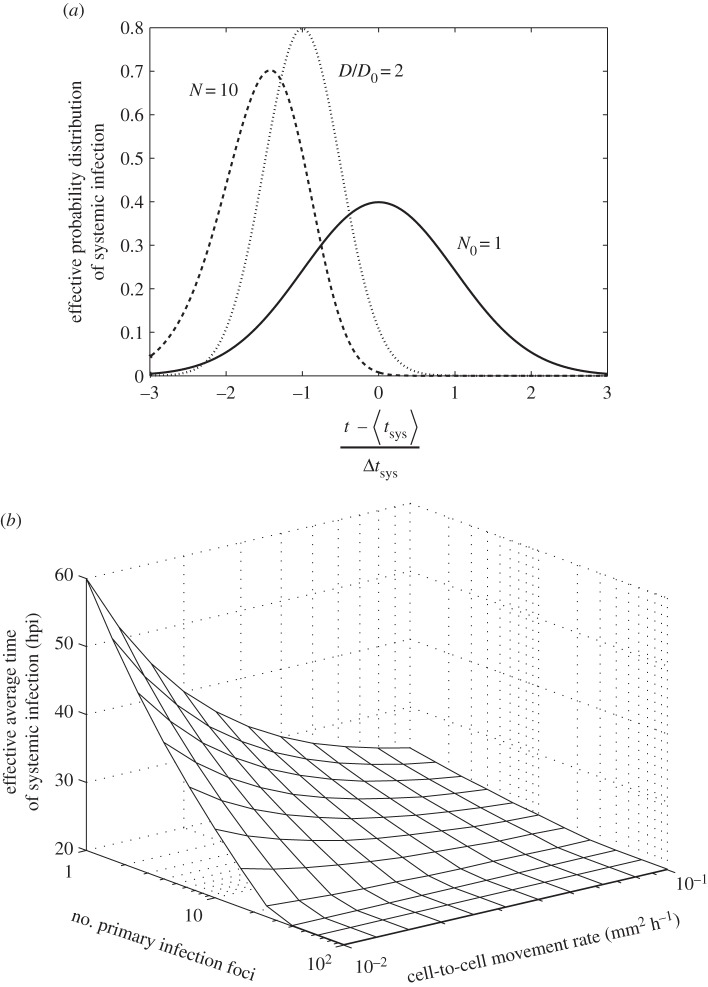
The model presented here is useful because it helps to distil the two key processes governing the timing of the onset of systemic infection of plant viruses, namely, the cell-to-cell movement rate in relation to the density of host vasculature (D) and the number of primary infection foci in the inoculated leaf (N). As the movement rate and number of foci increase, the onset of systemic infection will tend to be quicker and its variability will be reduced. However, the model also predicts that for large numbers of primary infection foci, the onset of systemic infection is limited by the latency period (T) rather than the cell-to-cell movement rate (figure 4). These model predictions have therefore implications for the evolution of plant viruses.

Figure 4.

Model predictions with the number of primary infection foci (N) and the cell-to-cell movement rate estimated as the effective diffusion coefficient (D) as variables. (a) Calculations with equation (2.9) of the effective probability distribution of systemic infection ((d/dt)P_sys(t)_N) for a reference system (solid line, variables with subscript 0), and when N = 10 (dashed line) and when D is duplicated (dotted line). (b) Model prediction of the effective average time of systemic infection (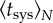) as a function of N and D (equation (2.10)). For this plot, we used μ = 0.40 mm², σ = 0.20 mm² and T = 20 hpi.

Whereas some plant viruses can be transmitted vertically, horizontal transmission depends on vectors [29] or contact between plants [30]. The intensity of between-host transmission will probably vary greatly in the field, strongly depending on the density of both plants and vectors. Plant viruses typically exclude superinfection by conspecific or closely related viruses [31,32], a phenomenon that even extends to simultaneous coinoculation [9]. Therefore, a virus that causes full-blown systemic infection is likely to exclude its competitors, making it plausible that the onset of systemic infection is an important fitness component under some conditions. Therefore, when high levels of transmission result in a large number of primary infection foci, our model suggests the key characteristic that will be under selection is latency (i.e. viruses with a faster replication in the first infected cell will be selected). The rate of cell-to-cell spread may then still be important for colonization of systemically infected tissues, but it likely will not affect the onset of systemic infection (figure 4). On the other hand, single primary infection focus typically results in low levels of transmission and systemic infections [9]. In this situation, the onset of systemic infection may not be an important fitness component either, because low infections levels will limit co-infection and therefore minimize the importance of within-host competition. Consequently, our results suggest that intraspecific competition will impose selection for rapid cell-to-cell movement only for a limited range of primary infection foci values (1 < N < 30). Moreover, the need to overcome host immune responses could, by itself, still drive selection for rapid cell-to-cell movement. Indeed, in some cases, the host plant can restrict the virus spread in the inoculated leaf (hypersensitive response), thus rapid cell-to-cell movement would help to surmount this barrier [33].

Funding statement

This work was supported by the grant no. BFU2012-30805 from Spain Ministerio de Economía y Competitividad (MINECO) to S.F.E. G.R. was supported by an EMBO long-term fellowship co-funded by Marie Curie actions (ALTF-1177-2011) and an AXA post-doctoral fellowship, and M.P.Z. by a Juan de la Cierva post-doctoral contract (JCI-2011-10379) from MINECO.