Computational modelling of epidermal stratification highlights the importance of asymmetric cell division for predictable and robust layer formation

Abstract

Skin is a complex organ tasked with, among other functions, protecting the body from the outside world. Its outermost protective layer, the epidermis, is comprised of multiple cell layers that are derived from a single-layered ectoderm during development. Using a new stochastic, multi-scale computational modelling framework, the anisotropic subcellular element method, we investigate the role of cell morphology and biophysical cell–cell interactions in the formation of this layered structure. This three-dimensional framework describes interactions between collections of hundreds to thousands of cells and (i) accounts for intracellular structure and morphology, (ii) easily incorporates complex cell–cell interactions and (iii) can be efficiently implemented on parallel architectures. We use this approach to construct a model of the developing epidermis that accounts for the internal polarity of ectodermal cells and their columnar morphology. Using this model, we show that cell detachment, which has been previously suggested to have a role in this process, leads to unpredictable, randomized stratification and that this cannot be abrogated by adjustment of cell–cell adhesion interaction strength. Polarized distribution of cell adhesion proteins, motivated by epithelial polarization, can however eliminate this detachment, and in conjunction with asymmetric cell division lead to robust and predictable development.

1. Introduction

Skin, the largest organ in our body, undergoes continuous self-renewal throughout our lives and can be repaired after injury. The epidermis, the outermost layer of the skin, provides an essential barrier function that protects us from water loss, infections and other environmental insults [1,2]. Within the epidermis, cells are arranged in a stereotypic, multi-layered pattern, with a single layer of basal cells sitting on an extracellular basement membrane, and multiple layers of suprabasal cells occupying the space closer to the outer surface [3]. Epidermal stem/progenitor cells, with probabilistic self-renewal and/or proliferative activities, reside in the basal layer [4,5]. These proliferative cells embark on the process of terminal differentiation as they withdraw from the cell cycle to first produce spinous cells, which occupy the layers immediately above basal cells and later go on to become granular cells, and ultimately cornified layers which constitute the physical permeability barrier for the organism. Homeostasis of the adult established epidermis is maintained by a combination of shedding of the outer dead, enucleated cells and the continual production of new cells by the basal layer that slowly move towards the surface [6]. Coordinated proliferation and differentiation within the basal layer as well as structural integrity of the outer layers are important determinants of barrier function, the disruption or defects of which results in death, diseases or skin conditions such as psoriasis and atopic dermatitis [7].

We consider here the early developmental processes that produce the layered epidermal structure. The skin epidermis is derived from a single-layered surface ectoderm during mid-embryogenesis when ectodermal cells commit to becoming epidermal basal cells [8]. Early-stage basal cells are multipotent, producing not only the interfollicular epidermis but also its appendages, including hair follicles, sebaceous glands and mammary glands. Within the developing epidermis, basal cells divide symmetrically, with the division plane being perpendicular to the skin surface (figure 1a), to produce two daughter basal cells in order to expand the single basal layer in proportion to the growth of the organism [6,9]. Past and recent studies have also identified embryonic basal cells in the mouse that undergo asymmetric division with division plane parallel to the skin surface [10,11]. These asymmetric cell divisions generate two distinct daughter cells, one basal and another intermediate spinous that assumes a suprabasal location. Distinct from spinous cells in the mature epidermis, intermediate spinous cells are transiently proliferative during development, which aids the rapid expansion of the epidermis [11,12]. The molecular and cellular mechanisms that control the epidermal stratification process have been under intensive study in recent years [4,8]. It is known that the relative frequency of symmetric versus asymmetric divisions depends on developmental stage [13] with symmetric division dominating early expansion and tissue maintenance while asymmetric division dominates at intermediate times [10,14–16]. What is less clear is how these different modes of division contribute to robust and efficient stratification of the early epidermis.

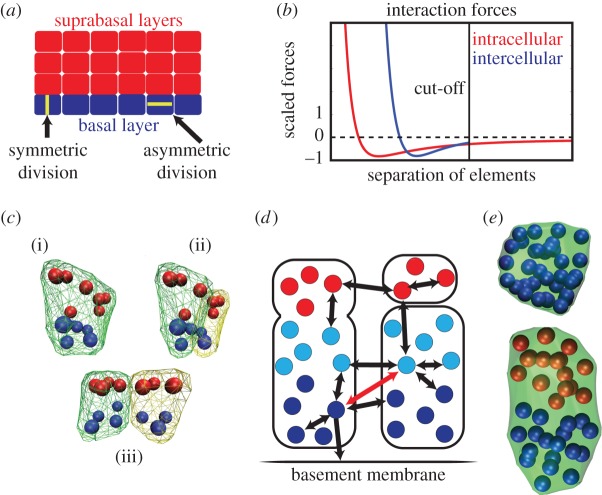
Figure 1.

Overview of the anisotropic subcellular element method. (a) Schematic of the stratified epidermis comprised of a single layer of basal cells and multiple layers of suprabasal cells. The highlighted basal cells depict the division planes for (a) symmetric division. (b) Scaled plot of the intercellular and intracellular forces acting on an element versus element separation. The intracellular force cut-off line is the separation at which we assume cell–cell adhesion no longer operates, so the force between elements in different cells is set to zero. (c) An illustration of the implementation of cell division. Part (i) shows a cell that is ready to divide, (ii) shows the same cell after it has distributed its elements to two daughter cells, but before any cell motion has occurred and (iii) shows the cell after the change from intracellular forces to intercellular forces has pushed the two daughter cells apart. (d) Schematic of forces. The arrows represent the forces acting on the pairs of element types with thicker arrows representing stronger forces. These forces are strongly repulsive at short range and attractive at longer ranges as shown in (c). The dark blue elements are the basal elements of the basal cells and adhere to the basement membrane by way of an external attractive force. The light blue elements are the apical elements of the basal cells and have a very weak repulsion from the basement membrane (not shown). The red elements are the elements destined to be part of suprabasal cells that do not interact with the membrane. When modelling cells with strong polarity the red arrow in (a) only provides a short-range repulsive force and no attractive force. Forces between pairs of element types not shown are strictly repulsive, preventing elements from overlapping. (e) Two cells with an identical number of elements (36) but comprised of one or two element types. The left cell is comprised of only a single element type to a round or cuboidal shape. The right is made up of two distinct element types (e.g. apical and basal). Their interaction rules lead to segregation and the resulting columnar shape.

In this work, we investigate the process of epidermal stratification using a mathematic modelling approach. Specifically, we explore and compare different potential strategies that might contribute to initial formation of suprabasal layers. This is inherently a (relatively) short-timescale question, and we do not consider issues of tissue maintenance or homeostasis, which occur beyond the initial developmental phase. We consider two simple, non-mutually exclusive mechanisms for how a basal cell might produce suprabasal cells: (i) it asymmetrically divides to produce a suprabasal cell as one of its daughters [10], or (ii) it detaches from the basement membrane and migrates upwards, later differentiating to become a suprabasal cell [17–19]. With the latter view, cell divisions remain symmetric, and detachment of individual cells leads to differentiation. Both are known to be present with the relative importance of each possibly dependent on specific conditions as well as the performance objectives of the epidermis at different stages of development. We focus on the mechanical elements required for robust and orderly layer formation, rather than the underlying biochemistry regulating those elements. To properly model the mechanical forces present during epidermal stratification, it is necessary to account for cell morphology and structure, movements, growth, division—symmetric and asymmetric—and various cell interactions including cadherin-mediated cell–cell adhesion and integrin-mediated cell to substratum adhesion [20]. To accomplish this, we develop a multi-scale modelling framework capable of incorporating all the discussed features in a modular way, so that differing hypotheses can be modelled and compared.

There are a number of modelling paradigms that can accomplish this to varying degrees. Particle methods [21,22], where cells are treated as point objects, track motions of cells and account for cell–cell interactions. These benefit from simplicity and numerical efficiency, but do not account for cell morphology and over simplify force interactions. Centre-based methods [23] extend these and represent cells as deformable ellipsoids. Both effectively endow each cell with three positional degrees of freedom, but centre-based methods endow each cell with three additional morphological or ‘shape’ degrees of freedom (one for each ellipsoidal axis). Centre-based methods can be extended to account for rudimentary mechanical cell properties such as conservation of size (e.g. volume), but have limited ability to represent more complex aspects of cell–cell interactions, cell–substrate interactions and differing modes of division.

Cellular potts methods (CPM) [24–27], alternatively known as the Glazier–Graner–Hogeweg model (GGH), are well suited for describing morphology, internal cell structure and complex interactions. These methods however take a probabilistic Hamiltonian approach to modelling cell motions and interactions, and do not directly describe force interactions, which is likely to be critically important in describing cell detachment. An alternative to the CPM is the recently developed subcellular element (SCE) method [28]. In this framework, each discrete cell is treated as a collection of an arbitrary number of volume elements interacting according to user-defined interactions. This methodology benefits from being grid free, using a more natural representation of forces, and the ability to describe many viscoelastic rheological cell properties [29]. The SCE method has the added benefit of avoiding many of the complexities associated with Hamiltonian formulations.

This methodology has been used to describe both single-cell dynamics [29] and multi-cellular systems. In the latter case, it has been applied to the dynamics of epithelial sheets [28], primitive streak formation in the chick embryo [30] and the effects of Notch signalling on intracellular gene networks controlling cell division [31]. In its original form, this methodology described cells as isotropic entities with no internal structure or preferred shape. Harvey et al. [32] extended this to describe swarming Myxococcus xanthus bacteria as an ordered chain of elements connected by torsion springs. This enforced an indicative bacterial rod-like cell shape that would bend as they collided and return to their original shape. Sweet et al. [33] extended it to describe platelets as heterogeneous entities with a single internal element surrounded by a shell of connected peripheral elements and subsequently observed the deformations and motions of these cells when subjected to a flow.

To investigate different mechanisms for epidermal layer formation driven by symmetric and asymmetric divisions, we propose an anisotropic extension of the SCE method that accounts for more complex internal cell structure and morphology by representing different parts of the cell with different types of elements that encode distinct mechanical interactions. The method is presented in a general context and used to model the development of a sheet of polarized, columnar basal cells followed by the formation of subsequent layers of cuboidal suprabasal cells. A parallel implementation of this method is presented along with performance results showing the method can take full advantage of common parallel architectures, dramatically improving performance. Using this model, we show that while both detachment and asymmetric division are capable of giving rise to the stratified epithelial structure, detachment alone leads to highly chaotic development and polar distribution of cell–cell adhesions has the potential to suppress this randomness.

This paper is organized as follows. In §2, we describe the general anisotropic subcellular element (ASCE) method, and the specific biological components that are included in this framework for this application. In §3, a brief description of the implementation of this model is provided. Section 4 describes results of simulations of different model variants, and §5 discusses implications of these results. A technical methods section is included to describe the details of all model variants and their implementation along with providing performance benchmarks.

2. Model description

We introduce anisotropic features into the SCE method, which we present next, to extend the original SCE method's capabilities' and account for more complex cell morphologies and intercellular interactions. Like the SCE, in the ASCE method, individual cells are comprised of a collection of volume elements. Unlike the original SCE, we take a view where each element is an object assigned a list of attributes describing it (for example, position is but one attribute). Interactions between pairs of elements representing both intra- and intercellular forces are then dependent on these attributes. The choice of attributes and forces then leads to a self-organized internal structure and evolution of the multi-cellular system.

2.1. Anisotropic subcellular element method

In the SCE method, each cell is constructed from a number of discrete ‘subcellular elements’ (X_i), with the number of elements (e.g. degrees of freedom) comprising each cell (C_i) determined by the level of detail required. The elements of the system interact as an over-damped (no inertia) Langevin system with the force governing the interaction between a pair of elements determined by the distance between them (r = |X_i − X_j|) and the choice of the force representation (F). Different forces govern interactions between pairs of elements in the same (F_intra(r)) cell or in different (F_inter(r)) cells [28,31,33]. Evolution of the system is then prescribed by a large coupled system of Langevin equations for all elements.

In the original SCE formulation, each element is assigned two attributes, position and an identifier for the cell it is contained in. The ASCE method extends this approach by assigning to each element additional attributes describing that element's type (where the list of element types is user-defined based on context). With only a single element type, intracellular forces will always be isotropic and in the absence of external forces, cells will always round up to a roughly spherical shape of preferred size (figure 1e, left-hand cell) indicative of the cuboidal morphologies seen in in vitro settings. In the application to come, each basal cell will be comprised of at least two element types with different properties. Elements of different types will be assigned different pairwise intracellular forces that cause the cell to self-organize (figure 1e, right cell). Additionally, different element types interact with the environment differently through element-type-dependent intercellular and external forces. The system is now comprised of a collection of elements each with three attributes: position (X_i), the cell it resides in (c(i)) and its type (τ(i)). The equations of motion for the ASCE method become

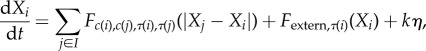where I is the set of all elements in the system, F is a pairwise force interaction between elements (i, j), F_extern,τ(i) is any external force that affects that element, η is a normalized stochastic white noise term and k is a noise magnitude representing the strength of thermodynamic fluctuations. The pairwise force F depends on these attributes and encompasses both intra- and intercellular forces. In cases where this force does not depend on (τ(i), τ(j)), the original SCE method is recovered.

2.2. Model components

We use this framework to construct a model of epithelial layer formation that includes (i) intracellular forces that determine cell shape and polarity, (ii) polarity-dependent intercellular adhesion forces that control cell interactions, (iii) external forces that provide cell–membrane adhesion and (iv) cell growth and division which are also potentially dependent on cell polarity. In simulations not presented, we have also incorporated random apoptosis events as well. This inclusion however served only to augment the net growth rate by the rate of apoptosis and did not affect qualitative results. As it is not clear whether apoptosis is present at this early stage, we have not included it in the following discussion. There are numerous other features present in later developmental stages we do not consider here as well. For example, it has been observed that suprabasal cells in the developed epidermis are nearly twice as large as basal cells [34], which could have potential effects on detachment rates. This and other properties could easily be incorporated in our extensible modelling framework. However, as it is not clear whether they are present at these early stages, we opt for parsimony.

2.2.1. Cell structure and adhesion forces

Each basal cell is endowed with two element types: basal and apical. Each attracts its own type and exerts a short-range repulsion on the opposite type, leading to a columnar morphology (figure 1e). We found that approximately 10 elements give enough detail to capture the distinction between columnar cells and cuboidal cells while maintaining computation times that are low enough to run the ensembles of hundreds of simulations (each with hundreds of cells) necessary to assess the influence of randomness on results. A modified Lennard–Jones force is used to model both inter- and intracellular forces, but with different effective ranges and strengths (figure 1b) that, in turn, affect morphology. Some elements within the basal category are further endowed with an attractive force to a fixed basement membrane, mimicking integrin-mediated cell–substrate adhesion. Suprabasal cells are assigned a third element type.

We consider two hypotheses for the form of basal cell–cell adhesion: polar and non-polar. In the former, we assume polarity separates each basal cell into two regions (apical and basal) with different adhesion properties. Then, only like regions of two different cells can interact, e.g. the apical region of one cell can adhere to the apical region of another but not with the basal region. This is implemented by only allowing attractive intercellular force interactions to occur between elements of the same type. In the latter (non-polar) regime, we assume polarity has no effect on the distribution of adhesion molecules, so that intercellular force interactions are independent of element type. Suprabasal cells are assumed to be isotropic and adhere both to each other and to the apical region of basal cells. A schematic of different pairwise element interactions are shown in figure 1d.

2.2.2. Cell growth, division and differentiation

We assume basal cells grow at a constant rate prior to dividing. To implement growth, two elements are added to each cell at regularly scheduled intervals. For symmetric growth (that is growth that will lead to symmetric division) of basal cells, one of each type of basal cell element (basal and apical) is added to the cell. For asymmetric growth of basal cells, two suprabasal elements are added to the cell. For growth of suprabasal cells, two suprabasal elements are added at each interval. As cell size increases, the probability that division will occur increases. Once a decision to divide is made, the type of division is determined by the make-up of the cell. Cells with only basal (resp. suprabasal) elements divide symmetrically into two basal (resp. suprabasal), cells with a roughly equal number of elements and a division plane roughly perpendicular to the basement membrane. Cells with both element types divide asymmetrically into a basal and suprabasal cell with a division plane at the border between the two element types (figure 1c). In the cases of cell detachment, differentiation to the suprabasal fate is assumed to occur and this is implemented by reassigning the type attribute of all elements when the cell reaches approximately one cell height from the basement membrane.

2.3. Model hypotheses

We consider a number of distinct models with different combinations of hypotheses for the form of cell–cell adhesion and the type of basal cell division. Cell–cell adhesion can be either polar or non-polar, whereas basal cell division can be either symmetric or asymmetric. We consider each of the four possible combinations of these two properties to determine which lead to robust, predictable formation of the stratified epithelium.

2.3.1. Symmetric division with non-polar adhesion

One hypothesis is that all cell–cell adhesions are uniformly distributed over the entire surface of each cell (non-polar) and that all cell divisions are symmetric. In this case, the only possible way for a suprabasal layer to form is for basal cells to detach and differentiate. Detachment can, in principle, be either a controlled process or a random process. If control were present, a signalling cue would have to be temporally regulated, so that the basal layer is sufficiently formed before detachment occurs. Further, it would have to act both locally, so that individual cells detach while leaving their neighbours behind, as well as globally, so that detachment occurs over the entire basal layer with consistent density and the suprabasal layer forms homogeneously. While Ca²⁺ has been suggested as a possible cue for detachment [18], it is unclear how its action is temporally regulated or if it is a sufficient cue to guide both orderly and robust layer formation. We therefore assume detachment is a random process initiated by local forces and thermal fluctuations rather than a regulated process.

2.3.2. Symmetric division with polar adhesion

In this case, we assume all cell divisions are symmetric, but that cell–cell adhesion is polarized. This is motivated by the possibility that cell–cell and cell–substrate adhesions influence each other [35,36] and the observation that aPKC and PAR3, which are known to affect localization of cadherin proteins [37], are polarized in basal cells [10]. We do not model internal components that give rise to polarity but instead directly assume basal (resp. apical) regions of a cell can form adhesions only with the basal (resp. apical) regions of neighbouring cells. With these hypotheses, the only source of suprabasal cells is still detachment followed by differentiation.

2.3.3. Switch from symmetric to asymmetric division with (non)polar adhesion

As discussed above, an alternative mechanism is that suprabasal cells result from asymmetric division of basal cells rather than detachment and differentiation. In this case, symmetric division of basal cells is still required to populate the basal layer and a signal would be required to initiate the switch from symmetric to asymmetric division. A temporal switch from mostly symmetric cell divisions to mostly asymmetric cell divisions indeed occurs coincidentally with the onset of epidermal stratification in mouse embryos [6]. Rather than model a specific molecular switch responsible for this change, we pre-assign it to occur when the basal layer reaches a predetermined size. Again, either non-polar or polar adhesion is possible and will be investigated. While suprabasal cells would result from basal cell division in this case, it is still conceivable that detachment followed by differentiation is the source of some portion of suprabasal cells.

3. Implementation

The mathematical formalization of this model takes the form of a large, stiff system of coupled ordinary differential equations. We use a second-order Runge–Kutta method to evolve this dynamical system and calculate the motion of the elements. We discretized the time evolution of the system dynamics, so there are approximately 3300 time steps per unit time, which is defined as the mean time for a single-cell division. This was chosen to be as course grained as possible without affecting simulation results. Because cell growth happens on a longer timescale than cellular dynamics, we fix the discrete growth steps to occur every 1000 time steps, see Methods for further detail.

By far, the most computationally intensive component of this method is computation of the pairwise force interactions, which scale as O(N²), where N is the number of subcellular elements in the system. In this application, this scaling is exacerbated by the fact that as the system evolves, cell numbers and hence N increase. Fortunately, this step is highly parallel, which has been exploited in past implementations of the original SCE [31]. While the extra complexity of the ASCE creates difficulties for GPU implementation (table 1), the computation can still be distributed over multiple CPUs. To exploit this, the force calculation task is implemented using OpenCL libraries, whereas less intensive serial tasks are performed in C++. We note that OpenCL uses a just in time compiler and detects the available resources at the time of execution prior to distributing the workload. Combined with the modular structure of this implementation, this enables simple adjustments to force files to be made without the need to recompile the main program. So, hypothesized model components and force interactions can be easily interchanged or modified. For the interested readers, a compilable version of the program used for our simulations can be found at http://cmcb.math.uci.edu/ASMC3D.html.

Table 1.

Time comparison of running the ASCE method with different numbers of elements for 100 000 timesteps. Each row gives the real time taken to compute 100 000 timesteps of cell movement for a sample system, the first row with eight CPU cores working in parallel, the second for a single CPU, and the third with an older generation GPU. Column 1 gives the times for a system consisting of one element in a single cell. Column 2 is for 10 elements of the same type in a single cell. Column 3 is for 100 elements of the same type evenly divided into 10 cells. Column 4 is for 1000 elements of the same type divided evenly into 100 cells. Column 5 is for 100 cells, each containing five elements of one type and five elements of another type. The first four columns indicate performance for the standard SCE method while the final column (*) indicates performance for ASCE with two element types.

	one element	10 elements	100 elements	1000 elements	2 × 500 elements*
eight CPU cores	0 min 5.612 s	0 min 12.44 s	0 min 29.531 s	10 min 23.523 s	11 min 41.174 s
one CPU core	0 min 4.269 s	0 min 5.195 s	0 min 57.132 s	77 min 33.166 s	79 min 54.411 s
GPU	0 min 15.128 s	0 min 15.095 s	1 min 8.371 s	28 min 43.597 s	57 min 47.117 s

4. Results

Given the array of possibilities for how cells divide, adhere to each other and adhere to a basement membrane, we use this highly flexible methodology to investigate which combinations of properties give rise to orderly layer formation. Specifically, we investigate the four models described in §2.3. All simulations begin with a single basal cell undergoing symmetric growth/division to establish a basal layer. For computational tractability, we consider a small section of the epithelium containing on the order of hundreds of cells rather than the entire epithelium. To keep layers from expanding laterally without bound, walls that constrain cell movements to this patch are included to mimic contact with identical adjacent sections.

4.1. Symmetric division with non-polar adhesion leads to unpredictable stratification

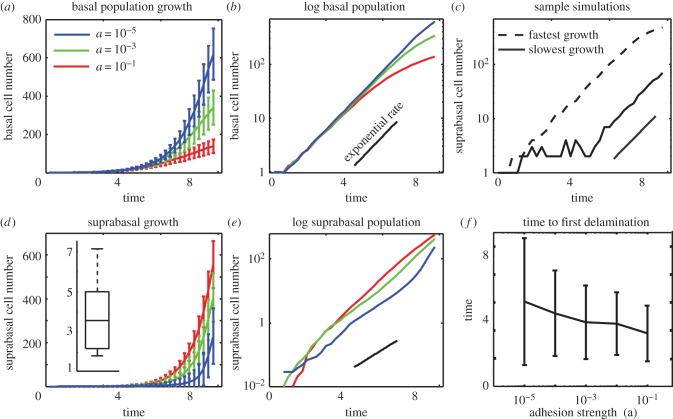
We first consider the hypothesis that all divisions are symmetric, adhesions are uniformly distributed on the cell membrane, and suprabasal cells result from detachment of basal cells. We find that while cell detachment leads to the development of multiple layers (figure 2), the location and more importantly timing of suprabasal layer formation is unpredictable. The stochastic effect of division and detachment leads to substantially different outcomes under identical simulation conditions (figure 2). To determine the extent of the timing variability, we performed an ensemble of 100 simulations each subjected to the same conditions and mechanics. Assuming the strength of cell–cell adhesion relative to cell–substrate adhesion affects local forces and in turn detachment, we replicated this ensemble simulation at logarithmically spaced values of cell–cell adhesion strength (figure 3).

Figure 2.

Time course images of layer formation from symmetric cell division. (a–c) Snapshots from a simulation where the first basal cell detachment occurs early. Because delamination occurred only in one area, the resulting second layer is concentrated in that area. Times: 3.2, 6.2 and 9.2 (time step 10.5 k, 20.5 k, 30.5 k). (d–f) An example where the first delamination occurs relatively late. The resulting second layer is patchy, lagging behind the upper layer in terms of growth. Times: 5.9, 7.4 and 8.9 (time step 19.5 k, 24.5 k, 29.5 k). (g–i) Example where detachment occurs in two locations at different times, leading to a patchy and uneven second layer. Times: 5.9, 7.7 and 9.2 (time step 19.5 k, 25.5 k,30.5 k).

Figure 3.

Symmetric cell division coupled with detachment. Time course data for the number of basal and suprabasal cells when all cell division is symmetric and layer formation results from delamination and subsequent division of basal cells. (a,d) Time course of simulation mean and variance data showing near exponential growth for both basal and suprabasal cell layers. The inset in (d) shows the maximal separation between two suprabasal cells at the first time point when five suprabasal cells are present. The data are normalized by an indicative cell diameter, so that separations are reported in normalized units of cell diameters. (b,e) Log₁₀ plot. Black line depicts the slope in log space (exponential growth rate) predicted based on simulations parameters. (c) Dashed (respectively full) curves represent cell numbers for the individual simulation that terminates with the maximal (resp. minimum) basal cell number. (f) Measure of the time to first basal cell detachment for different cell–cell adhesion strengths. Mean and variance are computed over 1000 simulations.

On average, both layers grow roughly exponentially. The growth rate of the basal layer (depicted by the logarithmic slope in figure 3b), however, is lower than that predicted by the division rate parameters, whereas the rate for the suprabasal layer is larger than expected. So, the suprabasal layer is continuously receiving cells from the basal layer. We also see significant variability in the number of cells in each layer at the final time, independent of adhesion strength. Adhesion strength does however have a profound effect on layer formation. Figure 3a,d shows that when cell–cell adhesions are weak, a large basal layer forms with few cells occupying the suprabasal layer. When it is strong, the suprabasal layer outgrows the basal layer.

To further characterize the effects of adhesion strength on detachment, we performed an ensemble of 1000 simulations and recorded the time to the first detachment event in each case (figure 3f). On average, the time to first detachment decreases as cell–cell adhesion strength increases. From a modelling standpoint, this results from the fact that cell–cell interactions are the only source of vertical forces capable of opposing cell–substratum adhesions. Interestingly, decreased adhesion strength leads to a substantial increase in the variability of detachment times. So while lower cell–cell adhesion on average promotes the formation of a basal layer (figure 3a), this comes with a commensurate increase in the unpredictability of layer formation. The extent of this unpredictability is demonstrated in figure 3c where the number of basal cells at the end of two specific simulations varies by a factor of more than five.

We also quantified the level of spatial variability in the layer formation process. To do so, we tracked the centre of mass of each cell (in the planar x,y-coordinates) and determined the maximal distance between suprabasal cells at the first time point when five suprabasal cells are present. We further determined the characteristic distance between two basal cells (e.g. the cell diameter) and normalized the maximal distance accordingly. This provides a measure of patchiness, where large maximal separations correspond to detachments in disparate locations. Results (figure 3d inset) show a substantial variability of this maximal distance, which ranges from two to seven cell diameters. To provide a relative scale, the mean number of basal cells present at the measured time point is 43. If placed in a square arrangement, a crude estimate for the size of the tissue is approximately 6.5 cell diameters in each direction. So, this mechanism gives rise to significant spatial patchiness.

Interestingly, we also note there is considerable deviation from exponential growth for the basal cell numbers as time progresses, especially in the large adhesion regime (figure 3b), suggesting increased detachment at larger cell numbers. Cell division and growth each produce a local pressure on the cells around them that contribute to detachment. When cell numbers are low, this pressure can be dissipated through the movement of the relatively few surrounding cells. When large numbers of tightly packed cells are present, however, it becomes more difficult to quickly dissipate a transient increase in local pressure through displacement, because more cells must be displaced, and the energetic path of least resistance would be to detach. The resulting increase in cell–cell forces thus promotes detachment. To verify that it is these local pressures rather than global pressures (resulting from the confining walls) that are responsible for this longer time deviation, we have performed identical simulations with the walls spatially confining the system removed. Results (not presented) show only a marginal reduction in final cell numbers and detachment rates. Thus, it is local proliferative pressures rather than global confinement pressures that are driving detachment. Given the level of temporal and spatial randomness observed here, we reject this as a model for robust, predictable layer formation.

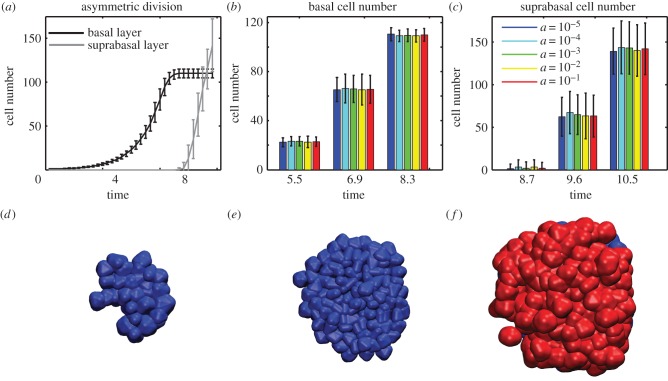
4.2. Polar cell–cell adhesion distribution coupled with symmetric division reduces unpredictability but hinders formation of suprabasal layers

We now consider the effect polar adhesion has on layer formation and in particular robustness and predictability of its formation. In this case, detachment of basal cells is almost completely abrogated (figure 4a,b). Thus, polar adhesion nearly eliminates the intrinsic variability associated with randomized early detachment. Further, this is nearly independent of adhesion strength (figure 4b,c). While this reduction in variability makes things more predictable and ensures consistent formation of a basal layer, the lack of randomized detachment hinders formation of subsequent layers. This defect is reminiscent of the p63 knockout (in mice) phenotype where development of suprabasal layers is severely impaired [5,38]. Interestingly, this mutation also completely abolishes asymmetric division [10], consistent with our results. Of course, once the basal layer is fully populated the only way to grow is up. Thus, continued proliferation will inevitably lead to random detachment and unpredictable layer formation similar to the symmetric, non-polar case (data not shown). We thus reject this as a model for layer formation and more generally suggest layer formation does not result from detachment and differentiation of basal cells.

Figure 4.

Asymmetric cell division coupled with polar adhesion. (a) Time course data for the number of basal and suprabasal cells when cell–cell adhesion is polarized and asymmetric cell division occurs once the basal layer reaches 100 cells in size. Mean and standard deviation of 100 simulations with a = 10⁻³. (b,c) Mean and variance of cell numbers at three time points for different values of cell–cell adhesion strength. (d–f) Time course images for layer formation via asymmetric cell division. Times: 6.2, 9.2 and 10.4 (timestep 20.5 k, 30.5 k, and 34.5 k).

4.3. Polar distribution of cell–cell adhesions coupled with a developmental switch to asymmetric division leads to robust, predictable stratification

We now consider the situation where an individual basal cell undergoes symmetric division until a threshold is reached. In simulations, this threshold directly depends on the number of basal cells (arbitrarily set as 100 cells). Once this threshold is reached, asymmetric division is implemented. In this setting, both isotropic and polarized adhesions are plausible. The switch to asymmetric division does not however affect detachment dynamics prior to that switch. The assumption of asymmetric division cannot therefore remove the unpredictability associated with non-polar adhesion. For this reason, we consider only the hypothesis that basal cell–cell adhesions exhibit a polar distribution, which was shown earlier to suppress detachment.

An ensemble of 100 simulations at logarithmically spaced adhesion strengths are again performed (figure 4). An initial exponential growth phase of the basal layer with a rate that very closely matches that prescribed by the division rate constants indicates very little detachment at any adhesion value. Non-zero values for the suprabasal size indicate there is a small amount of detachment, though only 1–10 cells per simulation have on average been accumulated in the suprabasal layer by the time asymmetric division is initiated, an order of magnitude fewer than the number of suprabasal cells resulting from detachment in the symmetric, non-polar case.

Once the threshold is reached, growth of the basal layer stops and after a growth-related lag, a suprabasal layer forms. Figure 4a,c shows considerable variance in the size of the suprabasal layer at specific time points. This however is related to variability in the time at which the threshold is reached rather than unpredictability of the underlying detachment process. This randomness does not grow with time and is not influenced by cell density. Thus, the two layers form in an orderly fashion (figure 4d–f) with the only source of unpredictability related to the precise timing of the switch from symmetric to asymmetric division, which is likely to be tightly controlled by external factors.

4.4. Formation of multiple layers

We have thus far found that polarized adhesion coupled with a switch from symmetric to asymmetric division leads to predictable formation of a single layer. This combination of mechanisms also leads to robust formation of multiple layers (figure 5). Here, we see a basal layer giving rise sequentially to multiple well-formed suprabasal layers. In contrast, the detachment-driven mechanism leads to highly heterogeneous distribution of cells in the layer resulting from strong stochastic variation.

Figure 5.

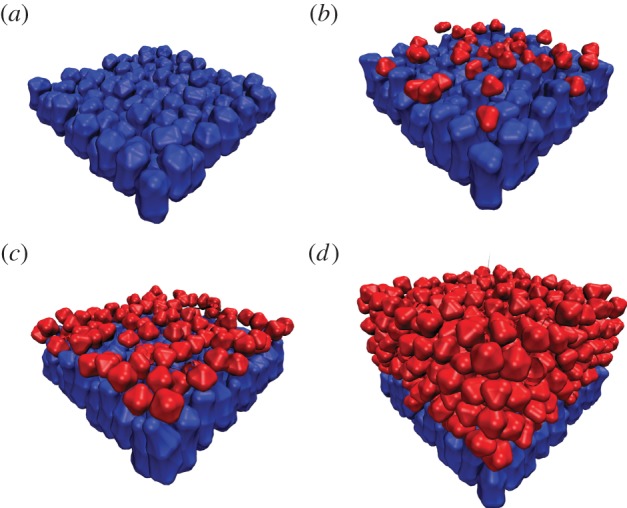
Growth of multiple suprabasal layers from a single basal layer. (a–d) Snapshots of a simulation at times 0.3, 4.5, 6.3 and 19.7 (timestep 1 k, 15 k, 21 k, 65 k). By time 4.5, the first suprabasal layer has formed, and by time 19.7, the stratified structure is evident. Alternative simulations with the same parameters lead to similar results.

5. Discussion

Epidermal development requires the formation of multiple stratified cell layers. We developed a multi-scale modelling framework to investigate the importance of and interactions between various biophysical factors involved in this process. In particular, we investigate the roles of asymmetric division and detachment/differentiation of basal cells in tissue stratification. Asymmetric division of the embryonic basal cells has been well documented, and its underlying molecular basis has been studied [10]. Experimental evidence supporting basal cell detachment, however, has largely come from in vitro studies [17–19]. As such, the in vivo significance of physical cell detachment, and more generally the role of mechanical cell–cell interactions are less understood. Furthermore, it is particularly difficult to probe the involvement of mechanical interactions experimentally given the difficulty of both measuring and manipulating those interactions. Our computational modelling results now offer important insights into this issue, and suggest asymmetric cell division to be a more advantageous mechanism than cell detachment in robustly producing a multi-layered epidermis. Furthermore, the methodology that we developed offers a useful framework to explore additional, more complicated scenarios and to generate new hypotheses that can be tested experimentally in the future.

Our simulation results show that layer formation driven solely by detachment is both highly unpredictable and irregular. This randomness is inherent in the source of detachment itself. We find that the cause of these detachments is local pressures induced by proliferation and growth. Because the timing of cell divisions and the subsequent chance of detachment are both somewhat random, the layer formation process itself is random and irregular. Further, manipulating the strength of cell–cell interactions does not rescue orderly layer formation.

Asymmetric division does lead to robust, predictable layer formation, consistent with observations that asymmetric division is present during both the development [10] and maintenance [39,40] of epidermal tissue. This however requires that the tendency for basal cell detachment to be suppressed. While manipulating cell–cell adhesion strengths does not alleviate this stochastic effect, we found polarized distribution of cell–cell adhesions to be highly effective at doing so. It is unclear what might be responsible for this feature, but asymmetric localization of polarity determinants such as the PAR complex has been observed in these cells [10], which could potentially affect localization of cadherins or other adhesion proteins. We thus propose that basal cell polarity serves not only to promote asymmetric division, but also to suppress unpredictability arising from randomized detachment of basal cells from the basement membrane.

It is important to note however that while asymmetric division may be the primary source of suprabasal cells, symmetric division of basal cells remains present during development and is vital to expanding the epidermis as the organism grows [6,9]. Adhesion polarity could thus represent a novel mechanism that allows the developing organism to robustly balance the needs of expanding the proliferative basal layer while at the same time forming subsequent protective layers. While it is challenging to measure cellular forces directly, observations of the subcellular localization of adhesion proteins (e.g. cadherins) would provide an indirect test of this hypothesis.

We also presented a highly flexible, multi-scale, stochastic modelling framework, referred to as the anisotropic subcellular element (ASCE) method. In this application, a range of assumptions on the internal structure of individual cells and the interactions between them were incorporated while maintaining the tractability and efficiency needed to observe dynamics of the resulting tissue comprised of hundreds of cells. Like the SCE method, this methodology benefits from (i) simple problem descriptions, because interactions are described directly by forces and (ii) parallelizability allowing for dramatic computation speedups in cases where many cells are involved. Unlike the standard SCE method, the ASCE is also (iii) highly flexible, allowing the user to account for more complex intra- and intercellular dynamics. This extension will likely be useful in other applications where either complex cell morphologies or multiple interacting cell types are present. The next step in this direction is to provide an efficient graphics processing unit (GPU) implementation of the ASCE method to take advantage of the hundreds to thousands of parallel processors available on modern GPUs.

6. Methods

6.1. Element types and interactions

For this model of epidermal growth, we used three element types, two types for the basal cells and one for the suprabasal cells. Within each cell, each type of element forms strong short-ranged bonds with elements of the same type, and weaker long-ranged bonds with elements of other types to hold the cell together. This discrepancy leads to aggregation of the individual element types and the resulting columnar morphology of basal cells. The full details of the interactions between elements are shown in table 2.

Table 2.

Forces used for element to element and element to membrane interactions. Column 1 lists the force being described. Column two is the equation used to calculate the force, where r is the distance between elements or between an element and the basement membrane. Column 3 gives the distance at which a force is set to zero because the interaction is out of range. Column 4 gives the equilibrium separation resulting from the force. Column 5 gives the maximum attractive strength that the force attains.

force	equation	cut-off distance	equilibrium separation	maximum attraction
basal cell element (basal) to membrane	30((2.512/r14) − 1)	none	2.19	30
basal cell element (apical) to membrane	min(0.04 − 0.005r, 0)	none	8	0
suprabasal element to membrane	min(3 − 0.5z, −0.1)	none	6	0.1
basal cell element to basal cell element (same type, intracellular)	((2.212/r14) − (2.23/r3))	none	1.91	0.794
basal cell element to basal cell element (same type, intercellular)	0.001 ((2.512/r14) − (2.56/r8))	3.5	2.5	3.25 × 10−5
basal cell element to basal cell element (cross type, intracellular)	0.8 ((312/r14) − (36/r6))	none	2.28	1.26
basal cell element to basal cell element (cross type, intercellular)	0.0002 ((3.512/r14) − (3.56/r8))	5.5	3.5	3.32 × 10−6
suprabasal cell element to suprabasal cell element (intracellular)	2((2.012/r14) − 1)	none	1.81	1
suprabasal cell element to suprabasal cell element (intercellular)	((3.212/r12) − (3.23/r3))	3.8	3.2	0.472
suprabasal cell element to basal cell element (intercellular)	((2.012/r12) − 1)	none	2.0	1
suprabasal cell element to basal cell element (intercellular)	((4.312/r12) − (4.33/r3))	5.5	4.3	0.472

6.2. Potentials and forces

The SCE method [28] used Morse potentials to determine both intercellular and intracellular forces. In addition to Morse potentials, other papers have used spring potentials [32,33] or Lennard–Jones potentials [33] to describe the forces between elements. The Lennard–Jones potential, also known as the 12–6 potential, has the form D_e((r_e/r)¹² – 2(r_e/r)⁶) and like the Morse potential was originally used to describe the force between neutral atoms. The force generated by this potential is F(r) = 12D_e((r_e/r)¹²(1/r) − (r_e/r)⁶(1/r)). The first term of this force provides a strong repulsion that gives the elements volume and prevents their overlap. The second term is a longer-range attractive force that provides adhesion between elements and cells. The equilibrium separation r_e, is the separation at which the force transitions from a repulsive force to an attracting force. This determines element ‘size’ and the separation between cells that are adhered to one another.

We use a modified Lennard–Jones-type potential for our model because it provides several distinct advantages over the Morse potential. The Lennard–Jones potential provides a repulsive force that increases to infinity as the separation of the elements goes to zero, giving each element a more distinct volume. Another advantage is that Lennard–Jones-type potentials provide more versatility than the Morse potential. The Morse potential has only two control parameters, the potential well depth and equilibrium separation. By viewing the exponents on each term in the Lennard–Jones potential as parameters however, it has two additional parameters to separately adjust the rates at which the repulsive force and attractive force increase and decrease. Unlike the attraction between neutral atoms, cell–cell adhesion does not drop off quickly over very short ranges. To include this in our model, we increased the effective range of the intracellular potential by changing the attractive term of the Lennard–Jones potential to r⁻³ (table 2). Although this change had the desired effect of reducing the sharp drop off of the attractive force past the equilibrium distance, it increased the effective range of the force to several cell lengths. Because cadherin-mediated cell–cell adhesion acts only over short distances, we added a range cut-off to intercellular forces after which the force drops to zero. In the polar adhesion regime, this range cut-off is set to be the equilibrium distance for interactions between elements of opposite types, so that there is never an attractive intracellular force between these elements, but the volume defining repulsive force remains intact.

The full list of the forces governing the interactions of the elements can be found it table 2. The specific parameters here are not derived from physical measurements. The subcellular elements comprising an individual cell are not representative of physiological structures. We thus chose intracellular force parameters that produce a stable cell and take the resulting cell size as a base length scale for the system. Further, adhesion forces are very difficult to measure and the concept of cell–cell separation is not precisely defined in the subcellular element framework (because the model cells do not have a well-defined membrane surface). We thus chose intercellular forces and parameters to maintain cell separations considerably smaller than the unit cell length scale of the system.

6.3. Cell growth and division

As discussed in §2.2.2, cell growth is implemented by adding elements of the appropriate type to each cell at 1000 time step (approx. one-third of the cell cycle length) intervals. When a basal cell is preparing for symmetric division, it has one membrane adhering basal element added at the centre of the basal section of the cell and apical element added at the centre of the apical portion of the cell. If it is preparing for asymmetric division, it will have two suprabasal elements added to its apical end. Suprabasal cells (which only undergo symmetric division) have two suprabasal elements added to them at the cell centre plus a small random offset preventing them from being added at exactly the same location, which would produce large forces that cause numerical issues. The new elements are likely to be placed closer than the equilibrium separation to other elements, in this case, the strong repulsive forces provided by the Lennard–Jones potential will quickly cause the elements in the cell to rearrange to accommodate the new elements. Every time a pair of elements is added to a cell there is a chance it will divide. If after growth the cell has eight or fewer elements, the probability of division is zero; otherwise, the probability of division given by p = 0.1 (n − 8), where n is the total number of elements in the cell in the case of symmetric division, and the number of suprabasal elements present in the cell for basal cells undergoing asymmetric division.

Implementation of division is a natural process in the ASCE method. For a symmetrically dividing cell, once the axis of division is determined, the elements of the cell are divided along this axis with half being assigned to one daughter cell and half being assigned to the other. This is a relabelling of the cell number attribute, with no repositioning taking place. After this relabelling, the change from intracellular potentials to intercellular potentials between elements in the daughter cells will cause them to move apart (figure 1b). When basal cells divide symmetrically, they do so with the basal elements and apical elements divided as evenly as possible between the daughter cells. When a basal cell undergoes asymmetric division, the suprabasal elements of the cell are assigned to a new suprabasal cell, leaving the original basal cell intact. When a suprabasal cell divides, the elements in the cell (there are only one type) are distributed as evenly as possible to the two daughter cells. The division of suprabasal cells is always symmetric.

6.4. Performance

In principle, the pairwise force calculation in the ASCE method can be distributed over M available processors to achieve an M-fold speed-up. In practice, there will be some performance loss associated with the complexity of having a number of different pairwise force descriptions determined by element attributes. This is however minimal in this application (table 1) and computation time scales nearly linearly with the number of processors. The original SCE and the ASCE methods demonstrate nearly identical performance scaling with respect to processor number. Thus, while the added complexity of the ASCE does increase computation times, this can be ameliorated with increased resources. This linear scaling is expected to taper off as the number of available processors increases owing to serial aspects of the computation dominating parallel aspects. When thousands of elements are present however, we expect this taper to occur at a relatively large number of processors, beyond the typical resources provided by high-performance desktops and small clusters.

6.5. Visualization

The ASCE represents cells as a collection of interacting elements. To visualize each individual cell in the context of the developing tissue, we render a surface representation of each cell individually. This is performed using the software package VMD [13]. The resulting surface is a simplified visual representation of the cell, not a direct representation of its membrane surface.

Funding statement

This work was supported by National Institutes of Health grants R01GM107264 and P50GM76516 and National Science Foundation grant DMS1161621.