Spatial Arrangement of Branches in Relation to Slope and Neighbourhood Competition

Abstract

To gain a better understanding of the effects of spatial structure on patterns of neighbourhood competition among hardwood trees, the three‐dimensional extension of primary branches was surveyed for ten community‐grown Castanea crenata (Fagaceae) trees with respect to the positioning of neighbouring branches and the slope of the forest floor. There were significantly more branches extending towards the lower side of the slope than towards the upper side, but structural properties such as branch length and vertical angle were not affected by slope. When horizontal extension of a branch towards its neighbour was compared for a C. crenata branch and a neighbouring heterospecific, the former was significantly narrower than the latter when the inter‐branch distance (horizontal distance between the base positions of two neighbouring branches) was short (< approx. 5 m). Castanea crenata branches tended to extend in a direction avoiding neighbouring branches of heterospecifics when the inter‐branch distance was short. Furthermore, for an inter‐branch distance <3 m, the horizontal extension of a C. crenata branch was less when it was neighbouring a heterospecific branch than when neighbouring a conspecific branch. These results suggest that horizontal extension of C. crenata branches is more prone to spatial invasion by nearby neighbouring branches of heterospecifics, and that the invasion can be lessened when C. crenata trees are spatially aggregated. The reason why such an arrangement occurs is discussed in relation to the later leaf‐flush of C. crenata compared with that of other species in the forest.

INTRODUCTION

Spatial patterns of plants have important effects on the dynamics of a plant community (Dale, 1999). Crowns of many plant species tend to develop towards open space (Aguilera and Lauenroth, 1993), hence competition patterns in plant communities can change in accordance with spatial distribution of neighbouring individuals (Silvertown et al., 1992; Rees et al., 1996; Tilman and Kareiva, 1997; Stoll and Prati, 2001). In the above‐ground part of forests, expansion of the total crown often determines the growth of a tree ( Sumida, 1993; Ottorini et al., 1996; Ito et al., 1997). Thus, many studies of interactions among tree crowns have concentrated on individual crowns without taking account of smaller components of each crown, such as individual branches and annual shoots; these studies have found that tree crowns grow away from near neighbours (Ishizuka, 1984; Mizunaga, 1992; Umeki, 1995a, b; Rouvinen and Kuuluvainen, 1997). In such individual crown‐based analyses, each crown is assumed to be a single entity with a somewhat round shape, and the ‘crown centre’ is often defined and used to explain or predict the direction of crown development under the influence of neighbours (Umeki, 1995a, b; Rouvinen and Kuuluvainen, 1997). However, to explain or model spatial development of crowns in detail, information on the extension of branches of target trees and their neighbouring trees is needed (Rouvinen and Kuuluvainen, 1997), since the process of crown expansion in forests depends on spatial development of each branch, which interacts locally with neighbours. Even if the potential for physiological processes (e.g. photosynthetic ability of leaves) is lower in a particular species than in its neighbours, the branch structure of the species can bring advantages for neighbourhood competition (Schulze et al., 1986; Bazzaz, 1996). Investigating branch structure would therefore help clarify patterns of neighbourhood competition (Schulze et al., 1986; Küppers, 1989; Tiwari and Shukla, 1995). Despite the importance of branch structure, however, it has been little studied (Sinoquet and Rivet, 1997; Sinoquet et al., 1997) in adult trees of hardwood species in forests with respect to neighbourhood competition patterns; this is mainly due to difficulties in measuring tree crowns three‐dimensionally in forests.

In an earlier study (Sumida et al., 2001), we showed that the crown width of Castanea crenata Sieb et Zucc (Japanese chestnut, Fagaceae) varied among canopy trees of a similar height in a secondary hardwood forest. We found that the difference in crown width of C. crenata could be explained by taking into account the difference in the mean horizontal distance between the crown base of a C. crenata tree and that of neighbouring crowns surrounding the C. crenata tree (Sumida et al., 2001). However, an analysis based on individual crowns is insufficient to analyse inter‐ and intraspecific interactions of neighbouring crowns because the shape of a crown is often irregular, being locally dependent on the spatial relationship with neighbouring branches. In this paper further analysis has been performed to clarify how branch extension in space is affected by neighbouring branches using three‐dimensional data. Effects of the direction of slope of the forest floor were also analysed as a possible spatial factor affecting branch structure. The ecological implications of the spatial structure of branches are discussed in terms of competition and survival of C. crenata. We also discuss why this branch structure has arisen in the developmental process of the forest in connection with patterns of leaf phenology of the species in the forest.

MATERIALS AND METHODS

Site description

The study site is located in Shokawa Village, Gifu Prefecture, in the cool–temperate deciduous forest zone of Japan (36°05′ N, 137°00′ E) at an elevation of approx. 1000 m. Annual mean temperature and precipitation (1989–1998) ranges from 6·3 to 8·2 °C and 1620 to 3070 mm, respectively (Kato et al., 1999). The forest is a secondary forest composed of deciduous hardwood trees approx. 30–100 years of age as of 1985. It suffered intense disturbance during the 1900s and 1940s and was then allowed to regenerate naturally (Komiyama, 1989). The forest canopy was closed when this study was conducted in 1998. A permanent plot with an area of 1 ha (approx. 100 m × 100 m) was established in the forest in 1983 to study the biomass and dynamics of deciduous broad‐leaved forests (Komiyama, 1993; Higo et al., 1995). Within this 1 ha plot, an area of approx. 20 m × 25 m was chosen as the study plot to include ten C. crenata trees. This species is very common in deciduous forests in Japan and is known to have relatively high light requirements (Segawa, 1985). It was one of the dominant tree species in the forest and the C. crenata trees were all canopy‐constructors in the study plot. Sixteen other canopy trees (seven species; Table 1) occurred as neighbouring trees, i.e. their crowns neighboured those of C. crenata. The canopy height in the study plot was approx. 20 m. Three‐dimensional coordinates (x, y, z) were determined for the study plot, with the positive direction of y being north and z vertical. The forest floor faced WSW (direction of negative values of x and y) with a slope of approx. 14°.

Table 1.

Tree height and number for Castanea crenata and the 16 deciduous trees neighbouring the crowns of C. crenata trees

Species	Tree height (range, m)	Number of trees	Family
Castanea crenata Sieb.et Zucc	16·5–19·8	10	Fagaceae
Acer pictum Thunb. Subsp. dissectum (Wesmael) Ohashi	9·2–15·7	4	Aceraceae
Aesculus turbinata Blume	11·1	1	Hippocastanaceae
Betula platyphylla Sukatchev var. japonica (Miq.) Hara	18·7, 19·3	2	Betulaceae
Cornus controversa Hemsley	16·0	1	Cornaceae
Populus sieboldii Miquel	20·0	1	Salicaceae
Quercus mongolica Fischer ex Turcz. var. crispula (Bl.) Ohashi	16·0–18·6	5	Fagaceae
Tilia japonica (Miq.) Simonkai	16·1, 19·1	2	Tiliaceae

Nomenclature follows Kitamura and Murata (1997a, b).

Measurements and calculations

Positions of trunks and branches were surveyed three‐dimensionally using a theodolite (T460D; Leica, Switzerland) equipped with a visible‐laser range finder (POWER DATA DISTO GSI; Leica, Heerbrugg, Switzerland). The diameter of the laser spot is 6 mm at a distance of 10 m, and it increases proportionally with increasing distance (Leica, 1997). Using the range finder, it is possible to measure distances up to 60 m without a reflector and the typical accuracy is ± 5 mm ( Leica, 1997). The three‐dimensional coordinates of the target where the red laser is spotted are calculated automatically. Using the visible laser it is possible to identify the exact target even in a dense forest.

In this paper, ‘trunk’ refers to the thickest stem of a tree, while a stem branching off the trunk is called the ‘primary branch’. When the primary branch forks, the thicker axis is regarded as the continuation of the primary branch. For all major live primary branches contributing to total crown construction (i.e. excluding relatively short ones that seemed to be epicormic shoots), the three‐dimensional position of their base, tip and of several turning points was recorded (Fig. 1A). Primary branches around the top of a trunk (approx. 2 m from the treetop) were not always measured because they were relatively short and thus often invisible. For species other than C. crenata, only primary branches extending towards neighbouring C. crenata trees were surveyed. Positional measurements for the trunk were made for the trunk base, at a height of 1·3 m, and for the treetop (Fig. 1A); tree heights (Table 1) were measured separately with a height pole. The theodolite was positioned at multiple points (‘survey points’) on the forest floor to survey a single tree from different sides. Since the built‐in frame of reference of the theodolite changes every time it is moved to a different survey point, the coordinates of all these survey points had to be linked to one another. Therefore, 15 arbitrarily chosen points (‘reference points’) were established on the forest floor, and the three‐dimensional coordinates of the reference points were determined by ordinary closed traverse survey. The positions of the survey points were then surveyed from some of the reference points to link them together. In this way, all the three‐dimensional data were finally converted into unified coordinates of the study area. The field measurements were conducted between July and early December 1998 (a total of 20 d).

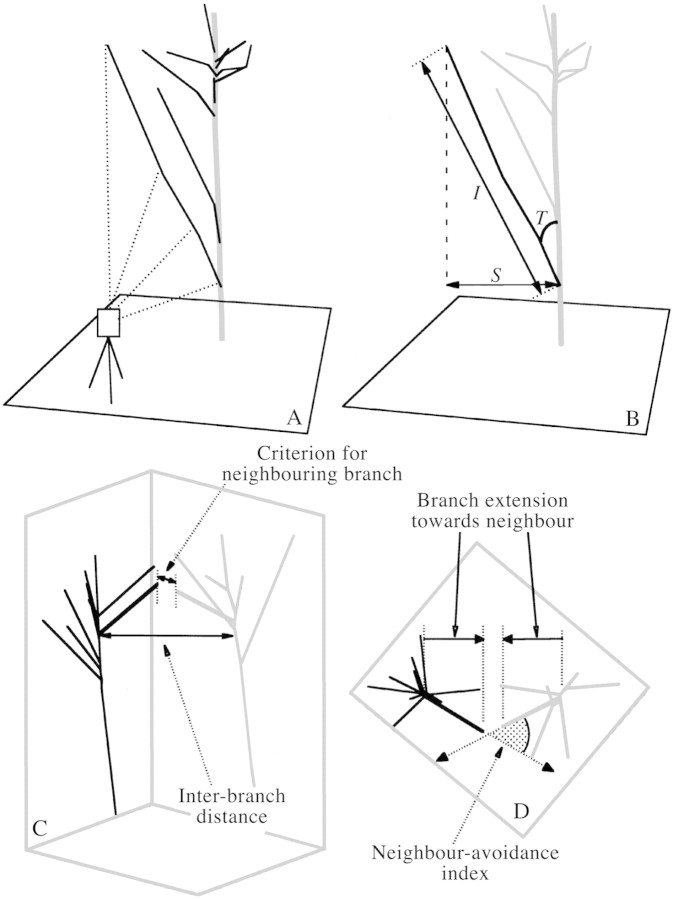
Fig. 1. Schematic illustration of the three‐dimensional measurement of tree structure, and definitions. A, The general structure of a tree was surveyed with a theodolite and whole‐tree structure was reconstructed. B, Branch angle (T), branch spread (s) and branch length (l). C, The neighbouring branch was defined on the basis of the smallest distance between branch tips, while the inter‐branch distance denotes the horizontal distance between branch bases. D, Aerial view of C. ‘Branch extension towards neighbour’ represents the horizontal extension of a target branch from its branch base towards the base of the neighbour branch. The neighbour‐avoidance index (shaded angle) is the supplementary angle (≤180°) of the interior angle between the two vectors showing the direction of horizontal extension of two neighbouring branches.

Since the laser was aimed at the surface of branches and trunks, measured positional data do not represent internal positions of the tree body. Hence positional data were rounded to the nearest 10 cm; because of the large size of trees this procedure does not significantly affect results.

Having obtained three‐dimensional data, the framework of the tree was reconstructed on a personal computer (Figs 1A and 2) using the three‐dimensional line‐graphics facility of a graphics package (DeltaGraph 4·5J; Japan Poladigital, Tokyo, Japan). Branch angle (T, °) and branch length (l, m) were then calculated for each primary branch (Fig. 1B). The branch angle is the angle between the vertical and the straight line from the base to tip of a primary branch. Branch length was represented by the length of the straight line between the base and the tip of the branch (Fig. 1B) because branches were generally straight and the difference between branch length so‐defined and the total length of the partial segments of a branch was only about 10 %. Branch spread (horizontal spread of each primary branch; s, m) was calculated, as in Fig.1 B, by

s = l sin(T)(1)

In analyses of the effect of slope of the forest floor, primary branches of C. crenata were classified according to the horizontal direction of branch extension: branches extending towards the upper side of the slope are termed ‘uphill branches’ (n = 15), while the others are ‘downhill branches’ (n = 37).

To evaluate the effects of the presence of nearby branches, the ‘neighbouring branch’ was defined. For each C. crenata branch, a branch of another tree whose branch tip was nearest to the tip of the target branch of C. crenata was chosen using the three‐dimensional data and was defined as the neighbouring branch (Fig. 1C). The nearest neighbour of a C. crenata branch was sometimes the top of the trunk, not the primary branch. Therefore, in analyses involving neighbouring branches, the part of the trunk above the base of the highest primary branch was regarded as a primary branch for the ten C. crenata trees. The base position of the top‐part of the trunk and that of the highest primary branch are the same in this case. The branch neighbouring a C. crenata branch can be either a heterospecific branch or a conspecific branch of another individual. The primary branches of C. crenata were classified into two groups according to the nature of the neighbouring branch, i.e. ‘C‐C branches’ (C. crenata neighbouring C. crenata, n = 32) and ‘C‐H branches’ (C. crenata neighbouring heterospecifics, n = 30). The branches of the other species neighbouring the C‐H branches are termed ‘H‐C branches’ (n = 30).

The ‘inter‐branch distance’, calculated as the horizontal distance between the base position of a target branch of C. crenata and that of its neighbouring branch, was employed to analyse how two neighbouring branches shared the space between them (Fig. 1C).

Extension of a branch of C. crenata towards its neighbouring branch was represented by the horizontal component of the vector from the base to tip of a C. crenata branch projected to the vertical plane including the positions of the bases of the two branches (Fig. 1D). This value is termed ‘branch extension towards neighbour’. A negative value means that a branch extends towards the opposite side of the neighbouring branch.

To evaluate the effect of neighbouring branches on the horizontal direction of branch extension, we calculated the interior angle (≤180°) between two vectors, each of which is the horizontal component of the vector from the base to tip of a C. crenata branch and that of its neighbouring branch, respectively. The supplementary angle (≤180°) of the interior angle, or the difference between the interior angle and 180°, is referred to as the ‘neighbour‐avoidance index’ (Fig. 1D). The neighbour‐avoidance index is minimum (0°) when each of the two neighbouring branches extends in the direction of the other branch’s base. The index increases as either of the branches extends in a direction that avoids its neighbour, and reaches its maximum value (180°) when the two branches extend in a parallel direction. Incidentally, there were no pairs of C. crenata and neighbouring branches that extended towards the opposite side of the other branch’s base in this study.

Given a target branch and its neighbouring branch, the latter’s neighbouring branch is not always the former. However, if each of these branches is the nearest neighbour of the other and both are C. crenata branches, then duplication of data in the neighbour‐avoidance index occurs because the same values are calculated for the target C. crenata branch and for its conspecific neighbouring branch on the basis of the difference between their horizontal directions. In this case, one set of duplicated data was excluded from the analyses. There were seven such cases out of the 32 C‐C branches (i.e. C. crenata branches neighbouring conspecifics), so that n = 25 for the neighbour‐avoidance index for C‐C branches.

RESULTS

Effects of slope on occurrence and direction of extension of C. crenata branches

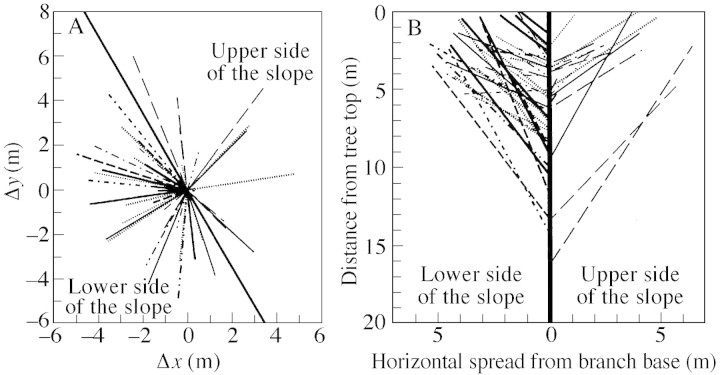
Figure 3A illustrates the horizontal direction and horizontal length of all primary branches of the ten C. crenata trees, with the base position of each branch fixed at the centre of the figure. The ratio of the number of downhill branches to the total number of branches (37/52) was significantly greater than 1/2 (P < 0·05; see Table 2), showing that more branches occurred on the lower side of the slope. However, comparing uphill and downhill branches, there were no significant differences in branch length, branch width, branch angle, height of the tip of a branch, and branch‐base position on the trunk (Fig. 3B, Table 2). These results are also confirmed by the following analyses.

Fig. 3. Horizontal and vertical view of all primary branches of the ten C. crenata trees. The number of uphill and downhill branches was 15 and 37, respectively. Different lines indicate different individual trees. A, Horizontal direction; length of the line is equivalent to branch spread. The thickest diagonal line separates uphill and downhill branches. B, Positions of the base and the tip of all the primary branches, represented by the distance from the top of the tree. Downhill and uphill branches are shown on the left and the right, respectively, of the figure. The horizontal axis shows horizontal extension, and the length of each straight line corresponds to branch length.

Table 2.

Structural properties of uphill (n = 15) and downhill (n = 37) branches of the ten C. crenata trees sampled

	Mean
Branch properties	Uphill	Downhill	Statistics*		Methods of tests
Branch length (m)	5·2	5·2	tS = 0·0605 (N.S.)	d.f. ≈ 21·12	Welch’s t‐test
Branch spread (m)	3·1	3·0	tS = 0·138 (N.S.)	d.f. ≈ 20·72	Welch’s t‐test
Branch angle to vertical (°)	40·8	43·4	TR = 383 (N.S.)		Wilcoxon rank sum test
Branch‐tip height† (m)	2·2	2·2	t = –0·107 (N.S.)	d.f. = 50	t‐test
Branch base position‡ (m)	6·2	6·1	TR = 390 (N.S.)		Wilcoxon rank sum test
	Proportion
Number of branches	15/52	37/52	u = 2·91 (P < 0·05)		Test of significanceof deviation froma binomial proportion of 1/2

*t_S, Welch’s t ‐value; T_R, Rank sum for smaller samples (= uphill branches); u, one‐tailed normal probability calculated from the number of uphill and downhill branches.

^†Height of the tip of a primary branch expressed as the distance from the top of the tree.

^‡Position of the branch base on the main trunk expressed as the distance from the top of the tree.

The relationship between horizontal spread (s) and length (l) of branches on the ten C. crenata trees could be approximated logarithmically:

s = a ln l + b(2)

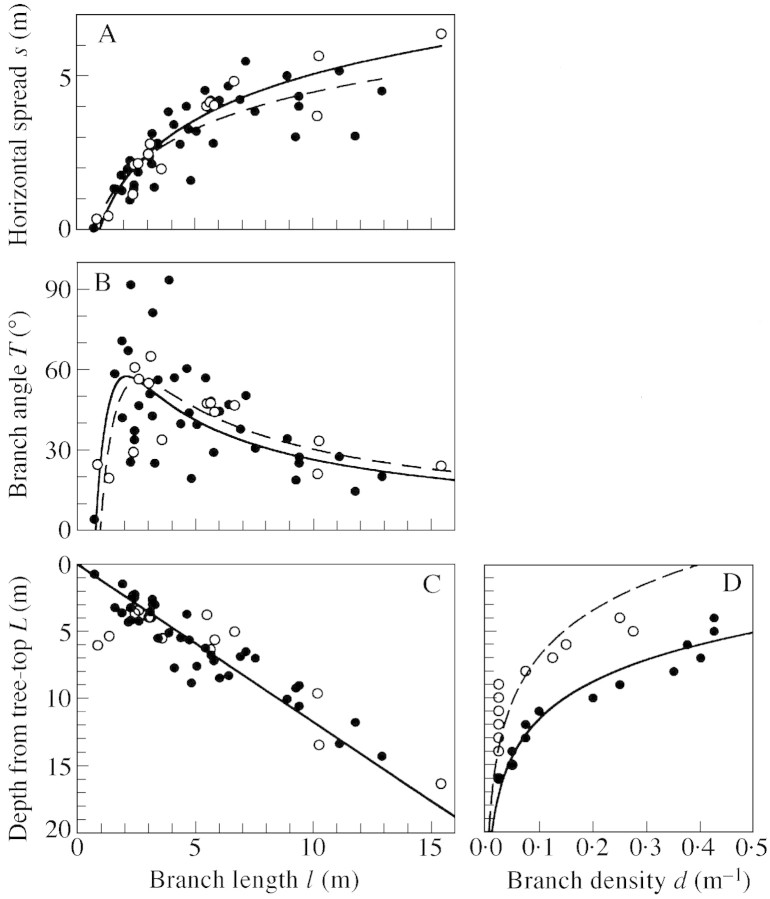
where a and b are constants. Regression lines for the uphill and downhill branches (Fig. 4A) were fitted by the least squares linear regression for s and ln l, and the significance of the regression was tested by ANOVA (P < 0·01). As shown by the convex shape of the regression lines (Fig. 4A), there was limited scope for increasing horizontal spread as branch length increased. Thus, long branches contribute little to the expansion of horizontal crown space. There were no statistical differences in the slopes (d.f. = 48, F = 1·860, P > 0·05) or the intercepts (d.f. = 49, F = 0·847, P > 0·05) of the regression lines between the uphill and downhill branches (ANCOVA).

Fig. 4. General structure of the C. crenata branches. In the four figures, filled circles and solid lines show the downhill branches (n = 37), and open circles and broken lines the uphill branches (n = 15). A, Relationship between branch length (l, m) and horizontal spread (s, m), approximated by s = a ln l + b. The (a, b) values were (1·76, 0·47) for downhill branches (R² = 0·693, d.f. = 36, F = 78·98, P < 0·01), and (2·18, 0·07) for uphill branches (R² = 0·893, d.f. = 14, F = 108·01, P < 0·01). B, Relationship between branch length (l, m) and branch angle from vertical (T, °). Theoretically deduced curves showing T = sin ^–1[(a ln l + b)/l] were drawn, where (a, b) values are those obtained from the s–l relationships in A. C, Relationship between branch length (l, m) and the basal position of the branch on the trunk represented by distance from the top of the tree (L, m). Regression lines are: l = 0·856L for downhill branches (R ² = 0·862, d.f. = 37, F = 224·16, P < 0·01) and l = 0·858L for uphill branches (R ² = 0·772, d.f. = 15, F = 47·38, P < 0·01). D, Relationship between branch density (d, m^–1) and the basal position of the branch on the trunk (L, m). The relationship was approximated by an exponential regression, ln d = –0·246L + 0·551 for the downhill branches (R² = 0·935, d.f. = 12, F = 158·78, P < 0·01) and ln d = –0·201L –0·920 for the uphill branches (R² = 0·666, d.f. = 12, F = 21·93, P < 0·01). The slopes were not significantly different (ANCOVA, d.f. = 22, F = 0·925, P > 0·05), but the intercepts were (ANCOVA, d.f. = 23, F = 35·53, P < 0·01). Note that in C and D the abscissa and ordinate are swapped for presentation.

The relationship between horizontal spread and branch length can be attributed to the relationship between branch angle (from vertical, T) and branch length. Figure 4B shows theoretical lines for the branch length–branch angle (l–T) relationship deduced by substituting s of eqn (2) into eqn (1) [s = l sin(T)], i.e.

T = sin^–1[(a ln l + b)/l](3)

where a and b are constants calculated in eqn (2). Branch angle tended to decrease with increasing branch length for branches over approx. 2 m long, i.e. long branches, which generally joined the trunk lower down, tended to assume an upright position. Branches measuring about 2 m tended to be more horizontal, while branches less than approx. 2 m long, which generally occurred near the top of the trunk, had a smaller branch angle (Fig. 4). Thus very short primary branches in the treetop tended to be vertical.

Branch length was significantly linearly related to base position of the primary branches on the trunk expressed by distance from the top of the tree (L) in both downhill (intercept = –0·18, slope = 0·880, R² = 0·862, d.f. = 36, F = 219·38, P < 0·01) and uphill branches (intercept = –0·41, slope = 0·906, R² = 0·775, d.f. = 14, F = 44·76, P < 0·01) (results not shown). The slopes (d.f. = 48, F = 0·046, P > 0·05) and intercepts (d.f. = 49, F = 0·024, P > 0·05) of these regressions did not differ significantly (ANCOVA). Since the intercepts of the regressions were not significantly different from zero (P > 0·05), the relationship was re‐approximated by proportional regression, l = 0·856L for the downhill branches (P < 0·01), and l = 0·858L for uphill branches (P < 0·01) (Fig. 4C). As the slope of the proportional equation shows, on average the length of primary branches is about 0·86 times the length of the trunk above the base of the branch, for both uphill and downhill branches. This suggests that the mean extension growth rates of the trunk and primary branches are similar.

We also investigated changes in linear density of branches with branch‐base position on the trunk. For each 1 m section of trunk from the top of the tree (distance from tree top, L), the mean number of primary branches was calculated for the ten C. crenata trees. Since this value represents the linear density of primary branches on the trunk, it is hereafter referred to as ‘branch density’. Because not all primary branches could be surveyed near the top of the trunk, data for L < 2 m were excluded. In calculating the value, moving averages of branch density in 4 m depth classes of L were taken. Figure 4D shows vertical changes in branch density on the trunk. The relationship could be approximated by an exponential equation for both the uphill (P < 0·01) and downhill (P < 0·01) branches (Fig. 4D), showing that branch density decreased exponentially on a trunk from the top downward. The slopes of these regressions for uphill and downhill branches were not significantly different (P > 0·05), but the intercepts were (P < 0·01) (Fig. 4D).

Results presented in Table 2 and Fig. 4 indicate that the direction of the slope of the forest floor affected the number of branches, but did not affect other structural properties of the branches. Therefore, differences in the uphill and downhill branches are not taken into account in the following analyses.

Effects of neighbouring branches on horizontal extension of C. crenata branches

Branch extension towards neighbour (Fig. 1D) decreased significantly with decreasing inter‐branch distance in both C‐H (Fig. 5A) and C‐C branches (Fig. 5B). The positive regressions (Table 3) suggest that horizontal extension of a branch became more limited the closer the neighbouring branch. The regression was also positive for H‐C branches, or branches of the other species neighbouring the C‐H branches (Fig. 5A). Although there were no significant differences among the three regressions (ANCOVA, d.f. = 88, F = 2·42, P > 0·05), more C‐H branches appear to have been extending in an opposite direction to the neighbour branch compared with H‐C branches, as shown by several negative values of branch extension when the inter‐branch distance was less than approx. 5 m (Fig. 5A). To confirm this trend, interspecific comparisons for branch extension towards the neighbour were made between C‐H branches and their neighbours (i.e. H‐C branches) by changing the data range of inter‐branch distance (Table 4). Results show that when inter‐branch distance was <5 m and the neighbouring branch of C. crenata was a heterospecific branch, then the horizontal spread of a branch towards its neighbour was significantly less in C. crenata than in the neighbouring heterospecifics. However, as the range of inter‐branch distance increased (see Table 4), differences became non‐significant. An intraspecific comparison of branch extension towards the neighbouring branch was conducted for C‐H branches and C‐C branches (Table 4). When the inter‐branch distance was <3 m, branch extension of C‐H branches was significantly less than that of C‐C branches. This means that horizontal branch extension towards a neighbouring branch was more limited when C. crenata branches were neighbouring heterospecifics than when neighbouring conspecifics. These results are consistent with the relationship between inter‐branch distance and the neighbour‐avoidance index. The neighbour‐avoidance index increased with decreasing inter‐branch distance for C‐H branches (P < 0·01; Fig. 5C, Table 3). On the other hand, the relationship was not significant for C‐C branches (P > 0·05; Fig. 5C, Table 3B). Thus, C. crenata branches tended to extend in a direction that avoided nearby neighbouring branches of heterospecifics, but this trend was not seen when C. crenata branches neighboured conspecific branches.

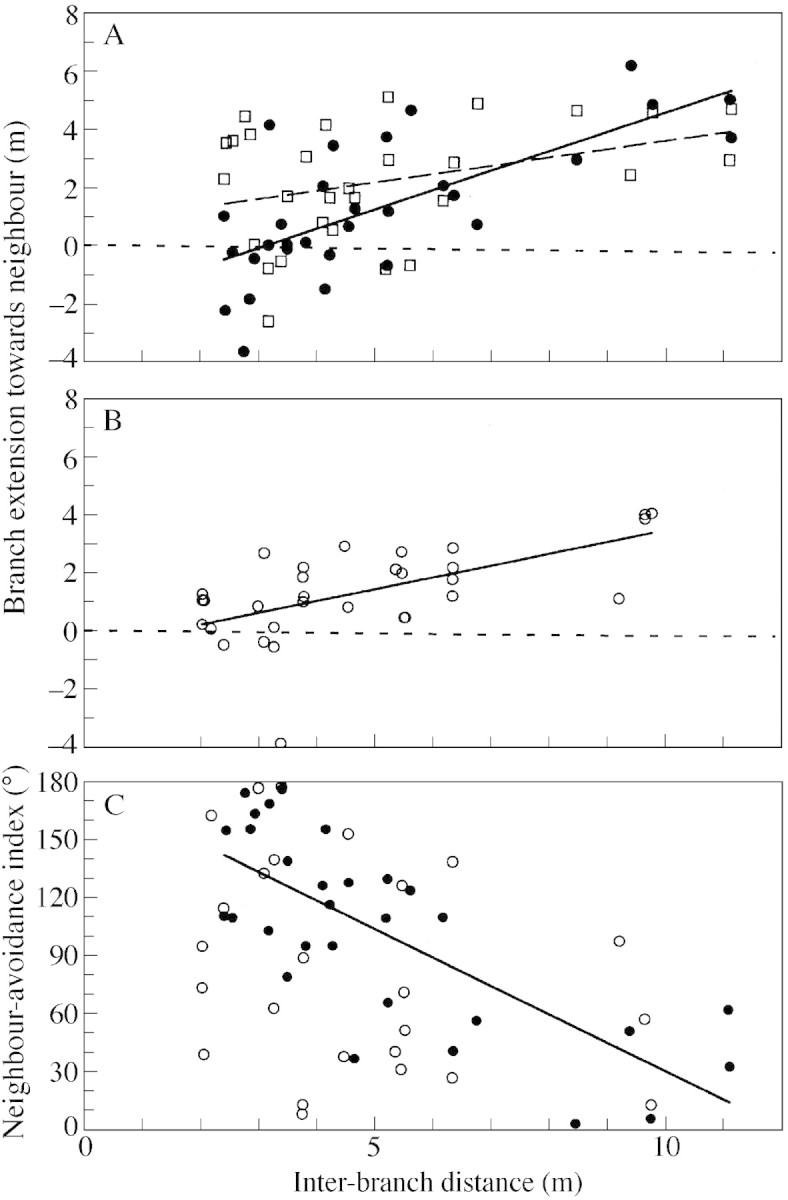
Fig. 5. Effects of inter‐branch distance on horizontal branch extension of C. crenata. In the figures, filled circles represent C‐H branches and open circles represent C‐C branches. Statistics for the regressions are given in Table 3. A, Relationship between inter‐branch distance and branch extension towards neighbour for C‐H branches (solid regression line) and H‐C branches (open squares and broken regression lines). B, Relationship between inter‐branch distance and branch extension towards neighbour for C‐C branches. C, Relationship between inter‐branch distance and neighbour‐avoidance index for C‐H and C‐C branches. The regression was not significant in the C‐C branches (Table 3).

Table 3.

Regression analysis of inter‐branch distance with branch extension towards neighbour (Fig. 5A, B) and neighbour avoidance index (Fig. 5C)

	Species	Branch category	Intercept	Slope	R 2	d.f.	F	P
Branch extension towards neighbour*	C. crenata	C‐H branches	–2·06	0·685	0·517	29	29·99	<0·01
	C. crenata	C‐C branches	–0·59	0·423	0·376	31	18·08	<0·01
	Other spp.	H‐C branches	0·77	0·304	0·143	29	4·682	<0·05
Neighbour avoidance index	C. crenata	C‐H branches	177·36	–14·50	0·551	29	34·42	<0·01
	C. crenata	C‐C branches	119·47	–7·24	0·094	24	2·391	N.S.

*The slopes (d.f. = 86, F = 2·58, P < 0·05) and intercepts (d.f. = 88, F = 2·42, P < 0·05) of the three regressions were not significantly different (ANCOVA).

Table 4.

Tests for intra‐ and interspecific differences in the values of branch extension towards neighbour

		Inter‐branch distance (m)
		<3	<4	<5	<6	<7	<10	<12
Interspecific	S	0	17	42	78	97	131	160
comparison	k	6	12	18	22	25	28	30
	Significance level	<0·05	<0·05	<0·05	N.S.	<0·05	N.S.	N.S.
Intraspecific	T R	28	141	296	465	602	791	911
comparison	n	7	16	18	24	28	32	32
	m	6	12	18	22	25	28	30
	Significance level	<0·05	N.S.	N.S.	N.S.	N.S.	N.S.	N.S.

Comparisons were made for different ranges of inter‐branch distances. The interspecific comparison tested differences between C‐H branches (C. crenata) and H‐C branches (other spp.) neighbouring each other; one‐tailed Wilcoxon signed‐ranks test with the alternative hypothesis that C‐H branches had a smaller value for branch extension than H‐C branches. S, Sum of (negative) signed‐ranks for C‐H branches; k, number of C‐H branches (= the number of H‐C branches). The intraspecific comparison for branches of C. crenata tested differences between the C‐C and C‐H branches; one‐tailed Wilcoxon rank sum test with the alternative hypothesis that C‐H branches had a smaller value for branch extension than C‐C branches. T_R, Total rank calculated for the C‐H branches; n and m, number of C‐C and C‐H branches, respectively. See also Fig. 5.

DISCUSSION

Effects of slope

Slope direction had a pronounced effect on branch number in C. crenata. More primary branches occurred on the lower side of the slope (Table 2). As shown in Fig. 4D, there was a consistent tendency for branch density to be lower in uphill compared with downhill branches, irrespective of position on the trunk. A possible explanation for this is that fewer branches were produced or survived on the upper side of the slope where they may be more shaded by the taller crowns that occur there. To confirm this, studies of branch demography (e.g. Koike, 1989; Suzuki, 2001) combined with measurements of light conditions and positions of branches would be necessary.

Another explanation for the difference in branch number is that it is not the effect of the slope, but is instead the effect of the main direction of incident solar light (Rouvinen and Kuuluvainen, 1997): more branches simply exist on the southern side (note that the slope direction was WSW). However, in a similar study in another hardwood forest, 80·7 % of the 180 primary branches of 20 Quercus serrata Murray trees extended towards the lower side of the slope, which faced north‐east with a slope of 24° (Togashi, 2000). Hence it is possible that slope direction rather than the southern aspect had the major effect in this study.

Vertical angle and length of C. crenata branches: implications for branch survival

The uphill and downhill branches had similar patterns of branch length and branch angle, but they differed in number (Fig. 4). This suggests that apart from the different horizontal directions of uphill and downhill branches, the major primary branches showed similar patterns of extension growth and branch angle, mainly dependent on the branch‐base position on the trunk (Fig. 4C), or on branch age. Extension growth of the existing branches may not have been affected by neighbours or the slope, probably because they could grow towards available open space, avoiding neighbouring branches (Fig. 5).

The tip of a long branch, which is generally joined to the lower part of the trunk and is thus older, can exist in the canopy layer owing to its upright angle (Figs 3B and 4B). This arrangement would contribute to the expansion of the live crown to a higher position in the canopy. However, it is clear that for a given branch length, there is a trade‐off between vertical extension by a more upright branch angle and horizontal extension by a more horizontal angle. Retaining longer branches does not lead to horizontal expansion of the crown due to their upright positioning (Figs 3 and 4A). However, given the relatively high light demands of C. crenata (Segawa, 1985), extending branches vertically is important for branch survival; branches extending horizontally would be shaded by neighbouring crowns, reducing the chances of survival. Hence the upright angle of longer branches of C. crenata is advantageous because it avoids being overtopped by neighbouring branches (Sumida et al., 2001).

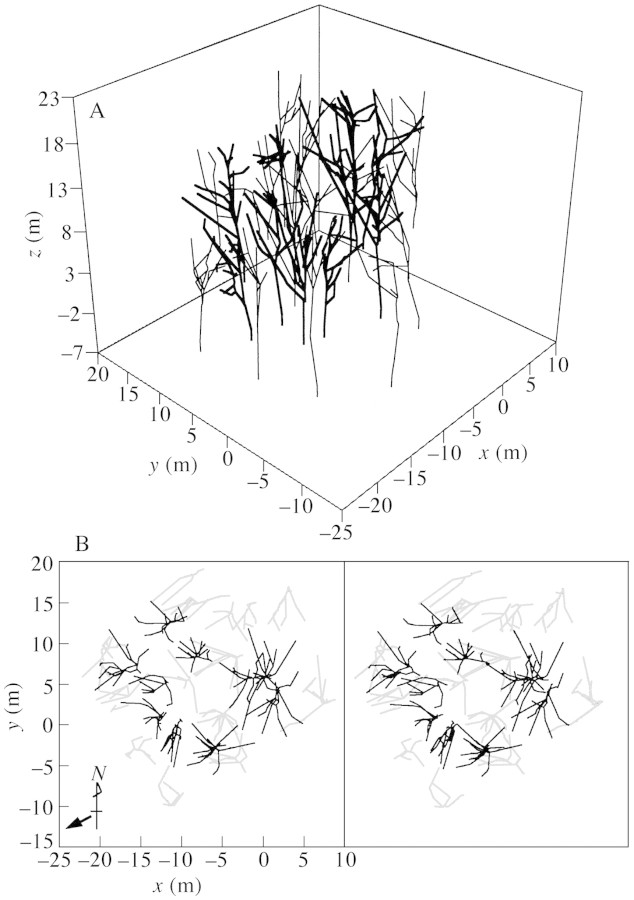
Trunks were also affected by the direction of the slope. As shown in Fig. 2B, trunks of many trees lean towards the lower side of the slope. In fact, the horizontal positions (x, y) of the crown bases of all ten C. crenata trees were biased towards the lower side of the slope (negative values of x and y) from their trunk‐base positions due to the lean of the trunk. The trunk below the crown base (mean height = 8·0 m, s.d. = 3·2 m) had an average lean of 7·1° (s.d. = 1·9°). While differences in branch length and branch angle were not detected between the uphill and downhill branches (Fig. 3, Table 2), the lean of the trunk could make the whole crown develop towards the lower side of the slope (Umeki, 1995a, b).

Fig. 2. Overview of the study plot reconstructed from the three‐dimensional data. A, A bird‘s‐eye view. B, A stereogram, viewed from above. Castanea crenata trees are indicated by solid lines. The thick arrow indicates the downhill slope.

Effects of neighbours on horizontal extension of C. crenata branches

If the horizontal distribution of individual trees of a given species in a community is aggregated, then the length of the periphery of the crown neighbouring heterospecific crowns is less than if trees are distributed regularly or randomly. That is, an aggregated distribution of individuals can lessen the probability that a branch meets a heterospecific neighbouring branch. In the case of C. crenata, branch extension towards the neighbour was more limited when the neighbouring branch was a heterospecific branch than when it was a conspecific branch (Fig. 5A, B and Table 4). This implies that development of a C. crenata crown is more limited when it is surrounded by crowns of heterospecifics. However, in the 1 ha study area, canopy trees of C. crenata (n = 43) were significantly aggregated on a scale of 1750 m², 348 m² and less [Morisita’s I‐δ analysis (Morisita, 1959); Teranishi, 1998]. In the area studied (approx. 500 m²) nine of the ten C. crenata trees had conspecific neighbouring branches, i.e. both C‐H and C‐C branches, owing to the aggregated distribution of C. crenata trees on the forest floor. Aggregation of conspecific individuals often profits less competitive species by increasing their survival and coexistence with other species in the community (Stoll and Prati, 2001). Similarly, aggregation of individual trees of C. crenata might increase their chance of survival through reduced limitation of crown expansion by heterospecifics. The occurrence of neighbouring conspecific crowns as a result of the aggregated distribution of individuals may in part account for the persistence of C. crenata in this forest, despite being less able to extend branches horizontally compared with neighbouring heterospecifics.

Branch extension

During crown structure development, the horizontal spread of C. crenata branches became narrower than that of heterospecifics. One possible explanation for this concerns differences in leaf phenology. Komiyama (1991) and Kato et al. (1999) investigated patterns of leaf phenology in 30+ tree species in the same forest. In 1997, leaf flush in C. crenata began at the beginning of June and ended in mid‐July (Kato et al., 1999). However, leaf flush in the neighbouring species began in May, and their leaves finished opening by mid‐June, about 1–1.5 months earlier than leaves of C. crenata. Leaves of C. crenata have also been observed to flush later than those of other canopy trees in a cool temperate forest in northern Japan, which has a similar species composition and mean annual temperature to our study forest (Kikuzawa, 1983). Ozawa et al. (2000) reported that the development of C. crenata leaves after bud break was slower than that of other dominant canopy species (Q. serrata and Carpinus laxiflora Blume), in a secondary forest in cool/warm temperate transitional region in central Japan. Thus it seems that C. crenata trees generally start opening their leaves after other neighbouring species have almost completed leaf expansion. It is therefore possible that the reason C. crenata branches neighbouring heterospecifics show a neighbour‐avoiding tendency while those neighbouring conspecifics do not when inter‐branch distance is short (Fig. 5C, Table 4) is as follows: annual shoots of C. crenata grow away from already‐existing foliage on nearby neighbouring shoots of heterospecifics to gain more light, and/or only shoots growing away from the neighbour survive because of the high light demands of C. crenata.

In summary, the later leaf‐flush of C. crenata may result in a more restricted horizontal expansion of a branch when it neighbours a close‐by heterospecific branch; this can lead to a narrow crown and ultimately to the decline of tree growth. However, the chances of C. crenata branches neighbouring heterospecifics are small because individual trees of C. crenata tend to be aggregated in the forest. Aggregation of trees may be responsible, in part, for the dominance of C. crenata in forests despite its late leaf‐flush pattern which appears disadvantageous for crown development.

Incidentally, in the 1 ha forest, the distribution of individual trees of canopy species that flushed later (n = 86; including 43 canopy trees of C. crenata) was more aggregated on the scale of <109 m² than that of other canopy trees that flushed earlier (n = 308) [Morisita’s I‐δ analysis Morisita (1959); Teranishi, 1998]. There might be a general tendency for tree species that flush later to have an aggregated distribution of individuals.

In this study we have demonstrated the importance of branch‐scale structure on inter‐crown interaction in hardwood communities. However, structural information alone can only provide an indirect explanation of community dynamics. Further analyses incorporating chronological investigations of structure and growth are necessary to clarify the mechanisms of competition and coexistence of tree species in forest communities.

ACKNOWLEDGEMENTS

We are grateful to Yukari Terada, Masato Mukai, Tomohiro Mano and other students of the Laboratory of Forest Ecology, Gifu University, for their assistance with fieldwork, and to Toshihiko Hara, Jun‐ichiro Suzuki, Hiroaki Ishii, Peter Stoll, Akira Osawa and Akio Takenaka for critical comments on an earlier draft. We also thank Hervé Sinoquet for useful comments on the manuscript. This research was supported by the Ministry of Education, Science, Sports and Culture, Japan, through a Grant‐in‐Aid for Scientific Research (B) (No.10440233), 1998–2001.

Received: 18 June 2001; Returned for revision: 2 August 2001; Accepted: 19 November 2001.