Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2002 Jul 1;90(1):99–110. doi: 10.1093/aob/mcf153

Tillering in Grain Sorghum over a Wide Range of Population Densities: Modelling Dynamics of Tiller Fertility

T A LAFARGE 1,*, G L HAMMER 2,3
PMCID: PMC4233857  PMID: 12125777

Abstract

The prediction of tillering is poor or absent in existing sorghum crop models even though fertile tillers contribute significantly to grain yield. The objective of this study was to identify general quantitative relationships underpinning tiller dynamics of sorghum for a broad range of assimilate availabilities. Emergence, phenology, leaf area development and fertility of individual main culms and tillers were quantified weekly in plants grown at one of four plant densities ranging from two to 16 plants m–2. On any given day, a tiller was considered potentially fertile (a posteriori) if its number of leaves continued to increase thereafter. The dynamics of potentially fertile tiller number per plant varied greatly with plant density, but could generally be described by three determinants, stable across plant densities: tiller emergence rate aligned with leaf ligule appearance rate; cessation of tiller emergence occurred at a stable leaf area index; and rate of decrease in potentially fertile tillers was linearly related to the ratio of realized to potential leaf area growth. Realized leaf area growth is the measured increase in leaf area, whereas potential leaf area growth is the estimated increase in leaf area if all potentially fertile tillers were to continue to develop. Procedures to predict this ratio, by estimating realized leaf area per plant from intercepted radiation and potential leaf area per plant from the number and type of developing axes, are presented. While it is suitable for modelling tiller dynamics in grain sorghum, this general framework needs to be validated by testing it in different environments and for other cultivars.

Key words: Sorghum bicolor L. Moench, plant density, thermal time, tiller emergence, cessation of tiller emergence, tiller fertility, leaf area index, source–sink relationships

INTRODUCTION

In crop models, predicting tiller dynamics is essential for accurate prediction of crop leaf area index (LAI) development, which in turn affects grain yield. Sorghum may have zero to four fertile tillers depending on growing conditions and variety (Hammer et al., 1993). Fertile tillers may account for a significant part of the total plant leaf area (up to 60 %) according to variety (Hammer et al., 1987), and of the total grain yield, with proportions ranging from 5 to 80 % depending on density (Lafarge et al., 2002). However, tiller dynamics are not dealt with accurately, if at all, in existing sorghum crop models. Some early models do not deal with tillering either because they consider sorghum to be a uniculm plant (e.g. SORGF; Arkin et al., 1983), or because they operate only in environmental conditions devoid of tiller production [e.g. CERES‐Sorghum (SAT); Birch et al., 1990]. Others have assumed that all axes in the canopy are homogeneous and have similar potential (Maas, 1993). Other models have considered the diminishing contribution of additional tillers in canopy development, but have used fertile tiller number as an input rather than attempting to predict it (Hammer and Muchow, 1994). An attempt was made to simulate tiller dynamics in sorghum in SORKAM using source–sink ratio concepts and assimilate translocation (Rosenthal et al., 1989). However, Heiniger et al. (1997a) showed that yield estimated using this model was insensitive to plant population levels, notably because of aspects associated with assimilate demand required per tiller. The authors tried to improve the modelling of tiller dynamics, but made only modest progress (Heiniger et al., 1997b).

Tiller emergence has generally been analysed on high tillering species, such as wheat, tall fescue or rice, in which primary (from main culm leaf axils), secondary (from primary tiller leaf axils) and even tertiary and quaternary tillers are often produced (Boone et al., 1990; Skinner and Nelson, 1994). It was observed that tiller emergence was driven first by tiller site formation at the base of every leaf associated with leaf production, and secondly by the number of buds that develop into tillers. The concept of site filling, expressed as number of new tillers per tiller per phyllochron (time between appearance of two consecutive leaves), was introduced by Davies (1974) and generalized by Neuteboom and Lantiga (1989). Site filling was maximized in spaced plants or early in seedling development (Skinner and Nelson, 1992) when a large number of tiller buds developed into tillers. Consequently, at this early stage of development, the tiller emergence rate was related to the leaf appearance rate (Davies and Thomas, 1983). In wheat and barley, tiller site formation has been related to leaf appearance on the main culm by a Fibonacci series to determine potential tiller emergence in spaced plants (Kirby et al., 1985; Boone et al., 1990). This approach implied (1) a linear relationship between tiller sites and leaf appearance for each culm; and (2) an identical rate of leaf appearance for each axis at any time (Masle‐Meynard and Sébillotte, 1981; Klepper et al., 1982; Kirby, 1995). So, before the occurrence of any stress, a linear relationship was observed between tiller emergence expressed on a logarithmic scale (relative tillering rate, RTR) and main culm leaf appearance, for tall fescue, wheat and perennial ryegrass (Skinner and Nelson, 1992; Bos and Neuteboom, 1998; Gautier et al., 1999). Because emergence of secondary tillers is exceptional in sorghum, the relationship between tiller emergence and leaf appearance has been shown to be almost linear (Major et al., 1982; Carberry et al., 1993).

The onset of a reduction in tiller emergence in response to detrimental environmental conditions has often been analysed in terms of deviation from the potential linear relationship in high tillering species (Kirby et al., 1985; Bos and Neuteboom, 1998; Gautier et al., 1999). If RTR were related to relative shoot growth rate (RGR), as it is in rice and tall fescue for example (Schnier et al., 1990; Sugiyama, 1995), a decrease in tiller emergence could be related to reduced RGR and cessation associated with a threshold RGR (6 % d–1) below which tiller senescence starts (Dingkuhn et al., 1991). This value proved to be stable for different varieties, sowing methods and levels of water limitation, but differed with growth stage and was only valid during the vegetative phase (Schnier et al., 1990). Other studies have indicated that cessation of tiller emergence is probably not the result of reduced assimilate availability in the plant. Deregibus et al. (1985) and Ballaré et al. (1987) observed that a decrease in tiller emergence occurred prior to any appreciable mutual shading and depletion of assimilate resources. Indeed, tiller (or stolon) production was reported to be reduced by a change in light quality for forage species, ryegrass, tall fescue, wheat, white clover and barley (Deregibus et al., 1985; Casal et al., 1986; Kasperbauer and Karlen, 1986; Robin et al., 1992; Davis and Simmons, 1994). The relationship between light quality and tiller emergence was confirmed when Casal et al. (1986) observed that an artificial increase in red light at the base of the plant enhanced tiller emergence, and when Gautier et al. (1995) observed that an artificial increase in far‐red light inhibited production of axes in clover. In fact, because green leaves absorb most of the red and reflect much of the far‐red light, the ratio of red : far‐red light decreases as density increases (Kasperbauer, 1987). While this situation has not yet been reported in sorghum, the nature of the response, the associated mechanism and evidence from numerous species indicate likely generality. Hence, it is likely that an architectural plant or canopy variable could account for the light quality mediated effect of plant competition on cessation of tiller emergence.

Tiller fertility has not been quantified in detail in most studies on tillering. In some cases, tiller number dynamics were observed from emergence to maturity, but no distinction was made between fertile and non‐fertile axes (Bauer et al., 1984; Schnier et al., 1990; Moot et al., 1996). In other cases, the proportion of fertile tillers was observed without any mention of tiller dynamics (Gerik and Neely, 1987; Mitchell et al., 1998; Wu et al., 1998). When both tiller dynamics and fertility were considered, cessation in development of individual tillers was either not identified (Cannell, 1969a; Ishag and Taha, 1974; Darwinkel, 1978), or was simply related to tiller age in very controlled conditions (Ong, 1984).

The central idea for predicting tiller fertility in this study was to explore the concept of potential leaf area development, which was established according to tiller developmental stage and the ensuing growing conditions. This potential could be contrasted with the realized leaf area that the plant could achieve at the same time given the assimilates available. Assimilate supply could be estimated independently of plant density and tiller number from leaf area index and light interception. Lafarge and Hammer (2002) observed that the stability, over a range of plant densities, in the extinction coefficient, radiation use efficiency, shoot assimilate partitioning and specific leaf area at the plant level for sorghum provided a reliable way to predict leaf area production regardless of plant density. This approach relates closely to concepts of source–sink interaction and assimilate balance in the plant. Once assimilates become limiting, cessation in the progression of tillers towards fertility would occur in a strict order regardless of plant density according to the common tiller hierarchy identified by Lafarge et al. (2002).

The objectives of this study were therefore: (1) to quantify the dynamics of tiller number per plant for a sorghum cultivar based on tiller emergence and fertility; and (2) to identify predictive relationships underpinning these dynamics for a wide range of assimilate supplies and light quality conditions established by growing plants at a wide range of densities in a field study. Care was taken to ensure that water and nutrient supplies were non‐limiting.

MATERIAL AND METHODS

Growing conditions and field measurements associated with the field experiment are detailed in Lafarge et al. (2002) and Lafarge and Hammer (2002). In brief, plants were grown at one of four densities, D1–D4, corresponding to two, four, eight and 16 plants m–2, with a non‐limiting supply of water and nutrients.

Description of the modelling approach

Definitions and structure.

Predicting tiller dynamics involves studing both tiller emergence and tiller senescence. Changes over time in live tiller number and potentially fertile tiller number per plant were determined by non‐destructive measurements. A tiller was considered alive on the day of measurement if one or more of its leaves was green. A tiller was considered potentially fertile (a posteriori) on the day of measurement if the number of fully expanded leaves had increased by the next measurement (1 week later). In this study, all tillers that ceased developing at any time did not resume growth again, so that once this had occurred the tiller was removed from the pool of potentially fertile tillers. A live tiller that failed to continue to develop was considered senescent. Kirby and Riggs (1978) and Lauer and Simmons (1988) identified non‐surviving tillers in a similar manner by observing the decline in leaf emergence before any visible signs of leaf senescence. Tillers that developed no more than two leaves (shoot dry weight <0·5 g) were not included here as they did not contribute significantly to assimilate balance of the plant. They were still heterotrophic at this stage as no associated nodal root had appeared (Klepper et al., 1984). Tiller dynamics were described and quantified using three variables: tiller emergence; cessation of tiller emergence; and decrease in number of potentially fertile tillers.

Tiller emergence

Tiller emergence was defined as the increase in tiller number per plant with time. The number of emerged tillers was recorded weekly on tagged plants in each plot and was related to thermal time and full expansion of leaves on the main culm (i.e. ligule appearance). Additional data from weekly quadrat harvests, measured before maximal tiller number per plant was obtained, were included so that observations on tiller emergence were available every 3–4 d at early stages. For the quadrat data, the number of fully expanded leaves on the main culm on the day of measurement was estimated from the regression of fully expanded leaf number on thermal time derived from measurements on tagged plants. Delay in onset of tiller emergence, expressed as the number of fully expanded leaves on the main culm estimated at the time of emergence of the first tiller, was determined as the x‐intercept of the linear regression of plant tiller number vs. the number of fully expanded main culm leaves.

Cessation of tiller emergence

During the period of tiller emergence, the number of emerged tillers could be approximated by a linear function on thermal time. The thermal time at which maximal tiller number per plant was achieved was defined as the thermal time at which the regression of the number of emerged tillers on thermal time reached the maximal tiller number. This was calculated by interpolation between consecutive measurements, which were up to 1 week apart.

Decrease in number of potentially fertile tillers

Using non‐destructive observations on tagged plants, the number of potentially fertile (Fig. 1) and senescent tillers was established a posteriori for each tiller origin and for plants at each density. The decrease in the number of potentially fertile tillers per plant was determined by regressing potentially fertile tiller number on thermal time. The decrease was taken as the average rate of decline between the thermal time at cessation of tiller emergence and the thermal time at which there was no further change in potentially fertile tiller number. This was determined from the slope of the associated linear regression for each replicate.

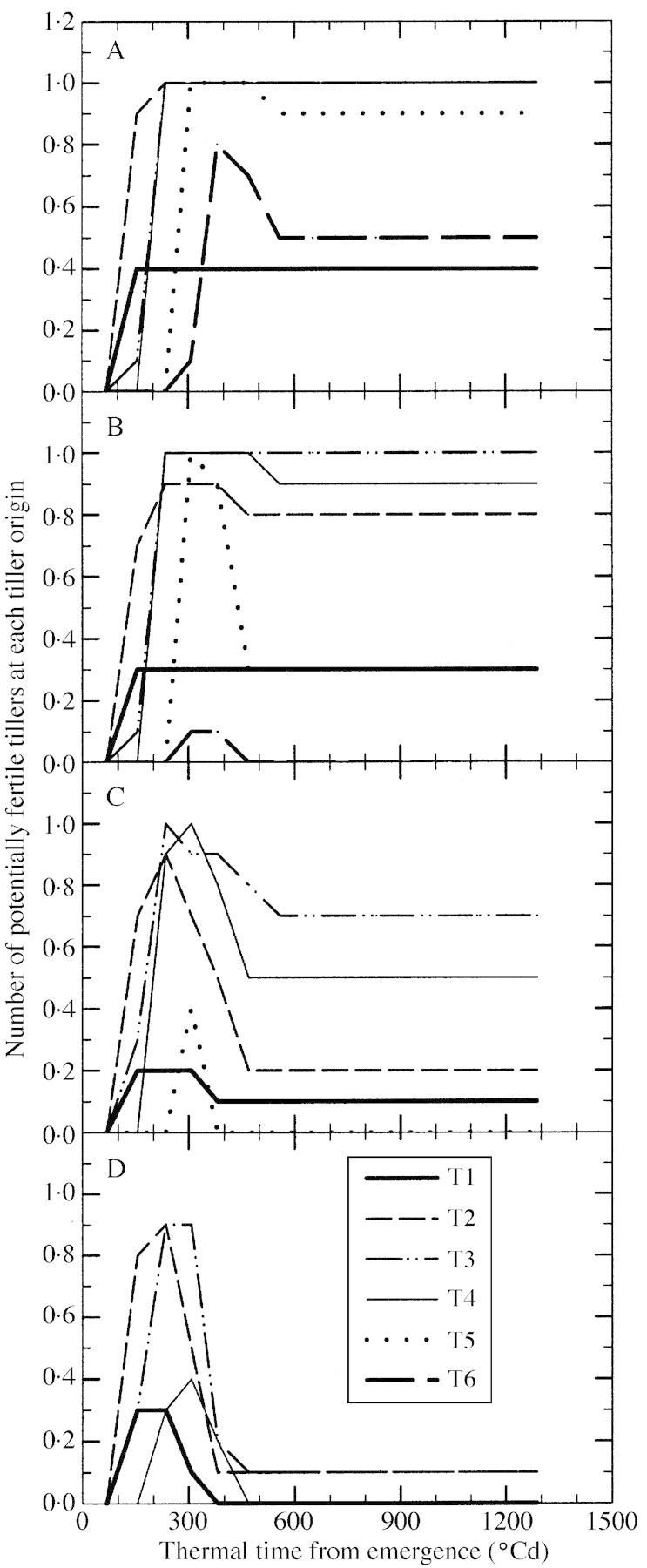
graphic file with name mcf153f1.jpg

Open in a new tab

Fig. 1. Change with thermal time from emergence in number of potentially fertile tillers for each tiller origin for plants grown at a density of two (A), four (B), eight (C) and 16 (D) plants m–2.

Dynamics of total leaf area per fertile culm

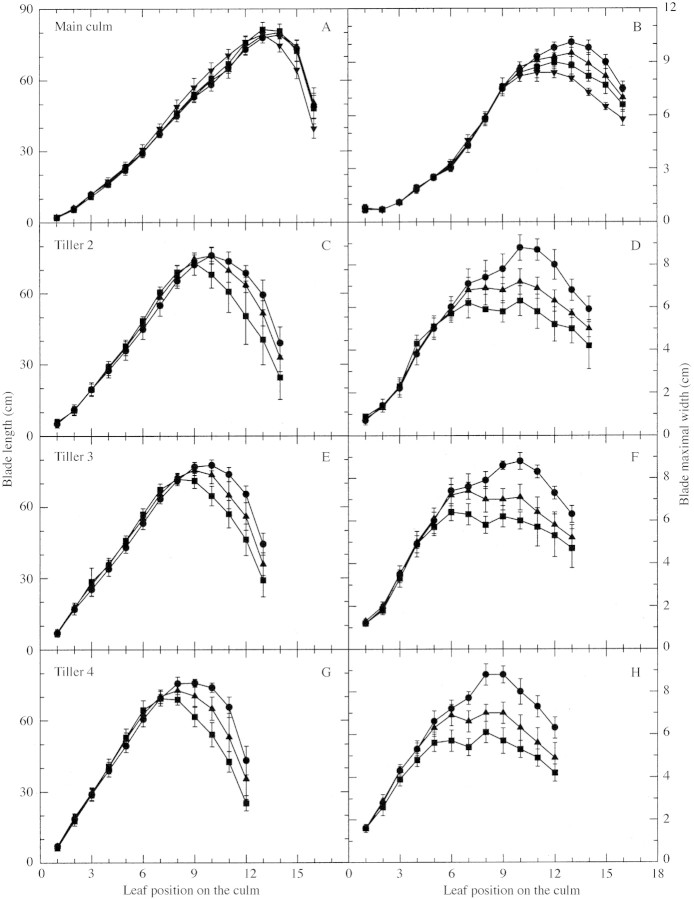
Total leaf area (Fig. 2) of fertile culms was estimated weekly from non‐destructive observations of the appearance of fully expanded leaves combined with the measured area of individual mature blades using the approach reported by Muchow and Carberry (1990). These authors noted that total leaf area of culms was best predicted using a known leaf size–leaf number relationship, by adding 1·6 to the number of fully expanded leaves before accumulating individual blade areas. In this way, the contribution of leaves not yet fully expanded was incorporated in the estimate of culm total leaf area. The area of individual mature blades on these plants was determined non‐destructively from measurements of length and maximal width of each blade. Blade area was calculated by multiplying length, maximal width, and a coefficient of allometry of 0·685 (Lafarge et al., 2002). Non‐destructive observation of total leaf area production on tagged plants avoided any confounding associated with leaf senescence that might occur with destructive sampling.

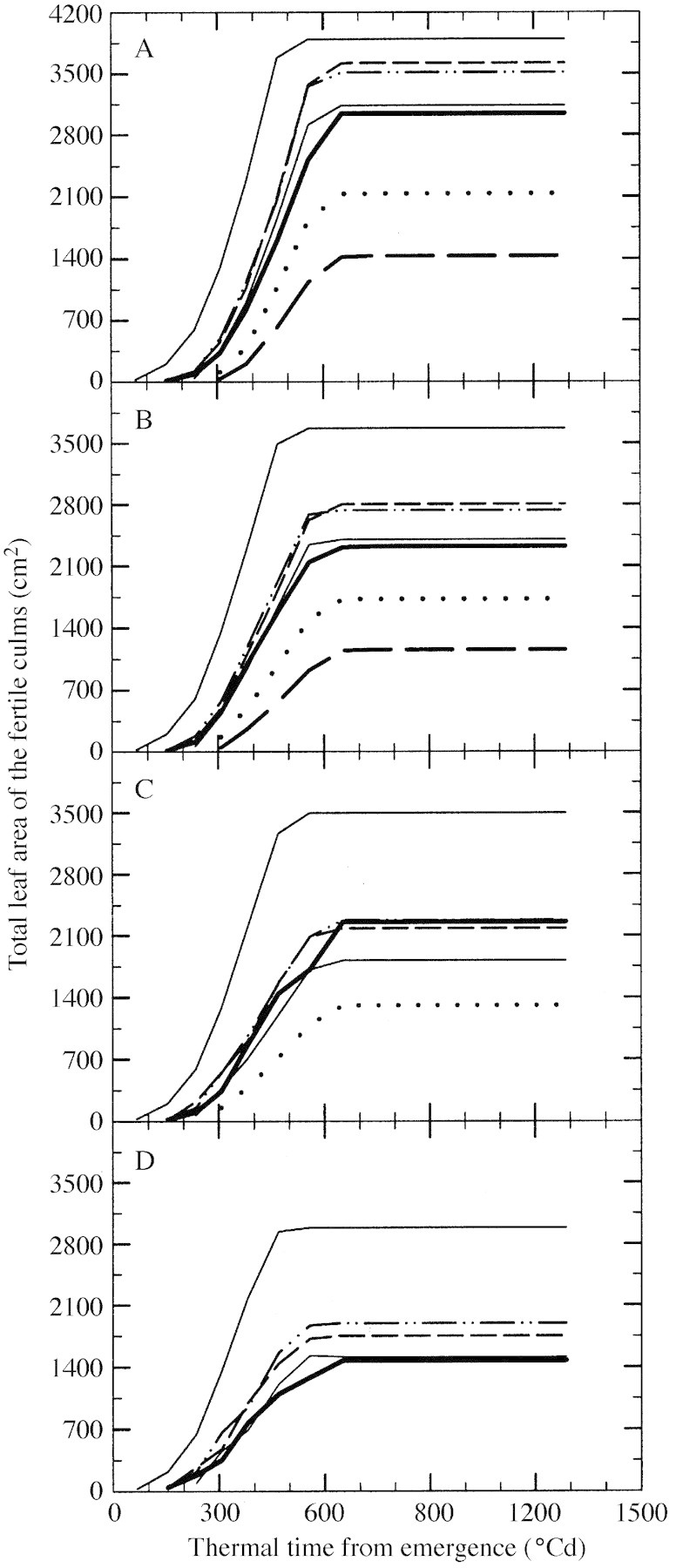
graphic file with name mcf153f2.jpg

Open in a new tab

Fig. 2. Change with thermal time from emergence in total leaf area of each fertile culm for plants grown at a density of two (A), four (B), eight (C) and 16 (D) plants m–2. The thin solid line represents the main culm; all other line styles for each tiller origin are as shown in Fig. 1.

Realized leaf area

Realized leaf area development on the tagged plants in each plot was calculated weekly, for the coming week, as the increase in plant leaf area between two consecutive observations. On the day of each observation, plant leaf area was calculated by accumulating the areas of all expanded and partially expanded, green and dead leaves on all culms that had appeared by that time. In a second method, the increase in realized plant leaf area was predicted daily, then weekly, independently of plant density, from initial leaf area index and incident radiation. This was based on a stable extinction coefficient (0·56) and radiation use efficiency (1·24 g MJ–1), combined with stable relationships with thermal time for shoot assimilate partitioning and specific leaf area (Lafarge and Hammer, 2002). Realized plant leaf area was estimated daily from the value of the plant leaf area ratio (LAR), which is the proportion of net above‐ground biomass partitioned to leaf area. A unique model of LAR on thermal time was fitted for this range of plant densities:

L = ae–bT + c

where L = LAR, T = thermal time, a = 307, b = 0·0026 and c = 11.

Potential leaf area

Potential leaf area development of the tagged plants in each plot was estimated weekly, for the coming week, as the increase in plant leaf area that would have occurred if all tillers that were potentially fertile on the day of an observation had continued to develop during the coming week. On the day of an observation, plant leaf area was calculated as noted above for the realized leaf area. The leaf area that would have developed on each culm a week later was determined from measurements, averaged per plot, of appearance rate of fully expanded leaves and leaf size carried out on the same type of tillers, grown in the same conditions, that had continued to develop during that week.

RESULTS

Plant density did not affect the rate of tiller emergence whereas cessation of tiller emergence was delayed as density decreased, and rate of decrease in number of potentially fertile tillers increased with density

Tiller emergence from the whorl started 120 °Cd after seedling emergence in all four plant densities (Fig. 3). Tiller number per plant increased at the same rate for all densities until a maximum number of tillers per plant was reached. The maximum number of live tillers per plant decreased with increasing density (Fig. 3A), being 5·3, 4·3, 3·4 and 2·5 for plants grown at a density of two, four, eight and 16 plants m–2, respectively. Live tiller number remained stable at this level for some time before tiller senescence commenced. The maximum number of potentially fertile tillers per plant was similar to the maximum number of live tillers, with values for the four density treatments of 5·3, 4·3, 3·2 and 2·4, respectively (Fig. 3B). However, the number of potentially fertile tillers decreased much sooner, especially at the higher densities. The decrease commenced immediately after emergence of the final tiller. The rate of decrease in the number of potentially fertile tillers per plant varied strongly with density. It increased from 0·017 to 0·108 tillers °Cd–1 as density increased from two to 16 plants m–2. The end of the decrease appeared synchronous among treatments and corresponded approximately to ligule appearance of the final leaf on the main culm. The number of fertile tillers per plant at maturity decreased with increasing density, with values of 4·9, 3·3, 1·5 and 0·2, respectively, for the four density treatments. The same values were observed for the number of live tillers per plant at maturity, indicating that tillers that had not become fertile were all dead at maturity (Fig. 3A). Final fertile tiller number per plant was already established by the time of full expansion of the final leaf on the main culm (Fig. 3B), whereas all emerged tillers were still alive at this time. Some non‐fertile tillers died only just before maturity, 700 °Cd after full expansion of the final leaf (Fig. 3A).

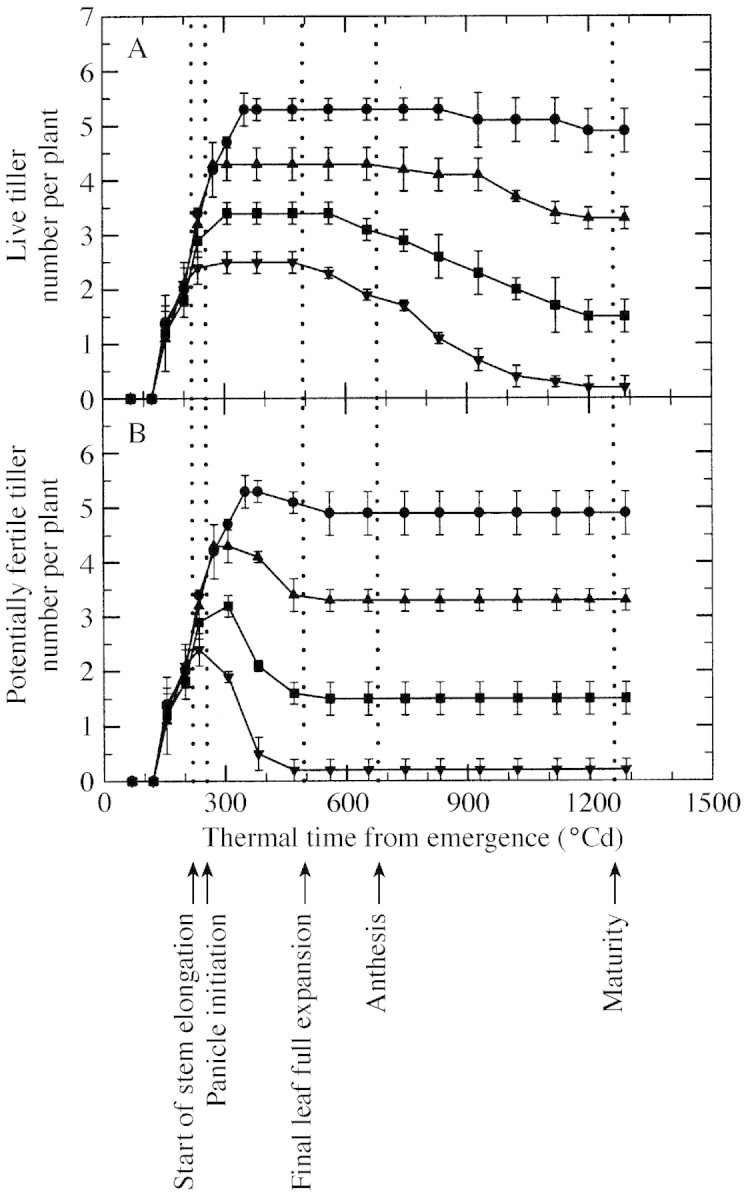
graphic file with name mcf153f3.jpg

Open in a new tab

Fig. 3. Change with thermal time from emergence in number of live tillers per plant (A) and number of potentially fertile tillers per plant (B) for plants grown at a density of two (circles), four (upward pointing triangles), eight (squares) and 16 (downward pointing triangles) plants m–2. Vertical lines represent s.e.m. of three replications. Timing of phenological events indicated by dotted lines relates to the main culm.

The modelling approach pursued here focused on the dynamics of potentially fertile tiller number per plant as these tillers were the ones that would contribute significantly to canopy development, crop growth and yield, and that would participate actively in source–sink interactions. Hence, three components that generate these dynamics were examined: tiller emergence; cessation of tiller emergence; and decrease in number of potentially fertile tillers per plant.

Tillers emerged linearly with thermal time at the same rate as fully expanded leaves appeared on the main culm, with no significant differences among density treatments

The number of emerged tillers per plant increased linearly with thermal time for the duration of tiller emergence at each density (Fig. 4A). Responses did not differ significantly among densities, so a single regression line was fitted. As the appearance of fully expanded leaves on the main culm also responded linearly to thermal time independently of plant density (Lafarge et al., 2002), a single linear regression was fitted for the number of emerged tillers on the number of fully expanded main culm leaves (Fig. 4B). The slope of this regression was 0·99, indicating one newly emerged tiller for each additional fully expanded leaf. Besides emergence of T3 occurred at the full expansion of leaf 6 on the main culm, irrespective of whether or not T1 and/or T2 was present. This indicated that emergence of a tiller occurred strictly at the same time as the appearance of the ligule of the leaf positioned three ranks above its subtending leaf. Delay in the onset of tiller emergence also did not differ significantly among densities; it was calculated as 3·9 fully expanded leaves on the main culm.

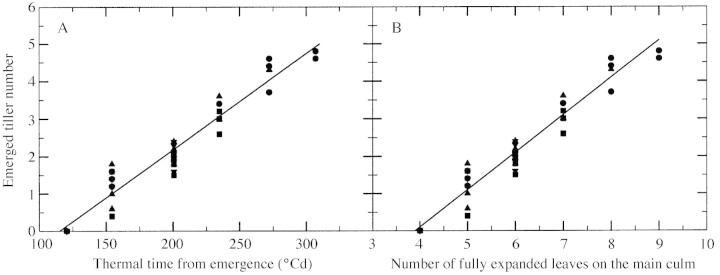
graphic file with name mcf153f4.jpg

Open in a new tab

Fig. 4. Change in emerged tiller number with thermal time from emergence (A) and with number of fully expanded leaves on the main culm (B) using data from each of the three replications at a density of two (circles), four (upward pointing triangles), eight (squares) and 16 (downward pointing triangles) plants m–2 before cessation of tiller emergence had occurred. Solid lines show the corresponding linear regressions; slopes are 0·026 for (A) and 0·99 for (B).

Cessation of tiller emergence occurred at a similar leaf area index regardless of plant density

Cessation of tiller emergence was examined in relation to canopy development (Fig. 5). The leaf area index (LAI) value at the time of cessation was determined for each field plot by linear interpolation between values of the two consecutive LAI measurements around this thermal time (see example for treatment means in Fig. 5 insert). The mean LAI values were 0·55, 0·72, 0·65 and 0·65 for plants grown at a density of two, four, eight and 16 plants m–2, respectively. When the individual data from the 12 plots were considered, a single LAI value of 0·64 ± 0·13, independent of plant population, was relevant to the timing of cessation of tiller emergence (Fig. 5). A similar result, 0·65 ± 0·14, was found if LAI at the time of cessation was determined using a logistic function fitted on values corresponding to the five LAI measurements closest to that time (data not shown).

graphic file with name mcf153f5.jpg

Open in a new tab

Fig. 5. Relationship between duration of the period from seedling emergence to cessation of tiller emergence and LAI calculated at the time of cessation of tiller emergence, using data from each of the three replications at a density of two (circles), four (upward pointing triangles), eight (squares) and 16 (downward pointing triangles) plants m–2. The vertical dashed line represents the mean LAI values. The inset shows change in LAI with thermal time from emergence and indicates the interpolation procedure used to estimate LAI at the time of cessation of tiller emergence. Data points are means, and bars represent s.e.m. of three replications.

Rate of decrease in number of potentially fertile tillers per plant was related to the ratio of realized to potential leaf area growth

A significant relationship was obtained between the rate of change in the number of potentially fertile tillers per plant and the ratio of realized to potential leaf area growth when realized leaf area was determined from direct leaf area measurement (Fig. 6). This relationship appeared to be linear (R2 = 0·80) and common for the large range of tillering responses. The rate of decrease in number of potentially fertile tillers per plant became greater as the ratio of realized to potential leaf area growth diminished and departed further from unity. When the realized leaf area was predicted via estimated light interception (Fig. 7), the relationship was retained, but with slightly increased scatter in the data (R2 = 0·68). However, the data based on predicted realized leaf area reflected closely the relationship determined using measured realized leaf area.

graphic file with name mcf153f6.jpg

Open in a new tab

Fig. 6. Relationship between rate of change in potentially fertile tiller number and ratio of realized/potential leaf area growth for data calculated in each of the three replications at a density of two (circles), four (upward pointing triangles), eight (squares) and 16 (downward pointing triangles) plants m–2. Solid line shows the fitted linear regression (R2 = 0·80).

graphic file with name mcf153f7.jpg

Open in a new tab

Fig. 7. Relationship between rate of change in potentially fertile tiller number and estimated ratio of realized/potential leaf area growth for data calculated in each of the three replications at a density of two (circles), four (upward pointing triangles), eight (squares) and 16 (downward pointing triangles) plants m–2. Realized leaf area was estimated from estimated light interception, using the extinction coefficient, radiation use efficiency and plant leaf area ratio, as reported by Lafarge and Hammer (2002). Otherwise data were calculated as for Fig. 6. The dotted line shows the linear regression of the reference response fitted in Fig. 6.

Dynamics of total plant leaf area for a plant grown at a given density did not differ from those of plants grown at lower densities with the same number of emerged tillers prior to the time at which the number of fertile tillers of that plant was fixed

The relationship between total leaf area per plant and accumulated thermal time was examined to determine whether a simulation of potential leaf area could be achieved independently of plant density. Total leaf area was calculated from fully expanded leaf number and individual leaf size for all fertile culms only, to exclude any effect of tiller senescence (see Materials and Methods). Accumulation of leaf area on main culms did not vary with plant population until 400 °Cd after emergence (Fig. 8A). After that time, differences in total leaf area on the main culm among plants grown at different densities increased until full expansion of the final leaf. Differences in total leaf area per plant were also examined for plants with main culm plus one fertile tiller (T3, Fig. 8B), main culm plus two fertile tillers (T3 and T4, Fig. 8C), and main culm plus three fertile tillers (T3, T4 and T2, Fig. 8D). The combinations of tillers used conforms with the tiller hierarchy identified previously (Lafarge et al., 2002). No difference in total leaf area for plants with two fertile tillers was observed among density treatments before 380 °Cd after emergence. Moreover, no difference was observed between plants grown at D1 and D2 before 450 °Cd. These times are similar to that at which fertile tiller number per plant was fixed (e.g. approx. 400 °Cd for plants in D4 and 450 °Cd for plants in D2; Fig. 3B). The situation was similar for plants with either one or three fertile tillers. For a given number of fertile tillers per plant, total plant leaf area dynamics at any plant density did not depart from that observed in plants grown in D1 up until about the time when fertile tiller number per plant was fixed. After that time, total plant leaf area increased less rapidly under high density conditions due to increasing competition. Hence, the dynamics in plants grown at a density of two plants m–2 could be used for predicting potential leaf area growth independently of plant density. Leaf area per plant for various plant tiller configurations under these conditions is presented in Fig. 8E as a reference for potential leaf area calculation. However, once fertile tiller number was fixed, total plant leaf area still varied significantly with varying plant density. For example, for a plant with two fertile tillers and with no difference in final leaf number, the range in total leaf area per plant varied from 6500 to 10 500 cm2 across density treatments (Fig. 8C). This variation in total leaf area was the result of a reduction in later blade size (reduced final length and maximal width of these blades; Fig. 9) at high density. Blade area development of all culms of any plant was affected at about the same time, given the known timing differences among culms in appearance of leaves. The main culm was five leaves ahead of tiller 2, which was one and two leaves ahead of tillers 3 and 4, respectively (Lafarge et al., 2002). In D3, the first leaf whose blade length was significantly reduced was leaf 10 for tiller 2 (Fig. 9C), leaf 9 for tiller 3 (Fig. 9E) and leaf 8 for tiller 4 (Fig. 9G), whereas no leaf was affected on the main culm, which developed 16 leaves (Fig. 9A). Also in D3, the first leaf whose blade width was significantly affected was leaf 11 for the main culm (Fig. 9B), leaf 7 for tiller 2 (Fig. 9D), leaf 6 for tiller 3 (Fig. 9F) and about leaf 5 for tiller 4 (Fig. 9H). Interestingly, the reduction in total blade area due to increasing density was mostly due to a reduction in blade width, which was consistently observed to occur three leaf positions earlier on each culm type than a reduction in blade length.

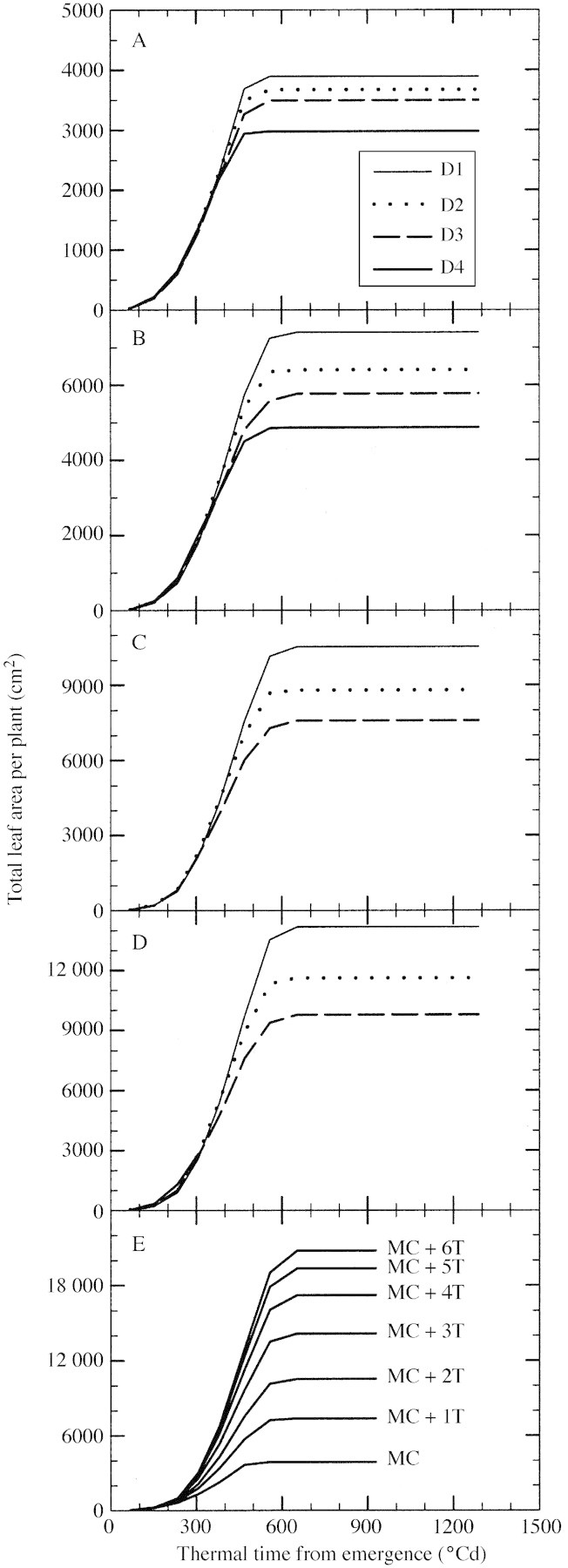
graphic file with name mcf153f8.jpg

Open in a new tab

Fig. 8. Total leaf area produced per plant vs. thermal time from emergence for plants with main culm only (A), main culm + one tiller (B), main culm + two tillers (C) and main culm + three tillers (D) grown at density of two (thin solid line), four (dotted line), eight (dashed line) and 16 (bold solid line) plants m–2, and for plants with seven different tillering configurations when grown at two plants m–2 (E).

graphic file with name mcf153f9.jpg

Open in a new tab

Fig. 9. Relationship between leaf position on the culm and leaf blade final length for leaves on the main culm (A), tiller 2 (C), tiller 3 (E) and tiller 4 (G), and relationship with maximal leaf blade width for leaves on the main culm (B), tiller 2 (D), tiller 3 (F) and tiller 4 (H) for plants grown at a density of two (circles), four (upward pointing triangles), eight (squares) and 16 (downward pointing triangles) plants m–2. Data points are the means of three replications and vertical lines represent s.e.m.

DISCUSSION

The framework used to analyse the dynamics of sorghum tillering was designed to facilitate prediction of the number of fertile tillers at maturity as early as possible in crop development. This framework was based on integrated responses at the plant level. Rather than focusing on total tiller dynamics, which has been common in previous work, this study focused on the number of potentially fertile tillers per plant, as this group of tillers contributes significantly to canopy development and grain yield. Field measurements were performed at a range of plant densities to quantify the time course of the number of potentially fertile tillers per plant for a range of assimilate availabilities. Although the number of fertile tillers per plant at maturity varied greatly among treatments (from 4·9 to 0·2 for plants grown at densities of two to 16 plants m–2), three underpinning determinants were sufficient to account for this variation and thus provided the basis for a modelling approach: (1) rate of tiller emergence; (2) time at which tiller emergence ceased; and (3) rate of decrease in number of potentially fertile tillers per plant.

Tiller emergence was linearly related to thermal time and to the number of fully expanded leaves on the main culm. A new tiller emerged whenever a new ligule appeared on the main culm, regardless of density. This observation suggested that each potential tiller had the capacity to emerge and grow for only a limited period. Similar qualitative results have been reported by Kirby and Faris (1972), Porter (1985) and Rickman et al. (1985), who found that each tiller on wheat had only one phyllochron during which it had the opportunity to initiate its development. Hence, in this cultivar of sorghum, tiller emergence can be simulated according to rate of appearance of fully expanded leaves once the first tiller has emerged. Under our experimental conditions, the onset of tiller emergence occurred after 3·9 fully expanded leaves, regardless of plant density. The associated mean air temperature, calculated between 50 and 150 °Cd after emergence, was 21·0 °C. Tiller emergence from lower axils, and hence subsequent fertility, has been reported to be highly affected by high temperature in sorghum (Downes, 1968), barley (Cannell, 1969b) and wheat (Bos and Neuteboom, 1998). The effect of temperature was partly confirmed when tiller production was analysed for plants sown on 11 Nov. 1998 in an extra experiment conducted at a density of ten plants m–2 using the same growing conditions as those described here. The onset of tiller emergence occurred after 4·2 fully expanded leaves, and the mean air temperature was 22·3 °C between 50 and 150 °Cd after emergence (data not shown). In particular, in the latter conditions, no plant developed a T1 and only 60 % developed a T2. While variation in other environmental factors may also have contributed to this difference, the effect of temperature on potential expansive growth of the main culm (greater with high temperature) may be one of the major determinants of the amount of assimilate available for tillering in young plants, where the potential assimilate supply is low. A hypothesis relating timing of the first tiller to emerge to availability of assimilate beyond the requirement of existing culms has been promoted by several authors (Cannell, 1969b; Major et al., 1982; Ong, 1984; Bos and Neuteboom, 1998).

Tiller emergence ceased at a stable (LAI) of 0·64 for plants at all four densities tested. Similarly, in a simulation model of perennial graminoid growth, Coughenour et al. (1984) limited tillering rate according to LAI values. In that model, the detrimental effect of canopy leaf area on tiller production occurred from a LAI of 1, which was consistent with published data. The response of tiller emergence to LAI could be explained by the sensitivity of sorghum to neighbouring plants via variation in light quality. Ballaré et al. (1987) observed a reduced red : far‐red ratio at low solar elevations for LAI values close to 1. This reduction was synchronous with a reduction in tiller production (Casal et al., 1986; Gautier et al., 1995). Contrary to the hypothesis of Ong (1984) for millet, and Kirby et al. (1985) and Boone et al. (1990) for wheat, there was no clear relationship between cessation of tiller emergence and stem elongation. In this study, apex height measured at the time of cessation was 0, 11, 38 and 51 mm for plants in D4, D3, D2 and D1 (data not shown). In fact, stem elongation is also known to be promoted by a decrease in the red : far‐red ratio (Ballaré et al., 1989; Kasperbauer and Karlen, 1994), and so both enhanced stem elongation and reduced branching have been reported to be consequences of a decrease in the red : far‐red ratio (Ballaré and Casal, 2000). However, internode elongation measured in this study appeared to be less sensitive to variation in light quality than tiller production (data not shown). It is likely that changes in light quality, as an early signal of the presence of neighbours, allowed the plant to avoid wasting assimilate in tillers that would be unlikely to survive and become fertile (Skinner and Simmons, 1993).

The rate of decrease in the number of potentially fertile tillers per plant was related to the ratio of realized to potential leaf area growth during the period of decrease. This ratio was used to reflect the balance between supply of, and demand for, shoot assimilate in the young plant where leaf area expansion is the major shoot sink. This approach was supported by the stability of shoot assimilate partitioning and specific leaf area observed at the plant level across plant densities between emergence and anthesis (Lafarge and Hammer, 2002). The ratio used here is similar in concept to the supply : demand ratio for water, which has been utilized effectively in crop models as an index of plant water status (Chapman et al., 1993). A number of other studies have utilized the notion of potential organ growth to quantify demand for assimilates. DeJong and Grossman (1994) determined carbohydrate demand of a fruit tree by estimating the collective growth potential of all individual growing organs. Heuvelink (1996) validated a tomato simulation model based on the hypothesis that dry matter distribution was regulated by the potential growth rates of plant organs, i.e. the growth rates at non‐limiting assimilate supply, and Tabourel‐Tayot and Gastal (1998) calculated assimilate demand from the amount of carbon and nitrogen required to produce a potential volume of tissue. The same approach was used in this study, where the potential growth in leaf area (demand) was estimated from the leaf area that would be produced between two observations if all potentially fertile tillers were to continue their development. These data do not exclude any possible direct effect of light quality on decrease in potentially fertile tiller number, given that this decrease started shortly after emergence of the final tiller, when no significant competition for assimilate was obvious. However, the possibility of the concept of source–sink balance as a major controller of tiller development was supported by the observed stable relationship of the rate of decrease in potentially fertile tiller number per plant with the ratio of realized to potential leaf area growth. Hence, this relationship, when determined from measured leaf area data, was considered as a reference response. Its utility in predicting and modelling tiller dynamics depends on the ability to predict realized and potential leaf area growth.

Prediction of realized leaf area per plant has been proposed via light interception, radiation use efficiency and plant leaf area ratio (Lafarge and Hammer, 2002). This method regenerated the reference response well. It was based on six parameters, stable over the large range of plant densities explored here, that were sufficient to predict an increase in leaf area from the initial leaf area index and incident radiation. The stability of radiation use efficiency for above‐ground dry matter accumulation meant that it was not necessary to consider root growth and respiration, in contrast to the approach used by DeJong and Grossman (1994).

Prediction of potential leaf area growth was proposed via dynamics of leaf area production of the whole plant for a given tiller number. Leaf area growth of fertile tillers, added to the plant according to the tiller hierarchy identified by Lafarge et al. (2002), did not depart from that observed at a density of two plants m–2 for any density conditions up until the time at which fertile tiller number per plant was fixed. Consequently, potential plant leaf area growth, in the developmental period associated with tillering, could be estimated for all densities using the potential defined under no, or limited, competition. This potential can be estimated well using a logistic function fitted against thermal time (see Dwyer and Stewart, 1986; Hammer et al., 1987).

CONCLUSIONS

This study provides a basis for modelling tiller dynamics in grain sorghum. It shows that the dynamics of the number of potentially fertile tillers per plant can be predicted from the intrinsic rate of tiller emergence, the timing of cessation of tiller emergence and the rate of decrease in potentially fertile tillers. The rate of tiller emergence aligned with appearance rate of fully expanded leaves on the main culm and commenced after about four main culm leaves had emerged, although commencement is likely to vary with environmental conditions. Tiller emergence ceased when the canopy leaf area index reached 0·64, and was probably associated with hormonal effects in response to changes in light quality (red : far‐red ratio). The rate of decrease in potentially fertile tillers was linearly related to the ratio of realized to potential leaf area growth, which was an indicator of the source–sink balance in young plants. Hence, this ratio provided a basis by which to predict the rate of decrease in the number of potentially fertile tillers. Any decrease will reduce the rate of potential leaf area growth until the balance point with realizable leaf area is reached. So, using only planting density, daily temperature and incident radiation as inputs, this framework provides a means to simulate fertile tiller dynamics in sorghum for a wide range of conditions. However, the concepts embodied in the general framework presented need to be validated with different cultivars and in different environments. This study also provided some insight for leaf area modelling. It was observed that once fertile tiller number was fixed, interplant competition effects were manifest mainly through leaf area of the fertile tillers. These effects resulted in variation in area of individual mature blades rather than in final leaf number, which was stable for any culm across density treatments. Both final length and maximal width of later blades were affected, although most variation was manifest in blade width.

Supplementary Material

Content Snapshot
supp_90_1_99__index.html (920B, html)

Received: 17 September 2001; Returned for revision: 22 November 2001; Accepted: 28 March 2002

References

  1. ArkinGF, Rosenthal WD, Jordan WR.1983. A sorghum leaf area model. Technical Paper 83–2098, ASAE, St Joseph, MI, USA.
  2. BallaréCL, Casal JJ.2000. Light signals perceived by crop and weed plants. Field Crops Research 67: 149–160. [Google Scholar]
  3. BallaréCL, Sanchez RA, Scopel AL, Casal JJ, Ghersa CM.1987. Early detection of neighbour plants by phytochrome perception of spectral changes in reflected sunlight. Plant, Cell and Environment 10: 551–557. [Google Scholar]
  4. BallaréCL, Scopel AL, Sanchez RA.1989. Photomodulation of axis extension in sparse canopies. Plant Physiology 89: 1324–1330. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. BauerA, Frank AB, Black AL.1984. Estimation of spring wheat leaf growth rates and anthesis from air temperature. Agronomy Journal 76: 829–835. [Google Scholar]
  6. BirchCJ, Carberry PS, Muchow RC, McCown RL, Hargreaves JNG.1990. Development and evaluation of a sorghum model based on CERES‐Maize in a semi‐arid tropical environment. Field Crops Research 24: 87–104. [Google Scholar]
  7. BooneMYL, Rickman RW, Whisler FD.1990. Leaf appearance rates of two winter wheat cultivars under high carbon dioxide conditions. Agronomy Journal 82: 718–724. [Google Scholar]
  8. BosHJ, Neuteboom JH.1998. Morphological analysis of leaf and tiller number dynamics of wheat (Triticum aestivum L.): response to temperature and light intensity. Annals of Botany 81: 131–139. [Google Scholar]
  9. CannellRQ.1969a The tillering pattern in barley varieties. I. Production, survival and contribution to yield by component tillers. Journal of Agricultural Science 72: 405–422. [Google Scholar]
  10. CannellRQ.1969b The tillering pattern in barley varieties. II. The effect of temperature, light intensity and daylength on the frequency of occurrence of the coleoptile node and second tillers in barley. Journal of Agricultural Science 72: 423–435. [Google Scholar]
  11. CarberryPS, Muchow RC, Hammer GL.1993. Modelling genotypic and environmental control of leaf area dynamics in grain sorghum. II. Individual leaf level. Field Crops Research 33: 311–328. [Google Scholar]
  12. CasalJJ, Sanchez RA, Deregibus VA.1986. The effect of plant density on tillering: the involvement of R/FR ratio and the proportion of radiation intercepted per plant. Environmental and Experimental Botany 26: 365–371. [Google Scholar]
  13. ChapmanSC, Hammer GL, Meinke H.1993. A sunflower simulation model: I. Model development. Agronomy Journal 85: 725–735. [Google Scholar]
  14. CoughenourMB, McNaughton SJ, Wallace LL.1984. Modelling primary production of perennial graminoids. Uniting physiological processes and morphometric traits. Ecological Modelling 23: 101–134. [Google Scholar]
  15. DarwinkelA.1978. Patterns of tillering and grain production of winter wheat at a wide range of plant densities. Netherlands Journal of Agricultural Science 26: 383–398. [Google Scholar]
  16. DaviesA.1974. Leaf tissue remaining after cutting and regrowth in perennial ryegrass. Journal of Agricultural Science 82: 165–172. [Google Scholar]
  17. DaviesA, Thomas H.1983. Rates of leaf and tiller production in young spaced perennial ryegrass plants in relation to soil temperature and solar radiation. Annals of Botany 57: 591–597. [Google Scholar]
  18. DavisMH, Simmons SR.1994. Tillering response of barley to shifts in light quality caused by neighbouring plants. Crop Science 34: 1604–1610. [Google Scholar]
  19. DeJongTM, Grossman YL.1994. A supply and demand approach to modelling annual reproductive and vegetative growth of deciduous fruit trees. HortScience 29: 12: 1435–1442. [Google Scholar]
  20. DeregibusVA, Sanchez RA, Casal JJ, Trlica MJ.1985. Tillering responses to enrichment of red light beneath the canopy in a humid natural grassland. Journal of Applied Ecology 22: 199–206. [Google Scholar]
  21. DingkuhnM, Schnier HF, de Datta SK, Dorffling K, Javellana C.1991. Relationships between ripening‐phase productivity and crop duration, canopy photosynthesis and senescence in transplanted and direct‐seeded lowland rice. Field Crops Research 26: 327–345. [Google Scholar]
  22. DownesRW.1968. The effect of temperature on tillering of grain sorghum seedlings. Australian Journal of Agricultural Research 19: 59–64. [Google Scholar]
  23. DwyerLM, Stewart DW.1986. Leaf area development in field‐grown maize. Agronomy Journal 78: 334–343. [Google Scholar]
  24. GautierH, Varlet‐Grancher C, Hazard L.1999. Tillering responses to the light environment and to defoliation in populations of perennial ryegrass (Lolium perenne L.) selected for contrasting leaf length. Annals of Botany 83: 423–429. [Google Scholar]
  25. GautierH, Varlet‐Grancher C, Gastal F, Moulia B.1995. Evolution of the leaf area index in a white clover and tall fescue intercrop: possible regulation by light quality. In: Sinoquet H, Cruz P, eds. Ecophysiology of tropical intercropping Versailles, France: INRA éditions, 275–284. [Google Scholar]
  26. GerikTJ, Neely CL.1987. Plant density effects on main culm and tiller development of grain sorghum. Crop Science 27: 1225–1230. [Google Scholar]
  27. HammerGL, Muchow RC.1994. Assessing climatic risk to sorghum production in water‐limited subtropical environments. I. Develop ment and testing of a simulation model. Field Crops Research 36: 221–234. [Google Scholar]
  28. HammerGL, Carberry PS, Muchow RC.1993. Modelling genotypic and environmental control of leaf area dynamics in grain sorghum. I. Whole plant level. Field Crops Research 33: 293–310. [Google Scholar]
  29. HammerGL, Hill K, Schrodter GN.1987. Leaf area production and senescence of diverse grain sorghum hybrids. Field Crops Research 17: 305–317. [Google Scholar]
  30. HeinigerRW, Vanderlip RL, Welch SM.1997a Developing guidelines for replanting grain sorghum: I. Validation and sensitivity analysis of the SORKAM sorghum growth model. Agronomy Journal 89: 75–83. [Google Scholar]
  31. HeinigerRW, Vanderlip RL, Welch SM, Muchow RC.1997b Developing guidelines for replanting grain sorghum: II. Improved method of simulating caryopsis weight and tiller number. Agronomy Journal 89: 84–92. [Google Scholar]
  32. HeuvelinkE.1996. Dry matter partitioning in tomato: validation of a dynamic simulation model. Annals of Botany 77: 71–80. [Google Scholar]
  33. IshagHM, Taha MB.1974. Production and survival of tillers of wheat and their contribution to yield. Journal of Agricultural Science 83: 117–124. [Google Scholar]
  34. KasperbauerMJ.1987. Far‐red light reflection from green leaves and effects on phytochrome‐mediated assimilate partitioning under field conditions. Plant Physiology 85: 350–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. KasperbauerMJ, Karlen DL.1986. Light‐mediated bioregulation of tillering and photosynthate partitioning in wheat.Physiologia Plantarum 66: 159–163. [Google Scholar]
  36. KasperbauerMJ, Karlen DL.1994. Plant spacing and reflected far‐red light effects on phytochrome‐regulated photosynthate allocation in corn seedlings. Crop Science 34: 1564–1569. [Google Scholar]
  37. KirbyEJM.1995. Factors affecting rate of leaf emergence in barley and wheat. Crop Science 35: 11–19. [Google Scholar]
  38. KirbyEJM, Faris DG.1972. The effect of plant density on tiller growth and morphology in barley. Journal of Agricultural Science 78: 281–288. [Google Scholar]
  39. KirbyEJM, Riggs TJ.1978. Developmental consequences of two‐row and six‐row ear type in spring barley. 2. Shoot apex, leaf and tiller development. Journal of Agricultural Science 91: 207–216. [Google Scholar]
  40. KirbyEJM, Appleyard M, Fellowes G.1985. Leaf emergence and tillering in barley and wheat. Agronomie 5: 193–200. [Google Scholar]
  41. KlepperB, Belford RK, Rickman RW.1984. Root and shoot development in winter wheat. Agronomy Journal 76: 117–122. [Google Scholar]
  42. KlepperB, Rickman RW, Peterson CM.1982. Quantitative characterisation of vegetative development in small cereal grains. Agronomy Journal 74: 789–792. [Google Scholar]
  43. LafargeT, Hammer GL.2002. Predicting plant leaf area production: shoot assimilate accumulation and partitioning, and specific leaf area, are stable for a wide range of sorghum population density. Field Crops Research (in press).
  44. LafargeT, Broad IJ, Hammer GL.2002. Tillering in grain sorghum over a wide range of population densities: identification of a common hierarchy for tiller emergence, leaf area development and fertility. Annals of Botany 90: 87–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. LauerJG, Simmons SR.1988. Photoassimilate partitioning by tillers and individual tiller leaves in field‐grown spring barley. Crop Science 28: 279–282. [Google Scholar]
  46. MaasSJ.1993. Parameterised model of gramineous crop growth: I. leaf area and dry mass simulation. Agronomy Journal 85: 348–353. [Google Scholar]
  47. MajorDJ, Hamman WM, Rood SB.1982. Effects of short duration chilling temperature exposure on growth and development of sorghum. Field Crops Research 5: 129–136. [Google Scholar]
  48. Masle‐MeynardJ, Sébillotte M.1981. Etude de l’hétérogénéité d’un peuplement de blé d’hiver. II. Origine des différentes catégories d’individus du peuplement; éléments de description de sa structure. Agronomie 1: 217–224. [Google Scholar]
  49. MitchellRB, Moser LE, Moore KJ, Redfearn DD.1998. Tiller demographics and leaf area index of four perennial pasture grasses. Agronomy Journal 90: 47–53. [Google Scholar]
  50. MootDJ, Henderson AL, Porter JR, Semenov MA.1996. Temperature, CO2 and the growth and development of wheat: changes in the mean and variability of growing conditions. Climatic Change 33: 351–368. [Google Scholar]
  51. MuchowRC, Carberry PS.1990. Phenology and leaf area development in a tropical grain sorghum. Field Crops Research 23: 221–237. [Google Scholar]
  52. NeuteboomJH, Lantiga EA.1989. Tillering potential and relationship between leaf and tiller production in perennial ryegrass. Annals of Botany 63: 265–279. [Google Scholar]
  53. OngCK.1984. Response to temperature in a stand of pearl millet (Pennisetum typhoïdes S. & H.). V. Development and fate of tillers. Journal of Experimental Botany 35: 83–90. [Google Scholar]
  54. PorterJR.1985. Approaches to modelling canopy development in wheat. In: Day W, Atkin RK, eds. Wheat growth modelling New York, USA: Plenum Press, 69–81. [Google Scholar]
  55. RickmanRW, Klepper B, Peterson CM.1985. Wheat seedling growth and developmental response to incident photosynthetically active radiation. Agronomy Journal 77: 283–287. [Google Scholar]
  56. RobinC, Varlet‐Grancher C, Gastal F, Flenet F, Guckert A.1992. Photomorphogenesis of white clover (Trifolium repens L.): phytochrome mediated effects on C‐assimilate partitioning. European Journal of Agronomy 1: 235–240. [Google Scholar]
  57. RosenthalWD, Vanderlip RL, Jackson BS, Arkin GF.1989. SORKAM: a grain sorghum growth model. Computer Software Documentation Serie MP‐1669. Texas Agricultural Experiment Station, College Station, TX, USA. [Google Scholar]
  58. SchnierM, Dingkuhn M, de Datta SK, Mengel K, Wijanco E, Javellana C.1990. Nitrogen economy and canopy carbon dioxide assimilation of tropical lowland rice. Agronomy Journal 82: 451–459. [Google Scholar]
  59. SkinnerRH, Nelson CJ.1992. Estimation of potential tiller production and site usage during tall fescue canopy development. Annals of Botany 70: 493–499. [Google Scholar]
  60. SkinnerRH, Nelson CJ.1994. Effect of tiller trimming on phyllochron and tillering regulation during tall fescue development. Crop Science 34: 1267–1273. [Google Scholar]
  61. SkinnerRH, Simmons SR.1993. Modulation of leaf elongation, tiller appearance and tiller senescence in spring barley by far‐red light. Plant, Cell and Environment 16: 555–562. [Google Scholar]
  62. SugiyamaS.1995. The relationship between growth and development of vegetative shoots in genotypes of tall fescue (Festuca arundinacea Schreb.). Annals of Botany 76: 553–558. [Google Scholar]
  63. Tabourel‐TayotF, Gastal F.1998. MecaNiCAL, a supply‐demand model of carbon and nitrogen partitioning applied to defoliated grass. 1. Model description and analysis. European Journal of Agronomy 9: 223–241. [Google Scholar]
  64. WuG, Wilson LT, McClung AM.1998. Contribution of rice tillers to dry matter accumulation and yield. Agronomy Journal 90: 317–323. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Content Snapshot
supp_90_1_99__index.html (920B, html)
supp_90.1.99_mcf181f11a.gif (55.6KB, gif)

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES