Quantitative Analysis of Shoot Development and Branching Patterns in Actinidia

Abstract

We developed a framework for the quantitative description of Actinidia vine architecture, classifying shoots into three types (short, medium and long) corresponding to the modes of node number distribution and the presence/absence of neoformed nodes. Short and medium shoots were self‐terminated and had only preformed nodes. Based on the cut‐off point between their two modes of node number distribution, short shoots were defined as having nine or less nodes, and medium shoots as having more than nine nodes. Long shoots were non‐terminated and had a number of neoformed nodes; the total number of nodes per shoot was up to 90. Branching patterns for each parent shoot type were represented by a succession of branching zones. Probabilities of different types of axillary production (latent bud, short, medium or long shoot) and the distributions of length for each branching zone were estimated from experimental data using hidden semi‐Markov chain stochastic models. Branching was acrotonic on short and medium parent shoots, with most axillary shoots being located near the shoot tip. For long parent shoots, branching was mesotonic, with most long axillary shoots being located in the transition zone between the preformed and neoformed part of the parent shoot. Although the shoot classification is based on node number distribution there was a marked difference in average (per shoot) internode length between the shoot types, with mean values of 9, 27 and 47 mm for short, medium and long shoots, respectively. Bud and shoot development is discussed in terms of environmental controls.

INTRODUCTION

Shoot morphology and the distribution of shoot types within the branching framework of a plant contribute to the characteristic form or architecture of that plant. An important role of architectural analyses is to identify genetically determined patterns of plant construction and to study how patterns of shoot growth and branching are modified by environment (Barthelemy et al., 1991). Stochastic models are often appropriate for these analyses because of the highly variable nature of shoot growth and branching patterns. In particular, hidden semi‐Markov chain models (Guédon, 1999) have been applied to represent distributions of axillary production (shoot types and latent buds) along parent shoots in apricot (Costes and Guédon, 1996) and apple (Godin et al., 1999). This modelling approach is based on the assumption that branching patterns can be represented by a succession of branching zones, with each zone being characterized by certain probabilities of different types of axillary production.

In this paper we analyse shoot development and branching patterns of Actinidia Lindl. (for an introduction to genus Actinidia, see Ferguson, 1990). Previously, much attention has been given to measurements and visual computer reconstructions of the three‐dimensional structure of kiwifruit vines (Actinidia deliciosa) and to analyses of the spatial distribution of plant organs in the vine canopy (Smith et al., 1992, 1994; Smith and Curtis, 1996). The focus of the current study was to quantify the main architectural features of Actinidia vines, in particular to provide definitions of specific shoot types and their distribution within the branching framework.

At the whole plant level, Actinidia conforms to the Champagnat architectural tree model (Hallé et al., 1978). This model is characterized by mixed axes, i.e. axes that have successive and distinct phases in their development. In the Champagnat model, the mixed axes have a spiral phyllotaxis and begin their growth with an orthotropic direction before they bend under their own weight. In Actinidia all branching is sympodial, with relay axes (dominant branches) developing in the region of curvature along the parent axes. Therefore, the vines are constructed by the superposition of such mixed axes, the proximal parts being included in the trunk and the distal parts becoming a branch. In horticulture, kiwifruit vines are trained onto pergola or T‐bar support structures (Sale and Lyford, 1990). A single trunk is usually maintained and initially two relay axes, called ‘leaders’ or ‘central leaders’ are trained horizontally in opposite directions along the support structures. New relay axes form along these leaders. Left to bend under their own weight, these axes are eventually tied down in winter to the support structures as ‘replacement canes’. The axillary shoots arising from these replacement canes in the following year produce the fruiting canopy. The fruiting canes are generally replaced with new relay axes (canes) during winter pruning, thus bringing the vine back to a similar structure at the beginning of each season. It is the pattern of development and distribution of axillary shoot types within this set framework that is of particular interest in horticulture, and the precise classification of the different shoot types is essential when analysing fruiting canopy development.

As with other deciduous species, in kiwifruit the current season’s shoots arise from axillary buds formed during the previous season and contain a number of preformed leaf primordia (Brundell, 1975; Snowball, 1997b; Walton and Fowke, 1993; Walton et al., 1997). Bud scales are generally located at nodes 1–4, with leaf and floral primordia developing between approx. nodes 5 and 12, depending on the species. At the time of budbreak, the active bud begins to swell and opens in 5–6 d. After 10–15 d, the bud develops into an open cluster containing a few leaves. Many shoots terminate soon after this time when their tips wither and die. Other shoots continue producing leaves until the end of the season, ending up with several more leaves than the number of preformed leaf primordia within the parent axillary bud (Snowball, 1997a, b). In Actinidia literature, these two shoots types are variously referred to as ‘determinate and indeterminate’ (Brundell, 1975), or ‘terminated and nonterminated’ (Ferguson, 1984). Although all shoots eventually self‐terminate (all shoot growth on Actinidia is sympodial), the difference between these two shoot types is in the timing of growth termination.

The final number of nodes per shoot in a homogeneous population of shoots (sampled from equivalent architectural positions) follows a distribution characterizing the random growth of shoots (deReffye et al., 1995). Unimodal (Fagus sylvatica, Hevea brasiliensis) or bimodal (Prunus avium, Populus nigra, Zelkova serrata) distributions have been obtained for different species, depending on whether the neoformed metamers were produced during shoot growth (deReffye et al., 1991, 1995). The proportion of shoots with neoformation (the weight of the second mode of the node number distribution) depended on their architectural position. For the above species, distributions of node number for preformed shoots were unimodal; however, for Actinidia species the corresponding distributions often have more then one mode (this can be interpreted from previous data on node number distributions for axillary shoots; see Fig. 2 in Snowball, 1997a). Hence further subdivision of terminated shoots into at least two types is required for Actinidia.

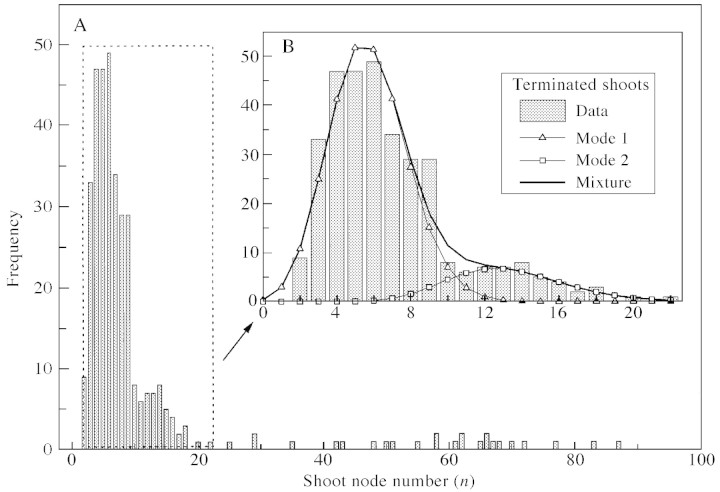
Fig. 2. Frequency distribution of final node number per axillary shoot. A, All axillary shoots from long parent shoots. B, Distribution for terminated axillary shoots represented by a mixture of binomial (Mode 1) and negative binomial (Mode 2) distributions (see Table 1 for parameters).

In this paper we consider two levels of description: the metamer level and the shoot level. Shoots represent annual increments of extension growth, and their component parts, metamers, consist of a node, an internode, a leaf and an axillary bud (White, 1979). Because descriptions at the metamer level can be prohibitively time consuming, reduction to descriptions at the shoot level are often warranted. Although such a reduction will result in less information on plant structure this can be overcome by careful classification of shoot types. In a case study with Actinidia chinensis Planch., we classify shoot types into short, medium and long according to modes of node number distribution, and we establish a relationship between shoot type and average internode length. We then model branching patterns on these different shoot types using a family of hidden semi‐Markov chain models (Guédon, 1999; Guédon et al., 2001).

MATERIALS AND METHODS

Data collection

Our approach is based on data collected by Snowball from a range of Actinidia spp. and genotypes, and published in summary form (Snowball, 1997a, b). To assist model development we collected a more detailed data set from one A. chinensis vine (accession no. CK01_01_01_01). This was the same female vine used by Snowball (1997a, b) at the HortResearch Kumeu Research Orchard (36°44′S, 174°35′E) near Auckland, New Zealand (Fig. 1A). The plant was a mature, field‐grown seedling trained onto a T‐bar support structure. The vine had been left with no pruning for the previous 3 years so we were able to select entire 2‐year‐old branching systems (branches) comprising a parent shoot produced in the previous year and its axillary shoots grown in the current year. Short, medium and long parent shoots were selected according to our preliminary classification: short and medium shoots were terminated, with maximum internode lengths <15 and >15 mm, respectively; long shoots were non‐terminated. For each parent shoot type, ten branches were collected in winter, after leaf‐fall. Branches with long parent shoots (Fig. 1B) were selected from several locations in the fruiting canopy, including some large ‘water‐shoots’ arising from near the base of the main trunk of the parent vine. Branches with medium and short parent shoots were all selected from the fruiting canopy of the parent vine.

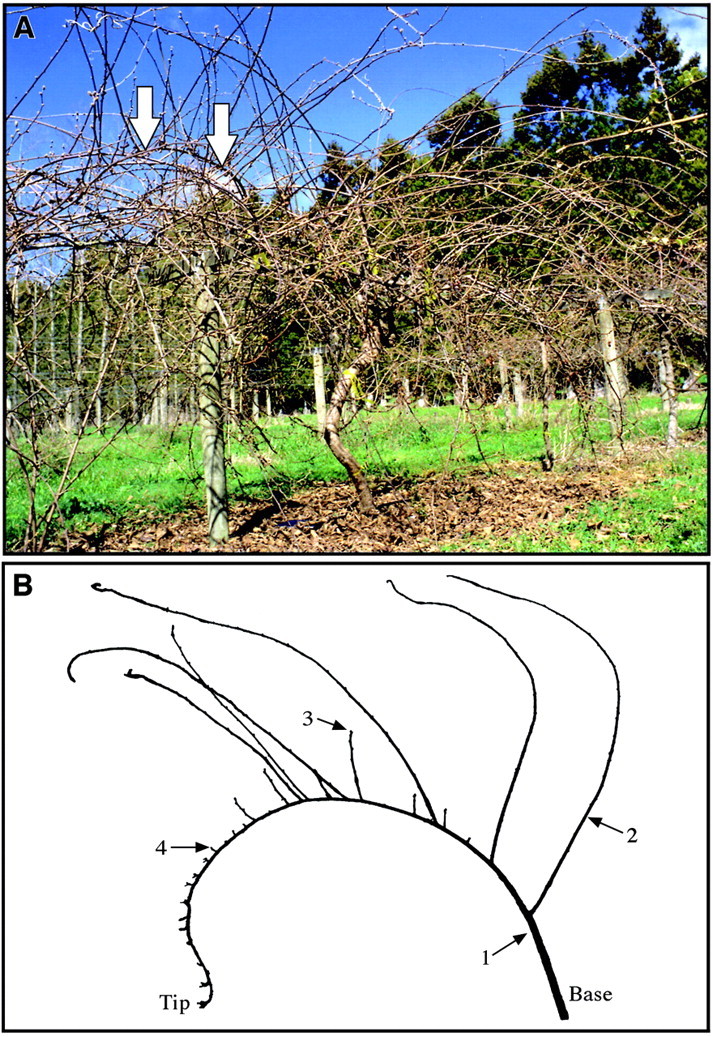
Fig. 1. A, Actinidia chinensis female vine growing at the HortResearch Kumeu Research Orchard near Auckland, New Zealand and left unpruned for 3 years. Arrows indicate a typical relay axis bent under its own weight. B, Two‐year‐old branch with long parent shoot (1). Long (2), medium (3) and short (4) axillary shoots are shown.

For each branch we recorded total length and number of nodes of the parent shoot. Nodes (buds) were numbered from the base of the parent shoot. The first bud was located below (proximal to) the first extended internode over approx. 15 mm long. Buds below this were not included in these counts as varying numbers (usually less than three) were either not visible beneath the bud shield or were left behind when the branch was cut from the vine. At each bud we recorded the presence or absence of an axillary shoot, and the distance of each axillary shoot from the base of the parent shoot. For each axillary shoot we recorded shoot type, node number (excluding those nodes not visible beneath the bud shield) and shoot length. It was unusual to find secondary or lammas shoots from a second growth flush of the axillary shoots, so when present we just recorded their location, number and combined length.

Node number distribution and classification of shoot types

Modelling in this section was carried out for a sub‐population of axillary shoots from long parent shoots. There were insufficient data to analyse axillary shoots on short and medium parent shoots in this way. Node number distribution for non‐terminated shoots was modelled by a negative binomial distribution. Node number distribution for terminated shoots was modelled by a mixture of discrete distributions using the STAT module of AMAPmod software (Godin and Guédon, 1999; see also introduction to AMAPmod methodology of measuring and analysing plant architecture in Godin et al., 1997). The number of modes (two in our case), the types of discrete distributions (binomial, negative binomial, etc.) and their parameters were determined on a best fit basis. A new classification of short and medium shoots (to replace our preliminary classification used for data collection) was established corresponding to the two modes of node number distribution obtained for terminated shoots. This new classification was used in all subsequent analyses including parent and axillary shoot types.

Modelling shoot length and average internode length

Total shoot length, L, as a function of node number, n, was modelled by a piece‐wise function L̂(n) consisting of a third degree polynomial segment and a linear segment smoothly connected (so that the first derivative was continuous at the point of connection). Model parameters including the point of connection were determined on the basis of the best fit using PROC NLIN (SAS, 1990). Average per shoot internode length was defined as a ratio of shoot length to its node number, l = (L/n). It was verified that l̂(n) = (L̂(n)/n) represented mean internode length for subpopulations of shoots S with a given node number n.

Internode length, l, for each sub‐population of shoots S(n) with a given node number n was assumed to be normally distributed. The corresponding standard deviation was modelled by a piece‐wise linear function σ̂(n) consisting of two segments corresponding to the segments of L̂(n). Namely, within the first segment standard deviation of internode length for each S(n) was calculated from experimental data and a linear model was fitted to these values. It was not possible to fit the model in the same way for the second segment because the sizes of S(n) were very small. We assumed homogeneity of variance for the second segment and estimated σ̂ using long shoots.

To confirm model compatibility and consistency of underlying assumptions, a probability density distribution function and a cumulative distribution function for internode length were calculated using fitted models for node number distributions together with models for mean internode length l̂(n) and standard deviation σ̂(n) (see Appendix). Calculated distributions were compared with corresponding distributions extracted from the data.

Effects of position on axillary shoot attributes

Analysis of positional effects was carried out for a sub‐population of axillary shoots from long parent shoots, since axillary shoots on terminated parent shoots were generally located close to the tips of the shoots. Effects of position along the parent shoot on node number of short and long axillary shoots were analysed using PROC GENMOD with identity link function (SAS, 1990). Residual values for each model were plotted against estimated values and visually examined to check for homogeneity of residual variance. Only data for medium shoots were not suitable for modelling with the identity link function.

Effects of axillary shoot position on its length were analysed taking into account the previously obtained relationship L̂(n) between shoot length and node number. For each axillary shoot type, multiple regression analysis was performed for shoot length as a function of L̂(n) and shoot position along the parent shoot. Residual values for each model were plotted and examined visually for homogeneity of variance.

Modelling distribution of axillary production along parent shoot axes

Observed branching of individual parent shoots was represented by sequences of categorical variable ‘type’ taking values 0, 1, 2 or 3, corresponding to latent bud, short shoot, medium shoot and long shoot, respectively. Preliminary examination of data indicated that terminated (short and medium) parent shoots had maximum branching density near the tip, whereas non‐terminated (long) parent shoots had maximum branching density towards the lower and middle sections. Accordingly, for terminated parent shoots the sequences of axillary production were ordered from the tip to the base of the parent shoot, while for non‐terminated parent shoots these sequences were ordered from the base to the tip. It was assumed that each parent shoot type comprised a succession of branching zones, with each zone characterized by a certain mixture of axillary production. These branching patterns were modelled by hidden semi‐Markov chains with the states corresponding to branching zones along parent shoots, defined by the following parameters: probabilities of types of axillary production within each zone; initial probabilities of a given zone being in the beginning of the sequence; distribution of length for each zone measured in number of nodes (occupancy distribution); and probabilities of zone i being followed by zone j (transition probabilities). For formal mathematical definitions of Markovian models and discussion of their application to branching patterns and axillary flowering sequences see Guédon (1999) and Guédon et al. (2001). This family of models was flexible enough to account for deviation of zone length distributions from geometric (which is the case with Markov chains). The term ‘hidden’ relates to the fact that zones were not always characterized by a single type of axillary production and therefore could not be observed directly. The number of states of each model for our data was chosen a priori, on the basis of examination of trends in axillary production, being two, three and four for short, medium and long parent shoot types, respectively. Model parameters for each model were estimated from the corresponding observed sequences of axillary production on the basis of maximum likelihood criteria, using the AMAPmod STAT module (Godin and Guédon, 1999; Guédon, 1999).

Branching zones and preformation

The preformed parts of long parent shoots contain metamers formed during the previous season. The probable location of the last preformed node on the parent shoot was estimated from the number of leaf initials within a bud (unpublished data provided by A. Snowball) and our data on maximum node number of preformed shoots. Location of branching zones and probability distributions of different types of axillary production were related to these preformed and neoformed parts of the long parent shoot.

RESULTS

Node number distribution

The frequency distribution of axillary shoot node number for long parent shoots was multi‐modal (Fig. 2; Table 1). The node number distribution for terminated axillary shoots was bimodal comprising a binomial mode and a negative binomial mode, with the weights of the modes being 0.845 and 0.155, respectively. Based on the cut‐off point between these modes, we defined short shoots as having nine or less nodes, and medium shoots as having more than nine nodes. Typical short and medium shoots are shown in Fig. 3. Non‐terminated (long) axillary shoots had up to 90 nodes and were characterized by a negative binomial node number distribution.

Table 1.

Modes of node number distributions for axillary shoots from long parent shoots

	Terminated axillary shoot				Non‐terminated
	First mode (B)		Second mode (NB)		axillary shoot
	Mean	s.d.	Mean	s.d.	Mean	s.d.
n	5·7	2·1	13·2	3·1	57·1	16·4

Type of distribution (B, binomial; NB, negative binomial) for each mode is given in parentheses. n, axillary shoot node number.

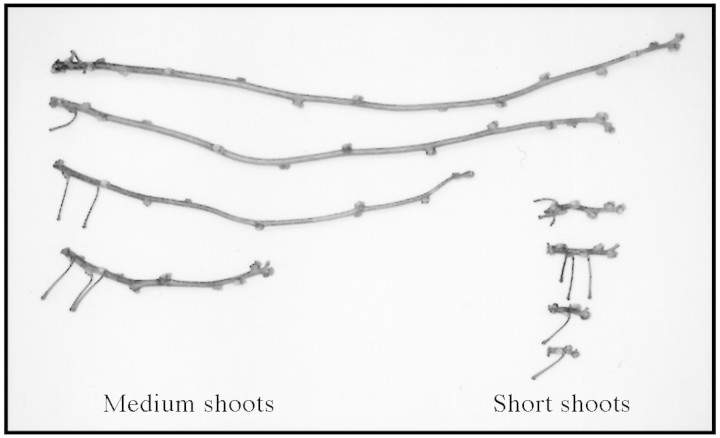
Fig. 3. Terminated shoots of Actinidia chinensis. Although short and medium shoots were classified on the basis of shoot node number, short shoots had, on average, shorter internodes (see Fig. 6).

Total axillary shoot length and internode length

Total shoot length L and average (per shoot) internode length l were measured in mm, thus all model coefficients correspond to this choice of units. The fitted model for total shoot length (Fig. 4) is given by:

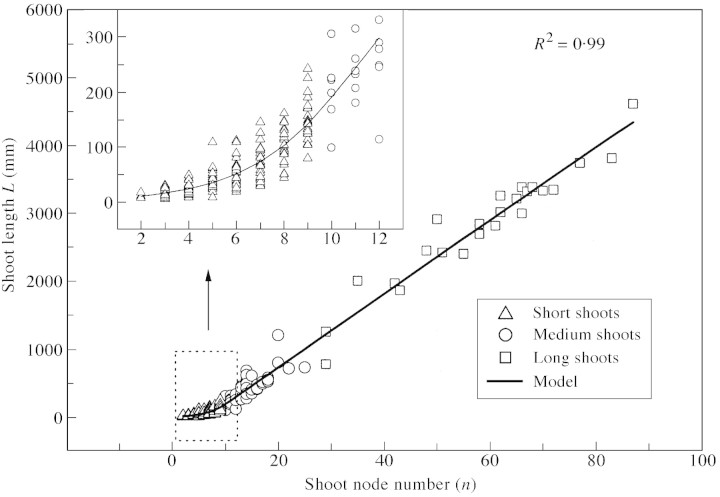
Fig. 4. Relationship between total length L and node number n of axillary shoots. Scatter graphs represent data and the line is a piece‐wise model, consisting of a third and a first order polynomial segment [eqn (1)] smoothly connected at n = 9.92.

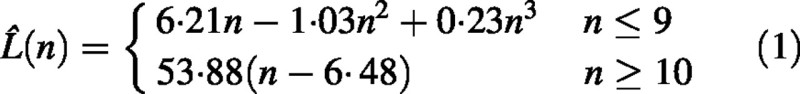
It follows from eqn (1) that the relationship between total length and node number for short shoots is non‐linear, while that for medium and long shoots is linear. From eqn (1) we get a model for internode length:

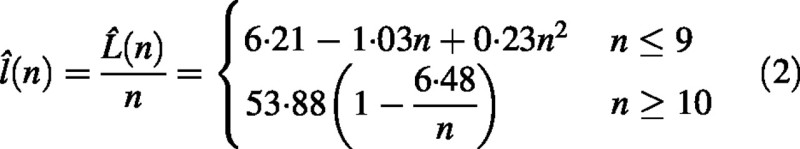
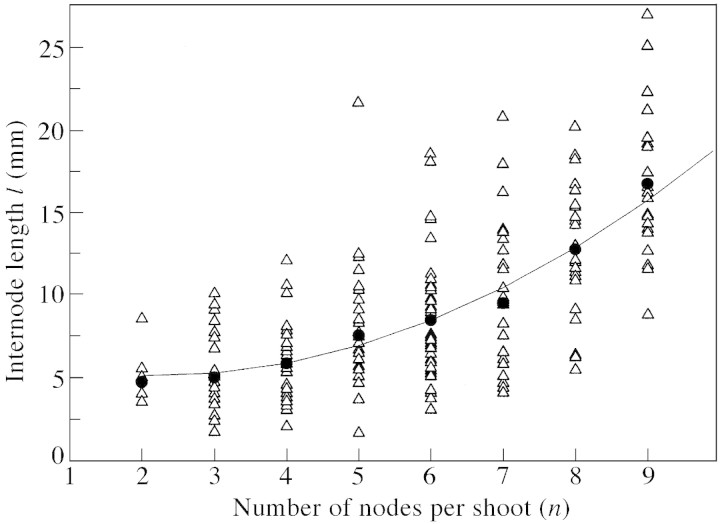
For short shoots, the quadratic function l̂(n) closely fitted (r² = 0·982) the mean value of internode length l̄(n) for sub‐populations of shoots with a given node number, S(n) (Fig. 5).

Fig. 5. Internode length of axillary shoots. (Average) internode length of individual shoots l calculated as a ratio of shoot length L to shoot node number n (triangles); mean value of internode length l̄ for sub‐populations of shoots with a given node number, S(n) (circles); model l̂ [eqn (2)] (—).

For n ≤ 9, the standard deviation of internode length σ̂(n) for sub‐populations of shoots with a given node number, S(n), was a linear function of n (r = 0·93). σ̂(n) for n > 9 was determined using data for long shoots. Finally

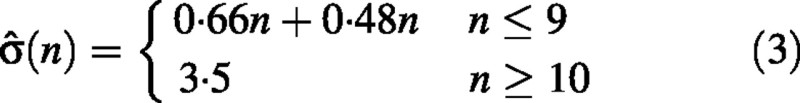
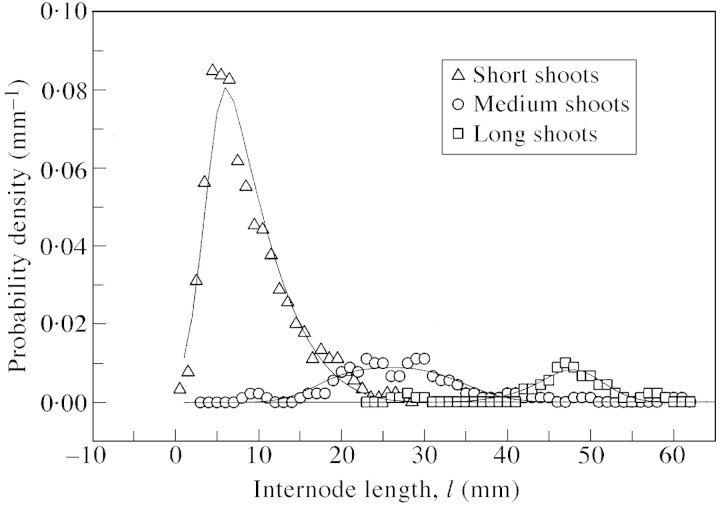
Internode length distributions for short, medium and long shoots calculated on the basis of the node number distribution and relationships [eqns (2) and (3)] showed good agreement with the corresponding distributions extracted from the data (Fig. 6). The correlation coefficient for calculated and observed internode length distributions (taking into account all shoots) was 0·962. This confirms our assumptions regarding the analytical form of eqn (3). Mean values of internode length for short, medium and long shoots were 9, 27 and 47 mm, respectively.

Fig. 6. Probability density function for average per shoot internode length, l. Line graphs represent distributions calculated from the node number distributions using relationship eqn (A1).

Shoot attributes

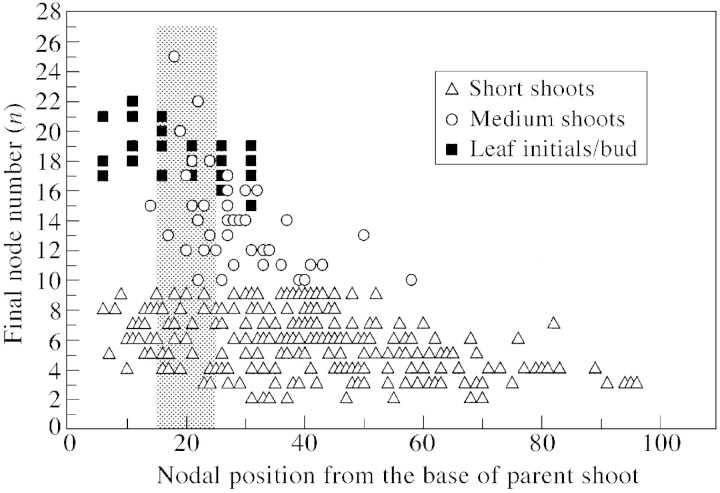
The final node number of terminated axillary shoots was affected by their position along the parent shoot (Fig. 7). Few medium shoots occurred in the preformed section of long parent shoots, whereas short shoots occurred in both preformed and neoformed sections. A comparison of Snowball’s data on number of leaf initials preformed within a bud with our data on final node number of terminated axillary shoots suggested that most shoots self‐terminated before all of the initials within the parent bud had elongated. Axillary shoots located in the lower preformed part of the parent shoot terminated well before all preformed leaf initials had extended, whereas many shoots located in the upper preformed and lower neoformed parts of the parent shoot were closer to having all preformed metamers elongated. Mean node number of medium axillary shoots at a given position appeared to correlate with the mean number of leaf initials within the axillary bud at this position. However, more data on the number of leaf initials are required to quantify this relationship. As with medium shoots, final node number of both short and long shoots decreased towards the tips of long parent shoots (Table 2).

Fig. 7. Effect of position on the long parent shoot on the node number of terminated axillary shoots. Data on number of leaf initials per bud, by courtesy of A. Snowball. Transition from the preformed to neoformed part of a long parent shoot takes place between nodes 15 and 25, (shaded area on graph). Compilation of A. Snowball’s data with the present data.

Table 2.

Effect of nodal position on long parent shoots on the final node number of short and long axillary shoots

	Axillary shoot type
Parameter	Short	Long
Intercept	7·3 ± 0·3	70 ± 5
Position from the base	–0·040 ± 0·006	–0·83 ± 0·17

Positional effects were analysed using generalized models (PROC GENMOD, SAS) with identity link function, P < 0·0001 for all parameters.

Position along parent shoots did not have a major effect on average internode length per shoot (data not presented).

Distribution of axillary production along parent shoot axes

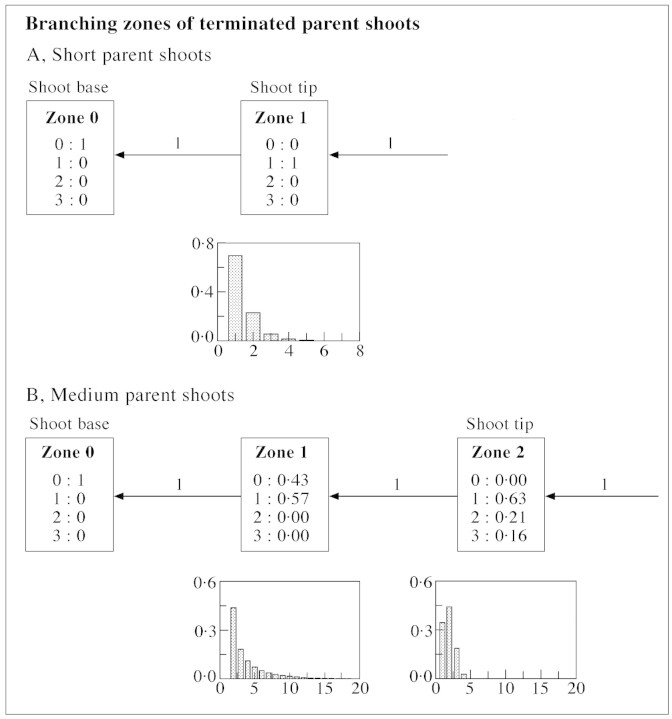
Within each parent shoot type the distribution of axillary production was not homogeneous, and varied between individual parent shoots (Fig. 8). Long and medium parent shoots produced all three axillary shoot types, whereas short parent shoots produced only short axillary shoots. Branching zones of long and medium parent shoots were represented by hidden semi‐Markov chain models (Figs 9 and 10B), as these zones could contain more than one type of axillary production. Representation of branching zones of short shoots was reduced to a semi‐Markov chain (Fig. 10A), as these contained just one axillary production type, latent bud or short shoot.

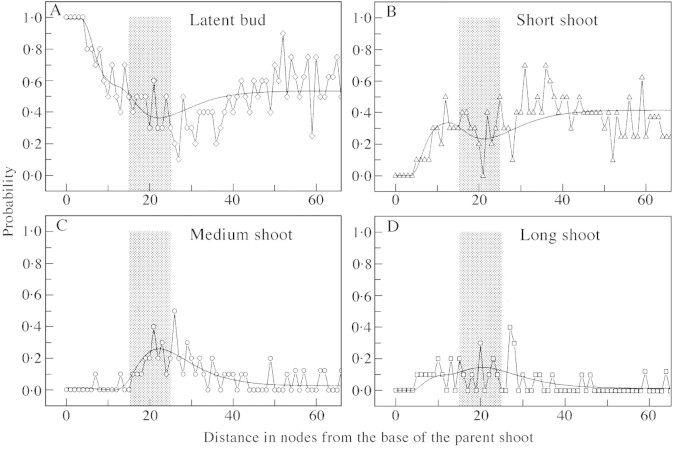
Fig. 8. Distribution of axillary production for long (A–C), medium (D–F), and short (G–I) parent shoots. Axillary production types 0, 1, 2 and 3 correspond to latent bud, short shoot, medium shoot, and long shoot, respectively.

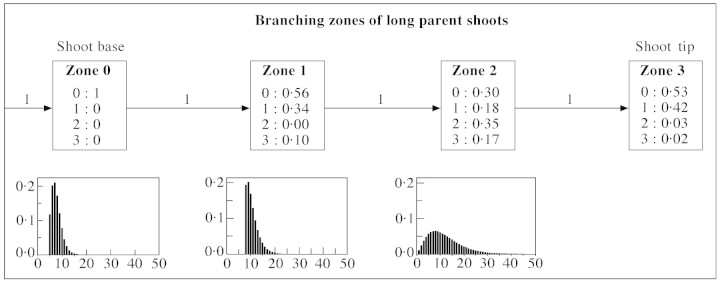
Fig. 9. Hidden semi‐Markov chain model representing branching pattern of long kiwifruit shoots. Boxes represent branching zones along the shoots, corresponding to the states of the model, with probabilities of different types of axillary production observed in each zone given within the zone boxes. The types of axillary production denoted by 0, 1, 2 and 3 correspond to latent bud, short shoot, medium shoot and long shoot, respectively. Arrows represent transitions between the zones with transition probabilities shown above. The far left arrow indicates that the initial state of the model corresponds to zone 0. The probability distributions for zone length measured in number of nodes are shown below the corresponding boxes.

Fig. 10. Semi‐Markov chain model (A) and hidden semi‐Markov chain model (B) representing branching patterns of short and medium shoots, respectively. Diagram notations are the same as for long parent shoots (Fig. 9) except that in the case of terminated shoots the initial states of the models correspond to the branching zones at the tips of the shoots, as indicated by arrows on the far right pointing to these zones.

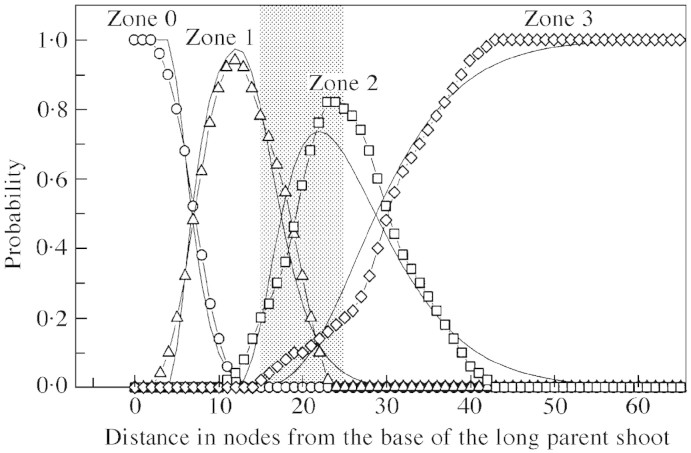
Branching on long parent shoots was essentially mesotonic with an unbranched zone at the base that included a section of bud scales and floral primordia development (zone 0, Fig. 9). A zone at the tip contained mainly short axillary shoots (zone 3, Fig. 9). Most long shoots occurred in two intermediate zones (zones 1 and 2, Fig. 9). The transition between these two intermediate zones corresponded to the transition from the preformed to the neoformed part of the parent shoot (Fig. 11). Indeed, from model parameters, the combined mean length of zones 0 and 1 was 18.5 nodes, which is close to 19.5—the number of leaf initials within the parent bud obtained for the same plant by Snowball (1997b), using buds sampled from the ten‐node region distal to the floral nodes (see Table 4 in Snowball, 1997b). The mean number of leaf initials calculated for a larger sample from the original data (presented in Fig. 7) was 18.4, which is even closer to our data for the combined length of zones 0 and 1.

Fig. 11. Probability distributions for branching zones of long parent shoots. Observed probabilities of zone 0 (circles), zone 1 (triangles), zone 2 (squares) and zone 3 (diamonds) were calculated on the basis of optimal segmentation of observed sequences of axillary production into branching zones. The corresponding theoretical probabilities (represented by line graphs) were calculated from the parameters of the corresponding hidden semi‐Markov chain model (Fig. 9). Transition from preformed to neoformed parts of the parent shoot takes place within the shaded area (see legend to Fig. 7).

As with long parent shoots, all terminated (short and medium) parent shoots had a non‐branched zone at their base. However, unlike long parent shoots, branching on short and medium parent shoots was acrotonic with a short zone at the tip characterized by 100 % branching. Only these two zones were required to represent branching patterns on short parent shoots (Fig. 10A). In medium parent shoots, the zone at the shoot tip bore a mixture of all three shoot types, and an intermediate zone (zone 1, Fig. 10B), which had short shoots only.

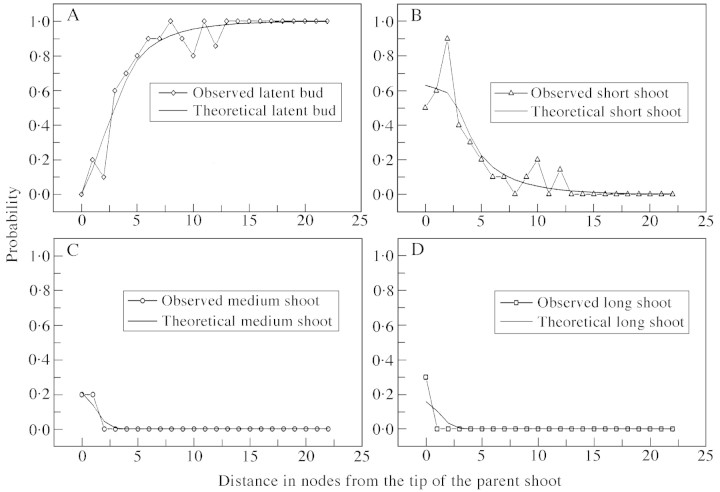
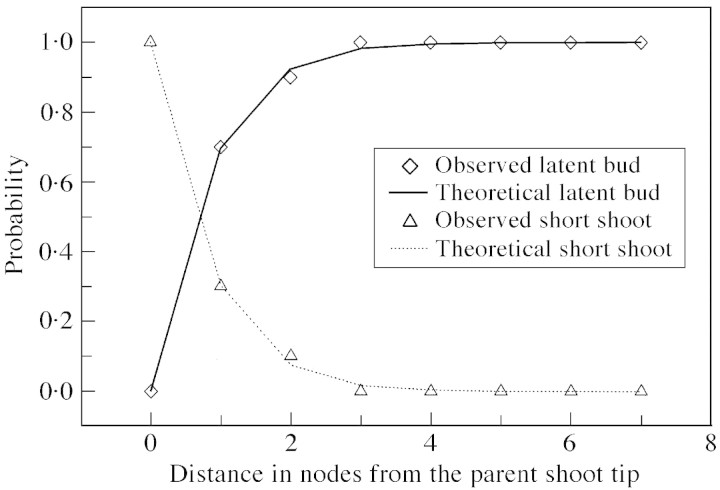
Theoretical probability distributions of the different types of axillary production for long, medium and short parent shoots calculated from the corresponding models showed good agreement with the observed probabilities extracted from the data (Figs 12–1314). Note that for long parent shoots these probabilities are expressed as functions of distance (measured in nodes) from the base of the parent shoot, whereas for short and medium shoots the probabilities are expressed in terms of distance from the tip of the parent shoot. The latter choice was more appropriate for terminated shoots that were variable in total node number with dense branching at the tips.

Fig. 12. Probability distributions of different types of axillary production for long parent shoots. Symbols represent probabilities extracted from the data, and line graphs are probabilities calculated from the corresponding hidden semi‐Markov chain model (Fig. 9). Transition from preformed to neoformed parts of the parent shoot takes place within the shaded area (see legend to Fig. 7).

Fig. 13. Probability distributions of different types of axillary production for medium parent shoots. Symbols represent probabilities extracted from the data, and line graphs are probabilities calculated from the corresponding hidden semi‐Markov chain model (Fig. 10B).

Fig. 14. Observed and theoretical probability distributions of different types of axillary production for short parent shoots. Symbols represent probabilities extracted from the data, and line graphs are probabilities calculated from the corresponding semi‐Markov chain model (Fig. 10A).

DISCUSSION

Classification of shoot types

The proposed classification of shoot types is based on the modes of node number distribution and does not rely on any pre‐set values of shoot attributes such as length or node number. It is therefore flexible enough to represent characteristic features of individual Actinidia species, such as the number of shoot types and their proportions in the total population of shoots. The classification also encompasses physiological processes that are underlying phenomena of preformation/neoformation and internode extension. Classification of shoots into short and long, based on the absence or presence of neoformation, was used previously for apricot by Costes and Guédon (1996). A characteristic feature of Actinidia chinensis is that the node number distribution for preformed shoots is bimodal and requires the introduction of a medium shoot type. Internode length (and its distribution within the plant structure) contributes to the characteristic form of plants and is therefore an important variable in modelling plant structure and function. Our study has shown that in A. chinensis internode length was determined more by shoot node number than by shoot position within the vine structure, with internode length distribution being split into three modes corresponding to the modes of the node number distribution.

Quantitative models of branching patterns

In our analyses, the branching structure of parent shoots is modelled by a succession of zones, which differ for each parent shoot type according to their development. This is particularly apparent in the case of long parent shoots where the first two branching zones correspond to the preformed part of the shoot and the most vigorously branched zone is located near the base of the neoformed part of the shoot. The median location of long shoots along the axes of long parent shoots is consistent with the definition of the Champagnat model. In this model, relay axes (dominant shoots) develop in the region of maximum curvature along the parent axes. It can be assumed from visual observations of vines that this median location corresponds to the curved portion of the long parent shoot. However, rather than just being associated with a change in curvature, increased production of long shoots in this median section may also be due to the pattern of parent shoot development and the transition from the preformed to the neoformed part of the parent shoot. Similar correlations between branching and parent shoot development were obtained for sylleptic branching (Génard et al., 1994) and for distribution of axillary production along fruiting shoots (Fournier et al., 1998) in peach; and for axillary production in young apple trees (Lauri and Térouanne, 1998).

Quantitative comparison of branching of different shoots is complicated by the fact that even within one parent shoot type there is a considerable variation in total node number. It is thus inappropriate to compare axillary production according to just nodal position on the parent shoot, especially between different shoot types. The number of nodes in the preformed part of long parent shoots also differs considerably between species, from, on average, 15 for A. guilinensis to 34.6 for A. melanandra (Snowball, 1997a). Modelling branching structure by a succession of zones gives a level of representation intermediate between shoot level and metamer level that takes into account this variability in shoot node number. It provides criteria for comparing patterns of axillary production for different shoot types, according to the number and characteristics of the branching zones and positions along the parent shoot, as related to shoot development (Fournier et al., 1998).

Budbreak

The probability of budbreak for a given bud did not appear to be related to the number of preformed metamers in the resting bud. For example, on long parent shoots the region of maximum branching does not coincide with the region of maximum metamer preformation identified by Snowball (unpubl. res.). Nor was the likelihood of the bud developing into a long shoot related to the number of preformed metamers in the resting bud. These probabilities were more related to the position of the bud along the preformed and neoformed sections of the parent shoot. Similarly, the final node number for preformed axillary shoots, although limited by the number of leaf primordia within the bud, depended mainly on their position along the parent shoot. Comparison of these two findings suggests that apart from buds in the basal ‘floral’ zone on each shoot, all axillary buds have equal potential to break, their development being triggered or interrupted by certain conditions of the external or internal environment. For example, increased light exposure increases bud break in kiwifruit shoots in the following year, and insufficient winter chilling considerably reduces the amount of bud break and delays its timing (McPherson et al., 1995).

Shoot development and climatic conditions

Temperature has a considerable effect on shoot extension (Morgan et al., 1985) and on the rate of leaf appearance and expansion of individual leaves (Seleznyova and Greer, 2001). This is particularly important for non‐terminated shoots, which continue to grow until the end of the season. In contrast, the maximum final node number of terminated shoots does not depend on the current season temperature as it is related to bud development and the number of leaf primordia preformed within buds during the previous season. Thus, site‐to‐site and year‐to‐year variations in the number of preformed primordia in buds are likely to be related to climatic conditions during bud development (Remphrey and Davidson, 1994). Because the majority of Actinidia shoots are preformed, a study of environmental effects on bud development is a prerequisite to an understanding of the climatic effects on vine dynamics.

CONCLUSIONS

This study has developed a framework for the quantitative description of Actinidia vine architecture. Shoot types have been defined and the families of stochastic models most suitable for representing branching patterns have been selected. This approach is being used to study the effects of kiwifruit pruning systems and rootstocks on shoot development and to quantify phenotypic differences in breeding populations.

ACKNOWLEDGEMENTS

We thank Dr Angela Snowball (previously HortResearch, Mt Albert) for use of her data sets, and Dr Paul Gandar, Dr Fraser Broom and Shirley Miller for discussions during the establishment of this work. This study was funded by the New Zealand Foundation for Research, Science and Technology, Contracts C06806 and C06X0006.

APPENDIX

Internode length distribution for a group of shoots within a range of node number n₁ ≤ n ≤ n₂, can be calculated by taking into account input from each of the sub‐populations of shoots S(n) with a given node number, n. Namely, the probability density distribution function for such a group can be presented in the form:

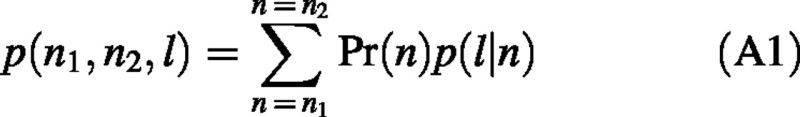
where Pr(n) is the probability that a shoot belongs to S(n), and p(l|n) is a probability density of a shoot from S(n) having internode length l. Note that the notion of probability density (measured in mm^–1) was used since internode length l is a continuous variable (for example, p(10|8) gives the probability of a shoot with eight nodes having an internode length between 9.5 and 10.5 mm). We used eqn (A1) to calculate internode length distributions for short, medium and long shoots. Pr(n) was determined as a fitted mixture of tree modes of the node number distribution of axillary shoots (Table 1), taking into account weights of the modes for the whole population of axillary shoots, so that

We assumed p(l|n) to be normally distributed with the mean l̂(n) given by eqn (2) and the standard deviation σ̂(n) given by eqn (3).

Received: 11 October 2001; Returned for revision: 16 November 2001; Accepted: 3 January 2002.