Sexual and Vegetative Reproduction of Hieracium pilosella L. under Competition and Disturbance: a Grid‐based Simulation Model

Abstract

We used a spatially explicit simulation model to examine the relative importance of vegetative and sexual reproduction in Hieracium pilosella L. Based on an understanding of the complex life cycle of this species and on data from in situ population dynamics in a calcareous grassland in NW Switzerland, we simulated growth and the relative contribution of clonal reproduction by stolons and reproduction by seeds across a gradient of increasing soil fertility. Competition by a clonal grass resulted in nearly complete exclusion of H. pilosella from the more fertile part of the simulation plot. Under low soil fertility, when grass could not survive, H. pilosella largely persisted by vegetatively produced rosettes. This pattern of a sharp separation of both species was shifted slightly in favour of H. pilosella by introducing random disturbances. Only by adding: (1) long‐distance seed dispersal, and (2) facilitation of seedling establishment in the vicinity of grass tussocks in vegetation gaps was a more realistic representation of field observations realised, with rosettes of H. pilosella grown from seeds occasionally distributed within dense grass vegetation. Phenotypic plasticity of stolon length was a decisive factor for the maintenance of H. pilosella populations. We conclude that a mixed strategy of clonal growth and reproduction by seeds in H. pilosella is necessary to maintain populations of this species in the presence of high interspecific competition and a shortage of open space.

INTRODUCTION

There is abundant evidence from interspecific comparisons that clonal reproduction is favoured under specific ecological conditions (Abrahamson, 1980). Advantages of clonal growth include the ability to rapidly colonize open habitats, to occupy space by forming dense patches or to forage for resources that are heterogeneously distributed (Hutchings, 1988). Sexual reproduction and the production of seeds remain important for most clonal species (Eriksson, 1989; Stöcklin and Bäumler, 1996). Therefore, the importance of clonality in plants ultimately depends on the way in which meristems and resources of a plant are committed to various functions and how establishment from seeds and vegetative reproduction contribute to population growth (Sackville Hamilton et al., 1987). Several studies have shown that within and between closely related species the importance of clonal and sexual reproduction can vary among habitats (e.g. Turkington, 1985; Sutherland and Vickery, 1988; Stöcklin, 1992, 1999; Eckert and Barrett, 1993; Krahulec, 1994). Variation in life‐history traits among individuals or different taxa of clonal species may be a result of selection pressure on genetic trade‐offs exerted by biotic and abiotic factors in contrasting habitats (Prati and Schmid, 2000), or may result from phenotypic variation (plasticity), particularly common for morphological traits in clonal plants (de Kroon and van Groenendael, 1990). However, the extent to which variation in vegetative and sexual reproduction reflects evolutionary patterns or environmental conditions is only poorly known (Silander, 1985; Mogie and Hutchings, 1990).

The widespread Hieracium pilosella L. is an especially good example of the variable importance of clonal and sexual reproductive traits. Within this species the number of viable seeds per rosette, the importance of clonal reproduction by stolons and stolon length are highly variable (Gadella, 1991). Population maintenance in Hieracium pilosella usually depends almost exclusively on clonal reproduction (Bishop et al., 1978). Nevertheless, stolon formation and the production of seeds are tightly coupled, and the balance between the production of seeds and stolons is strongly dependent on nutrient availability and density (Davy and Bishop, 1984; Bishop and Davy, 1985). The conditions under which reproduction by seeds is relevant for population maintenance or population growth remain unclear.

Here, we use a spatially explicit simulation model of the population dynamics in Hieracium pilosella to examine the relative importance of vegetative vs. sexual reproduction in relation to grass density. The model is designed with the intention of varying the biological parameters of clonal and sexual reproduction for a better understanding of their functional significance. Spatially discrete grid‐based simulation models (cellular models) allow for the investigation of temporal and spatial aspects of population dynamics and of competition. Such models have been used to investigate clonal spread (Oborny and Cain, 1997, and literature cited therein), the combination of sexual and vegetative reproduction (Harada and Iwasa, 1996; Winkler and Fischer, 1999) and interactions among clonally reproducing plants (Inghe, 1989; Herben, 1992; Winkler and Klotz, 1997a). A model of the dynamics of H. pilosella in dry grassland addressed the importance of favourable weather conditions for the onset of individual reproduction (Winkler and Klotz, 1997b). The present model is an adaptation of the Winkler–Klotz model to a more general question, and is therefore complemented by analytical difference equations (Winkler et al., 1999). Fitness measures (‘competitiveness’, C) derived from these equations allow us to explain the transition in species dominance along a gradient of soil properties.

We simulate population growth of Hieracium pilosella to assess the relative importance of clonal and sexual reproduction in this species in a gradient of increasing soil fertility and in competition with a clonal grass. We use field observations of the population dynamics of H. pilosella and information from the literature to parameterize the model and as a control for the realism of simulations. The model is then explored to answer specific questions related to the sexual and vegetative reproduction of Hieracium: (1) is the relative importance of clonal and sexual reproduction of H. pilosella modified by the strength of grass competition and by random disturbances; (2) does long‐distance seed dispersal and gap recruitment of Hieracium affect the vegetation pattern in the soil gradient; (3) how important is density‐dependent plasticity in stolon length for vegetative reproduction of Hieracium; and (4) what are the biological and environmental reasons for maintaining a mixed reproductive strategy vs. either an exclusively sexual or vegetative reproductive strategy in fictitious Hieracium species?

MATERIALS AND METHODS

The species

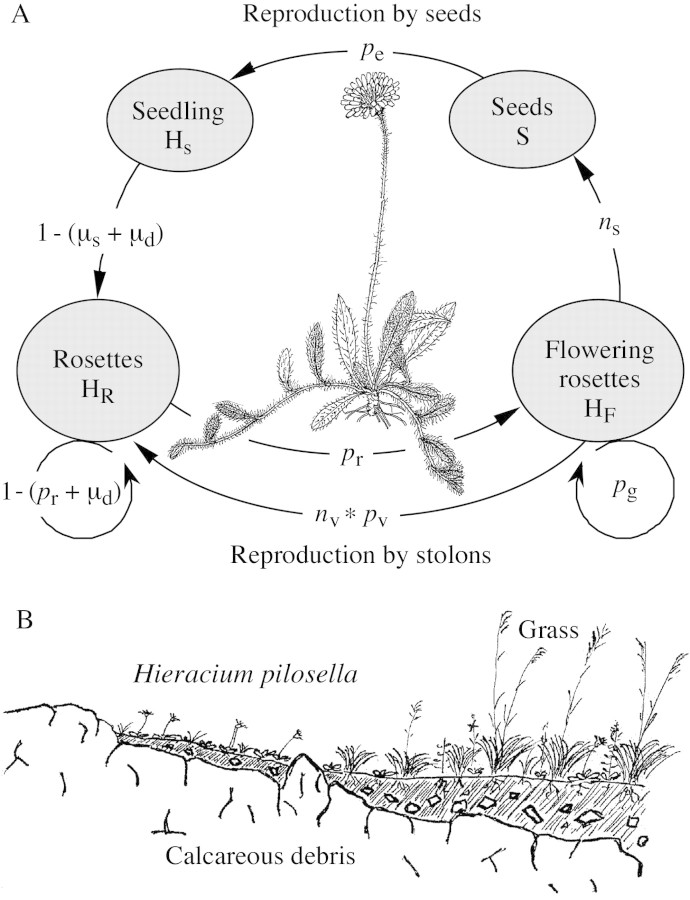
Hieracium pilosella L. (Asteraceae) is a widespread stoloniferous perennial that produces distinct rosettes on a slender rootstock (Bishop and Davy, 1994). The complex life cycle of the plant comprises four stage classes, and reproduction occurs both from seeds and clonal growth (Fig. 1). Non‐flowering rosettes originate either from seedlings or are produced vegetatively at the end of slender, leafy, sometimes branched stolons which can be up to 30 cm long. Rosettes are pressed firmly to the ground. Usually in late spring, the terminal apex of rosettes undergoes transition to flowering and produces one flower head (rarely two), while at the same time one or a few of the axillary meristems of the rosette leaves form stolons with new terminal rosettes. Sexual reproduction and clonal growth are therefore tightly coupled. After flowering, the rosettes decay and, after rooting of vegetatively produced rosettes, stolon connections decay. Occasionally, daughter rosettes may also develop in situ from the axillary buds of the parent rosette, without a stolon (Bishop and Davy, 1985; J.S. pers. obs.). In open grassland, favourable conditions (wet years) and vigorous clonal growth may result in dense populations of H. pilosella (Bishop et al., 1978).

Fig. 1. A, Life cycle of Hieracium pilosella L. with four stages (S, seeds; H_S, seedlings; H_R, non‐flowering rosettes; H_F, flowering rosettes), transition probabilities between these stages (p_e, germination and establishment probabilities; p_r, flowering probability; p_g, regeneration of flowering rosettes; p_v, establishment probability of stolons), fecundities (n_s, number of seeds per flowering rosette; n_v, number of stolons per flowering rosettes), and mortalities (µ_s, mortality of seedlings; µ_d, mortality due to disturbance). Note that all sequence steps of the life cycle can be realised within 1 year and that we do not consider the possibility of a seed bank. B, Schematic profile of the distribution of Hieracium and grass vegetation in a gradient of soil quality in calcareous grassland from observations in the field.

Empirical data for the simulation model

To parameterize the model we essentially used data collected during a demographic field study with Hieracium pilosella in an extensively grazed, nutrient‐poor calcareous grassland in NW Switzerland, 20 km south of Basel (Keller, 1997; Table 1). Such semi‐dry grassland in the Swiss Jura Mountains is dominated by Bromus erectus, a clonal grass forming tussocks. In November 1995, all 609 rosettes of H. pilosella in 25 plots (0·4 × 0·4 m) with variable densities of grass cover were measured and their growth and fate was followed until November 1996. The density of Hieracium in these plots was negatively correlated with the biomass of the dominant grass (r = –0·69, P < 0·001) and ranged from one to 63 rosettes per 0·16 m² plot. Low grass density at these sites indicates low soil fertility (Fig. 1B). Rosettes of H. pilosella in plots with dense grass vegetation were significantly larger than rosettes of H. pilosella on poor soil with only little grass present (r = 0·58, P < 0·01). Rosettes of H. pilosella were also larger when Hieracium density was low (r = –0·5, P < 0·05).

Table 1.

Growth and reproductive parameters of Hieracium pilosella L. used for the simulation model from demographic measurements in calcareous grassland in NW Switzerland and from an experiment on germination probability of seeds and seedling survival at the same site (Keller, 1997)

Parameter	Value	Source of data (Keller, 1997)
Growth rate of vegetative rosettes from March to June (mm d–1)	0·16	609 rosettes measured
Fraction of reproducing rosettes with:		225 rosettes flowering
one flower head	88 %
two flower heads	12 %
Percentage of reproducing rosettes with:		230 rosettes with stolons
one stolon	46 %
two stolons	45 %
three stolons	9 %
Ripe seeds per flower head (mean ± s.d.)	54 ± 23	Counts of 30 flower heads
Length of stolons (cm, mean ± s.d.)	4·8 ± 6·4	193 stolons measured
Probability of a rosette flowering within a year	0·36	Fate of marked rosettes (n = 609)
Flowering probability of a rosette with diameter		From a frequency distribution of
3 cm	0·08	flowering probability depending flowering probability depending
5 cm	0·65	on diameter of rosettes
Probability of establishment of a rosette produced from a stolon	0·58	Fate of observed stolons (n = 374)
% Germination of seeds in undisturbed grass vegetation (mean ± s.d.)	2·4 ± 4·3	Mean of 30 replicates in small plots (8 × 8 cm)
Seedling mortality until autumn (mean ± s.d.)	0·54 ± 0·38
% Seedling recruitment in plots with open soil prone to drought	0	No seedlings in such plots

See Materials and Methods for more details.

The population size of H. pilosella remained nearly stable from one year to another. Within a year, 36 % of the rosettes reproduced, subsequently died and were replaced by new ones, almost exclusively from vegetative reproduction. New rosettes originated mostly from stolons; approx. 10 % of dying rosettes regenerated directly from the rootstock. In plots with a high density of H. pilosella, germination and survival of seedlings was zero and H. pilosella persisted exclusively by clonal growth. Plots with a high density of H. pilosella were characterized by shallow soil prone to drought. The onset of reproduction was size‐dependent with a threshold diameter of rosettes of approx. 3 cm and a maximum flowering probability reached with a rosette diameter of 5 cm. Most of the flowering rosettes produced one flower head (88 %), the others two (12 %). The number of stolons per reproducing rosette was one (46 %), two (45 %) or three (9 %). Both the number of ripe seeds and the number of stolons increased significantly with rosette diameter (data not shown).

In an experiment at the same site, germination and survival probability of seedlings were examined in dense grass vegetation where H. pilosella occurs only occasionally. In November 1995, seeds of H. pilosella were sown at two densities (20 and 200) in small plots (8 × 8 cm, n = 120), either with an undisturbed grass cover or in gaps where all vegetation or only mosses had been removed. Germination of seeds and the survival of seedlings were followed until the following autumn. Germination occurred mostly during spring. The overall germination rate was 1·9 % (of the 12 600 seeds sown, 242 seedlings germinated) and tended to be higher when sowing density was low and with an undisturbed grass cover (2·4 %); however, the treatment effects were not significant. By the end of the summer, 52 % of all seedlings had died, independent of the vegetation cover. Of the remaining 117 seedlings, 75 % survived their first winter. At sites with a low or no grass cover, seeds of H. pilosella did not germinate, indicating a facilitation mechanism of grass for successful seedling establishment, similar to results obtained by Ryser (1993).

Additional information from Bishop and Davy (1994) and educated guesses (i.e. for seed dispersal distances and plasticity in stolon growth) were used for the formulation of simulation rules as indicated below.

AN OVERVIEW OF THE SPATIALLY EXPLICIT SIMULATION MODEL

Our approach combines grid‐based and continuous modelling. Vegetation dynamics are simulated in a two‐dimensional plane consisting of a grid of 200 × 50 cells of 1 × 1 cm (Fig. 2). Each cell can either be empty or host a rosette of Hieracium pilosella or grass vegetation. Dynamics are modelled in time steps of 1 year. Following the phenology of Hieracium in the field, each time step includes a sequence of stochastic growth, reproduction and mortality for Hieracium and the grass, as well as disturbance events affecting the simulation plane at random. All individual demographic and competitive events undergo demographic stochasticity (random decisions, or Poisson‐distributed number of seeds, stolons, or new grass patches). Growth and reproduction parameters are treated as continuous variables.

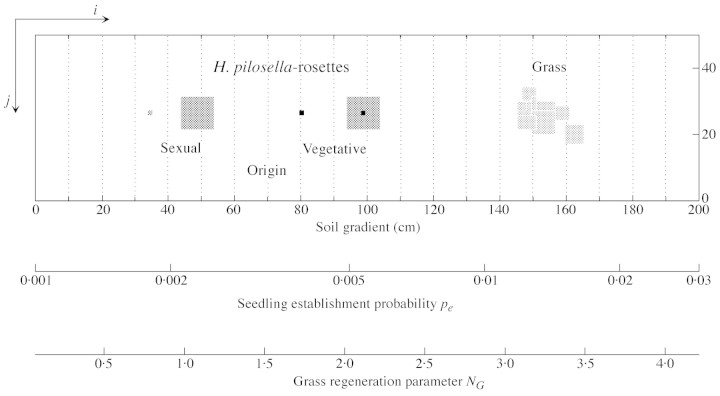
Fig. 2. Two dimensional (i, j) simulation plane (200 × 50 cells of 1 × 1 cm) with a gradient of soil fertility increasing from the left‐ to the right‐hand side. Seedling establishment probability p_e for Hieracium pilosella, and grass regeneration parameter N_G following the soil gradient are shown. The subsections along the gradient (i‐direction) are used in the calculation of vegetation cover in Fig. 4A and in the calculation of the number of Hieracium rosettes in Fig. 6. Dark‐grey patches represent Hieracium rosettes of minimum and maximum size. Centres of rosettes of sexual origin are denoted by a black spot (cell of 1 × 1 cm). Grass patches are represented in light grey.

A simulation time step is initiated with Hieracium rosettes and grass patches distributed over the cellular grid in a pattern resulting from the preceding time step. Rosettes or grass patches are characterized by the position of their centre in the grid, their radius R and their age A. The vegetation cover at the beginning of each time step reflects the situation in spring. All simulation results represent stationary states and were averaged over ten runs. Each run was averaged over a period of 300 years after an equilibration period of 300 years that started with an initial random distribution of Hieracium rosettes and grass patches over the simulation grid. The numeric results were averaged spatially: in ‘gradient simulations’ (Figs 4 and 6) over subsections indicated in Fig. 2, and in ‘patch simulations’ (Fig. 8) over the whole plot. The two‐dimensional representations of the vegetation pattern from simulations (Figs 3, 5 and 7) are snapshots from one time step. Parameters of the simulation model, derived from empirical data or set by scenarios, are listed in Table 2. The sensitivity of the model against changes of parameters was tested.

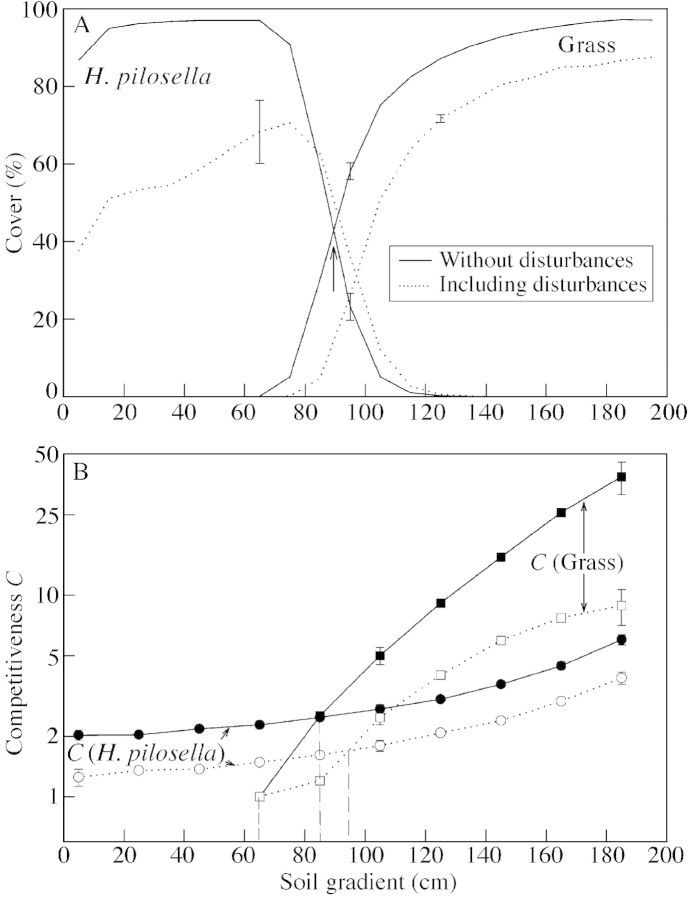
Fig. 4. Competition of Hieracium pilosella and grass in a gradient of soil fertility without (continuous line) and including (broken line) disturbance. A, Cover of competing species averaged over ten runs of 300 years computed for subsections along the soil gradient shown in Fig. 2. B, Competitiveness values C [eqns (1) and (3)]. The arrow in Fig. 4A denotes the point of intersection used for sensitivity analyses. The vertical dot‐dash lines in Fig. 4B indicate the points of intersection of the competitiveness values of the two species. They separate regions in a gradient of soil fertility where one species excludes the other in the long run. The vertical dashed line indicates the boundary for the presence of grass; left of it (C_G < 1) grass cannot establish.

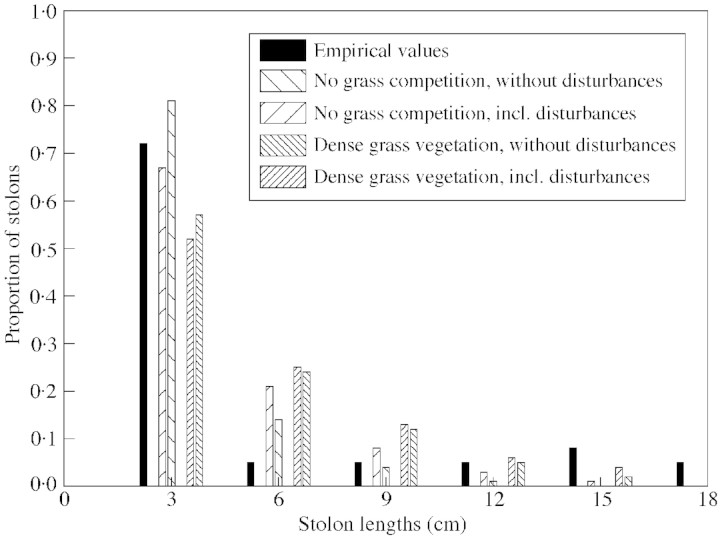
Fig. 8. Frequency distribution of stolon length of Hieracium pilosella from field observations (black bars) compared with values calculated from simulations averaged over 300 years (hatched bars) taking into account competition by grass, and low (p_e = 0·0055) and high (p_e = 0·015) soil fertilities leading to different grass densities.

Fig. 3. Vegetation pattern from simulations of competition between Hieracium and grass in a gradient of soil (standard scenario): A, without disturbances; B, including disturbances. The disturbance regime simulates plant mortality as a consequence of gap formation by cattle or other environmental influences and affects at random 8 % of all cells each year. Plotted are simulations with grass alone, Hieracium pilosella alone and both in competition. The patterns show vegetation distribution in a time step arbitrarily selected from stationary state simulations (for details of the model, see Materials and Methods). Hieracium rosettes are shaded dark grey with black spots indicating the centre of rosettes of sexual origin; grass patches are light grey.

Table 2.

Parameter values used in spatially explicit simulations

Parameters		Standard values	Source
ΔR0	Mean radius increase per year	3·0 (H. pilosella)	Table 1
		1·5 (grass)	Guess
σR	Standard deviation of radius increase	1·5	Table 1
R S	Threshold radius for reproduction	1·5	Table 1
δ	Increase parameter of reproduction probability	3·5	Table 1
R red	Radius reduction percentage for vegetative rosettes	0·2	Table 1
N V0	Mean number of stolons per reproductive rosette	2·0	Table 1
N S0	Resulting mean seed production	64	Table 1 (see Materials and Methods)
σd	Parameter of seed‐dispersal distribution	7·0	Guess
f t	Percentage of long‐distance seed dispersal	0	Standard scenario
		0·1	Modified standard scenario
ΔL	Step length of stolon growth	3·0	Table 1
p C	Probability of plastic stolon growth	0·75	Guess
p C	Regeneration probability of reproductive rosettes	0·1	Table 1
m	Mortality		See Materials and Methods
p e	Seedling establishment probability		See Fig. 2
µ	Juvenile mortality	0·35	Table 1
N G	Number of potential new grass tufts		See Fig. 2
c f	Facilitation coefficient for seedling establishment	1	Standard scenario
		1·15	Modified standard scenario
p T	Disturbance probability		See Materials and Methods
L T	Disturbance gap dimension		See Materials and Methods

Spatial parameters (Δ_0R, L_T, σ_R, R_S, δ, R_red, σ_d, Δ_L) are given in cell units (1 cm). Parameters are defined: (1) to match the findings of Table 1 or Keller, 1997, (2) by educated guesses or (3) by scenario assumptions. Variable model parameters (radius R, seed production, dispersal distances) are described in Materials and Methods. Parameters changing with the soil gradient are given in Fig. 2.

A gradient of soil fertility

The gradient of soil fertility used in ‘gradient simulations’ simulates changes in growth conditions from shallow to deep and moist soil conditions. ‘Gradient simulations’ used the grid of 200 cells in the i‐direction with a gradient for certain parameters and hence no dispersal torus, and 50 cells in the j‐direction without a gradient but with torus geometry (Fig. 2). Soil moisture conditions and soil fertility increasing from the left‐ to the right‐hand side of the simulation grid (Fig. 2) were assumed to influence the seedling establishment probability of Hieracium and the regeneration probability of the grass. Seedling establishment probability, p_e, increased from 0·001 to 0·03, and the number of potential new grass tufts N_G (grass regeneration parameter) changed from 0 to 4·2, where the highest value gave a 97 % grass cover when disturbances were absent. Limits of seedling establishment probability and of grass cover were derived from field observations (see above). To calculate stolon‐length distributions of Hieracium under different soil fertilities and to compute competitiveness values ‘patch simulations’ with a homogeneous grid of 100 × 50 cells and a torus geometry were used. In each ‘patch simulation’ there was a uniform seedling establishment probability p_e and grass regeneration parameter N_G.

Dynamics of Hieracium pilosella

A simulation time step for Hieracium starts in spring with rosette growth, i.e. an increase of the rosette radii, R, by Δ_R (where Δ_R is a normally distributed random number) and with competition of growing rosettes for cells not yet assigned to individual rosettes or grass. Rosettes of sexual origin grow more slowly in the first year after establishment than those of vegetative origin. When the rosette radius is larger than a threshold value, R_S, vegetative rosettes switch into the reproductive state with radius‐dependent probability p_r = (R – R_S)/δ. Vegetative rosettes that did not flower reduce their radius in autumn by R_red. Once per year, in summer, reproductive (flowering) rosettes produce stolons with a juvenile rosette at the apex as well as seeds. The stolon number, N_V, is a Poisson‐distributed random number with parameter N_V0. The number of seeds, N_S, is also a Poisson‐distributed number which depends on the resource state of a rosette (denoted by radius R). Both kinds of offspring production do not influence each other and are density independent. Seeds are dispersed into a transient seed bank in the vicinity of the mother rosettes (random disperal angle, and random distance decreasing along an exponential distribution with parameter σ_d), or as an additional assumption they are dispersed with probability f_t at random over the whole grid (long‐distance dispersal). Stolons grow away from the mother rosette with an internode length Δ_L and a randomly selected growth angle. If a cell that is a potential site of establishment for a juvenile is already occupied (i.e. covered by grass or another rosette) the stolon reacts plastically, with probability p_C, by at most four additional growth steps. Juvenile rosettes may compete for empty microsites. Juveniles that cannot establish after plastic search and competition will die. Their interactions with each other and with the vegetation already present mimic the density‐dependence of vegetative reproduction (Bishop and Davy, 1985). All seeds in the transient seed bank germinate in autumn, and seedlings are established with probability p_e if the germination site is empty. Because of lack of information we did not consider a permanent seed bank. In their first year after establishment, juvenile vegetative rosettes and juveniles from sexual reproduction undergo density‐independent mortality, µ. After reproduction, reproductive rosettes either die, or regenerate with probability p_g.

Dynamics of grass, and interactions with H. pilosella

Grass is considered as an assemblage of clonal patches covering a maximum of nine cells per patch after growth and competition for space in spring (Fig. 2). We do not consider any sexual reproduction for grass. Vegetative spread is formally expressed as an obligatory death of patches after each year combined with an immediate, density‐dependent formation and subsequent growth of N_G new patches starting from grid cells of old ones (Winkler and Klotz, 1997a). Parameter N_G determines local grass density. The limited lifespan of grass tufts and subsequent regrowth are features that allow the modelling of the fine‐scale spatial dynamics of grass. Grass is superior to Hieracium in competition for free cells, but it cannot exclude Hieracium rosettes from already occupied cells. Juvenile rosettes or seedlings of Hieracium cannot exclude grass. Grass is assumed to facilitate establishment of Hieracium seedlings in the immediate neighbourhood of grass patches (multiplication of establishment probability, p_e, by a factor c_f).

Disturbances

The disturbance regime simulates plant mortality caused by trampling of cattle and/or other environmental interferences. Disturbance patches of area L_T × L_T created with probability p_T around a cell kill all vegetation within their gap ranges in autumn after reproduction. We use a mixture of gap sizes including small (1 × 1), medium (4 × 4) and large (8 × 8) groups of empty cells, altogether resulting in 8 % disturbance mortality per year (Schläpfer et al., 1998).

ANALYTICAL DIFFERENCE‐EQUATION MODEL AND THE DEFINITION OF LONG‐TERM FITNESS

In parallel to the spatially explicit simulation model, an analytical difference‐equation model allows identification of the biological determinants of the simulation results. The equations give rise to fitness measures (‘population competitiveness’, C) where relative values of C_H and C_G predict the outcome of interspecific competition and exclusion of Hieracium and grass. If locally C < 1 for a species, then this plant cannot maintain its presence in this region by its local dynamics. This analytical model with its underlying assumptions, the relationship between both the simulation and analytical models, the correspondence of parameters and the numerical calculation of fitness have been described elsewhere (Winkler et al., 1999; Winkler and Fischer, 1999).

For H. pilosella the analytical approach allows for the separation of the consequences of vegetative, C_V, and sexual reproduction, C_S. Population competitiveness C_H (long‐term fitness under space limitation, or gross life‐time offspring production) can be derived as

C_H = C_V + C_S = wa_VF_V/ν + wa_Sp_e/ν(1)

Population competitiveness depends on the fraction, w, of reproductive rosettes; the rates, a_V and a_S, for production of both stolons and seeds; and on the probability of seedling establishment, p_e. Spatial non‐randomness of distribution processes are expressed by F_V (non‐random microsite utilization by juvenile rosettes), where F_V = 1 is the ‘null model’ value. Among other things, F_V > 1 may be a consequence of the plastic search behaviour of stolons, and F_V < 1 may be due to clumping of rosettes combined with short dispersal distances. The factor ν comprises all mortality events.

If we set in the underlying model equations F_V = 1 (no spatial effects), and if juvenile densities are low enough to neglect competition between establishing juveniles, the fraction of sexual offspring per time is calculated by:

B_S/B = (p_ea_S)/(p_ea_S+ a_V) ≈ (p_eN_S)/[p_eN_S (N_V + p_g)](2)

with the proportion p_g of regenerating rosettes added to vegetative reproduction.

Competitiveness of grass C_G is given by:

C_G = 1/f_G(3)

where f_G is the fraction of empty microsites when new grass tufts are formed. In contrast to C_H, there is no simple reduction of C_G on population dynamic parameters. To apply C_H and 1/f_G of eqns (1) and (3) as competitiveness (fitness) measures, theory demands (Winkler and Fischer, 1999) that all kinds of juveniles of all populations would compete for the same set of microsites. But the actual sequence of events, as given by the simulation model, is more complicated and limits any analytical fitness formulation. Nevertheless, numerical calculations (see Fig. 4 and Discussion) show that both fitness expressions are good predictors to explain patterns in species competition.

Values of species competitiveness, C_H and C_G, as well as their vegetative and sexual components, were calculated for each species separately from simulations in homogeneous local patches (‘patch simulations’) where values for the parameters N_G and p_e were selected to represent different positions on the soil gradient (Fig. 2).

RESULTS

Vegetation pattern on a soil gradient

The simulation excluding long‐distance dispersal and facilitation of seedling establishment in gaps (standard scenario) resulted in a distinctive distribution pattern of Hieracium and grass vegetation that was modified only slightly by disturbances (Figs 3 and 4A). Grass alone was restricted to the right (high‐fertility) part of the simulation grid. In the low‐fertility part of the grid the reproductive rate of grass was not high enough for a self‐sustaining population. The boundary between bare soil and vegetation remained rather sharp because of very low grass dispersal. On the other hand, Hieracium alone would fill the whole grid with an increasing number of rosettes of sexual origin towards the more fertile soil region. Competition resulted in a nearly complete exclusion of Hieracium from the more fertile part of the plot. The competitive impact of Hieracium on grass was relatively weak. On the low‐fertility part of the simulation grid, where grass could not be maintained, Hieracium largely persisted by vegetative rosettes. Only in a narrow boundary region could both species coexist. This overall pattern of a sharp separation of both species was shifted slightly in favour of Hieracium by the presence of disturbance. Both species suffered under the disturbance regime, but the grass performed even worse and showed a comparatively lower compensation for losses.

Competitive exclusion of Hieracium by the grass and the small extension of the transition zone with coexistence of both species is a consequence of the greater increase in competitiveness, C, of the grass depending on soil fertility (Fig. 4B). The increase in competitiveness of Hieracium from the left‐ to the right‐hand side of the simulation grid is only slight. The contribution of reproduction by seeds, C_HS, to the total competitiveness of Hieracium [eqn (1)] increases from the left‐ to the right‐hand side of the simulation grid, but this did not significantly affect total competitiveness of Hieracium. A competitive exclusion of grass by Hieracium is strengthened when disturbance is included in the model.

To test the model for sensitivity against parameter changes, the position of the point of intersection of species cover in Fig. 4A (X_I = 89 cm for undisturbed conditions, denoted by an arrow) was used as an indicator. A 10 % change of dispersal parameters Δ_L (above a threshold value of Δ_L = 2·0) and of σ_d as well as of seed production, N_S, had no significant effect on X_I (ΔX_I ≤ 0·5 cm). The effects of similar changes in juvenile mortality µ, reproduction threshold, R_S, and stolon number, N_V, were ΔX_I = 2·5, 1·5 and 5·0, respectively. The minimum value of N_V required to maintain a Hieracium population was N_V = 1·55. Even with very high stolon numbers (N_V ≈ 50) Hieracium could not fully exclude grass in the model habitat. Changing the plasticity probability p_C from 0 to 1 led to variation in X_I between 78 and 99 cm. An increase in the grass parameter ΔN_G, representing species’ response to changing abiotic conditions in the gradient, had a non‐linear effect: a ±10 % change shifted X_I from 89 to 82 or 101 cm, respectively. With a halving of ΔN_G, grass could not exist in the presence of Hieracium, whereas only by increasing this parameter by a factor of five, grass could fully exclude Hieracium.

Long‐distance seed dispersal and gap recruitment

The pattern shown in Fig. 3 (standard scenario) was modified by adding two assumptions: (1) long‐distance seed dispersal, and (2) facilitation of seedling establishment in the vicinity of grass tussocks in vegetation gaps. The penetration of Hieracium into grass vegetation was only slightly enhanced by some long‐distance seed transport (f_t = 0·1; Fig. 5A). Simulations showed that even a random distribution of all seeds over the whole plot (f_t = 1·0) would change only insignificantly the position and form of the sharp vegetation boundary. Establishment of Hieracium in gaps of otherwise dense grass vegetation was increased, at least in the transition zone between Hieracium and grass, if we assumed a facilitation of germination and seedling establishment in the vicinity of grass patches (c_f = 1·15; Fig. 5B). However, a combination of both long‐distance dispersal and facilitation modified the basic pattern to a more realistic representation of field observations, with Hieracium penetrating into the dense grass cover and with occasional Hieracium rosettes found in dense grass vegetation (Fig. 5C, modified standard scenario).

Fig. 5. Vegetation pattern from simulations of competition between Hieracium and grass in a gradient of soil fertility (including disturbance) with the following additional assumptions: A, long‐distance seed dispersal (10 % of produced seeds randomly dispersed over the whole plot); B, facilitation of seedling establishment in the vicinity of grass in vegetation gaps; C, combination of A and B (=modified standard scenario). Hieracium rosettes are shown in dark grey with black spots indicating the centre of rosettes of sexual origin; grass patches are light grey.

Relative importance of vegetative and sexual reproduction

The ratio of sexual to total offspring was determined by the soil property via the seedling establishment probability p_e (Fig. 6). Competition by grass causes a shift towards a much higher fraction of rosettes of sexual origin. In the presence of dense grass (right‐hand side of the simulation grid) only a small number of Hieracium rosettes are present, mostly of sexual origin. They result from occasional germination within gaps, but they do not give rise to subsequent vegetative spread. This suppression of vegetative spread of Hieracium is higher when the grass vegetation is denser. If there is no competition with grass, simulated values correspond well with the expected fraction calculated from eqn (2).

Fig. 6. The number of new Hieracium pilosella rosettes produced every year and the fraction of rosettes of sexual origin along a gradient of soil fertility calculated for the modified standard scenario with long‐distance seed dispersal and facilitation of seedling establishment included. Dashed lines, Scenario without disturbances; dotted lines, scenario with disturbance. The continuous line shows the expected fraction of Hieracium pilosella rosettes of sexual origin in the absence of grass [theoretical expectation according to eqn (2)]. Numbers and fractions were computed for subsections along the soil gradient shown in Fig. 2 and were averaged over ten runs of 300 years.

A 10 % change in the two parameters that ensured the presence of Hieracium in dense grass—the long‐distance dispersal parameter, f_t, and the facilitation parameter, c_f—affected offspring number (±1·0 and 4·0, respectively), but not the sexual fraction.

Exclusively sexual or exclusively vegetative reproduction

To maintain a population density similar to the standard scenario with vegetative reproduction alone, the mean number of stolons must be only slightly increased (N_V* = 2·3, instead of 2·0, regeneration included); whereas with sexual reproduction alone the number of seeds required per rosette (N_S*) is 200 (instead of 64). The spatial distribution of rosettes was very different in the two cases: rosettes of a ‘fictitious species’ with vegetative reproduction alone were aggregated in the competition‐free region, and rosettes of an exclusively sexually reproducing ‘fictitious species’ were crowded in the region with good soil conditions where there was strong competition with grass (Fig. 7).

Fig. 7. Vegetation pattern from simulations in a gradient of soil fertility using fictitious Hieracium species with either only vegetative or sexual reproduction. Values for exclusively sexual reproduction (N_S* = 200) and for exclusively vegetative reproduction (N_V* = 2·2 plus 10 % regenerating rosettes) were calculated in order to maintain an average population density of Hieracium similar to the standard scenario (see above, Fig. 3). Hieracium rosettes are shown in dark grey with black spots indicating the centre of rosettes of sexual origin; grass patches are light grey.

Vegetative growth of H. pilosella and variation in stolon length

In all simulations, rosettes of Hieracium are to a large extent of vegetative origin. Stolon length is density dependent and results from the ‘genetically fixed’ step length Δ_L and plastic behaviour when cells are already occupied (additional growth steps with probability p_c).

Simulations showed that Δ_L played an insignificant role: variations in Δ_L changed rosette densities by less than 5 %, irrespective of vegetation density. However, the capacity for plastic stolon elongation was a decisive factor in the performance of Hieracium. Without additional growth of stolons after establishment failure of a juvenile rosette (p_c = 0), the average density of Hieracium was reduced by 72 %. When disturbance was also included, Hieracium density was so low that the population could not survive in the presence of grass.

If plasticity is included, the realised stolon lengths were highly variable. There is good correspondence between the observed distribution of stolon length from the field and results from several simulations (Fig. 8). Simulations suggest that vegetation density is the decisive factor for stolon length distributions: the higher the vegetation density, the smaller the fraction of short stolons. Whether the vegetation was grass or Hieracium was not of importance.

DISCUSSION

Vegetation pattern and competitiveness

Salient features of the simulated vegetation pattern were the exclusion of one of the two species in different parts of the gradient and the formation of a sharp vegetation boundary between H. pilosella rosettes and grass tufts (Fig. 3) with only a restricted overlap zone.

The existence of sharp species boundaries is a common feature in species distribution (Wilson and Agnew, 1992). They may be related to human interference or to sharp boundaries in abiotic conditions. Both factors were ruled out by our field observations. Wilson and Agnew (1992) and Malanson (1997) have shown that sharp species boundaries may also result from a positive feedback in biological processes within a plant community. In their models, plants modified the environment in such a way that a continuous abiotic gradient became discontinuous. Lennon et al. (1997) explored the emergence of sharp species boundaries in a gradually changing environment using a metapopulation approach in which adjacent local populations were connected by dispersal of limited range.

In our model we extended these approaches, explaining boundaries from interactions of one species with its abiotic environment to interactions between different species. Grass alone had a distribution boundary determined by a similar mechanism to that discussed by Lennon et al. (1997). H. pilosella alone would be present over the whole gradient. But in the region where C_H < C_G, competition with grass reduces the growth rate of H. pilosella to below 1 and Hieracium dies out locally (Winkler and Fischer, 1999). Thus, the sharp boundaries in our model are a result of competitive interactions in a gradually changing environment. This general feature of our model is only quantitatively but not fundamentally affected by changes in the dynamic parameters of the species over a large region, or of the response of species to abiotic conditions along the gradient.

The pattern of species exclusion depends on the model assumption that both species are equivalent with respect to individual interactions (Winkler et al., 1999). This condition is, however, not strictly fulfilled: we realistically assumed that during growth grass patches are competitively superior to Hieracium rosettes. A stricter application of the assumption of equivalence among species had only minor effects on simulation results (data not shown).

Seedling establishment under competitive conditions

Long‐distance seed dispersal was limited to a small proportion of the seeds. It gave rise to only small, generally not self‐sustaining patches of H. pilosella in the grass area (Fig. 5A). Long‐distance dispersal, together with facilitation of recruitment in the vicinity of grass, led to a more realistic picture in the species distribution without changing the basic pattern of a relatively sharp boundary between the two species. The result of adding these two supplementary assumptions to the model matched the empirical observation of a regular presence of isolated H. pilosella individuals in more dense vegetation.

As a consequence of (almost) symmetrical individual competition in our model, fitness depends on the properties of the species itself. This species–individualistic view of fitness is abandoned by introducing positive interactions (facilitation; Callaway, 1998). Fitness of one species now depends on properties and the dynamics of the other species present. Although grass outcompeted H. pilosella in dense stands, it facilitated the establishment of H. pilosella in small gaps. Such a positive interaction results from the protection of seedlings against drought by established vegetation, and is well known in extreme climates like deserts or alpine screes (Franco and Nobel, 1988, 1989; Stöcklin and Bäumler, 1996). In semi‐dry calcareous grassland, facilitation of seedling establishment by neighbouring plants was observed by Keller (1997) and studied by Ryser (1993). He observed an improved establishment in microsites compared with larger gaps for a number of species.

Predominance of vegetative reproduction

In real populations (Bishop and Davy, 1994; Keller, 1997), and in our model, new rosettes of H. pilosella originate only rarely from seeds. Only in dense grass were H. pilosella rosettes not able to expand by stolon growth, and the maintenance of H. pilosella depended on seedling establishment. If there were disturbances, H. pilosella expanded vegetatively into the gaps created.

Stolon growth in the simulation model had a genetically fixed (internode length Δ_L) and a plastic component determining final stolon length (parameter p_C). Simulation results (population sizes as well as distribution patterns) depended only insignificantly on Δ_L. However, plasticity in stolon length was decisive for maintaining H. pilosella populations. The denser the environment of a reproducing rosette the longer were, on average, their stolons as more search steps were necessary to establish new rosettes (Fig. 8). Variation in stolon length is well known in Hieracium (Gadella, 1991). Density‐dependence of stolon length in H. pilosella was also mentioned by Bishop et al. (1978) but was not discussed further. Our results suggest that plasticity in stolon length is crucial for H. pilosella, particularly under competitive conditions. Morphological plasticity is common in clonal plants, particularly in spacers, those parts of clonal plants that interconnect ramets (de Kroon and van Groenendael, 1990). Such plasticity is frequently a result of environmental stimuli, resulting in what has been called the ‘foraging’ behaviour of plants, i.e. the ability to respond to environmental quality by escaping from poor sites and proliferating in richer sites (Hutchings, 1988). In our model, free space for establishing new rosette is the scarce resource determining plasticity in stolon length of H. pilosella.

Reasons for maintaining a mixed reproductive strategy

An obvious reason for maintaining seeds is the necessity for the colonization of new sites by long‐distance dispersal events. Our simulation results suggest that seedlings are also important for the maintenance of already established populations in the presence of high interspecific competition. A fictitious Hieracium species reproducing exclusively by stolons was crowded in the competition‐free zone; fictitious Hieracium reproducing exclusively by seeds was crowded in the region where competition with grass was strong. To maintain an exclusively sexual strategy, the number of seeds would have to be increased considerably. Seedling recruitment is supported by small gaps; however, facilitation of the survival of seedlings by protecting grass tussocks is probably even more important when soils are prone to drought. Eriksson (1997), reviewing published evidence, suggested that seedling recruitment is a significant part of the life cycle of many clonal plants, not only as a dispersal mechanism but also within already established populations. Our simulations support this idea for Hieracium. Reproduction by seeds is a necessity for the persistence of populations under strong interspecific competition and when there is a shortage of open space, conditions in which the plant is not able to expand by stolons.

CONCLUSIONS

Our grid‐based model allowed us to provide a realistic, dynamic and spatially explicit simulation of the behaviour of the clonal Hieracium pilosella in the field. Variable ramet size and the particular morphology determining vegetative and sexual reproduction are both taken into account by our model. We show that in competition with a clonal grass, sharp species boundaries may not only arise from abiotic conditions, but also from competitive interactions in a gradually changing environment. In H. pilosella, plasticity in stolon length is crucial for population maintenance, and vegetative reproduction is usually predominant. However, reproduction by seeds becomes important when interspecific competition is strong and when there is a shortage of open space, thus explaining why H. pilosella and closely related species continue to produce seeds.

ACKNOWLEDGEMENTS

We thank Monika Keller for her contribution to the observational data used for our model and H. Auge, M. Fischer, S. Pepin, W. Schütz and two anonymous reviewers for valuable comments on earlier versions of the manuscript.

Received: 21 August 2001; Returned for revision: 29 October 2001; Accepted: 18 January 2001.