Abstract
Kinetic parameters estimated from dynamic 18F-fluorodeoxyglucose PET acquisitions have been used frequently to assess brain function in humans. Neglecting partial volume correction (PVC) for a dynamic series has been shown to produce significant bias in model estimates. Accurate PVC requires a space-variant model describing the reconstructed image spatial point spread function (PSF) that accounts for resolution limitations, including non-uniformities across the field of view due to the parallax effect. For OSEM, image resolution convergence is local and influenced significantly by the number of iterations, the count density, and background-to-target ratio. As both count density and background-to-target values for a brain structure can change during a dynamic scan, the local image resolution may also concurrently vary. When PVC is applied post-reconstruction the kinetic parameter estimates may be biased when neglecting the frame-dependent resolution. We explored the influence of the PVC method and implementation on kinetic parameters estimated by fitting 18F-fluorodeoxyglucose dynamic data acquired on a dedicated brain PET scanner and reconstructed with and without PSF modelling in the OSEM algorithm. The performance of several PVC algorithms was quantified with a phantom experiment, an anthropomorphic Monte Carlo simulation, and a patient scan. Using the last frame reconstructed image only for regional spread function (RSF) generation, as opposed to computing RSFs for each frame independently, and applying perturbation GTM PVC with PSF based OSEM produced the lowest magnitude bias kinetic parameter estimates in most instances, although at the cost of increased noise compared to the PVC methods utilizing conventional OSEM. Use of the last frame RSFs for PVC with no PSF modelling in the OSEM algorithm produced the lowest bias in CMRGlc estimates, although by less than 5% in most cases compared to the other PVC methods. The results indicate that the PVC implementation and choice of PSF modelling in the reconstruction can significantly impact model parameters.
Keywords: partial volume effect correction, PET, cerebral-metabolism, quantitation, OSEM
1. Introduction
Calculation of kinetic parameters and the cerebral metabolic rate of glucose (CMRGlc) from dynamic 18F-fluorodeoxyglucose (18F-FDG) PET has been used extensively to estimate glucose utilization in the “normal” brain (e.g. healthy volunteers and mild dementia patients). Kinetic parameter calculation requires fitting a three compartment model (Phelps et al. 1979) to a full duration time activity curve (TAC) (i.e. starting immediately after injection) to estimate rate constants K1, k2, k3, and k4 representing 18F-FDG’s forward and reverse transport from the blood pool to tissue and its phosphorylation and dephosphorylation, respectively. 18F-FDG kinetic modelling has been found to have utility in both preclinical (Yu et al. 2009, Song et al. 2010) and clinical (Piert et al. 1996, Graham et al. 2002) neurological imaging studies. Mosconi et al. (2007) found that K1 and k3 were significantly reduced in several brain structures in mild Alzheimer’s disease patients compared with age matched subjects while Cornford et al. (1998) measured significantly reduced K1 and k3 values in seizure foci versus parameters derived from contralateral ROIs in patients being evaluated for the surgical treatment of intractable seizures.
Neglecting partial volume correction (PVC) for reconstructed images of a dynamic study has been shown to produce significant bias in kinetic parameter estimates (Rousset et al. 2000). Numerous PVC methods have been proposed (see Erlandsson et al. (2012) for a review); however, for the hybrid MR-PET system used in this study PVC methods which utilize the spatially registered high resolution anatomical information from MR images may offer optimal performance. We restrict our analysis to geometric transfer matrix (GTM) PVC algorithms which estimate mean ROI corrected uptake values through noiseless simulations of the PET system using as input unit filled images (binary maps or characteristic functions) generated from segmentations of each anatomical region contributing to spill-in and spill-out of the given ROI (Rousset et al. 1998). For TACs derived from images reconstructed with an analytic method such as FBP, PVC can be performed in post-reconstruction via such anatomic based GTM methods by estimating correction factors once and using these factors to correct for PV for all images in the time series. Accurate post-reconstruction PVC of FBP dynamic data in this manner is justified due to the independence of FBP image spatial resolution on the raw sinogram data. Application of PVC using a single calculation of correction factors assumes that patient motion during the dynamic acquisition is either negligible or corrected for, as misregistration between the anatomical and emission images can produce significant bias in corrected uptake values (Meltzer et al. 1999). If expectation maximization (EM) or ordered subsets EM iterative reconstructions are used, however, image spatial resolution independence is not maintained and PVC performance of dynamic image series may suffer bias.
Although ordered subsets expectation maximization (OSEM) reconstruction produces images with superior SNR compared with FBP (Hudson and Larkin 1994), spatial resolution convergence is local for OSEM and depends significantly on the background activity, count density, and size of the object being imaged (Boellaard et al. 2004). Yao et al. (2000) found that when background activity was added to rat brain data significantly more iterations were required to match image spatial resolution, at the cost of increased noise, versus when background activity was absent, while Gaitanis et al. (2010) demonstrated that resolution convergence was inversely related to the number of counts for a Hoffman brain phantom.
The performance of OSEM on 18F-FDG kinetic modelling has been evaluated previously (Boellaard et al. 2001) and was found to produce similar bias and variance results to FBP derived values for most conditions, although significantly higher bias was noted for cold regions with relatively high background activity levels. For PET systems where sinogram data has limited sinogram sampling due to gaps, however, FBP reconstructed images may have significant artefacts compared to OSEM estimates (Michel et al. 2000), greatly reducing the accuracy of FBP for kinetic modelling. For the camera of interest in this study, termed BrainPET, 44% of projection data is missing due to gaps between detector blocks (Catana et al. 2010). Although gap filling methods in sinogram space have been shown to reduce artefacts (Tuna et al. 2010, de Jong et al. 2003) in another dedicated brain scanner, the ECAT HRRT, this system lacks only ~10% of sinogram data and such methods are expected to be less effective for BrainPET.
During a dynamic imaging acquisition the noise and background to ROI activity concentration ratio can vary significantly between early and late frames, thereby potentially altering the local resolution convergence properties of the resulting OSEM reconstructed images on a frame-by-frame basis. The application of post-reconstruction PVC methods applied to each frame may subsequently propagate bias into kinetic parameter estimates if such frame-by-frame resolution convergence changes are not accounted for. We aim to explore the influence of the PVC method and implementation on kinetic parameter and CMRGlc values estimated from OSEM reconstructed dynamic BrainPET data. Few studies have examined the influence of PVC on kinetic modelling (Lehnert et al. 2012). Frouin et al. (2002) investigated the influence of two GTM PVC implementations in combination with analytical reconstruction on 18F-L-dopa and 11C-raclopride TAC quantification while Walker et al. (2011) assessed the influence of PSF modelling in OSEM reconstruction on bias in 11C-DASB and 15O-H2O patient dynamic scans. Thus, to our knowledge, this manuscript represents the first characterization of the effect of post-reconstruction PVC on kinetic modelling from images reconstructed with EM or OSEM.
Performance of kinetic modelling from OSEM images processed with several PVC methods was assessed with phantom, simulation, and subject data. Image bias as a function of the PVC algorithm and the background-to-target ratio was measured with acquisitions of a multi-compartment phantom filled with both 18F and 11C radionuclides, noise and bias performance of the PVC algorithms in a patient imaging scenario was quantified with multiple noisy realizations of a Monte Carlo brain simulation based on subject data from BrainPET, and the difference between kinetic parameters estimated from data processed with the PVC methods was calculated from a healthy volunteer scan.
2. Materials and methods
2.1. System description
The BrainPET (Siemens Healthcare Inc.) scanner is a stand alone PET system inserted into a 3-T MRI (MAGNETOM Trio, Siemens Medical) and has been described elsewhere (Catana et al. 2010). Briefly, the PET camera uses avalanche photodiodes (APDs) to decode lutetium oxyorthosilicate arrays of 12×12 elements (crystal size, 2.5 × 2.5 × 20 mm) arranged into a ring of 32 detector cassettes (6 axial detector blocks) producing effective transaxial and axial fields of view (FOVs) of 32 and 19.25 cm, respectively. Data is acquired in list-mode format and reconstructed with the ordinary Poisson OSEM 3D (OP-OSEM) algorithm (Byars et al. 2005) (span=9, maximum ring difference=67). Spatial resolution close to the center of FOV has been measured at ≤3.0 mm FWHM in all three dimensions based on line source measurements in air (Kolb et al. 2012).
2.2. Point spread function modelling
The OP-OSEM reconstruction was modified to include spatially variant point spread function (PSF) modelling in the image domain through the convolution of a spatially invariant 3D Gaussian and 2D radial motion blurring functions. The 3D Gaussian kernel accounted for resolution effects due to photon acolinearity, positron range, and the crystal face size, while the radial motion blurring modelled the degradation in radial resolution due to the parallax effect. The OP-OSEM algorithm was formulated as in Reader et al. (2003) to include PSF modelling of both kernels. Spatially variant PSFs have previously been modelled in image space (Kotasidis et al. 2011, Cloquet et al. 2010, Rapisarda et al. 2010) by parameter estimation of a set of simplified basis functions and as a function of the position in the scanner FOV. The method presented here differs from these implementations in that it requires the estimation of only two free parameters, and more importantly, these parameters are independent of the coordinate in scanner space. Consequently, the proposed implementation allows for significantly reduced computations and potentially increased robustness to local errors and noise in the parameter estimation and blurring matrix generation, although at the potential cost of reduced local model accuracy compared to prior methods. For the current implementation radial motion blurring was described as follows:
| (1) |
| (2) |
| (3) |
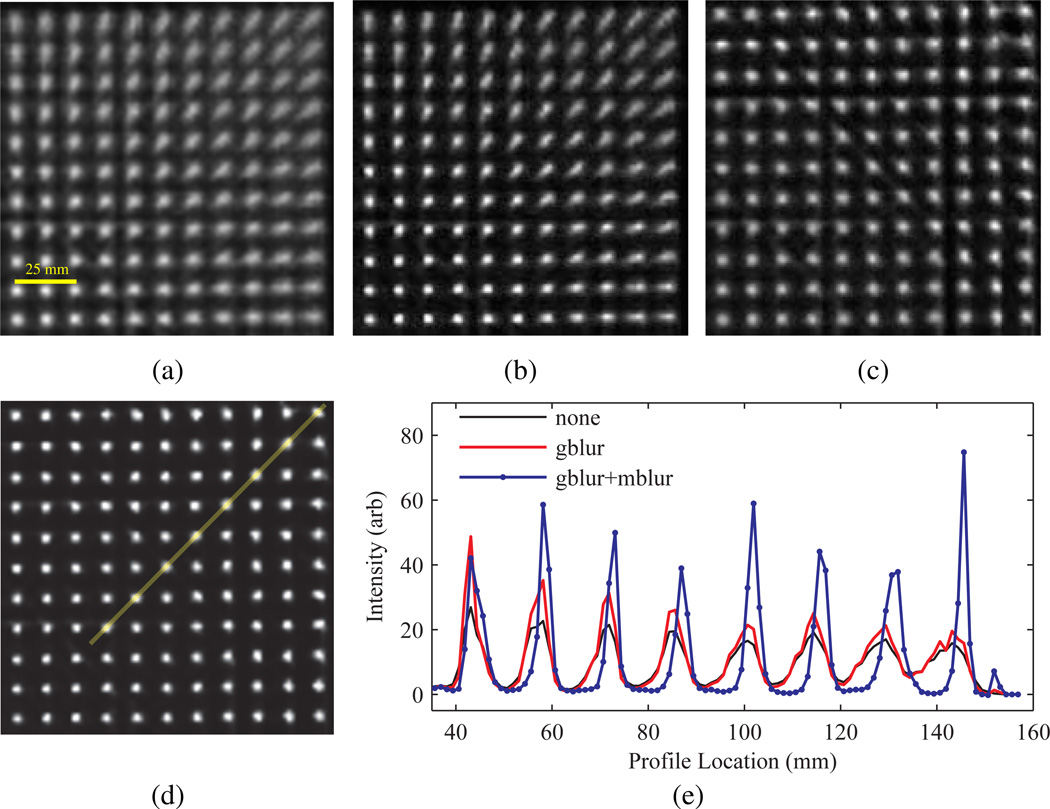
where Is (r) is the continuously defined smoothed image, r = [x y]T the 2D coordinate vector, I (r) the original image, l (r) the integration length, re the end coordinate, rc the center of the image, and b the radial blurring factor with ‖·‖2 symbolizing the L2-norm. The integration path, expressed in the argument of I, describes a radial line between r and re and the upper integration limit (l (r)) increases with the distance of r from rc. The result of the radial motion blurring function is shown in figure 1. PSF parameters were estimated by acquiring a total of 441 two minute duration 68Ge point source measurements from locations spanning the transaxial FOV. The optimal radial blurring factor was chosen by reconstructing 68Ge point source data with OP-OSEM with a range of b values, measuring the x and y resolutions at each source location, and choosing the value (b=1.067) that minimized the standard deviation computed over all locations. For the spatially invariant 3D Gaussian the FWHM was set to 3 mm and was chosen as an approximate match of the experimentally measured spatial resolution close to the center of FOV (Kolb et al. 2012). Figure 2 compares images for OP-OSEM reconstructions of the point source measurements with and without inclusion of the PSF models. A uniform background of 0.1% the point source maximum intensity was added to sinograms, from the forward projection of a digital uniform cylinder phantom filling the transaxial FOV, and subtracted after reconstruction to reduce potential bias from the OSEM non-negativity constraint. Use of the combined PSF model significantly improved radial resolution uniformity compared to application of the 3D Gaussian alone or no PSF.
Figure 1.
Example of the 2D radial motion blurring function in (1). (a) A simulated uniform grid of 5 mm diameter point sources spanning the BrainPET FOV before and (b) after application of radial motion blurring alone with b=1.067.
Figure 2.
Influence of PSF based OSEM on 68Ge point source measurement image quality. Transaxial images showing a quadrant of the FOV reconstructed with (a) no PSF modelling, and modelling of the (b) spatially invariant Gaussian PSF (gblur) alone, (c) radial motion blurring alone (mblur), and (d) a combination of the Gaussian and radial motion blur kernels, and (e) line profile comparison along band in (d) (profile location of 0 is at the center of the FOV).
2.3. Partial volume effect correction implementation
PVC was implemented with two variations of the GTM method (Rousset et al. 1998). In both approaches measured mean ROI values (b ∈ ℝK×1) are used to estimate the mean PVC values (a) as follows:
| (4) |
| (5) |
where K is the total number of ROIs considered,W ∈ ℝK×K is the GTM with elements wi,j, rsfj ∈ ℝN×1 is the regional spread function (RSF) N-voxel column vector image for ROI j, is the binary map for ROI i and ‖ · ‖1 is the L1-norm. The PVC values (a) are then estimated by calculating W−1 b. The two methods differ in how RSF images are computed. With the original approach, deemed “GTM” (Rousset et al. 1998), the RSF is computed as follows:
| (6) |
where ℛ and ℘ are the reconstruction and forward projector operators, respectively, and include PSF modelling. roij is the result of registering the binary image of the 3D ROI drawn on structure j from its native space (e.g. MR) to the PET frame of reference, while is a binary map generated from the threshold of roij. Through this methodology the tissue fraction effect (Soret et al. 2007) in the resulting PVC ROI values (W−1b), caused by downsampling the segmented brain structures from MR to the PET space, can be mitigated. In the second approach the influence of the background activity on resolution convergence is accounted for by using a perturbation method (Du et al. 2005), deemed “pGTM”, as follows:
| (7) |
| (8) |
where f ∈ ℝN×1 is the originally reconstructed 3D image without PVC, dj is the normalized perturbation factor, and p is the perturbation fraction. The goal of the pGTM approach is to generate an rsfj using the same series of OSEM update coefficients originally used to compute f. A large perturbation fraction (p) may significantly alter the update coefficients, while a very small p may induce rsfj to suffer from numerical precision errors due to nonlinear operations (e.g. thresholding) of the reconstruction or projection operators. The pGTM method was found to produce significantly less bias in PVC brain ROI values compared to the GTM approach for static Monte Carlo simulation SPECT data sets, particularly when PSF based OSEM was used (Du et al. 2005). Furthermore Du et al (2005) demonstrated that bias in pGTM PVC estimates was largely insensitive to the value p over three orders of magnitude.
2.4. Sensitivity of PVC to the target-to-background ratio
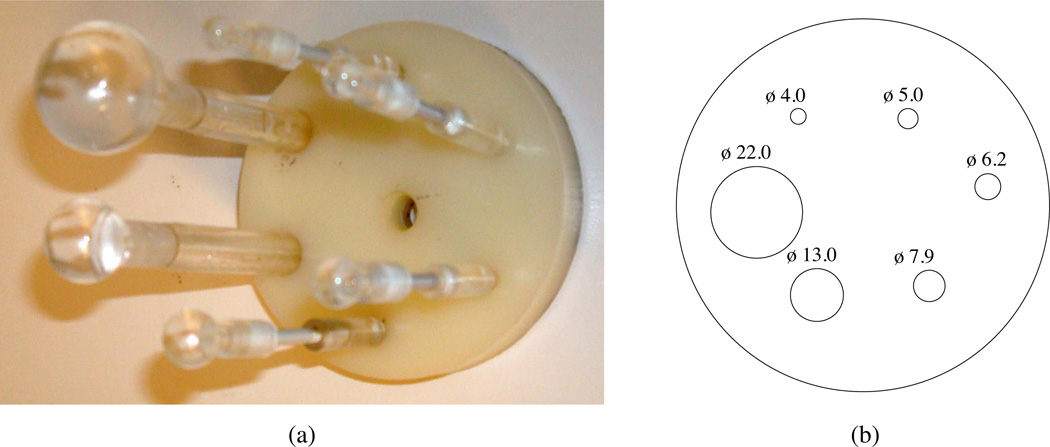
Bias as a function of the background-to-target ratio and application of different PVC methods was estimated from acquisitions of a phantom filled with both 18F and 11C radionuclides. The phantom was based on the image quality test object in the NEMA NU 2–2001 standards (National Electrical Manufactures Association 2001) and was composed of an insert of six hollow spheres with internal diameters ranging from 4.0–22.0 mm placed in a uniformly filled cylinder (D=9.6 cm). Figure 3 shows a photograph and schematic of the sphere phantom. The hollow spheres (targets) and background compartment were filled with 11C and 18F radionuclides, respectively, thereby allowing the background-to-target ratio to change dynamically during the course of PET imaging while other factors that may induce bias were significantly minimized (i.e. changes in tracer distribution and position). The phantom was filled with a total activity of 56 MBq (54 MBq of 18F and ~2 MBq of 11C) and background-to-target concentration ratio of 0.26 at the start of imaging, and scanned with both PET for 133 minutes and a 3D T2 weighted MR sequence (1 mm isotropic resolution) for ROI and µ-map generation.
Figure 3.
Sphere phantom used to determine the sensitivity of the PVC method to background-to-target changes. (a) Photograph and (b) schematic of the insert alone or placed in the background compartment, respectively, with internal diameter (ϕ) in mm.
Dynamic PET data was framed such that each resulting sinogram had ≈equal noise equivalent counts (NECs). As OSEM convergence is significantly influenced by count statistics, NECs are estimated from raw counts and are ∝SNR2 for OSEM reconstructions of uniform phantoms (Dahlbom et al. 2005), and the majority of counts in this instance were from the 18F background, resolution convergence variations on a frame-by-frame basis were expected to be largely due to the background-to-target changes and not count statistics. NECs (NECn) for each second n of the PET acquisition were estimated from global energy windowed prompts (Pd,n) and randoms (Rd,n) DAQ rates as follows:
| (9) |
where SF is the scatter fraction, and K(T+S) and KR are the scalar fraction of energy windowed trues plus scatters or randoms, respectively, with lines of response passing through the phantom. These fractions were assumed constant and calculated from a single set of sinograms framed from the complete acquisition time. Given an initial frame time a summed NEC (NECs) was calculated and sequential binning durations producing frames with ≈ equal summed NECs were estimated for each frame i by calculating the end summation limit (li) as follows:
| (10) |
ROIs comprising the fillable volume of the spheres and the background compartment (roij and ) were segmented from the MR images and a µ-map of the full phantom was generated from these segmented volumes assuming a uniform linear attenuation coefficient of 0.096 cm−1. Frames were reconstructed with PSF based OP-OSEM (subsets=8, iterations≤40 total, sampling=1.25 mm isotropic) with corrections for 18F tracer decay, branching fraction, dead-time, attenuation, randoms, and scatter, as estimated from the single scatter simulation (SSS) method (Watson et al. 1997) and post-reconstruction PVC applied as in section 2.3. The activity concentration ratio (ACR) of the spheres with respect to the 18F background was estimated by measuring tracer concentration in the MR segmented ROIs for the spheres and a total of five 10 mm circular ROIs (11 slices thick) drawn on the background at a central axial position where all spheres were visible. Bias in activity concentration ratios was estimated with respect to ground truth values calculated from initial well counter 18F and 11C activity measurements.
2.5. Influence of the PVC method on kinetic parameter estimation in patient imaging
2.5.1. Monte Carlo simulations
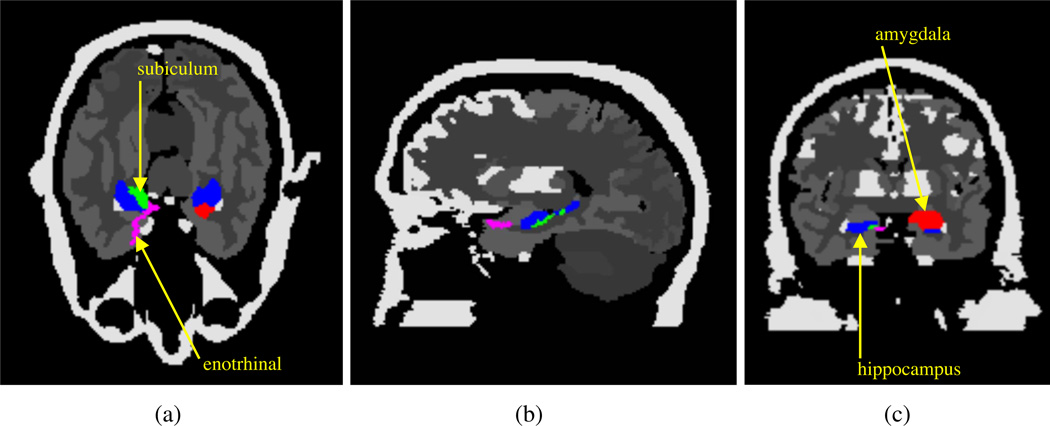
To determine how the choice of the PVC method influences estimation of kinetic parameters and CMRGlc in patient imaging, a dynamic acquisition with BrainPET was modeled with a Monte Carlo (MC) simulation. A digital Zubal phantom (Zubal et al. 1994) was used to model the activity and attenuation distributions, with normal and pathological 18F-FDG kinetic parameters assigned to various brain structures (table 1 in section 3.2.1) based on patient trials (Mosconi et al. 2007, Heiss et al. 1984). For the simulation study k4=0 for all structures. Additional structures were segmented manually in the Zubal phantom, including the right subiculum, left amygdala, and right entorhinal cortex, chosen for their measured hypometabolism in Alzheimer’s Disease patients. The attenuation distribution was generated from the Zubal phantom using single µ values for soft tissue (0.096 cm−1) and cortical bone (0.151 cm−1) (Catana et al. 2010). Figure 4 shows cross sections of the modified Zubal phantom.
Table 1.
Comparison of several PVC methods, with and without PSF modelling in the OSEM reconstruction, on the estimation of kinetic parameters and CMRGlc calculated after seventeen iterations for the Zubal phantom simulation. Results give bias ± CoV in percent unless otherwise noted.
| Structure | Method | K1 | k2 | k3 | CMRGlc |
|---|---|---|---|---|---|
| cerebellum | true | 0.0906 (ml/ccm/min) | 0.14108 (min−1) | 0.0460 (min−1) | 24.4496 (µmol/100 g/min) |
| wPSF–noPVC | −6.82 ± 0.64 | 7.65 ± 1.41 | 3.67 ± 1.00 | −9.45 ± 0.31 | |
| wPSF–GTM | 0.75 ± 0.64a* | 7.64 ± 1.42 | 3.26 ± 1.01 | −2.37 ± 0.31a* | |
| wPSF–ind pGTM | 4.39 ± 0.69b | 13.65 ± 1.51b* | 5.29 ± 1.05b | −1.51 ± 0.32b | |
| wPSF–last pGTM | 1.33 ± 0.65c | 7.71 ± 1.42c* | 3.27 ± 1.02c | −1.85 ± 0.31c | |
| noPSF–last pGTM | −6.87 ± 0.43d* | −7.09 ± 1.03d* | −0.73 ± 0.78d | −2.14 ± 0.24d | |
| noPSF–noPVC | −15.26 ± 0.42a* | −7.18 ± 0.99a* | 0.43 ± 0.74a | −10.12 ± 0.22a | |
| occipital lobes | true | 0.0827 (ml/ccm/min) | 0.1405 (min−1) | 0.0660 (min−1) | 29.1213 (µmol/100 g/min) |
| wPSF–noPVC | −17.93 ± 1.23 | 5.91 ± 2.99 | 0.85 ± 2.07 | −20.64 ± 0.43 | |
| wPSF–GTM | −8.83 ± 1.41a* | 4.54 ± 3.46 | 2.30 ± 2.39a | −10.16 ± 0.49a* | |
| wPSF–ind pGTM | 0.95 ± 1.64b* | 14.28 ± 3.97b* | 5.26 ± 2.63b | −4.60 ± 0.51b* | |
| wPSF–last pGTM | −3.61 ± 1.43c | 4.45 ± 3.51c* | 2.55 ± 2.42c | −4.80 ± 0.49 | |
| noPSF–last pGTM | −7.66 ± 0.80d | −9.01 ± 2.23d* | −1.54 ± 1.68d | −2.62 ± 0.37d | |
| noPSF–noPVC | −30.86 ± 0.62a* | −7.84 ± 1.71a* | −4.35 ± 1.30a* | −29.10 ± 0.29a* | |
| hippocampus | true | 0.0833 (ml/ccm/min) | 0.1457 (min−1) | 0.0578 (min−1) | 26.0669 (µmol/100 g/min) |
| wPSF–noPVC | −7.60 ± 3.57 | 6.03 ± 9.05 | −0.86 ± 6.73 | −11.93 ± 1.58 | |
| wPSF–GTM | −6.60 ± 4.05 | 5.67 ± 10.27 | −0.85 ± 7.62 | −10.74 ± 1.78a | |
| wPSF–ind pGTM | 2.52 ± 4.82b* | 7.93 ± 12.12 | 0.71 ± 8.38 | −2.37 ± 1.84b* | |
| wPSF–last pGTM | 1.44 ± 4.19 | 5.72 ± 10.71 | 0.04 ± 7.89 | −2.44 ± 1.81 | |
| noPSF–last pGTM | −4.47 ± 3.19d* | −5.64 ± 8.63d* | −1.91 ± 6.74 | −1.76 ± 1.54 | |
| noPSF–noPVC | −11.95 ± 2.41a | −6.07 ± 6.36a* | −3.64 ± 4.92 | −10.31 ± 1.16a | |
| temporal lobes | true | 0.0828 (ml/ccm/min) | 0.1356 (min−1) | 0.0661 (min−1) | 29.8955 (µmol/100 g/min) |
| wPSF–noPVC | −12.63 ± 0.57 | 3.23 ± 1.53 | 0.53 ± 1.00 | −14.18 ± 0.18 | |
| wPSF–GTM | −4.05 ± 0.63a* | 1.90 ± 1.70a | 1.39 ± 1.10a | −4.38 ± 0.19a* | |
| wPSF–ind pGTM | −0.60 ± 0.72b | 7.29 ± 1.86b* | 3.34 ± 1.13b | −3.08 ± 0.19b | |
| wPSF–last pGTM | −3.06 ± 0.64c | 1.82 ± 1.71c* | 1.52 ± 1.10c | −3.25 ± 0.19c | |
| noPSF–last pGTM | −8.57 ± 0.52d* | −11.50 ± 1.50d* | −2.39 ± 1.01d | −2.44 ± 0.18d | |
| noPSF–noPVC | −22.12 ± 0.43a* | −9.90 ± 1.22a* | −4.07 ± 0.85a | −18.80 ± 0.16a | |
| parietal lobes | true | 0.0864 (ml/ccm/min) | 0.1378 (min−1) | 0.0716 (min−1) | 32.5485 (µmol/100 g/min) |
| wPSF–noPVC | −14.84 ± 0.95 | 3.09 ± 2.58 | 0.96 ± 1.75 | −16.01 ± 0.31 | |
| wPSF–GTM | −5.56 ± 1.04a* | 1.84 ± 2.85 | 2.29 ± 1.91a | −5.27 ± 0.33a* | |
| wPSF–ind pGTM | 0.34 ± 1.22b* | 9.25 ± 3.24b* | 4.44 ± 2.06b | −2.61 ± 0.34b | |
| wPSF–last pGTM | −3.05 ± 1.04c | 1.87 ± 2.85c* | 2.34 ± 1.91c | −2.74 ± 0.33 | |
| noPSF–last pGTM | −8.58 0.66d* | −11.66 ± 1.84d* | −1.55 ± 1.27d | −1.94 ± 0.23d | |
| noPSF–noPVC | −23.54 ± 0.56a* | −10.41 ± 1.55a* | −3.82 ± 1.09a | −19.93 ± 0.21a | |
| RH subiculum | true | 0.0416 (ml/ccm/min) | 0.1457 (min−1) | 0.0289 (min−1) | 7.5954 (µmol/100 g/min) |
| wPSF–noPVC | 40.57 ± 23.65 | 31.16 ± 53.08 | 66.64 ± 32.90 | 75.81 ± 9.52 | |
| wPSF–GTM | 29.73 ± 38.90 | 58.63 ± 80.06 | 51.33 ± 45.62 | 33.00 ± 15.45a* | |
| wPSF–ind pGTM | 40.69 ± 54.83 | 69.87 ± 97.54 | 15.83 ± 66.76 | 8.52 ± 34.99b* | |
| wPSF–last pGTM | 46.28 ± 49.70 | 75.96 ± 89.66 | 22.17 ± 57.86 | 13.98 ± 28.73 | |
| noPSF–last pGTM | 24.53 ± 40.65 | 49.59 ± 81.38 | 14.27 ± 59.15 | 1.83 ± 27.74 | |
| noPSF–noPVC | 42.89 ± 13.53 | 7.66 ± 35.55 | 70.27 ± 23.67 | 108.08 ± 6.52a* | |
| LH amygdala | true | 0.0833 (ml/ccm/min) | 0.1457 (min−1) | 0.0289 (min−1) | 15.1908 (µmol/100 g/min) |
| wPSF–noPVC | −9.47 ± 7.90 | 1.26 ± 15.43 | 14.62 ± 12.74 | 0.27 ± 4.64 | |
| wPSF–GTM | −8.21 ± 8.74 | 1.58 ± 16.70 | 5.13 ± 14.32a* | −5.60 ± 5.59a* | |
| wPSF–ind pGTM | −0.18 ± 9.84b* | 3.51 ± 18.92 | 5.27 ± 15.36 | 1.26 ± 5.88b* | |
| wPSF–last pGTM | −0.76 ± 8.95 | 1.66 ± 17.01 | 3.64 ± 14.63 | 0.78 ± 5.75 | |
| noPSF–last pGTM | −8.37 ± 5.47d* | −9.68 ± 10.77d* | −1.77 ± 11.57 | −1.93 ± 5.05 | |
| noPSF–noPVC | −13.35 ± 4.29a | −10.61 ± 8.92a* | 19.19 ± 8.72 | 9.43 ± 3.28a* | |
| RH entorhinal cortex | true | 0.0208 (ml/ccm/min) | 0.1457 (min−1) | 0.0145 (min−1) | 2.0702 (µmol/100 g/min) |
| wPSF–noPVC | 127.98 ± 36.45 | 48.33 ± 83.85 | 320.90 ± 39.86 | 488.85 ± 9.04 | |
| wPSF–GTM | 69.71 ± 50.10a* | 94.30 ± 92.47 | 250.53 ± 74.62 | 202.53 ± 20.40a* | |
| wPSF–ind pGTM | 63.62 ± 78.20 | 75.20 ± 109.43 | 294.42 ± 160.12 | 94.67 ± 69.46b* | |
| wPSF–last pGTM | 95.25 ± 64.12 | 112.24 ± 94.77 | 164.99 ± 116.78 | 111.00 ± 58.49 | |
| noPSF–last pGTM | 36.49 ± 53.52d* | 80.39 ± 91.42 | 181.27 1± 58.30 | 38.92 ± 62.71d* | |
| noPSF–noPVC | 113.82 ± 11.07 | −1.83 ± 29.56a* | 292.17 ± 23.95 | 574.50 ± 5.93a* | |
Results significantly different (P-value <0.05) than wPSF–noPVC.
Results significantly different (P-value <0.05) than wPSF–GTM.
Results significantly different (P-value <0.05) than wPSF–ind pGTM.
Results significantly different (P-value <0.05) than wPSF–last pGTM.
(Absolute difference in percent bias for significant results ≥5.0%.)
Figure 4.
Modified Zubal phantom used in MC simulations. (a) Axial, (b) sagittal, and (c) coronal views with ntensity equal to the structure label number and added structures denoted.
The acquisition was simulated by generating a decay weighted “true” dynamic series, with time activity curves (TACs) for each structure calculated with the COMKAT package (Muzic and Cornelius 2001), assuming a three compartment model (Sokoloff et al. 1977) and using an analytical purely plasma arterial input function (AIF) generated as in (Feng et al. 1995). The cerebral blood volume effect (CBV) was not accounted for in the simulations. For each frame the 3D volume was blurred with the combined PSF and forward projected into sinogram space. Time binning of 4×30 seconds, 3×60 seconds, 2×150 seconds, 2×300 seconds, and 4×600 second was assumed. Figure 5 shows the normalized TACs and background-to-target ratios for several structures of the Zubal phantom.
Figure 5.
“true” TACs simulated for the Zubal phantom. (a) TACs and (b) background-to-target ratio, defined as the whole brain average activity concentration over that of a given structure, for several structures.
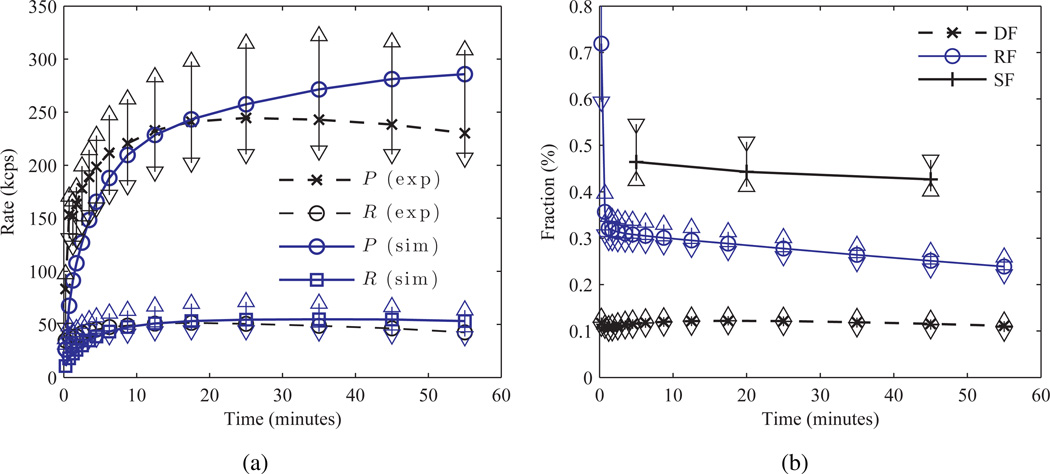
To accurately match Poisson count statistics for the simulation with those from patient acquisitions a set of 18F-FDG human BrainPET scans was utilized. A total of 7 dynamic scans of healthy volunteers (range of injection activities=[171, 191] MBq) were framed using the simulated data binning times and the prompts, randoms (R), and scatter (S) (estimated from the SSS sinograms) rates estimated. Figure 6 shows the rates and fractions from this subject analysis. The scatter (SF) and dead-time (DF) fractions were assumed constant for all frames of the simulation, and set to 43% and 12% respectively, while the randoms fraction (RFi) (median value from subject scans) varied from 70% to 20% over the course of the dynamic series. Randoms and scatter fractions were defined as RF = R/(T +S) and SF = S/(T +S), respectively, where T denotes the trues rate. The randoms (r0) and scatter (s0) distribution sinograms (not magnitude) with M elements in ℝM×1 were assumed constant and generated from the last five frames of variance reduced randoms sinograms from a single healthy subject scan, and the SSS scatter estimate of the acquisition time weighted average of all frames of the true Zubal images, respectively. The normalization sinogram was generated from BrainPET acquisitions of a 68Ge plane source as in (Catana et al. 2011). Simulated “true” frames (ti), previously uncorrected for attenuation and normalization, were scaled by a constant factor (fT) to match patient count rates by minimizing the root mean square error (RMSE) between the two cases of TACs composed of the sum of dead-time corrected trues and scatter frame rates. For each frame i, simulated prompts (pi ∈ ℝM×1), randoms (ri), and scatter (si) sinograms were generated as follows:
| (11) |
| (12) |
| (13) |
| (14) |
where cT, i is “true” frame scaling factor, and Ai is the acquisition time. Figure 6 compares experimental and scaled rates. A total of 30 noisy Poisson realizations was generated for each frame.
Figure 6.
Comparison of measured patient and simulated count rates and fractions. (a) Median patient (exp), with ±σ error bars around the mean, and simulated (sim) TAC prompts (P) and randoms (R), and (b) median patient dead-time (DF), randoms (RF), and scatter (SF) fractions.
The dynamic series were reconstructed with the PSF based OP-OSEM (subsets=8, terations≤25, sampling=1.25 mm isotropic) and PVC was applied with the following methods: GTM, pGTM with rsfj for all brain structures and W in (4) computed for each frame independently (“ind pGTM”), and pGTM with rsfj computed from a reconstructed mage (f in (7)) of the last frame alone and used to correct all frames (“last pGTM”). Use of the last frame alone forW generation significantly reduces total computation time for pGTM PVC of a dynamic series and may reduce noise propagation into mean ROI values (compared o early frames), but at the potential cost of increased bias due to resolution convergence differences with the frame being corrected. As the emission image from the last frame contains structures with the greatest differences in background-to-target ratios and number of counts compared to early frames, the last pGTM condition represents the worst case scenario for applying PVC to TACs using RSFs computed at one time point. Binary ROI images were generated directly from the structures of the Zubal phantom (), accounting for all structures in the phantom. RSF images (rsfj) were generated with the same OSEM parameters as the emission images and, in the case of pGTM, emission images with the same number of iterations were used as input. Emission and RSF images were also reconstructed with no PSF modelling in the OP-OSEM (“noPSF”) and the PVC methods applied as above. For the noPSF cases the forward projector (℘) in (6) and (7) maintained PSF modelling for RSF image generation. Kinetic parameters were estimated with an unweighted nonlinear least-squares (NLS) fitting, with initial parameters calculated with linearized least-squares (LLS) fitting as in (Muzic and Christian 2006), with COMKAT (Muzic and Cornelius 2001) for each brain structure from uncorrected and PVC images, and percent bias and coefficient of variation (CoV) computed with respect to the ground truth values (see table 1). NLS fitting was chosen due to its relatively low bias and noise performance, even at low count statistics, compared with other methods (Feng et al. 1995). Calculation of CMRGlc was performed as follows:
| (15) |
where K1, k2, and k3 are the kinetic parameter estimates, LC is the lumped coefficient and was set to 0.42 (Huang et al. 1980), and Cp is the capillary plasma glucose concentration and was assumed to be 4.81 µmol/ml (86.7 mg/dL) (Phelps et al. 1979). Bias and CoV of mean ROI values on a frame-by-frame basis were calculated and statistical significance between the results from the different PVC methods, and between data with and without PSF based OSEM, was determined through a student’s t-test (unpaired two-tailed), with P-value of <0.05 deemed significant.
2.5.2. Patient case comparison
The effect of the PVC method on kinetic parameter and CMRGlc values was quantified for a subject data set. Under an approved Institutional Review Board protocol, written consent was obtained from a healthy volunteer (male, 27 years old) and an arterial line was placed in the radial artery (opposite the arm intended for 18F-FDG injection) under local anaesthesia. The subject was positioned on the scanner, injected with 190 MBq 18F-FDG intravenously, and imaged with PET for 90 minutes. Simultaneously, the subject was scanned with MR using a multi-echo MPRAGE (MEMPRAGE) (TR=2.53s, TE1/TE2/TE3/TE4=1.64/3.5/5.36/7.22 ms TI1=1.2, 1 mm isotropic resolution) (van der Kouwe et al. 2008), dual-echo ultrashort echo time (DUTE) (TR=200ms, TE1/TE2=0.07/2.46 ms, 1.67 mm isotropic resolution, frame rate=0.33 Hz), and 2D echo planar imaging (EPI) (TR=3 s, TE=30 ms, 3.1×3.1×3.0 mm sampling, for affine motion estimates of the subject’s head) sequences. Arterial blood samples (2 ml samples) were drawn at the following time intervals: every 10 seconds for the first 3 minutes and at 5 minutes, 10 minutes, 30 minutes, 60 minutes, and 90 minutes after injection, immediately centrifuged (3200 RPM), and plasma samples’ activities measured with an automatic gamma counter (2480 WIZARD, Perkin Elmer).
PET sinograms were framed as in section 2.5.1 and each sinogram frame corrected for motion using the MR estimates as in (Catana et al. 2011), such that all raw sinogram data were registered to the same patient position before reconstruction. The µ-map was generated from the DUTEMR image as in (Catana et al. 2010), and PET images reconstructed with and without the PSF based OP-OSEM algorithm as in section 2.5.1. ROI and rsfj estimates for each structure were generated by first automatically segmenting MPRAGE data using the software suite FreeSurfer (Fischl et al. 2002), registering each segmented brain structure independently to the PET frame of reference via an a priori affine transformation with trilinear interpolation to get roij, and running the result through (6) or (7) to compute rsfj or thresholding the result by 0.1% of the maximum intensity to get in (5). GTM and pGTM PVC values for each frame were generated and kinetic parameters estimated as in section 2.5.1, except that the CBV was also included as a free parameter in the LLS and NLS fitting (Cai et al. 2002) as follows:
| (16) |
where Cs (t) represents the CBV influenced 18F-FDG concentration, the AIF, and the tissue 18F-FDG concentration as a function of time. CBV was estimated to reduce kinetic parameter bias in smaller structures where contribution to the total ROI count rate from plasma 18F-FDG may be significant. For consistency with the MC simulation study (section 2.5.1) k4 was set to zero for all structures during fitting.
3. Results
3.1. Sensitivity of PVC to the target-to-background ratio
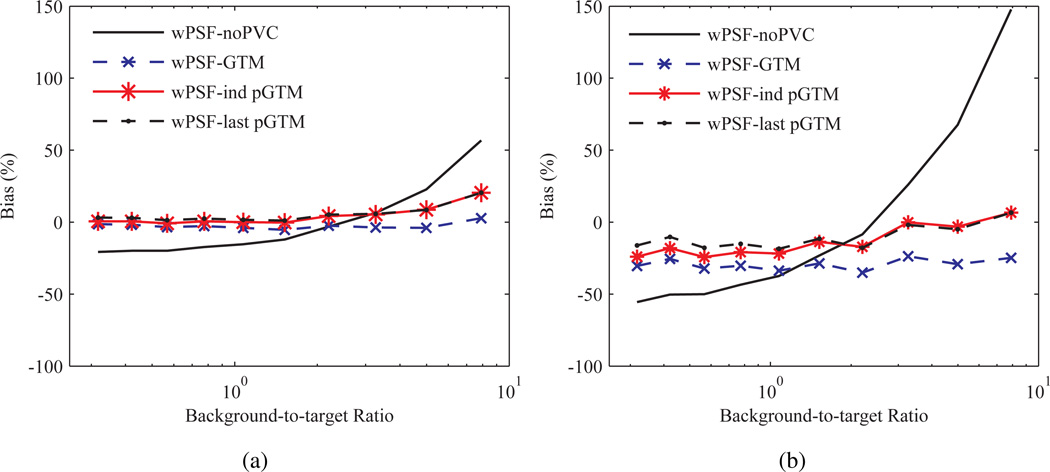
Bias in activity concentration ratios as a function of the background-to-target ratio and processed with several PVC methods, and PSF based OSEM, for two sphere sizes is shown in figure 7. For convenience results using PSF based OSEM and conventional OSEM are labelled “wPSF” and “noPSF”, respectively. Results with no post-reconstruction PVC are denoted as “noPVC” in this instance and throughout the manuscript and a perturbation fraction p of 10−3 was used for the pGTM PVC algorithms. Results are compared after 30 iterations, as fractional convergence for individual frames was estimated to be approximately ≤ 0.5% over the majority of background-to-target ratios and sphere sizes. Activity concentration ratio bias where no PVC was applied (noPVC) tended to increase as a function of the absolute background-to-target ratio and inversely with sphere diameter. Application of any of the PVC methods led to reduced magnitude and sensitivity to the background-to-target ratio of activity concentration ratio bias compared to noPVC, with noPVC, GTM, ind pGTM, and last pGTM producing RMSE bias averaged over all frames for the 6 mm sphere of 62.5, 29.6, 17.2 and 13.4%, respectively.
Figure 7.
Bias in the activity concentration ratio as a function of background-to-target ratio for spheres corrected with several PVC methods and PSF based OSEM. Results for spheres with (a) 22 mm and (b) 6.2 mm ID after 30 iterations. last pGTM represents the case where W was computed with f in (7) from a single background-to-target ratio of 7.9 and used to correct all frames. Other legend definitions are described in section 2.5.1
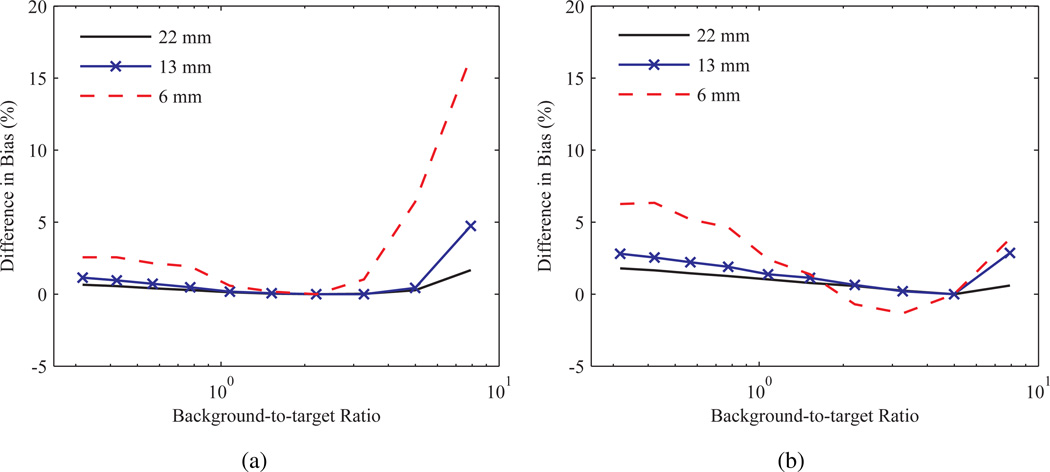
The differences in bias between data processed with wPSF ind pGTM and pGTM with W generated from a single frame and used in (4) to correct all frames is shown in figure 8. Images were chosen at background-to-target ratios of 2.2 and 5.0 for the latter case, as these values approximate the range of ratios over the course of the TAC for the entorhinal cortex in the Zubal phantom simulation (see figure 5). Use of a GTM matrix computed from a background-to-target ratio of 5.0 was found to minimize differences in activity concentration ratio bias between the pGTM methods, compared to when the lower bound of the background-to-target range was used, and the changes trended to increase inversely with sphere size. A similar comparison was made between wPSF ind pGTM and GTM (results not shown), demonstrating that bias between these methods increased as a function of background-to-target ratio and inversely with the sphere size, with a maximum value of 31.4% at a ratio of 7.9 measured for the 6 mm sphere.
Figure 8.
Difference in bias in the activity concentration ratio between wPSF–ind pGTM and pGTM with W generated at a single frame, as a function of background-to-target ratio for a range of spheres. Results for W computed at background-to-target ratios of (a) 2.2 and (b) 5.0 after 30 iterations.
3.2. Influence of the PVC method on kinetic parameter estimation in patient imaging
3.2.1. Monte Carlo simulations
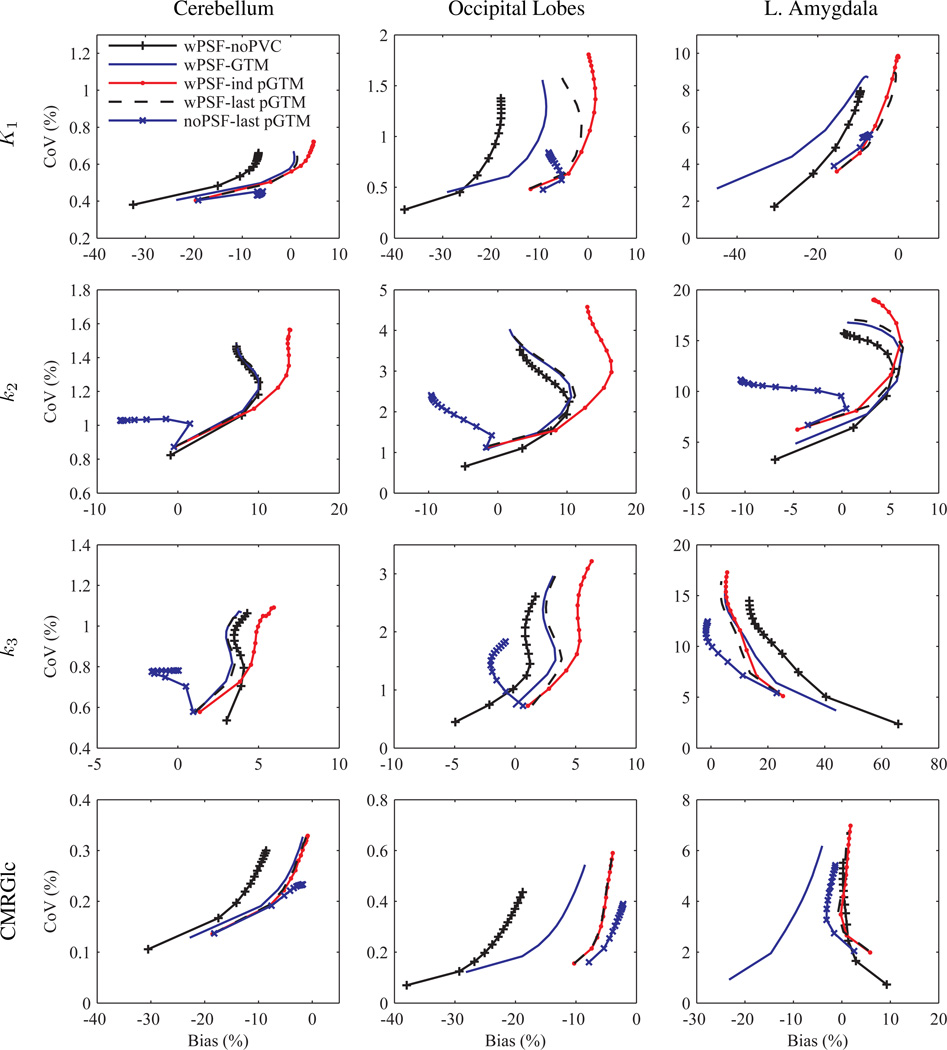
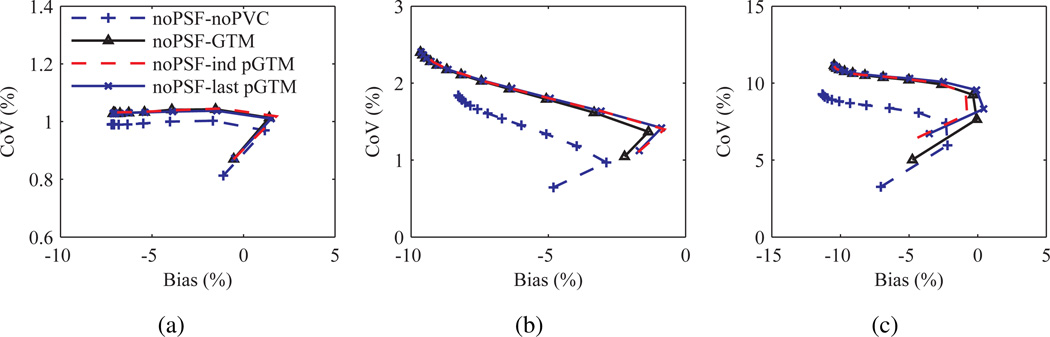
Figure 9 shows plots of CoV versus bias for kinetic parameter estimates of several structures calculated after application of the different PVC methods with and, and for one condition, without PSF based OSEM. A perturbation fraction p of 10−3 was used for the pGTM PVC algorithms. Significant differences were observed in the curves, with large magnitude differences in bias measured at late iterations in k2 estimates taken from images processed with wPSF–ind pGTM PVC compared with all other wPSF PVC methods. Differences in k2 bias were greatest for the relatively large volume cerebellar and cortical structures, with differences between wPSF ind and last pGTM PVC results for the cerebellum, occipital lobes, and parietal lobes measured at 6.6%, 11.5%, and 8.5%, respectively, after 25 iterations. We note that for CMRGlc estimates the differences in wPSF ind and last pGTM curves were minimal. For both k2 and k3 plots, with and without PSF based OSEM, bias was observed to not consistently decrease with iteration number, as is typically the case with ROI bias of individual images, and this was due to the very different resolution convergence rates of the early relative to the late frames. Figure 10 shows plots of CoV versus bias for k2 estimates for the different noPSF PVC methods. Contrary to the wPSF results there was minimal difference between the noPSF ind and last pGTM curves across all structures. Furthermore, at later iterations noPSF estimates showed reduced CoV compared to wPSF values processed with the same PVC method at matched iterations for all kinetic parameters, CMRGlc, and across all but the smallest volume structures.
Figure 9.
Variance versus bias for kinetic parameters from the Zubal phantom simulation processed with several PVC methods and with (wPSF) and without (noPSF) PSF modelling in the reconstruction. K1, k2, k3, and CMRGlc (in rows) for the cerebellum, occipital lobes, and left amygdala, respectively, with data points representing iterations 1 through 25, with a step size of 2. Iteration 1 is closest to zero CoV.
Figure 10.
Variance versus bias in k2 for the Zubal phantom simulation processed with several PVC methods and without PSF modelling in the reconstruction. Plots for the cerebellum (a), occipital lobes (b), and left amygdala (c), respectively, with data points representing iterations 1 through 25, with a step size of 2.
To focus the subsequent analysis the number of iterations to reach a fractional convergence of ≤0.5% for each kinetic parameter, structure, and PVC method combination was assessed. Results for wPSF indicated that the median number of iterations to reach this convergence threshold, calculated across all structures, was greatest for k2 and when ind pGTM was not used. Median number of iterations for wPSF–last pGTM were 11 (mode=9), 17 (mode=17), and 7 (mode=5) for K1, k2, and k3, respectively. The same analysis was performed for kinetic parameters estimated from images reconstructed without PSF modelling and it was determined that the number of iterations to reach the convergence threshold was greatest for k2 when GTM PVC was used, with median number of iterations equal to 11 (mode=11), 15 (mode=15), and 5 (mode=5) for K1, k2, and k3, respectively. Based on these findings, we restricted our analysis to results computed after 17 iterations.
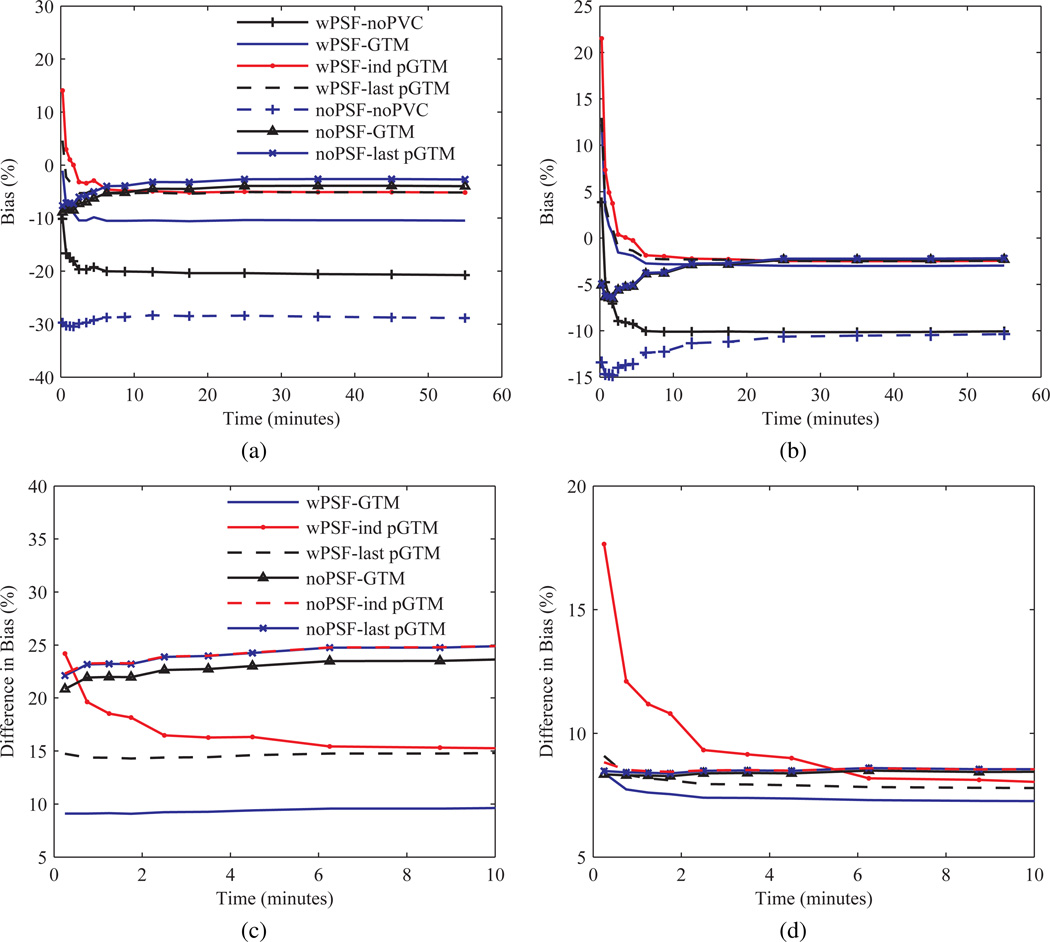
Kinetic parameters, CMRGlc values, and corresponding variances calculated after 17 iterations, with and without PSF based OSEM, are listed in table 1. For the PSF based OSEM case K1 estimates from wPSF–GTM PVC produced significantly lower bias (by an absolute difference in percent bias of ≥5%) than noPVC data for five of the structures considered, while wPSF–ind pGTM K1 values were significantly greater (more positive) than those calculated from GTM for all but the right subiculum and entorhinal cortex. For only the largest volume structures (e.g. the cerebellum, occipital lobes, temporal lobes, and parietal lobes) wPSF–last pGTM K1 estimates were significantly different than the wPSF–ind pGTM results. Changes in k2 were significant, with ≥5% bias differences, between wPSF ind pGTM and GTM or last pGTM PVC data for this same set of four relatively large volume structures, while significant differences in k3 meeting this bias criteria were only observed between GTM and noPVC data for the left amygdala. For CMRGlc the cerebellum and temporal lobes showed significant differences between wPSF ind and last pGTM data; however, significance with ≥5% absolute difference in bias was only observed between GTM and noPVC or ind pGTM data in more than half the cases. For the noPSF case there were no structures, kinetic parameters, or CMRGlc estimates where last pGTM results were significantly different, with ≥5% bias, than the ind pGTM or GTM values, thus only last pGTM values are reported. We note also that noPSF ind and last pGTM estimates were not significantly different for all conditions. noPSF–last pGTM K1 and k2 estimates were frequently underestimated, with greater magnitude bias by ≥5%(difference in absolute bias values) than wPSF–last pGTM for K1 in several cortical (cerebellum, temporal lobes, parietal lobes) and deep (hippocampus and left amygdala) structures, and for k2 in this same set of structures excluding the cerebellum and hippocampus and including the occipital lobes, while for k3 noPSF–last pGTM had significantly lower bias for only three of the large volume cortical structures. noPSF–last pGTM CMRGlc estimates had significantly lower magnitude bias than those of wPSF–last pGTM for larger cortical structures, the hippocampus, and the entorhinal cortex, although this was by an absolute difference of ≥5% in only the last case. For noise, overall all PVC methods, using the same reconstruction method, produced comparable CoV averaged over all structures, although for smaller structures (≤2 cc) data with no and ind pGTM PVC produced the lowest and highest CoV values respectively. noPSF results had lower CoV than wPSF kinetic parameters and CMRGlc values for all structures except for k3 for the entorhinal cortex and subiculum.
To determine the source of bias in the kinetic parameters the bias in TACs was quantified and compared for the different PVC methods. Figure 11 shows bias as a function of time for both the occipital lobes and cerebellum. Bias in the TACs for most structures was found to be largely independent of the frame number, however, at early frames (time <9 minutes) for the PSF based OSEM results bias increased (became more positive) inversely with the frame number for all PVC methods. For small hypometabolic structures with relatively large background-to-target changes over the course of the dynamic scan, such as the entorhinal cortex and the subiculum, magnitude bias increased as a function of time and varied for the different PVC methods, although not between the wPSF last and ind pGTM TACs. For the noPSF TACs bias tended to decrease (become more negative) inversely with the frame number for all the PVC methods at early frames, similarly starting at time <9 minutes, for all structures without significant spill-in (i.e. excluding white matter, the subiculum, and entorhinal cortex). Consequently, as bias was negative at later frames for large cortical structure and the hippocampus TACs, with and without PSF based OSEM, average magnitude bias at early frames was frequently less for wPSF, compared with noPSF, last pGTM. In order to improve visualization of bias differences between the TACs generated from the different PVC methods, the TACs in figure 11 (a) and (b) were subtracted by results with noPVC and are shown in figure 11 (c) and (d), respectively. These normalized TACs indicate that for the wPSF case the increase in bias in early frames was greatest for ind pGTM results compared with the other PVC methods. Notably, the difference in bias between wPSF ind and last pGTM for the second frame of the occipital lobe TACs was 5.3%. For the noPSF case ind and last pGTM curves were not significantly different across all frames and for all structures and showed <1% absolute difference across all frames except for the entorhinal cortex and subiculum.
Figure 11.
Bias for TACs from the Zubal phantom simulation processed with several PVC methods, and with and without PSF modelling in the OSEM reconstruction, calculated after seventeen iterations. Occipital lobes and cerebellum TAC bias over the full time duration, (a) and (b), or zoomed and subtracted by wPSF–noPVC for PSF based OSEM results or noPSF–noPVC for the noPSF curves, (c) and (d), respectively.
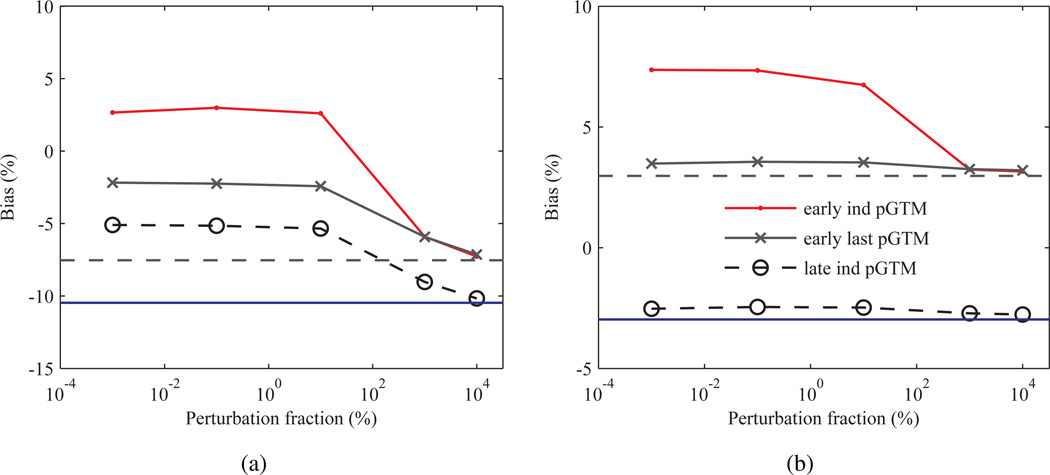
The bias in the pGTM method has been shown to be largely insensitive to the perturbation fraction p over a large range of values for a typical static brain acquisition (Du et al. 2005); however, the influence of p on bias for the low noise frames occurring at early TAC points has not been assessed. To determine if the increased bias in the ind pGTM TACs at early frames was due to a suboptimal choice in p, Zubal MC simulations were repeated with the p ranging from 10−3% to 104% for the 2nd and last frames and bias estimated. Figure 12 shows bias as a function of p for pGTM and GTM PVC methods with PSF based OSEM. Results demonstrated that even at early low count frames bias was relatively insensitive to change in p over nearly four orders of magnitude for both the cerebellum and occipital lobe. Bias for the wPSF ind and last pGTM methods approached GTM levels, as expected based on (7), for p > 101 %, and this drop was greater for the ind versus last pGTM PVC for the early frame. For several structures (i.e. the occipital lobe), bias crossed zero at the large p values for the 2nd frame corrected with wPSF–ind pGTM suggesting that p could be optimized on a frame-by-frame basis to reduce bias at early time points, although this same phenomenon was only observed for the left amygdala for the case of the last frame ind pGTM data.
Figure 12.
Bias as a function of the perturbation fraction, p in (8), for the Zubal phantom simulation calculated after seventeen iterations and with several PVC methods using PSF based OSEM. (a) Occipital lobe and (b) cerebellum bias at the second 30 s frame (early) and at the 10 min last frame (late), with GTM results shown as constant dashed and solid blue lines, respectively.
3.2.2. Patient case comparison
Table 2 gives kinetic parameters and CMRGlc values processed with the different PVC methods for a healthy subject scan. Sum of squared errors (SSE) estimates from the OLS fits are also shown. For the results with PSF based OSEM a number of structures were found to have ≥10% absolute difference between the ind and last pGTM k2 estimates including the cerebral cortex, putamina, amygdalae, accumbens areas, and the right pallidum, while only the right pallidum met this criteria for K1, the right pallidum and left putamen this inequality for k3, and no structures met this condition for CMRGlc. Relatively low counts throughout TACs of the smallest structures (e.g. the subicula), compared to large volume regions, consistently resulted in kinetic parameters at the limits of the OLS fitting and were not considered in this analysis. For the noPSF based OSEM case noPSF–last pGTM k2 estimates were found to have an absolute difference of ≥10% the wPSF–last pGTM results for all structures except the right amygdala, while this same set of structures excluding the cerebral cortex, right pallidum, and right accumbens area met this criteria for K1, the left caudate and right accumbens area met this inequality for k3, and only the right pallidum and right accumbens area this condition for CMRGlc. In the majority of structures where such differences were noted K1 and k2 estimates for noPSF–last pGTM were lower than the wPSF–last pGTM values.
Table 2.
Comparison of several PVC methods, with and without PSF modelling in the OSEM reconstruction, on the estimation of kinetic parameters, CMRGlc, and sum of squared errors (SSE) estimates calculated after seventeen iterations for a patient data set.
| Structure | Method |
K1 (ml/ccm/min) |
k2 (min−1) |
k3 (min−1) |
CMRGlc (µmol/100 g/min) |
SSE (kBq2/ml2) |
|---|---|---|---|---|---|---|
| L. Cerebral Cx | wPSF–noPVC | 0.0655 | 0.1675 | 0.0997 | 39.1042 | 0.2312 |
| wPSF–GTM | 0.0961 | 0.1595 | 0.1015 | 59.8688 | 0.4515 | |
| wPSF–ind pGTM | 0.1024 | 0.1814 | 0.1055 | 60.3343 | 0.4688 | |
| wPSF–last pGTM | 0.0961 | 0.1585 | 0.1018 | 60.1554 | 0.4482 | |
| noPSF–last pGTM | 0.0925 | 0.1344 | 0.0979 | 62.3943 | 0.5924 | |
| noPSF–noPVC | 0.0577 | 0.1427 | 0.0971 | 37.3807 | 0.2435 | |
| L. Cerebellum Cx | wPSF–noPVC | 0.0839 | 0.2014 | 0.0531 | 28.0280 | 0.5481 |
| wPSF–GTM | 0.1059 | 0.2009 | 0.0517 | 34.6912 | 0.8603 | |
| wPSF–ind pGTM | 0.1136 | 0.2228 | 0.0534 | 35.1400 | 1.0264 | |
| wPSF–last pGTM | 0.1066 | 0.2012 | 0.0517 | 34.8880 | 0.8708 | |
| noPSF–last pGTM | 0.0960 | 0.1784 | 0.0506 | 33.9481 | 0.7849 | |
| noPSF–noPVC | 0.0741 | 0.1781 | 0.0527 | 27.1159 | 0.4739 | |
| L. Caudate | wPSF–noPVC | 0.0511 | 0.1878 | 0.1289 | 33.3036 | 0.5213 |
| wPSF–GTM | 0.0587 | 0.1629 | 0.1356 | 42.7147 | 0.9990 | |
| wPSF–ind pGTM | 0.0641 | 0.1537 | 0.1260 | 46.2086 | 1.0754 | |
| wPSF–last pGTM | 0.0635 | 0.1556 | 0.1302 | 46.3388 | 1.1039 | |
| noPSF–last pGTM | 0.0463 | 0.0664 | 0.1051 | 45.3938 | 0.6634 | |
| noPSF–noPVC | 0.0389 | 0.1252 | 0.1300 | 31.7151 | 0.2701 | |
| L. Hippocampus | wPSF–noPVC | 0.0676 | 0.2936 | 0.0886 | 25.0987 | 1.0334 |
| wPSF–GTM | 0.0816 | 0.3109 | 0.0896 | 29.2274 | 2.3955 | |
| wPSF–ind pGTM | 0.0862 | 0.3227 | 0.0922 | 30.6723 | 2.7178 | |
| wPSF–last pGTM | 0.0845 | 0.3102 | 0.0912 | 30.7313 | 2.8456 | |
| noPSF–last pGTM | 0.0660 | 0.2479 | 0.0931 | 28.8470 | 1.6110 | |
| noPSF–noPVC | 0.0550 | 0.2452 | 0.0915 | 23.9255 | 0.5707 | |
| R. Cerebral Cx | wPSF–noPVC | 0.0651 | 0.1571 | 0.0951 | 39.2839 | 0.2688 |
| wPSF–GTM | 0.0956 | 0.1475 | 0.0960 | 60.3711 | 0.5468 | |
| wPSF–ind pGTM | 0.1032 | 0.1756 | 0.1021 | 60.7564 | 0.6130 | |
| wPSF–last pGTM | 0.0955 | 0.1473 | 0.0964 | 60.4565 | 0.5426 | |
| noPSF–last pGTM | 0.0943 | 0.1325 | 0.0940 | 62.6328 | 0.6848 | |
| noPSF–noPVC | 0.0578 | 0.1408 | 0.0937 | 36.9865 | 0.2697 | |
| R. Putamen | wPSF–noPVC | 0.0689 | 0.1750 | 0.0972 | 39.3951 | 0.6872 |
| wPSF–GTM | 0.0795 | 0.1706 | 0.0998 | 46.9706 | 1.2284 | |
| wPSF–ind pGTM | 0.0904 | 0.1992 | 0.1071 | 50.6441 | 1.7551 | |
| wPSF–last pGTM | 0.0861 | 0.1798 | 0.1041 | 50.5457 | 1.4497 | |
| noPSF–last pGTM | 0.0762 | 0.1575 | 0.1085 | 49.7703 | 1.1588 | |
| noPSF–noPVC | 0.0611 | 0.1557 | 0.1019 | 38.7259 | 0.5611 | |
| R. Pallidum | wPSF–noPVC | 0.0470 | 0.2280 | 0.1052 | 23.7441 | 1.2079 |
| wPSF–GTM | 0.0454 | 0.2526 | 0.1159 | 22.8484 | 3.1169 | |
| wPSF–ind pGTM | 0.0409 | 0.1824 | 0.1004 | 23.2326 | 3.4019 | |
| wPSF–last pGTM | 0.0463 | 0.2500 | 0.1163 | 23.5603 | 3.7224 | |
| noPSF–last pGTM | 0.0475 | 0.3357 | 0.1256 | 20.7136 | 3.0338 | |
| noPSF–noPVC | 0.0474 | 0.2305 | 0.1119 | 24.7973 | 0.8794 | |
| R. Amygdala | wPSF–noPVC | 0.0439 | 0.1321 | 0.0666 | 23.5401 | 0.6828 |
| wPSF–GTM | 0.0414 | 0.1112 | 0.0576 | 22.6269 | 1.5778 | |
| wPSF–ind pGTM | 0.0441 | 0.1205 | 0.0581 | 22.9622 | 1.9157 | |
| wPSF–last pGTM | 0.0415 | 0.1065 | 0.0558 | 22.8527 | 1.8100 | |
| noPSF–last pGTM | 0.0356 | 0.1069 | 0.0581 | 20.0899 | 1.7036 | |
| noPSF–noPVC | 0.0402 | 0.1285 | 0.0708 | 22.8689 | 0.5675 | |
| R. Accumbens area | wPSF–noPVC | 0.0514 | 0.1401 | 0.1002 | 34.3311 | 4.1506 |
| wPSF–GTM | 0.0501 | 0.1087 | 0.0938 | 37.1701 | 13.6719 | |
| wPSF–ind pGTM | 0.0490 | 0.0939 | 0.0858 | 37.4314 | 21.5727 | |
| wPSF–last pGTM | 0.0518 | 0.1121 | 0.0926 | 37.5091 | 17.6079 | |
| noPSF–last pGTM | 0.0524 | 0.2004 | 0.1400 | 34.4914 | 3.1352 | |
| noPSF–noPVC | 0.0515 | 0.1799 | 0.1263 | 34.0109 | 0.5391 | |
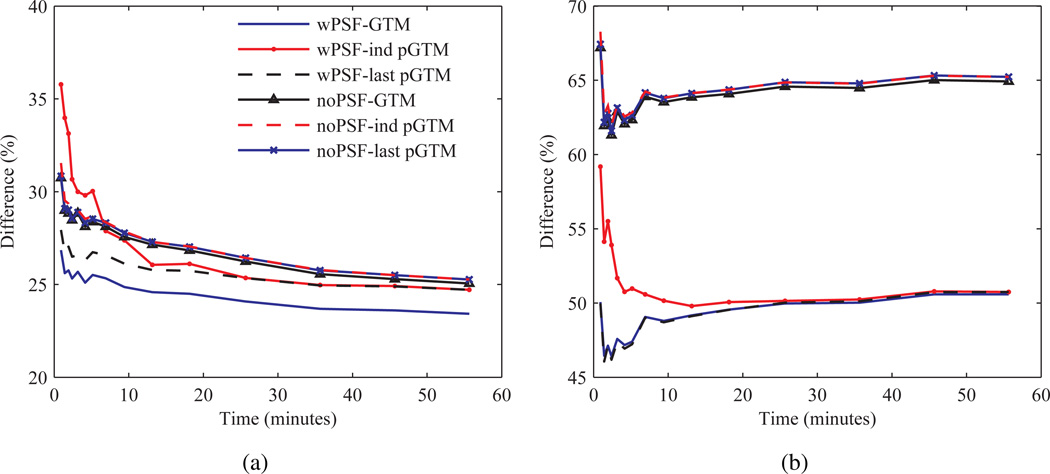
Figure 13 shows the TACs for the different PVC methods normalized (subtracted and divided) by the noPVC case for the subject scan. For the PSF based OSEM case the difference between the TACs was found to be inversely related to frame number for the ind pGTM data for time<13 minutes while the GTM and last pGTM PVC frames showed relatively constant difference over the course of the dynamic acquisition. For instance, the difference from the last to the first frame for the right cerebellum increased by 11.1% for images processed with wPSF–ind pGTM while both wPSF–GTM and wPSF–last pGTM had a difference of <3.5% between these time points. For all structures there was <5% change over the course of later frames (time>13 minutes). For the noPSF case ind and last pGTM curves showed a high degree of overlap across all frames and structures.
Figure 13.
TACs for the patient data processed with several PVC methods. (a) Right cerebellum and (b) right cerebral cortex TACs normalized (subtracted and divided) by wPSF–noPVC data for PSF based OSEM results or noPSF–noPVC for the noPSF curves, respectively.
4. Discussion
The results demonstrate that the method of PVC combined with the choice of PSF modelling in the reconstruction can have a significant effect on kinetic parameters estimated from OSEM reconstructed frames, and that this performance differential is unique to dynamic imaging. Notably, for PSF based OSEM applying ind versus last pGTM PVC led to large magnitude bias increases in k2 estimates for several structures as observed in both the subject scan and MC simulations, with reduced changes in K1 and k3. Furthermore, this differential in k2 increased with iteration number (past when fractional convergence for all parameters was ≥0.5%), demonstrating that lack of convergence was not a source of this phenomenon. Increased residual error in k2 for wPSF–ind pGTM was attributed to an inverse relationship of bias with respect to time for early frames, as k2 largely influences early TAC kinetics, while K1 and k3 affect the overall magnitude and late kinetics for TACs, respectively. For the MC simulation the difference in bias between the GTM and pGTM methods at late high count frames, with or without PSF modelling, were consistent with the performance analysis for static images (Du et al. 2005). Furthermore these differences were relatively constant with time except for comparisons of noPVC with GTM or pGTM PVC TACs for small hypometabolic structures with large background-to-target changes, such as the entorhinal cortex and the subiculum. Overall, using the last pGTM PVC with PSF based OSEM produced the lowest absolute bias averaged across all structures of interest and over K1, k2, k3, and CMRGlc as shown through the MC simulations, when the smallest structures (subiculum and entorhinal cortex) were ignored. The noPSF–last pGTM algorithm generally underestimated both K1 and k2 compared to wPSF–last pGTM estimates and these deficits were due to the increase in negative bias for noPSF TACs with decreasing frame number at early times points. Similarly, for the patient data set noPSF–last pGTM K1 and k2 estimates were found to be lower in numerous structures than those of wPSF–last pGTM. For the subiculum and the entorhinal cortex, data with noPSF–last pGTM produced the lowest absolute bias for K1 and CMRGlc, while noPSF-noPVC k2 estimates were most accurate, and last pGTM with either reconstruction method optimal for k3.
For optimal CMRGlc estimates alone noPSF–last pGTM PVC data produced significantly lower bias than the other methods for most structures, although with a difference in absolute bias of ≥5% compared with wPSF ind or last pGTM for only the entorhinal cortex. For the left amygdala, however, the wPSF–pGTM approaches were not significantly more accurate than the wPSF–noPVC CMRGlc value even though the structure underwent appreciable partial voluming. Consequently the high positive bias in K1 and k3 estimates for the left amygdala effectively cancelled through the CMRGlc calculation in (15).
Due to the fact that kinetic modelling was done on ROIs with a relatively large number of voxels, changes in noise as a function of the PVC method, when the same reconstruction method was used, were less relevant than differences in bias; however, we note that in all cases and particularly for smaller structures (e.g. the left amygdala, entorhinal cortex, and the subiculum) ind pGTM PVC tended to amplify CoV compared to the other implementations. Amplification of noise is inherent in all of the post-reconstruction PVC algorithms explored here due to the summation of weighted Poisson distributed ROI values (Rousset et al. 1998) when solving for a in (4) and the inversion of the frequently ill-conditioned GTM matrix (W) combined with noise propagation from the reconstructed images in the case of the pGTM PVC methods. Sattarivand et al (2012) assessed a modified GTM method (symmetric GTM), which was shown to have significantly less noise amplification than the classical GTM method for structures with small feature sizes, and this would likely translate into a similar reduction in noise amplification for kinetic parameter estimates. Use of PSF based OSEM led to an amplification of noise in most structures compared to noPSF kinetic parameters, which may be explained by the frequently measured increase in voxel covariance with PSF modelling (Rahmim et al. 2013). Such an increase in the variance of mean ROI values was also observed by Blinder et al (2012) in 11C-methylphenidate derived binding potential measurements of the striata of rats.
Performance differences in kinetic modelling between the PVC methods examined here were influenced more by changes in counts over the course of the TACs than variations in background-to-target ratios. As bias and noise free scatter and randoms estimates were used in the MC simulation, the changes in the counts in the emission data as a function of time constitute the main source of bias. For the majority of structures in the Zubal MC simulation, bias for the PSF based OSEM PVC algorithms increased (became more positive) as the number of counts decreased at early frames, and this occurred in combination with small changes in the background-to-target ratios. Furthermore, as shown by the 18F–11C phantom experiment (figure 8(b)), the bias of all wPSF methods (GTM, ind and last PGTM) was largely insensitive to a large range of background-to-target ratios for spheres as small as 6 mm ID. In contrast, for the noPSF PVC TACs bias became more negative with decreasing frame number for the cortical and low background-to-target deep brain structures, while for the white matter bias became more positive. The trend for the noPSF case can be attributed to the projection space domain non-negativity constraint employed in the OSEM algorithm, which has been shown to reduce contrast (effectively increase both spill-in and spill-out) for reconstructions of low count acquisitions using both attenuation weighted (Boellaard et al. 2001, Reilhac et al. 2008) and OP-OSEM (Grezes-Besset et al. 2007). For the wPSF TACs use of PSF modelling has been shown to decrease magnitude bias at low count statistics. For example, Walker et al. (2011) measured more than a 7% decrease in bias in the caudate head when using PSF based OSEM for 30 second frames from dynamic human 11C-DASB scans. We note that in our implementation parameters describing the Gaussian and motion blur kernels were chosen to match those exactly of the MC simulator, or closely approximate those in the experimental case, while for the study in (Walker et al. 2011) the resolution model FWHM was set to slightly lower magnitude than measured. Consequently, this may have led to an overcorrection of partial voluming and induced the positive bias observed at the earliest frames in this study. Together these results suggest that although ML reconstruction methods that allow for negative voxel values, such as AB-EMML (Erlandsson et al. 2000) and NEG-ML (Grezes-Besset et al. 2007), may significantly reduce bias at early low count frames for the noPSF PVC methods analysed here these reconstruction algorithms aren’t likely to lead to large decreases in positive bias for the wPSF PVC frames.
Significant differences in bias between wPSF ind and last pGTM PVC for ROI values at early frames for larger cortical structures were due primarily to overestimation of spill-out compared with spill-in activity. As ROIs from early frames for noPSF ind and last pGTM TACs showed negligible differences the use of PSF modelling in the reconstruction was primarily responsible for this phenomenon. An analysis of mean elements of the wPSF GTMs (wij) from the MC simulation for all structures demonstrated that for early frame wPSF–ind pGTM PVC, factors reflecting spill-out (i = j) were less than, and elements describing spill-in (i ≠ j) were greater than, those computed from last pGTM for a given structure i. Furthermore, the magnitude of the reductions and increases in spill-in and spill-out factors were found to be comparable. As cortical structures, for both the MC simulation and patient imaging, typically showed higher activity concentrations than the nearest neighbouring white matter structures, which were responsible for the majority of cortical spill-in, inversion of W and estimation of a in (4) resulted in the positively biased ind pGTM ROI values at early frames compared with those from last pGTM PVC. The combination of increased spill-in and reduced spill-out wij elements for a given structure suggest that the source of increased bias in wPSF–ind pGTM for early frames was due to increased magnitude spatial resolution, or decreased contrast, for the RSF images compared with their source reconstructed emission (f) and wPSF–last pGTM RSF images. Although smaller deep structures, such as the left amygdala, had significant overestimation of spill-out also, this was counteracted by larger spill-in effects compared with cortical volumes, particularly from neighbouring and relatively high activity concentration structures such as the hippocampi and temporal lobes in the case of the left amygdala. Among the largest cortical structures, the occipital lobe experienced the greatest magnitude difference in early frame concentrations between the wPSF pGTM methods due to it having the relatively smallest feature sizes.
There were several limitations in this study that may have influenced the results. For example, in the MC simulations we didn’t account for all the factors that affect reconstructed image SNR and resolution, including the following: noise in the scatter and randoms estimates, scatter from OFOV, inconsistencies between the forward and back projection models, and patient motion. Lack of inclusion of these components could have resulted in lower noise and bias, particularly at earlier frames, than encountered during patient imaging. Furthermore, we only considered a single patient phantom, with a single set of kinetic constants at one noise level, and the influence of cortical atrophy in different structures on kinetic modelling for data corrected with the investigated PVC methods was not explored. We did note a trend towards increased magnitude differences between kinetic parameters for the patient imaging case in several structures, notably in k2 for wPSF ind versus last pGTM for the amygdalae and putamina, and in K1 and k2 for for last pGTM with and without PSF modelling. As global count-rates were comparable for the patient scan and the MC simulation, differences in structure feature sizes, ground truth kinetic parameters, and the accuracy of the resolution model, likely caused these observed differences.
Although this study was restricted to the influence of the PVC method on 18F-FDG kinetic modelling for the BrainPET system, these results may have equal or greater impact for numerous tracers and/or PET systems with limited tomographic sampling where EM reconstruction methods are utilized. For instance, 11C-raclopride (Lammertsma et al. 1996), 18F-DOPA (Huang et al. 1991), and 11C-PiB (Price et al. 2005) all frequently merit TACs with low count frames at both early and late time points after tracer injection, which may lead to increased bias over a larger fraction of the dynamic acquisition than for 18F-FDG acquisitions if wPSF–ind pGTM is used over other PVC methods. Furthermore, PET systems with significant undersampling in sinogram space have been developed for applications in dedicated breast imaging (MacDonald et al. 2009) and in beam hadron therapy monitoring (Crespo et al. 2006), to name a few. Kinetic modelling may have utility for both scanners, and as these systems utilize MLEM reconstruction quantification of the resulting kinetic parameters may be influenced significantly by the choice of PVC.
5. Conclusions
The influence of the PVC method on 18F-FDG kinetic modelling from OSEM reconstructed images of dynamic brain acquisitions with BrainPET was estimated through phantom experiments, anthropomorphic MC simulations, and a subject scan. The results indicate that the choice of PVC method can have significant impact on kinetic parameter estimation. Using the last frame reconstructed image (f) only for RSF generation, as opposed to computing RSFs for each frame independently, and applying pGTM PVC with PSF based OSEM produced the lowest magnitude bias in most instances. The bias difference between these two PVC approaches was greatest magnitude for k2 and this was attributed to positive bias in the spatial resolution for the wPSF–ind pGTM RSF images compared with their source reconstructed emission volumes (f), due to relatively low counts in early frames. The improvement in bias for the wPSF–last pGTM method came at the cost of increased noise versus the noPSF-last pGTM approach. The noPSF-last pGTM approach produced optimal CMRGlc estimates, although by less than 5% compared to the other PVC methods. More research is required to determine how the choice of PVC may influence the kinetic modelling of tracers beyond 18F-FDG.
Acknowledgments
The authors thank Dr. Jacob Hooker and Steve Carlin for tracer synthesis, Grae Arabasz and Shirley Hsu for technical assistance and subject scanning, Patricia McCarthy for subject scanning, and Andrea Ferrero for use of the sphere phantom. Funding was provided in part by the National Institutes of Health (Grant No. NIH-NCI R01 CA137254-01A1 and NIH-NIBIB R01 EB014894-01A1).
References
- Blinder SAL, Dinelle K, Sossi V. Scanning rats on the high resolution research tomograph (HRRT): a comparison study with a dedicated micro-PET. Med. Phys. 2012;39(8):5073–5083. doi: 10.1118/1.4736802. [DOI] [PubMed] [Google Scholar]
- Boellaard R, Krak NC, Hoekstra OS, Lammertsma AA. Effects of noise, image resolution, and ROI definition on the accuracy of standard uptake values: a simulation study. J. Nucl. Med. 2004;45(9):1519–1527. [PubMed] [Google Scholar]
- Boellaard R, van Lingen A, Lammertsma AA. Experimental and clinical evaluation of iterative reconstruction (OSEM) in dynamic PET: quantitative characteristics and effects on kinetic modeling. J. Nucl. Med. 2001;42(5):808–817. [PubMed] [Google Scholar]
- Byars L, Sibomana M, Burbar Z, Jones J, Panin V, Barker W, Liow J, Carson R, Michel C. IEEE Nucl. Sci. Symp. Conf. Rec. Vol. 5. Fajardo, Puerto Rico: 2005. Variance reduction on randoms from delayed coincidence histograms for the HRRT; pp. 2622–2626. [Google Scholar]
- Cai WD, Feng DG, Fulton R, Siu WC. Generalized linear least squares algorithms for modeling glucose metabolism in the human brain with corrections for vascular effects. Comput. Meth. Prog. Bio. 2002;68(1):1–14. doi: 10.1016/s0169-2607(01)00160-2. [DOI] [PubMed] [Google Scholar]
- Catana C, Benner T, van der Kouwe A, Byars L, Hamm M, Chonde DB, Michel CJ, El Fakhri G, Schmand M, Sorensen AG. MRI-assisted PET motion correction for neurologic studies in an integrated MR-PET scanner. J. Nucl. Med. 2011;52(1):154–161. doi: 10.2967/jnumed.110.079343. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Catana C, van der Kouwe A, Benner T, Michel CJ, Hamm M, Fenchel M, Fischl B, Rosen B, Schmand M, Sorensen AG. Toward implementing an MRI-based PET attenuation-correction method for neurologic studies on the MR-PET brain prototype. J. Nucl. Med. 2010;51(9):1431–1438. doi: 10.2967/jnumed.109.069112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cloquet C, Sureau FC, Defrise M, Van Simaeys G, Trotta N, Goldman S. Non-gaussian space-variant resolution modelling for list-mode reconstruction. Phys. Med. Biol. 2010;55(17):5045–5066. doi: 10.1088/0031-9155/55/17/011. [DOI] [PubMed] [Google Scholar]
- Cornford EM, Gee MN, Swartz BE, Mandelkern MA, Blahd WH, Landaw EM, Delgado-Escueta AV. Dynamic [F-18]fluorodeoxyglucose positron emission tomography and hypometabolic zones in seizures: Reduced capillary influx. Ann. Neurol. 1998;43(6):801–808. doi: 10.1002/ana.410430615. [DOI] [PubMed] [Google Scholar]
- Crespo P, Shakirin G, Enghardt W. On the detector arrangement for in-beam PET for hadron therapy monitoring. Phys. Med. Biol. 2006;51(9):2143–2163. doi: 10.1088/0031-9155/51/9/002. [DOI] [PubMed] [Google Scholar]
- Dahlbom M, Schiepers C, Czernin J. Comparison of noise equivalent count rates and image noise. IEEE T. Nucl. Sci. 2005;52(5):1386–1390. [Google Scholar]
- de Jong H, Boellaard R, Knoess C, Lenox M, Michel C, Casey M, Lammertsma AA. Correction methods for missing data in sinograms of the HRRT PET scanner. IEEE T. Nucl. Sci. 2003;50(5):1452–1456. [Google Scholar]
- Du Y, Tsui BMW, Frey EC. Partial volume effect compensation for quantitative brain SPECT imaging. IEEE T. Med. Imaging. 2005;24(8):969–976. doi: 10.1109/TMI.2005.850547. [DOI] [PubMed] [Google Scholar]
- Erlandsson K, Buvat I, Pretorius PH, Thomas BA, Hutton BF. A review of partial volume correction techniques for emission tomography and their applications in neurology, cardiology and oncology. Phys. Med. Biol. 2012;57(21):R119–R159. doi: 10.1088/0031-9155/57/21/R119. [DOI] [PubMed] [Google Scholar]
- Erlandsson K, Visvikis D, Waddington W, Cullum I, Jarritt P, Polowsky L. IEEE Nucl. Sci. Symp. Conf. Rec. Vol. 2. Lyon, France: 2000. Low-statistics reconstruction with AB-EMML; pp. 15/249–15/253. [Google Scholar]
- Feng D, Ho D, Chen K, Wu L, Wang J, Liu R, Yeh S. An evaluation of the algorithms for determining local cerebral metabolic rates of glucose using positron emission tomography dynamic data. IEEE T. Med. Imaging. 1995;14(4):697–710. doi: 10.1109/42.476111. [DOI] [PubMed] [Google Scholar]
- Fischl B, Salat DH, Busa E, Albert M, Dieterich M, Haselgrove C, van der Kouwe A, Killiany R, Kennedy D, Klaveness S, Montillo A, Makris N, Rosen B, Dale AM. Whole brain segmentation: automated labeling of neuroanatomical structures in the human brain. Neuron. 2002;33(3):341–355. doi: 10.1016/s0896-6273(02)00569-x. [DOI] [PubMed] [Google Scholar]
- Frouin V, Comtat C, Reilhac A, Grégoire MC. Correction of partial-volume effect for PET striatal imaging: fast implementation and study of robustness. J. Nucl. Med. 2002;43(12):1715–1726. [PubMed] [Google Scholar]
- Gaitanis A, Kontaxakis G, Spyrou G, Panayiotakis G, Tzanakos G. Studying the properties of the updating coefficients in the OSEM algorithm for iterative image reconstruction in PET. Comput. Meth. Prog. Bio. 2010;99(3):219–229. doi: 10.1016/j.cmpb.2009.11.011. [DOI] [PubMed] [Google Scholar]
- Graham MM, Muzi M, Spence AM, O’Sullivan F, Lewellen TK, Link JM, Krohn KA. The FDG lumped constant in normal human brain. J. Nucl. Med. 2002;43(9):1157–1166. [PubMed] [Google Scholar]
- Grezes-Besset L, Nuyts J, Boellard R, Buvat I, Michel C, Pierre C, Costes N, Reilhac A. IEEE Nucl. Sci. Symp. Conf. Rec. Honolulu, Hawaii: 2007. Simulation-based evaluation of NEG-ML iterative reconstruction of low count PET data; pp. 3009–3014. [Google Scholar]
- Heiss WD, Pawlik G, Herholz K, Wagner R, Gldner H, Wienhard K. Regional kinetic constants and cerebral metabolic rate for glucose in normal human volunteers determined by dynamic positron emission tomography of [18F]-2-fluoro-2-deoxy-D-glucose. J. Cerebr. Blood. F. Met. 1984;4(2):212–223. doi: 10.1038/jcbfm.1984.30. [DOI] [PubMed] [Google Scholar]
- Huang SC, Phelps ME, Hoffman EJ, Sideris K, Selin CJ, Kuhl DE. Noninvasive determination of local cerebral metabolic rate of glucose in man. Am. J. Physiol. 1980;238(1):E69–E82. doi: 10.1152/ajpendo.1980.238.1.E69. [DOI] [PubMed] [Google Scholar]
- Huang S, Yu D, Barrio J, Grafton S, Melega W, Hoffman J, Satyamurthy N, Mazziotta J, Phelps M. Kinetics and modeling of l-6-[f-18] fluoro-dopa in human positron emission tomographic studies. J. Cerebr. Blood. F. Met. 1991;11(6):898–913. doi: 10.1038/jcbfm.1991.155. [DOI] [PubMed] [Google Scholar]
- Hudson HM, Larkin RS. Accelerated image reconstruction using ordered subsets of projection data. IEEE T. Med. Imaging. 1994;13(4):601–609. doi: 10.1109/42.363108. [DOI] [PubMed] [Google Scholar]
- Kolb A, Wehrl HF, Hofmann M, Judenhofer MS, Eriksson L, Ladebeck R, Lichy MP, Byars L, Michel C, Schlemmer HP, Schmand M, Claussen CD, Sossi V, Pichler BJ. Technical performance evaluation of a human brain PET/MRI system. Eur. Radiol. 2012;22(8):1776–1788. doi: 10.1007/s00330-012-2415-4. [DOI] [PubMed] [Google Scholar]
- Kotasidis FA, Matthews JC, Angelis GI, Noonan PJ, Jackson A, Price P, Lionheart WR, Reader AJ. Single scan parameterization of space-variant point spread functions in image space via a printed array: the impact for two PET/CT scanners. Phys. Med. Biol. 2011;56(10):2917–2942. doi: 10.1088/0031-9155/56/10/003. [DOI] [PubMed] [Google Scholar]
- Lammertsma AA, Bench CJ, Hume SP, Osman S, Gunn K, Brooks DJ, Frackowiak RSJ. Comparison of methods for analysis of clinical [C-11]raclopride studies. J. Cerebr. Blood. F. Met. 1996;16(1):42–52. doi: 10.1097/00004647-199601000-00005. [DOI] [PubMed] [Google Scholar]
- Lehnert W, Gregoire MC, Reilhac A, Meikle SR. Characterisation of partial volume effect and region-based correction in small animal positron emission tomography (PET) of the rat brain. NeuroImage. 2012;60(4):2144–2157. doi: 10.1016/j.neuroimage.2012.02.032. [DOI] [PubMed] [Google Scholar]
- MacDonald L, Edwards J, Lewellen T, Haseley D, Rogers J, Kinahan P. Clinical imaging characteristics of the positron emission mammography camera: PEM flex solo II. J. Nucl. Med. 2009;50(10):1666–1675. doi: 10.2967/jnumed.109.064345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meltzer CC, Kinahan PE, Greer PJ, Nichols TE, Comtat C, Cantwell MN, Lin MP, Price JC. Comparative evaluation of MR-based partial-volume correction schemes for PET. J. Nucl. Med. 1999;40(12):2053–2065. [PubMed] [Google Scholar]
- Michel C, Schmand M, Liu X, Sibomana M, Vollmar S, Knoss C, Lercher M, Watson C, Newport D, Casey M, Defrise M, Wienhard K, Heiss W. IEEE Nucl. Sci. Symp. Conf. Rec. Vol. 2. Lyon, France: 2000. Reconstruction strategies for the HRRT; pp. 207–212. [Google Scholar]
- Mosconi L, Tsui WH, Rusinek H, Santi SD, Li Y, Wang G, Pupi A, Fowler J, de Leon MJ. Quantitation, regional vulnerability, and kinetic modeling of brain glucose metabolism in mild alzheimer’s disease. Eur. J. Nucl. Med. Mol. I. 2007;34(9):1467–1479. doi: 10.1007/s00259-007-0406-5. [DOI] [PubMed] [Google Scholar]
- Muzic RFJ, Cornelius S. COMKAT: compartment model kinetic analysis tool. J. Nucl. Med. 2001;42(4):636–645. [PubMed] [Google Scholar]
- Muzic, Raymond FJ, Christian BT. Evaluation of objective functions for estimation of kinetic parameters. Med. Phys. 2006;33(2):342–353. doi: 10.1118/1.2135907. [DOI] [PubMed] [Google Scholar]
- National Electrical Manufactures Association. NEMA Standards Publication NU 2–2001: Performance Measurements of Positron Emission Tomographs. Rosslyn, VA: National Electrical Manufactures Association; 2001. [Google Scholar]
- Phelps ME, Huang SC, Hoffman EJ, Selin C, Sokoloff L, Kuhl DE. Tomographic measurement of local cerebral glucose metabolic rate in humans with (F-18)2-fluoro-2-deoxy-D-glucose: validation of method. Ann. Neurol. 1979;6(5):371–388. doi: 10.1002/ana.410060502. [DOI] [PubMed] [Google Scholar]
- Piert M, Koeppe RA, Giordani B, Berent S, Kuhl DE. Diminished glucose transport and phosphorylation in alzheimer’s disease determined by dynamic FDG-PET. J. Nucl. Med. 1996;37(2):201–208. [PubMed] [Google Scholar]
- Price JC, Klunk WE, Lopresti BJ, Lu X, Hoge JA, Ziolko SK, Holt DP, Meltzer CC, DeKosky ST, Mathis CA. Kinetic modeling of amyloid binding in humans using PET imaging and pittsburgh compound-b. J. Cerebr. Blood. F. Met. 2005;25(11):1528–1547. doi: 10.1038/sj.jcbfm.9600146. [DOI] [PubMed] [Google Scholar]
- Rahmim A, Qi J, Sossi V. Resolution modeling in PET imaging: Theory, practice, benefits, and pitfalls. Med. Phys. 2013;40(6):06430–1–06430–15. doi: 10.1118/1.4800806. PMID: 23718620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rapisarda E, Bettinardi V, Thielemans K, Gilardi MC. Image-based point spread function implementation in a fully 3D OSEM reconstruction algorithm for PET. Phys. Med. Biol. 2010;55(14):4131–4151. doi: 10.1088/0031-9155/55/14/012. [DOI] [PubMed] [Google Scholar]
- Reader A, Julyan P, Williams H, Hastings D, Zweit J. EM algorithm system modeling by image-space techniques for PET reconstruction. IEEE Transactions on Nuclear Science. 2003;50(5):1392–1397. [Google Scholar]
- Reilhac A, Tome S, Buvat I, Michel C, Keheren F, Costes N. Simulation-based evaluation of OSEM iterative reconstruction methods in dynamic brain PET studies. NeuroImage. 2008;39(1):359–368. doi: 10.1016/j.neuroimage.2007.07.038. [DOI] [PubMed] [Google Scholar]
- Rousset OG, Deep P, Kuwabara H, Evans AC, Gjedde AH, Cumming P. Effect of partial volume correction on estimates of the influx and cerebral metabolism of 6-[(18)F]fluoro-L-dopa studied with PET in normal control and parkinson’s disease subjects. Synapse. 2000;37(2):81–89. doi: 10.1002/1098-2396(200008)37:2<81::AID-SYN1>3.0.CO;2-#. [DOI] [PubMed] [Google Scholar]
- Rousset OG, Ma Y, Evans AC. Correction for partial volume effects in PET: principle and validation. J. Nucl. Med. 1998;39(5):904–911. [PubMed] [Google Scholar]
- Sattarivand M, Kusano M, Poon I, Caldwell C. Symmetric geometric transfer matrix partial volume correction for PET imaging: principle, validation and robustness. Phys. Med. Biol. 2012;57(21):7101–7116. doi: 10.1088/0031-9155/57/21/7101. [DOI] [PubMed] [Google Scholar]
- Sokoloff L, Reivich M, Kennedy C, Rosiers MHD, Patlak CS, Pettigrew KD, Sakurada O, Shinohara M. The [14C]deoxyglucose method for the measurement of local cerebral glucose utilization: theory, procedure, and normal values in the conscious and anesthetized albino rat. J. Neurochem. 1977;28(5):897–916. doi: 10.1111/j.1471-4159.1977.tb10649.x. [DOI] [PubMed] [Google Scholar]
- Song SL, Deng C, Wen LF, Liu JJ, Wang H, Feng D, Wong CYO, Huang G. F-18-FDG PET/CT-related metabolic parameters and their value in early prediction of chemotherapy response in a VX2 tumor model. Nucl. Med. Biol. 2010;37(3):327–333. doi: 10.1016/j.nucmedbio.2009.12.002. [DOI] [PubMed] [Google Scholar]
- Soret M, Bacharach SL, Buvat I. Partial-Volume effect in PET tumor imaging. J. Nucl. Med. 2007;48(6):932–945. doi: 10.2967/jnumed.106.035774. [DOI] [PubMed] [Google Scholar]
- Tuna U, Peltonen S, Ruotsalainen U. Gap-filling for the high-resolution PET sinograms with a dedicated DCT-domain filter. IEEE T. Med. Imaging. 2010;29(3):830–839. doi: 10.1109/TMI.2009.2037957. [DOI] [PubMed] [Google Scholar]
- van der Kouwe AJW, Benner T, Salat DH, Fischl B. Brain morphometry with multiecho MPRAGE. NeuroImage. 2008;40(2):559–569. doi: 10.1016/j.neuroimage.2007.12.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker MD, Asselin MC, Julyan PJ, Feldmann M, Talbot PS, Jones T, Matthews JC. Bias in iterative reconstruction of low-statistics PET data: benefits of a resolution model. Phys. Med. Biol. 2011;56(4):931–949. doi: 10.1088/0031-9155/56/4/004. [DOI] [PubMed] [Google Scholar]
- Watson CC, Newport D, Casey ME, DeKemp RA, Beanlands RS, Schmand M. Evaluation of simulation-based scatter correction for 3-D PET cardiac imaging. IEEE T. Nucl. Sci. 1997;44(1):90–97. [Google Scholar]
- Yao R, Seidel J, Johnson C, Daube-Witherspoon M, Green M, Carson R. Performance characteristics of the 3-D OSEM algorithm in the reconstruction of small animal PET images. IEEE T. Med. Imaging. 2000;19(8):798–804. doi: 10.1109/42.876305. [DOI] [PubMed] [Google Scholar]
- Yu AS, Lin HD, Huang SC, Phelps ME, Wu HM. Quantification of cerebral glucose metabolic rate in mice using f-18-FDG and small-animal PET. J. Nucl. Med. 2009;50(6):966–973. doi: 10.2967/jnumed.108.060533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zubal IG, Harrell CR, Smith EO, Rattner Z, Gindi G, Hoffer PB. Computerized three-dimensional segmented human anatomy. Med. Phys. 1994;21(2):299–302. doi: 10.1118/1.597290. [DOI] [PubMed] [Google Scholar]