Wanted: Scalable Tracers for Diffusion Measurements

Abstract

Scalable tracers are potentially a useful tool to examine diffusion mechanisms and to predict diffusion coefficients, particularly for hindered diffusion in complex, heterogeneous, or crowded systems. Scalable tracers are defined as a series of tracers varying in size but with the same shape, structure, surface chemistry, deformability, and diffusion mechanism. Both chemical homology and constant dynamics are required. In particular, branching must not vary with size, and there must be no transition between ordinary diffusion and reptation. Measurements using scalable tracers yield the mean diffusion coefficient as a function of size alone; measurements using nonscalable tracers yield the variation due to differences in the other properties. Candidate scalable tracers are discussed for two-dimensional (2D) diffusion in membranes and three-dimensional diffusion in aqueous solutions. Correlations to predict the mean diffusion coefficient of globular biomolecules from molecular mass are reviewed briefly. Specific suggestions for the 3D case include the use of synthetic dendrimers or random hyperbranched polymers instead of dextran and the use of core–shell quantum dots. Another useful tool would be a series of scalable tracers varying in deformability alone, prepared by varying the density of crosslinking in a polymer to make say “reinforced Ficoll” or “reinforced hyperbranched polyglycerol.”

Scalable Tracers

I argue that diffusion measurements in complex and heterogeneous fluids, particulaly cells, can be improved by the use of families of scalable tracers, that is, tracers in which a single property can be varied without significantly varying any of the other properties that affect diffusion. The basic problem is that nonscalable tracers are often used with the tacit assumption that they are scalable. Actual scalable tracers are needed to test this assumption. Diffusion measurements on scalable tracers will be advantageous in two distinct diffusion problems, predicting the diffusion of other species in the same complex fluid and using the diffusion measurements to characterize the complex fluid.

What Are Scalable Tracers?

The main properties of the tracer affecting diffusion are its size, shape, structure, surface chemistry, deformability, and diffusion mechanism. We consider two cases: tracers scalable in size and tracers scalable in deformability. These tracers are called “scalable” rather than “homologous” to emphasize that we need not only chemical homology but also constant dynamics and to emphasize that the series of tracers is explicitly designed so that one property can be varied while the others are held as constant as possible.

Specifically, tracers scalable in size are defined as a homologous series of tracers varying in size but with (a) constant shape; (b) constant structure, implying in particular that branching must not vary with size; (c) constant surface chemistry so a constant interaction with the environment, both attractive and repulsive, and a constant solvation shell;¹ (d) constant deformability; (e) constant dynamics, that is, no change in the diffusion mechanism with size, in particular no transition between ordinary diffusion and reptation.

Ideally the tracers would also be (f) uniform, with negligible variation in the properties affecting diffusion, and in particular (g) monodisperse, that is, uniform in size. Polydispersity ought to be an explicit variable, not just whatever the manufacturer, synthesis, or microorganism supplies; (h) metabolically inert, not metabolized by the cell, not modified by the cell, not affecting metabolism except as inert crowders, and not bound in mobile complexes or to the cytoskeleton (“bio-orthogonal”); (i) continuously variable in radius, though unfortunately tracers must be made out of atoms; (j) with tunable surface properties; (k) with a low tendency to associate or crystallize; (l) made by a scalable synthesis in which the size can be readily controlled by varying concentrations, reaction times, surfactants, or other reaction conditions; and (m) available in a wide range of sizes, covering the entire range of length scales needed for a cell or other complex fluid. If several types of tracers are needed to cover the size range of interest, the sizes of the types must overlap.

One example of a nonscalable tracer is a stiff linear polymer, which is chemically homologous for all degrees of polymerization, but the dynamics varies with the ratio of the polymer length to the persistence length. Another example is dextran, as will be discussed in detail in the text and Supporting Information 4. The structural limitation is that dextran branching increases with molecular weight, small dextrans have no long branches, and the solution properties depend strongly on a small number of long branches. The dynamic limitation is that a small dextran can undergo a transition between ordinary diffusion and reptation, depending on the environment.

For the common case of fluorescent tracers, it would be useful for the series to have the same fluorophore in the same immediate surroundings so the optical response and the signal-to-noise ratio are constant. Furthermore, it would be useful to have a tracer that can be labeled at a unique site: for a protein, a single lysine or cysteine, and for a polysaccharide, the reducing end. For labeling the reducing end, see Avaltroni et al.² and for nonspecific labeling of hydroxyls see de Belder and Granath.³ For a comprehensive general reference on the chemistry of labeling and crosslinking, see Hermanson.⁴ For examples of highly precise labeling of highly uniform polymers (unfortunately not water-soluble), see Zettl et al.⁵

For measurements in 2D systems like membranes, cylinders would be simplest, and for the 3D case, spheres. If cylinders can be used in a 3D system, it is straightforward to get a series of tracers scalable in length for lengths well below the persistence length, for example, DNA, a soluble α-helical protein, or a coiled polysaccharide like schizophyllan. But it is difficult to find a series of cylindrical tracers scalable in diameter.

Why Use Scalable Tracers?

What can be done with scalable tracers that cannot be done readily with nonscalable ones? I argue that measurements with scalable tracers ought to be used to examine fundamental diffusion mechanisms and to determine the effect of tracer size cleanly and unambiguously. Measurements with scalable tracers yield the diffusion coefficient D as a function of tracer size at fixed values of the other properties affecting diffusion: shape, structure, surface chemistry, deformability, and diffusion mechanism. Measurements with nonscalable tracers yield the variation of D at fixed size due to variation in the other properties. Thus, measurements with scalable tracers yield the mean of D as a function of tracer size; measurements with nonscalable tracers yield the standard deviation of D due to the other properties. For a new species of known size but unknown D, the combined measurements would provide a plausible estimate of D, with error bars.

Diffusion of globular proteins is sometimes treated this way, though not always explicitly. The Stokes–Einstein equation gives the mean D, the effect of shape is approximated in terms of ellipsoids of revolution, and the remaining factors give scatter. Alternatively, D may be computed from atomic structures.

Scope

We have defined scalable probes and outlined their advantages. Next we discuss precedents in the literature of size exclusion chromatography, renal filtration, crowding, and integral membrane proteins. Then we review candidate species for two-dimensional (2D) diffusion in membranes and three-dimensional (3D) diffusion in the cytoplasm and nucleus, briefly in the text and in detail in the Supporting Information. For the 3D case, the classes of tracers discussed are spherical (such as quantum dots and fluorescent beads), cylindrical (DNA, RNA), globular proteins, and finally carbohydrates and synthetic polymers, discussed together because similar techniques are used to characterize them. For diffusion and crowding researchers, the review of candidate species is a quick tour of the zoo of macromolecules and nanoparticles. For macromolecule and nanoparticle researchers, the review is a discussion of requirements in the hope that these workers will be able to make the appropriate species. Finally we discuss candidate species varying in deformability.

Diffusion and techniques of diffusion measurements are not discussed here. Diffusion physics is reviewed comprehensively in the outstanding work of Höfling and Franosch.⁶ Optical measurements of diffusion are reviewed briefly there. See also Saxton⁷ and for fluorescence correlation spectroscopy (FCS) the excellent but well-hidden review by Petrov and Schwille.⁸ For single-particle tracking (SPT), see Wieser and Schütz⁹ and Clausen and Lagerholm.¹⁰ For label-free SPT measurements by interferometric scattering microscopy, see Ortega-Arroyo and Kukura.¹¹ NMR diffusion measurements are discussed by Price¹² and NMR methods for membrane diffusion by Macdonald et al.¹³

The discussion is in terms of tracers to measure diffusion, but many of the same considerations apply to crowders. Scalable labels ought to be used for diffusion measurements in crowded systems, and the use of scalable crowders may be advantageous. Crowding affects reactions in several ways: the rate of diffusion of reactants to their initial encounter, the rate of recollision of reactants after an unreactive collision, the rate of reorientation of reactants, and the effects of crowding on thermodynamic equilibrium. To reduce to the simplest terms a field now worthy of international meetings, crowding is an example of Le Chatelier’s principle applied to a chemical reaction and the crowders themselves are subject to Le Chatelier’s principle. See Harve et al.¹⁴ for experiments on this. Zhou et al.¹⁵ review crowding.

Precedents for Scalable Tracers

Questions of scalability have shown up in the specific areas of size exclusion chromatography (SEC), renal filtration, crowding, and diffusion of transmembrane proteins in bilayers. The main variable is size, but shape and deformability are also important. Deformation is assumed to be on average symmetrical in the case of crowding and asymmetrical in the case of interactions with pores.

SEC is discussed here, and measurements of renal filtration are discussed here, in Tunable Deformability and in Supporting Information 6. Work in these areas provides important precedents for the ideas presented in this review, and one purpose of this review is to point out the importance of work in these seemingly specialized areas for general diffusion measurements. A scalable tracer as defined here meets the requirements set out in the SEC and renal filtration literature. The case of transmembrane proteins is considered in detail because this was the problem that led me to examine the question.

Size Exclusion Chromatography

Questions of scalability arise in calibration standards for size exclusion chromatography (gel permeation chromatography, gel filtration chromatography).¹⁶⁻¹⁸ In SEC, a known column is used to characterize an unknown tracer; in inverse SEC, a known tracer is used to characterize an unknown porous solid. The SEC retention time is determined by the degree of penetration of tracer into the pores of the stationary phase, so the size, shape, and flexibility of the standards are all important. In work on dendrimers as an SEC calibration standard, Dubin et al.¹⁶ gave the requirements as follows. The standard must be monodisperse. It must not be adsorbed by the stationary phase. And one must be able to determine its molecular dimensions unambiguously in terms of the Stokes–Einstein radius (biochemical community) or the viscosity radius (polymer community). Experimental results are discussed in the section on dendrimers of Supporting Information 4. Later work¹⁷ examined Ficoll and schizophyllan as SEC standards because they are among the few water-soluble uncharged nonhydrophobic macromolecules with a well-defined geometry. Here the requirements stated for SEC standards are similar: a monodisperse spherical molecule with negligible enthalpic interactions with the stationary phase and well-characterized size. The size must be constant, with no scission or aggregation.

Glomerular Permeability

Some of the most useful information about the properties discussed here as scalability comes from the field of renal filtration. The general question is explaining glomerular permselectivity, that is, the ability of the kidney to retain large proteins in the blood while allowing salt, water, and toxins to escape to the urine.^19,20 The standard approach is to use the behavior of simple tracers to characterize a complex tissue-level membrane. Specifically, a polydisperse tracer is administered in the blood, and the resulting tracer size distribution is measured in the blood and urine. This approach to measuring the sieving coefficient is described in a review as “remarkably reproducible, reliable, and elegant.”²¹ See for example Figure 1 of Ohlson et al.²² Their experiments on rat kidney show a major shift in distribution of Ficoll sizes between perfusate and urine, measured as elution volumes for an agarose column. This reference also discusses the complications of kidneys: a two-pore model is required (radii 4.6 nm and 8.0–8.7 nm) with a small proportion of the larger pores, and tracer charge is important. For charge effects, see also Axelsson et al.²³ Workers in this field have paid very serious attention to the effects of tracer size and flexibility, and some of their results are discussed later. The warning by Groszek et al.²⁰ about “confounding of the results of chemical modification on charge with effects on size and shape” fits well into the scalability requirements here.

The converse problem is also important, renal clearance. If a substance is to be used for medical diagnosis or treatment, one must know how rapidly it is cleared from the body by renal filtration and excretion in the urine. Arturson and Wallenius²⁴ and Mehvar and Shepard²⁵ examined clearance of dextrans. Imran Ul-Haq et al.²⁶ measured clearance of linear and hyperbranched polyglycerols, as well as linear poly(ethylene glycol) (PEG). Choi et al.²⁷ compared clearance of quantum dots with clearance of proteins and determined the effects of the quantum dot size and the organic coating.

Crowding

Results in the crowding literature resemble those in the kidney literature, as Elcock²⁸ pointed out in a review on crowding. In work on a scaled-particle model of solutions of hemoglobin plus dextran, the Ferrone group²⁹ argued that dextran can be approximated as a sphere with a volume that decreases as the dextran concentration increases.

A current theme in crowding research is the role of enthalpic interactions in addition to the purely entropic interactions that drive classical depletion interaction and crowding.³⁰⁻³² Scalable tracers may be useful as crowders because scalability requires varying the size at constant surface composition, making it possible to separate size effects from enthalpic effects, or as the review of Wirth and Gruebele³³ on quinary protein structure phrased it, to distinguish size-specific from sequence-specific properties. Wang et al.³⁴ provides a useful discussion of surface properties in the context of crowding. Rotational diffusion is a sensitive test for weak interactions.^35,36

The use of branch-on-branch crowders would be informative. Some workers have compared crowding by monomers and the corresponding polymers: ethylene glycol and various sizes of PEG,³⁶ or glucose and dextran.³¹ Branch-on-branch crowders would test the effect of topology. Another potential use of these crowders involves entanglement. Phillip and Schreiber³⁷ pointed out a fundamental difference among types of crowders: concentrated solutions of synthetic polymers form an entangled mesh but globular proteins in concentrated solutions retain their structure. As discussed later, the topology of branch-on-branch polymers drastically reduces entanglement, so the effects of entangled and nonentangled crowders could be compared at the same concentration and similar surface chemistry.

In connection with meshes and crowders, note that the importance of tracer size is well-known for diffusion in 3D networks. An elegant example is the SPT work of Wong et al.³⁸ on diffusion of spherical tracers in actin gels. Both mesh and tracer sizes could be adjusted, and the anomalous subdiffusion exponent was measured as a function of the ratio of tracer to mesh sizes. A similar argument can be applied to crowding, with the mean crowder spacing replacing the mesh size, though temporal fluctuations in the crowder spacing are likely to make the effect less clear-cut.

Recent work by Breydo et al.³⁹ examined the effect of crowder rigidity on protein conformation and aggregation, using dextran as a flexible crowder, hydroxypropyl celluose as a more rigid crowder, and Ficoll as an intermediate case. The crowders were chosen to be hydrophilic to minimize specific protein-crowder interactions and neutral to eliminate electrostatic interactions. This work is thus a precedent for scalable tracers and could be extended by use of crowders systematically scalable in deformability.

Although fluorescent labeling is not necessary for crowding measurements, any experiment on the effect of crowding on diffusion ought to include trace fluorescent crowder so that the diffusion of both the target molecule and the crowder can be measured.

Integral Membrane Proteins

Prominent theoretical papers on lateral diffusion in membranes include the classic work of Saffman and Delbrück,⁴⁰ who analyzed the hydrodynamics of 2D motion of a cylinder that is embedded in a thin high-viscosity membrane phase and extends into a low-viscosity aqueous phase of infinite extent. The major result is that D decreases with particle radius R only weakly, approximately as the logarithm of 1/R, in sharp contrast to 3D diffusion in bulk solution, where D ∝ 1/R. This work was generalized to tracers of arbitrary radius by Hughes et al.⁴¹ These results required messy numerics, so Petrov and Schwille⁴² devised simple analytic approximations and used them to analyze the experiments of Cicuta et al.⁴³ Petrov et al.⁴⁴ extended that work to rotational diffusion and analyzed their own experiments on rotational diffusion of gel domains. Quemeneur et al.⁴⁵ recently examined the dependence of diffusion on membrane curvature induced by transmembrane proteins. This work measured the effect of membrane tension on D and found no effect for aquaporin, which is curvature-neutral, but a major effect for a voltage-gated potassium channel that is curvature-coupled. This work gives a theoretical treatment of the curvature effect and discusses other theoretical extensions of the Saffman-Delbrück model.

Early experimental work on transmembrane protein diffusion by Vaz and Criado⁴⁶ compared diffusion of monomers, dimers, and tetramers of the acetylcholine receptor and supported the weak size dependence predicted by the Saffman-Delbrück model.

Johnson et al.⁴⁷ used video FRAP (fluorescence recovery after photobleaching) to measure diffusion coefficients of a variety of (nonscalable) lipid probes in synthetic lipid bilayers and in stratum corneum lipids. They presented their results and results from the literature as a plot of D versus molecular weight, and they fit the plot assuming that D was the sum of a power-law term dominant at low molecular weights and a Saffman-Delbrück term dominant at high molecular weights.

To test mechanisms of hindrance of diffusion in cells, Kucik et al.⁴⁸ studied diffusion in the plasma membrane of fish epidermal keratocytes by FRAP and SPT. The tracers used were (monovalent) succinyl Con A, and Con A-coated beads of various diameters: 40 nm gold, 190 nm latex, and 550 nm latex. Con A (concanavalin A) was chosen because it binds to many membrane glycoproteins so that the measurements were of general membrane proteins, not one specific protein. The contact area of beads with the membrane could not be measured directly, so the number of contacts was assumed to be proportional to the surface area of the bead. The measurements showed little size effect, implying that diffusion is controlled by viscosity, not hindrance by microcorrals or transient binding. Here viscosity was interpreted very generally, to include lipid viscosity, crowding effects, and hydrodynamic interactions. The tracers were scalable in the sense that all presumably bound the same set of glycoproteins, but the tracers were nonspecific by design.

A systematic study of D from the Petersen lab used a series of probes in which a homologous series of macrocyclic polyamide rings was synthesized and acyl chains or transmembrane helices were attached.^49,50 The high degree of geometric similarity made it possible to see the transition from a free area model for small tracers to Saffman-Delbrück behavior for large. The free area model calculates D in terms of the probability of lateral density fluctuations in the membrane large enough to accommodate motion of the diffusing species.⁵¹ But the matter is not yet settled. Later work questions the free area model; simulations⁵² and quasi-elastic neutron scattering⁵³ show concerted motion instead of jumps. To settle this matter, simulations and neutron scattering experiments using the Petersen probes would be useful.

Work by Gambin and collaborators challenged the Saffman-Delbrück size dependence.^54,55 This work lumped together results from Petersen’s tracers, α-helices, and β-barrels, even though an essential result of the work from the Petersen laboratory is that rigorous scalability is required to distinguish mechanisms of diffusion in membranes. Ramadurai et al.⁵⁶ measured diffusion of several transmembrane proteins and found D to be consistent with the Saffman-Delbrück model. This group^56,57 criticized the work of Gambin et al.⁵⁴ for the high fraction of immobile proteins and the use of a membrane made from a synthetic surfactant instead of phospholipids. Gambin et al.⁵⁸ and Reffay et al.⁵⁹ further discuss the use of such surfactants in later work on the effect of hydrophobic matching on diffusion and on protein–protein interactions in opposed membranes.

In my opinion, the main contribution of the Gambin work was to introduce β-barrels as tracers. It would be useful to do experiments with a strictly homologous series of β-barrels (identical strands) over a wider range of diameters (stoichiometric β-barrels: 8–24 strands in nature; maybe more artificially). For specifics see Candidate Tracers for Biomembranes and Supporting Information 1. In order to compare unequivocally the Petersen tracers, α-helices, and β-barrels, one must overlap the diameters. The experiments of Ramadurai et al.⁵⁶ seem carefully done within the limitation of using structurally different naturally occurring proteins. The biophysical questions are, how much do transmembrane helices differ among native membrane proteins, and how much effect do these differences have on diffusion? It would be useful to find the mean diffusion coefficients by measuring a strictly homologous series of transmembrane proteins, and the range of D by measuring a series with a constant number of transmembrane helices but different side chains, varying the composition over the full range found in nature. The experiments suggested here would be demanding, but they would provide an internally consistent data set covering a wide range of diameters, with diffusion measured by the same technique on the same instrument with the same calibration.

Candidate Tracers for Biomembranes

Why should one bother constructing a scalable series of membrane proteins if the Saffman-Delbrück treatment predicts a very weak dependence on radius? First, to provide an unambiguous test of the Saffman-Delbrück treatment and later developments. Second, to use in measurements of obstructed diffusion in the plasma membrane of cells, as discussed at the end of this section. The text summarizes candidate species, which are discussed in detail with full references in Supporting Information 1. An essential design constraint, especially for protein tracers, is that the tracers must not induce the formation of lipid domains, permanent or transient.

Self-Assembled Amphiphiles: Lipid Domains

Lipid domains may be considered self-assembled scalable tracers in membranes. The domain size varies almost continuously and changes with time, so the size of each domain must be measured along with its diffusion coefficient. Electrostatic repulsion may be important.

Peripheral Proteins

Another possibility is an artificial peripheral protein, in which the headgroup is some water-soluble scalable species such as a protein or a polysaccharide, and the headgroup is bound to the membrane by a lipid tail. An early example was stearoylated dextran.^60,61

Macrocyclic Polyamides

As discussed earlier, the Petersen laboratory constructed an excellent example of a scalable series, in which various sizes of macrocyclic amide rings were synthesized and each vertex was linked to a dodecyl chain⁴⁹ or a transmembrane helix.⁵⁰

Transmembrane α-Helices

The ideal building block for scalable transmembrane helix (TMH) probes would be a diffusionally neutral TMH, one with no tendency to aggregation or repulsion, and no tendency to drive lipid domain formation. Direct interactions such as van der Waals attractions and Coulomb interactions must be minimized. To avoid lipid-mediated interactions, hydrophobic matching is necessary. In the common case in which the vertical position of the TMH is determined by a pair of Trps, the Trp-Trp distance must also be matched to the distance between lipid carbonyls. In addition, oligomerization sites and hydrophobic surfaces promoting association must be designed to assemble the required number of TMHs but to give no further association. Designing and testing a diffusionally neutral series of scalable tracers would be an interesting test of our understanding of protein–lipid interactions.

Diffusion measurements have been made on a variety of natural proteins with different numbers of TMHs, recently in the work of Ramadurai et al.⁵⁶ on proteins ranging from 1 to 7 TMHs. Many larger proteins could be used. The E. coli lactose permease LacY has 12 TMHs. Aquaporin-1 is a tetramer in which each monomer is made up of six TMHs.⁶² The E. coli ammonia channel AmtB is a trimer with 11 TMHs per monomer. See the review of membrane protein structure by Vinothkumar and Henderson.⁶³ Such collections of proteins are not scalable, except to the extent that the side chains in naturally occurring TMHs do not affect diffusion. Maybe they do not, but this ought to be a question, not an assumption. Artificial multipass TMH proteins have been constructed, but the emphasis has been on adding functionality to a fixed structure of 4 TMHs.

Transmembrane β-Barrels

Transmembrane β-barrels may be a useful set of scalable membrane probes. These are proteins of the outer membrane of Gram-negative bacteria, mitochondria, and chloroplasts. They are made up of β-strands joined by loops. The barrel has a hydrophobic exterior and a hydrophilic interior. There are two classes of these proteins, small and giant. The small β-barrels known in nature range in size from 8 to 24 strands, so diffusion measurements could be made on naturally occurring proteins over a significant size range. Considerable work has been published on the modification of β-barrels to change the number and length of strands and the structure of loops. It appears feasible to design and build a series of rigorously scalable β-barrels with prescribed diameters, uniform loops, and uniform strands matched to the membrane thickness. Oligomerization sites must be removed, and the barrelheads for these barrels must be designed to give a circular cross section, to decrease or adjust flexibility, and to close the pores so that the tracers can be used in living cells. A logical extension of this work would be to try to increase the number of strands. In nature, larger structures occur in giant β-barrels, but these are more complicated structurally, stoichiometry is often variable, some self-assembly is required, and adjustment of the size is more difficult. (See Supporting Information 3.)

Proposed Percolation Experiment

Scalable biomembrane tracers would make possible highly refined measurements of obstructed diffusion and the percolation threshold in supported bilayers. The percolation threshold is the key parameter describing diffusion in the presence of immobile obstacles. As the obstacle concentration increases, the system approaches the percolation threshold. For point tracers, the percolation threshold is defined as the obstacle concentration at which long-range diffusion is blocked and only local diffusion is possible, in the limit of an infinite system. For tracers with a nonzero radius, the percolation threshold is defined in terms of the excluded area fraction, not just the area fraction of obstacles, so the threshold is highly sensitive to tracer size.⁶⁴

In the early days of work on supported bilayers, it was hoped that simple unequivocal diffusion measurements could be made on transmembrane proteins in supported bilayers. Unfortunately the transmembane proteins tended to adhere to the support and were immobilized. One response to this problem was to alter the support, as in the article “Double cushions preserve transmembrane protein mobility in supported bilayer systems.”⁶⁵

I propose exploiting this immobilization to make obstacles for a percolation experiment. Make supported bilayers with prescribed concentrations of transmembrane proteins, fluorescent-labeled so that immobilization can be verified. Then measure diffusion in the presence of these obstacles, using either a lipid tracer or a protein linked to glycosylphosphatidylinositol (GPI) so that the measurement is restricted to the distal leaflet. Presumably, the supported bilayer would be stable enough that it could be examined by super-resolution microscopy or atomic force microscopy to verify obstacle concentrations and to test randomness. Both obstacle concentration and tracer size can be varied, making possible a detailed characterization of obstructed diffusion.

Candidate Tracers for Cytoplasm and Nucleus

Candidate tracers for 3D aqueous systems such as the cytoplasm and the nucleus are discussed briefly here and in full detail in the Supporting Information. Supporting Information 2 discusses various spherical labels; Supporting Information 3, globular proteins; Supporting Information 4, carbohydrates and synthetic polymers; and Supporting Information 5, potential energy functions and scalability. References are given in the Supporting Information.

Spherical Labels

Various inherently spherical fluorescent labels are available.

Self-Assembled Amphiphiles: Lipid Droplets

Lipid droplets occur naturally in cells. Droplets have a high refractive index so they are detectable in SPT without labeling. They are often used in the physics literature for SPT measurements of diffusion in cytoplasm or for laser tweezer measurements of viscosity. Diameters are nonuniform, in the range 0.1–5 μm, so the size of each droplet must be measured along with its diffusion coefficient. The droplets consist of neutral lipids surrounded by a phospholipid monolayer. A major caveat: lipid droplets are not just inert spheres of fat but biologically active organelles with bound surface proteins, enough proteins to warrant proteomics studies.

Quantum Dots

Quantum dots (semiconductor nanocrystals) are highly useful probes, with a broad absorption peak, a narrow and tunable emission band, and a large absorption cross section. Blinking is a major limitation, but methods to eliminate nonfluorescent states are becoming available. The fluorescent core itself is small, but an inorganic shell is usually added to isolate the core from the environment, and further layers are added to make the structure hydrophilic and to attach the quantum dot to its cellular target. The core–shell structure provides a straightforward way to adjust the diameter in a scalable series, and methods are available to add shell material in a controlled manner.

Fluorescent Beads: Organic and Inorganic

Fluorescent beads are also useful, with a highly fluorescent species incorporated into say colloidal silica, polystyrene, or poly(methyl methacrylate) beads. These are the best set of scalable tracers commercially available, assuming that the proprietary chemistry is constant. The smallest ones seem to be 20–50 nm diameter and the largest, 5–25 μm, depending on the supplier. Much work has been published on the preparation of more specialized fluorescent beads, including core–shell structures well-suited to scalable tracer design.

Exotic (for Now)

More exotic fluorophores are being developed, including highly photostable nanodiamonds with a nitrogen vacancy center, and fluorescent metal nanoclusters. Methods to tune the size remain to be developed.

Gold Bead Scatterers

Colloidal gold is a strong light scatterer, long used as an SPT label. The minimum size is set by the strong size dependence of Rayleigh scattering. Core–shell structures might be useful to make large tracers.

Cylindrical Tracers

DNA and RNA can readily be used to make scalable cylindrical tracers of fixed diameter but here scalability requires structures that are uncharged and approximately spherical. Another possibility is plasmids. The diffusion coefficient of supercoiled plasmids varies with mass according to M^2/3, but in solution plasmids are intermediate between a flexible coil and a rigid structure, with “an enormous variety of rather irregular and dynamic configurations.”⁶⁶ Alternatively, cylindrical tracers with variable diameter could be made from cylindrical polymer brushes, by varying the side chain length for sufficiently stiff side chains. The topic was reviewed by Zhang and Müller⁶⁷ and by Sheiko et al.⁶⁸

Globular Proteins

Measurements of 3D diffusion in biological systems often use a variety of globular proteins, scalable only insofar as they happen to have the same shape and the same interaction with the other species present. Structures of some commonly used globular proteins are shown in Figure 1.

Figure 1.

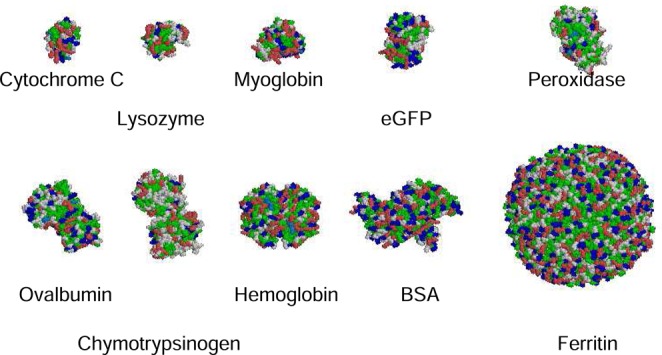
Space-filling structures of some globular proteins frequently used as tracers. All are to the same scale. Amino acids are color-coded according the classification in Rasmol: acidic in red, basic in blue, hydrophobic in green, and hetero groups in orange. Properties are given in Table 2 of Supporting Information 3.

The diffusion coefficient is given as a function of radius by the Stokes–Einstein equation. Corrections for shape can be obtained in terms of ellipsoids of revolution or from atomistic modeling. A rigorously scalable series of globular proteins would be useful and would be easier to design than a novel enzyme. An obvious possibility would be proteins with a string of linked α-helices, with hydrophobic surfaces chosen to drive folding into parallel helices, possibly with disulfide bonds to stiffen the linkages between helices. The length of the α-helices could be varied to make the final structure more spherical than disk-shaped. Such structures would build on existing work on the design of protein maquettes, which are simplified but functional synthetic proteins. (See Supporting Information 3 for references.)

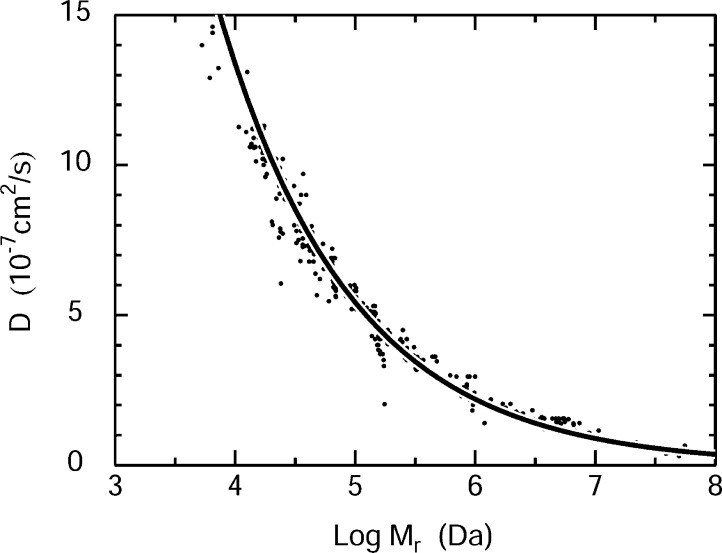
Figure 2 shows the cloud of data points, D versus log M_r, for a variety of globular biomolecules. The line is a power-law fit to these data points. An ideal set of scalable tracers would fall directly on such a line. The observed scatter in D represents the effect of nonscalability, plus the scatter due to experimental error in both D and M_r. See Figure S1 (panel c) of the Supporting Information 3 for details.

Figure 2.

Cloud of diffusion coefficients D as a function of log mass M_r for a variety of globular biomolecules ranging from ribonuclease to tobacco mosaic virus. The line is a least-squares power law fit. This figure is the cartoon version of Figure S1 (panel c) of Supporting Information 3. Full details are given there.

Supporting Information 3 discusses diffusion coefficients of globular proteins at length, including the prediction of D from molecular mass, proteome-scale analysis of diffusion coefficients, and candidate scalable tracers. It begins to answer the key question: are the usual sets of nonscalable globular proteins good enough, or is it worthwhile to make a set of scalable tracers?

Carbohydrates and Synthetic Polymers

We emphasize water-soluble biocompatible polymers such as polysaccharides, synthetic sugar copolymers, and PEG-like polymers that are often used as tracers. A simple linear chain gives a random coil with some persistence length. We need a more spherical structure, so branching or crosslinking is necessary.

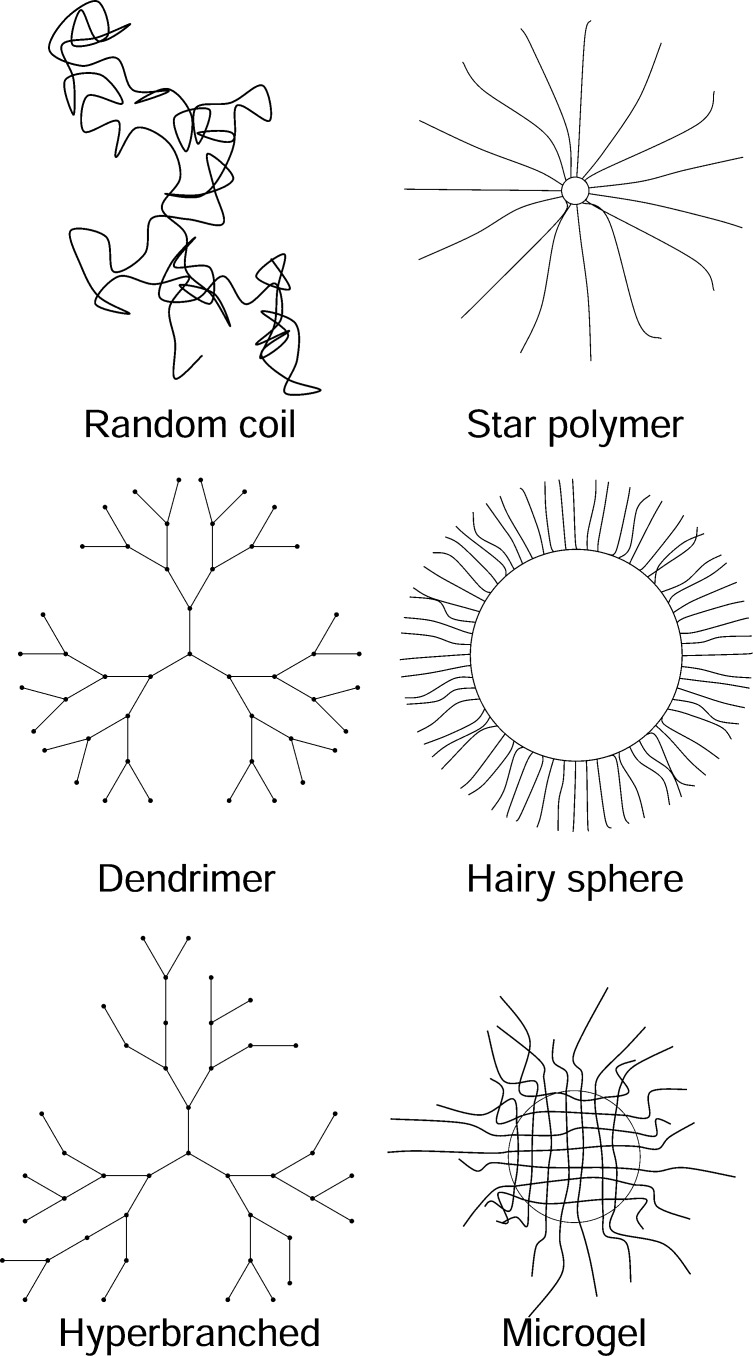
Figure 3 shows the polymer types in cartoon form, emphasizing the topology (inspired in part by figures in the review of Vlassopoulos and Fytas⁶⁹). Details of the various polymer types are given in Supporting Information 4, including structure, characterization, and diffusion measurements. The experimental characterization of polymer solution properties is outlined in Supporting Information 4 and characterization of polymers in terms of polymer–polymer interaction potentials in Supporting Information 5.

Figure 3.

Cartoons of the polymer structures discussed. Random coil, star polymer, dendrimer, hairy sphere (sterically stabilized colloid), hyperbranched polymer, microgel.

Dextran

Dextran is commonly used as a tracer and a crowder. It has been studied extensively by SEC, but its branching structure is not yet completely understood. Most of the branches are so short, one or two glucose residues, that they have little effect on solution properties. The major effect is from a small number of long branches. Small dextrans act as random coils because they are unlikely to have long branches; large dextrans have long branches and deviate from random-coil behavior. This complication directly affects the scalability of dextran. The limitations and alternatives to dextran are discussed in detail in the next section and Supporting Information 4.

Branch-on-Branch Polymers

Of particular interest here are several classes of branch-on-branch polymers. The advantage over linear polymers is that they are more nearly spherical, and there is no transition to reptation. The disadvantage is that there is no unique site for labeling after preparation. In structures built around a core, a fluorophore or an attachment site for a fluorophore can be built into the core.

Ficoll is a commercially available random copolymer of sucrose and epichlorohydrin. The epichlorohydrin treatment leads to branching and crosslinking. The structure is complex and hard to characterize in detail, but Ficoll has the favorable tracer properties of a branch-on-branch polymer, as argued in the renal filtration literature.

Dendrimers are iteratively branched polymers built from a core to which successive layers (generations) of branched monomers are attached. Ideally the branching is regular and deterministic. The core can include a fluorophore or a gold bead scattering center. The disadvantage is that obtaining this regular structure requires a complex and extensive synthesis, with each generation requiring an addition step and a purification step. Dendrimers are advantageous as scalable labels. All molecules in a given generation have the same structure and size. The surface composition is constant among generations, though the density of surface groups varies. The branching structure suppresses reptation and entanglement. Dendrimer solutions have a low viscosity because there is little entanglement.

Hyperbranched polymers are made by the polymerization of branched monomers to give a random, multiply branched structure. They can be thought of as random, imperfect dendrimers. Like dendrimers, they have many terminal groups. Their great advantage over dendrimers is that they can be made by a one-pot synthesis. Their disadvantage is polydispersity, though techniques to reduce polydispersity are known. A particularly important example here is hyperbranched polyglycerol, which has been studied extensively for biomedical applications because it is similar enough to PEG structurally that it is similarly biocompatible.

Dendrigraft (arborescent) polymers are a type of hyperbranched polymer in which the monomers are long and have many branch points, 10–15 versus 2–3 for conventional hyperbranched polymers. This is a convenient route to large polymers, in the range of 10 kDa to 100 MDa.

PEG is water-soluble and biocompatible, so PEG-like polymers have been prepared with many of the topologies just discussed, providing a favorable system for comparisons. Caution is required. Zhou et al.¹⁵ have argued that PEG interacts with nonpolar or hydrophobic residues in proteins, and this interaction limits its usefulness as a crowder. Phillip and Schreiber³⁷ present a contrary view. In any case, protein interactions with the PEG-like polymers must be tested.

Other Polymers

Star polymers consist of a core to which unbranched arms are attached. Star polymers interpolate between linear polymers and spheres. If one or two arms are used, the polymer is linear. As the number of arms increases, the polymer becomes more spherelike. A common type of stabilized colloid is a particle coated with soluble polymer chains so that entropic repulsion of the chains prevents aggregation. This “hairy sphere” can be regarded as a star polymer with many chains, all shorter than the sphere radius.

Microgels are multiply crosslinked polymer beads swollen in a good solvent. The size is controlled by carrying out the polymerization in a microemulsion. Microgels are potential scalable tracers, and they are a good example of stiffening due to crosslinking, as discussed in Tunable Deformability and Supporting Information 6.

Dextran Delenda Est?

To summarize the results from the renal filtration literature on tracers, dextran is deformable enough to allow reptation. Ficoll is less deformable and more spherical than dextran but more deformable than globular proteins.

I propose that in experiments on diffusion or crowding, dextran be replaced by a more highly branched polymer with shorter branches. Dendrimers, hyperbranched polymers, or dendrigraft polymers would all be suitable. The simplest starting points are Ficoll or hyperbranched polyglycerol. In any case, characterization of the material is essential. As discussed in Supporting Information 4, Fissell and collaborators have begun the characterization of Ficoll by SEC.^19,20 Dendrigraft polymers would be useful to reach large diameters. The advantages of highly branched polymers are as follows.

1. Shape

The hyperbranching constrains the polymer to be on average more spherical than the dextran random coil with a few long branches. A spherical structure inhibits entanglement, so the motion is simpler. Multidetector SEC measurements⁷⁰ showed that glycogens, which are hyperbranched, appeared to behave as a compact sphere and dextrans behave much more as a linear coil.

2. Analysis

Characterization of a polymer with a large number of short hyperbranches is likely to be easier than characterization of a polymer with a small number of long branches that have a large effect on solution properties. In SEC experiments on branched polymers and polysaccharides, Gaborieau and Castignolles⁷¹ found that the presence of few long-chain branches leads to poor separation, but separation of highly branched polymers is much better. The complexities of dextran structure (Supporting Information 4) lead me to ask, is dextran a calibration standard or a research problem? Hyperbranched polyglycerol might be preferable to Ficoll on grounds that the structure is simpler. See the discussion of Ficoll in Supporting Information 4 and references cited there, particularly the work of Holmberg and collaborators.⁷²⁻⁷⁴

3. Dynamics

Hyperbranching makes the dynamics more scalable. It constrains reptation far more than the few long branches in dextran do. Hindering the transition from conventional diffusion to reptation is essential to unambiguous diffusion measurements. Weiss et al.⁷⁵ ruled out dextrans as tracers on account of this transition. Xiao et al.⁷⁶ interpreted their diffusion measurements on large dextrans (282 kDa and 525 kDa) in brain extracellular space in terms of a crossover from normal diffusion to reptation.

An advantage of dextran over hyperbranched polyglycerol and Ficoll is that dextran has a unique site for fluorescent labeling, but polyglycerol and Ficoll do not. If the details of labeling matter, one must label hydroxyls generically and separate the different forms or build a unique label or labeling site into the polymer. Dextran can be labeled uniquely at the reducing end, though to get a higher number of fluorophores per molecule, it is often labeled via a generic reaction with hydroxyls.

My recommendations are mixed. Anyone considering the use of dextrans as tracers or crowders ought to read the reviews on dextran structure first. (See Supporting Information 4 for references.) But anyone doing diffusion experiments using hyperbranched polymers ought to do parallel experiments using dextrans and Ficoll to provide comparative data and to connect the results to previous work.

Tunable Deformability

Rationale

It would be useful to develop a series of homologous tracers with tunable deformability, so that deformability is an explicit, readily adjustable experimental variable. The problem has been recognized in various parts of the literature, though the terminology varies: softness, stiffness, flexibility, deformability, and compressibility. In a highly informative article in the kidney literature, Venturoli and Rippe²¹ use three of these terms in the abstract. We use “deformability” as the generic term and “compressibility” for the thermodynamically defined compressibility. For orientation, Supporting Information 6 includes a table of thermodynamic compressibilities for a variety of materials.

Extensive experimental work on deformability has been done in the context of renal filtration. For example, see Asgeirsson et al.⁷⁷ and the article entitled “Ficoll is not a rigid sphere” by Fissell et al.⁷⁸ Deformability has also been considered in SEC.¹⁶⁻¹⁸ In their FCS experiments on single-file diffusion of tracers in pores, DeSanto et al.⁷⁹ ought to have varied the deformability of the tracers. These workers were well aware of this issue, but well-characterized probes were not available.

An advantageous choice for these tracers is a series of polymers in which only the density of crosslinks is varied. A useful first approximation to the effect of crosslink density is the standard model of rubber elasticity.⁸⁰ See Vlassopoulos and Fytas⁶⁹ for a review of particle softness from the standpoint of soft matter physics and Vlassopoulos and Cloitre⁸¹ for the introduction to a special journal issue on “Bridging the gap between hard and soft colloids.”

Two practical questions immediately arise: how to measure the effect of crosslinking on the deformability of a species in solution, and what sort of crosslinking chemistry to use. We discuss these questions here and in more detail in Supporting Information 6.

How to Define and Measure Deformability

First we must consider how to define and measure deformability. The technique must measure global deformability, not local properties such as FRET between two sites on the tracer. Four methods are considered: size exclusion chromatography, ultrafiltration through nanopores, osmotic compression, and ultrasound. The methods measure physically different properties but any one method seems likely to give useful comparisons within a series of polymers with different degrees of crosslinking. The measurements are sensitive to hydration but the hydration ought to be approximately constant; a design goal for a scalable series of tracers is that the crosslinking is varied and surface properties are held constant. Atomic force microscopy measurements⁸² are excluded. The measurements themselves are direct, but the particles must first be adsorbed to a surface. The method thus brings in the particle-surface interaction as another variable.

Size Exclusion Chromatography

SEC is one possible method, but partition depends on the size, shape, and deformability of the macromolecule. Pore shape is often complex. The experiment is typically a measurement of solution properties as a function of elution volume (a measure of M_r) for a polydisperse macromolecule. So in my opinion SEC is not the preferred method, though it might be useful for relative measurements. One could usefully examine SEC using a scalable series of tracers varying in deformability, with the deformability characterized by one of the other methods.

Ultrafiltration through Nanopores

Another approach is to measure the passage of tracer through well-defined pores, either track-etched or nanofabricated. This approach is popular in the kidney literature because it uses probe behavior in artificial pores with known geometry and surface properties to characterize probes to be used to study complex natural pores. Tracers include linear macromolecules such as poly(vinylpyrrolidone) and poly(ethylene oxide), branched ones such as Ficoll, and more complex ones such as dextran. Their permeation is compared with that of a globular protein, and the results are often described in terms of hyperpermeability, that is, the degree to which tracers are more permeable than a globular protein of corresponding mass.^21,78 For other experimental work on diffusion of polymers in pores, see Shao and Baltus⁸³ and references cited there. Ultrafiltration is also used to characterize microgel beads, as discussed in Supporting Information 6.

There is an entropy cost to confining a tracer in a pore⁷⁸ and possibly an energy change due to the interaction of the tracer with the pore surface. This free-energy cost is paid by the pressure gradient imposed across the pores. Similarly, in measurements of DNA transport through nanopores, an electric field is applied to drive entry. The physical situation is thus distinct from that in the other measurements. But the Onsager regression hypothesis⁸⁴ states that relaxation of a random fluctuation follows the same law that relaxation from a small external perturbation of the same variable does. For example, the diffusion coefficients for self-diffusion and gradient diffusion are the same in the limit of small gradients.⁸⁴ Similarly, one would expect that for small pressure drops, the behavior in the ultrasonic and pore experiments is the same.

The transport of polymers through nanopores and nanochannels is a highly active area of research. Starting points in this literature are the review of Panja et al.,⁸⁵ the book of Muthukumar,⁸⁶ and some recent research papers.^87,88

Osmotic Compression

Some laboratories have measured deformability of crowders or microgels in terms of particle size as a function of osmotic pressure. For example, Harve et al.¹⁴ used dynamic light scattering (DLS) to measure crowder size as a function of crowder concentration for dextran, poly(vinylpyrrolidone), and Ficolls. At higher concentrations, the hydrodynamic radius R(hydro) decreased, much more strongly for dextran than for the Ficolls. The decrease was described as a “hyper-crowding state” in which crowding shrank the crowders. The advantage of osmotic compression is that it directly addresses the biophysical question of crowding effects on size. The disadvantage is that it addresses the biophysical question too directly, especially when the tracer size is measured by DLS, in which R(hydro) is calculated from the measured diffusion coefficient. Circularity notwithstanding, the method may be useful to monitor the effect of crosslinking density in a scalable series of tracers. To measure crosslinking effects, one would prepare a batch of scalable tracer with a prescribed fraction of crosslinker, and find R(hydro) by DLS as a function of crowder concentration. The crowder may be identical to the tracer or not, and the interpretation of the experiment is different in the two cases as discussed in Supporting Information 6.

Ultrasound

One appealing measure is the compressibility because it is rigorously defined from thermodynamics and is easy to measure.⁸⁹⁻⁹¹ The adiabatic compressibility is defined as

1

where V is volume, P is pressure, and S is entropy. The isothermal compressibility β_T is defined similarly. The compressibilities are related by standard thermodynamics,

2

where T is temperature, α is the thermal expansion coefficient, ρ is the density, and C_p is the heat capacity at constant pressure. The compressibility is by definition the reciprocal of the bulk elastic modulus. The isothermal compressibility relates the root-mean-square volume fluctation δ_V to the thermal energy kT as⁹²

3

Note that β_S can be zero or negative but β_T cannot; β_T = 0 would imply zero volume fluctations. For hard solids, β_S = β_T. The adiabatic compressibility is readily measured in solution by ultrasonics:

4

where U is the speed of sound, typically measured at frequencies in the 1–10 MHz range. Isothermal compressibilities are harder to measure. They can be obtained directly from measurements of partial specific volume as a function of pressure by densimetry or centrifugation or indirectly from measurements of β_S.

Time Scales

One way to compare the methods is in terms of the time scales of molecular motion involved. When a scalable tracer is used, the relevant timescale is the time for a tracer to interact with an obstacle. Fast motions, the ps and ns internal motions of the tracer, ought to be averaged over. All the methods do this but are somewhat different for slow motions. For SEC and ultrafiltration, the slow timescale is that of pore entry, confinement, and exit. For osmotic compression, the slow timescale is that of a tracer-crowder collision. For ultrasonics the slow timescale is set by the ultrasonic frequency.

How to Tune Deformability

We discuss three approaches to making a series of scalable tracers varying in deformability: modifying protein structure, varying monomer properties in synthetic polymers, and varying crosslinker density in synthetic polymers. The latter seems the simplest approach and most suited for proof of concept. This section is intended as a starting point and evidence of feasibility; specialists in these areas will have better ideas.

An inherent limitation of silica beads and the like is that the tunability of deformability is limited to small changes produced by changing the outermost coating to vary the particle–particle or particle–obstacle potential.

Proteins

An obvious way to adjust the compressibility of globular proteins is to vary the density of disulfide bridges. Making such a series of mutants is standard, as in the case of lysozyme.⁹³ Another approach involves mutating proteins to change cavity size. Clearly this would be an extreme approach just to make a series of scalable tracers, but the Royer laboratory has done extensive, careful work on this problem as a fundamental study of protein structure and folding.⁹⁴⁻⁹⁶ They have examined staphyococcal nuclease, SNase, as a model protein folding system and have made a series of mutants to study the partial molar expansivity α = (1/V)(∂V/∂T)_P. These mutants could also be used to study (1/V)(∂V/∂P)_S.

Synthetic Polymers: Monomers

One way to vary the deformability of a synthetic polymer is to vary monomer properties. For example, Behera and Ramakrishnan⁹⁷ prepared a series of hyperbranched polymers in which the segment length and deformability were varied. As the structures were varied, the density of branches and the degree of backfolding both varied. The products were characterized by SEC.

Synthetic Polymers: Cross-Linking

Varying the crosslink density seems simplest and most likely to produce a scalable series. Tuning deformability via crosslink density is well-known in the case of gels. The most obvious example is varying the elasticity of polyacrylamide gels.⁹⁸ Microgel properties are varied similarly. For example, Varga et al.⁹⁹ used light scattering to analyze poly(N-isopropylacrylamide) microgel particles with various degrees of crosslinking, and found that the structure was strongly dependent on crosslinking. For another example see Sierra-Martin et al.⁸²

One starting point is the commercial synthesis. Cross-linking of sucrose with epichlorohydrin is used to produce Ficoll, and crosslinking of dextran with epichlorohydrin is used to produce Sephadex.¹⁰⁰ I propose a simple approach: crosslink Ficoll using the same epichlorohydrin chemistry that was used to manufacture it. A convenient feature of the standard preparation is that it is done in an aqueous medium, though a nonaqueous solvent may be useful to promote crosslinking, as shown in work on crosslinking of starch in water or dimethyformamide.¹⁰¹ If Ficoll is used as the starting material, the properties of the “reinforced Ficoll” can be related to well-known properties of Ficoll. For a description of the reaction conditions, see the original patent.¹⁰² For general information on methods of synthesis and analysis, see the references in Supporting Information 4 and the patent literature. Alternatively, a distinct secondary crosslinker could be used.

Cross-linking chemistry is discussed extensively in the literature on modification of dextran and agarose for chromatography media. One application is crosslinking to make stiffer beads and improve flow in chromatographic columns. Another is activating the substrate to attach ligands for affinity chromatography; here crosslinking is an unwanted side effect. This literature is a valuable source of information on synthetic chemistry and analytical methods. The work must be modified to give the dilute limit, to optimize for crosslinking, and to measure deformability as a macromolecular property instead of a macroscopic property like flow in a column. References are given in Supporting Information 6.

Clearly the same chemistry can be used to randomly crosslink other polymers with multiple internal hydroxyls, to make, for example, “reinforced hyperbranched polyglycerol.” In general, the interior and periphery are chemically distinguishable in dendrimers but not in hyperbranched polymers. For hyperbranched polyglycerol, however, there is chemistry to select interior or exterior. See Supporting Information 6.

2D Case

It is not obvious how to devise a series of transmembrane tracers scalable in compressibility. Such a series would be useful to test the simulation results of Guigas and Weiss.¹⁰³ These authors pointed out that the standard Saffman-Delbrück treatment of diffusion in bilayers and its refinements all assume an incompressible tracer, and further argue that as a result of internal degrees of freedom of the tracer, D ∝ 1/R² at large R, not log 1/R as in the Saffman-Delbrück treatment. Here R is the tracer radius.

One possibility would be to make a series of β-barrels with a constant number of strands but with different protein segments inside the barrel, in the simplest case a barrel with and without a barrelhead. Compressibility and internal modes might best be described using computer modeling.

Conclusions and Specific Recommendations

Diffusion measurements, especially measurements of hindered diffusion, would be improved if two types of measurements were made and clearly distinguished: scalable tracers to test the effect of size alone and nonscalable tracers at fixed size to test the effect of shape, structure, surface chemistry, deformability, and diffusion mechanism. The first measurement gives the mean and is appropriate in studies of fundamental mechanisms. The second gives the standard deviation and is helpful for estimating the diffusion coefficient of a new species.

The emphasis here has been on approximately spherical tracers for diffusion measurements in 3D complex fluids. Measurements using such tracers would be useful for examining basic size dependence, but of course the diffusion of random coil proteins is fundamentally important in cells. The ideal experiment would compare random coil to spherical proteins using a series of proteins varying in disulfide crosslinking.

1. The simplest and most direct test of the ideas presented here would use polyglycerols—hyperbranched polymers, dendrimers, or both—starting with commercially available forms. The experiments would include a comparison of the polyglycerols to dextran and Ficoll to see whether the polyglycerols are good replacements. The potential advantages are (a) Branch-on-branch probes are more constrained than dextran to be on average spherical. (b) Branch-on-branch structure prevents reptation much more than a few long branches do. Snakes reptate. Snakes with bristles—a short-chain comb polymer, reptate. Porcupines, echidnas, and hedgehogs do not. Squid are intermediate, with the so-called teuthidic motion of Phillies.¹⁰⁴ (c) Characterization of a large number of short hyperbranches is likely to be easier than characterization of a small number of long branches that have a large effect on solution properties. Hyperbranched polyglycerol is a highly advantageous choice for work to develop scalable tracers, on account of its properties and the extensive research that has been carried out on it and related polymers.¹⁰⁵ See Supporting Information 4.

Diffusion measurements with dextrans and Ficoll ought to be made in parallel to provide comparative data and to connect to previous work. Measurements on PEG-like polymers would make a systematic study of topological effects possible. If these probes are to be used in crowding experiments, one ought to test for protein–polymer attraction.

2. Prepare a scalable series of transmembrane proteins and a scalable series of globular proteins. The author strongly encourages the experts in interactions of bilayers with transmembrane proteins, and the experts in engineering of soluble proteins, to design and build these probes.

3. Prepare a series of reinforced Ficoll and reinforced hyperbranched polyglycerol tracers with different degrees of crosslinking. Measure deformability by ultrasonics and measure diffusion as a function of deformability.

My own work is on the modeling of hindered diffusion, not diffusion experiments or tracer synthesis. This review is intended to bring attention to the problem and possible solutions, not to serve as territorial marking. I hope that this review will encourage experimentalists to try these approaches, and I hope that the discussion of scalable probes will lead to the use of better probes, even if the perfect scalable probe does not exist.

Biography

Michael J. Saxton received his B.S. in chemical physics from Michigan State and his A.M. in chemistry from Harvard. He served in the U.S. Army in Landstuhl, Germany, and received his Ph.D. in chemical physics from Harvard in 1976, working in the Karplus-Deutch group. He was then at Battelle Memorial Institute and the University of Connecticut. He has been a researcher at the University of California, Davis, in various units since 1979, and is now Research Chemist Emeritus.

His main research interest is modeling hindered diffusion in cells, primarily 2D diffusion in membranes. A particular interest is methods of analysis of single-particle tracking experiments.

Supporting Information Available

Detailed discussion with full references for the following topics: (1) Candidate Species for Biomembranes; (2) Candidate Species: Spherical Tracers; (3) Candidate Species: Globular Proteins; (4) Candidate Species: Carbohydrates and Synthetic Polymers; (5) Potentials; and (6) Tunable Deformability. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare the following competing financial interest(s): I own stock in General Electric, the manufacturer of Ficoll.

Funding Statement

National Institutes of Health, United States